1 Introduction

Quantum communication is one of the most striking applications of quantum information science [1]. As one branch of quantum communication, quantum teleportation aims to transport an unknown single-qubit state from a sender to a receiver with the help of a Bell state and classical communication. The original quantum teleportation protocol was presented by Bennett et al. [2] in 1993. A key ingredient in quantum teleportation is a quantum channel connecting Alice and Bob that is supposed to be a maximally entangled pure state [3–17]. Subsequently, many quantum teleportation schemes have been proposed by using different types of multiparty entangled state as a quantum channel [18–26]. In 2008, it was demonstrated that the cluster state may be useful in perfect teleportation of an arbitrary single and two qubit states [27]. In 2011, Nie et al. [28] had shown that the cluster state can also be used successfully to teleport a three-qubit GHZ state.

In this work, we demonstrate that a six-qubit cluster state can be used to realize the perfect teleportation of a special form of four-qubit state based on the six-qubit von-Neumann projective measurements and local unitary operations.

2 Quantum Teleportation of a Four-qubit State

Suppose Alice has a four-qubit state, which is given by

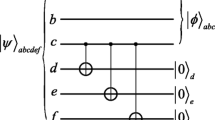
$$ \left| \uppsi \right\rangle_{abcd} =\left( {\alpha \left|0000 \right\rangle +\beta \left|0011 \right\rangle +\gamma \left|1100 \right\rangle +\delta \left|1111 \right\rangle } \right)_{abcd} , $$
(1)

where |α|2+|β|2+|γ|2+|δ|2 = 1. And Alice and Bob share a six-qubit cluster state

$$ \left|\mathcal{C} \right\rangle_{123456} =\frac{1}{2}\left( {\left|000000 \right\rangle +\left|001101 \right\rangle +\left|110010 \right\rangle -\left|111111 \right\rangle } \right)_{123456} , $$
(2)

the qubits a, b, c, d, 5 and 6 belong to Alice, qubits 1, 2, 3 and 4 belong to Bob, respectively. The joint state of the four-qubit state and the quantum channel is given by,

$$ {\begin{array}{lllllllllllllllll} \left| \Uppsi \right\rangle =\left|\uppsi \right\rangle_{abcd} \otimes \left|\mathcal{C} \right\rangle_{123456} \\ =\frac{1}{4}[ \left| \varphi^{1} \right\rangle_{abcd56} \left( \alpha \left|0000 \right\rangle +\beta \left|0011 \right\rangle +\gamma \left|1100 \right\rangle +\delta \left|1111 \right\rangle \right)_{1234} \\ +\left|\varphi^{2} \right\rangle_{abcd56} \left( \alpha \left|0000 \right\rangle -\beta \left|0011 \right\rangle +\gamma \left|1100 \right\rangle -\delta \left|1111 \right\rangle \right)_{1234} \\ +\left|\varphi^{3} \right\rangle_{abcd56} \left( \alpha \left|0000 \right\rangle +\beta \left|0011 \right\rangle -\gamma \left|1100 \right\rangle -\delta \left|1111 \right\rangle \right)_{1234} \\ +\left|\varphi^{4} \right\rangle_{abcd56} \left( \alpha \left|0000 \right\rangle -\beta \left|0011 \right\rangle -\gamma \left|1100 \right\rangle +\delta \left|1111 \right\rangle \right)_{1234} \\ +\left|\varphi^{5} \right\rangle_{abcd56} \left( \alpha \left|0011 \right\rangle +\beta \left|0000 \right\rangle +\gamma \left|1111 \right\rangle +\delta \left|1100 \right\rangle \right)_{1234} \\ +\left|\varphi^{6} \right\rangle_{abcd56} \left( \alpha \left|0011 \right\rangle -\beta \left|0000 \right\rangle +\gamma \left|1111 \right\rangle -\delta \left|1100 \right\rangle \right)_{1234} \\ +\left|\varphi^{7} \right\rangle_{abcd56} \left( \alpha \left|0011 \right\rangle +\beta \left|0000 \right\rangle -\gamma \left|1111 \right\rangle -\delta \left|1100 \right\rangle \right)_{1234} \\ +\left|\varphi{8} \right\rangle_{abcd56} \left( \alpha \left|0011 \right\rangle -\beta \left|0000 \right\rangle -\gamma \left|1111 \right\rangle +\delta \left|1100 \right\rangle \right)_{1234} \\ +\left|\varphi{9} \right\rangle_{abcd56} \left( \alpha \left|1100 \right\rangle +\beta \left|1111 \right\rangle +\gamma \left|1100 \right\rangle +\delta \left|0011 \right\rangle \right)_{1234} \\ +\left|\varphi{10} \right\rangle_{abcd56} \left( \alpha \left|1100 \right\rangle -\beta \left|1111 \right\rangle +\gamma \left|1100 \right\rangle -\delta \left|0011 \right\rangle \right)_{1234} \\ +\left|\varphi{11} \right\rangle_{abcd56} \left( \alpha \left|1100 \right\rangle +\beta \left|1111 \right\rangle -\gamma \left|1100 \right\rangle -\delta \left|0011 \right\rangle \right)_{1234} \\ +\left|\varphi{12} \right\rangle_{abcd56} \left( \alpha \left|1100 \right\rangle -\beta \left|1111 \right\rangle -\gamma \left|1100 \right\rangle +\delta \left|0011 \right\rangle \right)_{1234} \\ +\left|\varphi{13} \right\rangle_{abcd56} \left( \alpha \left|1111 \right\rangle +\beta \left|1100 \right\rangle +\gamma \left|0011 \right\rangle +\delta \left|0000 \right\rangle \right)_{1234} \\ +\left|\varphi{14} \right\rangle_{abcd56} \left( \alpha \left|1111 \right\rangle -\beta \left|1100 \right\rangle +\gamma \left|0011 \right\rangle -\delta \left|0000 \right\rangle \right)_{1234} \\ +\left|\varphi{15} \right\rangle_{abcd56} \left( \alpha \left|1111 \right\rangle +\beta \left|1100 \right\rangle -\gamma \left|0011 \right\rangle -\delta \left|0000 \right\rangle \right)_{1234} \\ +\left|\varphi{16} \right\rangle_{abcd56} \left( \alpha \left|1111 \right\rangle -\beta \left|1100 \right\rangle -\gamma \left|0011 \right\rangle +\delta \left|0000 \right\rangle \right)_{1234}] , \end{array}} $$
(3)

where |φ i〉 abcd56(i = 1,2,⋯ ,16) are mutually orthonormal six-qubit states in Alice’s possession given by,

$$ \left|\varphi^{1} \right\rangle=\frac{1}{2}(\mid 000000\rangle + \mid 001101\rangle +\mid 110010\rangle -\mid111111\rangle)_{abcd56}, $$
(4)
$$ \left|\varphi^{2} \right\rangle=\frac{1}{2}(\mid 000000\rangle - \mid 001101\rangle +\mid 110010\rangle +\mid111111\rangle)_{abcd56}, $$
(5)
$$ \left|\varphi^{3} \right\rangle=\frac{1}{2}(\mid 000000\rangle + \mid 001101\rangle - \mid 110010\rangle +\mid111111\rangle)_{abcd56}, $$
(6)
$$ \left|\varphi^{4} \right\rangle=\frac{1}{2}(\mid 000000\rangle - \mid 001101\rangle - \mid 110010\rangle -\mid111111\rangle)_{abcd56}, $$
(7)
$$ \left|\varphi^{5} \right\rangle =\frac{1}{2}(\mid 000001\rangle + \mid 001100\rangle + \mid 110011\rangle -\mid111110\rangle)_{abcd56}, $$
(8)
$$ \left|\varphi^{6} \right\rangle =\frac{1}{2}(\mid 000001\rangle - \mid 001100\rangle + \mid 110011\rangle +\mid111110\rangle)_{abcd56}, $$
(9)
$$ \left|\varphi^{7} \right\rangle =\frac{1}{2}(\mid 000001\rangle + \mid 001100\rangle - \mid 110011\rangle +\mid111110\rangle)_{abcd56}, $$
(10)
$$ \left| \varphi^{8} \right\rangle =\frac{1}{2}(\mid 000001\rangle - \mid 001100\rangle - \mid 110011\rangle -\mid111110\rangle)_{abcd56}, $$
(11)
$$ \left|\varphi^{9} \right\rangle =\frac{1}{2}(\mid 000010\rangle + \mid 001111\rangle + \mid 110000\rangle -\mid111101\rangle)_{abcd56}, $$
(12)
$$ \left|\varphi^{10} \right\rangle =\frac{1}{2}(\mid 000010\rangle - \mid 001111\rangle + \mid 110000\rangle +\mid111101\rangle)_{abcd56}, $$
(13)
$$ \left|\varphi^{11} \right\rangle =\frac{1}{2}(\mid 000010\rangle + \mid 001111\rangle - \mid 110000\rangle +\mid111101\rangle)_{abcd56}, $$
(14)
$$ \left|\varphi^{12} \right\rangle =\frac{1}{2}(\mid 000010\rangle - \mid 001111\rangle - \mid 110000\rangle -\mid111101\rangle)_{abcd56}, $$
(15)
$$ \left| \varphi^{13} \right\rangle =\frac{1}{2}(\mid 000011\rangle + \mid 001110\rangle + \mid 110001\rangle -\mid111100\rangle)_{abcd56}, $$
(16)
$$ \left| \varphi^{14} \right\rangle =\frac{1}{2}(\mid 000011\rangle - \mid 001110\rangle + \mid 110001\rangle +\mid111100\rangle)_{abcd56}, $$
(17)
$$ \left| \varphi^{15} \right\rangle =\frac{1}{2}(\mid 000011\rangle + \mid 001110\rangle - \mid 110001\rangle +\mid111100\rangle)_{abcd56}, $$
(18)
$$ \left| \varphi^{16} \right\rangle =\frac{1}{2}(\mid 000011\rangle - \mid 001110\rangle - \mid 110001\rangle -\mid111100\rangle)_{abcd56}, $$
(19)

After the measurement, Alice communicates her measured result via four classical bits to Bob. Bob then applies appropriate Pauli rotations to recover the original unknown four-qubit state. Alice’s measured results, her communicated results to Bob and Bob’s corresponding operations are listed in Table 1.

Table 1 Strategy for recovering the four-qubit state
Full size table

Table 1: Strategy for recovering the four-qubit state

3 Conclusion

In summary, we have shown that a restricted class of four-qubit state can be teleported by a six-qubit cluster state. In our scheme, only six-qubit von-Neumann projective measurements and local unitary operations are needed. We have explicitly calculated Alice’s measurement bases and the unitary operations required by Bob to reconstruct the unknown four-qubit state. We are also looking forward to generalize our schemes for quantum information splitting of an arbitrary four-qubit state by using eight-qubit cluster state as a quantum channel.