1 Introduction

The idea of transferring quantum states through quantum mechanical resources was given by Bennett et al. in 1993, in their celebrated work [1] where the teleportation protocol was introduced. Following this work many authors created several protocols for teleporting different types of quantum states [2,3,4,5,6,7,8,9,10,11,12,13,14,15,16,17,18,19,20,21,22,23,24,25,26]. Depending on the nature of the final result there are several types of teleportation process like controlled teleportation [2,3,4], bidirectional quantum teleportation [5,6,7,8,9], probabilistic teleportation [10,11,12,13], etc. In this paper we present a scheme of perfect asymmetric bidirectional controlled teleportation protocol.

Bidirectional teleportation is a quantum communication process in which two parties exchange the quantum states they possess. Zha et al. [6] established a protocol in which two parties can exchange arbitrary qubits in their possessions under the supervision of a controller. Several authors subsequently created protocols for mutual transfer of quantum states using different quantum channels [27,28,29].

Asymmetric bidirectional teleportation is a process by which mutual exchange of quantum states of different natures is done through the use of quantum entangled channels. Such a protocol was first created by Zhang et al. [30] in 2015 in which Alice transmits her single qubit entangled state to Bob and Bob wants to teleport his arbitrary two-qubit to Alice by using a maximally seven-qubit entangled state as quantum channel. Also in the same year 2015, Zhang et al. [31] demonstrated a bidirectional and asymmetric teleportation protocol where Alice transmits an arbitrary single qubit state to Bob and Bob transmits an arbitrary two-qubit entangled state to Alice via eight-qubit entangled state as a quantum channel. Afterwards Yang et al. [32] advanced a teleportation protocol in which Alice sends an arbitrary single qubit state to Bob and Bob sends an arbitrary two qubit state to Alice by using a seven-qubit entangled state as a quantum channel with the help of a controller Charlie. Several others asymmetric bidirectional teleportation protocols have published in the literature in references [33, 34]. A scheme of asymmetric quantum dialogue was presented by Banerjee et al. in [35].

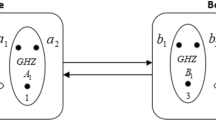
In our present work, we present a scheme of asymmetric bidirectional 3 ⇔ 2 qubit quantum teleportation protocol between Alice and Bob using 9-qubit cluster state with the help of the supervisor Charlie. In this scheme, the 9-qubit channel is initially shared by Alice and Bob and supervisor Charlie. Suppose that Alice and Bob have three entangled particles (a 1, a 2, a 3) and two entangled particles (b 1, b 2) respectively and want to exchange these states with each other under the controller Charlie. Following the protocol they exchange the entangled states in their possessions.

2 Asymmetric Bidirectional 3 ⇔ 2 Qubit Teleportation Protocol Between Alice and Bob Via 9-qubit Cluster State

Our scheme is described as follows. There are two parties Alice and Bob, who are in possessions of the three-qubit and two-qubit states\(|\psi \rangle _{a_{1}a_{2}a_{3}} = (x_{0}|000\rangle + x_{1}|111\rangle )\) and \(|\psi \rangle _{b_{1}b_{2}} = (y_{0}|00\rangle + y_{1}|11\rangle )\) respectively where x 0, x 1, y 0, y 1 are arbitrary complex coefficients with |x 0|2 + |x 1|2 = 1 and |y 0|2 + |y 1|2 = 1. Here the three qubits a 1, a 2, a 3 belong to Alice and the two qubits b 1, b 2 belong to Bob. In abbreviation, we indicate Alice’s three-qubit particle (a 1 a 2 a 3) and Bob’s two-qubit particle (b 1 b 2) by a and b respectively.

Alice wants to transmit her three qubit state to Bob and Bob wants to send his two qubit state to Alice through a single quantum channel consisting of 9-qubit cluster state shared between Alice, Bob and a supervisor Charlie. The channel is a cluster state having the form

\(|\psi \rangle _{123456789} = \frac {1}{2}[|000000000\rangle + |110100001\rangle + |001011110\rangle + |111111111\rangle ]_{123456789},\) where the qubits 2,4,6,8 belong to Alice, the qubits 3,5,7,9 belong to Bob and the qubit 1 belongs to the supervisor Charlie.

For convenience we rewrite the channel in the form as in the following. \(|\psi \rangle _{CA_{1}B_{1}A_{2}B_{2}A_{3}B_{3}A_{4}B_{4}} = \frac {1}{2}[|000000000\rangle + |110100001\rangle + |001011110\rangle + |111111111\rangle ],\) where the qubits A 1, A 2, A 3, A 4 belong to Alice, the qubits B 1, B 2, B 3, B 4 belong to Bob and the qubit C belongs to the supervisor Charlie.

Then the composite state of 14-qubits can be expressed as

$$\begin{array}{@{}rcl@{}} |\psi\rangle_{s} &=& |\psi\rangle_{a} \otimes |\psi\rangle_{b} \otimes |\psi\rangle_{CA_{1}B_{1}A_{2}B_{2}A_{3}B_{3}A_{4}B_{4}}\\ &=& \frac{1}{2}(x_{0}|000\rangle + x_{1}|111\rangle)\otimes(y_{0}|00\rangle + y_{1}|11\rangle)\otimes [|000000000\rangle + |110100001\rangle\\ &&+ |001011110\rangle + |111111111\rangle]. \end{array} $$
(1)

GHZ-states are given by

$$\begin{array}{@{}rcl@{}} &&|\phi^{\pm}\rangle = \frac{|000\rangle \pm |111\rangle}{\sqrt{2}}~~~~~~~~~~|\eta^{\pm}\rangle = \frac{|001\rangle \pm |110\rangle}{\sqrt{2}}\\ &&|\gamma^{\pm}\rangle = \frac{|010\rangle \pm |101\rangle}{\sqrt{2}}~~~~~~~~~~|\delta^{\pm}\rangle = \frac{|011\rangle \pm |100\rangle}{\sqrt{2}} \end{array} $$
(2)

Bell states are given by

$$\begin{array}{@{}rcl@{}} |\xi^{\pm}\rangle = \frac{|00\rangle \pm |11\rangle}{\sqrt{2}}~~~~~~~~~~~~~~~~~~|\nu^{\pm}\rangle = \frac{|01\rangle \pm |10\rangle}{\sqrt{2}}. \end{array} $$
(3)

The protocol is executed in the following way. Alice performs a measurement on her five qubits a 1, a 2, a 3, A 3, A 4 in the basis consisting of the following elements

$$\begin{array}{@{}rcl@{}} &&|\phi^{\pm}\rangle_{a_{1}a_{2}A_{3}}|\xi^{\pm}\rangle_{a_{3}A_{4}}~~~~~|\phi^{\pm}\rangle_{a_{1}a_{2}A_{3}}|\nu^{\pm}\rangle_{a_{3}A_{4}}\\ &&|\eta^{\pm}\rangle_{a_{1}a_{2}A_{3}}|\xi^{\pm}\rangle_{a_{3}A_{4}}~~~~~|\eta^{\pm}\rangle_{a_{1}a_{2}A_{3}}|\nu^{\pm}\rangle_{a_{3}A_{4}}\\ &&|\gamma^{\pm}\rangle_{a_{1}a_{2}A_{3}}|\xi^{\pm}\rangle_{a_{3}A_{4}}~~~~~|\gamma^{\pm}\rangle_{a_{1}a_{2}A_{3}}|\nu^{\pm}\rangle_{a_{3}A_{4}}\\ &&|\delta^{\pm}\rangle_{a_{1}a_{2}A_{3}}|\xi^{\pm}\rangle_{a_{3}A_{4}}~~~~~|\delta^{\pm}\rangle_{a_{1}a_{2}A_{3}}|\nu^{\pm}\rangle_{a_{3}A_{4}}. \end{array} $$
(4)

She then classically transmits her outcome of measurement to Bob and to the controller Charlie.

Then Bob performs a GHZ-state measurement on his three qubits b 1, b 2, B 4, that is, in the basis

$$\begin{array}{@{}rcl@{}} &&|\phi^{\pm}\rangle_{b_{1}b_{2}B_{4}} ~~~~~~~~~~|\eta^{\pm}\rangle_{b_{1}b_{2}B_{4}}\\ &&|\gamma^{\pm}\rangle_{b_{1}b_{2}B_{4}} ~~~~~~~~~~|\delta^{\pm}\rangle_{b_{1}b_{2}B_{4}}. \end{array} $$
(5)

Afterwards, Bob classically sends his measurement result to Alice and to the controller Charlie. After that Charlie performs a von-Numann measurement on his qubit C and transmits his measurement result classically to both Alice and Bob.

Alice and Bob, based on the results obtained in the measurements, perform appropriate unitary operations on the qubits A 1, A 2 and B 1, B 2, B 3 respectively and thereby exchange the states originally in their respective possessions. The protocol is thereby completed. It is described schematically in Fig. 1.

Fig. 1
figure 1

The schematic diagram of the asymmetric bidirectional quantum controlled teleportation protocol. Here (a)solid circles denote qubits, (b)bold black lines represent quantum entanglements and (c)dotted lines with arrows stand for transferring classical information

Full size image

The protocol is described in detail below.

Firstly Alice performs her measurement in the basis described in (4).

If Alice’s measurement result is \(|\phi ^{+}\rangle _{a_{1}a_{2}A_{3}}|\xi ^{+}\rangle _{a_{3}A_{4}} \), then the other particles are collapsed into the state

$$\begin{array}{@{}rcl@{}} |\zeta^{1}\rangle_{b_{1}b_{2}CA_{1}B_{1}A_{2}B_{2}B_{3}B_{4}} \,=\, (y_{0}|00\rangle \,+\, y_{1}|11\rangle) \frac{1}{2}[x_{0}|0000000\rangle&\,+\,&x_{0}|1101001\rangle~\,+\,~x_{1}|0010110\rangle\\ &+&x_{1}|1111111\rangle]. \end{array} $$

If Alice’s measurement result is \(|\phi ^{+}\rangle _{a_{1}a_{2}A_{3}}|\xi ^{-}\rangle _{a_{3}A_{4}} \), then the other particles are collapsed into the state

$$\begin{array}{@{}rcl@{}} |\zeta^{2}\rangle_{b_{1}b_{2}CA_{1}B_{1}A_{2}B_{2}B_{3}B_{4}} \,=\, (y_{0}|00\rangle \,+\, y_{1}|11\rangle) \frac{1}{2}[x_{0}|0000000\rangle&\,+\,&x_{0}|1101001\rangle~\,-\,~x_{1}|0010110\rangle\\ &\,-\,&x_{1}|1111111\rangle]. \end{array} $$

If Alice’s measurement result is \(|\phi ^{-}\rangle _{a_{1}a_{2}A_{3}}|\xi ^{+}\rangle _{a_{3}A_{4}}\), then the other particles are collapsed into the state

$$\begin{array}{@{}rcl@{}} |\zeta^{3}\rangle_{b_{1}b_{2}CA_{1}B_{1}A_{2}B_{2}B_{3}B_{4}} \,=\, (y_{0}|00\rangle \,+\, y_{1}|11\rangle) \frac{1}{2}[x_{0}|0000000\rangle&\,+\,&x_{0}|1101001\rangle~\,-\,~x_{1}|0010110\rangle\\ &\,-\,&x_{1}|1111111\rangle]. \end{array} $$

If Alice’s measurement result is \(|\phi ^{-}\rangle _{a_{1}a_{2}A_{3}}|\xi ^{-}\rangle _{a_{3}A_{4}} \), then the other particles are collapsed into the state

$$\begin{array}{@{}rcl@{}} |\zeta^{4}\rangle_{b_{1}b_{2}CA_{1}B_{1}A_{2}B_{2}B_{3}B_{4}} = (y_{0}|00\rangle \,+\, y_{1}|11\rangle) \frac{1}{2}[x_{0}|0000000\rangle&\,+\,&x_{0}|1101001\rangle~\,+\,~x_{1}|0010110\rangle\\ &\,+\,&x_{1}|1111111\rangle]. \end{array} $$

If Alice’s measurement result is \(|\eta ^{+}\rangle _{a_{1}a_{2}A_{3}}|\nu ^{+}\rangle _{a_{3}A_{4}} \), then the other particles are collapsed into the state

$$\begin{array}{@{}rcl@{}} |\zeta^{5}\rangle_{b_{1}b_{2}CA_{1}B_{1}A_{2}B_{2}B_{3}B_{4}} = (y_{0}|00\rangle \,+\, y_{1}|11\rangle) \frac{1}{2}[x_{0}|0010110\rangle&\,+\,&x_{0}|1111111\rangle~\,+\,~x_{1}|0000000\rangle\\ &\,+\,&x_{1}|1101001\rangle]. \end{array} $$

If Alice’s measurement result is \(|\eta ^{+}\rangle _{a_{1}a_{2}A_{3}}|\nu ^{-}\rangle _{a_{3}A_{4}} \), then the other particles are collapsed into the state

$$\begin{array}{@{}rcl@{}} |\zeta^{6}\rangle_{b_{1}b_{2}CA_{1}B_{1}A_{2}B_{2}B_{3}B_{4}} = (y_{0}|00\rangle \,+\, y_{1}|11\rangle) \frac{1}{2}[x_{0}|0010110\rangle&\,+\,&x_{0}|1111111\rangle~\,-\,~x_{1}|0000000\rangle\\ &\,-\,&x_{1}|1101001\rangle].\\ \end{array} $$

If Alice’s measurement result is \(|\eta ^{-}\rangle _{a_{1}a_{2}A_{3}}|\nu ^{+}\rangle _{a_{3}A_{4}} \), then the other particles are collapsed into the state

$$\begin{array}{@{}rcl@{}} |\zeta^{7}\rangle_{b_{1}b_{2}CA_{1}B_{1}A_{2}B_{2}B_{3}B_{4}} = (y_{0}|00\rangle \,+\, y_{1}|11\rangle) \frac{1}{2}[x_{0}|0010110\rangle&\,+\,&x_{0}|1111111\rangle~\,-\,~x_{1}|0000000\rangle\\ &\,-\,&x_{1}|1101001\rangle]. \end{array} $$

If Alice’s measurement result is \(|\eta ^{-}\rangle _{a_{1}a_{2}A_{3}}|\nu ^{-}\rangle _{a_{3}A_{4}} \), then the other particles are collapsed into the state

$$\begin{array}{@{}rcl@{}} |\zeta^{8}\rangle_{b_{1}b_{2}CA_{1}B_{1}A_{2}B_{2}B_{3}B_{4}} = (y_{0}|00\rangle \,+\, y_{1}|11\rangle) \frac{1}{2}[x_{0}|0010110\rangle&\,+\,&x_{0}|1111111\rangle~\,+\,~x_{1}|0000000\rangle\\ &\,+\,&x_{1}|1101001\rangle]. \end{array} $$

The other possibilities in the measurement of Alice do not appear in view of the fact that the combined state |ψ〉 s in (1) can be expressed as

$$\begin{array}{@{}rcl@{}} |\psi\rangle_{s}&=&|\phi^{+}\rangle_{a_{1}a_{2}A_{3}}|\xi^{+}\rangle_{a_{3}A_{4}}|\zeta^{1}\rangle+ |\phi^{+}\rangle_{a_{1}a_{2}A_{3}}|\xi^{-}\rangle_{a_{3}A_{4}}|\zeta^{2}\rangle\\ &&+|\phi^{-}\rangle_{a_{1}a_{2}A_{3}}|\xi^{+}\rangle_{a_{3}A_{4}}|\zeta^{3}\rangle+ |\phi^{-}\rangle_{a_{1}a_{2}A_{3}}|\xi^{-}\rangle_{a_{3}A_{4}}|\zeta^{4}\rangle\\ &&+|\eta^{+}\rangle_{a_{1}a_{2}A_{3}}|\nu^{+}\rangle_{a_{3}A_{4}}|\zeta^{5}\rangle+ |\eta^{+}\rangle_{a_{1}a_{2}A_{3}}|\nu^{-}\rangle_{a_{3}A_{4}}|\zeta^{6}\rangle\\ &&+|\eta^{-}\rangle_{a_{1}a_{2}A_{3}}|\nu^{+}\rangle_{a_{3}A_{4}}|\zeta^{7}\rangle+ |\eta^{-}\rangle_{a_{1}a_{2}A_{3}}|\nu^{-}\rangle_{a_{3}A_{4}}|\zeta^{8}\rangle.\\ \end{array} $$

Alice sends her measurement result to Bob and Charlie by classical means.

We note that not all the states corresponding to the different measurement outcomes are different. The states (|ζ 1〉,|ζ 4〉);(|ζ 2〉,|ζ 3〉);(|ζ 5〉,|ζ 8〉);(|ζ 6〉,|ζ 7〉) are identical. So we consider next only |ζ 1〉,|ζ 2〉,|ζ 5〉,|ζ 6〉 as measurement outcomes.

After that Bob performs his measurement in the basis described in (5). We consider the measurement of Bob in different cases obtained from Alice’s measurement.

Case 1 ::

When |ζ 1〉 is obtained after Alice’s measurement. If Bob’s measurement result is |ϕ +〉, then the other particles are collapsed into the state \(|\zeta ^{1},\phi ^{+}\rangle _{CA_{1}B_{1}A_{2}B_{2}B_{3}} {}={} \frac {1}{2}[x_{0}y_{0}|000000\rangle ~{}+{}~x_{0} y_{1}|110100\rangle ~{}+{}~x_{1}y_{0}|001011\rangle ~{}+{}~x_{1} y_{1}|111111\rangle ]\). If Bob’s measurement result is |ϕ −〉, then the other particles are collapsed into the state \(|\zeta ^{1},\phi ^{-}\rangle _{CA_{1}B_{1}A_{2}B_{2}B_{3}} {}={} \frac {1}{2}[x_{0}y_{0}|000000\rangle ~{}-{}~x_{0} y_{1}|110100\rangle ~{}+{}~x_{1}y_{0}|001011\rangle ~{}-{}~x_{1} y_{1}|111111\rangle ].\) If Bob’s measurement result is |η +〉, then the other particles are collapsed into the state \(|\zeta ^{1},\eta ^{+}\rangle _{CA_{1}B_{1}A_{2}B_{2}B_{3}} {}={} \frac {1}{2}[x_{0}y_{0}|110100\rangle ~{}+{}~x_{0} y_{1}|000000\rangle ~{}+{}~x_{1}y_{0}|111111\rangle ~{}+{}~x_{1} y_{1}|001011\rangle ].\) If Bob’s measurement result is |η −〉, then the other particles are collapsed into the state \(|\zeta ^{1},\eta ^{-}\rangle _{CA_{1}B_{1}A_{2}B_{2}B_{3}} {}={} \frac {1}{2}[x_{0}y_{0}|110100\rangle ~{}-{}~x_{0} y_{1}|000000\rangle ~{}+{}~x_{1}y_{0}|111111\rangle ~{}-{}~x_{1} y_{1}|001011\rangle ].\)

Case 2 ::

When |ζ 2〉 is obtained after Alice’s measurement. If Bob’s measurement result is |ϕ +〉, then the other particles are collapsed into the state \(|\zeta ^{2},\phi ^{+}\rangle _{CA_{1}B_{1}A_{2}B_{2}B_{3}} {}={} \frac {1}{2}[x_{0}y_{0}|000000\rangle ~{}+{}~x_{0} y_{1}|110100\rangle ~{}-{}~x_{1}y_{0}|001011\rangle ~{}-{}~x_{1} y_{1}|111111\rangle ]\). If Bob’s measurement result is |ϕ −〉, then the other particles are collapsed into the state \(|\zeta ^{2},\phi ^{-}\rangle _{CA_{1}B_{1}A_{2}B_{2}B_{3}} {}={} \frac {1}{2}[x_{0}y_{0}|000000\rangle ~{}-{}~x_{0} y_{1}|110100\rangle ~{}-{}~x_{1}y_{0}|001011\rangle ~{}+{}~x_{1} y_{1}|111111\rangle ]\). If Bob’s measurement result is |η +〉, then the other particles are collapsed into the state \(|\zeta ^{2},\eta ^{+}\rangle _{CA_{1}B_{1}A_{2}B_{2}B_{3}} {}={} \frac {1}{2}[x_{0}y_{0}|110100\rangle ~{}+{}~x_{0} y_{1}|000000\rangle ~{}-{}~x_{1}y_{0}|111111\rangle ~{}-{}~x_{1} y_{1}|001011\rangle ]\). If Bob’s measurement result is |η −〉, then the other particles are collapsed into the state \(|\zeta ^{2},\eta ^{-}\rangle _{CA_{1}B_{1}A_{2}B_{2}B_{3}} {}={} \frac {1}{2}[x_{0}y_{0}|110100\rangle ~{}-{}~x_{0} y_{1}|000000\rangle ~{}-{}~x_{1}y_{0}|111111\rangle ~{}+{}~x_{1} y_{1}|001011\rangle ]\).

Case 3 ::

When |ζ 5〉 is obtained after Alice’s measurement. If Bob’s measurement result is |ϕ +〉, then the other particles are collapsed into the state \(|\zeta ^{5},\phi ^{+}\rangle _{CA_{1}B_{1}A_{2}B_{2}B_{3}} {}={} \frac {1}{2}[x_{0}y_{0}|001011\rangle ~{}+{}~x_{0} y_{1}|111111\rangle ~{}+{}~x_{1}y_{0}|000000\rangle ~{}+{}~x_{1} y_{1}|110100\rangle ]\). If Bob’s measurement result is |ϕ −〉, then the other particles are collapsed into the state \(|\zeta ^{5},\phi ^{-}\rangle _{CA_{1}B_{1}A_{2}B_{2}B_{3}} {}={} \frac {1}{2}[x_{0}y_{0}|001011\rangle ~{}-{}~x_{0} y_{1}|111111\rangle ~{}+{}~x_{1}y_{0}|000000\rangle ~{}-{}~x_{1} y_{1}|110100\rangle ]\). If Bob’s measurement result is |η +〉, then the other particles are collapsed into the state \(|\zeta ^{5},\eta ^{+}\rangle _{CA_{1}B_{1}A_{2}B_{2}B_{3}} {}={} \frac {1}{2}[x_{0}y_{0}|111111\rangle ~{}+{}~x_{0} y_{1}|001011\rangle ~{}+{}~x_{1}y_{0}|110100\rangle ~{}+{}~x_{1} y_{1}|000000\rangle ]\). If Bob’s measurement result is |η −〉, then the other particles are collapsed into the state \(|\zeta ^{5},\eta ^{-}\rangle _{CA_{1}B_{1}A_{2}B_{2}B_{3}} {}={} \frac {1}{2}[x_{0}y_{0}|111111\rangle ~{}-{}~x_{0} y_{1}|001011\rangle ~{}+{}~x_{1}y_{0}|110100\rangle ~{}-{}~x_{1} y_{1}|000000\rangle ]\).

Case 4 ::

When |ζ 6〉 is obtained after Alice’s measurement. If Bob’s measurement result is |ϕ +〉, then the other particles are collapsed into the state \(|\zeta ^{6},\phi ^{+}\rangle _{CA_{1}B_{1}A_{2}B_{2}B_{3}} {}={} \frac {1}{2}[x_{0}y_{0}|001011\rangle ~{}+{}~x_{0} y_{1}|111111\rangle ~{}-{}~x_{1}y_{0}|000000\rangle ~{}-{}~x_{1} y_{1}|110100\rangle ]\). If Bob’s measurement result is |ϕ −〉, then the other particles are collapsed into the state \(|\zeta ^{6},\phi ^{-}\rangle _{CA_{1}B_{1}A_{2}B_{2}B_{3}} {}={} \frac {1}{2}[x_{0}y_{0}|001011\rangle ~{}-{}~x_{0} y_{1}|111111\rangle ~{}-{}~x_{1}y_{0}|000000\rangle ~{}+{}~x_{1} y_{1}|110100\rangle ]\). If Bob’s measurement result is |η +〉, then the other particles are collapsed into the state \(|\zeta ^{6},\eta ^{+}\rangle _{CA_{1}B_{1}A_{2}B_{2}B_{3}} {}={} \frac {1}{2}[x_{0}y_{0}|111111\rangle ~{}+{}~x_{0} y_{1}|001011\rangle ~{}-{}~x_{1}y_{0}|110100\rangle ~{}-{}~x_{1} y_{1}|000000\rangle ]\). If Bob’s measurement result is |η −〉, then the other particles are collapsed into the state \(|\zeta ^{6},\eta ^{-}\rangle _{CA_{1}B_{1}A_{2}B_{2}B_{3}} {}={} \frac {1}{2}[x_{0}y_{0}|111111\rangle ~{}-{}~x_{0} y_{1}|001011\rangle ~{}-{}~x_{1}y_{0}|110100\rangle ~{}+{}~x_{1} y_{1}|000000\rangle ]\).

The other possibilities in the measurement of Bob do not appear in view of the fact that in each cases of Bob measurement can be expressed as

$$\begin{array}{@{}rcl@{}} |\zeta^{1}\rangle &\,=\,& |\phi^{+}\rangle_{b_{1}b_{2}B_{4}}|\zeta^{1},\phi^{+}\rangle~\,+\,~|\phi^{-}\rangle_{b_{1}b_{2}B_{4}}|\zeta^{1},\phi^{-}\rangle ~\,+\,~|\eta^{+}\rangle_{b_{1}b_{2}B_{4}}|\zeta^{1},\eta^{+}\rangle~\,+\,~|\eta^{-}\rangle_{b_{1}b_{2}B_{4}}|\zeta^{1},\eta^{-}\rangle.\\ |\zeta^{2}\rangle &\,=\,& |\phi^{+}\rangle_{b_{1}b_{2}B_{4}}|\zeta^{2},\phi^{+}\rangle~\,+\,~|\phi^{-}\rangle_{b_{1}b_{2}B_{4}}|\zeta^{2},\phi^{-}\rangle ~\,+\,~|\eta^{+}\rangle_{b_{1}b_{2}B_{4}}|\zeta^{2},\eta^{+}\rangle~\,+\,~|\eta^{-}\rangle_{b_{1}b_{2}B_{4}}|\zeta^{2},\eta^{-}\rangle.\\ |\zeta^{5}\rangle &\,=\,& |\phi^{+}\rangle_{b_{1}b_{2}B_{4}}|\zeta^{5},\phi^{+}\rangle~\,+\,~|\phi^{-}\rangle_{b_{1}b_{2}B_{4}}|\zeta^{5},\phi^{-}\rangle ~\,+\,~|\eta^{+}\rangle_{b_{1}b_{2}B_{4}}|\zeta^{5},\eta^{+}\rangle~\,+\,~|\eta^{-}\rangle_{b_{1}b_{2}B_{4}}|\zeta^{5},\eta^{-}\rangle.\\ |\zeta^{6}\rangle &\,=\,& |\phi^{+}\rangle_{b_{1}b_{2}B_{4}}|\zeta^{6},\phi^{+}\rangle~\,+\,~|\phi^{-}\rangle_{b_{1}b_{2}B_{4}}|\zeta^{6},\phi^{-}\rangle ~\,+\,~|\eta^{+}\rangle_{b_{1}b_{2}B_{4}}|\zeta^{6},\eta^{+}\rangle~\,+\,~|\eta^{-}\rangle_{b_{1}b_{2}B_{4}}|\zeta^{6},\eta^{-}\rangle.\\ \end{array} $$

From the above it is seen that only |ϕ ±〉 and |η ±〉 appear in Bob’s measurement. The other basis elements do not appear. Bob then classically sends his measurement result to Alice and Charlie.

Finally, Charlie performs a von Neumann measurement on his qubit C in the measurement basis

$$\begin{array}{@{}rcl@{}} |\pm\rangle_{C} = \frac{1}{\sqrt{2}}(|0\rangle \pm |1\rangle)_{C}. \end{array} $$

Charlie then sends his measurement results to Alice and Bob.

After that Alice and Bob apply unitary operations on the qubits in their possessions to complete the exchange of their states.

We illustrate the protocol through a case in the following. Let us assume that Alice’s measurement result is \(|\eta ^{+}\rangle _{a_{1}a_{2}A_{3}}|\nu ^{+}\rangle _{a_{3}A_{4}}\), where the other particles are collapsed into the state

$$\begin{array}{@{}rcl@{}} |\zeta^{5}\rangle_{b_{1}b_{2}CA_{1}B_{1}A_{2}B_{2}B_{3}B_{4}} &=& (y_{0}|00\rangle + y_{1}|11\rangle) \frac{1}{2}[x_{0}|0010110\rangle\\&&+ x_{0}|1111111\rangle~+~x_{1}|0000000\rangle~+~x_{1}|1101001\rangle]. \end{array} $$

After that suppose Bob’s measurement result is \(|\phi ^{-}\rangle _{b_{1}b_{2}B_{4}}\), then the other particles collapse into the state

$$\begin{array}{@{}rcl@{}} |\zeta^{5},\phi^{-}\rangle_{CA_{1}B_{1}A_{2}B_{2}B_{3}} &=& \frac{1}{2}[x_{0}y_{0}|001011\rangle~-~x_{0} y_{1}|111111\rangle\\&&+~x_{1}y_{0}|000000\rangle~-~x_{1} y_{1}|110100\rangle]_{CA_{1}B_{1}A_{2}B_{2}B_{3}}. \end{array} $$

Then the supervisor Charlie performs his measurement in which he obtains the result |+〉 C which he transmits to Alice and Bob classically.

Then the other states are collapsed to \(\frac {1}{2\sqrt {2}}(y_{0}|00\rangle ~-~y_{1}|11\rangle )_{A_{1}A_{2}}\otimes (x_{0}|111\rangle ~+~x_{1}|000\rangle )_{B_{1}B_{2}B_{3}}\).

After that Alice and Bob perform appropriate unitary operation \((\sigma _{z}\otimes \sigma _{0})_{{A_{1}A_{2}}}\), and \((\sigma _{x}\otimes \sigma _{x}\otimes \sigma _{x})_{{B_{1}B_{2}B_{3}}}\) respectively.

The protocol is fully described for all cases in the Table 1.

Table 1 Description of the whole protocol
Full size table

3 Discussion and Conclusion

The principal resource of the protocol is the entangled channel the preparation of which is an important aspect of quantum communication theory. There are several experimental methods of creating entanglements some of which are noted in [36,37,38,39]. Further there are entanglement concentration protocols (abbreviated as ECPs) through which we can increase the amount of entanglement in certain situations [40,41,42]. The Bell-states [43, 44] and GHZ-states [45, 46] are important categories of quantum entangled states which have been taken up for exchange in the present protocol. In this work we use a nine-qubit quantum channel for the purpose of an asymmetric exchange of a Bell-state and a GHZ-state between two parties. Although the task in the present paper is different from the asymmetric bidirectional teleportation protocols given by Yang et al. [32] and Li et al. [34], we note the following comparison in terms of efficiency. The efficiency of the protocol is given by the formula \(\tau _{effic} = \frac {q_{s}}{q_{u} + b_{t}}\), where q s is the number of qubits that consist of the quantum information to be shared, q u is the number of the qubits that is used as the quantum channel (except for those chosen for security checking) and b t is the number of classical bits transmitted [44, 47]. Based on the above formula our efficiency is \(\tau = \frac {5}{21}\), while the efficiency of the protocol Yang et al. [32] and Li et al. [34] are \(\tau _{(Yang)} = \frac {3}{17}\) and \(\tau _{(Li)} = \frac {1}{6}\) respectively. The necessity of a channel having higher number qubits is due to the fact that we attempt more complex task of exchanging two-qubit and three-qubit entangled states compared to those in [32] and [34]. But this does not necessarily reduce the efficiency of the protocol as in our present case. Our quantum communication channel is a nine-qubit entangled state which belongs to a family of states known as cluster states described in [48, 49]. The present protocol has a controller Charlie. He has a very special role to play in the completion of the protocol where his measurement result, which is a one-qubit von Neumann measurement, has to be communicated to both the parties for their decisions on the choices of the unitary operations to be executed at their respective ends. This can not be done in the absence of the classical information received from the controller. We note another feature of our protocol which is that not all possible outcomes of the corresponding basis appear in the measurement. This leads to a substantial simplification of the protocol. This feature is explicitly mentioned in the corresponding places in the description of the protocol.