Analytical soliton solutions of the fractional order dual-mode nonlinear Schrödinger equation with time-space conformable sense by some procedures

Abstract

This paper considers the fractional order dual-mode nonlinear Schrödinger equation (FDMNLSE) with cubic law nonlinearity. The FDMNLSE interprets the concurrent propagation of two-mode waves instead of a single wave. Throughout this work, the fractional derivative is given in terms of time and space conformable sense. The FDMNLSE introduces three physical parameters: dispersive factor, phase speed, and nonlinearity. This new model has many applications in nonlinear physics and fiber optics. We will use two methods to get new optical solutions: the generalized exponential rational function method (GERFM) and the functional variable method (FVM). Using the GERFM, we get unique wave solutions in the forms of shock wave solutions, singular soliton solutions, singular periodic waves, and exponential function solutions. Thanks to FVM, we reach bright optical soliton solutions, singular optical soliton solutions, and periodic singular wave solutions, and the restraint conditions for solutions are reported. The analytical outcomes are supplemented with numerical simulations of the got solutions to understand the dynamic behavior of obtained solutions. The results of this study may have a high-importance application while handling the other nonlinear partial differential equations (NLPDEs).

1 Introduction

NLPDEs are of great significance to our modern world. Accordingly, the problem of building new approaches to solve these equations is an essential matter in applied mathematics and mathematical physics. The new exact solutions of nonlinear equations supply a better understanding of the tools of nonlinear physical phenomena in engineering and science. We recognize that the extraordinary concentration of investigators in this area of investigation plays a magnific role and significance.

In recent years, nonlinear evolution equations (NLEEs) have become a favorite research topic in diverse engineering and physical sciences fields. Because these types of equations model every natural phenomenon. Their solutions allow us to understand better and analyze our universe. Investigators are keenly interested in developing additional effectual ways of determining solutions to nonlinear prototypes. Better awareness is being delivered to solitary wave solutions because the NLEEs have successfully demonstrated the connected physical system’s behavior in many science areas. The nonlinear Schrödinger equation (NLSE) is one of the most vital NLEEs encountered in studying nonlinear optics. The most recent of these can be given as an example of Logarithmic transformations (Seadawy et al. 2023), Sub-ODE method (Aziz et al. 2023), Differential transform method (DTM) (Zahran et al. 2023), Extended simple equation method (Zahran and Bekir 2022; Ahmed et al. 2022). The NLSE is a universal model that portrays many physical nonlinear systems. The NLSE is one of the equations characterizing the evolution of slowly altering packets of quasi-monochromatic waves in weakly nonlinear media with dispersion. During the past few decades, examinations on optical solitons have become widespread among investigators in the physical sciences. Another performance of this equation is in pattern formation, which has been used to model some nonequilibrium pattern-forming systems.

Fractional calculus has gained considerable concentration in recent times. The origin of fractional calculus dates back to the 1600 s, first seen in a letter from Leibnitz to L’Hospital. Afterward, Abel, Fourier, Liouville, Leibnitz, Weyl, and Riemann contributed to this theory. Abel gave the first applications of fractional calculus in 1823. Researchers have been working on fractional calculus and developing new operators such as Riemann-Liouville derivatives (Salah et al. 2019), Caputo-Fabrizio derivatives (Baleanu et al. 2020), Atangana-Baleanu derivatives (Scott 2005), and Conformable fractional derivatives (CFDs) (Zhao and Luo 2017).

Varied fractional-order prototypes are employed in applied sciences and engineering because they better illustrate real-world problems. The CFD is favorably applicable for solving complicated prototypes. It also facilitates us to achieve an opinion of how physical phenomena act. This derivative is discovered to be extra attractive and marked than the earlier mounted ones. The CFD conveys many luxuries when it is used to model many physical problems because the differential equations with CFDs are easier to solve numerically than those connected with the Caputo fractional derivative or Riemann-Liouville.

Up to now, many effective analytical approaches for the NLPDEs and the nonlinear ordinary differential equations (NODEs) have been offered as Paul-Painleve approach method (Zahran et al. 2023), Lie group analysis technique (Adeyemo and Khalique 2023), Hirota bilinear method (Wang 2023), Split-step method (Bourdine et al. 2022), New extended generalized Kudryashov technique (Seadawy et al. 2021), Generalized auxiliary equation strategy (Khater et al. 2019), Modification of variational iteration algorithm-I (Ahmad et al. 2020), Multistage optimal homotopy asymptotic method (Wang et al. 2022; Shah et al. 2020), Improved tanh method (Islam et al. 2022), Extended tanh method (Saha et al. 2021), Extended Jacobi elliptic expansion function scheme (Zafar 2020), Haar wavelet collocation method (HWCM) (Liu et al. 2021; Ahsan et al. 2021), Finite difference method (Zaher et al. 2021; Raslan and Ali 2020). Also, different powerful mathematical methods were applied to solve the PDEs with integer or fractional order offered as Rational $(G^{\prime }/G)$-expansion method (Islam et al. 2021), The analytical soliton solutions (Yépez-Martínez et al. 2022), Extended Riccati scheme (Islam et al. 2022), First integral approach (Aderyani et al. 2022), Sub-equation approach (Yépez-Martínez et al. 2022), Rational-expansion approach (Islam et al. 2022), Meshless approach (Ahmad et al. 2020a, b; Nawaz Khan et al. 2020), Generalized Riccati equation (GRE) together with the basic simplest equation method (SEM) (Osman et al. 2020), Modified first integral scheme (Yépez-Martínez et al. 2018), Fractional iteration algorithm-I (Ahmad et al. 2020), Variational Iteration algorithm-I (Ahmad et al. 2020), Local meshless method (Inc et al. 2020).

Two-mode or, sometimes named, dual-mode type equations have recently attracted noticeably more investigation in the nonlinear sciences. Because dual-mode equations in the present design survey the extemporaneous wave interactions. Jaradat et al. (2018) got dual-mode optical soliton solutions for their prototype by utilizing the tanh-coth expansion technique. Employing simplified Hirota’s technique, Wazwaz reached multiple kink solutions of dual-mode Sharma–Tasso–Olver (DM-STO) equation and dual-mode fourth-order Burgers (TMBE-4th) Wazwaz (2018). Javid et al. (2021) accepted dual-wave soliton solutions for dual-mode RNLSE by utilizing the $\exp (-\phi )$-expansion approach. Kopçasız and Yaşar (2023) used the Lie symmetry procedure on the DMNLSE to discover the infinitesimal generators using the invariance condition. Then, they transformed the DMNLSE into an ODE employing accepted generators and similarity reduction concepts. Later, thanks to the multiplier technique, they obtained the conserved quantities’ densities and fluxes.

In this study, we deal with FDMNLSE with cubic law nonlinearity. The FDMNLSE is defined as

$$\begin{aligned}{} & {} i(D_{t}^{2\gamma }W-s^{2}D_{x}^{2\gamma }W)+\left( D_{t}^{\gamma }\left\{ \digamma \left( \left| W\right| ^{2}\right) W\right\} -\pi sD_{x}^{\gamma }\left\{ \digamma \left( \left| W\right| ^{2}\right) W\right\} \right) \nonumber \\{} & {} \quad +\left( D_{t}^{\gamma }\left\{ \frac{1}{2}D_{x}^{2\gamma }W\right\} -\theta sD_{x}^{\gamma }\left\{ \frac{1}{2}D_{x}^{2\gamma }W\right\} \right) =0. \end{aligned}$$

(1)

Here $W=W(x,t)$ is a complex function that stands for the envelope field with temporal variable t and the propagation distance x, i is an imaginary unit and $\ i^{2}=-1.$ Also, $\left| \pi \right| \le \pm 1$ is a nonlinearity factor, $\left| \theta \right| \le \pm 1$ is a dispersive factor,$\ s\ge 0$ is an interaction phase speed (Kopçasız and Yaşar 2022a).

Dual-mode kind equations have newly attracted appreciably more investigation in the nonlinear sciences. Because dual-mode equations in the existing configuration probe the spontaneous wave relations. There are considerably different works connected with the dual-mode Korteweg-de Vries equation (Kopçasız and Yaşar 2022b; Kopçasız et al. 2022; Zayed and Shohib 2020; Alquran and Jaradat 2019).

The major goal of this study is to extract the diverse exact solutions to the FDMNLSE with cubic law nonlinearity. The FDMNLSE interprets the concurrent propagation of two-mode waves instead of a single wave. We will apply two analytical methods: GERFM and the FVM.

The overall composition of this paper is organized as follows. Section 2 is dedicated to the properties of the conformable fractional derivatives. Section 3 suggests a concise introduction to the GERFM and the FVM. In Sect. 4, the proposed strategies are employed to construct the soliton solutions. Physical interpretations and concluding remarks are offered in Sect. 5.

2 The conformable fractional derivative (CFD)

The concept with some properties of the fractional derivative of conformal type (Zheng et al. 2019; Khalil et al. 2014) is given as:

Definition 1

Let $u:(0,\infty )\rightarrow {\mathbb {R}},$ then the conformable fractional derivative of u of order $\gamma$ is defined as

$$\begin{aligned} D_{x}^{\gamma }(u(x))=\underset{\epsilon \rightarrow 0}{\lim }\frac{ u(x+\epsilon x^{1-\gamma })-u(x)}{\epsilon } \end{aligned}$$

in which $x>0$ and order of derivative depicted by $\gamma$ also $0<\gamma \le 1.$ The properties of discussed definition follow the next theorems.

If y(x) and z(x) are $\gamma -$differentiable functions at any point $x>0$ for all $\gamma \in (0,1].$ Then

Theorem 2

• (T1) $D_{x}^{\gamma }(x^{n})=nx^{n-\gamma }$

• (T2) $D_{x}^{\gamma }(\lambda )=0,$ in which $\lambda$ is any arbitrary constant.

• (T3) $D_{x}^{\gamma }(\varkappa _{1}y(x)+\varkappa _{2}z(x))=\varkappa _{1}D_{x}^{\gamma }(y(x))+\varkappa _{2}D_{x}^{\gamma }(z(x)),$ $\forall \varkappa _{1},\varkappa _{2}\in {\mathbb {R}}.$

• (T4) $D_{x}^{\gamma }(y(x).z(x))=y(x)D_{x}^{\gamma }(z(x))+z(x)D_{x}^{\gamma }(y(x)).$

• (T5) $D_{x}^{\gamma }\left(\frac{y(x)}{z(x)}\right)=\frac{z(x)D_{x}^{\gamma }(y(x))-y(x)D_{x}^{\gamma }(z(x))}{z^{2}(x)}.$ If u is differentiable, then $D_{x}^{\gamma }y(x)=x^{1-\gamma }\frac{dy(x)}{dx}.$

Theorem 3

Presume $y(x),z(x):(0,\infty )\rightarrow {\mathbb {R}}$ be differentiable and also $\gamma$-differentiable functions, then the following rule holds:

$$\begin{aligned} D_{x}^{\gamma }(y(x).z(x))=x^{1-\gamma }z^{\prime }(t)y^{\prime }(h(t)). \end{aligned}$$

3 Methodologies

3.1 The outline of technique I: GERFM

This procedure was first proposed by Ghanbari and his colleague in the article (Ghanbari and Inc 2018). So far, many partial differential equations (PDEs) have been studied by using this technique (Ghanbari et al. 2021; Younas et al. 2021; Kumar and Niwas 2022; Ghanbari 2021). We will review how to use the method below.

Phase 1. Suppose we have a fractional order NLEE in the form:

$$\begin{aligned} \Omega (W(x,t),D_{x}^{\gamma }\{W(x,t)\},D_{t}^{\gamma }\{W(x,t)\},D_{x}^{2\gamma }\{W(x,t)\},...)=0. \end{aligned}$$

(2)

Phase 2. Using the transformations $W(x,t)=V(\xi )$ and $\xi =\frac{ (x^{\gamma }-at^{\gamma })}{\gamma }$, Eq. (2) becomes a NODE given by:

$$\begin{aligned} \Omega (V,V^{\prime },V^{\prime \prime },...)=0. \end{aligned}$$

(3)

Phase 3. We assume that Eq. (3) admits the exact solution giving by

$$\begin{aligned} V(\xi )=A_{0}+\overset{N}{\underset{k=1}{\sum }}A_{k}\Lambda (\xi )^{k}+ \overset{N}{\underset{k=1}{\sum }}B_{k}\Lambda (\xi )^{-k}, \end{aligned}$$

(4)

in which

$$\begin{aligned} \Lambda (\xi )=\frac{h_{1}e^{f_{1}\xi }+h_{2}e^{f_{2}\xi }}{h_{3}e^{f_{3}\xi }+h_{4}e^{f_{4}\xi }}. \end{aligned}$$

(5)

Unknown coefficients $A_{0},$ $A_{k},$ $B_{k}(1\le i\le N)$ and $h_{i},f_{i}(1\le i\le 4)$ are real (or complex) constants to be evaluated, such that Eq. (4) satisfies the NODE Eq. (3).

Phase 4. Besides, the positive integer N is calculated by the principles of balancing.

Substituting Eq. (4) together with Eq. (5) into Eq. (3) and gathering all terms, the left-hand side of the resultant equation is converted into polynomial equation $K(\varsigma _{1},\varsigma _{2},\varsigma _{3},\varsigma _{4})=0$ as to $\varsigma _{i}=e^{f_{i}\xi }$ for $i=1,..,4.$ Taking each coefficient of K to zero, we reach a set of algebraic equations.

Phase 5. Solving the algebraic equations in Phase 4 with the aid of a symbolic computation package and then inserting non-trivial solutions in Eq. (4), the explicit shape of the solutions of Eq. (2) will be extracted.

3.2 The outline of technique II: FVM

The FVM was first presented by Zerarka et al. (2010). This procedure has been further developed by many authors (Mirzazadeh et al. 2016; Liu and Chen 2013; Neirameh 2023).

Suppose we have a fractional order NLEE in the form:

$$\begin{aligned} \Omega _{1}(W(x,t),D_{x}^{\gamma }\{W(x,t)\},D_{t}^{\gamma }\{W(x,t)\},D_{x}^{2\gamma }\{W(x,t)\},...)=0. \end{aligned}$$

(6)

Here $\Omega _{1}$ is a polynomial in W(x, t) and its partial derivatives. The main phases of this approach can be explained as follows:

Phase 1. We use the wave transformation

$$\begin{aligned} W(x,t)=V(\xi ),\quad \xi =\frac{(x^{\gamma }-at^{\gamma })}{\gamma }, \end{aligned}$$

(7)

to reduce Eq. (6) to the next NODE:

$$\begin{aligned} \Omega _{2}(V,V_{\xi },V_{\xi \xi },...)=0, \end{aligned}$$

(8)

where $\Omega _{2}$ is a polynomial in $V(\xi )$ and its total derivatives, while $V_{\xi }=\frac{dV}{d\xi },$ $V_{\xi \xi }=\frac{d^{2}V}{d\xi ^{2}}$ and so on.

Phase 2. We transform in which the unknown function $V(\xi )$ is regarded as a functional variable in the form:

$$\begin{aligned} V_{\xi }=\Gamma (V) \end{aligned}$$

(9)

and some successively derivatives of $V(\xi )$ are as follows:

$$\begin{aligned} V_{\xi \xi }= & {} \frac{1}{2}(\Gamma ^{2})^{\prime },\nonumber \\ V_{\xi \xi \xi }= & {} \frac{1}{2}(\Gamma ^{2})^{\prime \prime }\sqrt{\Gamma ^{2}},\nonumber \\ V_{\xi \xi \xi \xi }= & {} \frac{1}{2}[(\Gamma ^{2})^{\prime \prime \prime }\Gamma ^{2}+(\Gamma ^{2})^{\prime \prime }(\Gamma ^{2})^{\prime }], \end{aligned}$$

(10)

and so on, in which “$^{\prime }$” stands for $\frac{d}{dV}$.

Phase 3. We put Eq. (9) and Eq. (10) into Eq. (8) to reduce it to the subsequent NODE:

$$\begin{aligned} \Omega _{3}(V,\Gamma ,\Gamma ^{\prime },\Gamma ^{\prime \prime },\Gamma ^{\prime \prime \prime },...)=0. \end{aligned}$$

(11)

After integration, Eq. (11) provides the expression of $\Gamma$, and this in turn together with Eq. (9) gives the appropriate solutions of Eq. (6).

4 Mathematical discussion for the fractional order nonlinear model

Under the cubic law, $\digamma (W)=W$, thus Eq. (1) become next

$$\begin{aligned}{} & {} i\left( D_{t}^{2\gamma }W-s^{2}D_{x}^{2\gamma }W)+(D_{t}^{\gamma }\left\{ \left| W\right| ^{2}W\right\} -\pi sD_{x}^{\gamma }\left\{ \left| W\right| ^{2}W\right\} \right) \nonumber \\{} & {} \quad +\left( D_{t}^{\gamma }\left\{ \frac{1}{2}D_{x}^{2\gamma }W\right\} -\theta sD_{x}^{\gamma }\left\{ \frac{1}{2}D_{x}^{2\gamma }W\right\} \right) =0. \end{aligned}$$

(12)

By making the fractional-order complex wave transformation

$$\begin{aligned} W(x,t) = & {} e^{i\alpha \frac{(x^{\gamma }+\eta t^{\gamma })}{\gamma }}V(\xi ),\nonumber \\ \xi (x,t) = & {} \frac{(x^{\gamma }-at^{\gamma })}{\gamma },\text { } \end{aligned}$$

(13)

on Eq. (12) and split up real and imaginary parts, we reach the next NODEs:

$$\begin{aligned}{} & {} (-2\eta ^{2}-2s^{2}+\theta s\alpha -\alpha \eta )\alpha ^{2}V+(-2\pi s+2\eta )\alpha V^{3}+(2a^{2}-2s^{2}+\alpha \eta -2\alpha a-3\alpha \theta s)V^{\prime \prime }=0, \end{aligned}$$

(14)

$$\begin{aligned}{} & {} (4\eta a+4s^{2}+3\alpha \theta s-2\alpha \eta +\alpha a)\alpha V-2(\pi s+a)V^{3}-(a+\theta s)V^{\prime \prime }=0. \end{aligned}$$

(15)

From the Eq. (15), we have $\pi =\theta =-\frac{a}{s}$, $\eta =\frac{ \alpha a-2\,s^{2}}{2a-\alpha }$ and plugging them into Eq. (14), then Eq. (12) is reached to a NODE

$$\begin{aligned}{} & {} a(s+a)(a-s)(2a-\alpha )V^{\prime \prime }\nonumber \\{} & {} \quad +(-5\alpha as^{2}+2s^{4}+2s^{2}a^{2}+s^{2}\alpha ^{2}+\alpha a^{3})\alpha ^{2}V+(s+a)(a-s)(2a-\alpha )\alpha V^{3}=0\text {.} \end{aligned}$$

(16)

4.1 Main outcomes of solving model Eq. (12) using technique I

According to Phase 4, Eq. (16) presents $N=1$. Therefore, Phase 3 gives us

$$\begin{aligned} V(\xi )=A_{0}+A_{1}\Lambda (\xi )+\frac{B_{1}}{\Lambda (\xi )}. \end{aligned}$$

(17)

Category 1

When we take $h:[-1,0,1,1]$ and f : [0, 0, 1, 0], then Eq. (5) changes into

$$\begin{aligned} \Lambda =-\frac{1}{1+e^{\xi }}. \end{aligned}$$

(18)

For getting the values of parameters, we need to solve algebraic equations with the aid of Maple and the pursuing set of solutions can be delivered as

$$\begin{aligned} A_{0}= & {} \pm \,\frac{1}{2}\sqrt{-\frac{2a}{\alpha }},\quad A_{1}=\pm\, \frac{2a}{\alpha \sqrt{-\frac{2a}{\alpha }}},\quad B_{1}=0,\\ s= & {} \pm\, \frac{\sqrt{2}}{4\alpha }\left( \begin{array}{c} -4a^{2}\alpha ^{2}+10a\alpha ^{3}-2\alpha ^{4}-2a^{2}+a\alpha \\ +\left( \begin{array}{c} 16\alpha ^{4}a^{4}-112a^{3}\alpha ^{5}+116a^{2}\alpha ^{6}-40a\alpha ^{7}+4\alpha ^{8}+48a^{4}\alpha ^{2} \\ -64a^{3}\alpha ^{3}+28\alpha ^{4}a^{2}-4a\alpha ^{5}+4a^{4}-4a^{3}\alpha +a^{2}\alpha ^{2} \end{array} \right) ^{\frac{1}{2}} \end{array} \right) ^{\frac{1}{2}}. \end{aligned}$$

Inserting these above values of $A_{0},$ $A_{1},$ $B_{1}$ into Eq. (17), we have

$$\begin{aligned} V(\xi )=\frac{1}{2}\sqrt{-\frac{2a}{\alpha }}+\frac{2a}{\alpha \sqrt{-\frac{ 2a}{\alpha }}}\times \left( -\frac{1}{1+e^{\xi }}\right) . \end{aligned}$$

(19)

By using the Eq. (19) together with Eq. (13), then, the exponential function can be expressed as

$$\begin{aligned} W_{1}(x,t)=\left\{ \frac{1}{2}\sqrt{-\frac{2a}{\alpha }}+\frac{2a}{\alpha \sqrt{-\frac{2a}{\alpha }}}\times \left( -\frac{1}{1+e^{\frac{(x^{\gamma }-at^{\gamma })}{\gamma }}}\right) \right\} \times e^{i\alpha \frac{ (x^{\gamma }+\eta t^{\gamma })}{\gamma }} \end{aligned}$$

(20)

provided that $a\alpha <0$.

Category 2

When we choose $h=[1,1,1,-1]$ and $f=[1,-1,1,-1]$, then Eq. (5) modify into

$$\begin{aligned} \Lambda =\frac{e^{\xi }+e^{-\xi }}{e^{\xi }-e^{-\xi }}. \end{aligned}$$

(21)

The next Sub-category are scheduled:

Sub-category 2.1

$$\begin{aligned}{} & {} A_{0}=0,\quad A_{1}=B_{1}=\pm\, \sqrt{-\frac{2a}{\alpha }},\\{} & {} s=\pm\, \frac{1}{2\alpha }\left( \begin{array}{c} -\,2a^{2}\alpha ^{2}+5a\alpha ^{3}-\alpha ^{4}-16a^{2}+8a\alpha \\ \pm\, \left( \begin{array}{c} 4\alpha ^{4}a^{4}-28a^{3}\alpha ^{5}+29a^{2}\alpha ^{6}-10a\alpha ^{7}+\alpha ^{8}+192a^{4}\alpha ^{2}-256a^{3}\alpha ^{3} \\ +\,112\alpha ^{4}a^{2}-16a\alpha ^{5}+256a^{4}-256a^{3}\alpha +64a^{2}\alpha ^{2} \end{array} \right) ^{\frac{1}{2}} \end{array} \right) ^{\frac{1}{2}}. \end{aligned}$$

Inserting these above values of $A_{0},$ $A_{1},$ $B_{1}$ into Eq. (17), we have

$$\begin{aligned} V(\xi )=\sqrt{-\frac{2a}{\alpha }}\times \left( \frac{e^{\xi }+e^{-\xi }}{ e^{\xi }-e^{-\xi }}\right) +\sqrt{-\frac{2a}{\alpha }}\times \left( \frac{ e^{\xi }+e^{-\xi }}{e^{\xi }-e^{-\xi }}\right) ^{-1}. \end{aligned}$$

(22)

By using the Eq. (22) together with Eq. (13), we attain the singular soliton solution as

$$\begin{aligned} W_{2,1}(x,t)=\left\{ \begin{array}{c} \sqrt{-\frac{2a}{\alpha }}\times \left( \frac{e^{\frac{(x^{\gamma }-at^{\gamma })}{\gamma }}+e^{-\frac{(x^{\gamma }-at^{\gamma })}{\gamma }}}{ e^{\frac{(x^{\gamma }-at^{\gamma })}{\gamma }}-e^{-\frac{(x^{\gamma }-at^{\gamma })}{\gamma }}}\right) \\ +\sqrt{-\frac{2a}{\alpha }}\times \left( \frac{e^{\frac{(x^{\gamma }-at^{\gamma })}{\gamma }}+e^{-\frac{(x^{\gamma }-at^{\gamma })}{\gamma }}}{ e^{\frac{(x^{\gamma }-at^{\gamma })}{\gamma }}-e^{-\frac{(x^{\gamma }-at^{\gamma })}{\gamma }}}\right) ^{-1} \end{array} \right\} \times e^{i\alpha \frac{(x^{\gamma }+\eta t^{\gamma })}{\gamma }} \end{aligned}$$

(23)

provided that $a\alpha <0$.

Sub-category 2.2

$$\begin{aligned}{} & {} A_{0}=A_{1}=0,\quad B_{1}=\pm\, \sqrt{-\frac{2a}{\alpha }},\\{} & {} s=\pm \frac{1}{2\alpha }\left( \begin{array}{c} -2a^{2}\alpha ^{2}+5a\alpha ^{3}-\alpha ^{4}-4a^{2}+2a\alpha \\ \pm \,\left( \begin{array}{c} 4\alpha ^{4}a^{4}-28a^{3}\alpha ^{5}+29a^{2}\alpha ^{6}-10a\alpha ^{7}+\alpha ^{8}+48a^{4}\alpha ^{2} \\ -\,64a^{3}\alpha ^{3}+28\alpha ^{4}a^{2}-4a\alpha ^{5}+16a^{4}-16a^{3}\alpha +4a^{2}\alpha ^{2} \end{array} \right) ^{\frac{1}{2}} \end{array} \right) ^{\frac{1}{2}}. \end{aligned}$$

Substituting the values of $A_{0},$ $A_{1},$ $B_{1}$ into Eq. (17), we have

$$\begin{aligned} V(\xi ) = \pm \sqrt{-\frac{2a}{\alpha }}\times \left( \frac{e^{\xi }+e^{-\xi } }{e^{\xi }-e^{-\xi }}\right) ^{-1}. \end{aligned}$$

(24)

Using the Eq. (24) together with Eq. (13), we discover the singular soliton solution as

$$\begin{aligned} W_{2,2}(x,t)=\left\{ \pm \sqrt{-\frac{2a}{\alpha }}\times \left( \frac{e^{ \frac{(x^{\gamma }-at^{\gamma })}{\gamma }}+e^{-\frac{(x^{\gamma }-at^{\gamma })}{\gamma }}}{e^{\frac{(x^{\gamma }-at^{\gamma })}{\gamma } }-e^{-\frac{(x^{\gamma }-at^{\gamma })}{\gamma }}}\right) ^{-1}\right\} \times e^{i\alpha \frac{(x^{\gamma }+\eta t^{\gamma })}{\gamma }} \end{aligned}$$

(25)

provided that $a\alpha <0$.

Category 3

For $h=[-3,-1,1,1]$ and $f=[1,-1,1,-1]$, then Eq. (5) transform into

$$\begin{aligned} \Lambda =\frac{-3e^{\xi }-e^{-\xi }}{e^{\xi }+e^{-\xi }}. \end{aligned}$$

(26)

The next Sub-category are planned:

Sub-category 3.1

$$\begin{aligned}{} & {} A_{0}=\pm\, \frac{4a}{\alpha \sqrt{-\frac{2a}{\alpha }}},\quad A_{1}=\pm\, \sqrt{-\frac{2a}{\alpha }},\quad B_{1}=0,\\{} & {} s=\pm\, \frac{1}{2\alpha }\left( \begin{array}{c} -2a^{2}\alpha ^{2}+5a\alpha ^{3}-\alpha ^{4}-4a^{2}+2a\alpha \\ \pm \left( \begin{array}{c} 4\alpha ^{4}a^{4}-\,28a^{3}\alpha ^{5}+29a^{2}\alpha ^{6}-10a\alpha ^{7}+\alpha ^{8}+48a^{4}\alpha ^{2}-64a^{3}\alpha ^{3} \\ +28\alpha ^{4}a^{2}-4a\alpha ^{5}+16a^{4}-16a^{3}\alpha +4a^{2}\alpha ^{2} \end{array} \right) ^{\frac{1}{2}} \end{array} \right) ^{\frac{1}{2}}. \end{aligned}$$

Substituting the values of $A_{0},$ $A_{1},$ $B_{1}$ into Eq. (17), we have

$$\begin{aligned} V(\xi )=\frac{4a}{\alpha \sqrt{-\frac{2a}{\alpha }}}+\sqrt{-\frac{2a}{\alpha }}\times \left( \frac{-3e^{\xi }-e^{-\xi }}{e^{\xi }+e^{-\xi }}\right) . \end{aligned}$$

(27)

Using the Eq. (27) together with Eq. (13), then, we obtain the shock wave solution as

$$\begin{aligned} W_{3,1}(x,t)=\left\{ \frac{4a}{\alpha \sqrt{-\frac{2a}{\alpha }}}+\sqrt{- \frac{2a}{\alpha }}\times \left( \frac{-3e^{\frac{(x^{\gamma }-at^{\gamma }) }{\gamma }}-e^{-\frac{(x^{\gamma }-at^{\gamma })}{\gamma }}}{e\frac{ (x^{\gamma }-at^{\gamma })}{\gamma }+e^{-\frac{(x^{\gamma }-at^{\gamma })}{ \gamma }}}\right) \right\} \times e^{i\alpha \frac{(x^{\gamma }+\eta t^{\gamma })}{\gamma }} \end{aligned}$$

(28)

provided that $a\alpha <0$.

Sub-category 3.2

$$\begin{aligned}{} & {} A_{0}= \pm \,2\sqrt{-\frac{2a}{\alpha }},\quad A_{1}=0,\quad B_{1}=\pm \,3\sqrt{-\frac{2a}{\alpha }},\\{} & {} s=\pm\, \frac{1}{2\alpha }\left( \begin{array}{c} -2a^{2}\alpha ^{2}+5a\alpha ^{3}-\alpha ^{4}-4a^{2}+2a\alpha \\ \pm\, \left( \begin{array}{c} 4\alpha ^{4}a^{4}-28a^{3}\alpha ^{5}+29a^{2}\alpha ^{6}-10a\alpha ^{7}+\alpha ^{8}+48a^{4}\alpha ^{2}-64a^{3}\alpha ^{3} \\ +28\alpha ^{4}a^{2}-4a\alpha ^{5}+16a^{4}-16a^{3}\alpha +4a^{2}\alpha ^{2} \end{array} \right) ^{\frac{1}{2}} \end{array} \right) ^{\frac{1}{2}}. \end{aligned}$$

Substituting the values of $A_{0},$ $A_{1},$ $B_{1}$ into Eq. (17), we have

$$\begin{aligned} V(\xi )=2\sqrt{-\frac{2a}{\alpha }}+3\sqrt{-\frac{2a}{\alpha }}\times \left( \frac{-3e^{\xi }-e^{-\xi }}{e^{\xi }+e^{-\xi }}\right) ^{-1}. \end{aligned}$$

(29)

Using the Eq. (29) together with Eq. (13), we get the shock wave solution as

$$\begin{aligned} W_{3,2}(x,t)=\left\{ 2\sqrt{-\frac{2a}{\alpha }}+3\sqrt{-\frac{2a}{\alpha }} \times \left( \frac{-3e^{\frac{(x^{\gamma }-at^{\gamma })}{\gamma }}-e^{- \frac{(x^{\gamma }-at^{\gamma })}{\gamma }}}{e^{\frac{(x^{\gamma }-at^{\gamma })}{\gamma }}+e^{-\frac{(x^{\gamma }-at^{\gamma })}{\gamma }}} \right) ^{-1}\right\} \times e^{i\alpha \frac{(x^{\gamma }+\eta t^{\gamma }) }{\gamma }} \end{aligned}$$

(30)

provided that $a\alpha <0$.

Category 4

On selecting $h=[2,0,1,-1]$ and $f=[1,0,1,-1]$, then Eq. (5) turns into

$$\begin{aligned} \Lambda =\frac{2e^{\xi }}{e^{\xi }-e^{-\xi }}. \end{aligned}$$

(31)

Proceeding as the outline of technique I, we reach

$$\begin{aligned}{} & {} A_{0}=\pm\, \frac{2a}{\alpha \sqrt{-\frac{2a}{\alpha }}},\quad A_{1}=\pm\, \sqrt{-\frac{2a}{\alpha }},\quad B_{1}=0,\\{} & {} s=\pm\, \frac{1}{2\alpha }\left( \begin{array}{c} -2a^{2}\alpha ^{2}+5a\alpha ^{3}-\alpha ^{4}-4a^{2}+2a\alpha \\ \pm\, \left( \begin{array}{c} 4\alpha ^{4}a^{4}-28a^{3}\alpha ^{5}+29a^{2}\alpha ^{6}-10a\alpha ^{7}+\alpha ^{8}+48a^{4}\alpha ^{2}-64a^{3}\alpha ^{3} \\ +28\alpha ^{4}a^{2}-4a\alpha ^{5}+16a^{4}-16a^{3}\alpha +4a^{2}\alpha ^{2} \end{array} \right) ^{\frac{1}{2}} \end{array} \right) ^{\frac{1}{2}}. \end{aligned}$$

Substituting the values of $A_{0},$ $A_{1},$ $B_{1}$ into Eq. (17), we have

$$\begin{aligned} V(\xi )=\frac{2a}{\alpha \sqrt{-\frac{2a}{\alpha }}}+\sqrt{-\frac{2a}{\alpha }}\times \left( \frac{2e^{\xi }}{e^{\xi }-e^{-\xi }}\right) . \end{aligned}$$

(32)

Using the Eq. (32) together with Eq. (13), we attain the singular soliton solution as

$$\begin{aligned} W_{4}(x,t)=\left\{ \frac{2a}{\alpha \sqrt{-\frac{2a}{\alpha }}}+\sqrt{-\frac{ 2a}{\alpha }}\times \left( \frac{2e^{\frac{(x^{\gamma }-at^{\gamma })}{ \gamma }}}{e^{\frac{(x^{\gamma }-at^{\gamma })}{\gamma }}-e^{-\frac{ (x^{\gamma }-at^{\gamma })}{\gamma }}}\right) \right\} \times e^{i\alpha \frac{(x^{\gamma }+\eta t^{\gamma })}{\gamma }} \end{aligned}$$

(33)

provided that $a\alpha <0$.

Category 5

On selecting $h=[1,2,1,1]$ and $f=[-1,1,-1,1]$, then Eq. (5) convert into

$$\begin{aligned} \Lambda =\frac{2e^{\xi }+e^{-\xi }}{e^{\xi }+e^{-\xi }}. \end{aligned}$$

(34)

The subsequent Sub-category are planned:

Sub-category 5.1

$$\begin{aligned}{} & {} A_{0}=\pm\, \frac{6a}{\alpha \sqrt{-\frac{2a}{\alpha }}},\quad A_{1}=\pm\, 2\sqrt{-\frac{2a}{\alpha }},\quad B_{1}=0,\\{} & {} s=\pm\, \frac{1}{2\alpha }\left( \begin{array}{c} -2a^{2}\alpha ^{2}+5a\alpha ^{3}-\alpha ^{4}-4a^{2}+2a\alpha \\ \pm\, \left( \begin{array}{c} 4\alpha ^{4}a^{4}-28a^{3}\alpha ^{5}+29a^{2}\alpha ^{6}-10a\alpha ^{7}+\alpha ^{8}+48a^{4}\alpha ^{2}-64a^{3}\alpha ^{3} \\ +28\alpha ^{4}a^{2}-4a\alpha ^{5}+16a^{4}-16a^{3}\alpha +4a^{2}\alpha ^{2} \end{array} \right) ^{\frac{1}{2}} \end{array} \right) ^{\frac{1}{2}}. \end{aligned}$$

Substituting the values of $A_{0},$ $A_{1},$ $B_{1}$ into Eq. (17), we have

$$\begin{aligned} V(\xi )=\frac{6a}{\alpha \sqrt{-\frac{2a}{\alpha }}}+2\sqrt{-\frac{2a}{ \alpha }}\times \left( \frac{2e^{\xi }+e^{-\xi }}{e^{\xi }+e^{-\xi }}\right) . \end{aligned}$$

(35)

Using the Eq. (35) together with Eq. (13), in this way, the next shape is derived as the shock wave solution

$$\begin{aligned} W_{5,1}(x,t)=\left\{ \frac{6a}{\alpha \sqrt{-\frac{2a}{\alpha }}}+2\sqrt{- \frac{2a}{\alpha }}\times \left( \frac{2e^{\frac{(x^{\gamma }-at^{\gamma })}{ \gamma }}+e^{-^{\frac{(x^{\gamma }-at^{\gamma })}{\gamma }}}}{e^{\frac{ (x^{\gamma }-at^{\gamma })}{\gamma }}+e^{-^{\frac{(x^{\gamma }-at^{\gamma }) }{\gamma }}}}\right) \right\} \times e^{i\alpha \frac{(x^{\gamma }+\eta t^{\gamma })}{\gamma }} \end{aligned}$$

(36)

provided that $a\alpha <0$.

Sub-category 5.2

$$\begin{aligned}{} & {} A_{0}=\pm\, 3\sqrt{-\frac{2a}{\alpha }},\quad A_{1}=0,\quad B_{1}=\pm\, 4\sqrt{-\frac{2a}{\alpha },}\\{} & {} s=\pm\, \frac{1}{2\alpha }\left( \begin{array}{c} -2a^{2}\alpha ^{2}+5a\alpha ^{3}-\alpha ^{4}-4a^{2}+2a\alpha \\ \pm\, \left( \begin{array}{c} 4\alpha ^{4}a^{4}-28a^{3}\alpha ^{5}+29a^{2}\alpha ^{6}-10a\alpha ^{7}+\alpha ^{8}+48a^{4}\alpha ^{2}-64a^{3}\alpha ^{3} \\ +28\alpha ^{4}a^{2}-4a\alpha ^{5}+16a^{4}-16a^{3}\alpha +4a^{2}\alpha ^{2} \end{array} \right) ^{\frac{1}{2}} \end{array} \right) ^{\frac{1}{2}}. \end{aligned}$$

Inserting these values in Eq. (17), yields

$$\begin{aligned} V(\xi )=3\sqrt{-\frac{2a}{\alpha }}+4\sqrt{-\frac{2a}{\alpha }}\times \left( \frac{2e^{\xi }+e^{-\xi }}{e^{\xi }+e^{-\xi }}\right) ^{-1}. \end{aligned}$$

(37)

Accordingly, we get the shock wave solution as

$$\begin{aligned} W_{5,2}(x,t)=\left\{ 3\sqrt{-\frac{2a}{\alpha }}+4\sqrt{-\frac{2a}{\alpha }} \times \left( \frac{2e^{\frac{(x^{\gamma }-at^{\gamma })}{\gamma }}+e^{- \frac{(x^{\gamma }-at^{\gamma })}{\gamma }}}{e^{\frac{(x^{\gamma }-at^{\gamma })}{\gamma }}+e^{-\frac{(x^{\gamma }-at^{\gamma })}{\gamma }}} \right) ^{-1}\right\} \times e^{i\alpha \frac{(x^{\gamma }+\eta t^{\gamma }) }{\gamma }} \end{aligned}$$

(38)

provided that $a\alpha <0$.

Category 6

Considering $h=[i,-i,1,1]$ and $f=[i,-i,i,-i]$, from Eq. (5) we accomplished

$$\begin{aligned} \Lambda =\frac{ie^{i\xi }-ie^{-i\xi }}{e^{i\xi }+e^{-i\xi }}. \end{aligned}$$

(39)

Sub-category 6.1

$$\begin{aligned}{} & {} A_{0}=0,\quad A_{1}=B_{1}=\pm\, \sqrt{-\frac{2a}{\alpha }},\\{} & {} s=\pm\, \frac{1}{2\alpha }\left( \begin{array}{c} -2a^{2}\alpha ^{2}+5a\alpha ^{3}-\alpha ^{4}-8a^{2}+4a\alpha \\ \pm\, \left( \begin{array}{c} 4\alpha ^{4}a^{4}-28a^{3}\alpha ^{5}+29a^{2}\alpha ^{6}-10a\alpha ^{7}+\alpha ^{8}+96a^{4}\alpha ^{2}-128a^{3}\alpha ^{3} \\ +56\alpha ^{4}a^{2}-8a\alpha ^{5}+64a^{4}-64a^{3}\alpha +16a^{2}\alpha ^{2} \end{array} \right) ^{\frac{1}{2}} \end{array} \right) ^{\frac{1}{2}}. \end{aligned}$$

Substituting the values of $A_{0},$ $A_{1},$ $B_{1}$ into Eq. (17), we have

$$\begin{aligned} V(\xi )=\sqrt{-\frac{2a}{\alpha }}\times \left( \frac{ie^{i\xi }-ie^{-i\xi } }{e^{i\xi }+e^{-i\xi }}\right) +\sqrt{-\frac{2a}{\alpha }}\times \left( \frac{ie^{i\xi }-ie^{-i\xi }}{e^{i\xi }+e^{-i\xi }}\right) ^{-1}. \end{aligned}$$

(40)

Using the Eq. (40) together with Eq. (13), then, we discover the singular periodic wave solution as

$$\begin{aligned} W_{6,1}(x,t)=\left\{ \begin{array}{c} \sqrt{-\frac{2a}{\alpha }}\times \left( \frac{ie^{i\frac{(x^{\gamma }-at^{\gamma })}{\gamma }}-ie^{-i\frac{(x^{\gamma }-at^{\gamma })}{\gamma }} }{e^{i\frac{(x^{\gamma }-at^{\gamma })}{\gamma }}+e^{-i\frac{(x^{\gamma }-at^{\gamma })}{\gamma }}}\right) \\ +\sqrt{-\frac{2a}{\alpha }}\times \left( \frac{ie^{i\frac{(x^{\gamma }-at^{\gamma })}{\gamma }}-ie^{-i\frac{(x^{\gamma }-at^{\gamma })}{\gamma }} }{e^{i\frac{(x^{\gamma }-at^{\gamma })}{\gamma }}+e^{-i\frac{(x^{\gamma }-at^{\gamma })}{\gamma }}}\right) ^{-1} \end{array} \right\} \times e^{i\alpha \frac{(x^{\gamma }+\eta t^{\gamma })}{\gamma }} \end{aligned}$$

(41)

provided that $a\alpha <0$.

Sub-category 6.2

$$\begin{aligned}{} & {} A_{0}=A_{1}=0,\quad B_{1}=\pm\, \sqrt{-\frac{2a}{\alpha }},\\{} & {} s=\pm\, \frac{1}{2\alpha }\left( \begin{array}{c} -2a^{2}\alpha ^{2}+5a\alpha ^{3}-\alpha ^{4}+4a^{2}-2a\alpha \\ \pm\, \left( \begin{array}{c} 4\alpha ^{4}a^{4}-28a^{3}\alpha ^{5}+29a^{2}\alpha ^{6}-10a\alpha ^{7}+\alpha ^{8}-48a^{4}\alpha ^{2}+64a^{3}\alpha ^{3} \\ -28\alpha ^{4}a^{2}+4a\alpha ^{5}+16a^{4}-16a^{3}\alpha +4a^{2}\alpha ^{2} \end{array} \right) ^{\frac{1}{2}} \end{array} \right) ^{\frac{1}{2}}. \end{aligned}$$

Inserting the values of $A_{0},$ $A_{1},$ $B_{1}$ into Eq. (17), we have

$$\begin{aligned} V(\xi )=\sqrt{-\frac{2a}{\alpha }}\times \left( \frac{ie^{i\xi }-ie^{-i\xi } }{e^{i\xi }+e^{-i\xi }}\right) ^{-1}. \end{aligned}$$

(42)

Using the Eq. (40) together with Eq. (13), we attain the singular periodic wave solution as

$$\begin{aligned} W_{6,2}(x,t)=\left\{ \sqrt{-\frac{2a}{\alpha }}\times \left( \frac{ie^{i \frac{(x^{\gamma }-at^{\gamma })}{\gamma }}-ie^{-i\frac{(x^{\gamma }-at^{\gamma })}{\gamma }}}{e^{i\frac{(x^{\gamma }-at^{\gamma })}{\gamma } }+e^{-i\frac{(x^{\gamma }-at^{\gamma })}{\gamma }}}\right) ^{-1}\right\} \times e^{i\alpha \frac{(x^{\gamma }+\eta t^{\gamma })}{\gamma }} \end{aligned}$$

(43)

provided that $a\alpha <0$.

Sub-category 6.3

$$\begin{aligned}{} & {} A_{0}=B_{1}=0,\quad A_{1}=\pm\, \sqrt{-\frac{2a}{\alpha }},\\{} & {} s=\pm\, \frac{1}{2\alpha }\left( \begin{array}{c} -2a^{2}\alpha ^{2}+5a\alpha ^{3}-\alpha ^{4}+4a^{2}-2a\alpha \\ \pm\, \left( \begin{array}{c} 4\alpha ^{4}a^{4}-28a^{3}\alpha ^{5}+29a^{2}\alpha ^{6}-10a\alpha ^{7}+\alpha ^{8}-48a^{4}\alpha ^{2}+64a^{3}\alpha ^{3} \\ -28\alpha ^{4}a^{2}+4a\alpha ^{5}+16a^{4}-16a^{3}\alpha +4a^{2}\alpha ^{2} \end{array} \right) ^{\frac{1}{2}} \end{array} \right) ^{\frac{1}{2}}. \end{aligned}$$

Substituting the values of $A_{0},$ $A_{1},$ $B_{1}$ into Eq. (17), we have

$$\begin{aligned} V(\xi )=\sqrt{-\frac{2a}{\alpha }}\times \left( \frac{ie^{i\xi }-ie^{-i\xi } }{e^{i\xi }+e^{-i\xi }}\right) . \end{aligned}$$

(44)

By use of Eq. (44) together with Eq. (13), we reach the singular periodic wave solution as

$$\begin{aligned} W_{6,3}(x,t)=\left\{ \sqrt{-\frac{2a}{\alpha }}\times \left( \frac{ie^{i \frac{(x^{\gamma }-at^{\gamma })}{\gamma }}-ie^{-i\frac{(x^{\gamma }-at^{\gamma })}{\gamma }}}{e^{i\frac{(x^{\gamma }-at^{\gamma })}{\gamma } }+e^{-i\frac{(x^{\gamma }-at^{\gamma })}{\gamma }}}\right) \right\} \times e^{i\alpha \frac{(x^{\gamma }+\eta t^{\gamma })}{\gamma }} \end{aligned}$$

(45)

provided that $a\alpha <0$.

Category 7

As long as, if it is allocated $h=[-1-i,1-i,-1,1]$ and $f=[i,-i,i,-i]$, from Eq. (5) we establish

$$\begin{aligned} \Lambda =\frac{-(1+i)e^{i\xi }+(1-i)e^{-i\xi }}{-e^{i\xi }+e^{-i\xi }} \end{aligned}$$

(46)

The subsequent Sub-category are planned:

Sub-category 7.1

$$\begin{aligned}{} & {} A_{0}=\pm\, \frac{2a}{\alpha \sqrt{-\frac{2a}{\alpha }}},\quad A_{1}=\pm\, \sqrt{-\frac{2a}{\alpha }},\quad B_{1}=0,\\{} & {} s=\pm\, \frac{1}{2\alpha }\left( \begin{array}{c} -2a^{2}\alpha ^{2}+5a\alpha ^{3}-\alpha ^{4}+4a^{2}-2a\alpha \\ \pm\, \left( \begin{array}{c} 4\alpha ^{4}a^{4}-28a^{3}\alpha ^{5}+29a^{2}\alpha ^{6}-10a\alpha ^{7}+\alpha ^{8}-48a^{4}\alpha ^{2}+64a^{3}\alpha ^{3} \\ -28\alpha ^{4}a^{2}+4a\alpha ^{5}+16a^{4}-16a^{3}\alpha +4a^{2}\alpha ^{2} \end{array} \right) ^{\frac{1}{2}} \end{array} \right) ^{\frac{1}{2}}. \end{aligned}$$

Plugging the values of $A_{0},$ $A_{1},$ $B_{1}$ into Eq. (17), we have

$$\begin{aligned} V(\xi )=\frac{2a}{\alpha \sqrt{-\frac{2a}{\alpha }}}+\sqrt{-\frac{2a}{\alpha }}\times \left( \frac{-(1+i)e^{i\xi }+(1-i)e^{-i\xi }}{-e^{i\xi }+e^{-i\xi }} \right) . \end{aligned}$$

(47)

By use of Eq. (47) together with Eq. (13), we get the singular periodic wave solution as

$$\begin{aligned} W_{7,1}(x,t)=\left\{ \frac{2a}{\alpha \sqrt{-\frac{2a}{\alpha }}}+\sqrt{- \frac{2a}{\alpha }}\times \left( \frac{-(1+i)e^{i\frac{(x^{\gamma }-at^{\gamma })}{\gamma }}+(1-i)e^{-i\frac{(x^{\gamma }-at^{\gamma })}{ \gamma }}}{-e^{i\frac{(x^{\gamma }-at^{\gamma })}{\gamma }}+e^{-i\frac{ (x^{\gamma }-at^{\gamma })}{\gamma }}}\right) \right\} \times e^{i\alpha \frac{(x^{\gamma }+\eta t^{\gamma })}{\gamma }} \end{aligned}$$

(48)

provided that $a\alpha <0$.

Sub-category 7.2

$$\begin{aligned}{} & {} A_{0}=\pm\, \sqrt{-\frac{2a}{\alpha }},\quad A_{1}=0,\quad B_{1}=\pm\, 2\sqrt{-\frac{2a}{\alpha }},\\{} & {} s=\pm\, \frac{1}{2\alpha }\left( \begin{array}{c} -2a^{2}\alpha ^{2}+5a\alpha ^{3}-\alpha ^{4}+4a^{2}-2a\alpha \\ \pm\, \left( \begin{array}{c} 4\alpha ^{4}a^{4}-28a^{3}\alpha ^{5}+29a^{2}\alpha ^{6}-10a\alpha ^{7}+\alpha ^{8}-48a^{4}\alpha ^{2}+64a^{3}\alpha ^{3} \\ -28\alpha ^{4}a^{2}+4a\alpha ^{5}+16a^{4}-16a^{3}\alpha +4a^{2}\alpha ^{2} \end{array} \right) ^{\frac{1}{2}} \end{array} \right) ^{\frac{1}{2}}. \end{aligned}$$

Plugging the values of $A_{0},$ $A_{1},$ $B_{1}$ into Eq. (17), we have

$$\begin{aligned} V(\xi )=\pm\, \sqrt{-\frac{2a}{\alpha }}\pm\, 2\sqrt{-\frac{2a}{\alpha }}\times \left( \frac{-(1+i)e^{i\xi }+(1-i)e^{-i\xi }}{-e^{i\xi }+e^{-i\xi }}\right) ^{-1}. \end{aligned}$$

(49)

By using Eq. (49) together with Eq. (13), then, we reach the singular periodic wave solution as

$$\begin{aligned} W_{7,2}(x,t)= & {} \left\{ \pm\, \sqrt{-\frac{2a}{\alpha }}\pm\, 2\sqrt{-\frac{2a}{ \alpha }}\times \left( \frac{-(1+i)e^{i\frac{(x^{\gamma }-at^{\gamma })}{ \gamma }}+(1-i)e^{-i\frac{(x^{\gamma }-at^{\gamma })}{\gamma }}}{-e^{i\frac{ (x^{\gamma }-at^{\gamma })}{\gamma }}+e^{-i\frac{(x^{\gamma }-at^{\gamma })}{ \gamma }}}\right) ^{-1}\right\} \nonumber \\{} & {} \times e^{i\alpha \frac{(x^{\gamma }+\eta t^{\gamma })}{\gamma }} \end{aligned}$$

(50)

provided that $a\alpha <0$.

Category 8

For $h=[2-i,2+i,1,1]$ and $f=[i,-i,i,-i]$, then Eq. (5) converts into

$$\begin{aligned} \Lambda =\frac{(2-i)e^{i\xi }+(2+i)e^{-i\xi }}{e^{i\xi }+e^{-i\xi }}. \end{aligned}$$

(51)

The next Sub-category are planned:

Sub-category 8.1

$$\begin{aligned}{} & {} A_{0}=\pm\, \frac{4a}{\alpha \sqrt{-\frac{2a}{\alpha }}},\quad A_{1}=\pm\, \sqrt{-\frac{2a}{\alpha }},\quad B_{1}=0,\\{} & {} s=\pm\, \frac{1}{2\alpha }\left( \begin{array}{c} -2a^{2}\alpha ^{2}+5a\alpha ^{3}-\alpha ^{4}+4a^{2}-2a\alpha \\ \pm\, \left( \begin{array}{c} 4\alpha ^{4}a^{4}-28a^{3}\alpha ^{5}+29a^{2}\alpha ^{6}-10a\alpha ^{7}+\alpha ^{8}-48a^{4}\alpha ^{2}+64a^{3}\alpha ^{3} \\ -28\alpha ^{4}a^{2}+4a\alpha ^{5}+16a^{4}-16a^{3}\alpha +4a^{2}\alpha ^{2} \end{array} \right) ^{\frac{1}{2}} \end{array} \right) ^{\frac{1}{2}}. \end{aligned}$$

Inserting the values of $A_{0},$ $A_{1},$ $B_{1}$ into Eq. (17), we have

$$\begin{aligned} V(\xi )=\frac{4a}{\alpha \sqrt{-\frac{2a}{\alpha }}}+\sqrt{-\frac{2a}{\alpha }}\times \left( \frac{(2-i)e^{i\xi }+(2+i)e^{-i\xi }}{e^{i\xi }+e^{-i\xi }} \right) . \end{aligned}$$

(52)

Using Eq. (52) together with Eq. (13), we attain the singular periodic wave solution as

$$\begin{aligned} W_{8,1}(x,t)=\left\{ \frac{4a}{\alpha \sqrt{-\frac{2a}{\alpha }}}+\sqrt{- \frac{2a}{\alpha }}\times \left( \frac{(2-i)e^{i\frac{(x^{\gamma }-at^{\gamma })}{\gamma }}+(2+i)e^{-i\frac{(x^{\gamma }-at^{\gamma })}{ \gamma }}}{e^{i\frac{(x^{\gamma }-at^{\gamma })}{\gamma }}+e^{-i\frac{ (x^{\gamma }-at^{\gamma })}{\gamma }}}\right) \right\} \times e^{i\alpha \frac{(x^{\gamma }+\eta t^{\gamma })}{\gamma }} \end{aligned}$$

(53)

provided that $a\alpha <0$.

Sub-category 8.2

$$\begin{aligned}{} & {} A_{0}=\pm\, 2\sqrt{-\frac{2a}{\alpha }},\quad A_{1}=0,\quad B_{1}=\pm\, 5\sqrt{-\frac{2a}{\alpha }},\\{} & {} s=\pm\, \frac{1}{2\alpha }\left( \begin{array}{c} -2a^{2}\alpha ^{2}+5a\alpha ^{3}-\alpha ^{4}+4a^{2}-2a\alpha \\ \pm\, \left( \begin{array}{c} 4\alpha ^{4}a^{4}-28a^{3}\alpha ^{5}+29a^{2}\alpha ^{6}-10a\alpha ^{7}+\alpha ^{8}-48a^{4}\alpha ^{2}+64a^{3}\alpha ^{3} \\ -28\alpha ^{4}a^{2}+4a\alpha ^{5}+16a^{4}-16a^{3}\alpha +4a^{2}\alpha ^{2} \end{array} \right) ^{\frac{1}{2}} \end{array} \right) ^{\frac{1}{2}}. \end{aligned}$$

Substituting the values of $A_{0},$ $A_{1},B_{1}$ into Eq. (17), we have

$$\begin{aligned} V(\xi )=2\sqrt{-\frac{2a}{\alpha }}+5\sqrt{-\frac{2a}{\alpha }}\times \left( \frac{(2-i)e^{i\xi }+(2+i)e^{-i\xi }}{e^{i\xi }+e^{-i\xi }}\right) ^{-1}. \end{aligned}$$

(54)

By use of Eq. (54) together with Eq. (13), then, we obtain the singular periodic wave solution as

$$\begin{aligned} W_{8,2}(x,t)=\left\{ 2\sqrt{-\frac{2a}{\alpha }}+5\sqrt{-\frac{2a}{\alpha }} \times \left( \frac{(2-i)e^{i\frac{(x^{\gamma }-at^{\gamma })}{\gamma } }+(2+i)e^{-i\frac{(x^{\gamma }-at^{\gamma })}{\gamma }}}{e^{i\frac{ (x^{\gamma }-at^{\gamma })}{\gamma }}+e^{-i\frac{(x^{\gamma }-at^{\gamma })}{ \gamma }}}\right) ^{-1}\right\} \times e^{i\alpha \frac{(x^{\gamma }+\eta t^{\gamma })}{\gamma }} \end{aligned}$$

(55)

provided that $a\alpha <0$.

Category 9

If we take $h=[2-i,-2-i,1,-1]$ and $f=[-i,i,-i,i]$, from Eq. (5), we attain

$$\begin{aligned} \Lambda =\frac{(2-i)e^{-i\xi }-(2+i)e^{i\xi }}{e^{-i\xi }-e^{i\xi }}. \end{aligned}$$

(56)

We get

Sub-category 9.1

$$\begin{aligned}{} & {} A_{0}=\pm\, \frac{4a}{\alpha \sqrt{-\frac{2a}{\alpha }}},\quad A_{1}=\pm\, \sqrt{-\frac{2a}{\alpha }},\quad B_{1}=0,\\{} & {} s=\pm\, \frac{1}{2\alpha }\left( \begin{array}{c} -2a^{2}\alpha ^{2}+5a\alpha ^{3}-\alpha ^{4}+4a^{2}-2a\alpha \\ \pm\, \left( \begin{array}{c} 4\alpha ^{4}a^{4}-28a^{3}\alpha ^{5}+29a^{2}\alpha ^{6}-10a\alpha ^{7}+\alpha ^{8}-48a^{4}\alpha ^{2}+64a^{3}\alpha ^{3} \\ -28\alpha ^{4}a^{2}+4a\alpha ^{5}+16a^{4}-16a^{3}\alpha +4a^{2}\alpha ^{2} \end{array} \right) ^{\frac{1}{2}} \end{array} \right) ^{\frac{1}{2}}. \end{aligned}$$

Substituting the values of $A_{0},$ $A_{1},$ $B_{1}$ into Eq. (17), we have

$$\begin{aligned} V(\xi )=\frac{4a}{\alpha \sqrt{-\frac{2a}{\alpha }}}+\sqrt{-\frac{2a}{\alpha }}\times \left( \frac{(2-i)e^{-i\xi }-(2+i)e^{i\xi }}{e^{-i\xi }-e^{i\xi }} \right) . \end{aligned}$$

(57)

Using Eq. (57) together with Eq. (13), we get the singular periodic wave solution as

$$\begin{aligned} W_{9,1}(x,t)=\left\{ \frac{4a}{\alpha \sqrt{-\frac{2a}{\alpha }}}+\sqrt{- \frac{2a}{\alpha }}\times \left( \frac{(2-i)e^{-i\frac{(x^{\gamma }-at^{\gamma })}{\gamma }}-(2+i)e^{i\frac{(x^{\gamma }-at^{\gamma })}{\gamma }}}{e^{-i\frac{(x^{\gamma }-at^{\gamma })}{\gamma }}-e^{i\frac{(x^{\gamma }-at^{\gamma })}{\gamma }}}\right) \right\} \times e^{i\alpha \frac{ (x^{\gamma }+\eta t^{\gamma })}{\gamma }} \end{aligned}$$

(58)

provided that $a\alpha <0$.

Sub-category 9.2

$$\begin{aligned}{} & {} A_{0}=\pm\, 2\sqrt{-\frac{2a}{\alpha }},\quad A_{1}=0,\quad B_{1}=\pm\, 5\sqrt{-\frac{2a}{\alpha }},\\{} & {} s=\pm\, \frac{1}{2\alpha }\left( \begin{array}{c} -2a^{2}\alpha ^{2}+5a\alpha ^{3}-\alpha ^{4}+4a^{2}-2a\alpha \\ \pm\, \left( \begin{array}{c} 4\alpha ^{4}a^{4}-28a^{3}\alpha ^{5}+29a^{2}\alpha ^{6}-10a\alpha ^{7}+\alpha ^{8}-48a^{4}\alpha ^{2}+64a^{3}\alpha ^{3} \\ -28\alpha ^{4}a^{2}+4a\alpha ^{5}+16a^{4}-16a^{3}\alpha +4a^{2}\alpha ^{2} \end{array} \right) ^{\frac{1}{2}} \end{array} \right) ^{\frac{1}{2}}. \end{aligned}$$

Substituting the values of $A_{0},$ $A_{1},$ $B_{1}$ into Eq. (17), we have

$$\begin{aligned} V(\xi )=2\sqrt{-\frac{2a}{\alpha }}+5\sqrt{-\frac{2a}{\alpha }}\times \left( \frac{(2-i)e^{-i\xi }-(2+i)e^{i\xi }}{e^{-i\xi }-e^{i\xi }}\right) . \end{aligned}$$

(59)

By use of Eq. (59) together with Eq. (13), then, we obtain the singular periodic wave solution as

$$\begin{aligned} W_{9,2}(x,t)=\left\{ 2\sqrt{-\frac{2a}{\alpha }}+5\sqrt{-\frac{2a}{\alpha }} \times \left( \frac{(2-i)e^{-i\frac{(x^{\gamma }-at^{\gamma })}{\gamma } }-(2+i)e^{i\frac{(x^{\gamma }-at^{\gamma })}{\gamma }}}{e^{-i\frac{ (x^{\gamma }-at^{\gamma })}{\gamma }}-e^{i\frac{(x^{\gamma }-at^{\gamma })}{ \gamma }}}\right) ^{-1}\right\} \times e^{i\alpha \frac{(x^{\gamma }+\eta t^{\gamma })}{\gamma }} \end{aligned}$$

(60)

provided that $a\alpha <0$.

Category 10

When we take $h=[-2,-1,1,1]$ and $f=[0,1,0,1]$, then Eq. (5) changes into

$$\begin{aligned} \Lambda =\frac{-2-e^{\xi }}{1+e^{\xi }}. \end{aligned}$$

(61)

We obtain

Sub-category 10.1

$$\begin{aligned}{} & {} A_{0}=\pm\, \frac{3}{2}\sqrt{-\frac{2a}{\alpha }},\quad A_{1}=\pm\, \sqrt{- \frac{2a}{\alpha }},\quad B_{1}=0,\\{} & {} s=\pm\, \frac{\sqrt{2}}{4\alpha }\left( \begin{array}{c} -4a^{2}\alpha ^{2}+10a\alpha ^{3}-2\alpha ^{4}-2a^{2}+a\alpha \\ +\left( \begin{array}{c} 16\alpha ^{4}a^{4}-112a^{3}\alpha ^{5}+116a^{2}\alpha ^{6}-40a\alpha ^{7}+4\alpha ^{8} \\ +48a^{4}\alpha ^{2}-64a^{3}\alpha ^{3}+28\alpha ^{4}a^{2}-4a\alpha ^{5}+4a^{4}-4a^{3}\alpha +a^{2}\alpha ^{2} \end{array} \right) ^{\frac{1}{2}} \end{array} \right) ^{\frac{1}{2}}. \end{aligned}$$

Substituting the values of $A_{0},$ $A_{1},$ $B_{1}$ into Eq. (17), we have

$$\begin{aligned} V(\xi )=\frac{3}{2}\sqrt{-\frac{2a}{\alpha }}+\sqrt{-\frac{2a}{\alpha }} \times \left( \frac{-2-e^{\xi }}{1+e^{\xi }}\right) . \end{aligned}$$

(62)

Using Eq. (62) together with Eq. (13), then, the exponential function solution can be expressed as

$$\begin{aligned} W_{10,1}(x,t)=\left\{ \frac{3}{2}\sqrt{-\frac{2a}{\alpha }}+\sqrt{-\frac{2a}{ \alpha }}\times \left( \frac{-2-e^{\frac{(x^{\gamma }-at^{\gamma })}{\gamma } }}{1+e^{\frac{(x^{\gamma }-at^{\gamma })}{\gamma }}}\right) \right\} \times e^{i\alpha \frac{(x^{\gamma }+\eta t^{\gamma })}{\gamma }} \end{aligned}$$

(63)

provided that $a\alpha <0$.

Sub-category 10.2

$$\begin{aligned}{} & {} A_{0}=\pm\, \frac{3}{2}\sqrt{-\frac{2a}{\alpha }},\quad A_{1}=0,\quad B_{1}=\pm\, 2\sqrt{-\frac{2a}{\alpha }},\\{} & {} s=\pm\, \frac{\sqrt{2}}{4\alpha }\left( \begin{array}{c} -4a^{2}\alpha ^{2}+10a\alpha ^{3}-2\alpha ^{4}-2a^{2}+a\alpha \\ +\left( \begin{array}{c} 16\alpha ^{4}a^{4}-112a^{3}\alpha ^{5}+116a^{2}\alpha ^{6}-40a\alpha ^{7}+4\alpha ^{8} \\ +48a^{4}\alpha ^{2}-64a^{3}\alpha ^{3}+28\alpha ^{4}a^{2}-4a\alpha ^{5}+4a^{4}-4a^{3}\alpha +a^{2}\alpha ^{2} \end{array} \right) ^{\frac{1}{2}} \end{array} \right) ^{\frac{1}{2}}. \end{aligned}$$

Plugging the values of $A_{0},$ $A_{1},$ $B_{1}$ into Eq. (17), we have

$$\begin{aligned} V(\xi )=\pm\, \frac{3}{2}\sqrt{-\frac{2a}{\alpha }}\pm\, \sqrt{-\frac{2a}{\alpha }}\times \left( \frac{-2-e^{\xi }}{1+e^{\xi }}\right) ^{-1}. \end{aligned}$$

(64)

By using Eq. (62) together with Eq. (13), the exponential function solution is obtained as

$$\begin{aligned} W_{10,2}(x,t)=\left\{ \pm\, \frac{3}{2}\sqrt{-\frac{2a}{\alpha }}\pm\, \sqrt{- \frac{2a}{\alpha }}\times \left( \frac{-2-e^{\frac{(x^{\gamma }-at^{\gamma }) }{\gamma }}}{1+e^{\frac{(x^{\gamma }-at^{\gamma })}{\gamma }}}\right) ^{-1}\right\} \times e^{i\alpha \frac{(x^{\gamma }+\eta t^{\gamma })}{\gamma }} \end{aligned}$$

(65)

provided that $a\alpha <0$.

4.2 Main outcomes of solving model Eq. (12) using technique II

Equation(16) can be written as

$$\begin{aligned}{} & {} a(a-s)(a+s)(2a-\alpha )V_{\xi \xi }\nonumber \\{} & {} \quad +(-5\alpha as^{2}+2s^{4}+2s^{2}a^{2}+s^{2}\alpha ^{2}+\alpha a^{3})\alpha ^{2}V+(a-s)(s+a)(2a-\alpha )\alpha V^{3}=0\text {.} \end{aligned}$$

(66)

Following Eq. (10), it is effortless to deduce from Eq. (66) an expression for the function $\Gamma (V)$

$$\begin{aligned}{} & {} a(a-s)(s+a)(2a-\alpha )\frac{1}{2}(\Gamma ^{2})^{\prime }\nonumber \\{} & {} \quad +(-5\alpha as^{2}+2s^{4}+2s^{2}a^{2}+s^{2}\alpha ^{2}+\alpha a^{3})\alpha ^{2}V+(s+a)(a-s)(2a-\alpha )\alpha V^{3}=0\text {.} \end{aligned}$$

(67)

After integrating Eq. (67) concerning the constant of integration to zero, products

$$\begin{aligned} \Gamma (V)= & {} \sqrt{-\frac{(a^{3}\alpha +2a^{2}s^{2}-5a\alpha s^{2}+\alpha ^{2}s^{2}+2s^{4})\alpha ^{2}}{a(s+a)(a-s)(2a-\alpha )}}\nonumber \\{} & {} V\sqrt{1+\frac{ (s+a)(a-s)(2a-\alpha )V^{2}}{2\alpha (a^{3}\alpha +2a^{2}s^{2}-5a\alpha s^{2}+\alpha ^{2}s^{2}+2s^{4})}}. \end{aligned}$$

(68)

Then, making the change of variables

$$\begin{aligned} \Upsilon (\xi )=\frac{(s+a)(a-s)(2a-\alpha )}{2\alpha (a^{3}\alpha +2a^{2}s^{2}-5a\alpha s^{2}+\alpha ^{2}s^{2}+2s^{4})}V^{2}, \end{aligned}$$

and using the transformation $V_{\xi }=\Gamma (V)$, we have

$$\begin{aligned} V_{\xi }=\sqrt{-\frac{(a^{3}\alpha +2a^{2}s^{2}-5a\alpha s^{2}+\alpha ^{2}s^{2}+2s^{4})\alpha ^{2}}{a(a-s)(a+s)(2a-\alpha )}}V\sqrt{1+\Upsilon (\xi )}. \end{aligned}$$

(69)

Integration of Eq. (69) leads to

$$\begin{aligned} V(\xi )= & {} \sqrt{\frac{2\alpha (a^{3}\alpha +2a^{2}s^{2}-5a\alpha s^{2}+\alpha ^{2}s^{2}+2s^{4})}{(\alpha -2a)(a^{2}-s^{2})}} \\{} & {} \times \sec h\left[ \sqrt{\frac{(a^{3}\alpha +2a^{2}s^{2}-5a\alpha s^{2}+\alpha ^{2}s^{2}+2s^{4})\alpha ^{2}}{a(\alpha -2a)(\alpha ^{2}-s^{2})}} (\xi _{0}+\xi )\right] ^{2}, \nonumber \end{aligned}$$

(70)

and

$$\begin{aligned} V(\xi )= & {} \sqrt{-\frac{2\alpha (a^{3}\alpha +2a^{2}s^{2}-5a\alpha s^{2}+\alpha ^{2}s^{2}+2s^{4})}{(\alpha -2a)(a^{2}-s^{2})}} \\{} & {} \times \csc h\left[ \sqrt{\frac{(a^{3}\alpha +2a^{2}s^{2}-5a\alpha s^{2}+\alpha ^{2}s^{2}+2s^{4})\alpha ^{2}}{a(\alpha -2a)(\alpha ^{2}-s^{2})}} (\xi _{0}+\xi )\right] ^{2}, \nonumber \end{aligned}$$

(71)

where $\xi _{0}$ is a constant of integration.

Thus, we get bright soliton solutions and singular soliton solutions for the FDMNLSE, respectively, as follows

$$\begin{aligned} W_{11}^{\pm\, }(x,t)= & {} \sqrt{\frac{2\alpha (a^{3}\alpha +2a^{2}s^{2}-5a\alpha s^{2}+\alpha ^{2}s^{2}+2s^{4})}{(\alpha -2a)(a^{2}-s^{2})}} \\{} & {} \times \sec h\left[ \sqrt{\frac{(a^{3}\alpha +2a^{2}s^{2}-5a\alpha s^{2}+\alpha ^{2}s^{2}+2s^{4})\alpha ^{2}}{a(\alpha -2a)(\alpha ^{2}-s^{2})}} \left(\xi _{0}+\frac{(x^{\gamma }-at^{\gamma })}{\gamma }\right)\right] ^{2}\nonumber \\{} & {} \times e^{i\alpha \frac{(x^{\gamma }+\eta t^{\gamma })}{\gamma }}, \nonumber \end{aligned}$$

(72)

and

$$\begin{aligned} W_{12}^{\pm\, }(x,t)= & {} \sqrt{-\frac{2\alpha (a^{3}\alpha +2a^{2}s^{2}-5a\alpha s^{2}+\alpha ^{2}s^{2}+2s^{4})}{(\alpha -2a)(a^{2}-s^{2})}} \\{} & {} \times \csc h\left[ \sqrt{\frac{(a^{3}\alpha +2a^{2}s^{2}-5a\alpha s^{2}+\alpha ^{2}s^{2}+2s^{4})\alpha ^{2}}{a(\alpha -2a)(\alpha ^{2}-s^{2})}} \left(\xi _{0}+\frac{(x^{\gamma }-at^{\gamma })}{\gamma }\right)\right] ^{2}\nonumber \\{} & {} \times e^{i\alpha \frac{(x^{\gamma }+\eta t^{\gamma })}{\gamma }}, \nonumber \end{aligned}$$

(73)

where the constraint relation between the soliton parameters is given by $\alpha ^{2}(a^{3}\alpha +2a^{2}s^{2}-5a\alpha s^{2}+\alpha ^{2}s^{2}+2\,s^{4})\times a(\alpha -2a)(\alpha ^{2}-s^{2})>0.$

It is easy to see that solutions Eqs.(72) and (73) can reduce to the following periodic singular waves:

$$\begin{aligned} W_{13}^{\pm\, }(x,t)= & {} \sqrt{\frac{2\alpha (a^{3}\alpha +2a^{2}s^{2}-5a\alpha s^{2}+\alpha ^{2}s^{2}+2s^{4})}{(\alpha -2a)(a^{2}-s^{2})}} \\{} & {} \times \sec \left[ \sqrt{\frac{(a^{3}\alpha +2a^{2}s^{2}-5a\alpha s^{2}+\alpha ^{2}s^{2}+2s^{4})\alpha ^{2}}{a(2a-\alpha )(\alpha ^{2}-s^{2})}} \left(\xi _{0}+\frac{(x^{\gamma }-at^{\gamma })}{\gamma }\right)\right] ^{2}\nonumber \\{} & {} \times e^{i\alpha \frac{(x^{\gamma }+\eta t^{\gamma })}{\gamma }} \nonumber \end{aligned}$$

(74)

and

$$\begin{aligned} W_{14}^{\pm\, }(x,t)= & {} \sqrt{\frac{2\alpha (a^{3}\alpha +2a^{2}s^{2}-5a\alpha s^{2}+\alpha ^{2}s^{2}+2s^{4})}{(\alpha -2a)(a^{2}-s^{2})}} \\{} & {} \times \csc \left[ \sqrt{\frac{(a^{3}\alpha +2a^{2}s^{2}-5a\alpha s^{2}+\alpha ^{2}s^{2}+2s^{4})\alpha ^{2}}{a(2a-\alpha )(\alpha ^{2}-s^{2})}} \left(\xi _{0}+\frac{(x^{\gamma }-at^{\gamma })}{\gamma }\right)\right] ^{2}\nonumber \\{} & {} \times e^{i\alpha \frac{(x^{\gamma }+\eta t^{\gamma })}{\gamma }} \nonumber \end{aligned}$$

(75)

where the constraint relation between the soliton parameters is given by $a(\alpha -2a)(\alpha ^{2}-s^{2})\times (a^{3}\alpha +2a^{2}s^{2}-5a\alpha s^{2}+\alpha ^{2}s^{2}+2\,s^{4})\alpha ^{2}<0$.

5 Physical interpretations and concluding remarks

In this examination, we studied the FDMNLSE with cubic law nonlinearity, which interprets the propagation of two distinct waves moving simultaneously with the interaction of embedded phase speed. The significant achievements of the paper were determined via two efficient procedures based on the GERFM and FVM.

Up till now, many different effective methods have been used by investigators to discover analytical solutions for this prototype. The authors of Lu et al. (2019), and Raza et al. (2020), which are related to our model, obtained the soliton solution by using the $\exp (-\Phi (\xi ))$-expansion method. Suppose one pays attention to our study. In that case, many new solutions with physical properties, such as shock wave solutions, singular soliton solutions, singular periodic wave solutions, exponential function solutions, and bright optical soliton solutions are revealed. In this context, exponential function solution Eqs. (20), (63), and (65), singular soliton solution Eqs.(23), (25), (33), and (73), shock wave solution Eqs.(28), ( 30), (36), and (38), singular periodic wave solution Eqs.(40), (43), (45), (48), (50), (52), (55), (58), (60), (74), and (75), bright soliton solutions Eq. (72) were obtained. Also, we offered the dynamic behavior of analytical solitons in the shape of graphic miniatures for the accepted solutions by selecting an appropriate choice of variables. These graphs enable researchers in this field to have a better physical interpretation of this fractional-order complex model. Furthermore, the strategies used in this article are specific, efficacious, and productive approaches in seeking the exact solitary wave solutions for many fractional-order NLPDEs. Moreover, these accepted solutions will be applicable to study analytically other fractional order NLPDEs in mathematical physics, plasma physics, applied sciences, nonlinear dynamics, and engineering. Also, the acquired outcomes are beneficial in ocean engineering to understand the investigation of wave propagation and are paramount for the reality of numerical and practical results. The obtained solutions are entirely novel for the FDMNLSE that are not reported by the other studies. We confirmed obtained outcomes with the help of Maple by putting them back into the original equation. In the future, we will probe the more exotic exact solution form for the FDMNLSE containing perturbation terms.

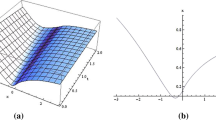
Figure 1. The 3d plots for the solution $\left| W_{1}(x,t)\right|$ in Eq. (20) when $\gamma =0.5,$ $\gamma =0.75,$ $\gamma =0.99,$ respectively, and $a=-1,$ $\alpha =1,$ $\eta =1,$ $\xi =\frac{x^{\gamma }+at^{\gamma }}{^{\gamma }}.$

Figure 2. The contour plots for the solution $\left| W_{1}(x,t)\right|$ in Eq. (20) when $\gamma =0.5,$ $\gamma =0.75,$ $\gamma =0.99,$ respectively, and $a=-1,$ $\alpha =1,$ $\eta =1,$ $\xi =\frac{x^{\gamma }+at^{\gamma }}{^{\gamma }}.$

Figure 3. The density plots for the solution $\left| W_{1}(x,t)\right|$ in Eq. (20) when $\gamma =0.5,$ $\gamma =0.75,$ $\gamma =0.99,$ respectively, and $a=-1,$ $\alpha =1,$ $\eta =1,$ $\xi =\frac{x^{\gamma }+at^{\gamma }}{^{\gamma }}.$

Figure 4. The 2d plots for the solution $\left| W_{1}(x,t)\right|$ in Eq. (20) when $\gamma =0.5,$ $\gamma =0.75,$ $\gamma =0.99,$ respectively, and $a=-1,$ $\alpha =1,$ $\eta =1,$ $\xi =\frac{x^{\gamma }+at^{\gamma }}{^{\gamma }}.$

Figure 5. The 3d,  contour, density, and 2d plots for the solution $\left| W_{2,1}(x,t)\right|$ in Eq. (23) when $\gamma =0.5,$ $a=-1,$ $\alpha =1,$ $\eta =1,$ $\xi =\frac{x^{\gamma }+at^{\gamma }}{ ^{\gamma }}.$

Figure 6. The 3d,  contour, density, and 2d plots for the solution $\left| W_{3,1}(x,t)\right|$ in Eq. (28) when $\gamma =0.5,$ $a=-1,$ $\alpha =1,$ $\eta =1,$ $\xi =\frac{x^{\gamma }+at^{\gamma }}{ ^{\gamma }}.$

Figure 7. The 3d,  contour, density, and 2d plots for the solution $\left| W_{4}(x,t)\right|$ in Eq. (33) when $\gamma =0.5,$ $a=-1,$ $\alpha =1,$ $\eta =1,$ $\xi =\frac{x^{\gamma }+at^{\gamma }}{ ^{\gamma }}.$

Figure 8. The 3d,  contour, density, and 2d plots for the solution $\left| W_{5,1}(x,t)\right|$ in Eq. (36) when $\gamma =0.5,$ $a=-1,$ $\alpha =1,$ $\eta =1,$ $\xi =\frac{x^{\gamma }+at^{\gamma }}{ ^{\gamma }}.$

Figure 9. The 3d,  contour, density, and 2d plots for the solution $\left| W_{6,1}(x,t)\right|$ in Eq. (41) when $\gamma =0.5,$ $a=-1,$ $\alpha =1,$ $\eta =1,$ $\xi =\frac{x^{\gamma }+at^{\gamma }}{ ^{\gamma }}.$

Figure 10. The 3d,  contour, density, and 2d plots for the solution $\left| W_{7,1}(x,t)\right|$ in Eq. (48) when $\gamma =0.5,$ $a=-1,$ $\alpha =1,$ $\eta =1,$ $\xi =\frac{x^{\gamma }+at^{\gamma }}{ ^{\gamma }}.$

Figure 11. The 3d,  contour, density, and 2d plots for the solution $\left| W_{8,1}(x,t)\right|$ in Eq. (53) when $\gamma =0.5,$ $a=-1,$ $\alpha =1,$ $\eta =1,$ $\xi =\frac{x^{\gamma }+at^{\gamma }}{ ^{\gamma }}.$

Figure 12. The 3d,  contour, density, and 2d plots for the solution $\left| W_{10,1}(x,t)\right|$ in Eq. (63) when $\gamma =0.5,$ $a=-1,$ $\alpha =1,$ $\eta =1,$ $\xi =\frac{x^{\gamma }+at^{\gamma }}{ ^{\gamma }}.$

Figure 13. The 3d,  contour, density, and 2d plots for the solution $\left| W_{11}^{\pm\, }(x,t)\right|$ in Eq. (72) when $\gamma =0.5,$ $s=1,$ $a=2,$ $\alpha =3,$ $\eta =4,$ $\xi =\frac{x^{\gamma }+at^{\gamma }}{^{\gamma }}.$

Figure 14. The 3d,  contour, density, and 2d plots for the solution $\left| W_{12}^{\pm\, }(x,t)\right|$ in Eq. (73) when $\gamma =0.5,$ $s=1,$ $a=2,$ $\alpha =3,$ $\eta =4,$ $\xi _{0}=1,$ $\xi =\frac{ x^{\gamma }+at^{\gamma }}{^{\gamma }}.$

Figure 15. The 3d,  contour, density, and 2d plots for the solution $\left| W_{14}^{\pm\, }(x,t)\right|$ in Eq. (75) when $\gamma =0.5,$ $s=1,$ $a=2,$ $\alpha =3,$ $\eta =4,$ $\xi _{0}=1$ $\xi =\frac{ x^{\gamma }+at^{\gamma }}{^{\gamma }}.$

Fig. 1

The 3d plots for the solution $\left| W_{1}(x,t)\right|$ in Eq. (20)

Fig. 2

The contour plots for the solution $\left| W_{1}(x,t)\right|$ in Eq. (20)

Fig. 3

The density plots for the solution $\left| W_{1}(x,t)\right|$ in Eq. (20)

Fig. 4

The 2d plots for the solution $\left| W_{1}(x,t)\right|$ in Eq. (20)

Fig. 5

The 3d, contour, density, and 2d plots for the solution $\left| W_{2,1}(x,t)\right|$ in Eq. (23)

Fig. 6

The 3d, contour, density, and 2d plots for the solution $\left| W_{3,1}(x,t)\right|$ in Eq. (28)

Fig. 7

The 3d, contour, density, and 2d plots for the solution $\left| W_{4}(x,t)\right|$ in Eq. (33)

Fig. 8

The 3d, contour, density, and 2d plots for the solution $\left| W_{5,1}(x,t)\right|$ in Eq. (36)

Fig. 9

The 3d, contour, density, and 2d plots for the solution $\left| W_{6,1}(x,t)\right|$ in Eq. (41)

Fig. 10

The 3d, contour, density, and 2d plots for the solution $\left| W_{7,1}(x,t)\right|$ in Eq. (48)

Fig. 11

The 3d, contour, density, and 2d plots for the solution $\left| W_{8,1}(x,t)\right|$ in Eq. (53)

Fig. 12

The 3d, contour, density, and 2d plots for the solution $\left| W_{10,1}(x,t)\right|$ in Eq. (63)

Fig. 13

The 3d, contour, density, and 2d plots for the solution $\left| W_{11}^{\pm\, }(x,t)\right|$ in Eq. (72)

Fig. 14

The 3d, contour, density, and 2d plots for the solution $\left| W_{12}^{\pm\, }(x,t)\right|$ in Eq. (73)

Fig. 15

The 3d, contour, density, and 2d plots for the solution $\left| W_{14}^{\pm\, }(x,t)\right|$ in Eq. (75)