1 Introduction

Recently, a new family of nonlinear equations under the name “two-mode” or “dual-mode” have been established. The members of this family are nonlinear partial differential equations of second order in the time coordinate. It describes the propagations of two different nonlinear wave modes simultaneously. The KdV equation of second order in time was the first established two-mode equation [1, 2]

$$\begin{aligned}&u_{tt}-s^2 u_{xx}+\left( \frac{\partial }{\partial t}-\alpha s \frac{\partial }{\partial x}\right) u u_x\nonumber \\&\quad +\left( \frac{\partial }{\partial t}-\beta s \frac{\partial }{\partial x}\right) u_{xxx}=0, \end{aligned}$$
(1.1)

where \(u=u(x,t)\) is a field function, s the interaction phase velocity, \(\alpha \) the nonlinearity factor, and \(\beta \) the dispersive factor with \(s\ge 0\), \(|\alpha | \le 1\), \(|\beta | \le 1\), and we refer to Eq. (1.1) as the two-mode KdV equation (TMKdV). The TMKdV has been constructed as a related topic to Hirota–Satsuma model [3], which describes the interaction of two long waves with different dispersion factors and concluded that if there is no interaction between these two waves, no effect of one wave on the other, then these waves obey the KdV equations. Indeed, if \(s=0\) in (1.1) “no interaction” and integrating once with respect to the time t, we get the standard KdV equation

$$\begin{aligned} u_t+u u_x+u_{xxx}=0. \end{aligned}$$
(1.2)

Inspired by TMKdV (1.1), Korsunsky and Wazwaz [1, 4] suggested a two-mode generator learned as follows. Any nonlinear equation obeys the form

$$\begin{aligned} u_t+N(u,u_x,\ldots )+L(u_{xx},u_{xxx},\ldots )=0, \end{aligned}$$
(1.3)

where \(N,\ L\) are, respectively, the nonlinear and linear operators. Then, the two-mode version of (1.3) takes the form

$$\begin{aligned}&u_{tt}-s^{2}u_{xx}+\left( \frac{\partial }{\partial t}-\alpha s \frac{\partial }{\partial x}\right) N(u,u_{x},\ldots )\nonumber \\&\qquad +\left( \frac{\partial }{\partial t} -\beta s \frac{\partial }{\partial x}\right) L(u_{xx},u_{xxx},\ldots )=0. \end{aligned}$$
(1.4)

Consequently, some new real-valued two-mode models are established [5,6,7,8,9,10,11,12] and soliton–kink, multiple soliton–kink solutions are obtained to these models by applying simplified Hirota and tanh-expansion methods. The contributions on two-mode equations conducted in the aforementioned studies were limited to extract only solitary wave solutions restricted with some constraint conditions. Motivated by the existing literature, there was only one attempt to extend the two-mode concept on complex-valued model. In [13], a two-mode Schrödinger (TMNLS) with power Kerr law is established and both dark and singular soliton solutions are obtained. Therefore, we aim to further explore TMNLS with different types of the Kerr laws and conduct some graphical justifications.

The nonlinear Schrödinger (NLS) is a physical model that plays a key role in engineering sciences, dynamics and nonlinear optics. The general form of NLS reads [14,15,16,17]

$$\begin{aligned} i q_t+\frac{1}{2} q_{xx}+F(|q|^2) q=0, \end{aligned}$$
(1.5)

where the function F is the nonlinearity Kerr function and q is a complex-type envelope function. In this context, we consider two types of F: the square-root law when \(F(\tau )=\sqrt{\tau }\) and the dual-power law when \(F(\tau )=\tau + v \tau ^2\).

Now, by means of Eqs. (1.3) and (1.4), the generalized dual-mode Schrödinger is second order in time and has the form

$$\begin{aligned}&i\left( q_{tt}-s^2 q_{xx}\right) +\frac{1}{2}\left( \frac{\partial }{\partial t}-\beta s \frac{\partial }{\partial x} \right) \{ q_{xx}\}\nonumber \\&\qquad +\left( \frac{\partial }{\partial t}-\alpha s \frac{\partial }{\partial x} \right) \{F(|q|^2) q\}=0, \end{aligned}$$
(1.6)

The dual-mode (1.6) (DMNLS) models the spread of directional absorption or amplification of dual-wave pulses with distributed dispersion and nonlinearity and interaction phase velocity. We aim to study the dynamics of DMNLS for two types of the real-valued algebraic function F. The square-root Kerr

$$\begin{aligned}&i\left( q_{tt}-s^2 q_{xx}\right) +\frac{1}{2}\left( \frac{\partial }{\partial t}-\beta s \frac{\partial }{\partial x} \right) \{ q_{xx}\}\nonumber \\&\qquad +\left( \frac{\partial }{\partial t}-\alpha s \frac{\partial }{\partial x} \right) \{|q| q\}=0, \end{aligned}$$
(1.7)

and the dual-power Kerr

$$\begin{aligned}&i\left( q_{tt}-s^2 q_{xx}\right) +\frac{1}{2}\left( \frac{\partial }{\partial t}-\beta s \frac{\partial }{\partial x} \right) \{ q_{xx}\}\nonumber \\&\qquad +\left( \frac{\partial }{\partial t}-\alpha s \frac{\partial }{\partial x} \right) \{(|q|^2+v |q|^4)q\}=0. \end{aligned}$$
(1.8)

Equation (1.7) is used to study soliton turbulence, and Eq. (1.8) describes the interaction between Langmuir waves and electrons [18].

Fig. 1
figure 1

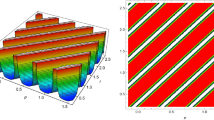
Multiplicative of the dual-waves obtained for the real part of q(x, t) (2.6) by increasing the phase velocity: \(s=0.5,\ 1,\ 2,\ 3\) respectively

Full size image

2 Dual-mode Schrödinger with square-root Kerr

The envelope function \(q=q(x,t)\) in (1.7) is of complex-valued type, so we may write q as

$$\begin{aligned} q(x,t)=e^{i \eta } p(\zeta ), \end{aligned}$$
(2.1)

where \(\eta =\lambda (x+w t)\) and \(\zeta =x- c t\). Substituting (2.1) in (1.7) and separating real and imaginary parts will lead us to a system of two differential equations with p being the dependent real-valued function and \(\zeta \) the independent variable

$$\begin{aligned} 0= & {} \lambda ^2 (2 s^2 + s \beta \lambda - w (2 w + \lambda )) p(\zeta )\nonumber \\&+\, 2 (w - s \alpha ) \lambda p^2(\zeta ) + (2 c^2 - 2 s^2 \nonumber \\&- \,2 c \lambda + w \lambda - 3 s \beta \lambda ) p''(\zeta ),\nonumber \\ 0= & {} (\lambda (4 s^2 + 4 c w + c \lambda - 2 w \lambda + 3 s \beta \lambda ) \nonumber \\&- \,4 (c + s \alpha ) p(\zeta )) p'(\zeta ) - (c + s \beta ) p'''(\zeta ). \end{aligned}$$
(2.2)

Now we seek solutions to the above system by employing two methods: the tanh-expansion and the Kudryashov expansion schemes.

2.1 Tanh-solution I

The tanh-scheme suggests the solution of (2.2) to be of the form

$$\begin{aligned} p(\zeta )=\sum _{i=0}^n a_i Y^i, \end{aligned}$$
(2.3)

where \(Y=\tanh (\mu \zeta )\) and satisfies the followings relations

$$\begin{aligned} Y'= & {} \mu (1-Y^2),\nonumber \\ Y''= & {} -2 \mu ^2 Y (1-Y^2),\nonumber \\ Y'''= & {} -2 \mu ^3 (1-Y^2)(1-3Y^2). \end{aligned}$$
(2.4)

Balancing the terms \(p^2\) and \(p''\) or \(p p'\) and \(p'''\) gives \(n=2\) in (2.3). We insert (2.3) and (2.4) in (2.2) and collect coefficients of the same power of Y. Setting each obtained coefficient to zero will produce a nonlinear algebraic system in the unknowns \(a_0,\ a_1,\ a_2,\ \lambda ,\ \mu ,\ w\) and c. By solving this algebraic system, we obtain the following outcomes

$$\begin{aligned} \alpha= & {} \beta =\pm 1,\nonumber \\ a_0= & {} 0,\ \ a_1=\ \texttt {free},\ \ a_2=-3 \mu ^2 ,\nonumber \\ c= & {} -\beta s,\ \ \lambda =-2 w,\ \ \mu =\ \texttt {free},\ \ w=\beta s. \end{aligned}$$
(2.5)

Therefore, the tanh-solution of DMNLS with square-root Kerr law (1.7) is given by

$$\begin{aligned} q(x,t)= & {} e^{-2 i s(x \pm s t)} \left( a_1 \tanh (\mu (x\pm s t))\right. \nonumber \\&\left. -3\mu ^2 \tanh ^2(\mu (x\pm s t)) \right) . \end{aligned}$$
(2.6)

Graphical analysis regarding (2.6) reveals that the increase in the phase velocity is accompanied by a clone of the dual-waves in a multiplicative manner, see Fig. 1.

Fig. 2
figure 2

Behaviors of dual-waves obtained for the real part of q(x, t) (2.14) by increasing the phase velocity: \(s=1,\ 2,\ 3\), respectively

Full size image

2.2 Kudryashov solution I

We aim to apply Kudryashov expansion technique [19, 20] to study more possible solutions to (1.7). This scheme suggests the solution of (2.2) as a polynomial of the variable Y

$$\begin{aligned} p(\zeta )=\sum _{i=0}^n A_i Y^i,\ \ Y=Y(\zeta ). \end{aligned}$$
(2.7)

The variable Y satisfies the differential equation

$$\begin{aligned} Y'=\mu Y(Y-1). \end{aligned}$$
(2.8)

Solving (2.8) gives

$$\begin{aligned} Y(\zeta )=\frac{1}{1-d e^{\mu \zeta }}. \end{aligned}$$
(2.9)

The index n is to be determined by applying order balance procedure which is in our case \(n=2\), and accordingly, we write (2.7) as

$$\begin{aligned} p(\zeta )= & {} A_0 +A_1 Y +A_2 Y^2. \end{aligned}$$
(2.10)

Differentiating both (2.8) and (2.10) implicitly leads to

$$\begin{aligned} Y''= & {} \mu ^2 Y(Y-1)(2Y-1),\nonumber \\ Y'''= & {} \mu ^3 Y(Y-1)(6Y^2-6Y+1), \end{aligned}$$
(2.11)

and

$$\begin{aligned} p'(z)= & {} A_1 Y' +2 A_2 Y Y', \nonumber \\ p''(z)= & {} A_1 Y'' +2 A_2 (Y Y''+(Y')^2), \nonumber \\ p'''(z)= & {} A_1 Y''' +2 A_2 (3Y' Y''+Y Y''') \end{aligned}$$
(2.12)

Now, we insert (2.8) through (2.12) in (2.2) to get a polynomial in Y. By setting each coefficient of \(Y^i\) to zero, a nonlinear algebraic system is obtained. Seeking a solution to this system, we get

$$\begin{aligned} \alpha= & {} \ \beta =\ \gamma =\ \pm 1,\nonumber \\ A_0= & {} 0,\ A_1=-A_2\ =\ 3 m^2,\nonumber \\ \lambda= & {} \ -2s,\ c=\ w\ =\ s \gamma ,\ \mu =\ \texttt {free}. \end{aligned}$$
(2.13)

Therefore, a new solution of DMNLS (1.7) is

$$\begin{aligned} q(x,t)= & {} -3 \mu ^2 e^{-2 i s(x \pm s t)}\nonumber \\&\times \left( \frac{1}{1-d e^{\mu (x\pm s t)}}-1\right) \frac{1}{1-d e^{\mu (x\pm s t)}}.\nonumber \\ \end{aligned}$$
(2.14)

Figure 2 presents the behavior of the dual-waves for the real part of (2.14) when \(s=\ 1,\ 2,\ 3\), respectively.

3 Dual-mode Schrödinger with dual-power Kerr

We follow the same steps considered in the preceding section. Substituting (2.1) in (1.8) produces the system

$$\begin{aligned} 0= & {} \lambda ^2 (2 s^2 + s \beta \lambda - w (2 w + \lambda )) p(\zeta ) \nonumber \\&+\, 2 (w - s \alpha ) \lambda p^3(\zeta ) + 2 m \lambda (w - s \alpha ) p^5(\zeta )\nonumber \\&+\, (2 c^2 - 2 s^2 - 2 c \lambda + w \lambda - 3 s \beta \lambda ) p''(\zeta ),\nonumber \\ 0= & {} (\lambda (4 s^2 + 4 c w + c \lambda - 2 w \lambda + 3 s \beta \lambda )\nonumber \\&-\, 6 (c + s \alpha ) p^2(\zeta ) - 10 m (c + s \alpha ) p^4(\zeta )) p'(\zeta ) \nonumber \\&-\, (c + s \beta ) p'''(\zeta ). \end{aligned}$$
(3.1)
Fig. 3
figure 3

Multiplicative of the dual-waves obtained for the real part of q(x, t) (3.6) by increasing the phase velocity: \(s=0.1,\ 1,\ 3,\ 5\), respectively

Full size image

We solve (3.1) by applying the tanh-technique. Considering the suggested solution given in (2.3) and performing the balance step, we get \(m=\frac{1}{2}\) which is not applicable for the tanh-scheme. Therefore, we introduce the following new transformation

$$\begin{aligned} p(\zeta )=f^{\frac{1}{2}} (\zeta ). \end{aligned}$$
(3.2)

Now we replace \(p(\zeta )\) in (3.1) by \(f(\zeta )\) to retrieve a new system

$$\begin{aligned} 0= & {} \lambda ^2 (2 s^2 + s \beta \lambda - w (2 w + \lambda )) f^2(\zeta ) \nonumber \\&+\, 2 (w - s \alpha ) \lambda f^3(\zeta ) + 2 m \lambda (w - s \alpha ) f^4(\zeta )\nonumber \\&-\,\frac{1}{4} (2 c^2 - 2 s^2 - 2 c \lambda + w \lambda - 3 s \beta \lambda )\nonumber \\&((f'(\zeta ))^2-2f(\zeta ) f''(\zeta )),\nonumber \\ 0= & {} \frac{1}{2} f^2(zeta) f'(\zeta )(\lambda (4 s^2 + 4 c w \nonumber \\&+\, c \lambda - 2 w \lambda + 3 s \beta \lambda ) - 6 (c + s \alpha ) f(\zeta )\nonumber \\&-\, 10 m (c + s \alpha ) f^2(\zeta )) -\frac{1}{8} (c + s \beta )(3 (f'(\zeta ))^3\nonumber \\&-\,6 f(\zeta )f'(\zeta )f''(\zeta ) +4 f^2(\zeta ) f'''(\zeta )). \end{aligned}$$
(3.3)

The tanh-solution of this new system is

$$\begin{aligned} f(\zeta )=b_0+b_1 Y. \end{aligned}$$
(3.4)
Fig. 4
figure 4

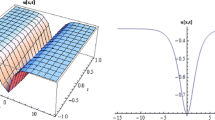
2D profile solutions for the DMNLS with dual-power Kerr law obtained in (3.6)

Full size image

Y is defined as in (2.4). Inserting (3.4) in (3.3) and performing the algebraic computations, we arrive at the following results

$$\begin{aligned} \alpha= & {} \beta =\pm 1,\nonumber \\ b_0= & {} 0,\ \ b_1=\ \texttt {free},\nonumber \\ c= & {} -\beta s,\ \ \lambda =\ \texttt {free} ,\ \ \mu =\ \texttt {free},\ \ w=\beta s.\nonumber \\ \end{aligned}$$
(3.5)

Accordingly, the tanh-solution of DMNLS with dual-power Kerr law (1.8) is given by

$$\begin{aligned} q(x,t)=e^{\lambda i (x+\beta s t)} \sqrt{b_1 \tanh (\mu (x+\beta s t)) }. \end{aligned}$$
(3.6)

3D plots of the real part of the obtained solution (3.6) asserts the multiplicative phenomena by gradually increasing in the phase velocity, see Fig. 3.

4 Conclusion

A new dual-mode Schrödinger (DMNLS) equation with nonlinearity Kerr laws of types square-root and dual-power is introduced for the first time. The new model describes the propagation of two different waves with embedded interaction phase velocity. Solitary dual-wave solutions are obtained to DMNLS equation by means of two different schemes: the tanh-expansion and Kudryashov expansion techniques.

3D plots of the obtained solutions are provided. Also, we studied geometrically the impact of the phase velocity on the interaction between the obtained dual-waves and concluded an intersecting physical phenomenon: doubling the number of these obtained dual-waves by increasing the phase velocity within the same coordinates region.

To study the formality and nature of the resulting waves of this model, we consider 2D profile solutions for the dual-power Kerr law depicted in (3.6) and conclude that both waves have the same shape and we may refer to these two waves as right-wave and left-wave as shown in Fig. 4.

The insights of the current work’s findings can be linked to the development of transmitting data through telecommunication integrated systems. The phenomenon of doubling the dual-waves may be used as a carrier wave of certain data transmitted to different directions.