1 Introduction

In real life, there are many diverse and complicated physical phenomena that can be best modeled by nonlinear Schrödinger (NLS) equations including higher-order nonlinear and dispersion terms. So, the NLS equations have a widespread application in various branches of natural and engineering sciences. Different forms of the NLS equations have commonly come across in nonlinear optics (Leble and Reichel 2009; Dörfler et al. 2011), quantum mechanics (Ohsumi 2019; Chen et al. 2007), plasma physics (Lee et al. 2007; Do Ó et al. 2009) and telecommunication (Zhou 2014; Yin et al. 2017; Tala-Tebue et al. 2018), etc. So, many researchers focus on solving the equations to interpret the dynamics of the solutions. In the literature, there are many produced methods and their versions called extended, modified, improved and generalized, etc. (Cesar et al. 2022; Hajar et al. 2021, 2022; Tarla et al. 2022; Kalim et al. 2021; Ozdemir et al. 2021; Ali et al. 2022; Cinar et al. 2021, 2022a, b; Mahak and Akram 2019; Liu et al. 2018; Biswas et al. 2016; Biswas and Arshed 2018; Korkmaz et al. 2020; Akbar et al. 2021; Raslan 2017; Tarla et al. 2022; Tariq et al. 2018, 2022a, b; Ozisik et al. 2022a).

One of these equations is the Chen–Lee–Liu (CLL) equation which was introduced in 1979 by Chen et al. (1979, 1987) as follows:

$$\begin{aligned} i \frac{\partial u}{\partial t}+\alpha _{1} \frac{\partial ^{2} u}{\partial x^{2}}+i \alpha _{2} \left|u \right|^{2} \frac{\partial u}{\partial x}=0, i=\sqrt{-1}, \end{aligned}$$
(1)

where \(u=u(\mathrm {x}, \mathrm {t})\) is a complex-valued function and \(\alpha _{1}, \alpha _{2}\) are real values and they come from group velocity dispersion and nonlinear dispersion terms, respectively. Besides t represents the temporal variable and x is the spatial variable which is propagation distance. If it is considered that \(\alpha _{1}=\alpha _{2}=1\), then Eq. (1) converts into the well-known regular Chen–Lee–Liu form. As it is known that Eq. (1) is also called the second derivative nonlinear Schrödinger equation (DNLSII) (Shuwei et al. 2011; Zhang et al. 2015; Gadzhiev et al. 1986). The CLL equation is important in that it represents a model controlling the propagation of the optical pulse with only a self-steepening effect (SSE) but no self-phase modulation (SPM). Especially in 2007, experimentally revealing the physical interpretation of the optical expression, which the DNLSII equation represents rather than being an equation only theoretically or mathematically, has increased the importance of the CLL equation and pioneered the formation of many forms of the CLL equation. Such as, an integrable coupled derivative NLS equation (Sakovich and Sakovich 2005; Feng 2012), DNLSII equation (Liu et al. 2019; Zhou et al. 2022), an integrable coupled CLL model (Tsuchida and Wadati 1999; Alrashed et al. 2022), perturbed CLL (Esen et al. 2021; Yépez-Martínez 2021), CLL in birefringent fiber (Yildirim 2019), higher-order CLL equation (Zhang et al. 2022), conservation laws of CLL equation Arnous et al. 2022), fractional CLL equation (Hussain et al. 2020; Yusuf et al. 2019). It should also be noted here that DNLSII has a wide range of applications, not only in optics but also in the modeling of weak nonlinear propagating water waves (Guo et al. 2014; Xia et al. 2021; Trulsen et al. 2000).

The Chen–Lee–Liu equation describes the propagation in nonlinear optical fibers (Mohamed et al. 2022; Akinyemi et al. 2021), besides it may appears in meta-materials, optical couplers and optoelectronic devices (Baskonus et al. 2021). In this study, we deal with the dimensionless perturbed Chen–Lee–Liu equation defined as Chen et al. (1979), Biswas (2018):

$$\begin{aligned} i\frac{\partial u}{\partial t} +\alpha _{1} \frac{\partial ^{2} u}{\partial x^{2} } +i\alpha _{2} \left|u\right|^{2} \frac{\partial u}{\partial x} =i\left( \gamma _{1} \frac{\partial u}{\partial x} +\gamma _{2} \frac{\partial \left( \left|u\right|^{2n} u\right) }{\partial x} +\gamma _{3} \frac{\partial \left|u\right|^{2n} }{\partial x} u\right) ,\; i=\sqrt{-1}, \end{aligned}$$
(2)

where \(u=u(x,t)\) is a complex function and the parameters \(\alpha _{1},\alpha _{2}\) are the coefficient of the group velocity dispersion and nonlinear dispersion term, respectively. The coefficients \(\gamma _1,\gamma _2, \text {and} \,\gamma _3\) are the inter-modal dispersion (IMD), the self-steepening and nonlinear dispersion terms, respectively. In addition, the all parameters are real values and n, the parameter of full nonlinearity, refers the density of complex function.

In the literature, the considered perturbed CLL equation has been solved via some other methods such as the first integral (Kudryashov 2019), Jacobi and the Weierstrass elliptic functions (Kudryashov 2021), Jacobi elliptic function method Tarla et al. (2022), generalized exponential rational function method (Tarla et al. 2022), both modified \(G/G'\)-expansion and modified Kudryashov methods (Yokus et al. 2021), the generalized Kudryashov and \(\exp (-\varphi (\eta ))\)-expansion methods (Baskonus et al. 2021). Besides, Yildirim et al. (2020) studied the considered equation by using different techniques that are Riccati, Sine-Gordon, F-Expansion, functional variable, Exp- expansion, trial equation and modified simple equation technique. As can be seen from the references in Yildirim et al. (2020), Kudryashov (2019), Biswas (2018), Kudryashov (2021), Tarla et al. (2022), Tarla et al. (2022), Yokus et al. (2021), Baskonus et al. (2021), the existing studies in the literature generally focus on the existence of some soliton solutions of the perturbed CLL equation with different refractive indexes or obtaining soliton solutions by applying different methods.

The aim of this study is not only focused on the soliton solution of the perturbed CLL equation, but also to examine the effects of terms of the inter-modal, self-steepening and nonlinear dispersion on the soliton behavior represented by the perturbed CLL equation. In this respect, no such review and results presented in this article have been reported for the perturbed CLL equation before.

In this study, the enhanced modified extended tanh expansion method (eMETEM) (Ozisik et al. 2022b) has been applied to construct some soliton solutions of the perturbed CLL equation. Extracting the effects of the coefficients of the inter-modal, self-steepening and nonlinear dispersion terms on soliton dynamics will encourage further studies.

The remaining part is arranged as follows: The algorithm of the method is described in Sect. 2. We apply the proposed method to perturbed CLL equation in Sect. 3. The results of the paper and the plots of the obtained solutions are explained in Sect. 4. We give a conclusion in the final section.

2 Review of the enhanced modified extended tanh expansion method

  • Step 1: Let us deal with the general form of a NLPDE and the wave transformations, respectively:

    $$\begin{aligned} H\left( U,\frac{\partial U}{\partial t} ,\frac{\partial U}{\partial x} ,\frac{\partial ^{2} U}{\partial t^{2} } ,\frac{\partial ^{2} U}{\partial x^{2} } ,\frac{\partial ^{2} U}{\partial x\partial t} ,\ldots \right) =0, \end{aligned}$$
    (3)
    $$\begin{aligned} U= U\left( x,t\right) = Y\left( \varepsilon \right) , \quad \varepsilon =p_{1} x+p_{2} t, \end{aligned}$$
    (4)

    where \(p_{1},p_{2}\) are the wave number and the velocity of the wave, respectively. Substituting the wave transformations in Eq. (4) into Eq. (3), we acquire a nonlinear ordinary differential (ODE) as follows:

    $$\begin{aligned} J\left( Y\left( \varepsilon \right) ,Y'\left( \varepsilon \right) ,Y''\left( \varepsilon \right) ,\ldots \right) =0, \end{aligned}$$
    (5)

    where the sign \(^\prime \) represents the derivatives of \(Y\left( \varepsilon \right) \) w.r.t. \(\varepsilon \).

  • Step 2: The solutions of the ODE in Eq. (5) can be supposed by the following form:

    $$\begin{aligned} Y\left( \varepsilon \right) =A_{0} +\sum _{i=1}^{m}A_{i} \Psi ^{i} (\varepsilon ) +\sum _{i=1}^{m}B_{i} \Psi ^{-i} (\varepsilon ). \end{aligned}$$
    (6)

    Here, \(A_{0},A_1, \ldots ,A_{m} ,B_{1} ,\ldots ,B_{m} \) are real parameters to be determined (\(A_{m}\) and \( B_{m}\) should not be zero, simultaneously) and m is a positive integer to be found by balancing the highest derivative term and the highest power nonlinear term in Eq. (5). Besides, \(\Psi (\varepsilon )\) is a function that satisfies the following Riccati differential equation:

    $$\begin{aligned} \frac{d\Psi (\varepsilon )}{d\varepsilon } =\gamma + \left[ \Psi (\varepsilon )\right] ^{2}, \end{aligned}$$
    (7)

    where \(\gamma \) is a nonzero real value.

  • Step 3: Equation (7) admits the solutions which are given in Table 1.

    Table 1 The solutions of Eq. (7)
    Full size table

    where \(\gamma , \alpha , \beta \) and \(\varepsilon _{0}\) are real values and \(\lambda =\mp 1\).

  • Step 4: Substituting Eq. (6) and its related derivatives into Eq. 5 and considering Eq. (7), a polynomial in \(\Psi (\varepsilon )\) are acquired. Collecting the coefficients of \(\Psi (\varepsilon )\) with the same power and equating each coefficient to zero, an algebraic equations system are derived.

  • Step 5: When the set of algebraic equations in Step 4 is solved, the unknowns \({{A}_{0}},{{A}_{1}},\ldots ,{{A}_{m}}\), \({{B}_{1}},{{B}_{2}},\ldots ,{{B}_{m}},{{p}_{1}},{{p}_{2}},\gamma ,\alpha , \beta \) and \(\varepsilon _0\) are determined. Substituting the values of the unknowns into Eq. (6) and considering Eq. (4), the solutions of the NLPDE in Eq. (3) are found.

3 Application of the method

Let us take \(n=1\) in the perturbed CLL equation that is given in Eq. (2) and consider the following wave transformation:

$$\begin{aligned} u(x,t)=e^{i\theta } U\left( \varepsilon \right) ,\; \varepsilon =\eta \left( x-vt\right) ,\; \theta =-kx+\beta t+\varphi , \end{aligned}$$
(8)

where \(U\left( \varepsilon \right) , \eta , v, \theta , k, \beta \) and \(\varphi \) are the amplitude of the wave, the wave number, velocity, phase component, the frequency, the wave number and phase constant. Substituting the travelling wave transformation in Eq. (8) into Eq. (2), one can obtain real and imaginary parts as follows:

$$\begin{aligned} \eta ^{2} \alpha _{1} U''\left( \varepsilon \right) -U\left( \varepsilon \right) \left( k\left( \gamma _{2} -\alpha _{2} \right) \left( U\left( \varepsilon \right) \right) ^{2} +k^{2} \alpha _{1} +k\gamma _{1} +\beta \right) =0, \end{aligned}$$
(9)
$$\begin{aligned} -2\eta \left( \left( \left( 3/2\right) \gamma _{2} +\gamma _{3} -\left( 1/2\right) \alpha _{2} \right) \left( U\left( \varepsilon \right) \right) ^{2} +k\alpha _{1} +v/2+\left( 1/2\right) \gamma _{1} \right) U'\left( \varepsilon \right) =0. \end{aligned}$$
(10)

Integrating the Eq. 10 once and taking the integration constant as zero, we have:

$$\begin{aligned} -\eta \left( 3\gamma _{2} + 2\gamma _{3} \alpha _{2} \right) \left( U\left( \varepsilon \right) \right) ^{3} -3 \eta \left( 2k\alpha _{1} +v+\gamma _{1} \right) U\left( \varepsilon \right) =0. \end{aligned}$$
(11)

From Eq. 11, one can get:

$$\begin{aligned} v=-2k\alpha _{1} -\gamma _{1}, \end{aligned}$$
(12)
$$\begin{aligned} \alpha _{2} =3\gamma _{2} +2\gamma _{3}. \end{aligned}$$
(13)

Under the constraints in Eqs. (12), (13), we take in to account the Eq. (9) as the ODE representation of Eq. (2):

$$\begin{aligned} \eta ^{2} \alpha _{1} U''-k\left( \gamma _{2} -\alpha _{2} \right) U^{3} -\left( k^{2} \alpha _{1} +k\gamma _{1} +\beta \right) U=0, \end{aligned}$$
(14)

where \(U= U\left( \varepsilon \right) \). When we balance the terms \(U''\) and \(U^{3} \) in Eq. (14) by considering Eq. (6), (7), we attain \(m=1\).

So, the solutions of Eq. (14) are supposed to be a form as follows:

$$\begin{aligned} U\left( \varepsilon \right) =A_{0} +A_{1} \Psi (\varepsilon )+B_{1} \frac{1}{\Psi (\varepsilon )}. \end{aligned}$$
(15)

Substituting the Eq. (15) and its derivatives into Eq. (14), we attain the polynomial in \(\Psi (\varepsilon )\) by taking Eq. (7) a consideration. Gathering each term with the same power of \(\Psi ^{i} (\varepsilon )\) and equating each coefficient to zero, one can get a system of algebraic equation system as:

$$\begin{aligned} \begin{array}{l} {\Psi ^{-3} (\varepsilon ): \quad B_{1} \left( k\delta B_{1} {}^{2} +\gamma ^{2} \eta ^{2} \alpha _{1} \right) =0} ,\\ {\Psi ^{-2} (\varepsilon ): \quad kA_{0} B_{1} {}^{2} \delta =0},\\ {\Psi ^{-1} (\varepsilon ): \quad -B_{1} \left( k^{2} \alpha _{1} +\left( -6 A_{1} \delta B_{1} -6 A_{0}^2 \delta +\gamma _{1} \right) k-2 \gamma \eta ^{2} \alpha _{1} +\beta \right) =0} ,\\ {\Psi ^{0} (\varepsilon ): \quad -A_{0} \left( k^{2} \alpha _{1} +\left( -2 \delta A_{0}^{2} -12 A_{1} B_{1} (\gamma _{2}+ \gamma _{3}) +\gamma _{1} \right) k+\beta \right) =0}, \\ {\Psi ^{1} (\varepsilon ): \quad -\left( k^{2} \alpha _{1} +\left( -6 A_{1} \delta B_{1}-6 A_{0}^2 \delta )+\gamma _{1} \right) k-2 \gamma \eta ^{2} \alpha _{1} +\beta \right) A_{1} =0} ,\\ {\Psi ^{2} (\varepsilon ): \quad kA_{0} A_{1} {}^{2} \delta =0} ,\\ {\Psi ^{3} (\varepsilon ): \quad A_{1} \left( k\delta A_{1} {}^{2} +\eta ^{2} \alpha _{1} \right) =0,} \end{array} \end{aligned}$$
(16)

where \(\delta = \gamma _{2} +\gamma _{3}\).

When we solve the system above by Maple, the unknowns \(A_{0} ,A_{1} ,B_{1}, \alpha _1, \gamma , \gamma _1, \gamma _2, \gamma _3, k\) and \(\beta \) are determined. The some of solution sets are given below:

$$\begin{aligned} Cset^{1}&=\left\{ \beta =-4 \eta ^{2} \gamma \alpha _{1} -k^{2} \alpha _{1} -k\gamma _{1}, A_{0} =0, A_{1} =\frac{\eta }{k\delta } \sqrt{-k\delta \alpha _{1} }, B_{1} =\gamma A_{1}\right\} ,\nonumber \\ Cset^{2}&=\left\{ \beta = \frac{-\eta ^{2} \left( 4\gamma \delta ^{2} A_{1} {}^{4} - \gamma _{1} \delta A_{1} {}^{2} +\eta ^{2} \alpha _{1} {}^{2} \right) \alpha _{1} }{A_{1} {}^{4} \delta ^{2} } , k=-\frac{\eta ^{2} \alpha _{1} }{A_{1} {}^{2} \delta } , A_{0} =0,B_{1} =\gamma A_{1} \right\} , \nonumber \\ Cset^{3}&=\left\{ \beta = \frac{\left( 8\gamma \delta ^{2} A_{1} {}^{4} + \gamma _{1} \delta A_{1} {}^{2} - \eta ^{2} \alpha _{1} {}^{2} \right) \eta ^{2} \alpha _{1} }{A_{1} {}^{4} \delta ^{2} } , k=-\frac{\eta ^{2} \alpha _{1} }{A_{1} {}^{2} \delta }, A_{0} =0,B_{1} =-\gamma A_{1} \right\} . \end{aligned}$$
(17)

For \(j=1,2,\ldots ,15\), substituting the \(\Psi _{j} (\varepsilon )\) in Table 1 into Eq. (15) and using the sets above, we get the solutions \(\Psi _{j} (\varepsilon )\) of the ODE in Eq. (14). Then, using wave transformations in Eq. (8), we acquire the following solutions \(u_j(x,t)\) of the perturbed CLL equation in Eq. (2):

$$\begin{aligned} u_{1} (x,t)= \chi \left( A_{0} -A_{1} \sqrt{-\gamma } \tanh \left( \Psi _{\tau }\right) -\frac{B_{1} }{\sqrt{-\gamma } \tanh \left( \Psi _{\tau }\right) } \right) , \end{aligned}$$
(18)
$$\begin{aligned} u_{2}(x,t)=\chi \left( A_{0} -A_{1} \sqrt{-\gamma } \mathrm{coth}\left( \Psi _{\tau }\right) -\frac{B_{1} }{\sqrt{-\gamma } \mathrm{coth}\left( \Psi _{\tau }\right) } \right) , \end{aligned}$$
(19)
$$\begin{aligned} u_{3} (x,t)=\chi \left( {A_{0} -A_{1} \sqrt{-\gamma } \left( \tanh \left( 2 \Psi _{\tau }\right) +i\mu {{{\,\mathrm{sech}\,}}}\left( 2 \Psi _{\tau }\right) \right) } {-\frac{B_{1} }{\sqrt{-\gamma } \left( \tanh \left( 2 \Psi _{\tau }\right) +i\mu {{{\,\mathrm{sech}\,}}}\left( 2 \Psi _{\tau }\right) \right) } } \right) , \end{aligned}$$
(20)
$$\begin{aligned} u_{4}(x,t)= \chi \left( A_{0} +A_{1} \frac{\gamma -\sqrt{-\gamma } \tanh \left( \Psi _{\tau }\right) }{1+\sqrt{-\gamma } \tanh \left( \Psi _{\tau }\right) } +B_{1} \frac{1+\sqrt{-\gamma } \tanh \left( \Psi _{\tau }\right) }{\gamma -\sqrt{-\gamma } \tanh \left( \Psi _{\tau }\right) } \right) , \end{aligned}$$
(21)
$$\begin{aligned} u_{5} (x,t)=\chi \left( A_{0} +A_{1} \frac{\sqrt{-\gamma } \left( 5-4 \cosh \left( 2 \Psi _{\tau }\right) \right) }{3+4 \sinh \left( 2 \Psi _{\tau }\right) } +B_{1} \frac{3+4 \sinh \left( 2 \Psi _{\tau }\right) }{\sqrt{-w} \left( 5-4 \cosh \left( 2 \Psi _{\tau }\right) \right) } \right) , \end{aligned}$$
(22)
$$\begin{aligned} u_{6} (x,t)=\chi \left( {A_{0} +A_{1} \frac{\mu \sqrt{C_1} -a\sqrt{-\gamma } \cosh \left( 2 \Psi _{\tau }\right) }{a\sinh \left( 2 \Psi _{\tau }\right) +b} } {+B_{1} \frac{a\sinh \left( 2 \Psi _{\tau }\right) +b}{\mu \sqrt{C_1} -a\sqrt{-\gamma } \cosh \left( 2 \Psi _{\tau }\right) } } \right) , \end{aligned}$$
(23)
$$\begin{aligned} u_{7} (x,t)=\chi \left( A_{0} +A_{1} \left( \frac{C_2}{a} - \frac{2 C_2 }{a+\cosh \left( 2 \Psi _{\tau }\right) -\mu \sinh \left( 2 \Psi _{\tau }\right) } \right) +\frac{B_{1} }{\frac{C_2}{a} -2 \frac{C_2 }{a+\cosh \left( 2 \Psi _{\tau }\right) -\mu \sinh \left( 2 \Psi _{\tau }\right) } } \right) , \end{aligned}$$
(24)
$$\begin{aligned} u_{8} (x,t)=\chi \left( A_{0} +A_{1} \sqrt{\gamma } \tan \left( \Omega _{\tau }\right) +\frac{B_{1} }{\sqrt{\gamma } \tan \left( \Omega _{\tau }\right) } \right) , \end{aligned}$$
(25)
$$\begin{aligned} u_{9} (x,t)=\chi \left( A_{0} -A_{1} \sqrt{\gamma } \cot \left( \Omega _{\tau }\right) -\frac{B_{1} }{\sqrt{\gamma } \cot \left( \Omega _{\tau }\right) } \right) , \end{aligned}$$
(26)
$$\begin{aligned} u_{10} (x,t)=\chi \left( A_{0} +A_{1} \sqrt{\gamma } \left( \tan \left( 2 \Omega _{\tau }\right) +\mu \sec \left( 2 \Omega _{\tau }\right) \right) +\frac{B_{1} }{\sqrt{\gamma } \tan \left( 2 \Omega _{\tau }\right) +\mu \sec \left( 2 \Omega _{\tau }\right) } \right) , \end{aligned}$$
(27)
$$\begin{aligned} u_{11} (x,t)=\chi \left( A_{0} -A_{1} \frac{\sqrt{\gamma } \left( 1-\tan \left( \Omega _{\tau }\right) \right) }{1+\tan \left( \Omega _{\tau }\right) } -B_{1} \frac{1+\tan \left( \Omega _{\tau }\right) }{\sqrt{\gamma } \left( 1-\tan \left( \Omega _{\tau }\right) \right) } \right) , \end{aligned}$$
(28)
$$\begin{aligned} u_{12} (x,t)=\chi \left( A_{0} +A_{1} \frac{\sqrt{\gamma } \left( 4-5 \cos \left( 2 \Omega _{\tau }\right) \right) }{3+5 \sin \left( 2 \Omega _{\tau }\right) } +B_{1} \frac{3+5 \sin \left( 2 \Omega _{\tau }\right) }{\sqrt{\gamma } \left( 4-5 \cos \left( 2 \Omega _{\tau }\right) \right) } \right) , \end{aligned}$$
(29)
$$\begin{aligned} u_{13} (x,t)=\chi \left( A_{0} +A_{1} \frac{\mu \sqrt{\left( a^{2} -b^{2} \right) w} -a\sqrt{w} \cos \left( 2 \Omega _{\tau }\right) }{a\sin \left( 2 \Omega _{\tau }\right) +b} +B_{1} \frac{a\sin \left( 2 \Omega _{\tau }\right) +b}{\mu \sqrt{\left( a^{2} -b^{2} \right) w} -a\sqrt{w} \cos \left( 2 \Omega _{\tau }\right) } \right) , \end{aligned}$$
(30)
$$\begin{aligned} u_{14} (x,t)=\chi \left( {A_{0} +A_{1} \left( i\mu \sqrt{\gamma } -\frac{2 i\mu a\sqrt{\gamma } }{a+\cos \left( 2 \Omega _{\tau }\right) -i\mu \sin \left( 2 \Omega _{\tau }\right) } \right) } {+\frac{B_{1} }{\left( i\mu \sqrt{\gamma } -\frac{2 i\mu a\sqrt{\gamma } }{a+\cos \left( 2 \Omega _{\tau }\right) -i\mu \sin \left( 2 \Omega _{\tau }\right) } \right) } } \right) , \end{aligned}$$
(31)
$$\begin{aligned} u_{15} (x,t) =-\frac{1}{x-vt}, \end{aligned}$$
(32)

where \(\chi =e^{i\left( \beta t-kx+\phi \right) }, v=-2 k\alpha _{1} -\gamma _{1}, C_1=-\left( a^{2} +b^{2} \right) \gamma ,C_2=\mu a\sqrt{-\gamma }, \Omega _{\tau }= \sqrt{\gamma } \eta \left( x-vt\right) \) and \(\Psi _{\tau }=\sqrt{-\gamma } \eta \left( x-vt\right) \).

4 Results and discussion

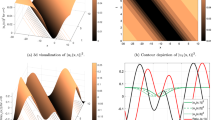
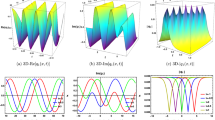
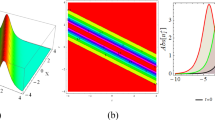
In this paper, we have successfully produced some solutions of the considered equation via the enhanced modified extended tanh expansion method. Besides, the effects of the coefficients of inter-modal dispersion, self-steepening and the nonlinear dispersion terms have been investigated. The codes of the method’s algorithm have been written by Maple. Selecting appropriate parameters and using Matlab, we have plotted many graphs of the obtained solutions. To explain the behavior of the obtained solutions, we have created various figures and have made detail interpretations. Each of the given graphics in Figs. 1, 2, 3 and 4 contains 6 sub-figures. These are modulus part in 3D (sub-figure (a)), contour of modulus part in 3D (sub-figure (b)), 2D of modulus part for \(t_f=1,2,3\) (solid black to dotted lines), 2D of imaginary part for \(t=1\) (blue line) and 2D of the real part for \(t=1\) (green line), together in (sub-figure (c)), respectively. The sub-figures (d)–(e)–(f) are the graphs showing the effect of the \(\gamma _1,\gamma _2\) and \(\gamma _3\) on the obtained soliton in sub-figure (a).

Figure 1 is the graph of the combination of \(u_3(x,t)\) in Eq. (20) and \(Cset^1\) in Eq. (17) for the parameter values \(\gamma =-0.1,\gamma _1=\gamma _2=\gamma _3=\varphi =\eta =1,\alpha _1=2,k=-1\). Fig. 1a–c (black solid to dotted lines) represents the bright soliton plot for \(\left|u_3(x,t)\right|\). From Fig. 1c, it can be seen that the soliton has traveling wave property and moves to the right. Figure 1d is the first graph created to examine the effects of the coefficients (\(\gamma _1,\gamma _2,\gamma _3\)) of inter-modal dispersion, the self-steepening and nonlinear dispersion terms on soliton behavior, respectively, which is the main purpose of this study. It is aimed to examine the effect of the \(\gamma _1\) on the bright soliton presented with Fig. 1a. For this purpose, 0.30, 0.60 and 0.90 values (dotted lines for negative values, solid lines for positive values) are assigned to the coefficients. From Fig. 1d, it is observed that there is no change in the vertical amplitude of the soliton when the \(\gamma _1\) is both negative or positive, the soliton maintains its bright soliton character, its skirts remain on the horizontal axis, and the horizontal distance between the soliton’s skirts is preserved. When \(\gamma _1\) is negative and increasing, the soliton changes position to the left depending on the increase in \(\gamma _1\) (dashed orange to black lines). In case the \(\gamma _1\) is positive and increasing, the soliton shows a similar position change to the left depending on the increase in \(\gamma _1\) (solid black to orange lines). Thus, in both cases (\(\gamma _1\) negative or positive) the coefficient of inter-modal dispersion term has a similar effect on the bright soliton. Figure 1e includes review belongs to \(\gamma _2\) which is the coefficient of the self-steepening dispersion term. The value for \(\gamma _2\) is also chosen as 0.30, 0.60 and 0.90 (dotted lines for negative values, solid lines for positive values). Unlike the previous review, it is seen that the change in the self-steepening dispersion term coefficient has a significant effect on the bright soliton obtained in the Fig. 1a. At first glance, this effect is observed as the change in the vertical amplitude of the soliton. When Fig. 1 is examined in detail, when \(\gamma _2\) gets negative and increasing values, the soliton maintains its bright soliton character, but there is a change in its vertical amplitude (position of the peak), and this change is observed in the form of a decrease in amplitude (vertical downward displacement of the peak point) depending on its increasing values (dashed orange to black lines). In the case that \(\gamma _2\) takes positive and increasing values, the soliton maintains its bright soliton character, there is a change in its vertical amplitude (position of the peak), and this change is a decrease in the amplitude (vertical downward displacement of the peak) depending on the increasing values of \(\gamma _2\) (solid black to orange lines). Therefore, for the self-steepening term coefficient \(\gamma _2\), if it continues to take increasing values in both cases (negative or positive) for the examined case, the amplitude of the soliton will continue to decrease, in other words, the peak of the soliton will approach the horizontal axis and the soliton will become flattered. We can say that it will evolve into a new appearance, and if the increase in \(\gamma _2\) continues, the soliton will gradually lose its bright soliton feature. Therefore, in terms of soliton transmission, it has an important effect in terms of preserving the character and amplitude of the soliton signal (soliton pulse) to be transmitted, and it is of great importance to select and control this coefficient depending on the interaction with other nonlinear terms. Figure 1f shows the effect of our analysis for the nonlinear dispersion term coefficient \(\gamma _3\). If Fig. 1f is examined in detail, we can categorically make similar comments made for \(\gamma _2\). When \(\gamma _3\) is both negative and positive, the soliton shows a position change to the left depending on the increasing values of \(\gamma _3\).

Fig. 1
figure 1

Some graphical representations of \(u_3(x,t)\) in Eq. (20) by selecting \(Cset^1\) in Eq. (17) for the parameters \(\gamma =-0.1, \gamma _1= \gamma _2=\gamma _3=\varphi =\eta =1, \alpha _1=2,k=-1\) and the effects of \(\gamma _1, \gamma _2, \gamma _3\)

Full size image

Figure 2 is the graph of the combination of \(u_5(x,t)\) in Eq. (22) and \(Cset^2\) in Eq. (17) for the parameters \(\gamma =-0.1, \gamma _1=0.1, \gamma _2=2, \gamma _3=3, \alpha _1=2,\eta =1,A_1=1,\varphi =-1\). Figure 2a–c (black lines) are 3D, contour 2D graphics of \(\left|u_5(x,t)\right|\). As in the previous section, \(Im(u_5(x,1))\) (blue line), \(Re(u_5(x,1))\) (green line) are given by Fig. 2c. All three graphics reflect the singular soliton character. This singularity is up directional (\(+\infty \)) for both sides of the singular point for \(\left|u_5(x,t)\right|\). \(Im(u_5(x,1))\) and \(Re(u_5(x,1))\) are down directional (\(-\infty \)) on the left of the singular point, and up directional (\(+\infty \)) on the right of the singular point. 2d reflects the effect on the singular soliton obtained in Fig. 2a with the inter-modal dispersion term coefficient \(\gamma _1\). Similarly, the values 0.30, 0.60 and 0.90 are chosen. In both cases of \(\gamma _1\) (negative or positive), the singular soliton character is preserved and the soliton is shifted to the left depending on the increase. 2e shows the examination of the case where \(\gamma _2\) is 0.50, 1.00 and 2.00 (dotted lines for negative, solid lines for positive). In case \(\gamma _2\) is both negative and positive, the soliton shows a position change to the left depending on the increasing values of \(\gamma _2\). In Fig. 2f, the similar analysis is made for \(\gamma _3\) for values of 0.50, 1.50 and 3.00. When \(\gamma _3\) is negative and increasing (dashed lines), the soliton behavior does not show a behavior similar to the previously examined cases. For \(\gamma _3=-3.0\), it is on the far left (dashed black), for \(\gamma _3=-1.5\) it is on the far right (dashed green) and then for \(\gamma _3=-0.5\) it is dashed orange. As it can be seen from the graph, when \(\gamma _3\) is positive and increasing, it shifts to the left between graphs \(\gamma _3=-3.0\) and \(\gamma _3=-1.5\) with smaller amounts depending on the increasing values of \(\gamma _3\) (solid black to orange lines). With Fig. 2f, we can attribute this situation, which occurs especially when \(\gamma _3\) is negative, to the interaction between nonlinear terms in such problems and the difficulty of controlling these terms during this interaction.

Fig. 2
figure 2

Some graphical representations of \(u_5(x,t)\) in Eq. (22) by selecting \(Cset^2\) in Eq. (17) for the parameters \(\gamma =-0.1, \gamma _1=0.1, \gamma _2=2, \gamma _3=3, \alpha _1=2,\eta =1,A_1=1,\varphi =-1\) and the effects of \(\gamma _1, \gamma _2, \gamma _3\)

Full size image

Figure 3 is the graph of the combination of \(u_{10}(x,t)\) in Eq. (27) and \(Cset^1\) in Eq. (17) for the parameters \(\gamma =-0.1, \gamma _1=0.1, \gamma _2=2, \gamma _3=3, \alpha _1=2,\eta =1, k=\varphi =-1\) and the effects of \(\gamma _1, \gamma _2, \gamma _3\). Figure 3 generally reflects the periodic singular soliton image. The effect of \(\gamma _1\) is examined in Fig. Fig. 3d, and the soliton shows a position change to the left depending on the increasing values of \(\gamma _1\), both positive and negative. Figure 3e, f are graphs that reflect the effects of \(\gamma _2\) and \(\gamma _3\), respectively. In both graphs, depending on the increasing values (negative or positive) for both \(\gamma _2\) and \(\gamma _3\), no horizontal position change is observed for the soliton, but there is a change in its vertical amplitude. It is possible to see this change from the skirt parts of the soliton. When \(\gamma _2\) and \(\gamma _3\) are negative and increasing, the amplitude decreases (dashed orange to black lines). And when the parameters are positive, the amplitude decreases. But this effect is observed as a smaller change (solid black to orange lines).

Fig. 3
figure 3

Some graphical representations of \(u_{10}(x,t)\) in Eq. (27) by selecting \(Cset^{1}\) in Eq. (17) for the parameters \(\gamma =-0.1, \gamma _1=0.1, \gamma _2=2, \gamma _3=3, \alpha _1=2,\eta =1, k=\varphi =-1\) and the effects of \(\gamma _1, \gamma _2, \gamma _3\)

Full size image

Lastly, Fig. 4 is the graph of the combination of \(u_{14}(x,t)\) in Eq. (31) and \(Cset^3\) in Eq. (17) for the parameters \(\gamma =0.1, \gamma _1=1, \gamma _2=2, \gamma _3=3, \alpha _1=2,\eta =1, k=-1,\varphi =1\). Periodic bright soliton character is generally observed in Fig. 4. Similarly, the graph of Fig. 4d is divided into the effect of \(\gamma _1\) and when \(\gamma _1\) is both positive or negative, the position of the solution changes to the left depending on the increasing values of \(\gamma _1\). Figure 4e shows the effect of \(\gamma _2\). When \(\gamma _2\) gets negative and increasing values, there is a change in the horizontal position of the soliton, but this change does not occur regularly (regularly to the left or right) depending on the increasing values of \(\gamma _2\). Because if the graph of \(\gamma _2=-2.00\) (dashed black line) is on the left, the graph of \(\gamma _2=-1.00\) (dashed green line) is on the right, and the graph of \(\gamma _2=-0.50\) (dashed orange line) is observed between these two graphs. This does not happen when \(\gamma _2\) takes positive and increasing values (solid black to orange lines). 4f shows the effect of \(\gamma _3\) and the soliton changes to the left depending on the increasing values of \(\gamma _3\) when \(\gamma _3\) is both negative and positive. We would also like to emphasize here that all solution functions obtained between Eqs. (18), (32) satisfy the main equation, Eq. (2), with each solution set given in Eq. (17).

Fig. 4
figure 4

Some graphical representations of \(u_{14}(x,t)\) in Eq. (31) by selecting \(Cset^3\) in Eq. (17) for the parameters \(\gamma =0.1, \gamma _1=1, \gamma _2=2, \gamma _3=3, \alpha _1=2,\eta =1, k=-1,\varphi =1\) and the effects of \(\gamma _1, \gamma _2, \gamma _3\)

Full size image

5 Conclusion

The existing studies in the literature focus on obtaining solutions of the perturbed Chen–Lee–Liu equation. In addition to obtaining the soliton solution of the perturbed CLL equation, the main purpose of this work is to investigate the impact of inter-modal, self-steepening, and nonlinear dispersion components on the soliton behavior represented by the considered equation. In this study, we have successfully obtained the bright, singular, periodic singular and periodic bright solitons of the perturbed Chen–Lee–Liu equation by applying the modified extended tanh expansion method. After obtaining the specified soliton types, 2D graphs of soliton behaviors have been drawn by giving different values to the coefficients of these terms in order to examine the effect of each term. It should also be noted that the numerical values given to the coefficients have been assigned to ensure both the limitations of the problem and the method and to preserve the soliton shape obtained within the area of the study. Therefore, making this choice often involves many difficulties and complexities in itself. In this aspect, the investigation of the effect of the inter-modal, self-steepening and nonlinear dispersion terms on soliton behaviors for the perturbed Chen–Lee–Liu equation has not been studied and the results within the scope of this study have not been presented. We believe that the gained results within the scope of the study will be useful for studies on problems modeling many physical phenomena in this area.