On some optical soliton structures to the Lakshmanan-Porsezian-Daniel model with a set of nonlinearities

Abstract

In this work, the Lakshmanan-Porsezian-Daniel model is investigated which is the generalization of the non-linear Schrödinger model, to describes the dynamical behavior of optical solitons. The extended modified auxiliary equation mapping method is employed to develop some new exact solitary wave solutions to the complex model with the ker law, the parabolic law and the anti-cubic law nonlinearities. As a result, dark solitons, light solitons, singular solitons, solitary wave, periodic solitary wave, rational function, and elliptic function solutions are established. In the current era of communications network technology and nonlinear optics, the applied strategy appears to be a more powerful and efficient approach for achieving exact optical solutions to a number of diversified contemporary models.

1 Introduction

Nonlinear evolution equations (NLEES) are of key importance due to their significant role in diverse disciplines of science and technology. The nonlinear wave structures have fascinated many researchers in recent decades due to their diverse properties observed in various disciplines of contemporary sciences. In the presence of solitary waves, the nonlinear evolution models are utilized to simulate the effect of surface for deep water and weakly nonlinear dispersive long waves. Therefore, the exact solutions of such models play a vital role of study of dynamical structures and further properties of physical phenomenon occurring several fields to name a few, electromagnetism, physical chemistry, geophysics, ionised physics, elastic medium, fluid motion, fluid mechanics, elastic medium, nuclear physics, electrochemistry, optical fibres, energy physics, chemical mechanics, gravity, biostatistics, statistical and natural physics (Chen et al. 2021; Ali and Gómez-Aguilar 2021; Yépez-Martínez et al. 2022; Islam et al. 2021a, b; Lü et al. 2021a, b; Yin et al. 2020; Li et al. 2010; Hosseini et al. 2018; Wazwaz 2014; Ivezić et al. 2019; Chen et al. 2021).

With the recent developments in various contemporary analytical methodologies, solitons plays a key role to understand the nonlinear phenomenon of many crucial structures in an exceptional way. The major feature of solitons is that they have nearly the same forms and speeds after colliding; also, the production of optical solitons is linked to optical frequency. Kink solutions are asymptotic waves that ascend or descend from one asymptotic state to the next, and they also approach a constant at infinity. Kink solutions, like classical particles, have a constant shape; nevertheless, their widths shrink, which can change. Solitons are transmitted as dark ones in the normal dispersion domain, but as bright ones in the anomalous dispersion domain. With the rapid advancement of information technology and telecommunications, the optical solitons play an important rule in understanding the dynamics of nonlinear wave propagation through a variety of wave-guides. The polarization of pulse propagation over trans-oceanic and trans-continental distances is an inherent problem with the dynamics of pulse propagation. This is due to a number of factors, including fiber diameter randomness, rough handling of optical fibers, and so on (Seadawy and Cheemaa 2019; Naher and Abdullah 2012; Wazwaz 2004; Ahmed et al. 2019; Kudryashov 2019; Sun et al. 2021; Zafar et al. 2022; Ahmad et al. 2021; Khater et al. 2021; Khodadad et al. 2021).

To investigate the behaviour of nonlinear models, researchers from all over the world discovered a variety of the numerical and analytical methods, such as the modified auxiliary equation method (Mahak and Akram 2020; Khater et al. 2019a, b), the optional decoupling condition approach (Lü and Chen 2021), the sub-equation method (Akinyemi et al. 2021), the extended trial function method (Ekici and Sonmezoglu 2019; Biswas et al. 2019; Nawaz et al. 2018), the modified kudryashov method (Kumar et al. 2018), the generalized riccati equation expansion method (Yong et al. 2003), the extended simple equation method (Lu et al. 2017; Zayed and Shohib 2019), the hirota bilinear method (Lü and Chen 2021; Jin-Ming and Yao-Ming 2011; El-Labany et al. 2018), the extended rational sinh-cosh method (Rezazadeh et al. 2019; Mahak and Akram 2019), the modified khater method (Khater et al. 2021) and so on.

The Lakshmanan-Porsezian-Daniel (LPD) model studies the optical solitons shine bright lights on the telecommunications industry (Inegbedion and Obadiaru 2019; Asimakopoulos and Whalley 2017) to govern the dynamics of the pulse transmission (Li et al. 2018; Bandelow et al. 2020; Weckbrodt et al. 2018) through optical fibers (Buck 2004; Liu et al. 2019), the Photonic-crystal fiber (Wang et al. 2016; Bulbul et al. 2021) and the meta materials (Cui et al. 2010; Ma and Cui 2020) for the transcontinental (Wang et al. 2020) and transoceanic distance (Lindo 2020). Because of the important roles that models play in our day-to-day operations or activities, it is also crucial to discuss the characteristics of the models that occurs in ocean dynamics Olbers et al. (2012); Kamenkovich (2011).

A. Biswas et al. have applied two integration strategies namely the extended Jacobi’s elliptic function approach and $exp(-\phi (\eta ))$-expansion method to construct dark and singular optical solitons solutions to the LPD model for Kerr nonlinearity (Biswas et al. 2018). In literature, a variety of interesting approaches have been implemented to analyse this model analytical such as the (Yépez-Martínez et al. 2022), the modified simple equation method (Biswas et al. 2018), the sine-Gordon equation method (Yildirim et al. 2021), the semi-inverse variational principle (Alzahrani and Belic 2021), the generalized projective Riccati equations method (Akram et al. 2021), the modified extended direct algebraic method (Hubert et al. 2018) and several others.

In our work, the extended modified auxiliary equation mapping (AEM) method (Akram and Sarfraz 2021; Al-Munawarah and Arabia 2021) is employed to study the LPD model (Rezazadeh et al. 2018) reads

$$\begin{aligned} i q_t+\mu _1 q_{\text {xx}}+\mu _2 q_{xt}+\mu _3F\left( |q|^2q\right)= & {} \alpha q^* (q_x)^2 +\sigma q_{xxxx}+\beta |q_x|^2 q \nonumber \\&+\gamma |q|^2q_{xx} +\lambda q^2 q^*_{xx}+\delta |q|^4 q, \end{aligned}$$

(1)

where q(x, t) represents the complex valued wave function. The first factor on the left side reflects the temporal evolution of the optical pulse, whereas the coefficients $\mu _1$ and $\mu _2$ represent the group-velocity dispersion and spatiotemporal dispersion respectively. Also $\sigma$ is the fourth-order dispersion and $\delta$ is the two-photon absorption. The functional F is the source of nonlinearity which is a real-valued algebraic function.

2 The extended modified AEM method

Firstly consider the NPDE of the form

$$\begin{aligned} P(u,u_{t},u_x,u_y,u_{xx},...)=0, \end{aligned}$$

(2)

where P is the polynomial of u(x, y, t).

To attain the exact traveling wave solution, consider the traveling wave transformation of the form

$$\begin{aligned} u(x,y,t)=u(\xi ), \quad \xi =\sum _{i=0}^m \kappa _i x_i, \end{aligned}$$

(3)

where $\kappa _i$, $i=0,1,2,...,m$ are the constants. By using this transformation Eq. (2) reduce to nonlinear ODE of the form

$$\begin{aligned} Q(u,u',u'',u''',...)=0. \end{aligned}$$

(4)

Where Q is the polynomial in $u(\xi )$ along with its derivatives w.r.t $\xi$.

Then we suppose the solution of Eq. (4) that will be expressed as

$$\begin{aligned} u(\xi )= & {} \sum _{k=0}^n a_k \psi ^k(\xi )+\sum _{k=-1}^{-n} b_{-k} \psi ^k(\xi )\nonumber \\&+\sum _{k=2}^n c_k \psi ^{k-2}(\xi ) \psi '(\xi )+\sum _{k=1}^n d_k \left( \frac{\psi '(\xi )}{\psi (\xi )}\right) ^k. \end{aligned}$$

(5)

where $a_k, b_k, c_k$ and $d_k$ are the arbitrary constants to be determined.

Here $\psi (\xi )$ satisfies the following generalized solution,

$$\begin{aligned} \psi '(\xi )^2=\delta _1 \psi (\xi )^2+\delta _2 \psi (\xi )^3+\delta _3 \psi (\xi )^4, \end{aligned}$$

(6)

where $\delta _1, \delta _2$ and $\delta _3$ are the constants to be determined. We have the following steps to attain the solution.

• 1. First we find the positive integer “n” by balancing the highest derivative and the highest nonlinear term of the Eq. (4).

• 2. Inserting Eq. (5) with its desired derivatives along with Eq. (6) into Eq. (4) and by collecting the same power terms ${\psi '(\xi )\psi (\xi )}$ and by equalizing them to zero, we have a system of algebraic equations. By solving the obtained system we attain a set of values of the constants $a_k, b_k, c_k$ and $d_k$.

• 3. By substituting all the obtained values in Eq. (5) we find the solution of the Eq. (2).

3 Applications to the LPD model

Consider the transformation

$$\begin{aligned} q(x,t)=u(\xi ) e^{i \phi (x,t)}\, \text {and}\, q^*(x,t)=U(\xi ) e^{-i \phi (x,t)}, \end{aligned}$$

(7)

where

$$\begin{aligned} \xi =x-\nu t \,\text {and}\, \phi =\theta + \omega t -\kappa x. \end{aligned}$$

(8)

In Eq. (8) $\phi$ is the phase component of the soliton, $\kappa$ is the frequency of soliton, while $\omega$ is the wave number, $\theta$ is the phase constant and $\nu$ is the velocity of the soliton.

Substituting Eq. (8) into Eq. (1) and then splitting into real and imaginary parts yields a pair of relations. The real part gives

$$\begin{aligned}&-U'' \left( 6 \kappa ^2 \sigma -\mu _2 \nu +\mu _1\right) -U \left( -\kappa ^4 \sigma -\kappa ^2 \mu _1+\kappa \mu _2 \omega -\omega \right) \nonumber \\&\quad - \mu _3 F(u^2) u-\kappa ^2 u^3 (\alpha -\beta +\gamma +\lambda )+\sigma U^{\prime \prime \prime }+\delta U^5\nonumber \\&\quad +u^2 (\gamma +\lambda ) u''+u (\alpha +\beta ) \left( u'\right) ^2=0, \end{aligned}$$

(9)

while the imaginary part gives

$$\begin{aligned} 4 \kappa \sigma u^{\prime \prime \prime }+u' \left( \kappa \mu _2 \nu -4 \kappa ^3 \sigma -2 \kappa \mu _1+\mu _2 \omega -\nu \right) +2 \kappa u^2 u' (\alpha +\gamma -\lambda )=0. \end{aligned}$$

(10)

Setting the coefficients of the linearly independent functions to zero in Eqs. (9) and (10), we get

$$\begin{aligned}&\alpha +\beta =0,\\&\gamma +\lambda =0,\\&\sigma =0,\\&\alpha +\gamma -\lambda =0, \end{aligned}$$

and consequently the soliton speed falls out to be

$$\begin{aligned} \nu =\frac{\mu _2 \omega -2 \kappa \mu _1}{1-\kappa \mu _2},\quad b k\ne 1. \end{aligned}$$

Hence the Eq. (9) reduces to

$$\begin{aligned} \mu _3 u F\left( u^2\right) -\delta u^5-4 \gamma \kappa ^2 u^3+\left( \mu _1-\mu _2 \nu \right) u''+u \left( \kappa \mu _2 \omega -\kappa ^2 \mu _1-\omega \right) =0. \end{aligned}$$

(11)

3.1 Ker law

Assume $F(u)=u$. The Eq. (1) reduces to

$$\begin{aligned} i q_t+\mu _1 q_{xx}+\mu _2 q_{xt}+\mu _3 |q|^2 q= & {} -2 \gamma q^* q_x^2 +2 \gamma |q_x|^2 q+\gamma |q|^2 q_{xx} \nonumber \\&-\gamma q^2 q_{xx}^*+\delta |q|^4 q, \end{aligned}$$

(12)

and Eq. (11) reduces to

$$\begin{aligned} \left( \mu _1-\mu _2 \nu \right) u''+u \left( -\kappa ^2 \mu _1+\kappa \mu _2 \omega -\omega \right) +u^3 \left( \mu _3-4 \gamma \kappa ^2\right) -\delta u^5=0, \end{aligned}$$

(13)

by setting $u=V^{\frac{1}{2}}$, the Eq. (13) becomes

$$\begin{aligned}&\left( \mu _1-\mu _2 \nu \right) \left( 2 V V''-\left( V'\right) ^2\right) +4 V^2 \left( -\kappa ^2 \mu _1+\kappa \mu _2 \omega -\omega \right) \nonumber \\&\quad +4 V^3 \left( \mu _3-4 \gamma \kappa ^2\right) -4 \delta V^4=0. \end{aligned}$$

(14)

By homogenous balance principle we get the positive integer $n=1$, so we suppose the solution of the form

$$\begin{aligned} V=a_0+a_1 \psi (\xi )+\frac{b_1}{\psi (\xi )}+d_1 \left( \frac{ \psi '(\xi )}{\psi (\xi )}\right) , \end{aligned}$$

(15)

where $a_0,~a_1,~b_1$ and $d_1$ are the constants to be determined. Substituting Eq. (15) along with its desired derivatives into Eq. (14) and by collecting the coefficients of $\psi (\xi ) \psi '(\xi )$ we get an algebraic system of equations. By solving that system, the following cases arise

• Family I

  $$\begin{aligned} \psi (\xi )=-\frac{4 \delta _1 e^{\sqrt{\delta _1} \xi }}{\delta _2^2 \left( -e^{2 \sqrt{\delta _1} \xi }\right) +2 \delta _2 e^{\sqrt{\delta _1} \xi }+4 \delta _1 \delta _3 e^{2 \sqrt{\delta _1} \xi }-1}. \end{aligned}$$

• Case I $a_0=\frac{3 \left( \mu _2^2 \mu _3-4 \gamma \right) }{8 \delta \mu _2^2},~a_1= 0,~b_1= 0,~d_1= \frac{\sqrt{3} \sqrt{\mu _1-\mu _2 \nu }}{2 \sqrt{\delta }},~\kappa = -\frac{1}{\mu _2},$

  $\omega = \frac{48 \gamma ^2-24 \gamma \mu _3 \mu _2^2-16 \delta \mu _1 \mu _2^2+3 \mu _3^2 \mu _2^4}{32 \delta \mu _2^4},~\delta _1= \frac{3 \left( \mu _2^2 \mu _3-4 \gamma \right) {}^2}{16 \delta \mu _2^4 \left( \mu _1-\mu _2 \nu \right) },~\delta _2= 0,~\delta _3= 0,$

  substituting values in Eq. (15) also using $u=V^{\frac{1}{2}}$ and by applying the reverse transformation (7), we get our solutions

  $$\begin{aligned}&q_{1}(x,t)=e^{i \phi } \sqrt{\frac{3 \left( \mu _2^2 \mu _3-4 \gamma \right) }{8 \delta \mu _2^2}+\frac{\sqrt{3} e^{\sqrt{\delta _1} (-\xi )} \sqrt{\delta _1^3 e^{2 \sqrt{\delta _1} \xi }} \sqrt{\mu _1-\mu _2 \nu }}{2 \sqrt{\delta } \delta _1}}, \end{aligned}$$

  (16)
  $$\begin{aligned}&q^*_{1}(x,t)=e^{-i \phi } \sqrt{\frac{3 \left( \mu _2^2 \mu _3-4 \gamma \right) }{8 \delta \mu _2^2}+\frac{\sqrt{3} e^{\sqrt{\delta _1} (-\xi )} \sqrt{\delta _1^3 e^{2 \sqrt{\delta _1} \xi }} \sqrt{\mu _1-\mu _2 \nu }}{2 \sqrt{\delta } \delta _1}}. \end{aligned}$$

  (17)

• Case II $a_0= \frac{3 \left( \mu _2^2 \mu _3-4 \gamma \right) }{8 \delta \mu _2^2},~a_1= 0,~b_1= 0,~d_1= -\frac{\sqrt{3} \sqrt{\mu _1-\mu _2 \nu }}{2 \sqrt{\delta }},~\kappa = -\frac{1}{\mu _2},$

  $\omega = \frac{48 \gamma ^2-24 \gamma \mu _3 \mu _2^2-16 \delta \mu _1 \mu _2^2+3 \mu _3^2 \mu _2^4}{32 \delta \mu _2^4},~\delta _1= \frac{3 \left( \mu _2^2 \mu _3-4 \gamma \right) {}^2}{16 \delta \mu _2^4 \left( \mu _1-\mu _2 \nu \right) },~\delta _2= 0,~\delta _3= 0,$

  substituting values in Eq. (15) also using $u=V^{\frac{1}{2}}$ and by applying the reverse transformation (7), we get our solutions

  $$\begin{aligned}&q_{2}(x,t)=e^{i \phi } \sqrt{\frac{3 \left( \mu _2^2 \mu _3-4 \gamma \right) }{8 \delta \mu _2^2}-\frac{\sqrt{3} e^{\sqrt{\delta _1} (-\xi )} \sqrt{\delta _1^3 e^{2 \sqrt{\delta _1} \xi }} \sqrt{\mu _1-\mu _2 \nu }}{2 \sqrt{\delta } \delta _1}}, \end{aligned}$$

  (18)
  $$\begin{aligned}&q^*_{2}(x,t)=e^{-i \phi } \sqrt{\frac{3 \left( \mu _2^2 \mu _3-4 \gamma \right) }{8 \delta \mu _2^2}-\frac{\sqrt{3} e^{\sqrt{\delta _1} (-\xi )} \sqrt{\delta _1^3 e^{2 \sqrt{\delta _1} \xi }} \sqrt{\mu _1-\mu _2 \nu }}{2 \sqrt{\delta } \delta _1}}. \end{aligned}$$

  (19)

• Case III $a_1=0,~b_1=0,~d_1=\frac{\sqrt{3} \sqrt{\mu _1-\mu _2 \nu }}{2 \sqrt{\delta }},~\kappa =\frac{\sqrt{3 \mu _3-8 a_0 \delta }}{2 \sqrt{3} \sqrt{\gamma }},~\delta _1=\frac{4 a_0^2 \delta }{3 \left( \mu _1-\mu _2 \nu \right) },$

  $\omega =\frac{\left( 8 a_0 \delta \left( 2 a_0 \gamma +\mu _1\right) -3 \mu _1 \mu _3\right) \left( \mu _2 \sqrt{9 \mu _3-24 a_0 \delta }+6 \sqrt{\gamma }\right) }{6 \sqrt{\gamma } \left( \mu _2^2 \left( 8 a_0 \delta -3 \mu _3\right) +12 \gamma \right) },~\delta _2=0,~\delta _3=0,$

  substituting values in Eq. (15) also using $u=V^{\frac{1}{2}}$ and by applying the reverse transformation (7), we get our solutions

  $$\begin{aligned}&q_{3}(x,t)=e^{i \phi } \sqrt{a_0+\frac{\sqrt{3} e^{\sqrt{\delta _1} (-\xi )} \sqrt{\delta _1^3 e^{2 \sqrt{\delta _1} \xi }} \sqrt{\mu _1-\mu _2 \nu }}{2 \sqrt{\delta } \delta _1}}, \end{aligned}$$

  (20)
  $$\begin{aligned}&q^*_{3}(x,t)=e^{-i \phi } \sqrt{a_0+\frac{\sqrt{3} e^{\sqrt{\delta _1} (-\xi )} \sqrt{\delta _1^3 e^{2 \sqrt{\delta _1} \xi }} \sqrt{\mu _1-\mu _2 \nu }}{2 \sqrt{\delta } \delta _1}}. \end{aligned}$$

  (21)

• Case IV $a_1=0,~b_1=0,~d_1=\frac{\kappa \left( \sqrt{3} \sqrt{\mu _1-\mu _2 \nu }\right) }{2 \sqrt{\delta }},~\kappa =-\frac{\sqrt{3 \mu _3-8 a_0 \delta }}{2 \sqrt{3} \sqrt{\gamma }},~\delta _2=0,~\delta _3=0,$

  $\omega =\frac{\left( 8 a_0 \delta \left( 2 a_0 \gamma +\mu _1\right) -3 \mu _1 \mu _3\right) \left( 6 \sqrt{\gamma }-\mu _2 \sqrt{9 \mu _3-24 a_0 \delta }\right) }{6 \sqrt{\gamma } \left( \mu _2^2 \left( 8 a_0 \delta -3 \mu _3\right) +12 \gamma \right) },~\delta _1=\frac{4 a_0^2 \delta }{3 \left( \mu _1-\mu _2 \nu \right) },$

  substituting values in Eq. (15) also using $u=V^{\frac{1}{2}}$ and by applying the reverse transformation (7), we get our solutions

  $$\begin{aligned}&q_{4}(x,t)=e^{i \phi } \sqrt{a_0+\frac{\sqrt{3} e^{\sqrt{\delta _1} (-\xi )} \sqrt{\delta _1^3 e^{2 \sqrt{\delta _1} \xi }} \sqrt{\mu _1-\mu _2 \nu }}{2 \sqrt{\delta } \delta _1}}, \end{aligned}$$

  (22)
  $$\begin{aligned}&q^*_{4}(x,t)=e^{-i \phi } \sqrt{a_0+\frac{\sqrt{3} e^{\sqrt{\delta _1} (-\xi )} \sqrt{\delta _1^3 e^{2 \sqrt{\delta _1} \xi }} \sqrt{\mu _1-\mu _2 \nu }}{2 \sqrt{\delta } \delta _1}}. \end{aligned}$$

  (23)

• Case V $a_1=0,~b_1=0,~d_1=-\frac{\sqrt{3} \sqrt{\mu _1-\mu _2 \nu }}{2 \sqrt{\delta }},\kappa =\frac{\sqrt{3 \mu _3-8 a_0 \delta }}{2 \sqrt{3} \sqrt{\gamma }},~\delta _2=0,~\delta _3=0,$

  $\omega =\frac{\left( 8 a_0 \delta \left( 2 a_0 \gamma +\mu _1\right) -3 \mu _1 \mu _3\right) \left( \mu _2 \sqrt{9 \mu _3-24 a_0 \delta }+6 \sqrt{\gamma }\right) }{6 \sqrt{\gamma } \left( \mu _2^2 \left( 8 a_0 \delta -3 \mu _3\right) +12 \gamma \right) },~\delta _1=\frac{4 a_0^2 \delta }{3 \left( \mu _1-\mu _2 \nu \right) },$

  substituting values in Eq. (15) also using $u=V^{\frac{1}{2}}$ and by applying the reverse transformation (7), we get our solutions

  $$\begin{aligned}&q_{5}(x,t)=e^{i \phi } \sqrt{a_0-\frac{\sqrt{3} e^{\sqrt{\delta _1} (-\xi )} \sqrt{\delta _1^3 e^{2 \sqrt{\delta _1} \xi }} \sqrt{\mu _1-\mu _2 \nu }}{2 \sqrt{\delta } \delta _1}}, \end{aligned}$$

  (24)
  $$\begin{aligned}&q^*_{5}(x,t)=e^{-i \phi } \sqrt{a_0-\frac{\sqrt{3} e^{\sqrt{\delta _1} (-\xi )} \sqrt{\delta _1^3 e^{2 \sqrt{\delta _1} \xi }} \sqrt{\mu _1-\mu _2 \nu }}{2 \sqrt{\delta } \delta _1}}. \end{aligned}$$

  (25)

• Case VI $a_1=0,~b_1=0,~d_1=-\frac{\sqrt{3} \sqrt{\mu _1-\mu _2 \nu }}{2 \sqrt{\delta }},~\kappa =-\frac{\sqrt{3 \mu _3-8 a_0 \delta }}{2 \sqrt{3} \sqrt{\gamma }},~\delta _2=0,~\delta _3=0,$

  $\omega =\frac{\left( 8 a_0 \delta \left( 2 a_0 \gamma +\mu _1\right) -3 \mu _1 \mu _3\right) \left( 6 \sqrt{\gamma }-\mu _2 \sqrt{9 \mu _3-24 a_0 \delta }\right) }{6 \sqrt{\gamma } \left( \mu _2^2 \left( 8 a_0 \delta -3 \mu _3\right) +12 \gamma \right) },~\delta _1=\frac{4 a_0^2 \delta }{3 \left( \mu _1-\mu _2 \nu \right) },$

  substituting values in Eq. (15) also using $u=V^{\frac{1}{2}}$ and by applying the reverse transformation (7), we get our solutions

  $$\begin{aligned}&q_{6}(x,t)=e^{i \phi } \sqrt{a_0-\frac{\sqrt{3} e^{\sqrt{\delta _1} (-\xi )} \sqrt{\delta _1^3 e^{2 \sqrt{\delta _1} \xi }} \sqrt{\mu _1-\mu _2 \nu }}{2 \sqrt{\delta } \delta _1}}, \end{aligned}$$

  (26)
  $$\begin{aligned}&q^*_{6}(x,t)=e^{-i \phi } \sqrt{a_0-\frac{\sqrt{3} e^{\sqrt{\delta _1} (-\xi )} \sqrt{\delta _1^3 e^{2 \sqrt{\delta _1} \xi }} \sqrt{\mu _1-\mu _2 \nu }}{2 \sqrt{\delta } \delta _1}}. \end{aligned}$$

  (27)

• Family II

  $$\begin{aligned} \psi (\xi )=\frac{4 \delta _1 e^{\sqrt{\delta _1} \xi }}{-2 \delta _2 e^{\sqrt{\delta _1} \xi }+e^{2 \sqrt{\delta _1} \xi }+\delta _2^2-4 \delta _1 \delta _3}. \end{aligned}$$

• Case I $a_0=\frac{3 \left( \mu _2^2 \mu _3-4 \gamma \right) }{8 \delta \mu _2^2},~a_1= 0,~b_1= 0,~d_1= \frac{\sqrt{3} \sqrt{\mu _1-\mu _2 \nu }}{2 \sqrt{\delta }},~\kappa = -\frac{1}{\mu _2},$

  $\omega = \frac{48 \gamma ^2-24 \gamma \mu _3 \mu _2^2-16 \delta \mu _1 \mu _2^2+3 \mu _3^2 \mu _2^4}{32 \delta \mu _2^4},~\delta _1= \frac{3 \left( \mu _2^2 \mu _3-4 \gamma \right) {}^2}{16 \delta \mu _2^4 \left( \mu _1-\mu _2 \nu \right) },~\delta _2= 0,~\delta _3= 0,$

  substituting values in Eq. (15) also using $u=V^{\frac{1}{2}}$ and by applying the reverse transformation (7), we get our solutions

  $$\begin{aligned}&q_{7}(x,t)=e^{i \phi } \sqrt{\frac{3 \left( \mu _2^2 \mu _3-4 \gamma \right) }{8 \delta \mu _2^2}+\frac{\sqrt{3} e^{\sqrt{\delta _1} \xi } \sqrt{\delta _1^3 e^{-2 \sqrt{\delta _1} \xi }} \sqrt{\mu _1-\mu _2 \nu }}{2 \sqrt{\delta } \delta _1}}, \end{aligned}$$

  (28)
  $$\begin{aligned}&q^*_{7}(x,t)=e^{-i \phi } \sqrt{\frac{3 \left( \mu _2^2 \mu _3-4 \gamma \right) }{8 \delta \mu _2^2}+\frac{\sqrt{3} e^{\sqrt{\delta _1} \xi } \sqrt{\delta _1^3 e^{-2 \sqrt{\delta _1} \xi }} \sqrt{\mu _1-\mu _2 \nu }}{2 \sqrt{\delta } \delta _1}}. \end{aligned}$$

  (29)

• Case II $a_0= \frac{3 \left( \mu _2^2 \mu _3-4 \gamma \right) }{8 \delta \mu _2^2},~a_1= 0,~b_1= 0,~d_1= -\frac{\sqrt{3} \sqrt{\mu _1-\mu _2 \nu }}{2 \sqrt{\delta }},~\kappa = -\frac{1}{\mu _2},$

  $\omega = \frac{48 \gamma ^2-24 \gamma \mu _3 \mu _2^2-16 \delta \mu _1 \mu _2^2+3 \mu _3^2 \mu _2^4}{32 \delta \mu _2^4},~\delta _1= \frac{3 \left( \mu _2^2 \mu _3-4 \gamma \right) {}^2}{16 \delta \mu _2^4 \left( \mu _1-\mu _2 \nu \right) },~\delta _2= 0,~\delta _3= 0,$

  substituting values in Eq. (15) also using $u=V^{\frac{1}{2}}$ and by applying the reverse transformation (7), we get our solutions

  $$\begin{aligned}&q_{8}(x,t)=e^{i \phi } \sqrt{\frac{3 \left( \mu _2^2 \mu _3-4 \gamma \right) }{8 \delta \mu _2^2}-\frac{\sqrt{3} e^{\sqrt{\delta _1} \xi } \sqrt{\delta _1^3 e^{-2 \sqrt{\delta _1} \xi }} \sqrt{\mu _1-\mu _2 \nu }}{2 \sqrt{\delta } \delta _1}}, \end{aligned}$$

  (30)
  $$\begin{aligned}&q^*_{8}(x,t)=e^{-i \phi } \sqrt{\frac{3 \left( \mu _2^2 \mu _3-4 \gamma \right) }{8 \delta \mu _2^2}-\frac{\sqrt{3} e^{\sqrt{\delta _1} \xi } \sqrt{\delta _1^3 e^{-2 \sqrt{\delta _1} \xi }} \sqrt{\mu _1-\mu _2 \nu }}{2 \sqrt{\delta } \delta _1}}. \end{aligned}$$

  (31)

• Case III $a_1=0,~b_1=0,~d_1=\frac{\sqrt{3} \sqrt{\mu _1-\mu _2 \nu }}{2 \sqrt{\delta }},~\kappa =\frac{\sqrt{3 \mu _3-8 a_0 \delta }}{2 \sqrt{3} \sqrt{\gamma }},~\delta _1=\frac{4 a_0^2 \delta }{3 \left( \mu _1-\mu _2 \nu \right) },$

  $\omega =\frac{\left( 8 a_0 \delta \left( 2 a_0 \gamma +\mu _1\right) -3 \mu _1 \mu _3\right) \left( \mu _2 \sqrt{9 \mu _3-24 a_0 \delta }+6 \sqrt{\gamma }\right) }{6 \sqrt{\gamma } \left( \mu _2^2 \left( 8 a_0 \delta -3 \mu _3\right) +12 \gamma \right) },~\delta _2=0,~\delta _3=0,$

  substituting values in Eq. (15) also using $u=V^{\frac{1}{2}}$ and by applying the reverse transformation (7), we get our solutions

  $$\begin{aligned}&q_{9}(x,t)=e^{i \phi } \sqrt{a_0+\frac{\sqrt{3} e^{\sqrt{\delta _1} \xi } \sqrt{\delta _1^3 e^{-2 \sqrt{\delta _1} \xi }} \sqrt{\mu _1-\mu _2 \nu }}{2 \sqrt{\delta } \delta _1}}, \end{aligned}$$

  (32)
  $$\begin{aligned}&q^*_{9}(x,t)=e^{-i \phi } \sqrt{a_0+\frac{\sqrt{3} e^{\sqrt{\delta _1} \xi } \sqrt{\delta _1^3 e^{-2 \sqrt{\delta _1} \xi }} \sqrt{\mu _1-\mu _2 \nu }}{2 \sqrt{\delta } \delta _1}}. \end{aligned}$$

  (33)

• Case IV $a_1=0,~b_1=0,~d_1=\frac{\kappa \left( \sqrt{3} \sqrt{\mu _1-\mu _2 \nu }\right) }{2 \sqrt{\delta }},~\kappa =-\frac{\sqrt{3 \mu _3-8 a_0 \delta }}{2 \sqrt{3} \sqrt{\gamma }},~\delta _2=0,~\delta _3=0,$

  $\omega =\frac{\left( 8 a_0 \delta \left( 2 a_0 \gamma +\mu _1\right) -3 \mu _1 \mu _3\right) \left( 6 \sqrt{\gamma }-\mu _2 \sqrt{9 \mu _3-24 a_0 \delta }\right) }{6 \sqrt{\gamma } \left( \mu _2^2 \left( 8 a_0 \delta -3 \mu _3\right) +12 \gamma \right) },~\delta _1=\frac{4 a_0^2 \delta }{3 \left( \mu _1-\mu _2 \nu \right) },$

  substituting values in Eq. (15) also using $u=V^{\frac{1}{2}}$ and by applying the reverse transformation (7), we get our solutions

  $$\begin{aligned}&q_{10}(x,t)=e^{i \phi } \sqrt{a_0+\frac{\sqrt{3} e^{\sqrt{\delta _1} \xi } \sqrt{\delta _1^3 e^{-2 \sqrt{\delta _1} \xi }} \sqrt{\mu _1-\mu _2 \nu }}{2 \sqrt{\delta } \delta _1}}, \end{aligned}$$

  (34)
  $$\begin{aligned}&q^*_{10}(x,t)=e^{-i \phi } \sqrt{a_0+\frac{\sqrt{3} e^{\sqrt{\delta _1} \xi } \sqrt{\delta _1^3 e^{-2 \sqrt{\delta _1} \xi }} \sqrt{\mu _1-\mu _2 \nu }}{2 \sqrt{\delta } \delta _1}}. \end{aligned}$$

  (35)

• Case V $a_1=0,~b_1=0,~d_1=-\frac{\sqrt{3} \sqrt{\mu _1-\mu _2 \nu }}{2 \sqrt{\delta }},\kappa =\frac{\sqrt{3 \mu _3-8 a_0 \delta }}{2 \sqrt{3} \sqrt{\gamma }},~\delta _2=0,~\delta _3=0,$

  $\omega =\frac{\left( 8 a_0 \delta \left( 2 a_0 \gamma +\mu _1\right) -3 \mu _1 \mu _3\right) \left( \mu _2 \sqrt{9 \mu _3-24 a_0 \delta }+6 \sqrt{\gamma }\right) }{6 \sqrt{\gamma } \left( \mu _2^2 \left( 8 a_0 \delta -3 \mu _3\right) +12 \gamma \right) },~\delta _1=\frac{4 a_0^2 \delta }{3 \left( \mu _1-\mu _2 \nu \right) },$

  substituting values in Eq. (15) also using $u=V^{\frac{1}{2}}$ and by applying the reverse transformation (7), we get our solutions

  $$\begin{aligned}&q_{11}(x,t)=e^{i \phi } \sqrt{a_0-\frac{\sqrt{3} e^{\sqrt{\delta _1} \xi } \sqrt{\delta _1^3 e^{-2 \sqrt{\delta _1} \xi }} \sqrt{\mu _1-\mu _2 \nu }}{2 \sqrt{\delta } \delta _1}}, \end{aligned}$$

  (36)
  $$\begin{aligned}&q^*_{11}(x,t)=e^{-i \phi } \sqrt{a_0-\frac{\sqrt{3} e^{\sqrt{\delta _1} \xi } \sqrt{\delta _1^3 e^{-2 \sqrt{\delta _1} \xi }} \sqrt{\mu _1-\mu _2 \nu }}{2 \sqrt{\delta } \delta _1}}. \end{aligned}$$

  (37)

• Case VI $a_1=0,~b_1=0,~d_1=-\frac{\sqrt{3} \sqrt{\mu _1-\mu _2 \nu }}{2 \sqrt{\delta }},~\kappa =-\frac{\sqrt{3 \mu _3-8 a_0 \delta }}{2 \sqrt{3} \sqrt{\gamma }},~\delta _2=0,~\delta _3=0,$

  $\omega =\frac{\left( 8 a_0 \delta \left( 2 a_0 \gamma +\mu _1\right) -3 \mu _1 \mu _3\right) \left( 6 \sqrt{\gamma }-\mu _2 \sqrt{9 \mu _3-24 a_0 \delta }\right) }{6 \sqrt{\gamma } \left( \mu _2^2 \left( 8 a_0 \delta -3 \mu _3\right) +12 \gamma \right) },~\delta _1=\frac{4 a_0^2 \delta }{3 \left( \mu _1-\mu _2 \nu \right) },$

  substituting values in Eq. (15) also using $u=V^{\frac{1}{2}}$ and by applying the reverse transformation (7), we get our solutions

  $$\begin{aligned}&q_{12}(x,t)=e^{i \phi } \sqrt{a_0-\frac{\sqrt{3} e^{\sqrt{\delta _1} \xi } \sqrt{\delta _1^3 e^{-2 \sqrt{\delta _1} \xi }} \sqrt{\mu _1-\mu _2 \nu }}{2 \sqrt{\delta } \delta _1}}, \end{aligned}$$

  (38)
  $$\begin{aligned}&q^*_{12}(x,t)=e^{-i \phi } \sqrt{a_0-\frac{\sqrt{3} e^{\sqrt{\delta _1} \xi } \sqrt{\delta _1^3 e^{-2 \sqrt{\delta _1} \xi }} \sqrt{\mu _1-\mu _2 \nu }}{2 \sqrt{\delta } \delta _1}}. \end{aligned}$$

  (39)

3.2 Parabolic law

Assume $F(u)=c_1 u+c_2 u^2$. The Eq. (1) reduces to

$$\begin{aligned}&i q_t+\mu _1 q_{xx}+\mu _2 q_{xt}+\left( c_1|q|^2+c_2|q|^4\right) *q=\end{aligned}$$

(40)

$$\begin{aligned}&-2 \gamma q^* q_x^2 +2 \gamma |q_x|^2 q+\gamma |q|^2q_{xx}-\gamma q^2 q^*_{xx}+\delta |q|^4 q, \end{aligned}$$

(41)

and Eq. (11) reduces to

$$\begin{aligned}&\left( \mu _1-\mu _2 \nu \right) u''+u \left( \kappa \mu _2 \omega -\kappa ^2 \mu _1-\omega \right) \nonumber \\&\quad +u^3 \left( c_1-4 \gamma \kappa ^2\right) +u^5 \left( c_2-\delta \right) =0. \end{aligned}$$

(42)

By setting $u=V^{\frac{1}{2}}$, the Eq. (42) becomes

$$\begin{aligned}&\left( \mu _1-\mu _2 \nu \right) \left( 2 V V''-\left( V'\right) ^2\right) +4 V^2 \left( -\kappa ^2 \mu _1+\kappa \mu _2 \omega -\omega \right) \nonumber \\&\quad +4 V^3 \left( c_1-4 \gamma \kappa ^2\right) +4 V^4 \left( c_2-\delta \right) =0. \end{aligned}$$

(43)

By homogenous balance principle we get the positive integer $n=1$, so we suppose the solution of the form

$$\begin{aligned} V=a_0+a_1 \psi (\xi )+\frac{b_1}{\psi (\xi )}+d_1 \left( \frac{ \psi '(\xi )}{\psi (\xi )}\right) , \end{aligned}$$

(44)

where $a_0,~a_1,~b_1$ and $d_1$ are the constants to be determined. Substituting Eq. (44) along with its desired derivatives into Eq. (43) and by collecting the coefficients of $\psi (\xi ) \psi '(\xi )$ we get an algebraic system of equations. By solving that system, the following cases arise

• Family I

  $$\begin{aligned} \psi (\xi )=-\frac{4 \delta _1 e^{\sqrt{\delta _1} \xi }}{\delta _2^2 \left( -e^{2 \sqrt{\delta _1} \xi }\right) +2 \delta _2 e^{\sqrt{\delta _1} \xi }+4 \delta _1 \delta _3 e^{2 \sqrt{\delta _1} \xi }-1}. \end{aligned}$$

• Case I $a_1=0,b_1=0,d_1=-\frac{\sqrt{3} \sqrt{\mu _1-\mu _2 \nu }}{2 \sqrt{\delta -c_2}},\delta _1=\frac{4 a_0^2 \left( \delta -c_2\right) }{3 \left( \mu _1-\mu _2 \nu \right) },\delta _2=0,\delta _3=0,$

  $\omega =\frac{-16 a_0^2 \gamma c_2+16 a_0^2 \gamma \delta -8 a_0 c_2 \mu _1+8 a_0 \delta \mu _1-3 c_1 \mu _1}{2 \sqrt{3} \sqrt{\gamma } \mu _2 \sqrt{8 a_0 c_2-8 a_0 \delta +3 c_1}+12 \gamma },\kappa =-\frac{\sqrt{8 a_0 c_2-8 a_0 \delta +3 c_1}}{2 \sqrt{3} \sqrt{\gamma }},$

  substituting values in Eq. (44) also using $u=V^{\frac{1}{2}}$ and by applying the reverse transformation (7), we get our solutions

  $$\begin{aligned}&q_{13}(x,t)=e^{i \phi } \sqrt{a_0-\frac{\sqrt{3} e^{\sqrt{\delta _1} (-\xi )} \sqrt{\delta _1^3 e^{2 \sqrt{\delta _1} \xi }} \sqrt{\mu _1-\mu _2 \nu }}{2 \delta _1 \sqrt{\delta -c_2}}}, \end{aligned}$$

  (45)
  $$\begin{aligned}&q^*_{13}(x,t)=e^{-i \phi } \sqrt{a_0-\frac{\sqrt{3} e^{\sqrt{\delta _1} (-\xi )} \sqrt{\delta _1^3 e^{2 \sqrt{\delta _1} \xi }} \sqrt{\mu _1-\mu _2 \nu }}{2 \delta _1 \sqrt{\delta -c_2}}}. \end{aligned}$$

  (46)

• Case II $a_1=0,b_1=0,d_1=\frac{\sqrt{3} \sqrt{\mu _1-\mu _2 \nu }}{2 \sqrt{\delta -c_2}},\delta _1=\frac{4 a_0^2 \left( \delta -c_2\right) }{3 \left( \mu _1-\mu _2 \nu \right) },\delta _2=0,\delta _3=0,$ $\omega =\frac{-16 a_0^2 \gamma c_2+16 a_0^2 \gamma \delta -8 a_0 c_2 \mu _1+8 a_0 \delta \mu _1-3 c_1 \mu _1}{2 \sqrt{3} \sqrt{\gamma } \mu _2 \sqrt{8 a_0 c_2-8 a_0 \delta +3 c_1}+12 \gamma },\kappa =-\frac{\sqrt{8 a_0 c_2-8 a_0 \delta +3 c_1}}{2 \sqrt{3} \sqrt{\gamma }},$ substituting values in Eq. (44) also using $u=V^{\frac{1}{2}}$ and by applying the reverse transformation (7), we get our solutions

  $$\begin{aligned}&q_{14}(x,t)=e^{i \phi } \sqrt{a_0+\frac{\sqrt{3} e^{\sqrt{\delta _1} (-\xi )} \sqrt{\delta _1^3 e^{2 \sqrt{\delta _1} \xi }} \sqrt{\mu _1-\mu _2 \nu }}{2 \delta _1 \sqrt{\delta -c_2}}}, \end{aligned}$$

  (47)
  $$\begin{aligned}&q^*_{14}(x,t)=e^{-i \phi } \sqrt{a_0+\frac{\sqrt{3} e^{\sqrt{\delta _1} (-\xi )} \sqrt{\delta _1^3 e^{2 \sqrt{\delta _1} \xi }} \sqrt{\mu _1-\mu _2 \nu }}{2 \delta _1 \sqrt{\delta -c_2}}}. \end{aligned}$$

  (48)

• Case III $a_1=0,b_1=0,d_1=\frac{\sqrt{3} \sqrt{\mu _1-\mu _2 \nu }}{2 \sqrt{\delta -c_2}},\delta _1=\frac{4 a_0^2 \left( \delta -c_2\right) }{3 \left( \mu _1-\mu _2 \nu \right) },\delta _2=0,\delta _3=0,$

  $\omega =\frac{16 a_0^2 \gamma c_2-16 a_0^2 \gamma \delta +8 a_0 c_2 \mu _1-8 a_0 \delta \mu _1+3 c_1 \mu _1}{2 \left( \sqrt{3} \sqrt{\gamma } \mu _2 \sqrt{8 a_0 c_2-8 a_0 \delta +3 c_1}-6 \gamma \right) },\kappa =\frac{\sqrt{8 a_0 c_2-8 a_0 \delta +3 c_1}}{2 \sqrt{3} \sqrt{\gamma }},$

  substituting values in Eq. (44) also using $u=V^{\frac{1}{2}}$ and by applying the reverse transformation (7), we get our solutions

  $$\begin{aligned}&q_{15}(x,t)=e^{i \phi } \sqrt{a_0+\frac{\sqrt{3} e^{\sqrt{\delta _1} (-\xi )} \sqrt{\delta _1^3 e^{2 \sqrt{\delta _1} \xi }} \sqrt{\mu _1-\mu _2 \nu }}{2 \delta _1 \sqrt{\delta -c_2}}}, \end{aligned}$$

  (49)
  $$\begin{aligned}&q^*_{15}(x,t)=e^{-i \phi } \sqrt{a_0+\frac{\sqrt{3} e^{\sqrt{\delta _1} (-\xi )} \sqrt{\delta _1^3 e^{2 \sqrt{\delta _1} \xi }} \sqrt{\mu _1-\mu _2 \nu }}{2 \delta _1 \sqrt{\delta -c_2}}}. \end{aligned}$$

  (50)

• Family II

  $$\begin{aligned} \psi (\xi )=\frac{4 \delta _1 e^{\sqrt{\delta _1} \xi }}{-2 \delta _2 e^{\sqrt{\delta _1} \xi }+e^{2 \sqrt{\delta _1} \xi }+\delta _2^2-4 \delta _1 \delta _3}. \end{aligned}$$

• Case I $a_1=0,b_1=0,d_1=-\frac{\sqrt{3} \sqrt{\mu _1-\mu _2 \nu }}{2 \sqrt{\delta -c_2}},\delta _1=\frac{4 a_0^2 \left( \delta -c_2\right) }{3 \left( \mu _1-\mu _2 \nu \right) },\delta _2=0,\delta _3=0,$

  $\omega =\frac{-16 a_0^2 \gamma c_2+16 a_0^2 \gamma \delta -8 a_0 c_2 \mu _1+8 a_0 \delta \mu _1-3 c_1 \mu _1}{2 \sqrt{3} \sqrt{\gamma } \mu _2 \sqrt{8 a_0 c_2-8 a_0 \delta +3 c_1}+12 \gamma },\kappa =-\frac{\sqrt{8 a_0 c_2-8 a_0 \delta +3 c_1}}{2 \sqrt{3} \sqrt{\gamma }},$

  substituting values in Eq. (44) also using $u=V^{\frac{1}{2}}$ and by applying the reverse transformation (7), we get our solutions

  $$\begin{aligned}&q_{16}(x,t)=e^{i \phi } \sqrt{a_0-\frac{\sqrt{3} e^{\sqrt{\delta _1} \xi } \sqrt{\delta _1^3 e^{-2 \sqrt{\delta _1} \xi }} \sqrt{\mu _1-\mu _2 \nu }}{2 \delta _1 \sqrt{\delta -c_2}}}, \end{aligned}$$

  (51)
  $$\begin{aligned}&q^*_{16}(x,t)=e^{-i \phi } \sqrt{a_0-\frac{\sqrt{3} e^{\sqrt{\delta _1} \xi } \sqrt{\delta _1^3 e^{-2 \sqrt{\delta _1} \xi }} \sqrt{\mu _1-\mu _2 \nu }}{2 \delta _1 \sqrt{\delta -c_2}}}. \end{aligned}$$

  (52)

• Case II $a_1=0,b_1=0,d_1=\frac{\sqrt{3} \sqrt{\mu _1-\mu _2 \nu }}{2 \sqrt{\delta -c_2}},\delta _1=\frac{4 a_0^2 \left( \delta -c_2\right) }{3 \left( \mu _1-\mu _2 \nu \right) },\delta _2=0,\delta _3=0,$

  $\omega =\frac{-16 a_0^2 \gamma c_2+16 a_0^2 \gamma \delta -8 a_0 c_2 \mu _1+8 a_0 \delta \mu _1-3 c_1 \mu _1}{2 \sqrt{3} \sqrt{\gamma } \mu _2 \sqrt{8 a_0 c_2-8 a_0 \delta +3 c_1}+12 \gamma },\kappa =-\frac{\sqrt{8 a_0 c_2-8 a_0 \delta +3 c_1}}{2 \sqrt{3} \sqrt{\gamma }},$

  substituting values in Eq. (44) also using $u=V^{\frac{1}{2}}$ and by applying the reverse transformation (7), we get our solutions

  $$\begin{aligned}&q_{17}(x,t)=e^{i \phi } \sqrt{a_0+\frac{\sqrt{3} e^{\sqrt{\delta _1} \xi } \sqrt{\delta _1^3 e^{-2 \sqrt{\delta _1} \xi }} \sqrt{\mu _1-\mu _2 \nu }}{2 \delta _1 \sqrt{\delta -c_2}}}, \end{aligned}$$

  (53)
  $$\begin{aligned}&q^*_{17}(x,t)=e^{-i \phi } \sqrt{a_0+\frac{\sqrt{3} e^{\sqrt{\delta _1} \xi } \sqrt{\delta _1^3 e^{-2 \sqrt{\delta _1} \xi }} \sqrt{\mu _1-\mu _2 \nu }}{2 \delta _1 \sqrt{\delta -c_2}}}. \end{aligned}$$

  (54)

• Case III $a_1=0,b_1=0,d_1=\frac{\sqrt{3} \sqrt{\mu _1-\mu _2 \nu }}{2 \sqrt{\delta -c_2}},\delta _1=\frac{4 a_0^2 \left( \delta -c_2\right) }{3 \left( \mu _1-\mu _2 \nu \right) },\delta _2=0,\delta _3=0,$

  $\omega =\frac{16 a_0^2 \gamma c_2-16 a_0^2 \gamma \delta +8 a_0 c_2 \mu _1-8 a_0 \delta \mu _1+3 c_1 \mu _1}{2 \left( \sqrt{3} \sqrt{\gamma } \mu _2 \sqrt{8 a_0 c_2-8 a_0 \delta +3 c_1}-6 \gamma \right) },\kappa =\frac{\sqrt{8 a_0 c_2-8 a_0 \delta +3 c_1}}{2 \sqrt{3} \sqrt{\gamma }},$

  substituting values in Eq. (44) also using $u=V^{\frac{1}{2}}$ and by applying the reverse transformation (7), we get our solutions

  $$\begin{aligned}&q_{18}(x,t)=e^{i \phi } \sqrt{a_0+\frac{\sqrt{3} e^{\sqrt{\delta _1} \xi } \sqrt{\delta _1^3 e^{-2 \sqrt{\delta _1} \xi }} \sqrt{\mu _1-\mu _2 \nu }}{2 \delta _1 \sqrt{\delta -c_2}}}, \end{aligned}$$

  (55)
  $$\begin{aligned}&q^*_{18}(x,t)=e^{-i \phi } \sqrt{a_0+\frac{\sqrt{3} e^{\sqrt{\delta _1} \xi } \sqrt{\delta _1^3 e^{-2 \sqrt{\delta _1} \xi }} \sqrt{\mu _1-\mu _2 \nu }}{2 \delta _1 \sqrt{\delta -c_2}}}. \end{aligned}$$

  (56)

3.3 Anti-cubic law

Assume $F(u)=\frac{c_1}{u^2}++c_2 u+c_3 u^2$, the Eq. (1) reduces to

$$\begin{aligned}&i q_t+\mu _1 q_{xx}+\mu _2 q_{xt}+\left( c_1 |q|^{-4}+c_2|q|^2+c_3 |q|^4\right) *q \nonumber \\&\quad =-2 \gamma q^* q_x^2+2 \gamma |q_x|^2q+\gamma |q|^2 q_{xx}-\gamma q^2 q^*_{xx}+\delta |q|^4 q, \end{aligned}$$

(57)

and Eq. (11) reduces to

$$\begin{aligned}&\left( \mu _1-\mu _2 \nu \right) u''+u \left( -\kappa ^2 \mu _1+\kappa \mu _2 \omega -\omega \right) \nonumber \\&\quad +u^3 \left( c_2-4 \gamma \kappa ^2\right) +c_1 u^{-3}+u^5 \left( c_3-\delta \right) =0. \end{aligned}$$

(58)

By setting $u=V^{\frac{1}{2}}$, the Eq. (58) becomes

$$\begin{aligned}&\left( \mu _1-\mu _2 \nu \right) \left( 2 V V''-\left( V'\right) ^2\right) +4 V^2 \left( -\kappa ^2 \mu _1+\kappa \mu _2 \omega -\omega \right) \nonumber \\&\quad +4 V^3 \left( c_2-4 \gamma \kappa ^2\right) +4 c_1+4 V^4 \left( c_3-\delta \right) =0. \end{aligned}$$

(59)

By homogenous balance principle we get the positive integer $n=1$, so we suppose the solution of the form

$$\begin{aligned} V=a_0+a_1 \psi (\xi )+\frac{b_1}{\psi (\xi )}+d_1 \left( \frac{ \psi '(\xi )}{\psi (\xi )}\right) , \end{aligned}$$

(60)

where $a_0,~a_1,~b_1$ and $d_1$ are the constants to be determined. Substituting Eq. (60) along with its desired derivatives into Eq. (59) and by collecting the coefficients of $\psi (\xi ) \psi '(\xi )$ we get an algebraic system of equations. By solving that system, the following cases arise

• Family I

  $$\begin{aligned} \psi (\xi )=-\frac{4 \delta _1 e^{\sqrt{\delta _1} \xi }}{\delta _2^2 \left( -e^{2 \sqrt{\delta _1} \xi }\right) +2 \delta _2 e^{\sqrt{\delta _1} \xi }+4 \delta _1 \delta _3 e^{2 \sqrt{\delta _1} \xi }-1}. \end{aligned}$$

• Case I $a_1=0,b_1=0,d_1=-\frac{\sqrt{3} \sqrt{\mu _1-\mu _2 \nu }}{2 \sqrt{\delta -c_3}},\gamma =\frac{8 a_0 \left( c_3-\delta \right) +3 c_2}{12 \kappa ^2},$

  $\delta _1=\frac{4 \left( a_0^2 \left( \delta -c_3\right) \left( \mu _1-\mu _2 \nu \right) +\sqrt{3} \sqrt{c_1 \left( \delta -c_3\right) \left( \mu _1-\mu _2 \nu \right) {}^2}\right) }{3 \left( \mu _1-\mu _2 \nu \right) {}^2},\delta _2=0,\delta _3=0,$

  $\omega =\frac{\left( \mu _1-\mu _2 \nu \right) \left( 4 a_0^2 \left( \delta -c_3\right) -3 \kappa ^2 \mu _1\right) -2 \sqrt{3} \sqrt{c_1 \left( \delta -c_3\right) \left( \mu _1-\mu _2 \nu \right) {}^2}}{3 \left( \kappa \mu _2-1\right) \left( \mu _2 \nu -\mu _1\right) },$

  substituting values in Eq. (60) also using $u=V^{\frac{1}{2}}$ and by applying the reverse transformation (7), we get our solutions

  $$\begin{aligned}&q_{19}(x,t)=e^{i \phi } \sqrt{a_0-\frac{\sqrt{3} e^{\sqrt{\delta _1} (-\xi )} \sqrt{\delta _1^3 e^{2 \sqrt{\delta _1} \xi }} \sqrt{\mu _1-\mu _2 \nu }}{2 \delta _1 \sqrt{\delta -c_3}}}, \end{aligned}$$

  (61)
  $$\begin{aligned}&q^*_{19}(x,t)=e^{-i \phi } \sqrt{a_0-\frac{\sqrt{3} e^{\sqrt{\delta _1} (-\xi )} \sqrt{\delta _1^3 e^{2 \sqrt{\delta _1} \xi }} \sqrt{\mu _1-\mu _2 \nu }}{2 \delta _1 \sqrt{\delta -c_3}}}. \end{aligned}$$

  (62)

• Case II $a_1=0,b_1=0,d_1=\frac{\sqrt{3} \sqrt{\mu _1-\mu _2 \nu }}{2 \sqrt{\delta -c_3}},\gamma =\frac{8 a_0 \left( c_3-\delta \right) +3 c_2}{12 \kappa ^2},$

  $\delta _1=\frac{4 \left( a_0^2 \left( \delta -c_3\right) \left( \mu _1-\mu _2 \nu \right) +\sqrt{3} \sqrt{c_1 \left( \delta -c_3\right) \left( \mu _1-\mu _2 \nu \right) {}^2}\right) }{3 \left( \mu _1-\mu _2 \nu \right) {}^2},\delta _2=0,\delta _3=0,$

  $\omega =\frac{\left( \mu _1-\mu _2 \nu \right) \left( 4 a_0^2 \left( \delta -c_3\right) -3 \kappa ^2 \mu _1\right) -2 \sqrt{3} \sqrt{c_1 \left( \delta -c_3\right) \left( \mu _1-\mu _2 \nu \right) {}^2}}{3 \left( \kappa \mu _2-1\right) \left( \mu _2 \nu -\mu _1\right) },$

  substituting values in Eq. (60) also using $u=V^{\frac{1}{2}}$ and by applying the reverse transformation (7), we get our solutions

  $$\begin{aligned}&q_{20}(x,t)=e^{i \phi } \sqrt{a_0+\frac{\sqrt{3} e^{\sqrt{\delta _1} (-\xi )} \sqrt{\delta _1^3 e^{2 \sqrt{\delta _1} \xi }} \sqrt{\mu _1-\mu _2 \nu }}{2 \delta _1 \sqrt{\delta -c_3}}}, \end{aligned}$$

  (63)
  $$\begin{aligned}&q^*_{20}(x,t)=e^{-i \phi } \sqrt{a_0+\frac{\sqrt{3} e^{\sqrt{\delta _1} (-\xi )} \sqrt{\delta _1^3 e^{2 \sqrt{\delta _1} \xi }} \sqrt{\mu _1-\mu _2 \nu }}{2 \delta _1 \sqrt{\delta -c_3}}}. \end{aligned}$$

  (64)

• Case III $a_0=-\frac{1}{2} \sqrt{\frac{3 \mu _1 \mu _2^2 \left( \delta -c_3\right) -2 \sqrt{3} \sqrt{c_1 \mu _2^8 \left( \delta -c_3\right) {}^3}}{\mu _2^4 \left( \delta -c_3\right) {}^2}},a_1=0,b_1=0,d_1=-\frac{\sqrt{3} \sqrt{\mu _1-\mu _2 \nu }}{2 \sqrt{\delta -c_3}},$

  $\gamma =\frac{1}{12} \mu _2^2 \left( 4 \left( \delta -c_3\right) \sqrt{\frac{3 \mu _1 \mu _2^2 \left( \delta -c_3\right) -2 \sqrt{3} \sqrt{c_1 \mu _2^8 \left( \delta -c_3\right) {}^3}}{\mu _2^4 \left( \delta -c_3\right) {}^2}}+3 c_2\right) ,\kappa =\frac{1}{\mu _2},$

  $\delta _1=\frac{\mu _1 \mu _2^2 \left( c_3-\delta \right) +2 \sqrt{3} \sqrt{c_1 \mu _2^8 \left( \delta -c_3\right) {}^3}}{\mu _2^4 \left( \delta -c_3\right) \left( \mu _2 \nu -\mu _1\right) },\delta _2=0,\delta _3=0,$

  substituting values in Eq. (60) also using $u=V^{\frac{1}{2}}$ and by applying the reverse transformation (7), we get our solutions

  $$\begin{aligned} q_{21}(x,t)= & {} e^{i \phi } \times \Bigg (-\frac{\sqrt{3} e^{\sqrt{\delta _1} (-\xi )} \sqrt{\delta _1^3 e^{2 \sqrt{\delta _1} \xi }} \sqrt{\mu _1-\mu _2 \nu }}{2 \delta _1 \sqrt{\delta -c_3}}\nonumber \\&\quad -\frac{1}{2} \sqrt{\frac{3 \mu _1 \mu _2^2 \left( \delta -c_3\right) -2 \sqrt{3} \sqrt{c_1 \mu _2^8 \left( \delta -c_3\right) {}^3}}{\mu _2^4 \left( \delta -c_3\right) {}^2}}\Bigg )^{\frac{1}{2}}, \end{aligned}$$

  (65)
  $$\begin{aligned} q^*_{21}(x,t)= & {} e^{-i \phi } \times \Bigg (-\frac{\sqrt{3} e^{\sqrt{\delta _1} (-\xi )} \sqrt{\delta _1^3 e^{2 \sqrt{\delta _1} \xi }} \sqrt{\mu _1-\mu _2 \nu }}{2 \delta _1 \sqrt{\delta -c_3}}\nonumber \\&\quad -\frac{1}{2} \sqrt{\frac{3 \mu _1 \mu _2^2 \left( \delta -c_3\right) -2 \sqrt{3} \sqrt{c_1 \mu _2^8 \left( \delta -c_3\right) {}^3}}{\mu _2^4 \left( \delta -c_3\right) {}^2}}\Bigg )^{\frac{1}{2}}. \end{aligned}$$

  (66)

• Case IV $a_0=-\frac{1}{2} \sqrt{\frac{3 \mu _1 \mu _2^2 \left( \delta -c_3\right) -2 \sqrt{3} \sqrt{c_1 \mu _2^8 \left( \delta -c_3\right) {}^3}}{\mu _2^4 \left( \delta -c_3\right) {}^2}},a_1=0,b_1=0,d_1=\frac{\sqrt{3} \sqrt{\mu _1-\mu _2 \nu }}{2 \sqrt{\delta -c_3}},$

  $\gamma =\frac{1}{12} \mu _2^2 \left( 4 \left( \delta -c_3\right) \sqrt{\frac{3 \mu _1 \mu _2^2 \left( \delta -c_3\right) -2 \sqrt{3} \sqrt{c_1 \mu _2^8 \left( \delta -c_3\right) {}^3}}{\mu _2^4 \left( \delta -c_3\right) {}^2}}+3 c_2\right) ,\kappa =\frac{1}{\mu _2},$

  $\delta _1=\frac{\mu _1 \mu _2^2 \left( c_3-\delta \right) +2 \sqrt{3} \sqrt{c_1 \mu _2^8 \left( \delta -c_3\right) {}^3}}{\mu _2^4 \left( \delta -c_3\right) \left( \mu _2 \nu -\mu _1\right) },\delta _2=0,\delta _3=0,$

  substituting values in Eq. (60) also using $u=V^{\frac{1}{2}}$ and by applying the reverse transformation (7), we get our solutions

  $$\begin{aligned} q_{22}(x,t)&= {} e^{i \phi } \times \left(\frac{\sqrt{3} e^{\sqrt{\delta _1} (-\xi )} \sqrt{\delta _1^3 e^{2 \sqrt{\delta _1} \xi }} \sqrt{\mu _1-\mu _2 \nu }}{2 \delta _1 \sqrt{\delta -c_3}} \right. \nonumber \\&\quad - \left.\frac{1}{2} \sqrt{\frac{3 \mu _1 \mu _2^2 \left( \delta -c_3\right) -2 \sqrt{3} \sqrt{c_1 \mu _2^8 \left( \delta -c_3\right) {}^3}}{\mu _2^4 \left( \delta -c_3\right) {}^2}}\right)^{\frac{1}{2}}, \end{aligned}$$

  (67)
  $$\begin{aligned} q^*_{22}(x,t)&= {} e^{-i \phi }\times \left(\frac{\sqrt{3} e^{\sqrt{\delta _1} (-\xi )} \sqrt{\delta _1^3 e^{2 \sqrt{\delta _1} \xi }} \sqrt{\mu _1-\mu _2 \nu }}{2 \delta _1 \sqrt{\delta -c_3}} \right. \nonumber \\&\quad - \left. \frac{1}{2} \sqrt{\frac{3 \mu _1 \mu _2^2 \left( \delta -c_3\right) -2 \sqrt{3} \sqrt{c_1 \mu _2^8 \left( \delta -c_3\right) {}^3}}{\mu _2^4 \left( \delta -c_3\right) {}^2}}\right)^{\frac{1}{2}}. \end{aligned}$$

  (68)

• Case V $a_0=\frac{1}{2} \sqrt{\frac{3 \mu _1 \mu _2^2 \left( \delta -c_3\right) -2 \sqrt{3} \sqrt{c_1 \mu _2^8 \left( \delta -c_3\right) {}^3}}{\mu _2^4 \left( \delta -c_3\right) {}^2}},a_1=0,b_1=0,d_1=-\frac{\sqrt{3} \sqrt{\mu _1-\mu _2 \nu }}{2 \sqrt{\delta -c_3}},$

  $\gamma =\frac{1}{12} \mu _2^2 \left( 4 \left( c_3-\delta \right) \sqrt{\frac{3 \mu _1 \mu _2^2 \left( \delta -c_3\right) -2 \sqrt{3} \sqrt{c_1 \mu _2^8 \left( \delta -c_3\right) {}^3}}{\mu _2^4 \left( \delta -c_3\right) {}^2}}+3 c_2\right) ,\kappa =\frac{1}{\mu _2},$

  $\delta _1=\frac{\mu _1 \mu _2^2 \left( c_3-\delta \right) +2 \sqrt{3} \sqrt{c_1 \mu _2^8 \left( \delta -c_3\right) {}^3}}{\mu _2^4 \left( \delta -c_3\right) \left( \mu _2 \nu -\mu _1\right) },\delta _2=0,\delta _3=0,$

  substituting values in Eq. (60) also using $u=V^{\frac{1}{2}}$ and by applying the reverse transformation (7), we get our solutions

  $$\begin{aligned} q_{23}(x,t)= & {} e^{i \phi }\times \Bigg (\frac{1}{2} \sqrt{\frac{3 \mu _1 \mu _2^2 \left( \delta -c_3\right) -2 \sqrt{3} \sqrt{c_1 \mu _2^8 \left( \delta -c_3\right) {}^3}}{\mu _2^4 \left( \delta -c_3\right) {}^2}}\nonumber \\&\quad -\frac{\sqrt{3} e^{\sqrt{\delta _1} (-\xi )} \sqrt{\delta _1^3 e^{2 \sqrt{\delta _1} \xi }} \sqrt{\mu _1-\mu _2 \nu }}{2 \delta _1 \sqrt{\delta -c_3}}\Bigg )^{\frac{1}{2}}, \end{aligned}$$

  (69)
  $$\begin{aligned} q^*_{23}(x,t)= & {} e^{-i \phi }\times \Bigg (\frac{1}{2} \sqrt{\frac{3 \mu _1 \mu _2^2 \left( \delta -c_3\right) -2 \sqrt{3} \sqrt{c_1 \mu _2^8 \left( \delta -c_3\right) {}^3}}{\mu _2^4 \left( \delta -c_3\right) {}^2}}\nonumber \\&\quad -\frac{\sqrt{3} e^{\sqrt{\delta _1} (-\xi )} \sqrt{\delta _1^3 e^{2 \sqrt{\delta _1} \xi }} \sqrt{\mu _1-\mu _2 \nu }}{2 \delta _1 \sqrt{\delta -c_3}}\Bigg )^{\frac{1}{2}}. \end{aligned}$$

  (70)

• Case VI $a_0=\frac{1}{2} \sqrt{\frac{3 \mu _1 \mu _2^2 \left( \delta -c_3\right) -2 \sqrt{3} \sqrt{c_1 \mu _2^8 \left( \delta -c_3\right) {}^3}}{\mu _2^4 \left( \delta -c_3\right) {}^2}},a_1=0,b_1=0,d_1=\frac{\sqrt{3} \sqrt{\mu _1-\mu _2 \nu }}{2 \sqrt{\delta -c_3}}$

  $\gamma =\frac{1}{12} \mu _2^2 \left( 4 \left( c_3-\delta \right) \sqrt{\frac{3 \mu _1 \mu _2^2 \left( \delta -c_3\right) -2 \sqrt{3} \sqrt{c_1 \mu _2^8 \left( \delta -c_3\right) {}^3}}{\mu _2^4 \left( \delta -c_3\right) {}^2}}+3 c_2\right) ,\kappa =\frac{1}{\mu _2},$

  $\delta _1=\frac{\mu _1 \mu _2^2 \left( c_3-\delta \right) +2 \sqrt{3} \sqrt{c_1 \mu _2^8 \left( \delta -c_3\right) {}^3}}{\mu _2^4 \left( \delta -c_3\right) \left( \mu _2 \nu -\mu _1\right) },\delta _2=0,\delta _3=0,$

  substituting values in Eq. (60) also using $u=V^{\frac{1}{2}}$ and by applying the reverse transformation (7), we get our solutions

  $$\begin{aligned} q_{24}(x,t)= & {} e^{i \phi }\times \Bigg (\frac{\sqrt{3} e^{\sqrt{\delta _1} (-\xi )} \sqrt{\delta _1^3 e^{2 \sqrt{\delta _1} \xi }} \sqrt{\mu _1-\mu _2 \nu }}{2 \delta _1 \sqrt{\delta -c_3}}\nonumber \\&\quad +\frac{1}{2} \sqrt{\frac{3 \mu _1 \mu _2^2 \left( \delta -c_3\right) -2 \sqrt{3} \sqrt{c_1 \mu _2^8 \left( \delta -c_3\right) {}^3}}{\mu _2^4 \left( \delta -c_3\right) {}^2}}\Bigg )^{\frac{1}{2}}, \end{aligned}$$

  (71)
  $$\begin{aligned} q^*_{24}(x,t)&= {} e^{-i \phi }\times \left(\frac{\sqrt{3} e^{\sqrt{\delta _1} (-\xi )} \sqrt{\delta _1^3 e^{2 \sqrt{\delta _1} \xi }} \sqrt{\mu _1-\mu _2 \nu }}{2 \delta _1 \sqrt{\delta -c_3}} \right. \nonumber \\&\quad +\left. \frac{1}{2} \sqrt{\frac{3 \mu _1 \mu _2^2 \left( \delta -c_3\right) -2 \sqrt{3} \sqrt{c_1 \mu _2^8 \left( \delta -c_3\right) {}^3}}{\mu _2^4 \left( \delta -c_3\right) {}^2}}\right)^{\frac{1}{2}}. \end{aligned}$$

  (72)

• Case VII $a_0=-\frac{1}{2} \sqrt{\frac{3 \mu _1 \mu _2^2 \left( \delta -c_3\right) +2 \sqrt{3} \sqrt{c_1 \mu _2^8 \left( \delta -c_3\right) {}^3}}{\mu _2^4 \left( \delta -c_3\right) {}^2}},a_1=0,b_1=0,d_1=-\frac{\sqrt{3} \sqrt{\mu _1-\mu _2 \nu }}{2 \sqrt{\delta -c_3}},$

  $\gamma =\frac{1}{12} \mu _2^2 \left( 4 \left( \delta -c_3\right) \sqrt{\frac{3 \mu _1 \mu _2^2 \left( \delta -c_3\right) +2 \sqrt{3} \sqrt{c_1 \mu _2^8 \left( \delta -c_3\right) {}^3}}{\mu _2^4 \left( \delta -c_3\right) {}^2}}+3 c_2\right) ,\kappa =\frac{1}{\mu _2},$

  $\delta _1=\frac{\mu _1 \mu _2^2 \left( c_3-\delta \right) -2 \sqrt{3} \sqrt{c_1 \mu _2^8 \left( \delta -c_3\right) {}^3}}{\mu _2^4 \left( \delta -c_3\right) \left( \mu _2 \nu -\mu _1\right) },\delta _2=0,\delta _3=0,$

  substituting values in Eq. (60) also using $u=V^{\frac{1}{2}}$ and by applying the reverse transformation (7), we get our solutions

  $$\begin{aligned} q_{25}(x,t)&= {} e^{i \phi }\times \left(-\frac{\sqrt{3} e^{\sqrt{\delta _1} (-\xi )} \sqrt{\delta _1^3 e^{2 \sqrt{\delta _1} \xi }} \sqrt{\mu _1-\mu _2 \nu }}{2 \delta _1 \sqrt{\delta -c_3}} \right. \nonumber \\&\quad -\left. \frac{1}{2} \sqrt{\frac{3 \mu _1 \mu _2^2 \left( \delta -c_3\right) +2 \sqrt{3} \sqrt{c_1 \mu _2^8 \left( \delta -c_3\right) {}^3}}{\mu _2^4 \left( \delta -c_3\right) {}^2}}\right)^{\frac{1}{2}}, \end{aligned}$$

  (73)
  $$\begin{aligned} q^*_{25}(x,t)&= {} e^{-i \phi }\times \left (-\frac{\sqrt{3} e^{\sqrt{\delta _1} (-\xi )} \sqrt{\delta _1^3 e^{2 \sqrt{\delta _1} \xi }} \sqrt{\mu _1-\mu _2 \nu }}{2 \delta _1 \sqrt{\delta -c_3}} \right. \nonumber \\ & \quad -\left. \frac{1}{2} \sqrt{\frac{3 \mu _1 \mu _2^2 \left( \delta -c_3\right) +2 \sqrt{3} \sqrt{c_1 \mu _2^8 \left( \delta -c_3\right) {}^3}}{\mu _2^4 \left( \delta -c_3\right) {}^2}}\right)^{\frac{1}{2}}. \end{aligned}$$

  (74)

• Case VIII $a_0=-\frac{1}{2} \sqrt{\frac{3 \mu _1 \mu _2^2 \left( \delta -c_3\right) +2 \sqrt{3} \sqrt{c_1 \mu _2^8 \left( \delta -c_3\right) {}^3}}{\mu _2^4 \left( \delta -c_3\right) {}^2}},a_1=0,b_1=0,d_1=\frac{\sqrt{3} \sqrt{\mu _1-\mu _2 \nu }}{2 \sqrt{\delta -c_3}},$

  $\gamma =\frac{1}{12} \mu _2^2 \left( 4 \left( \delta -c_3\right) \sqrt{\frac{3 \mu _1 \mu _2^2 \left( \delta -c_3\right) +2 \sqrt{3} \sqrt{c_1 \mu _2^8 \left( \delta -c_3\right) {}^3}}{\mu _2^4 \left( \delta -c_3\right) {}^2}}+3 c_2\right) ,\kappa =\frac{1}{\mu _2},$

  $\delta _1=\frac{\mu _1 \mu _2^2 \left( c_3-\delta \right) -2 \sqrt{3} \sqrt{c_1 \mu _2^8 \left( \delta -c_3\right) {}^3}}{\mu _2^4 \left( \delta -c_3\right) \left( \mu _2 \nu -\mu _1\right) },\delta _2=0,\delta _3=0,$

  substituting values in Eq. (60) also using $u=V^{\frac{1}{2}}$ and by applying the reverse transformation (7), we get our solutions

  $$\begin{aligned} q_{26}(x,t) &= {} e^{i \phi } \times \left(\frac{\sqrt{3} e^{\sqrt{\delta _1} (-\xi )} \sqrt{\delta _1^3 e^{2 \sqrt{\delta _1} \xi }} \sqrt{\mu _1-\mu _2 \nu }}{2 \delta _1 \sqrt{\delta -c_3}} \right. \nonumber \\&\quad - \left. \frac{1}{2} \sqrt{\frac{3 \mu _1 \mu _2^2 \left( \delta -c_3\right) +2 \sqrt{3} \sqrt{c_1 \mu _2^8 \left( \delta -c_3\right) {}^3}}{\mu _2^4 \left( \delta -c_3\right) {}^2}}\right)^{\frac{1}{2}}, \end{aligned}$$

  (75)
  $$\begin{aligned} q^*_{26}(x,t)&= {} e^{-i \phi } \times \left(\frac{\sqrt{3} e^{\sqrt{\delta _1} (-\xi )} \sqrt{\delta _1^3 e^{2 \sqrt{\delta _1} \xi }} \sqrt{\mu _1-\mu _2 \nu }}{2 \delta _1 \sqrt{\delta -c_3}} \right. \nonumber \\&\quad - \left. \frac{1}{2} \sqrt{\frac{3 \mu _1 \mu _2^2 \left( \delta -c_3\right) +2 \sqrt{3} \sqrt{c_1 \mu _2^8 \left( \delta -c_3\right) {}^3}}{\mu _2^4 \left( \delta -c_3\right) {}^2}}\right)^{\frac{1}{2}}. \end{aligned}$$

  (76)

• Case IX $a_0=\frac{1}{2} \sqrt{\frac{3 \mu _1 \mu _2^2 \left( \delta -c_3\right) +2 \sqrt{3} \sqrt{c_1 \mu _2^8 \left( \delta -c_3\right) {}^3}}{\mu _2^4 \left( \delta -c_3\right) {}^2}},a_1=0,b_1=0,d_1=-\frac{\sqrt{3} \sqrt{\mu _1-\mu _2 \nu }}{2 \sqrt{\delta -c_3}},$

  $\gamma =\frac{1}{12} \mu _2^2 \left( 4 \left( c_3-\delta \right) \sqrt{\frac{3 \mu _1 \mu _2^2 \left( \delta -c_3\right) +2 \sqrt{3} \sqrt{c_1 \mu _2^8 \left( \delta -c_3\right) {}^3}}{\mu _2^4 \left( \delta -c_3\right) {}^2}}+3 c_2\right) ,\kappa =\frac{1}{\mu _2},$

  $\delta _1=\frac{\mu _1 \mu _2^2 \left( c_3-\delta \right) -2 \sqrt{3} \sqrt{c_1 \mu _2^8 \left( \delta -c_3\right) {}^3}}{\mu _2^4 \left( \delta -c_3\right) \left( \mu _2 \nu -\mu _1\right) },\delta _2=0,\delta _3=0,$

  substituting values in Eq. (60) also using $u=V^{\frac{1}{2}}$ and by applying the reverse transformation (7), we get our solutions

  $$\begin{aligned} q_{27}(x,t)& = {} e^{i \phi }\times \left (\frac{1}{2} \sqrt{\frac{3 \mu _1 \mu _2^2 \left( \delta -c_3\right) +2 \sqrt{3} \sqrt{c_1 \mu _2^8 \left( \delta -c_3\right) {}^3}}{\mu _2^4 \left( \delta -c_3\right) {}^2}} \right. \nonumber \\&\quad - \left. \frac{\sqrt{3} e^{\sqrt{\delta _1} (-\xi )} \sqrt{\delta _1^3 e^{2 \sqrt{\delta _1} \xi }} \sqrt{\mu _1-\mu _2 \nu }}{2 \delta _1 \sqrt{\delta -c_3}}\right)^{\frac{1}{2}}, \end{aligned}$$

  (77)
  $$\begin{aligned} q^*_{27}(x,t) &= {} e^{-i \phi } \times \left(\frac{1}{2} \sqrt{\frac{3 \mu _1 \mu _2^2 \left( \delta -c_3\right) +2 \sqrt{3} \sqrt{c_1 \mu _2^8 \left( \delta -c_3\right) {}^3}}{\mu _2^4 \left( \delta -c_3\right) {}^2}} \right. \nonumber \\&- \left. \frac{\sqrt{3} e^{\sqrt{\delta _1} (-\xi )} \sqrt{\delta _1^3 e^{2 \sqrt{\delta _1} \xi }} \sqrt{\mu _1-\mu _2 \nu }}{2 \delta _1 \sqrt{\delta -c_3}}\right)^{\frac{1}{2}}. \end{aligned}$$

  (78)

• Case X $a_0=\frac{1}{2} \sqrt{\frac{3 \mu _1 \mu _2^2 \left( \delta -c_3\right) +2 \sqrt{3} \sqrt{c_1 \mu _2^8 \left( \delta -c_3\right) {}^3}}{\mu _2^4 \left( \delta -c_3\right) {}^2}},a_1=0,b_1=0,d_1=\frac{\sqrt{3} \sqrt{\mu _1-\mu _2 \nu }}{2 \sqrt{\delta -c_3}},$ $\gamma =\frac{1}{12} \mu _2^2 \left( 4 \left( c_3-\delta \right) \sqrt{\frac{3 \mu _1 \mu _2^2 \left( \delta -c_3\right) +2 \sqrt{3} \sqrt{c_1 \mu _2^8 \left( \delta -c_3\right) {}^3}}{\mu _2^4 \left( \delta -c_3\right) {}^2}}+3 c_2\right) ,\kappa =\frac{1}{\mu _2},$ $\delta _1=\frac{\mu _1 \mu _2^2 \left( c_3-\delta \right) -2 \sqrt{3} \sqrt{c_1 \mu _2^8 \left( \delta -c_3\right) {}^3}}{\mu _2^4 \left( \delta -c_3\right) \left( \mu _2 \nu -\mu _1\right) },\delta _2=0,\delta _3=0,$

  substituting values in Eq. (60) also using $u=V^{\frac{1}{2}}$ and by applying the reverse transformation (7), we get our solutions

  $$\begin{aligned} q_{28}(x,t) &= {} e^{i \phi }\times \left (\frac{\sqrt{3} e^{\sqrt{\delta _1} (-\xi )} \sqrt{\delta _1^3 e^{2 \sqrt{\delta _1} \xi }} \sqrt{\mu _1-\mu _2 \nu }}{2 \delta _1 \sqrt{\delta -c_3}} \right. \nonumber \\&\quad + \left. \frac{1}{2} \sqrt{\frac{3 \mu _1 \mu _2^2 \left( \delta -c_3\right) +2 \sqrt{3} \sqrt{c_1 \mu _2^8 \left( \delta -c_3\right) {}^3}}{\mu _2^4 \left( \delta -c_3\right) {}^2}}\right)^{\frac{1}{2}}, \end{aligned}$$

  (79)
  $$\begin{aligned} q^*_{28}(x,t)&= {} e^{-i \phi }\times \left(\frac{\sqrt{3} e^{\sqrt{\delta _1} (-\xi )} \sqrt{\delta _1^3 e^{2 \sqrt{\delta _1} \xi }} \sqrt{\mu _1-\mu _2 \nu }}{2 \delta _1 \sqrt{\delta -c_3}} \right. \nonumber \\&\quad + \left. \frac{1}{2} \sqrt{\frac{3 \mu _1 \mu _2^2 \left( \delta -c_3\right) +2 \sqrt{3} \sqrt{c_1 \mu _2^8 \left( \delta -c_3\right) {}^3}}{\mu _2^4 \left( \delta -c_3\right) {}^2}}\right)^{\frac{1}{2}}. \end{aligned}$$

  (80)

• Family II

  $$\begin{aligned} \psi (\xi )=\frac{4 \delta _1 e^{\sqrt{\delta _1} \xi }}{-2 \delta _2 e^{\sqrt{\delta _1} \xi }+e^{2 \sqrt{\delta _1} \xi }+\delta _2^2-4 \delta _1 \delta _3}. \end{aligned}$$

• Case I $a_1=0,b_1=0,d_1=-\frac{\sqrt{3} \sqrt{\mu _1-\mu _2 \nu }}{2 \sqrt{\delta -c_3}},\gamma =\frac{8 a_0 \left( c_3-\delta \right) +3 c_2}{12 \kappa ^2},$

  $\delta _1=\frac{4 \left( a_0^2 \left( \delta -c_3\right) \left( \mu _1-\mu _2 \nu \right) +\sqrt{3} \sqrt{c_1 \left( \delta -c_3\right) \left( \mu _1-\mu _2 \nu \right) {}^2}\right) }{3 \left( \mu _1-\mu _2 \nu \right) {}^2},\delta _2=0,\delta _3=0,$

  $\omega =\frac{\left( \mu _1-\mu _2 \nu \right) \left( 4 a_0^2 \left( \delta -c_3\right) -3 \kappa ^2 \mu _1\right) -2 \sqrt{3} \sqrt{c_1 \left( \delta -c_3\right) \left( \mu _1-\mu _2 \nu \right) {}^2}}{3 \left( \kappa \mu _2-1\right) \left( \mu _2 \nu -\mu _1\right) },$

  substituting values in Eq. (60) also using $u=V^{\frac{1}{2}}$ and by applying the reverse transformation (7), we get our solutions

  $$\begin{aligned}&q_{29}(x,t)=e^{i \phi } \sqrt{a_0-\frac{\sqrt{3} e^{\sqrt{\delta _1} \xi } \sqrt{\delta _1^3 e^{-2 \sqrt{\delta _1} \xi }} \sqrt{\mu _1-\mu _2 \nu }}{2 \delta _1 \sqrt{\delta -c_3}}}, \end{aligned}$$

  (81)
  $$\begin{aligned}&q^*_{29}(x,t)=e^{-i \phi } \sqrt{a_0-\frac{\sqrt{3} e^{\sqrt{\delta _1} \xi } \sqrt{\delta _1^3 e^{-2 \sqrt{\delta _1} \xi }} \sqrt{\mu _1-\mu _2 \nu }}{2 \delta _1 \sqrt{\delta -c_3}}}. \end{aligned}$$

  (82)

• Case II $a_1=0,b_1=0,d_1=\frac{\sqrt{3} \sqrt{\mu _1-\mu _2 \nu }}{2 \sqrt{\delta -c_3}},\gamma =\frac{8 a_0 \left( c_3-\delta \right) +3 c_2}{12 \kappa ^2},$

  $\delta _1=\frac{4 \left( a_0^2 \left( \delta -c_3\right) \left( \mu _1-\mu _2 \nu \right) +\sqrt{3} \sqrt{c_1 \left( \delta -c_3\right) \left( \mu _1-\mu _2 \nu \right) {}^2}\right) }{3 \left( \mu _1-\mu _2 \nu \right) {}^2},\delta _2=0,\delta _3=0,$

  $\omega =\frac{\left( \mu _1-\mu _2 \nu \right) \left( 4 a_0^2 \left( \delta -c_3\right) -3 \kappa ^2 \mu _1\right) -2 \sqrt{3} \sqrt{c_1 \left( \delta -c_3\right) \left( \mu _1-\mu _2 \nu \right) {}^2}}{3 \left( \kappa \mu _2-1\right) \left( \mu _2 \nu -\mu _1\right) },$

  substituting values in Eq. (60) also using $u=V^{\frac{1}{2}}$ and by applying the reverse transformation (7), we get our solutions

  $$\begin{aligned}&q_{30}(x,t)=e^{i \phi } \sqrt{a_0+\frac{\sqrt{3} e^{\sqrt{\delta _1} \xi } \sqrt{\delta _1^3 e^{-2 \sqrt{\delta _1} \xi }} \sqrt{\mu _1-\mu _2 \nu }}{2 \delta _1 \sqrt{\delta -c_3}}}, \end{aligned}$$

  (83)
  $$\begin{aligned}&q^*_{30}(x,t)=e^{-i \phi } \sqrt{a_0+\frac{\sqrt{3} e^{\sqrt{\delta _1} \xi } \sqrt{\delta _1^3 e^{-2 \sqrt{\delta _1} \xi }} \sqrt{\mu _1-\mu _2 \nu }}{2 \delta _1 \sqrt{\delta -c_3}}}. \end{aligned}$$

  (84)

• Case III $a_0=-\frac{1}{2} \sqrt{\frac{3 \mu _1 \mu _2^2 \left( \delta -c_3\right) -2 \sqrt{3} \sqrt{c_1 \mu _2^8 \left( \delta -c_3\right) {}^3}}{\mu _2^4 \left( \delta -c_3\right) {}^2}},a_1=0,b_1=0,d_1=-\frac{\sqrt{3} \sqrt{\mu _1-\mu _2 \nu }}{2 \sqrt{\delta -c_3}},$

  $\gamma =\frac{1}{12} \mu _2^2 \left( 4 \left( \delta -c_3\right) \sqrt{\frac{3 \mu _1 \mu _2^2 \left( \delta -c_3\right) -2 \sqrt{3} \sqrt{c_1 \mu _2^8 \left( \delta -c_3\right) {}^3}}{\mu _2^4 \left( \delta -c_3\right) {}^2}}+3 c_2\right) ,\kappa =\frac{1}{\mu _2},$

  $\delta _1=\frac{\mu _1 \mu _2^2 \left( c_3-\delta \right) +2 \sqrt{3} \sqrt{c_1 \mu _2^8 \left( \delta -c_3\right) {}^3}}{\mu _2^4 \left( \delta -c_3\right) \left( \mu _2 \nu -\mu _1\right) },\delta _2=0,\delta _3=0,$

  substituting values in Eq. (60) also using $u=V^{\frac{1}{2}}$ and by applying the reverse transformation (7), we get our solutions

  $$\begin{aligned} q_{31}(x,t)&= {} e^{i \phi }\times \left(-\frac{\sqrt{3} e^{\sqrt{\delta _1} \xi } \sqrt{\delta _1^3 e^{-2 \sqrt{\delta _1} \xi }} \sqrt{\mu _1-\mu _2 \nu }}{2 \delta _1 \sqrt{\delta -c_3}} \right. \nonumber \\ &\quad - \left. \frac{1}{2} \sqrt{\frac{3 \mu _1 \mu _2^2 \left( \delta -c_3\right) -2 \sqrt{3} \sqrt{c_1 \mu _2^8 \left( \delta -c_3\right) {}^3}}{\mu _2^4 \left( \delta -c_3\right) {}^2}}\right)^{\frac{1}{2}}, \end{aligned}$$

  (85)
  $$\begin{aligned} q^*_{31}(x,t) &= {} e^{-i \phi } \times \left(-\frac{\sqrt{3} e^{\sqrt{\delta _1} \xi } \sqrt{\delta _1^3 e^{-2 \sqrt{\delta _1} \xi }} \sqrt{\mu _1-\mu _2 \nu }}{2 \delta _1 \sqrt{\delta -c_3}} \right. \nonumber \\&\quad - \left. \frac{1}{2} \sqrt{\frac{3 \mu _1 \mu _2^2 \left( \delta -c_3\right) -2 \sqrt{3} \sqrt{c_1 \mu _2^8 \left( \delta -c_3\right) {}^3}}{\mu _2^4 \left( \delta -c_3\right) {}^2}}\right)^{\frac{1}{2}}. \end{aligned}$$

  (86)

• Case IV $a_0=-\frac{1}{2} \sqrt{\frac{3 \mu _1 \mu _2^2 \left( \delta -c_3\right) -2 \sqrt{3} \sqrt{c_1 \mu _2^8 \left( \delta -c_3\right) {}^3}}{\mu _2^4 \left( \delta -c_3\right) {}^2}},a_1=0,b_1=0,d_1=\frac{\sqrt{3} \sqrt{\mu _1-\mu _2 \nu }}{2 \sqrt{\delta -c_3}},$

  $\gamma =\frac{1}{12} \mu _2^2 \left( 4 \left( \delta -c_3\right) \sqrt{\frac{3 \mu _1 \mu _2^2 \left( \delta -c_3\right) -2 \sqrt{3} \sqrt{c_1 \mu _2^8 \left( \delta -c_3\right) {}^3}}{\mu _2^4 \left( \delta -c_3\right) {}^2}}+3 c_2\right) ,\kappa =\frac{1}{\mu _2},$

  $\delta _1=\frac{\mu _1 \mu _2^2 \left( c_3-\delta \right) +2 \sqrt{3} \sqrt{c_1 \mu _2^8 \left( \delta -c_3\right) {}^3}}{\mu _2^4 \left( \delta -c_3\right) \left( \mu _2 \nu -\mu _1\right) },\delta _2=0,\delta _3=0,$

  substituting values in Eq. (60) also using $u=V^{\frac{1}{2}}$ and by applying the reverse transformation (7), we get our solutions

  $$\begin{aligned} q_{32}(x,t)&= {} e^{i \phi } \times \left(\frac{\sqrt{3} e^{\sqrt{\delta _1} \xi } \sqrt{\delta _1^3 e^{-2 \sqrt{\delta _1} \xi }} \sqrt{\mu _1-\mu _2 \nu }}{2 \delta _1 \sqrt{\delta -c_3}} \right. \nonumber \\&\quad - \left. \frac{1}{2} \sqrt{\frac{3 \mu _1 \mu _2^2 \left( \delta -c_3\right) -2 \sqrt{3} \sqrt{c_1 \mu _2^8 \left( \delta -c_3\right) {}^3}}{\mu _2^4 \left( \delta -c_3\right) {}^2}}\right)^{\frac{1}{2}}, \end{aligned}$$

  (87)
  $$\begin{aligned} q^*_{32}(x,t) &= {} e^{-i \phi }\times \left(\frac{\sqrt{3} e^{\sqrt{\delta _1} \xi } \sqrt{\delta _1^3 e^{-2 \sqrt{\delta _1} \xi }} \sqrt{\mu _1-\mu _2 \nu }}{2 \delta _1 \sqrt{\delta -c_3}} \right. \nonumber \\&\quad - \left. \frac{1}{2} \sqrt{\frac{3 \mu _1 \mu _2^2 \left( \delta -c_3\right) -2 \sqrt{3} \sqrt{c_1 \mu _2^8 \left( \delta -c_3\right) {}^3}}{\mu _2^4 \left( \delta -c_3\right) {}^2}}\right)^{\frac{1}{2}}. \end{aligned}$$

  (88)

• Case V $a_0=\frac{1}{2} \sqrt{\frac{3 \mu _1 \mu _2^2 \left( \delta -c_3\right) -2 \sqrt{3} \sqrt{c_1 \mu _2^8 \left( \delta -c_3\right) {}^3}}{\mu _2^4 \left( \delta -c_3\right) {}^2}},a_1=0,b_1=0,d_1=-\frac{\sqrt{3} \sqrt{\mu _1-\mu _2 \nu }}{2 \sqrt{\delta -c_3}},$

  $\gamma =\frac{1}{12} \mu _2^2 \left( 4 \left( c_3-\delta \right) \sqrt{\frac{3 \mu _1 \mu _2^2 \left( \delta -c_3\right) -2 \sqrt{3} \sqrt{c_1 \mu _2^8 \left( \delta -c_3\right) {}^3}}{\mu _2^4 \left( \delta -c_3\right) {}^2}}+3 c_2\right) ,\kappa =\frac{1}{\mu _2},$

  $\delta _1=\frac{\mu _1 \mu _2^2 \left( c_3-\delta \right) +2 \sqrt{3} \sqrt{c_1 \mu _2^8 \left( \delta -c_3\right) {}^3}}{\mu _2^4 \left( \delta -c_3\right) \left( \mu _2 \nu -\mu _1\right) },\delta _2=0,\delta _3=0,$

  substituting values in Eq. (60) also using $u=V^{\frac{1}{2}}$ and by applying the reverse transformation (7), we get our solutions

  $$\begin{aligned} q_{33}(x,t)&= {} e^{i \phi }\times \left(\frac{1}{2} \sqrt{\frac{3 \mu _1 \mu _2^2 \left( \delta -c_3\right) -2 \sqrt{3} \sqrt{c_1 \mu _2^8 \left( \delta -c_3\right) {}^3}}{\mu _2^4 \left( \delta -c_3\right) {}^2}} \right. \nonumber \\&\quad - \left. \frac{\sqrt{3} e^{\sqrt{\delta _1} \xi } \sqrt{\delta _1^3 e^{-2 \sqrt{\delta _1} \xi }} \sqrt{\mu _1-\mu _2 \nu }}{2 \delta _1 \sqrt{\delta -c_3}}\right)^{\frac{1}{2}}, \end{aligned}$$

  (89)
  $$\begin{aligned} q^*_{33}(x,t) &= {} e^{-i \phi }\times \left(\frac{1}{2} \sqrt{\frac{3 \mu _1 \mu _2^2 \left( \delta -c_3\right) -2 \sqrt{3} \sqrt{c_1 \mu _2^8 \left( \delta -c_3\right) {}^3}}{\mu _2^4 \left( \delta -c_3\right) {}^2}} \right. \nonumber \\& \quad - \left. \frac{\sqrt{3} e^{\sqrt{\delta _1} \xi } \sqrt{\delta _1^3 e^{-2 \sqrt{\delta _1} \xi }} \sqrt{\mu _1-\mu _2 \nu }}{2 \delta _1 \sqrt{\delta -c_3}}\right)^{\frac{1}{2}}. \end{aligned}$$

  (90)

• Case VI $a_0=\frac{1}{2} \sqrt{\frac{3 \mu _1 \mu _2^2 \left( \delta -c_3\right) -2 \sqrt{3} \sqrt{c_1 \mu _2^8 \left( \delta -c_3\right) {}^3}}{\mu _2^4 \left( \delta -c_3\right) {}^2}},a_1=0,b_1=0,d_1=\frac{\sqrt{3} \sqrt{\mu _1-\mu _2 \nu }}{2 \sqrt{\delta -c_3}}$

  $\gamma =\frac{1}{12} \mu _2^2 \left( 4 \left( c_3-\delta \right) \sqrt{\frac{3 \mu _1 \mu _2^2 \left( \delta -c_3\right) -2 \sqrt{3} \sqrt{c_1 \mu _2^8 \left( \delta -c_3\right) {}^3}}{\mu _2^4 \left( \delta -c_3\right) {}^2}}+3 c_2\right) ,\kappa =\frac{1}{\mu _2},$

  $\delta _1=\frac{\mu _1 \mu _2^2 \left( c_3-\delta \right) +2 \sqrt{3} \sqrt{c_1 \mu _2^8 \left( \delta -c_3\right) {}^3}}{\mu _2^4 \left( \delta -c_3\right) \left( \mu _2 \nu -\mu _1\right) },\delta _2=0,\delta _3=0,$

  substituting values in Eq. (60) also using $u=V^{\frac{1}{2}}$ and by applying the reverse transformation (7), we get our solutions

  $$\begin{aligned} q_{34}(x,t)&= {} e^{i \phi } \times \left(\frac{\sqrt{3} e^{\sqrt{\delta _1} \xi } \sqrt{\delta _1^3 e^{-2 \sqrt{\delta _1} \xi }} \sqrt{\mu _1-\mu _2 \nu }}{2 \delta _1 \sqrt{\delta -c_3}} \right. \nonumber \\&\quad + \left. \frac{1}{2} \sqrt{\frac{3 \mu _1 \mu _2^2 \left( \delta -c_3\right) -2 \sqrt{3} \sqrt{c_1 \mu _2^8 \left( \delta -c_3\right) {}^3}}{\mu _2^4 \left( \delta -c_3\right) {}^2}}\right)^{\frac{1}{2}}, \end{aligned}$$

  (91)
  $$\begin{aligned} q^*_{34}(x,t)&= {} e^{-i \phi }\times \left (\frac{\sqrt{3} e^{\sqrt{\delta _1} \xi } \sqrt{\delta _1^3 e^{-2 \sqrt{\delta _1} \xi }} \sqrt{\mu _1-\mu _2 \nu }}{2 \delta _1 \sqrt{\delta -c_3}} \right. \nonumber \\&\quad + \left. \frac{1}{2} \sqrt{\frac{3 \mu _1 \mu _2^2 \left( \delta -c_3\right) -2 \sqrt{3} \sqrt{c_1 \mu _2^8 \left( \delta -c_3\right) {}^3}}{\mu _2^4 \left( \delta -c_3\right) {}^2}}\right)^{\frac{1}{2}}. \end{aligned}$$

  (92)

• Case VII $a_0=-\frac{1}{2} \sqrt{\frac{3 \mu _1 \mu _2^2 \left( \delta -c_3\right) +2 \sqrt{3} \sqrt{c_1 \mu _2^8 \left( \delta -c_3\right) {}^3}}{\mu _2^4 \left( \delta -c_3\right) {}^2}},a_1=0,b_1=0,d_1=-\frac{\sqrt{3} \sqrt{\mu _1-\mu _2 \nu }}{2 \sqrt{\delta -c_3}},$

  $\gamma =\frac{1}{12} \mu _2^2 \left( 4 \left( \delta -c_3\right) \sqrt{\frac{3 \mu _1 \mu _2^2 \left( \delta -c_3\right) +2 \sqrt{3} \sqrt{c_1 \mu _2^8 \left( \delta -c_3\right) {}^3}}{\mu _2^4 \left( \delta -c_3\right) {}^2}}+3 c_2\right) ,\kappa =\frac{1}{\mu _2},$

  $\delta _1=\frac{\mu _1 \mu _2^2 \left( c_3-\delta \right) -2 \sqrt{3} \sqrt{c_1 \mu _2^8 \left( \delta -c_3\right) {}^3}}{\mu _2^4 \left( \delta -c_3\right) \left( \mu _2 \nu -\mu _1\right) },\delta _2=0,\delta _3=0,$

  substituting values in Eq. (60) also using $u=V^{\frac{1}{2}}$ and by applying the reverse transformation (7), we get our solutions

  $$\begin{aligned} q_{35}(x,t) &= {} e^{i \phi }\times \left(-\frac{\sqrt{3} e^{\sqrt{\delta _1} \xi } \sqrt{\delta _1^3 e^{-2 \sqrt{\delta _1} \xi }} \sqrt{\mu _1-\mu _2 \nu }}{2 \delta _1 \sqrt{\delta -c_3}} \right. \nonumber \\&\quad - \left. \frac{1}{2} \sqrt{\frac{3 \mu _1 \mu _2^2 \left( \delta -c_3\right) +2 \sqrt{3} \sqrt{c_1 \mu _2^8 \left( \delta -c_3\right) {}^3}}{\mu _2^4 \left( \delta -c_3\right) {}^2}}\right)^{\frac{1}{2}}, \end{aligned}$$

  (93)
  $$\begin{aligned} q^*_{35}(x,t)& = {} e^{-i \phi }\times \left(-\frac{\sqrt{3} e^{\sqrt{\delta _1} \xi } \sqrt{\delta _1^3 e^{-2 \sqrt{\delta _1} \xi }} \sqrt{\mu _1-\mu _2 \nu }}{2 \delta _1 \sqrt{\delta -c_3}} \right. \nonumber \\&- \left. \frac{1}{2} \sqrt{\frac{3 \mu _1 \mu _2^2 \left( \delta -c_3\right) +2 \sqrt{3} \sqrt{c_1 \mu _2^8 \left( \delta -c_3\right) {}^3}}{\mu _2^4 \left( \delta -c_3\right) {}^2}}\right)^{\frac{1}{2}}. \end{aligned}$$

  (94)

• Case VIII $a_0=-\frac{1}{2} \sqrt{\frac{3 \mu _1 \mu _2^2 \left( \delta -c_3\right) +2 \sqrt{3} \sqrt{c_1 \mu _2^8 \left( \delta -c_3\right) {}^3}}{\mu _2^4 \left( \delta -c_3\right) {}^2}},a_1=0,b_1=0,d_1=\frac{\sqrt{3} \sqrt{\mu _1-\mu _2 \nu }}{2 \sqrt{\delta -c_3}},$

  $\gamma =\frac{1}{12} \mu _2^2 \left( 4 \left( \delta -c_3\right) \sqrt{\frac{3 \mu _1 \mu _2^2 \left( \delta -c_3\right) +2 \sqrt{3} \sqrt{c_1 \mu _2^8 \left( \delta -c_3\right) {}^3}}{\mu _2^4 \left( \delta -c_3\right) {}^2}}+3 c_2\right) ,\kappa =\frac{1}{\mu _2},$

  $\delta _1=\frac{\mu _1 \mu _2^2 \left( c_3-\delta \right) -2 \sqrt{3} \sqrt{c_1 \mu _2^8 \left( \delta -c_3\right) {}^3}}{\mu _2^4 \left( \delta -c_3\right) \left( \mu _2 \nu -\mu _1\right) },\delta _2=0,\delta _3=0,$

  substituting values in Eq. (60) also using $u=V^{\frac{1}{2}}$ and by applying the reverse transformation (7), we get our solutions

  $$\begin{aligned} q_{36}(x,t)= & {} e^{i \phi }\times \left(\frac{\sqrt{3} e^{\sqrt{\delta _1} \xi } \sqrt{\delta _1^3 e^{-2 \sqrt{\delta _1} \xi }} \sqrt{\mu _1-\mu _2 \nu }}{2 \delta _1 \sqrt{\delta -c_3}} \right. \nonumber \\&\quad - \left. \frac{1}{2} \sqrt{\frac{3 \mu _1 \mu _2^2 \left( \delta -c_3\right) +2 \sqrt{3} \sqrt{c_1 \mu _2^8 \left( \delta -c_3\right) {}^3}}{\mu _2^4 \left( \delta -c_3\right) {}^2}}\right)^{\frac{1}{2}}, \end{aligned}$$

  (95)
  $$\begin{aligned} q^*_{36}(x,t)&= {} e^{-i \phi }\times \left (\frac{\sqrt{3} e^{\sqrt{\delta _1} \xi } \sqrt{\delta _1^3 e^{-2 \sqrt{\delta _1} \xi }} \sqrt{\mu _1-\mu _2 \nu }}{2 \delta _1 \sqrt{\delta -c_3}} \right. \nonumber \\&\quad - \left. \frac{1}{2} \sqrt{\frac{3 \mu _1 \mu _2^2 \left( \delta -c_3\right) +2 \sqrt{3} \sqrt{c_1 \mu _2^8 \left( \delta -c_3\right) {}^3}}{\mu _2^4 \left( \delta -c_3\right) {}^2}}\right)^{\frac{1}{2}}. \end{aligned}$$

  (96)

• Case IX $a_0=\frac{1}{2} \sqrt{\frac{3 \mu _1 \mu _2^2 \left( \delta -c_3\right) +2 \sqrt{3} \sqrt{c_1 \mu _2^8 \left( \delta -c_3\right) {}^3}}{\mu _2^4 \left( \delta -c_3\right) {}^2}},a_1=0,b_1=0,d_1=-\frac{\sqrt{3} \sqrt{\mu _1-\mu _2 \nu }}{2 \sqrt{\delta -c_3}},$

  $\gamma =\frac{1}{12} \mu _2^2 \left( 4 \left( c_3-\delta \right) \sqrt{\frac{3 \mu _1 \mu _2^2 \left( \delta -c_3\right) +2 \sqrt{3} \sqrt{c_1 \mu _2^8 \left( \delta -c_3\right) {}^3}}{\mu _2^4 \left( \delta -c_3\right) {}^2}}+3 c_2\right) ,\kappa =\frac{1}{\mu _2},$

  $\delta _1=\frac{\mu _1 \mu _2^2 \left( c_3-\delta \right) -2 \sqrt{3} \sqrt{c_1 \mu _2^8 \left( \delta -c_3\right) {}^3}}{\mu _2^4 \left( \delta -c_3\right) \left( \mu _2 \nu -\mu _1\right) },\delta _2=0,\delta _3=0,$

  substituting values in Eq. (60) also using $u=V^{\frac{1}{2}}$ and by applying the reverse transformation (7), we get our solutions

  $$\begin{aligned} q_{37}(x,t)&= {} e^{i \phi }\times \left(\frac{1}{2} \sqrt{\frac{3 \mu _1 \mu _2^2 \left( \delta -c_3\right) +2 \sqrt{3} \sqrt{c_1 \mu _2^8 \left( \delta -c_3\right) {}^3}}{\mu _2^4 \left( \delta -c_3\right) {}^2}} \right. \nonumber \\&\quad - \left. \frac{\sqrt{3} e^{\sqrt{\delta _1} \xi } \sqrt{\delta _1^3 e^{-2 \sqrt{\delta _1} \xi }} \sqrt{\mu _1-\mu _2 \nu }}{2 \delta _1 \sqrt{\delta -c_3}}\right)^{\frac{1}{2}}, \end{aligned}$$

  (97)
  $$\begin{aligned} q^*_{37}(x,t)& = {} e^{-i \phi }\times \left(\frac{1}{2} \sqrt{\frac{3 \mu _1 \mu _2^2 \left( \delta -c_3\right) +2 \sqrt{3} \sqrt{c_1 \mu _2^8 \left( \delta -c_3\right) {}^3}}{\mu _2^4 \left( \delta -c_3\right) {}^2}} \right. \nonumber \\&\quad - \left. \frac{\sqrt{3} e^{\sqrt{\delta _1} \xi } \sqrt{\delta _1^3 e^{-2 \sqrt{\delta _1} \xi }} \sqrt{\mu _1-\mu _2 \nu }}{2 \delta _1 \sqrt{\delta -c_3}}\right)^{\frac{1}{2}}. \end{aligned}$$

  (98)

• Case X $a_0=\frac{1}{2} \sqrt{\frac{3 \mu _1 \mu _2^2 \left( \delta -c_3\right) +2 \sqrt{3} \sqrt{c_1 \mu _2^8 \left( \delta -c_3\right) {}^3}}{\mu _2^4 \left( \delta -c_3\right) {}^2}},a_1=0,b_1=0,d_1=\frac{\sqrt{3} \sqrt{\mu _1-\mu _2 \nu }}{2 \sqrt{\delta -c_3}},$

  $\gamma =\frac{1}{12} \mu _2^2 \left( 4 \left( c_3-\delta \right) \sqrt{\frac{3 \mu _1 \mu _2^2 \left( \delta -c_3\right) +2 \sqrt{3} \sqrt{c_1 \mu _2^8 \left( \delta -c_3\right) {}^3}}{\mu _2^4 \left( \delta -c_3\right) {}^2}}+3 c_2\right) ,\kappa =\frac{1}{\mu _2},$

  $\delta _1=\frac{\mu _1 \mu _2^2 \left( c_3-\delta \right) -2 \sqrt{3} \sqrt{c_1 \mu _2^8 \left( \delta -c_3\right) {}^3}}{\mu _2^4 \left( \delta -c_3\right) \left( \mu _2 \nu -\mu _1\right) },\delta _2=0,\delta _3=0,$

  substituting values in Eq. (60) also using $u=V^{\frac{1}{2}}$ and by applying the reverse transformation (7), we get our solutions

  $$\begin{aligned} q_{38}(x,t)&= {} e^{i \phi }\times \left(\frac{\sqrt{3} e^{\sqrt{\delta _1} \xi } \sqrt{\delta _1^3 e^{-2 \sqrt{\delta _1} \xi }} \sqrt{\mu _1-\mu _2 \nu }}{2 \delta _1 \sqrt{\delta -c_3}} \right. \nonumber \\&\quad + \left. \frac{1}{2} \sqrt{\frac{3 \mu _1 \mu _2^2 \left( \delta -c_3\right) +2 \sqrt{3} \sqrt{c_1 \mu _2^8 \left( \delta -c_3\right) {}^3}}{\mu _2^4 \left( \delta -c_3\right) {}^2}}\right)^{\frac{1}{2}}, \end{aligned}$$

  (99)
  $$\begin{aligned} q^*_{38}(x,t)& = {} e^{-i \phi }\times \left (\frac{\sqrt{3} e^{\sqrt{\delta _1} \xi } \sqrt{\delta _1^3 e^{-2 \sqrt{\delta _1} \xi }} \sqrt{\mu _1-\mu _2 \nu }}{2 \delta _1 \sqrt{\delta -c_3}} \right. \nonumber \\&\quad + \left. \frac{1}{2} \sqrt{\frac{3 \mu _1 \mu _2^2 \left( \delta -c_3\right) +2 \sqrt{3} \sqrt{c_1 \mu _2^8 \left( \delta -c_3\right) {}^3}}{\mu _2^4 \left( \delta -c_3\right) {}^2}}\right)^{\frac{1}{2}}. \end{aligned}$$

  (100)

4 Discussion and results

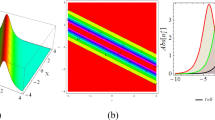
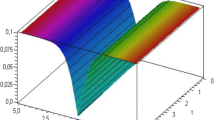
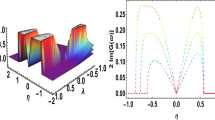
In this section, the graphical representations of LPD model have been illustrated. The extended modified AEM method is applied to get the exact solitary wave solutions for the set of values. The results attained here are the soliton wave solutions, bright solitons, dark solitons, multi solitons, periodic solitary wave, rational function and elliptic function solutions for some appropriated values of parameters. The 3D, contour and 2D graphs visualizes the nature of nonlinear waves constructed from Eq. (1).

Fig. 1

Absolute graphical solution of $q_{1}(x,y,t)$ for the values of $\gamma =3$, $\theta =2$, $\mu _1=4$, $\mu _2=-2$, $\mu _3=1$, $\delta =4$

Fig. 2

Real graphical solution of $q_{2}(x,y,t)$ for the values of $\gamma =-3$, $\theta =2$, $\mu _1=4$, $\mu _2=-2$, $\mu _3=1$, $\delta =4$

Fig. 3

Imaginary graphical solution of $q^*_{2}(x,y,t)$ for the values of $\gamma =-3$, $\theta =2$, $\mu _1=4$, $\mu _2=-2$, $\mu _3=1$, $\delta =4$

Fig. 4

Absolute graphical solution of $q_{3}(x,y,t)$ for the values of $\gamma =3$, $\theta =2$, $\mu _1=1$, $\mu _2=1$, $\mu _3=2$, $\delta =4$, $a_0=-0.1$

Fig. 5

Absolute graphical solution of $q_{4}(x,y,t)$ for the values of $\gamma =3$, $\theta =2$, $\mu _1=2$, $\mu _2=1$, $\mu _3=3$, $\delta =0.1$, $a_0=-1$

Fig. 6

Absolute graphical solution of $q^*_{4}(x,y,t)$ for the values of $\gamma =3$, $\theta =2$, $\mu _1=2$, $\mu _2=1$, $\mu _3=3$, $\delta =0.1$, $a_0=-1$

Fig. 7

Absolute graphical solution of $q_{5}(x,y,t)$ for the values of $\gamma =3$, $\theta =2$, $\mu _1=1$, $\mu _2=1$, $\mu _3=1$, $\delta =4$, $a_0=0.1$

Fig. 8

Absolute graphical solution of $q^*_{5}(x,y,t)$ for the values of $\gamma =3$, $\theta =2$, $\mu _1=1$, $\mu _2=1$, $\mu _3=1$, $\delta =4$, $a_0=0.1$

Fig. 9

Absolute graphical solution of $q_{6}(x,y,t)$ for the values of $\gamma =3$, $\theta =2$, $\mu _1=2$, $\mu _2=1$, $\mu _3=3$, $\delta =0.1$, $a_0=1$

Fig. 10

Absolute graphical solution of $q^*_{6}(x,y,t)$ for the values of $\gamma =3$, $\theta =2$, $\mu _1=2$, $\mu _2=1$, $\mu _3=3$, $\delta =0.1$, $a_0=1$

Fig. 11

Real graphical solution of $q_{7}(x,y,t)$ for the values of $\gamma =3$, $\theta =2$, $\mu _1=1$, $\mu _2=3$, $\mu _3=1$, $\delta =0.5$

Fig. 12

Imaginary graphical solution of $q^*_{7}(x,y,t)$ for the values of $\gamma =3$, $\theta =2$, $\mu _1=1$, $\mu _2=3$, $\mu _3=1$, $\delta =0.5$

Fig. 13

Real graphical solution of $q_{8}(x,y,t)$ for the values of $\gamma =-3$, $\theta =2$, $\mu _1=4$, $\mu _2=-2$, $\mu _3=1$, $\delta =4$

Fig. 14

Imaginary graphical solution of $q^*_{8}(x,y,t)$ for the values of $\gamma =-3$, $\theta =2$, $\mu _1=4$, $\mu _2=-2$, $\mu _3=1$, $\delta =4$

Fig. 15

Real graphical solution of $q_{10}(x,y,t)$ for the values of $\gamma =3$, $\theta =2$, $\mu _1=2$, $\mu _2=1$, $\mu _3=3$, $\delta =0.1$, $a_0=-1$

Fig. 16

Imaginary graphical solution of $q^*_{10}(x,y,t)$ for the values of $\gamma =3$, $\theta =2$, $\mu _1=2$, $\mu _2=1$, $\mu _3=3$, $\delta =0.1$, $a_0=-1$

Fig. 17

Real graphical solution of $q_{12}(x,y,t)$ for the values of $\gamma =3$, $\theta =2$, $\mu _1=2$, $\mu _2=1$, $\mu _3=3$, $\delta =0.1$, $a_0=1$

Fig. 18

Imaginary graphical solution of $q^*_{12}(x,y,t)$ for the values of $\gamma =3$, $\theta =2$, $\mu _1=2$, $\mu _2=1$, $\mu _3=3$, $\delta =0.1$, $a_0=1$

5 Conclusion

In this work, the extended modified auxiliary equation mapping approach is utilized to study the Lakshmanan-Porsezian-Daniel model with the Ker law, parabolic law and anti-cubic law of nonlinearity. As a result, a variety of exact solutions are established in the form of dark solitons, light solitons, solitary wave, periodic solitary wave, rational function, and complex function solutions, for details see Figs. 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14, 15, 16, 17 and 18. The obtained solutions conforms that the applied technique is more powerful and efficient approach for obtaining the exact optical solutions to a variety of nonlinear problems emerging in the contemporary era of communications network technology and nonlinear optics. In future, other methodologies and nonlinearity laws may be used to explore such model, thus there is still a lot of fresh work to be done on it.