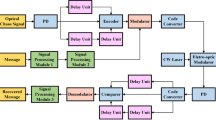
Abstract
This paper proposes an optical secure communication scheme based on chaos synchronization. Nonlinear Schrödinger equation is an important model for optical communication. Our theoretical analysis and numerical simulation show that when the nonlinear Schrödinger equation is perturbed by multiple frequencies, the optical solitons becomes chaotic despite that optical soliton is usual preferred for long-distance transmission. By taking the generated chaotic signals as communication carrier, a master slave system for optical secure communication is designed. A feedback controller is applied to the slave system. Sufficient conditions for chaos synchronization are then proved. It is discovered that the synchronization speed is closely linked with parameters of the nonlinear Schrödinger equation.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction
The nonlinear Schrödinger (NLS) equation has many important applications in various fields, such as plasma physics (Mathieu and Masahito 2014), optical fiber communication (Wang and Yang 2015), fluid and solid mechanics (Nottale 2009). Hederi et al. (2016) studied the efficiency of exponential time differencing schemes for nonlinear Schrödinger equations. Solitonic dynamics and excitations of the NLS equation with third-order dispersion in non-Hamiltonian PT-symmetric potentials were determined (Chen and Yan 2016).
For the cases of communication models, the NLS equation is an excellent option. The NLS equation admits optical solitons which can achieve ultra-long-distance and large-capacity communications. In addition,the security communication is highly required by the practical application of optical solitons in many aspects from state secrets to personal privacy. Secure communication modeled by the NLS equation is an important research field, hence it is the main interest of this paper.
Chaos synchronization technology is an important method for secure communications. This technology has been applied to many models such as the Duffing equation (Wu et al. 2007; Ahn 2009) and the Lorenz system (Wang et al. 2015). The key point of chaos synchronization is that chaos will be obtained as a signal carrier and then synchronization is devised for the decryption stage.
Secure communication has been studied using chaotic maps and continuous dynamical models. In Mahmoud et al. (2009), the case of two complex nonlinear oscillators was studied using active control and global synchronization techniques. Their results showed that the error is globally stable. By the Lyapunov stability theory, secure communication of a general complex dynamical network with coupling delays was investigated and the delay-dependent criteria were derived via adopting the free weighting matrix approach (Wang and Guan 2010). Secure communication of two identical stochastic Duffing oscillators with bounded random parameters was considered, and a feedback control strategy was adopted to synchronize chaotic responses of two identical equivalent deterministic systems (Wu et al. 2007; Wembe and Yamapi 2009; Sun 2012).
It is important to study optical secure communication modeled by the perturbed NLS equation. On one hand, we find that chaos is difficult to be excited in other systems. The chaotic signal can only be produced under special conditions. A slight change in the parameters or environment may eliminate the original chaos. These facts have negative effects on the design of stable and effective chaotic secure communication mechanisms. On the other hand, fiber optical secure communication has rarely been studied because the model uses the partial differential equation, while the classical secure communication is based on ordinary differential equations.
This paper focuses on designing an efficient mechanism for the optical signal secure communication by chaos synchronization. There are two objectives of this paper. The first is to find an effective method to generate chaos. It is noted that many models can induce chaos under periodic perturbation by the Melnikov method, and chaos appears when the homoclinic orbit breaks. By the dynamical theory, optical soliton corresponds to a homoclinic orbit. So we want to know whether the optical soliton turns into chaos or not, under periodic perturbation. The second is to use chaos synchronization technology to achieve optical secure communication modeled by the NLS equation. Chaos synchronization of the NLS equation has rarely been mentioned in the literature. In our previous studies (Yin and Zhao 2014; Wu et al. 2008), we found that the reduced nonlinear Schrodinger equation is similar to the Duffing equation. Owing to the similarity between the NLS equation and the Duffing equation, it is possible to achieve the chaos synchronization by the NLS equation.
The rest of this paper is organized as follows. In Sect. 2, we study an effective way to generate chaos by the Melnikov method, which is verified by numerical results. In Sect. 3, we study chaos synchronization by feedback control. Results show that using chaos synchronization technology can achieve optical secure communication modeled by the nonlinear Schrödinger equation. We arrive a conclusion in Sect. 4.
2 Chaos generated by perturbing the NLS equation
2.1 The perturbed NLS equation and unperturbed NLS equation
We consider the following perturbed NLS equation
in which, \(\varepsilon = \varepsilon (x)\) is a general expression given by
where \(\frac{d}{\sqrt{N} }\) and \(\omega _i\) denote the amplitude and the frequency, respectively. The reason for using Eq. (2) is that the power of \(\varepsilon (x)\) equals to \(\frac{d^2}{2}\), which allows us to focus on the richness of the frequency, while the perturbed power is kept as constant and independent of N.
Assume that Eq. (1) has traveling wave solutions in the form
The chaotic behavior is given by the following equation:
where “\(\prime\)” denotes the derivative with respect to x. By using the transformation \(\beta = {\alpha }'\), Eq. (3) is transformed into a set of two autonomous differential equations as below
When \(\varepsilon = 0\), Eq. (4) becomes an unperturbed system
System (5) has the following Hamiltonian function
2.2 Existence of solitary waves in the unperturbed system
Lemma 1
For any negative \({\varOmega },\) system ( 5 ) admits two homoclinic orbits associated with two solitary waves.
Proof
The equilibrium points of system (5) are considered as follows by using dynamic method. System (5) has three equilibrium points \(E_1 (\sqrt{ - {\varOmega }} ,0)\), \(E_2 ( - \sqrt{ - {\varOmega }} ,0)\) and \(E_3 (0,0)\). Let \(J_i\) be the Jacobian matrix at the corresponding \(E_i, i=1,2,3\) and we obtain
It is easy to find that eigenvalues of \(J_i\) are \(\lambda \left( {J_1 } \right) = \lambda \left( {J_2 } \right) = \pm \sqrt{4{\varOmega }}\) and \(\lambda \left( {J_3 } \right) = \pm \sqrt{ - 2{\varOmega }}\). So \(E_1\) and \(E_2\) are centers and \(E_3\) is a saddle for any negative \({\varOmega }\). Hence there are two homoclinic orbits \(T_{\hom }^\pm = [\phi _{h1}^\pm (t),\phi _{h2}^\pm (t)]\) passing through the saddle point \(E_3\).
According to the bifurcation theory, system (5) has two solitary waves followed by two homoclinic orbits: the positive solitary wave achieves its crest at \(\alpha = \sqrt{ - 4{\varOmega }}\) and the negative solitary wave has the valley at \(\alpha = - \sqrt{ - 4{\varOmega }}\).
2.3 Existence of chaos in the perturbed system
Next, we will consider the existence of chaos in the perturbed Eq. (3) by using the Melnikov method.
Consider that \(\varepsilon\) is a small perturbed parameter, and the unperturbed homoclinic orbits are written as \((\alpha ,\beta ) = (\alpha _0 (x),\beta _0 (x))\). According to the Melnikov method, a Melnikov function for Eq. (3) is defined as
where \(I_i = \int _{\;0}^{\; + \infty } {\alpha _0^2 } (x)\cos (w_i x)dx\) is a function of \(w_i .\)
According to the Melnikov method, chaos occurs if \(M(x_0 ) = 0\) and \({M}'(x_0 ) \ne 0\) for some \(x_0\). We observe that \(M(0) = 0\) and \({M}'(0) = \frac{dw_i^2 }{\sqrt{N} }\sum \nolimits _{i = 1}^N {I_i }\) is a function of \(w_i .\) The proof of the existence of chaos will be completed if \(I{ }_i > 0.\) By Lemma 1, we can obtain the expression of the homoclinic orbit as: \(\alpha _0 (t) = \sqrt{ - 2{\varOmega }} \cdot \sec h(\sqrt{ - 2{\varOmega }} \cdot x).\) So we have
From the facts above, we find that \(x_0 = 0\) satisfies Eq. (7) for any positive integer N. The proof of the existence of chaos is completed. \(\square\)
2.4 Numerical simulations
To illustrate the existence of chaos, we will investigate the phase portraits and the Lyapunov exponents of Eq. (3) numerically. Parameters are taken as \({\varOmega }= - 0.9\), \(d = 0.2\) with the initial condition \((x_0 ,y_0 ) = (0.2,3.9).\)
The phase portraits are shown in Fig. 1. For the chosen \(N=1,3,5,9\), the broken homoclinic orbits imply that Eq. (3) is chaotic.
Remark 1
The sign of the parameter \({\varOmega }\) has important value for the generation of chaos. According to Lemma 1, we find that for negative \({\varOmega },\) the system has homoclinic orbits, and the homoclinic orbits produce chaos in any periodic disturbance.
The Lyapunov exponents are shown in Fig. 2. All Lyapunov exponents are positive so that the motion of system (3) is chaotic. The corresponding time series are shown in Fig. 3. It also shows the existence of chaos.
Phase portraits of Eq. (4) for different values of N
Time series of Eq. (4) for different values of N
Remark 2
Chaos is also influenced by different values of the parameter d. From Fig. 2b, the Lyapunov exponent increases as d increase. Therefore the larger perturbation amplitude, the higher degree of chaos.
Remark 3
The number of the interference items N has little effect on the chaos. From Fig. 2, Lyapunov exponents do not change obviously for different values of N. The reason may be that the number of perturbations increases while the perturbation energy remains constant \(\frac{d^2}{2}.\)
Remark 4
The magnitude of the absolute value of the parameter \({\varOmega }\) has an important effect on the degree of chaos. There is a threshold \({\varOmega }_0\) such that the degree of chaos is enlarged when \({\varOmega }< {\varOmega }_0,\) that is, \({\varOmega }\) is close to zero. \({\varOmega }\) has little effect on the degree of chaos when its value reaches and exceeds \({\varOmega }_0.\)
3 Criteria for the chaos synchronization
We find that nonlinear Schrödinger equation can produce chaos in the conventional periodic interference environment. It’s a quite good secure communication model. So it is easy to choose the useful signal from chaotic signal. The more complex the chaotic signals, the securer the communication is. Chaos synchronization by feedback control is applied to increase the complexity of chaotic signal so that secure communication is achieved.
3.1 Construction of synchronization system
We rewrite Eq. (3) to an equivalent for matrix equation
with \(\alpha = (\alpha _1 ,\alpha _2 )^T \in R^2,\)
where \(\delta (x) = - 2{\varOmega }+ \varepsilon \sum \limits _{i = 1}^N {\cos (w_i x)} .\)
Now we construct a synchronization scheme for two equations with a linear state error feedback controller u(x) as follows:
where \(u(x) = K(\alpha - \gamma ),\) which is the extreme case of drive/response mismatch. \(\gamma = (\gamma _1 ,\gamma _2 )^T \in R^2\) is the state variable and \(K \in R^{2\times 2}\) denotes a constant control matrix.
Define the error variable \(e = \alpha - \gamma\). Since
with \(F(x) = 2(\alpha _1^2 + \alpha _1 \gamma _1 + \gamma _1^2 )\), we obtain a time-varying error system
Our aim is to select the control matrix K such that the trajectory \(\alpha (x)\) trends to \(\gamma (x)\) regardless of the choice of the initial condition \(\alpha (0)\) and \(\gamma (0),\) that is,
where \(\left\| \cdot \right\|\) denotes Euclidean norm of a vector.
3.2 Sufficient conditions of chaos synchronization
For convenience, we denote that a matrix \(P > 0\) if each element of P is positive.
Theorem 1
The master–slave scheme Eq. ( 10 ) achieves global chaos synchronization if there exist a symmetric matrix \(0 < P = \left( {{\begin{array}{*{20}l} {p_{11} } &{}\quad {p_{12} } \\ {p_{21} } &{}\quad {p_{22} } \\ \end{array} }} \right) \in R^{2\times 2}\) and a control matrix \(K = \left( {{\begin{array}{*{20}l} {k_{11} } &{}\quad {k_{12} } \\ {k_{21} } &{}\quad {k_{22} } \\ \end{array} }} \right) \in R^{2\times 2}\) such that the following inequalities are satisfied
Proof
Considering a quadratic Lyapunov function
The derivative of V(e) with respect to time along the trajectory of the error Eq. (12) equals
It is noted that \(\dot{V}(e) < 0\) if
According to the Lyapunov stability theory, the inequality (17) represents a sufficient condition for global asymptotic stability of the linear time-varying error Eq. (12) at the origin.
From Eqs. (9) and (11), we have
Since Y is symmetric, \(Y < 0\) if and only if
From Fig. 1, we know that the trajectory of chaotic system (3) is bounded, which implies that there exists a constant \(m > 0\) satisfying \(\left| {\alpha _1 (x)} \right| < m\) for any \(x \ge 0\). Hence, we have
where m is positive integer. Again \(p_{ii} > 0(i = 1,2)\) on the condition that \(P > 0\). Hence
Therefore the inequalities (18)–(20) hold if the inequalities (14)–(16) are satisfied. This completes the proof. \(\square\)
Corollary 1
The master slave scheme Eq. ( 10 ) achieves global chaos synchronization if a control matrix \(K = diag\left\{ {k_1 ,k_2 } \right\}\) and a symmetric positive definite matrix are selected such that
Proof
The inequalities (21)–(23) can be obtained according to the inequalities (14)–(16) with \(k_{11} = k_1 ,k_{22} = k_2 ,\) and \(k_{12} = k_{21} = 0._{ }\) The proof is completed. \(\square\)
Corollary 2
The master slave scheme Eq. ( 10 ) achieves global chaos synchronization if a control matrix \(K = diag\left\{ {k,k} \right\}\) and a symmetric positive definite matrix \(P = \left( {{\begin{array}{*{20}l} {p_{11} } &{}\quad {p_{12} } \\ {p_{21} } &{}\quad {p_{22} } \\ \end{array} }} \right)\) are selected such that
Proof
Letting \(k_1 = k_2 = k\) in the partial synchronization conditions Eqs (21) and (21), we can obtain the inequality (24).
For \(k > 0\), given by inequality (24), we have
Hence the inequalities (24) can be obtained by the partial synchronization condition Eq. (22) with \(k_1 = k_2 = k.\)
Since \(p_{11} p_{22} - p_{12}^2 > 0\), the solution k to inequality (24) exists. The proof is completed. \(\square\)
We select \(p_{12} = 0\) and \(p_{11} = p_{22} (\left| {2{\varOmega }} \right| + \left| {d\sqrt{N} } \right| + 6m^2) > 0\) to construct a symmetric positive definite matrix
Using this matrix we can obtain the following algebraic synchronization criterion by Eqs. (23) and (24)
3.3 Numerical simulations of chaos synchronization
Now we illustrate the performance of chaotic secure communication system by using MATLAB.
Chaos synchronization of system (12) for parameters \({\varOmega }= - 0.5,d = 0.2,N=1\) with different parameter k. a Error \(e_1\). b Error \(e_2\)
Chaos synchronization of system (12) for parameters \(k=13.2,d = 0.2,N=1\) with different parameter \({\varOmega }\). a Error \(e_1\). b Error \(e_2\)
Chaos synchronization of system (12) for parameters \({\varOmega }= - 0.5,k=13.2,N=1\) with different parameter d. a Error \(e_1\). b Error \(e_2\)
Chaos synchronization of system (12) for parameters \({\varOmega }= - 0.5,d = 0.2,k=13.2\) with interference item \(N = 1,3,5,9\). a Error \(e_1\). b Error \(e_2\)
Remark 5
We find that synchronization is closely linked with system parameters. The larger the control parameter k is, or the closer the parameter \({\varOmega }\) is to zero, or the smaller the amplitude of the disturbance is, and the faster the system is synchronized. However, the number of cosine waves of the interference term does not affect the synchronization speed (Figs. 4, 5, 6).
4 Conclusions
In this paper, we have proposed and investigated a new chaotic secure communication scheme based on the nonlinear Schrödinger equation. The sufficient criteria for chaos synchronization of the master–slave system have been obtained. Numerical simulations demonstrate the accuracy of those sufficient criteria. For the design of fiber-optic secure communication, we can select a close-to-zero negative \({\varOmega }\) and in order to obtain the greater complexity of chaotic signal. Meanwhile, chaos synchronization can be achieved at a faster rate under this condition. So the optimal choice is to take a small negative of the parameter \({\varOmega }\) (Fig. 7).
References
Ahn, C.K.: A new chaos synchronization method for Duffing oscillator. IEICE Electr. Expr. 6, 1355–1360 (2009)
Chen, Y., Yan, Z.Y.: Solitonic dynamics and excitations of the nonlinear Schrödinger equation with third-order dispersion in non-hermitian PT-symmetric potentials. Sci. Rep. 6, 23478 (2016). doi:10.1038/srep23478
Hederi, M., Islas, A.L., Reger, K., Schober, C.M.: Efficiency of exponential time differencing schemes for nonlinear Schrödinger equations. Math. Comput. Simul. 127, 101–113 (2016)
Mahmoud, G.M., Mahmoud, E.E., Farghaly, A.A., Aly, S.A.: Chaotic synchronization of two complex nonlinear oscillators. Chaos Solitons Fractals 42, 2858–2864 (2009)
Mathieu, C., Masahito, O.: Instability of ground states for a quaslinear Schrödinger equation. Differ. Integral Equ. 27, 613–624 (2014)
Nottale, L.: Generalized quantum potentials. J. Phys. A Math. Theor. 42, 275306 (2009)
Sun, Y.J.: A novel chaos synchronization of uncertain mechanical systems with parameter mismatchings, external excitations, and chaotic vibrations. Commun. Nonlinear Sci. Numer. Simul. 17, 496–504 (2012)
Wang, B.X., Guan, Z.H.: Chaos synchronization in general complex dynamical networks withcoupling delays. Nonlinear Anal. Real World Appl. 11, 1925–1932 (2010)
Wang, X.L., Yang, J.: Exact spatiotemporal soliton solutions to the generalize three-dimensional nonlinear Schrödinger equation in optical fiber communication. Adv. Differ. Equ. 2015, 347 (2015)
Wang, S.B., Wang, X.Y., Zhou, Y.: A memristor-based complex Lorenz system and its modified projective synchronization. Entropy 17, 7628–7644 (2015)
Wembe, E.T., Yamapi, R.: Chaos synchronization of resistively coupled Duffing systems: numerical and experimental investigations. Commun. Nonlinear Sci. Numer. Simul. 14, 1439–1453 (2009)
Wu, C.L., Fang, T., Rong, H.W.: Chaos synchronization of two stochastic Duffing oscillators by feedback control. Chaos Solitons Fractals 32, 1201–1207 (2007)
Wu, X.F., Cai, J.P., Wang, M.H.: Global chaos synchronization of the parametrically excited duffing oscillators by linear state error feedback control. Chaos Solitons Fractals 36, 121–128 (2008)
Yin, J.L., Zhao, L.W.: Dynamic behaviors of the shock compacton in the nonlinearly Schrödinger equation with a source term. Phys. Lett. A 378, 3516–3522 (2014)
Acknowledgements
This work is supported by the National Nature Science Foundations of China (Nos. 11101191 and 71673116), the Natural Science Foundation of Jiangsu Province (No. SBK2015021674) and Jiangsu Qing Lan Project.
Author information
Authors and Affiliations
Corresponding author
Rights and permissions
About this article
Cite this article
Yin, J., Duan, X. & Tian, L. Optical secure communication modeled by the perturbed nonlinear Schrödinger equation. Opt Quant Electron 49, 317 (2017). https://doi.org/10.1007/s11082-017-1111-7
Received:
Accepted:
Published:
DOI: https://doi.org/10.1007/s11082-017-1111-7