1 Introduction

In recent years, major advances have been observed in studies on analytical solutions of nonlinear partial differential equations (NLPDEs). These equations are mathematical models of physical phenomena that occur in interdisciplinary fields of mathematics. Analytical solutions of these equations provide information about the character of the physical event that describes the equation. Therefore, scientists work hard to obtain the solutions of these equations. Thanks to these studies of scientists, many analytical methods have been developed. Solving NLPDEs are more difficult and time consuming than solving ODEs. To overcome these difficulties, NLPDEs are converted into ODEs. Scientists usually use a variable transformation to do this transformation. In many of these analytical methods are used linear or nonlinear ordinary differential equations as an arbitrary equation. Analytical solutions of the investigated problem are obtained by making use of different types solution functions of these arbitrary equations. When some researchers use the riccati differential equation or the second order ordinary differential equation as the arbitrary equation, they obtain different trigonometric, hyperbolic and rational solution functions of the problem under consideration. Different analytical methods have been developed according to the selection of these arbitrary equations. For example, some methods have been developed using different types of \(G^{\prime\prime} + \lambda G^{\prime} + \mu G = 0.\) Some of these methods: \(\left( {{{G^{\prime}} \mathord{\left/ {\vphantom {{G^{\prime}} G}} \right. \kern-\nulldelimiterspace} G}} \right)\)-expansion method (Durur 2020a), \(\left( {{{G^{\prime}} \mathord{\left/ {\vphantom {{G^{\prime}} {G^{2} }}} \right. \kern-\nulldelimiterspace} {G^{2} }}} \right)\)-expansion method (Rehman et al. 2020), \(\left( {{1 \mathord{\left/ {\vphantom {1 {G'}}} \right. \kern-\nulldelimiterspace} {G'}}} \right)\)-expansion method (Durur et al. 2020b), Sumudu transform (Yavuz and Ozdemir 2018), heat balance integral method (Yavuz and Sene 2020), the sinh-Gordon function method (Yokuş et al. 2020), generalized exponential rational function method (Duran 2021a), \(\left( {m + G^{\prime}/G} \right)\)-expansion method (Ismael et al. 2020), \(\left( {m + 1/G^{\prime}} \right)\)-expansion method (Durur et al. 2020c), \(\left( {{{G^{\prime}} \mathord{\left/ {\vphantom {{G^{\prime}} {G,{1 \mathord{\left/ {\vphantom {1 G}} \right. \kern-\nulldelimiterspace} G}}}} \right. \kern-\nulldelimiterspace} {G,{1 \mathord{\left/ {\vphantom {1 G}} \right. \kern-\nulldelimiterspace} G}}}} \right)\)-expansion method (Duran 2020; Duran 2021b; Duran 2021c). Some scientists are presented different versions of these methods according to the selected solution function in the literature, such as extended, improved and generalized. In this sense, some methods are modified simple equation method (Kayum et al. 2021), modified extended tanh-function method (Seadawy et al. 2017), modified hyperbolic-function expansion method (Chen et al. 2019), complex method (Gu et al. 2017), Haar wavelet method (Pervaiz and Aziz 2020; Kirs et al. 2018), Bäcklund method (Rezazadeh et al. 2021), new auxiliary equation method (Kumar et al. 2020) and many more methods (Guerrero Sánchez et al. 2020; Hosseini et al. 2021, 2020a, 2020b; Yavuz and Yokus 2020; Yokus et al. 2019; Kudryashov 2020a, 2020b; Yokuş and Kaya 2020; Modanli 2019; Vahidi et al. 2020).

In this study, we consider the CLL equation that has many applications in plasma and optical fiber (Triki 2018a). This equation was first published in 1979 (Chen et al. 1979). Especially in the last few years, many studies have been conducted on the solutions of this equation. The mathematical model of the phenomena we encounter in plasma physics and fiber optics corresponds to a nonlinear differential equation such as the CLL equation. By applying analytical methods to a nonlinear differential equation, soliton solutions are obtained. When these soliton solutions are examined, special cases of these solutions are obtained, depending on the wave propagation parameter, height and density. We can classify these special cases as dark, bright and singular solitons (Yıldırım 2020). Bright and dark solitons are related to the intensity of the wave. While bright solitons indicate an increase, dark solitons indicate a decrease in the intensity of the wave (Triki et al. 2017; Triki 2018b). Singular solitons are a special case and are the result of a balance between the speed of the wave and its height (Biswas 2018).

In this article, authors established the soliton wave solutions of the following perturbed CLL equation that represents the propagation of an optical pulse in plasma and optical fiber:

$$ iq_{t} + aq_{{xx}} + ib\left| q \right|^{2} q_{x} = i\left[ {\lambda q_{x} + \theta \left( {\left| q \right|^{{2m}} q} \right)_{x} + \sigma \left( {\left| q \right|^{{2m}} } \right)_{x} q} \right], $$
(1)

the x and t coordinates are the wave propagation distance and time variable, respectively. \(q = q\left( {x,t} \right)\) is the complex wave function dependent on these independent coordinates. \(a\) is the velocity propagation parameter and \(b\) is the nonlinear dispersion parameter. \(\sigma\), \(\theta\) and \(\lambda\) on the right side of the equation are coefficients of nonlinear dispersion, self-steeping for short pulses and the inter-modal dispersion, respectively. In addition, the nonlinearity parameter \(m\) in the above equation defines the density for complex wave function (Yıldırım et al. 2020). One of the most important models for studying soliton propagation through optical fibers is Schrödinger's equation (Yıldırım et al. 2020). When the Schrödinger equation is examined, it is defined in different ways according to its derivative property. In particular, the CLL equation (Yıldırım et al. 2020) we deal with in this study is a special case of the Schrödinger equation.

In this study, two different analytical methods are used to obtain the traveling wave solutions of the CLL equation. These methods are Modified \(\left( {{1 \mathord{\left/ {\vphantom {1 {G'}}} \right. \kern-\nulldelimiterspace} {G'}}} \right)\)-expansion method and Modified Kudryashov methods. The classical \(\left( {{1 \mathord{\left/ {\vphantom {1 {G'}}} \right. \kern-\nulldelimiterspace} {G'}}} \right)\)-expansion method was brought into literature in 2011 with the Ph.D. thesis (Yokus 2011). Kudryashov has conducted many studies to obtain exact solutions of the NLPDEs (Kudryashov 1988, 1990, 1991, 1993, 2020c). As a result of these studies, the method was presented by Kudryashov in 2004 (Kudryashov 2004). Since the subject we deal with in this study is the improvement of Kudryashov's solution, we can call this the modified Kudryashov method (Kabir et al. 2011). Considering the fact that two analytical methods produce similar solutions with different methods, in this study the solutions produced by using modified versions of both analytical methods are compared.

2 The Modified Kudryashov method

Suppose you have a NLPDE in the form below

$$ T\left( {q,q_{t} ,q_{x} ,q_{{xx}} ,...} \right) = 0, $$
(2)

where \(q = q\left( {x,t} \right)\). We give the basic steps of this method (Kudryashov 1988, 1990, 1991, 1993, 2020c, 2004) in the follow:


Step 1 By using the wave transformation

$$ q\left( {x,t} \right) = U\left( \xi \right)e^{{i\varphi \left( {x,t} \right)}} ,\quad \xi = \eta \left( {x - vt} \right),\quad \varphi \left( {x,t} \right) = - \kappa x + wt + s, $$
(3)

where \(\kappa ,w,v,s\) are constants and we can transform it the following ODE for \(U\left( \xi \right)\):

$$ S\left( {U,U^{\prime},U^{\prime\prime},...} \right) = 0. $$
(4)

Step 2 We suppose that Eq. (4) has the formal solution

$$ U\left( \xi \right) = a_{0} + \sum\limits_{{i = 1}}^{n} {(a_{i} Q\left( \xi \right)^{i} + a_{{ - i}} Q\left( \xi \right)^{{ - i}} )} , $$
(5)

where \(a_{i} ,a_{{ - i}} ,\quad i = \left\{ {1,...,n} \right\}\) are constants to be determined, such that \(a_{n} \ne 0\;or\;a_{{ - n}} \ne 0,\) and \(Q\left( \xi \right)\) is the solution of the Eq.

$$ Q^{\prime}\left( \xi \right) = \left[ {Q^{2} \left( \xi \right) - Q\left( \xi \right)} \right]\ln \tau , $$
(6)

Equation (6) has solutions

$$ Q\left( \xi \right) = \frac{1}{{1 \pm \tau ^{\xi } }}, $$
(7)

where \(\tau > 0,\;\tau \ne 1\) is a number.


Step 3 We identify the positive integer n in Eq. (5) taking into account the homogeneous balance between the nonlinear terms and the highest order derivatives in Eq. (4).


Step 4 Surrogating Eq. (5) with Eq. (6) into Eq. (4), we compute all the required derivatives \(U^{\prime},U^{\prime\prime},...\) of the \(U\left( \xi \right)\). As a result of this, we obtain a polynomial of \(Q^{j} \left( \xi \right),\;\left( {j = 0,1,2,...} \right)\). In this polynomial obtained, we add all the terms of the same powers of \(Q^{j} \left( \xi \right)\) and equal them to zero, we attain a system of algebraic equations that may be solved by computer package program to attain the unknown parameters \(a_{i} ,a_{{ - i}} ,\quad i = \left\{ {1,...,n} \right\}\), k and v. As a result, we get exact solutions of the Eq. (2).

3 The Modified \(1/G^{\prime}\)-expansion method

Consider the form of NLPDEs,

$$ \diamondsuit \left( {q,\frac{{\partial q}}{{\partial t}},\frac{{\partial q}}{{\partial x}},\frac{{\partial ^{2} q}}{{\partial x^{2} }},...} \right) = 0. $$
(8)

Let \(q\left( {x,t} \right) = U\left( \xi \right)e^{{i\varphi \left( {x,t} \right)}} ,\quad \xi = \eta \left( {x - vt} \right),\quad \varphi \left( {x,t} \right) = - \kappa x + wt + s,\) here \(v\) is the velocity of the wave and constant. We may transform it the following ODE for \(U\left( \xi \right)\):

$$ N\left( {U,U^{\prime},U^{\prime\prime},...} \right) = 0. $$
(9)

The solution of Eq. (9) is supposed that with the form

$$ U\left( \xi \right) = a_{0} + \sum\limits_{{i = 1}}^{n} {\left( {a_{i} \left( {\frac{1}{{G^{\prime}}}} \right)^{i} + a_{{ - i}} \left( {\frac{1}{{G^{\prime}}}} \right)^{{ - i}} } \right)} , $$
(10)

where \(a_{i} ,\;a_{{ - i}} ,\quad i = \left\{ {1,...,n} \right\}\) are scalars, \(G = G\left( \xi \right)\) ensures following second-order IODE

$$ G^{\prime\prime} + \lambda G^{\prime} + \gamma = 0, $$
(11)

here \(\gamma\) and \(\lambda\) are constants to be determined,

$$ \frac{1}{{G^{\prime}\left( \xi \right)}} = \frac{1}{{ - \frac{\gamma }{\lambda } + A\cosh \left[ {\xi \lambda } \right] - A\sinh \left[ {\xi \lambda } \right]}} $$
(12)

The software for Eq. (12) in exponential form is as follows

$$ \frac{1}{{G^{\prime}\left( \xi \right)}} = \frac{1}{{ - \frac{\gamma }{\lambda } + A\;e^{{ - \xi \lambda }} }} $$
(12a)

The wanted derivatives of Eq. (10) are calculated and written into Eq. (9), obtaining a polynomial with \(\left( {{1 \mathord{\left/ {\vphantom {1 {G^{\prime}}}} \right. \kern-\nulldelimiterspace} {G^{\prime}}}} \right)\). Equating the coefficients of this polynomial to zero, an algebraic system of equations is created. The Equation is solved via the package program and the default Eq. (9) is put in its place in the solution function. Eventually, the solutions of Eq. (8) are found.

4 Application of Modified Kudryashov Method

We consider Eq. (1). By using

$$ q\left( {x,t} \right) = U\left( \xi \right)e^{{i\varphi \left( {x,t} \right)}} ,\quad \xi = \eta \left( {x - vt} \right), $$
(13)

where the amplitude component is \(U\left( \xi \right)\), with v being the speed, while phase component

$$ \varphi \left( {x,t} \right) = - \kappa x + wt + s, $$
(14)

where the parameters \(s,w,\kappa\) sequentially correspond to the phase, wave number and frequency. Inserting Eq. (2) into Eq. (1), the real and imaginary equations are

$$ a\eta ^{2} U^{\prime\prime} - \left( {w + a\kappa ^{2} + \kappa \lambda } \right)U + b\kappa U^{3} - \kappa \theta U^{{2m + 1}} = 0, $$
(15)
$$ - v - 2a\kappa - \lambda + bU^{2} - \left( {2m\theta + \theta + 2\sigma m} \right)U^{{2m}} = 0, $$
(16)

respectively. Where m is the nonlinearity parameter representing the exact density. The higher the density m, the stronger nonlinear term is obtained. In Eq. (16), the velocity of optical solitons in the form of \(v = - 2a\kappa - \lambda\) is obtained. Also, in Eq. (15), the structure of optic solitons is constructed. If you pay attention to the Eq. (16), it becomes \(b = 0\) when \(m \ne 1\) is selected. In this case, the nonlinear distribution parameter in Eq. (1) disappears and the equation is reduced to a simpler form. In this case, it may cause changes in its physical structure. In this study, \(m = 1\) was chosen to guarantee the existence of the analytical solution.

For use the balancing rule, Eqs. (15) and (16) are Modified to

$$ a\eta ^{2} U^{\prime\prime} - \left( {w + a\kappa ^{2} + \kappa \lambda } \right)U + 2\kappa \left( {\theta + \sigma } \right)U^{3} = 0, $$
(17)

and

$$ v = - 2a\kappa - \lambda ,\quad b = 3\theta + 2\sigma , $$
(18)

By adjusting \(m = 1\).

The profile of the optical solitons is recovered with the help of integrating the Eq. (7) while the speed of the optical solitons is emerged from the Eq. (18). In Eq. (18), we get the balancing term \(n = 1\) and by considering in the Eq. (5),

$$ U\left( \xi \right) = a_{0} + a_{1} Q\left( \xi \right) + a_{2} \frac{1}{{Q\left( \xi \right)}}, $$
(19)

if Eq. (19) is written in Eq. (17) and if necessary adjustments are made, the following systems of equations may be written:

$$ \begin{aligned} & Const:\; - ak^{2} a_{0} - wa_{0} - k\lambda a_{0} - 2k\theta a_{0}^{3} - 2k\sigma a_{0}^{3} - a\eta ^{2} \log \left[ \tau \right]^{2} a_{2} - 12k\theta a_{0} a_{1} a_{2} - 12k\sigma a_{0} a_{1} a_{2} = 0, \\ & \frac{1}{{Q\left[ \xi \right]}}:\; - ak^{2} a_{2} - wa_{2} - k\lambda a_{2} + a\eta ^{2} \log \left[ \tau \right]^{2} a_{2} - 6k\theta a_{0}^{2} a_{2} - 6k\sigma a_{0}^{2} a_{2} - 6k\theta a_{1} a_{2}^{2} - 6k\sigma a_{1} a_{2}^{2} = 0, \\ & \frac{1}{{Q\left[ \xi \right]^{2} }}:\; - 6k\theta a_{0} a_{2}^{2} - 6k\sigma a_{0} a_{2}^{2} = 0, \\ & \frac{1}{{Q\left[ \xi \right]^{3} }}:\; - 2k\theta a_{2}^{3} - 2k\sigma a_{2}^{3} = 0, \\ \end{aligned} $$
(20)
$$ \begin{aligned} & Q\left[ \xi \right]:\; - ak^{2} a_{1} - wa_{1} - k\lambda a_{1} + a\eta ^{2} \log \left[ \tau \right]^{2} a_{1} - 6k\theta a_{0}^{2} a_{1} - 6k\sigma a_{0}^{2} a_{1} - 6k\theta a_{1}^{2} a_{2} - 6k\sigma a_{1}^{2} a_{2} = 0, \\ & Q\left[ \xi \right]^{2} :\; - 3a\eta ^{2} \log \left[ \tau \right]^{2} a_{1} - 6k\theta a_{0} a_{1}^{2} - 6k\sigma a_{0} a_{1}^{2} = 0, \\ & Q\left[ \xi \right]^{3} :\;2a\eta ^{2} \log \left[ \tau \right]^{2} a_{1} - 2k\theta a_{1}^{3} - 2k\sigma a_{1}^{3} = 0. \\ \end{aligned} $$

\(a_{0} ,a_{1} ,\;a_{2}\) and \(a,k,\theta ,\sigma ,\lambda ,\eta ,w\) constants are obtained from Eq. (20) the system utilizing a software program.


Case 1: If

$$ a_{1} = 0,\quad a_{2} = - a_{0} ,\quad w = - ak^{2} - k\lambda + a\eta ^{2} \log \left[ \tau \right]^{2} ,\quad \sigma = - \theta ,\quad v = - 2ak - \lambda ,\quad b = 3\theta + 2\sigma ; $$
(21)

replacing values (21) into (19), we get traveling wave soliton for Eq. (1)

$$ q_{1} \left( {x,t} \right) = e^{{i\left( {s - kx + t\left( { - ak^{2} - k\lambda + a\eta ^{2} \log \left[ \tau \right]^{2} } \right)} \right)}} \left( {a_{0} - \left( {1 + \tau ^{{\eta \left( {x - t\left( { - 2ak - \lambda } \right)} \right)}} } \right)a_{0} } \right). $$
(22)

The solution presented with Eq. (22) is known as traveling wave solution in the literature.


Case 2: If

$$ a_{2} = 0,\quad w = - k\lambda ,\quad \sigma = - \theta ,\quad a = 0,\quad v = - 2ak - \lambda ,\quad b = 3\theta + 2\sigma , $$
(23)

replacing values (23) into (19), we get traveling wave soliton for Eq. (1)

$$ q_{2} \left( {x,t} \right) = e^{{i\left( {s - kx - kt\lambda } \right)}} \left( {a_{0} + \frac{{a_{1} }}{{1 + \tau ^{{\eta \left( {x + t\lambda } \right)}} }}} \right). $$
(24)

The solution presented with Eq. (24) is known as traveling wave solution in the literature.

Figures 1 and 2 present the graphs of the solitary wave representing the stationary wave at any moment by giving special values to the constants in Eqs. (22)–(24), which is the complex traveling wave solution in exponential form.

Fig. 1
figure 1

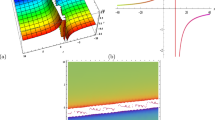
Real and imaginary parts of 3-D, 2-D and contour graphs for the Eq. (22) for \(s = 0.5,\;k = 1,\;\eta = 1,\;a = 2,\;a_{0} = 1,\;\tau = 1.1,\;\lambda = 1\;\)

Full size image
Fig. 2
figure 2

Real and imaginary parts of 3-D, 2-D and contour graphs of the Eq. (24) for \(s = 0.5,\;k = 1,\;\eta = 2,\;a_{1} = 5,\;a_{0} = 5,\;\tau = 1.1,\;\lambda = 1\)

Full size image

5 Implementation of the Modified \(\left( {\frac{1}{{G'}}} \right)\)-expansion method

Let's take Eq. (17) here, \(n = 1\) is attained with respect to the homogeneous balance principle. In Eq. (10), the following situation is obtained:

$$ U\left( \xi \right) = a_{0} + a_{1} \left( {\frac{1}{{G^{\prime}}}} \right) + a_{2} G^{\prime}. $$
(25)

Substituting Eq. (25) in Eq. (17) and the coefficients of Eq. (1) are set to zero, the following systems of equations can be written:

$$ \begin{aligned} & Const:\; - ak^{2} a_{0} - wa_{0} - k\lambda a_{0} - 2k\theta a_{0}^{3} - 2k\sigma a_{0}^{3} + a\eta ^{2} \mu \gamma a_{2} \\ & \quad \quad \quad \quad \quad - 12k\theta a_{0} a_{1} a_{2} - 12k\sigma a_{0} a_{1} a_{2} = 0, \\ & \frac{1}{{G^{\prime}\left[ \xi \right]}}:\; - ak^{2} a_{1} - wa_{1} - k\lambda a_{1} + a\eta ^{2} \gamma ^{2} a_{1} - 6k\theta a_{0}^{2} a_{1} - 6k\sigma a_{0}^{2} a_{1} \\ & \quad \quad \quad \quad \quad - 6k\theta a_{1}^{2} a_{2} - 6k\sigma a_{1}^{2} a_{2} = 0, \\ & \frac{1}{{G^{\prime}\left[ \xi \right]^{2} }}:\;3a\eta ^{2} \mu \gamma a_{1} - 6k\theta a_{0} a_{1}^{2} - 6k\sigma a_{0} a_{1}^{2} = 0, \\ & \frac{1}{{G^{\prime}\left[ \xi \right]^{3} }}:\;2a\eta ^{2} \mu ^{2} a_{1} - 2k\theta a_{1}^{3} - 2k\sigma a_{1}^{3} = 0, \\ & G^{\prime}\left[ \xi \right]:\; - ak^{2} a_{2} - wa_{2} - k\lambda a_{2} + a\eta ^{2} \gamma ^{2} a_{2} - 6k\theta a_{0}^{2} a_{2} - 6k\sigma a_{0}^{2} a_{2} \\ & \quad \quad \quad \quad \quad - 6k\theta a_{1} a_{2}^{2} - 6k\sigma a_{1} a_{2}^{2} = 0, \\ & G^{\prime}\left[ \xi \right]^{2} :\; - 6k\theta a_{0} a_{2}^{2} - 6k\sigma a_{0} a_{2}^{2} = 0, \\ & G^{\prime}\left[ \xi \right]^{3} :\; - 2k\theta a_{2}^{3} - 2k\sigma a_{2}^{3} = 0. \\ \end{aligned} $$
(26)

\(a_{0} ,a_{1} ,\;a_{2}\) and \(c,v,\gamma ,w,\kappa ,\alpha ,\lambda\) constants are obtained from Eq. (25) the system utilizing a software program.


Case 1: If

$$ a_{1} = 0,\quad w = - ak^{2} - k\lambda + a\eta ^{2} \gamma ^{2} ,\quad \sigma = - \theta ,\quad \mu = \frac{{\gamma a_{0} }}{{a_{2} }},\quad v = - 2ak - \lambda ,\quad b = 3\theta + 2\sigma , $$
(27)

Modifying values Eq. (27) in Eq. (25) and we have the complex hyperbolic type traveling wave solution for Eq. (1):

$$ q_{3} \left( {x,t} \right) = e^{{i\left( {s - kx + t\left( { - ak^{2} - k\lambda + a\eta ^{2} \gamma ^{2} } \right)} \right)}} \left( {a_{0} + \left( {Ae^{{ - \eta \left( {x - t\left( { - 2ak - \lambda } \right)} \right)\gamma }} - \frac{{a_{0} }}{{a_{2} }}} \right)a_{2} } \right). $$
(28)

The graphic presented in Fig. 3 is complex hyperbolic type traveling wave representing the stationary wave at any time.

Fig. 3
figure 3

Real and imaginary parts of 3-D, 2-D and contour graphs of the Eq. (28) for \(s = 0.5,\;k = 0.6,\;\eta = 0.4,\;a = 1,\;a_{0} = 2,\;\gamma = 1,\;\lambda = - 0.5,\;a_{2} = 1,\;A = 2.5\;\)

Full size image

Case 2: If

$$ a_{0} = 0,\quad w = - ak^{2} - k\lambda + a\eta ^{2} \gamma ^{2} ,\quad \sigma = - \theta ,\quad \mu = 0,\quad v = - 2ak - \lambda ,\quad b = 3\theta + 2\sigma , $$
(29)

replacing values (33) into (25), we get complex hyperbolic traveling wave solution for Eq. (1)

$$ q_{4} \left( {x,t} \right) = e^{{i\left( {s - kx + t\left( { - ak^{2} - k\lambda + a\eta ^{2} \gamma ^{2} } \right)} \right)}} \left( {\frac{{e^{{\eta \left( {x - t\left( { - 2ak - \lambda } \right)} \right)\gamma }} a_{1} }}{A} + Ae^{{ - \eta \left( {x - t\left( { - 2ak - \lambda } \right)} \right)\gamma }} a_{2} } \right). $$
(30)

The graphic presented in Fig. 4 is complex hyperbolic type traveling wave representing the stationary wave at any time.

Fig. 4
figure 4

Real and imaginary parts of 3-D, 2-D and contour graphs for the Eq. (30) for \(s = 0.5,\;k = 0.6,\;\eta = 0.4,\;a = 1,\;\gamma = - 0.3,\;\lambda = 1,\;a_{1} = 1,\;a_{2} = 1,\;A = 1.5\;\)

Full size image

Case 3: If

$$ a_{1} = 0,\quad w = - ak^{2} - k\lambda + a\eta ^{2} \gamma ^{2} ,\quad \sigma = - \theta ,\quad \mu = \frac{{\gamma a_{0} }}{{a_{2} }},\quad v = - 2ak - \lambda ,\quad b = 3\theta + 2\sigma , $$
(31)

replacing values (30) into (25), we get complex hyperbolic traveling wave solution for Eq. (1)

$$ q_{5} \left( {x,t} \right) = e^{{i\left( {s - kx + t\left( { - ak^{2} - k\lambda + a\eta ^{2} \gamma ^{2} } \right)} \right)}} \left( {a_{0} + \left( \begin{gathered} A\cosh \left[ {\eta \left( {x - t\left( { - 2ak - \lambda } \right)} \right)\gamma } \right] \hfill \\ - A\sinh \left[ {\eta \left( {x - t\left( { - 2ak - \lambda } \right)} \right)\gamma } \right] - \frac{{a_{0} }}{{a_{2} }} \hfill \\ \end{gathered} \right)a_{2} } \right). $$
(32)

The graphic presented in Fig. 5 is complex hyperbolic type traveling wave representing the stationary wave at any time.

Fig. 5
figure 5

Real and imaginary of 3-D, 2-D and contour graphs of the Eq. (32) for \(s = 0.5,\;k = 0.6,\;\eta = 0.4,\;a = 1,\;\gamma = 0.1,\;\lambda = 1,\;a_{0} = 1,\;a_{2} = 1,\;A = 1.5\;\)

Full size image

Case 4: If

$$ a_{0} = 0,\quad a_{2} = 0,\quad w = - ak^{2} - k\lambda + a\eta ^{2} \gamma ^{2} ,\quad \sigma = - \theta ,\quad \mu = 0,\quad v = - 2ak - \lambda ,\quad b = 3\theta + 2\sigma , $$
(33)

replacing values (33) into (25), we get complex hyperbolic traveling wave solution for Eq. (1)

$$ q_{6} \left( {x,t} \right) = \frac{{e^{{i\left( {s - kx + t\left( { - ak^{2} - k\lambda + a\eta ^{2} \gamma ^{2} } \right)} \right)}} a_{1} }}{{A\cosh \left[ {\eta \left( {x - t\left( { - 2ak - \lambda } \right)} \right)\gamma } \right] - A\sinh \left[ {\eta \left( {x - t\left( { - 2ak - \lambda } \right)} \right)\gamma } \right]}}. $$
(34)

The graphic presented in Fig. 6 is complex hyperbolic type traveling wave representing the stationary wave at any time.

Fig. 6
figure 6

Real and imaginary of 3-D, 2-D and contour graphs of the Eq. (34) for \(s = 0.5,\;k = 0.6,\;\eta = 0.5,\;a = 1,\;\gamma = - 0.2,\;\lambda = 1,\;a_{1} = 1,\;A = 1.5\;\)

Full size image

6 Results and discussions

Traveling wave solutions have an important place in Soliton's theory. Many researchers have focused on the solutions of partial differential equations. In this study, we have produced the traveling wave solutions by successfully applying the Modified \(1/G^{\prime}\)-expansion and Modified Kudryashov methods of the nonlinear Perturbed CLL equation. A modified version of both analytical methods were applied for the first time. At the end of this application, we found that both analytic methods are reliable, applicable, effective and useful. There are similarities and differences between the solutions produced by both analytical methods. While the base equation used in the Modified \(1/G^{\prime}\)-expansion is Eq. (11), it is Eq. (6) in the Modified Kudryashov method. Although the base equations used are different, there are also similarities in the solutions. When the solution format given by (12.a) Eq. (6) in the Modified \(1/G^{\prime}\)- expansion method is compared with the solution format given by the Eq. (7) of the Modified Kudryashov method, having the constants in the Eq. (12.a) carries a more general solution. However, we can conclude that base a in Eq. (7) is a free parameter and it is a more general solution compared to the Modified \(1/G^{\prime}\)- expansion method. Although the solutions produced by both analytical methods are similar, they add different interpretations in terms of physical meaning. This is also a wealth of mathematics. Both analytical methods have similar aspects. For example, we can list as classical wave transformation, balance principle, obtaining algebraic equation system. Its different aspects require that the base equations are different and therefore the assumed solutions differ. In the Modified Kudryashov method, Eq. (6) as the base equation and the default solution function of equation is given by Eq. (7). On the other hand, in the Modified \(1/G^{\prime}\)- expansion method, the Eq. (11) is given as the base equation and the default solution functions of the Eqs. (12) and (12a) are given. If we discuss the advantages and disadvantages of the methods, we can say that both methods are at the same level in terms of transaction complexity. Qualitatively, both methods produce traveling wave solutions and quantitatively the number of solutions produced by the Modified \(1/G^{\prime}\)-expansion method is higher. The solutions presented in this study are hyperbolic type complex traveling wave solutions. The term that affects the Eq. (32) directly in the real part and indirectly in the imaginary part is the coefficient “a”. The most important reason for choosing the parameter “a” here is that Eq. (1) represents the velocity propagation parameter of the traveling wave obtained. In particular, the parameter “a” is the coefficient of the term \(q_{{xx}}\), which is not formed as a result of the operation of the method and directly represents the spread in Eq. (1). Therefore, changes in the parameter “a” directly affect the mechanism. In the classical wave transformation presented in Eq. (3), \(\eta\) represents the amplitude of the wave. This parameter is also the most important parameter affecting the speed (\(v\)) of the wave. On the other hand, the parameter “\(\eta\)” was obtained as a result of the operation of the method that Eq. (1) does not contain. Since wave propagation is directly related to velocity (\(v\)) and frequency (\(w\)), the effect of parameter “\(\eta\)” on solitons was investigated. Also, the term that directly affects both the real and imaginary parts of the solution presented with Eq. (32) is the term “\(\eta\)”. Let's examine the effect of changes in both “\(\eta\)” and coefficient “a” on wave behavior. First, let's explain the behavior changes of the coefficient “a” representing the wave propagation speed in the solitary wave solution with the help of 3-dimensional simulation. In Fig. 7, the behavior of the wave is presented for different values of the wave propagation velocity coefficient “a” in Eq. (1). In addition, the velocity value that causes the occurrence of the physical phenomenon called refraction in wave behavior can be observed in the simulation below.

Fig.7
figure 7

Simulation of 3D graphs of the Eq. (32) for \(s = 0.5,\;k = - 1.5,\;\eta = 0.4,\;\tau = 0.1,\;\lambda = 1,\;a_{0} = 1,\;a_{2} = 1,\;A = 1.5,\;k = - 1.5\)

Full size image

As we observed in Fig. 7, the most important factor affecting the real part is the coefficient of the \(q_{{xx}}\) term in the Eq. (1). For \(a = 1.5\), the wavelength and amplitude that provide the transfer of energy from one point to another in Fig. 7 exhibit classical wave behavior. When the propagation velocity value is \(a = 2.5\), the wavelength becomes shorter and the amplitude increases. While exhibiting similar behaviors for \(a < 3.112\), distortion and breakage occur at the end points of the wave for \(a = 3.112\). As a result, as the speed of the wave increases, the length of the wave decreases and the amplitude increases. The speed exhibits irregular wave behavior after a certain value. Depending on the velocity propagation parameter, while creating the simulation in Fig. 7, the parameters except the coefficient “a” are taken as constant. Secondly, let's explain the behavior changes in the solitary wave solution within different values of the constant \(\eta\), which is a variable of the wave frequency affecting the complex part, with the help of 3-dimensional simulation.

As we observed in Fig. 8, one of the most important factors affecting both the real and the imaginary part is that by increasing the expression of the wave amplitude variable \(\eta\), it is observed that disorders in wave behavior occur and physical refraction occurs at \(\eta = 1.72\) value. When Fig. 8 is observed, \(\eta = 1.6\) and \(\eta = 1.71\) values exhibit similar behaviors despite the increase in the amplitude of the wave. For \(\eta = 1.72\), there is an irregular wave behavior in the real part of the traveling wave solution. In this case, it can be said that the average amplitude of the wave for the fixed values other than \(\eta\) will be at most 1.71. The sensitivity of this value can be increased. While creating the simulation in Fig. 8 that affects the amplitude, the parameters except the coefficient \(\eta\) are taken as constant. In this study, it has been verified that there are complex traveling wave solutions in the CLL equation, which is a nonlinear partial differential equation. After giving physical meanings to the coefficients in traveling wave solutions obtained in our study, these solutions can play a more important role in plasma and optical fiber. Wave propagates through an energy-limiting guide structure such as an optical fiber in an optical effect. The mathematical form of the wave in an area where the phase constant is effective is as follows:

$$ q\left( {x,t} \right) = A_{n} \;U\left( {m\left( {x - vt} \right)} \right)e^{{i\left( { - \kappa x + wt} \right)}} . $$
Fig. 8
figure 8

Simulation of 3D graphs of the Eq. (32) for \(a = 0.5,\;s = 0.5,\;k = - 1.5,\;\tau = 0.1,\;\lambda = 1,\;a_{0} = 1,\;a_{2} = 1,\;A = 1.5\)

Full size image

where \(A_{n}\) represents the maximum width of the area in which the wave propagates, \(U\left( {x,t} \right)\) represents the time-dependent envelope. \(\kappa\) represents the phase constant. In this study, \(U\left( {x,t} \right)\) is the hyperbolic type mathematical model of the envelope that shapes the impulse in the time domain (Band and Trippenbach 1996). In this study, the time-dependent envelope is of hyperbolic type and can be seen in the solutions presented. Also, the graph of traveling wave solutions is presented both in real and imaginary forms. Because it is to take into account the effect of the phase constant that causes the traveling wave to form. In addition, if the graph of the module of the traveling wave had been drawn, we would have presented the graphs of the time-dependent envelope.

The variation of the complex wave function for different values of the wave propagation \(\left( \lambda \right)\) and velocity propagation parameters “a” is shown in Fig. 1. When Fig. 1 is examined, it can be seen that the value of “b”, which is the nonlinear propagation parameter, is defined by the relationship between the nonlinear propagation coefficient \(\left( \sigma \right)\) and self steeping parameter for short pulses \(\left( \theta \right)\). In addition, the effects of changes in parameters and transformations in plasma and optical fiber were examined on figures. In this study, traveling wave solutions and interpretations are presented for m = 1 density. In future studies, wave changes can be investigated for different values of intensity m, which is a nonlinear parameter for complex wave function.

7 Conclusions

In this article, complex traveling wave solutions of the perturbed CLL equation were obtained by using Modified \(1/G^{\prime}\)-expansion and Modified Kudryashov methods. Special solutions were obtained when the constants were matched with the real number in the solutions produced. These special solutions were presented with 3D, 2D and contour graphs. The advantages and disadvantages of both analytical methods were discussed. Besides, the different and common aspects of both analytic methods were examined. In addition, a solitary wave was produced by giving special values to the parameters in the hyperbolic type complex traveling wave solution. Simulations for different values of the amplitute and velocity propagation parameters of the single wave were presented in Figs. 7 and 8. For \(a = 3.112\) in Fig. 7 and for \(\eta = 1.72\) in Fig. 8, the values that cause break in the wave were calculated. Many complex operations such as drawing graphics and solving algebraic equation systems were overcome by computer software programs. It was concluded that both analytical methods could be recommended for NLPDEs in the future.