1 Introduction

In last few years, the propagation behavior of laser beams in oceanic turbulence has attracted much attention due to their potential applications in underwater wireless optical communication and imaging systems (Nikishov and Nikishov 2000; Lacroix et al. 2010; Tang and Zhao 2015; Baykal 2016a, b). The influence of temperature and salinity fluctuations on propagation of laser beams, including the degree of polarization, mutual coherence function, spreading, and the scintillation index, have widely been investigated. Up to now, the propagation properties of various types of laser beams in an oceanic environment have been reported, such as those for radially polarized Gaussian beams (Tang and Zhao 2013), Gaussian Schell-model vortex beam (Huang et al. 2014), stochastic electromagnetic vortex beams (Xu and Zhao 2014), partially coherent flat-topped vortex hollow beam (Liu et al. 2015), partially coherent annular decentered beams (Yang et al. 2015), partially coherent Hermite–Gaussian linear array beams (Huang et al. 2015), hollow Gaussian beams (Li et al. 2019), cosine-Gaussian-correlated Schell-model beams (Ding et al. 2015), partially coherent Lorentz–Gauss vortex beams (Liu et al. 2017a), partially coherent four-petal Gaussian vortex beams (Liu et al. 2017b), random electromagnetic multi-Gaussian Schell-model vortex beam (Liu and Wang 2018), flat-topped beams (Baykal 2020) and Airy beams with power exponential phase vortex (Wang et al. 2021). Besides, a new beam model named vortex-cosh-Gaussian beam (vChGB) has been freshly investigated by us (Hricha et al. 2020). Compared to the standard Gaussian beam, vChGB possesses two additional key parameters, namely the decentered parameter b and the topological charge number M. The vortex charge of the beam leads to spiraling wave fronts, which results in an orbital angular momentum. Further, under special values of b and M, the field of vChGB can be reduced to many known laser beams such as vortex-Gaussian beam (Zhou et al. 2013), cosh-Gaussian beam (Casperson et al. 1997), or Gaussian beam (Siegman 1986). In the source plane, with a small value of b (saying b < 1) the intensity profile of vChGB is Gaussian vortex-like, whereas when b is large (b > 4), the beam profile becomes four-petal-like. In the intermediate case, i.e., when b takes a moderate value, the beam profile will be square hollow-like. Upon propagation, the vChGB profile is preserved in near-field, and its stability range can be controlled by adjusting the parameters b and M. In far field, the vChGB evolves into a multi-lobe structure whose shape is closely connected to the beam parameters. Such propagation properties of the vChGB may be beneficial to applications in optical trapping, micromanipulation, beam splitting, and optical communications.

The propagation properties of a vChGB through different optical media have been investigated (Hricha et al. 2020, 2021; Lazrek et al. 2021). However, to the best of our knowledge, its propagation properties in the oceanic turbulence have not been reported yet, so, this will be the subject of the present work. We aim in this paper to investigate the influence of oceanic turbulence on the propagation properties of a vChGB. The evolution properties of the beam through oceanic turbulence, and the effects of the turbulence strength of the sea-water in addition to the initial beam parameters on the average intensity distribution are investigated numerically and theoretically. In the second Section of the manuscript, a theoretical analysis based on the extended Huygens–Fresnel integral and Rytov method for the propagation of a vChGB in oceanic turbulence is made, and the corresponding analytical expression of the average intensity is derived. In Sect. 3, the evolution behaviour of the intensity distribution as well as the spreading of a vChGB in oceanic turbulence are analysed with illustrative numerical examples. The main results obtained are highlighted in the conclusion part.

2 Propagation of a vChGB through oceanic turbulence

In the Cartesian coordinate system, the electric field of a vChGB in the source plane z = 0 can be written as (Hricha et al. 2020).

$$ E\left( {r_{0} ,z = 0} \right) = \cosh \left( {b\frac{{x_{0} }}{{\omega_{0} }}} \right)\cosh \left( {b\frac{{y_{0} }}{{\omega_{0} }}} \right)\,e^{{ - \left( {\frac{{x_{0}^{2} + y_{0}^{2} }}{{\omega_{0}^{2} }}} \right)}} \left( {x_{0} + iy_{0} } \right)^{M} $$
(1)

where \(r_{0} = \left( {x_{0} {\kern 1pt} {\kern 1pt} ,{\kern 1pt} y_{0} {\kern 1pt} {\kern 1pt} } \right)\) is the position vector at the source plane, and \(\omega_{0}\) is the waist radius of the Gaussian part. b is the decentered parameter associated to the cosh part. M denotes the topological charge of the beam.

Within the framework of the paraxial approximation, and according to the extended Huygens–Fresnel diffraction integral, the propagation of a vChGB through the oceanic turbulence along the z-axis can be formulated as (Born and Wolf 1990; Andrews and Philips 1998).

$$ E\left( {\vec{r},z} \right) = - \frac{ik}{{2\pi z}}\exp \left( { - i\,k\,z} \right)\,\int_{ - \infty }^{ + \infty } {\int_{ - \infty }^{ + \infty } {E\left( {\vec{r}_{0} ,0} \right)\exp \left[ { - \frac{ik}{{2z}}\left( {\vec{r}_{0} - \vec{r}} \right)^{2} + \psi \left( {\vec{r}_{0} ,\vec{r},z} \right)} \right]} } d\vec{r}_{0} $$
(2)

where \(\vec{r} = (x,y)\) are the position vector in the receiver plane, z is the distance between the initial plane and the receiver plane, and \(d\vec{r}_{0} = dx_{0} dy_{0}\) is the elementary surface in the initial plane z = 0. \(\psi \left( {\vec{r}_{0} ,\vec{r},z} \right)\) is the Rytov solution that represents the random part for the complex phase of a spherical wave spreading from the source plane to the output plane, \(k = \frac{2\pi }{\lambda }\) is the wave number and \(\lambda\) is the wavelength.

The average intensity of a vChGB in the receiver plane can be written as.

$$ \left\langle {I\left( {\vec{r},z} \right)} \right\rangle = \left\langle {E\left( {r,z} \right)\,E*\left( {r,z} \right)} \right\rangle $$
(3)

where * and \(\left\langle . \right\rangle\) denote the complex conjugation and the ensemble average over the medium statistics, respectively.

Substituting Eq. (2) into Eq. (3), one obtains

$$ \begin{gathered} \left\langle {I\left( {\vec{r},z} \right)} \right\rangle = \frac{{k^{2} }}{{4\pi^{2} z^{2} }}\int\limits_{ - \infty }^{ + \infty } {\,\int\limits_{ - \infty }^{ + \infty } {} } \int\limits_{ - \infty }^{ + \infty } {\,\int\limits_{ - \infty }^{ + \infty } {} } E_{0} \left( {x_{01} ,y_{01} ,0} \right)E_{0} *\left( {x_{02} ,y_{02} ,0} \right) \hfill \\ \,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\, \times \,\exp \left[ { - \frac{ik}{{2z}}\left\{ {\left( {x_{01} - x} \right)^{2} + \left( {y_{01} - y} \right)^{2} - \left( {x_{02} - x} \right)^{2} - \left( {y_{02} - y} \right)^{2} } \right\}} \right] \hfill \\ \,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\, \times \left\langle {\exp \left[ {\psi \left( {\vec{r}_{01} ,\vec{r}} \right) + \psi *\left( {\vec{r}_{02} ,\vec{r}} \right)} \right]} \right\rangle d\vec{r}_{01} d\vec{r}_{02} \,\,, \hfill \\ \end{gathered} $$
(4)

\(d\vec{r}_{0i} {\kern 1pt} = dx_{0i} dy_{0i}\)(with i = 1 or 2) are elementary surfaces in the initial plane z = 0.

The term in angle brackets of Eq. (4) can be expressed as (Andrews and Philips 1998).

$$ \left\langle {\exp \left[ {\psi \left( {x_{01} ,y_{01} ,x,y} \right) + \psi *\left( {x_{02} ,y_{02} ,x,y} \right)} \right]} \right\rangle {\kern 1pt} {\kern 1pt} = {\kern 1pt} {\kern 1pt} \exp \left\{ { - \frac{1}{{\rho_{0}^{2} }}\left[ {\left( {x_{01} - x_{02} } \right)^{2} + \left( {y_{01} - y_{02} } \right)^{2} } \right]} \right\} $$
(5)

where \(\rho_{0} = \left[ {\frac{{\pi^{2} k^{2} z}}{3}\int_{0}^{ + \infty } {d\kappa \kappa^{3} \Phi \left( \kappa \right)} } \right]^{{{{ - 1} \mathord{\left/ {\vphantom {{ - 1} 2}} \right. \kern-\nulldelimiterspace} 2}}}\) is the coherence length of a spherical wave propagating in oceanic turbulence, with \(\kappa\) is the spatial frequency, and \(\Phi \left( \kappa \right)\) is the one-dimensional spatial power spectrum of the refractive index fluctuations, which for an homogeneous and isotropic turbulent ocean is given by (Nikishov and Nikishov 2000).

$$ \Phi \left( \kappa \right) = 0.388 \times 10^{ - 8} \varepsilon^{{ - {{11} \mathord{\left/ {\vphantom {{11} 3}} \right. \kern-\nulldelimiterspace} 3}}} \left[ {1 + 2.35\,\left( {\kappa \eta } \right)^{{{2 \mathord{\left/ {\vphantom {2 3}} \right. \kern-\nulldelimiterspace} 3}}} } \right]\,f\left( {\kappa ,\varsigma ,\chi_{T} } \right) $$
(6)

where \(\varepsilon\) is the rate of dissipation of turbulent kinetic energy per unit mass of fluid, which may vary in the range from \(10^{ - 10} m^{2} s^{ - 3}\) to \(10^{ - 1} m^{2} s^{ - 3}\). \(\eta = 10^{ - 3}\) is the Kolmogorov inner scale, and.

$$ f\left( {\kappa ,\varsigma ,\chi_{T} } \right) = \frac{{\chi_{T} }}{{\varsigma^{2} }}\left[ {\varsigma^{2} \exp \left( { - A_{T} \delta } \right) + \exp \left( { - A_{S} \delta } \right) - 2\varsigma \exp \left( { - A_{TS} \delta } \right)} \right] $$
(7)

with \(\chi_{T}\) is the rate of dissipation of mean square temperature varying in the range from \(10^{ - 4} K^{2} s^{ - 1}\) to \(10^{ - 10} K^{2} s^{ - 1}\), \(\delta = 8.284\left( {\kappa \eta } \right)^{{{4 \mathord{\left/ {\vphantom {4 3}} \right. \kern-\nulldelimiterspace} 3}}} + 12.978\left( {\kappa \eta } \right)^{2}\),\(A_{T} = 1.863 \times 10^{ - 2}\), \(A_{S} = 1.9 \times 10^{ - 4}\), and \(A_{TS} = 9.41 \times 10^{ - 3}\), \(\varsigma\) describes the relative strength of temperature and salinity fluctuations, which in the ocean water varies in the range from -5 to 0. The zero value corresponding to the case when salinity-driven turbulence dominates, and -5 value describes the case when temperature-driven turbulence prevails.

Substituting Eq. (1) into Eq. (4), and using the binomial formula (Abramowitz and Stegun 1964):

$$\left( {x_{0} {\kern 1pt} + {\kern 1pt} iy_{0} } \right)^{M} {\kern 1pt} = {\kern 1pt} \sum\limits_{l = 0}^{M} {C_{l}^{M} } x_{0}^{l} \left( {iy_{0} } \right)^{{_{M - l} }}$$
(8a)

where

$$ C_{l}^{M} = {\kern 1pt} \frac{M!}{{l!\left( {M - l} \right)!}} $$
(8b)

and after rearanging the integrand function, one can obtain

$$ \left\langle {I\left( {\vec{r},z} \right)} \right\rangle = \left( {\frac{k}{2\pi z}} \right)^{2} \sum\limits_{l = 0}^{M} {C_{l}^{M} \sum\limits_{n = 0}^{M} {C_{n}^{M} } } \,W_{l,n} \left( {x,z} \right)\,W_{M - l,M - n} \left( {y,z} \right), $$
(9)

where

$$ \begin{gathered} W_{l,n} \left( {v,z} \right) = \int_{ - \infty }^{ + \infty } {\int_{ - \infty }^{ + \infty } {v_{01}^{l} } } v_{02}^{n} \cosh \left( {\frac{{bv_{01} }}{{\omega_{0} }}} \right)\cosh \left( {\frac{{bv_{02} }}{{\omega_{0} }}} \right)\exp \left( { - \alpha \,v_{01}^{2} + \frac{ikv}{z}v_{01} } \right) \hfill \\ \,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\, \times \exp \left\{ { - \alpha^{ * } v_{02}^{2} + \left( { - \frac{ikv}{z} + \frac{{2v{}_{01}}}{{\rho_{0}^{2} }}} \right)v_{02} } \right\}\,dv_{01} dv_{02} \hfill \\ \end{gathered} $$
(10)

in which v represents either x or y, and \(\alpha\) is the auxiliary parameter given by

$$ \alpha = \frac{ik}{{2z}} + \frac{1}{{\omega_{0}^{2} }} + \frac{1}{{\rho_{0}^{2} }}\, $$
(11)

Equation (10) can be rewritten in the form

$$ W_{l,n} \left( {v,z} \right) = \int_{ - \infty }^{ + \infty } {v_{01}^{l} } \cosh \left( {\frac{{bv_{01} }}{{\omega_{0} }}} \right)\exp \left( { - \alpha \,v_{01}^{2} + \frac{ikv}{z}v_{01} } \right)\,Q_{n} \,\left( {v_{01} ,z} \right)dv_{01} $$
(12)

where

\(Q_{n} \,\left( {v_{01} ,z} \right)\) is an one-variable integral expression given by

$$ Q_{n} \,\left( {v_{01} ,z} \right) = \int_{ - \infty }^{ + \infty } {v_{02}^{n} } \cosh \left( {\frac{{bv_{02} }}{{\omega_{0} }}} \right)\exp \left\{ { - \alpha^{ * } v_{02}^{2} + \left( { - \frac{ikv}{z} + \frac{{2v{}_{01}}}{{\rho_{0}^{2} }}} \right)v_{02} } \right\}dv_{02} $$
(13)

Using the explicit form of cosh function: \(\cosh \left( u \right) = \frac{1}{2}\left[ {\exp \left( u \right) + \exp \left( { - u} \right)} \right]\), Eq. (13) can be expressed as

$$ Q_{n} \,\left( {v_{01} ,z} \right) = \frac{1}{2}\left[ {Q_{n}^{ + } \left( {v_{01} ,z} \right) + Q_{n}^{ - } \,\left( {v_{01} ,z} \right)} \right] $$
(14)

with

$$ Q_{n}^{ \pm } \left( {v_{01} ,z} \right) = \int_{ - \infty }^{ + \infty } {v_{02}^{n} } \exp \left\{ { - \alpha^{ * } v_{02}^{2} + 2\beta_{v01} v_{02} } \right\}dv_{02} $$
(15a)

and

$$ \beta_{v01} = - \frac{ikv}{{2z}} + \frac{{v{}_{01}}}{{\rho_{0}^{2} }} \pm \frac{b}{{2\omega_{0} }} $$
(15b)

By using the following integral equation (Belafhal et al. 2020)

$$ \int\limits_{ - \infty }^{ + \infty } {x^{n} e^{{ - px^{2} + 2qx}} } dx = e^{{\frac{{q^{2} }}{p}}} \sqrt {\frac{\pi }{p}} \left( {\frac{1}{2i\sqrt p }} \right)^{n} H_{n} \left( {\frac{iq}{{\sqrt p }}} \right) $$
(16)

where \(H_{n} \left( . \right)\) is the Hermite polynomial of n-order, the integral of Eq. (15a) is carried out, and Eq. (10) can be expressed as

$$ \begin{gathered} W_{l,n} \left( {v,z} \right) = \frac{1}{2}\sqrt {\frac{\pi }{{\alpha^{ * } }}} \left( {\frac{1}{{2i\sqrt {\alpha^{ * } } }}} \right)^{n} \int_{ - \infty }^{ + \infty } {v_{01}^{l} } \cosh \left( {\frac{{bv_{01} }}{{\omega_{0} }}} \right)\exp \left( { - \alpha \,v_{01}^{2} + \frac{ikv}{z}v_{01} } \right)\, \hfill \\ \,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\left[ {\exp \left\{ {\frac{{\left( {\beta_{v01}^{ + } } \right)^{2} }}{{\alpha^{ * } }}} \right\}H_{n} \left( {\frac{{i\beta_{v01}^{ + } }}{{\sqrt {\alpha^{ * } } }}} \right) + \exp \left\{ {\frac{{\left( {\beta_{v01}^{ - } } \right)^{2} }}{{\alpha^{ * } }}} \right\}H_{n} \left( {\frac{{i\beta_{v01}^{ - } }}{{\sqrt {\alpha^{ * } } }}} \right)} \right]dv_{01} \hfill \\ \end{gathered} $$
(17)

Now, by recalling the following series expansions of the Hermite polynomial (Gradshteyn and Ryzhik 1994).

$$ H_{m} \left( x \right) = \sum\limits_{j = 0}^{{\left[ {{\raise0.7ex\hbox{$m$} \!\mathord{\left/ {\vphantom {m 2}}\right.\kern-\nulldelimiterspace} \!\lower0.7ex\hbox{$2$}}} \right]}} {\frac{{( - 1)^{j} m!}}{{j!\left( {m - 2j} \right)!}}\left( {2x} \right)^{m - 2j} } $$
(18)
$$ \begin{gathered} W_{l,n} \left( {v,z} \right) = \frac{1}{4}\sqrt {\frac{\pi }{{\alpha^{ * } }}} \sqrt {\frac{\pi }{a}} \,\left( {\frac{1}{{2i\sqrt {\alpha^{ * } } }}} \right)^{n} \sum\limits_{s = 0}^{{\left[ \frac{n}{2} \right]}} {\frac{{\left( { - 1} \right)^{s\,} \,n\,!}}{{s!\,\left( {n - 2s} \right)\,!}}} \,\left( {\frac{2i}{{\sqrt {\alpha^{ * } } }}} \right)^{n - 2s} \sum\limits_{j = 0}^{n - 2s} {C_{j}^{n - 2s} \,\left( {\frac{1}{2i\sqrt a }} \right)^{l + j} \left( {\frac{1}{{\rho_{0}^{2} }}} \right)^{j} \,} \hfill \\ \times \left\{ \begin{gathered} \exp \left\{ {\frac{1}{{\alpha^{ * } }}\left( {\frac{ - ikv}{{2z}} + \frac{b}{{2\omega_{0} }}} \right)^{2} } \right\}\left[ {\exp \left\{ {\frac{{\left( {f_{1v}^{ + } } \right)^{2} }}{a}} \right\}H_{l + j} \left( {\frac{{if_{1v}^{ + } }}{\sqrt a }} \right) + \exp \left\{ {\frac{{\left( {f_{1v}^{ - } } \right)^{2} }}{a}} \right\}H_{l + j} \left( {\frac{{if_{1v}^{ - } }}{\sqrt a }} \right)} \right] \hfill \\ + \exp \left\{ {\frac{1}{{\alpha^{ * } }}\left( {\frac{ - ikv}{{2z}} - \frac{b}{{2\omega_{0} }}} \right)^{2} } \right\}\left[ {\exp \left\{ {\frac{{\left( {f_{2v}^{ + } } \right)^{2} }}{a}} \right\}H_{l + j} \left( {\frac{{if_{2v}^{ + } }}{\sqrt a }} \right) + \exp \left\{ {\frac{{\left( {f_{2v}^{ - } } \right)^{2} }}{a}} \right\}H_{l + j} \left( {\frac{{if_{2v}^{ - } }}{\sqrt a }} \right)} \right]\, \hfill \\ \end{gathered} \right\} \hfill \\ \,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\, \hfill \\ \end{gathered} $$
(19)

with

$$ a = \alpha - \frac{1}{{\rho_{0}^{4} \alpha^{ * } }} $$
(20a)
$$ f_{1v}^{ \pm } = \frac{1}{{\rho_{0}^{2} \alpha^{ * } }}\left( {\frac{ - ikv}{{2z}} + \frac{b}{{2\omega_{0} }}} \right) + \left( {\frac{ikv}{{2z}} \pm \frac{b}{{2\omega_{0} }}} \right) $$
(20b)

and

$$ f_{2v}^{ \pm } = \frac{1}{{\rho_{0}^{2} \alpha^{ * } }}\left( {\frac{ - ikv}{{2z}} - \frac{b}{{2\omega_{0} }}} \right) + \left( {\frac{ikv}{{2z}} \pm \frac{b}{{2\omega_{0} }}} \right) $$
(20c)

The direct substituting from Eq. (19) into Eq. (9) will give the analytical expression of a vChGB propagating in oceanic turbulence (the explicit formula is not presented here to save space). From the obtained formula, it can be seen that the beam depends on the oceanic turbulence strength and the initial beam parameters in addition to the propagation distance z. This will allow us to analyse the propagation properties of a vChGB in oceanic turbulence.

From the main analytical formula derived above, one can distinguish the special cases following:

  • The case b = 0, Eq. (9) will give the corresponding formula for the hollow Gaussian vortex beam, which can be expressed as

    $$ \left\langle {I\left( {\vec{r},z} \right)} \right\rangle = \left( \frac{k}{2z} \right)^{2} \frac{1}{{\alpha^{ * } a}}\left( {\frac{1}{{2i\sqrt {\alpha^{ * } } }}} \right)^{M} \sum\limits_{l = 0}^{M} {C_{l}^{M} \sum\limits_{n = 0}^{M} {C_{n}^{M} } } \,R_{l,n} \left( {x,z} \right)\,R_{M - l,M - n} \left( {y,z} \right), $$
    (21)

    where

    $$ R_{l,n} \left( {v,z} \right) = \exp \left( {Bv^{2} } \right)\sum\limits_{s = 0}^{{\left[ \frac{n}{2} \right]}} {\frac{{\left( { - 1} \right)^{s\,} \,n\,!}}{{s!\,\left( {n - 2s} \right)\,!}}} \,\left( {\frac{2i}{{\sqrt {\alpha^{ * } } }}} \right)^{n - 2s} \sum\limits_{j = 0}^{n - 2s} {C_{j}^{n - 2s} \,\left( {\frac{1}{2i\sqrt a }} \right)^{l + j} \left( {\frac{1}{{\rho_{0}^{2} }}} \right)^{j} \,} H_{l + j} \left( {\frac{iA}{{\sqrt a }}v} \right) $$
    (22a)
    $$ A = \frac{ik}{{2z}}\left( {1 - \frac{1}{{\alpha^{ * } \rho_{0}^{2} }}} \right) $$
    (22b)

    and

    $$ B = \frac{{A^{2} }}{a} - \frac{{k^{2} }}{{4\alpha^{ * } z^{2} }} $$
    (22c)

    It should be noted that we have checked numerically that Eq. (21) is consistent with Eq. (16) of Ref. (Li et al. 2019) even though they are different in the form.

  • The case when M = 0, Eq. (9) will yield the propagation equation for the cosh-Gaussian beam in oceanic turbulence.

3 Numerical examples and analysis

In this section, based on the formulas derived above, the evolution properties of a vChGB propagating through the oceanic turbulence are illustrated with numerical calculations. As is previously indicated, the initial vChGB can have two types of profile depending on the value the parameter b: the initial beam is Gaussian-like for small values of b (typically when b = 0.1) while for a large value of b (typically, b = 4), the profile is four-petal like. Consequently, in the following, the two initial beam configurations are examined, separately. Unless it is specified, the calculation parameters are set arbitrarily as \(\omega_{0} = 2\,cm\), M = 1,\(\lambda = 417\,nm\), \(\varepsilon = 10^{ - 7}\), \(\chi_{T} = 10^{ - 9}\) and \(\varsigma = - 2.5\).

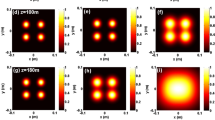
Figures 1 and 2 show the normalized average intensity (with contour graph and one-dimensional representation) of vChGBs propagating through oceanic turbulence for the two initial beam configurations. From the plots in the top row of Fig. 1, one can see that a beam with small b configuration can keep its dark center at short propagation distances (see plot (a.1)), but as the propagation distance is further increased, the beam will lose gradually its initial hollow dark-like profile and evolves into Gaussian-like beam (see plot a3-a5). The plots in bottom row of Fig. 1 show that the beam with large b configuration can retain its four­petal profile for the first transmission process, but with increasing the propagation distance the light petals get closer and bond, and finally in the far-field the beam morphed into a flat-topped profile-like (see plots Fig. 1b.5 and Fig. 2 (2b)). These results demonstrate that the propagation of a vChGB is influenced by the turbulent medium with respect to that corresponding to the free space.

Fig. 1
figure 1

Normalized intensity of a vChGB with M = 1 in oceanic turbulence for z = 0.1 km, 0.3 km, 0,6 km, 0.9 km and 1.2 km. Top row for b = 0.1, and bottom row for b = 4

Full size image
Fig. 2
figure 2

Normalized intensity in x-direction of vChGB propagating through oceanic turbulence. a for b = 0.1, and (b) for b = 4.The other parameters are the same as in Fig. 1

Full size image

The effect of changing the vortex charge M on the spreading properties of a vChGB in the oceanic turbulence is illustrated in Figs. 3 and 4 for the small b and large b configurations, respectively.

Fig. 3
figure 3

The average intensity of a vChGB in a oceanic turbulence for different values of the topological charge M with \(\omega_{0} = 0.02\,\,m\), \(\lambda = 417\,\,nm\) \(\varepsilon = 10^{ - 7}\),\(\chi_{T} = 10^{ - 9}\), \(\varsigma = - 2.5\) and b = 0.1

Full size image
Fig. 4
figure 4

The same as Fig. 3 except b = 4

Full size image

It can be seen that the rise speed of the central peak intensity becomes slower as M is larger; this means that a beam with larger M can keep its initial profile better than the one with smaller M. Also, one can see form these figures that a vChGB with large b is less perturbed by the oceanic turbulence at short propagation distances compared to that with small b configuration.

For further analyzing the beam evolution properties in the turbulent medium, we have carried out in Fig. 5 the variation of the on-axis intensity as a function of the propagation distance. The other parameters calculations are the same as in Figs. 3 and 4. It can be readily seen from the plots that the on-axis intensity is zero at short propagation distances, but gradually increases with increasing the propagation process until it reaches a maximum value. Then, the peak intensity decreases naturally with propagation distance due to the diffraction process. It is clearly observed that for the beam with small b configuration (see Fig. 5b), the rise speed of the central peak intensity is slower when the topological charge M is larger. Nevertheless, the on-axis intensity of the propagated beam is less sensitive to the value of M for the large b configuration.

Fig. 5
figure 5

The normalized axial intensity versus propagation distance z of a vChGB in oceanic turbulence with \(\omega_{0} = 0.02\,\,m\), \(\lambda = 417\,\,nm\) \(\varepsilon = 10^{ - 7}\),\(\chi_{T} = 10^{ - 9}\) and \(\varsigma = - 2.5\)

Full size image
Fig. 6
figure 6

Normalized on-axis average intensity of a vChGB in oceanic turbulence versus z for different values of the rate of dissipation of mean-square temperature \(\chi_{T}\), with \(\omega_{0} = 0.02\,\,m\), \(\lambda = 417\,\,nm\), \(\varepsilon = 10^{ - 7}\) and \(\varsigma = - 2.5\), rows (a–d) for M = 1, (b–e) for M = 2 and (c–f) for M = 3

Full size image
Fig. 7
figure 7

Normalized on-axis average intensity of the perturbed vChGB versus propagation distance z for different values of the ratio of temperature to salinity \(\varsigma\), with \(\omega_{0} = 0.02\,\,m\), \(\lambda = 417\,\,nm\) \(\varepsilon = 10^{ - 7}\), and \(\chi_{T} = 10^{ - 9}\), rows a–d) for M = 1, (b–e) for M = 2 and (c–f) for M = 3

Full size image
Fig. 8
figure 8

On-axis average intensity of the perturbed vChGB versus propagation distance z for different values of \(\varepsilon\), rows a–d for M = 1, b–e for M = 2 and (c-f) for M = 3. for different values of the b-parameter (a): b = 0.1 and b: b = 4 versus the topological charge M

Full size image

In order to investigate the influence of the strength of the oceanic turbulence on the propagation behaviour of a vChGB in the turbulent ocean, we have depicted in Figs. 6, 7 and 8 the normalized on-axis intensity of the beam (with M = 1, 2 and 3) for different values of the sea water parameters (\(\chi_{T}\), \(\varsigma\) and \(\varepsilon\)). From Figs. (6) and (7), it is shown that when the dissipation rate of mean-square temperature \(\chi_{T}\) or the ratio of temperature to salinity \(\varsigma\) increases, the rising speed of the central peak becomes faster until reaching the maximum value, and with further propagation distance the decline rate of the intensity curve is faster. In addition, it is found that the beam propagating in the turbulent ocean with larger value of the dissipation rate of turbulent kinetic energy per unit mass of fluid \(\varepsilon\) evolves slower into Gaussian-like beam.

The evolution of the on-axis intensity of a vChGB propagating through oceanic turbulence versus the beam waist radius ω0 is depicted in Fig. 9. It can be seen that the profile of evolution and the position of maximum of the on-axis intensity are shifted toward large propagation distance when ω0 is increased. In addition, one can note also that the intensity curve becomes wider as when ω0 is larger. This means that the beam can retain its dark centre longer, and the rise speed of the central peak intensity is slower when ω0 is larger. Thus increasing the beam waist may be beneficial for improving the transmission of the beam in oceanic turbulence.

Fig. 9
figure 9

Normalized on-axis average intensity of a vChGB in oceanic turbulence versus propagation distance for different values of \(\omega_{0}\), rows (a–d) for M = 1, (b–e) for M = 2 and (c–f) for M = 3

Full size image

Finally, the influence of wavelength λ on the propagation properties of a vChGB in oceanic turbulence is illustrated in Figs. 10 and 11, where we have depicted the evolutions of the normalized on-axis intensity versus the propagation distance for some values of λ in the visible spectrum (\(\lambda = 417{\kern 1pt} {\kern 1pt} nm\), \(488{\kern 1pt} {\kern 1pt} {\kern 1pt} nm\), \(532{\kern 1pt} {\kern 1pt} {\kern 1pt} nm\) and \(633{\kern 1pt} {\kern 1pt} {\kern 1pt} nm\)). From Fig. 10, one can note at first glance that the on-axis intensity is less sensitive to wavelength.

Fig. 10
figure 10

Normalized on-axis average intensity of a vChGB with M = 1 in oceanic turbulence versus z for different values of \(\lambda\): a for b = 0.1, (b) for b = 4

Full size image
Fig. 11
figure 11

As in Fig. 10 with zoom in on the region near maximum intensity position

Full size image

However, the zoom of the variation region shown in Fig. 11 indicates that the rise speed of the central peak intensity becomes slower and the intensity profile moves toward small propagation distance when λ is augmented.

4 Conclusion

In summary, based on the extended Huygens–Fresnel diffraction integral and Rytov theory the propagation properties of a vChGB in oceanic turbulence are investigated theoretically and numerically. The analytical formula of the average intensity for the beam propagating in oceanic turbulence is derived in detail. The evolution behavior of the intensity distribution of a vChGB in oceanic turbulence is analyzed numerically as a function of the turbulence strength, initial beam parameters, and the propagation distance. The results reveal that a vChGB propagating in oceanic turbulence can keep its initial dark-hollow profile at short propagation distances, and evolves into Gaussian-like beam in far-field. It is shown that when the oceanic turbulence strength increases (i.e., by increasing the parameters \(\chi_{T}\) and \(\varsigma\) or decreasing the parameter \(\varepsilon\)) or the initial source parameters b, M, ω0 and λ decrease, the rising speed of the central peak becomes stronger. The results obtained in this paper would be conducive for further understanding the propagation properties of a vChGB in turbulent ocean, which are useful for optical underwater communication and remote sensing domain, imaging, and so on.