1 Introduction

The study of the properties of laser beams propagating in oceanic turbulence is an important research topic in the application of underwater wireless optical communication and sensing. The influences of oceanic turbulence on the propagation of laser beams are very complicated, but it is convenient to study the propagation properties of laser beams based on the power spectrum of oceanic turbulence [1]. Recently, the propagation properties of laser beams in oceanic turbulence have been widely studied and analyzed. The polarization properties of stochastic beams have been investigated by O. Korotkova et al. [2]. Zhao et al. have studied the intensity and polarization properties of radially polarized beam [3], stochastic electromagnetic vortex beam [4] and astigmatic stochastic electromagnetic beam [5] propagating in oceanic turbulence. The influences of oceanic turbulence on the evolution properties of vortex beam have been studied by many researchers, such as Gaussian Schell-model vortex beam [6], partially coherent flat-topped vortex hollow beam [7], partially coherent four-petal Gaussian vortex beam [8], flat-topped vortex hollow beam [9], and partially coherent Lorentz–Gauss vortex beam [10]. Due to the advantage of high power, the propagation properties of array beams in oceanic turbulence have been widely investigated, such as partially coherent Hermite–Gaussian linear array beam [11], Gaussian array beam [12,13,14], phase-locked partially coherent radial flat-topped array laser beams [15], and radial phased-locked partially coherent Lorentz–Gauss array beam [16]. The propagation properties of mutual coherence function of laser beam [17] and higher order mode laser beam [18] in oceanic turbulence have been studied by Baykal. The propagation properties of partially coherent cylindrical vector beam in oceanic turbulence have been studied by Cai et al. [19]. Liu et al. have investigated the evolution properties of chirped Gaussian pulsed beam [20], Lorentz beam [21], partially coherent four-petal Gaussian beam [22], and partially coherent Lorentz–Gauss beam [23] propagating in oceanic turbulence. In this work, the random electromagnetic multi-Gaussian Schell-model (REMGSM) vortex beam has first been introduced, and the average intensity and polarization properties of REMGSM vortex beam propagating in oceanic turbulence have been studied using the numerical examples.

2 REMGSM vortex beam

In the Cartesian coordinate system, the z-axis is set as the propagation axis, the cross-spectral density matrix of a random electromagnetic beam at the source plane z = 0 can be characterized by the \(2 \times 2\) electric cross-spectral density matrix:

$$\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\leftrightarrow}$}} {W} \left( {{\mathbf{r}_{10}},{\mathbf{r}_{20}},0} \right)=\left[ {\begin{array}{*{20}{c}} {{W_{xx}}\left( {{\mathbf{r}_{10}},{\mathbf{r}_{20}},0} \right)}&{{W_{xy}}\left( {{\mathbf{r}_{10}},{\mathbf{r}_{20}},0} \right)} \\ {{W_{yx}}\left( {{\mathbf{r}_{10}},{\mathbf{r}_{20}},0} \right)}&{{W_{yy}}\left( {{\mathbf{r}_{10}},{\mathbf{r}_{20}},0} \right)} \end{array}} \right],$$
(1)

where

$${W_{\alpha \beta }}\left( {{\mathbf{r}_{10}},{\mathbf{r}_{20}},0} \right)=\left\langle {{E_\alpha }\left( {{\mathbf{r}_{10}},0} \right)E_{\beta }^{ * }\left( {{\mathbf{r}_{20}},0} \right)} \right\rangle \mathop {}\nolimits_{{}}^{{}} \left( {\alpha ,\beta =x,y} \right),$$
(2)

where \({\mathbf{r}_0}=\left( {{x_0},{y_0}} \right)\) is the position vector at the source plane z = 0; \({E_x}\left( {{\mathbf{r}_{10}},0} \right)\) and \({E_y}\left( {{\mathbf{r}_{10}},0} \right)\) denote the components of electric field along x-axis and y-axis, respectively; the asterisk stands for the complex conjugate and the angular brackets stand for the average over the ensemble of realizations of fluctuating electric field.

The element of the cross-spectral density matrix of the REMGSM vortex beam at the source plane z = 0 can be written as

$$\begin{aligned} {W_{\alpha \beta }}\left( {{\mathbf{r}_{10}},{\mathbf{r}_{20}},0} \right)&={A_\alpha }{A_\beta }{B_{\alpha \beta }}\frac{1}{{C_{0}^{2}}}\exp \left( { - \frac{{x_{{10}}^{2}+x_{{20}}^{2}}}{{w_{0}^{2}}} - \frac{{y_{{10}}^{2}+y_{{20}}^{2}}}{{w_{0}^{2}}}} \right)\\&\quad\times{\left( {{x_{10}}+i{y_{10}}} \right)^M}{\left( {{x_{20}} - i{y_{20}}} \right)^M} \hfill \\&\quad \times \sum\limits_{{n=1}}^{N} {\left( {\begin{array}{*{20}{c}} N \\ n \end{array}} \right)\frac{{{{\left( { - 1} \right)}^{n - 1}}}}{n}} \exp \left[ { - \frac{{{{\left( {{x_{10}} - {x_{20}}} \right)}^2}}}{{2n\sigma _{{\alpha \beta }}^{2}}} - \frac{{{{\left( {{y_{10}} - {y_{20}}} \right)}^2}}}{{2n\sigma _{{\alpha \beta }}^{2}}}} \right], \hfill \\ \end{aligned}$$
(3)

where M is the topological charge; N is the index of multi-Gaussian Schell-model beam; \({\sigma _{\alpha \beta }}\) is the positive constant characterizing the spatial coherence length; \({A_\alpha }\) and \({A_\beta }\) are the amplitudes of the electric field vector components; \({B_{\alpha \beta }}\) is the correlation coefficient, which can be expressed as

$$\begin{gathered} {B_{\alpha \beta }}=1\mathop {}\nolimits_{{}}^{{}} \left( {\alpha =\beta } \right) \hfill \\ \left| {{B_{\alpha \beta }}} \right| \ne 1\mathop {}\nolimits_{{}}^{{}} \left( {\alpha \ne \beta } \right) \hfill \\ \end{gathered}$$
(4)

and the coefficient \({C_0}\) in Eq. (3) can be written as

$${{\text{C}}_0}=\sum\limits_{{n=1}}^{N} {\left( {\begin{array}{*{20}{c}} N \\ n \end{array}} \right)\frac{{{{\left( { - 1} \right)}^{n - 1}}}}{n}} .$$
(5)

The vortex term in Eq. (3) can be expressed by the following equation [24]:

$${\left( {x+iy} \right)^M}=\sum\limits_{{l=0}}^{M} {\frac{{M!{i^l}}}{{l!\left( {M - l} \right)!}}{x^{M - l}}{y^l}} .$$
(6)

3 Propagation of a REMGSM vortex beam in oceanic turbulence

Based on the extended Huygens–Fresnel principle, the element of the cross-spectral density matrix of the REMGSM vortex beam propagating in oceanic turbulence at the receiver plane z can be written as [2,3,4,5,6,7,8,9,10,11,12]

$$\begin{gathered} {W_{\alpha \beta }}\left( {{\mathbf{r}_1},{\mathbf{r}_2},z} \right)=\frac{{{k^2}}}{{4{\pi ^2}{z^2}}}\int_{{ - \infty }}^{{+\infty }} {\int_{{ - \infty }}^{{+\infty }} {\int_{{ - \infty }}^{{+\infty }} {\int_{{ - \infty }}^{{+\infty }} {{W_{\alpha \beta }}\left( {{\mathbf{r}_{10}},{\mathbf{r}_{20}},0} \right)} } } } \hfill \\ \mathop {}\nolimits_{{}}^{{}} \times \,\exp \left[ { - \frac{{ik}}{{2z}}{{\left( {{\mathbf{r}_1}-{\mathbf{r}_{10}}} \right)}^2}+\frac{{ik}}{{2z}}{{\left( {{\mathbf{r}_2}-{\mathbf{r}_{20}}} \right)}^2}} \right] \hfill \\ \mathop {}\nolimits_{{}}^{{}} \times \,\left\langle {\exp \left[ {\psi \left( {{\mathbf{r}_{10}},{\mathbf{r}_1}} \right)+{\psi ^ * }\left( {{\mathbf{r}_{20}},{\mathbf{r}_2}} \right)} \right]} \right\rangle d{\mathbf{r}_{10}}d{\mathbf{r}_{20}}, \hfill \\ \end{gathered}$$
(7)

where \({W_{\alpha \beta }}\left( {{\mathbf{r}_1},{\mathbf{r}_2},z} \right)\) is the element of the cross-spectral density matrix of the REMGSM vortex beam at the receiver plane z; \(k={{2\pi } \mathord{\left/ {\vphantom {{2\pi } \lambda }} \right. \kern-0pt} \lambda }\) is the wave number with \(\lambda\) being the wavelength; \(\mathbf{r}=\left( {x,y} \right)\) is the position vector at the receiver plane z ; \(\psi \left( {{\mathbf{r}_0},\mathbf{r}} \right)\) is the complex phase perturbation due to the random media; the last term in sharp brackets of Eq. (7) denotes the average influence of all the turbulent medium, and which can be expressed as

$$\begin{gathered} \left\langle {\exp \left[ {\psi \left( {{\mathbf{r}_{10}},{\mathbf{r}_1}} \right)+{\psi ^ * }\left( {{\mathbf{r}_{20}},{\mathbf{r}_2}} \right)} \right]} \right\rangle =\exp \left\{ - \right.\frac{{{\pi ^2}{k^2}z}}{3}\int\limits_{0}^{\infty } {d\kappa {\kappa ^3}} \Phi \left( \kappa \right) \hfill \\ \mathop {}\nolimits_{{}}^{{}} \mathop {}\nolimits_{{}}^{{}} \mathop {}\nolimits_{{}}^{{}} \mathop {}\nolimits_{{}}^{{}} \left. {\left[ {{{\left( {{\mathbf{r}_{10}} - {\mathbf{r}_{20}}} \right)}^2}+\left( {{\mathbf{r}_{10}} - {\mathbf{r}_{20}}} \right)\left( {{\mathbf{r}_1} - {\mathbf{r}_2}} \right)+{{\left( {{\mathbf{r}_1} - {\mathbf{r}_2}} \right)}^2}} \right]} \right\}, \hfill \\ \end{gathered}$$
(8)

where \(\Phi \left( \kappa \right)\) is the one-dimensional spatial power spectrum of refractive index for oceanic turbulence, \(\kappa\) is spatial frequency, and \(\Phi \left( \kappa \right)\) can be written as

$$\begin{gathered} \Phi \left( \kappa \right)=0.388 \times {10^{ - 8}}{\varepsilon ^{{{ - 1} \mathord{\left/ {\vphantom {{ - 1} 3}} \right. \kern-0pt} 3}}}{\kappa ^{{{ - 11} \mathord{\left/ {\vphantom {{ - 11} 3}} \right. \kern-0pt} 3}}}\left[ {1+2.35{{\left( {\kappa \eta } \right)}^{{2 \mathord{\left/ {\vphantom {2 3}} \right. \kern-0pt} 3}}}} \right] \hfill \\ \mathop {}\nolimits_{{}}^{{}} \mathop {}\nolimits_{{}}^{{}} \times \frac{{{\chi _T}}}{{{\varsigma ^2}}}\left[ {{\varsigma ^2}\exp \left( { - {A_T}\delta } \right)+\exp \left( { - {A_S}\delta } \right) - 2\varsigma \exp \left( { - {A_{TS}}\delta } \right)} \right], \hfill \\ \end{gathered}$$
(9)

where \(\varepsilon\) is the rate of dissipation of kinetic energy per unit mass of fluid, which may vary in the range from \({10^{ - 1}}{{\text{m}}^{\text{2}}}{{\text{s}}^{ - {\text{3}}}}\) to \({10^{ - 10}}{{\text{m}}^{\text{2}}}{{\text{s}}^{ - {\text{3}}}}\); \({\chi _T}\) is the rate of dissipation of mean-squared temperature taking value in the range from \({10^{ - 4}}{{\text{K}}^{\text{2}}}{{\text{s}}^{ - {\text{1}}}}\) to \({10^{ - 10}}{{\text{K}}^{\text{2}}}{{\text{s}}^{ - {\text{1}}}}\); \(\varsigma\) is the ratio of temperature and salinity fluctuations to the refractive index spectrum, which in the ocean waters can vary in the range from − 5 to 0 in the oceanic turbulence, 0 value corresponding to the case when salinity-driven turbulence prevails, −5 value corresponding to the case when temperature-driven turbulence dominates; and \(\eta ={10^{ - 3}}\) is the Kolmogorov microscale (inner scale), and\({A_T}=1.863 \times {10^{ - 2}}\), \({A_S}=1.9 \times {10^{ - 4}}\), \({A_{TS}}=9.41 \times {10^{ - 3}}\), \(\delta =8.284{\left( {\kappa \eta } \right)^{{4 \mathord{\left/ {\vphantom {4 3}} \right. \kern-0pt} 3}}}+12.978{\left( {\kappa \eta } \right)^2}\). In Eq. (9), we can define [6,7,8,9]

$$\rho _{0}^{2}=\frac{3}{{{\pi ^2}{k^2}z\int\limits_{0}^{\infty } {d\kappa {\kappa ^3}} \Phi \left( \kappa \right)}}.$$
(10)

By substituting Eq. (3) into Eq. (7), and recalling the following equations [24],

$$\int_{{ - \infty }}^{{+\infty }} {{x^n}\exp \left( { - p{x^2}+2qx} \right)dx} =n!\exp \left( {\frac{{{q^2}}}{p}} \right){\left( {\frac{q}{p}} \right)^n}\sqrt {\frac{\pi }{p}} \sum\limits_{{k=0}}^{{\left[ {\frac{n}{2}} \right]}} {\frac{1}{{k!\left( {n - 2k} \right)!}}} {\left( {\frac{p}{{4{q^2}}}} \right)^k},$$
(11)
$${H_{2d}}\left( x \right)=\sum\limits_{{l=0}}^{d} {\frac{{{{\left( { - 1} \right)}^l}\left( {2d} \right)!}}{{l!\left( {2d - 2l} \right)!}}} {\left( {2x} \right)^{2d - 2l}}.$$
(12)

The element of the cross-spectral density matrix of the REMGSM vortex beam propagating in oceanic turbulence at the receiver plane z can be derived as

$$\begin{aligned} W_{{\alpha \beta }} \left( {{\mathbf{r}}_{1} ,{\mathbf{r}}_{2} ,z} \right) & = \frac{{k^{2} }}{{4\pi ^{2} z^{2} }}\exp \left[ { - \frac{{ik}}{{2z}}\left( {x_{1}^{2} + y_{1}^{2} } \right) + \frac{{ik}}{{2z}}\left( {x_{2}^{2} + y_{2}^{2} } \right)} \right] \\ & \quad \times {\kern 1pt} \exp \left[ { - \frac{{\left( {x_{1} - x_{2} } \right)^{2} + \left( {y_{1} - y_{2} } \right)^{2} }}{{\rho _{0}^{2} }}} \right] \\ & \quad \times {\kern 1pt} A_{\alpha } A_{\beta } B_{{\alpha \beta }} \frac{1}{{C_{0}^{2} }}\sum\limits_{{n = 1}}^{N} {\left( {\begin{array}{*{20}c} N \\ n \\ \end{array} } \right)\frac{{\left( { - 1} \right)^{{n - 1}} }}{n}} \sum\limits_{{l = 0}}^{M} {\frac{{M!i^{l} }}{{l!\left( {M - l} \right)!}}} \\ & \quad \times {\kern 1pt} \sum\limits_{{m = 0}}^{M} {\frac{{M!\left( { - i} \right)^{m} }}{{m!\left( {M - m} \right)!}}} W_{\alpha } \left( {x,z} \right)W_{\beta } \left( {y,z} \right), \\ \end{aligned}$$
(13)

where

$$\begin{gathered} {W_\alpha }\left( {x,z} \right)=\sqrt {\frac{\pi }{{{a_{\alpha x1}}}}} \left( {M - l} \right)!{\left( {\frac{1}{{{a_{\alpha x1}}}}} \right)^{M - l}}\sum\limits_{{s=0}}^{{\left[ {\frac{{M - l}}{2}} \right]}} {\frac{1}{{s!\left( {M - l - 2s} \right)!}}} {\left( {\frac{{{a_{\alpha x1}}}}{4}} \right)^s} \hfill \\ \exp \left\{ {\frac{1}{{{a_{\alpha x1}}}}{{\left[ {\frac{{ik}}{{2z}}{x_1} - \frac{{{x_1} - {x_2}}}{{2\rho _{0}^{2}}}} \right]}^2}} \right\}\sum\limits_{{t=0}}^{{M - l - 2s}} {\frac{{\left( {M - l - 2s} \right)!}}{{t!\left( {M - l - 2s - t} \right)!}}{{\left( {\frac{{ik}}{{2z}}{x_1} - \frac{{{x_1} - {x_2}}}{{2\rho _{0}^{2}}}} \right)}^{M - l - 2s - t}}} \hfill \\ {\left( {\frac{1}{{2n\sigma _{{\alpha \beta }}^{2}}}+\frac{1}{{\rho _{0}^{2}}}} \right)^t}\sqrt {\frac{\pi }{{{a_{\alpha x2}}}}} {2^{ - \left( {M - m+t} \right)}}{i^{\left( {M - m+t} \right)}}\exp \left( {\frac{{c_{{\alpha x}}^{2}}}{{{a_{\alpha x2}}}}} \right){\left( {\frac{1}{{{a_{\alpha x2}}}}} \right)^{0.5\left( {M - m+t} \right)}}{H_{M - m+t}}\left( { - \frac{{i{c_{\alpha x}}}}{{\sqrt {{a_{\alpha x2}}} }}} \right) \hfill \\ \end{gathered}$$
(14)

with

$${a_{\alpha x1}}=\frac{1}{{w_{0}^{2}}}+\frac{1}{{2n\sigma _{{\alpha \beta }}^{2}}}+\frac{1}{{\rho _{0}^{2}}}+\frac{{ik}}{{2z}},$$
(15a)
$${a_{\alpha x2}}=\frac{1}{{w_{0}^{2}}}+\frac{1}{{2n\sigma _{{\alpha \beta }}^{2}}}+\frac{1}{{\rho _{0}^{2}}} - \frac{{ik}}{{2z}} - \frac{1}{{{a_{\alpha x1}}}}\left( {\frac{1}{{2n\sigma _{{\alpha \beta }}^{2}}}+\frac{1}{{\rho _{0}^{2}}}} \right),$$
(15b)
$${c_{\alpha x}}=\frac{1}{{{a_{\alpha x1}}}}\left( {\frac{{ik}}{{2z}}{x_1} - \frac{{{x_1} - {x_2}}}{{2\rho _{0}^{2}}}} \right)\left( {\frac{1}{{2n\sigma _{{\alpha \beta }}^{2}}}+\frac{1}{{\rho _{0}^{2}}}} \right) - \frac{{ik}}{{2z}}{x_2}+\frac{{{x_1} - {x_2}}}{{2\rho _{0}^{2}}}$$
(15c)

and

$$\begin{gathered} {W_\beta }\left( {y,z} \right)=\sqrt {\frac{\pi }{{{a_{\beta y1}}}}} l!{\left( {\frac{1}{{{a_{\beta y1}}}}} \right)^l}\sum\limits_{{s=0}}^{{\left[ {\frac{l}{2}} \right]}} {\frac{1}{{s!\left( {l - 2s} \right)!}}} {\left( {\frac{{{a_{\beta y1}}}}{4}} \right)^s} \hfill \\ \exp \left\{ {\frac{1}{{{a_{\beta y1}}}}{{\left[ {\frac{{ik}}{{2z}}{y_1} - \frac{{{y_1} - {y_2}}}{{2\rho _{0}^{2}}}} \right]}^2}} \right\}\sum\limits_{{t=0}}^{{l - 2s}} {\frac{{\left( {l - 2s} \right)!}}{{t!\left( {l - 2s - t} \right)!}}{{\left( {\frac{{ik}}{{2z}}{y_1} - \frac{{{y_1} - {y_2}}}{{2\rho _{0}^{2}}}} \right)}^{l - 2s - t}}} \hfill \\ {\left( {\frac{1}{{2n\sigma _{{\alpha \beta }}^{2}}}+\frac{1}{{\rho _{0}^{2}}}} \right)^t}\sqrt {\frac{\pi }{{{a_{\beta y2}}}}} {2^{ - \left( {m+t} \right)}}{i^{\left( {m+t} \right)}}\exp \left( {\frac{{c_{{\beta y}}^{2}}}{{{a_{\beta y2}}}}} \right){\left( {\frac{1}{{{a_{\beta y2}}}}} \right)^{0.5\left( {m+t} \right)}}{H_{m+t}}\left( { - \frac{{i{c_{\beta y}}}}{{\sqrt {{a_{\beta y2}}} }}} \right) \hfill \\ \end{gathered}$$
(16)

with

$${a_{\beta y1}}=\frac{1}{{w_{0}^{2}}}+\frac{1}{{2n\sigma _{{\alpha \beta }}^{2}}}+\frac{1}{{\rho _{0}^{2}}}+\frac{{ik}}{{2z}},$$
(17a)
$${a_{\beta y2}}=\frac{1}{{w_{0}^{2}}}+\frac{1}{{2n\sigma _{{\alpha \beta }}^{2}}}+\frac{1}{{\rho _{0}^{2}}} - \frac{{ik}}{{2z}} - \frac{1}{{{a_{\beta y1}}}}\left( {\frac{1}{{2n\sigma _{{\alpha \beta }}^{2}}}+\frac{1}{{\rho _{0}^{2}}}} \right),$$
(17b)
$${c_{\beta y}}=\frac{1}{{{a_{y1}}}}\left( {\frac{{ik}}{{2z}}{y_1} - \frac{{{y_1} - {y_2}}}{{2\rho _{0}^{2}}}} \right)\left( {\frac{1}{{2n\sigma _{{\alpha \beta }}^{2}}}+\frac{1}{{\rho _{0}^{2}}}} \right) - \frac{{ik}}{{2z}}{y_2}+\frac{{{y_1} - {y_2}}}{{2\rho _{0}^{2}}}..$$
(17c)

Equations (15a), (15b), (15c), (16), (17a), (17b), and (17c) are the analytical expressions for the element of the cross-spectral density matrix of the REMGSM vortex beam propagating in oceanic turbulence at the receiver plane z.

The average intensity distribution of the REMGSM vortex beam propagating in oceanic turbulence at the point \(\left( {\mathbf{r},z} \right)\) with \({\mathbf{r}_1}={\mathbf{r}_2}=\mathbf{r}\) can be given by [25]

$$I\left( {\mathbf{r},z} \right)={W_{xx}}\left( {\mathbf{r},\mathbf{r},z} \right)+{W_{yy}}\left( {\mathbf{r},\mathbf{r},z} \right).$$
(18)

The spectral degree of polarization at the point \(\left( {\mathbf{r},z} \right)\) can be written as [25]

$$P\left( {\mathbf{r},z} \right)=\sqrt {1 - \frac{{4\det \overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\leftrightarrow}$}} {W} \left( {\mathbf{r},\mathbf{r},z} \right)}}{{{{\left[ {Tr\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\leftrightarrow}$}} {W} \left( {\mathbf{r},\mathbf{r},z} \right)} \right]}^2}}}} .$$
(19)

4 Numerical results and analyses

In this section, to investigate the evolution properties of a REMGSM vortex beam propagating in oceanic turbulence, we carry out the numerical calculations using the derived equations. In the following numerical calculations, unless other explanation, the parameters are set as \(\lambda =417\,{\text{nm}}\), \({w_0}=2 \,{\text{mm}}\), \({A_x}=1\), \({A_y}=0.5\), \({B_{xx}}={B_{yy}}=1\), \({B_{xy}}=0.5\exp \left( {{{i\pi } \mathord{\left/ {\vphantom {{i\pi } 3}} \right. \kern-0pt} 3}} \right)\), \({\sigma _{xx}}={\sigma _{yy}}=\sigma\), N = 3, M = 2, \({\chi _T}={10^{ - 9}}{{\text{K}}^{\text{2}}}{{\text{s}}^{ - 1}}\), \(\varepsilon ={10^{ - 7}}{{\text{m}}^{\text{2}}}{{\text{s}}^{ - 3}}\), and \(\varsigma = - 2.5\).

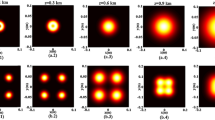
The 3D normalized intensity and corresponding contour graph of a REMGSM vortex beam with \(\sigma =2\,{\text{mm}}\) propagating in oceanic turbulence have been shown in Fig. 1. One can see that the normalized intensity pattern of a REMGSM vortex beam remains as the original dark hollow center at the short propagation distance (Fig. 1a); and as the propagation distance increases, the dark hollow center will gradually disappear (Fig. 1b, c); at last, the normalized intensity pattern of a REMGSM vortex beam will evolve into a flat-topped beam (Fig. 1d). The evolution properties of a REMGSM vortex beam through oceanic turbulence are similar to the multi-Gaussian Schell-model vortex beam through random media [26].

Fig. 1
figure 1

Normalized intensity and contour graph of a REMGSM vortex beam propagating in oceanic turbulence with \(\sigma =2\,{\text{mm}}\). a \(z=10\,{\text{m}}\), b \(z=50\,{\text{m}}\), c \(z=100\,{\text{m}}\), d \(z=180\,{\text{m}}\)

Full size image

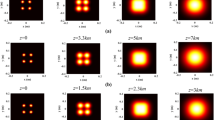
The influences of beam parameters \(\sigma\), M and N on the normalized intensity of a REMGSM vortex beam propagating in oceanic turbulence are illustrated in Figs. 2, 3, and 4, respectively. From Fig. 2, one sees that the REMGSM vortex beam with the smaller coherence length will lose its initial dark hollow center pattern more rapidly (Fig. 2b), and the fully coherent beam (\(\sigma =\inf\)) can keep its dark hollow center at the long propagation distance (Fig. 2d). From Fig. 3, one finds that the REMGSM vortex beam with \(\sigma =1\,{\text{mm}}\) and smaller topological charge M will lose its dark hollow pattern faster (Fig. 3b). While in the influences of the beam order N of Fig. 4, one finds that the REMGSM vortex beam with higher beam order N will lose the initial dark hollow center and evolve into Gaussian beam slower (Fig. 4a, b, red line), and the REMGSM vortex beam with the different N will all evolve into the Gaussian beam in the far field. But, by comparing Figs. 3 and 4, it is found the influence of beam order N on the normalized intensity of REMGSM vortex beam is not evidenced compared to the beam parameter M.

Fig. 2
figure 2

Cross section of a REMGSM vortex beam propagating in oceanic turbulence for the different \(\sigma\). a \(z=10\,{\text{m}}\), b \(z=50\,{\text{m}}\), c \(z=100\,{\text{m}}\), d \(z=180\,{\text{m}}\)

Full size image
Fig. 3
figure 3

Cross section of a REMGSM vortex beam propagating in oceanic turbulence with \(\sigma =1\,{\text{mm}}\) for the different M. a \(z=10\,{\text{m}}\), b \(z=20\,{\text{m}}\), c \(z=50\,{\text{m}}\), d \(z=100\,{\text{m}}\)

Full size image
Fig. 4
figure 4

Cross section of a REMGSM vortex beam propagating in oceanic turbulence with \(\sigma {\text{=1}}\,{\text{mm}}\) for the different N. a \(z=10\,{\text{m}}\), b \(z=20\,{\text{m}}\), c \(z=50\,{\text{m}}\), d \(z=100\,{\text{m}}\)

Full size image

To investigate the influences of oceanic turbulence on the normalized intensity of the REMGSM vortex beam, the normalized intensity of the REMGSM vortex beam with \(\sigma =2\,{\text{mm}}\) propagating in oceanic turbulence for the different \({\chi _T}\),\(\varepsilon\), and \(\varsigma\) are given in Figs. 5, 6, and 7, respectively. Form Fig. 5, it is found that the REMGSM vortex beam propagating in oceanic turbulence with larger \({\chi _T}\) will evolve into flat-topped beam faster, and then evolve into Gaussian-like beam. From Fig. 6, it can be seen that the beam propagation in oceanic turbulence with smaller \(\varepsilon\) will evolve into Gaussian-like beam faster. Figure 7 shows the influence of the relative strength of temperature and salinity fluctuations \(\varsigma\) on the propagation of the REMGSM vortex beam, one can find that the beam propagation in oceanic turbulence with larger \(\varsigma\) will evolve into Gaussian-like beam faster. Thus, from Figs. 5, 6, and 7, one can see that the REMGSM vortex beam propagation in oceanic turbulence with the increase of oceanic parameters \({\chi _T}\) and \(\varsigma\) or the decrease of oceanic parameter\(\varepsilon\) will lose its initial dark hollow center pattern faster, and evolve into flat-topped beam and Gaussian-like beam more rapidly. When oceanic parameters \({\chi _T}\) and \(\varsigma\) increase, or oceanic parameter\(\varepsilon\) decreases, the strength of oceanic turbulence will become stronger.

Fig. 5
figure 5

Cross section of a REMGSM vortex beam with \(\sigma =2\,{\text{mm}}\) propagating in oceanic turbulence for the different \({\chi _T}\). a \(z=20\,{\text{m}}\), b \(z=80\,{\text{m}}\)

Full size image
Fig. 6
figure 6

Cross section of a REMGSM vortex beam with \(\sigma =2\,{\text{mm}}\) propagating in oceanic turbulence for the different \(\varepsilon\). a \(z=50\,{\text{m}}\), b \(z=120\,{\text{m}}\)

Full size image
Fig. 7
figure 7

Cross section of a REMGSM vortex beam with \(\sigma =2\,{\text{mm}}\) propagating in oceanic turbulence for the different \(\varsigma\). a \(z=50\,{\text{m}}\), b \(z=120\,{\text{m}}\)

Full size image

The spectral degrees of polarization of the REMGSM vortex beam propagating in oceanic turbulence are shown in Figs. 8 and 9, respectively. The spectral degree of polarization distribution of the REMGSM vortex beam with \(\sigma =2\,{\text{mm}}\) through oceanic turbulence is not uniform (Fig. 8), and the spectral degree of polarization will change as the propagation distance increases. From Fig. 9, it is found that the on-axis spectral degree of polarization of the REMGSM vortex beam with \(\sigma =1\,{\text{mm}}\) for the different N and M will decrease as the propagation distance increases, the spectral degree of polarization of the REMGSM vortex beam with larger beam order N will decrease faster than the beam with smaller beam order N; while the spectral degree of the REMGSM vortex beam with larger topological charge M will decrease slower, the beam with large topological charge M can remain in its initial on-axis spectral degree better during the beam propagating in oceanic turbulence.

Fig. 8
figure 8

The spectral degree of polarization and corresponding contour graphs of a REMGSM vortex beam with \(\sigma =2\,{\text{mm}}\) propagating in oceanic turbulence. a \(z=20\,{\text{m}}\), b \(z=100\,{\text{m}}\)

Full size image
Fig. 9
figure 9

The on-axis spectral degree of polarization of a REMGSM vortex beam with \(\sigma =2\,{\text{mm}}\) propagating in oceanic turbulence. a For the different N, b for the different M

Full size image

5 Summary

In this paper, the new kind beam called the REMGSM vortex beam has been introduced. The elements of the cross-spectral density matrix of the REMGSM vortex beam propagating in oceanic turbulence have been derived, and the evolution properties of the REMGSM vortex beam have been analyzed using numerical examples. The results show that the REMGSM vortex beam propagating in stronger oceanic turbulence (the increase of oceanic parameters \({x_T}\) and \(\varsigma\) or the decrease of oceanic parameter \(\varepsilon\)) will lose its dark hollow center pattern and evolve into a flat-topped beam and Gaussian-like beam faster as the propagation distance z increases. And it is also found that the spectral degree of polarization of the REMGSM vortex beam for the different N and M will decrease as the propagation distance increases.