Propagation of radially polarized beams in the oceanic turbulence

Abstract

Based on the extended Huygens–Fresnel principle and the unified theory of coherence and polarization of light, we investigate the propagation properties of a radially polarized beam through turbulent ocean. Analytic formulae for the spectral density, the spectral degree of polarization, and the beam characteristics of such a beam on propagation are discussed. It is shown that under the influence of oceanic turbulence, the radially polarized beam will change to a partially polarized one and the beam profile will approach to a Gaussian distribution.

1 Introduction

The research of radially polarized beams is a subject of considerable importance due to its potential applications in area such as high-resolution microscopy [1], particle trapping and acceleration [2, 3], single fluorescent molecule [4], and acceleration techniques[5, 6]. Various methods for generating a laser beam with radial polarization have been reported [1, 7, 8], and the propagation properties of coherent and partially coherent radially polarized beams through free space, turbulent atmosphere, and paraxial optical system have been widely studied [9–14].

On the other hand, the propagation of laser beams has been discussed extensively, both in free space [15–17] and through a medium (see, for examples, atmospheric turbulence [18–20], optical fibers [21], chiral media [22], and compound photonic crystal [23]). As one kind of random medium, oceanic turbulence attracted more and more attention. It is shown that the spatial power spectrum of the refractive index fluctuations of oceanic waters is generally determined not only by the temperature fluctuations but also by the salinity fluctuations [24, 25]. Therefore, some interesting phenomena may emerge as laser beams propagating through the oceanic waters. However, to the best of our knowledge, the propagation properties of a radially polarized beam in the oceanic turbulence have not been reported.

In this manuscript, we will study the propagation of a radially polarized doughnut beam in the oceanic turbulence. The spectral density, the degree of polarization, and the beam characteristic parameters (i.e., the mean-squared beam width and PIB) will be investigated in detail.

2 Theoretical analyses

In the Cartesian coordinate system, the electric field of the radially polarized beam at the source plane z = 0 can be expressed as [26]

$$ {\mathbf{E}}(x,y,0) = E_{x} {\mathbf{e}}_{x} + E_{y} {\mathbf{e}}_{y} = E_{0} \left[ {\frac{x}{{\omega_{0} }}\exp \left( { - \frac{{r^{2} }}{{\omega_{0}^{2} }}} \right){\mathbf{e}}_{x} + \frac{y}{{\omega_{0} }}\exp \left( { - \frac{{r^{2} }}{{\omega_{0}^{2} }}} \right){\mathbf{e}}_{y} } \right], $$

(1)

where r ² = x ² + y ², ω ₀ denotes the beam waist size of a Gaussian beam, and E ₀ is a constant.

Assume that the beam propagates into the half-space z ≥ 0 close to the positive z direction. The second-order coherence and polarization properties of the beam may be characterized by a 2 × 2 cross-spectral density matrix [27]

$$ \overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\leftrightarrow}$}} {W} ({\mathbf{r}}_{1} ,{\mathbf{r}}_{2} ,z) = [W_{ij} ({\mathbf{r}}_{1} ,{\mathbf{r}}_{2} ,z)] = [\langle E_{i}^{*} ({\mathbf{r}}_{1} ,z)E_{j} ({\mathbf{r}}_{2} ,z)\rangle ],\quad \left( {i = x, y; j = x, y} \right) $$

(2)

where the asterisk denotes the complex conjugate, and the angular brackets stand for the average over the ensemble of realizations of the fluctuating electric field. E = (E _x , E _y ) is a member of the statistical ensemble of the fluctuating component of the transverse electric field.

On substituting from Eq. (1) into Eq. (2), one can obtain the element of cross-spectral density matrix in the source plane z = 0, by the following expressions:

$$ W_{xx} ({\mathbf{r}}_{10} ,{\mathbf{r}}_{20} ,0) = \frac{{E_{0}^{2} x_{10} x_{20} }}{{\omega_{0}^{2} }}\exp \left( { - \frac{{{\mathbf{r}}_{10}^{2} + {\mathbf{r}}_{20}^{2} }}{{\omega_{0}^{2} }}} \right), $$

(3a)

$$ W_{xy} ({\mathbf{r}}_{10} ,{\mathbf{r}}_{20} ,0) = \frac{{E_{0}^{2} x_{10} y_{20} }}{{\omega_{0}^{2} }}\exp \left( { - \frac{{{\mathbf{r}}_{10}^{2} + {\mathbf{r}}_{20}^{2} }}{{\omega_{0}^{2} }}} \right), $$

(3b)

$$ W_{yx} ({\mathbf{r}}_{10} ,{\mathbf{r}}_{20} ,0) = \frac{{E_{0}^{2} y_{10} x_{20} }}{{\omega_{0}^{2} }}\exp \left( { - \frac{{{\mathbf{r}}_{10}^{2} + {\mathbf{r}}_{20}^{2} }}{{\omega_{0}^{2} }}} \right), $$

(3c)

$$ W_{yy} ({\mathbf{r}}_{10} ,{\mathbf{r}}_{20} ,0) = \frac{{E_{0}^{2} y_{10} y_{20} }}{{\omega_{0}^{2} }}\exp \left( { - \frac{{{\mathbf{r}}_{10}^{2} + {\mathbf{r}}_{20}^{2} }}{{\omega_{0}^{2} }}} \right). $$

(3d)

When a radially polarized beam propagates in the oceanic turbulence, the elements of the cross-spectral density matrix can be obtained by using the extended Huygens–Fresnel diffraction integral [28]

$$ \begin{aligned} W_{{ij}} ({\mathbf{r}}_{1} ,{\mathbf{r}}_{2} ,z) & = \left( {\frac{k}{{2\pi z}}} \right)^{2} \iint {{\text{d}}{\mathbf{r}}_{{10}} }\iint {{\text{d}}{\mathbf{r}}_{{20}} }W_{{ij}} ({\mathbf{r}}_{{10}} ,{\mathbf{r}}_{{20}} ,0)\exp \left[ { - ik\frac{{({\mathbf{r}}_{1} - {\mathbf{r}}_{{10}} )^{2} - ({\mathbf{r}}_{2} - {\mathbf{r}}_{{20}} )^{2} }}{{2z}}} \right] \\ \quad \times {\text{exp}}\left[ { - \frac{{\pi ^{2} k^{2} z}}{3}({\mathbf{r}}_{{10}} - {\mathbf{r}}_{{20}} )^{2} } \right]\int {\kappa ^{3} } \Phi _{n} (\kappa ){\text{d}}\kappa \\ & \; = \left( \frac{k}{{2\pi z}}\right)^{2} \iint {{\text{d}}{\mathbf{r}}_{{10}} }\iint {{\text{d}}{\mathbf{r}}_{{20}} }W_{{ij}} \left({\mathbf{r}}_{{10}} ,{\mathbf{r}}_{{20}} ,0 \right)\exp \left[ { - ik\frac{{({\mathbf{r}}_{1} - {\mathbf{r}}_{{10}} )^{2} - ({\mathbf{r}}_{2} - {\mathbf{r}}_{{20}} )^{2} }}{{2z}}} \right] \times \exp \left[ { - \frac{1}{{\rho _{0}^{2} }}({\mathbf{r}}_{{10}} - {\mathbf{r}}_{{20}} )^{2} } \right] \\ \end{aligned} $$

(4)

where ${\text{d}}{\mathbf{r}}_{10} {\text{d}}{\mathbf{r}}_{20} = {\text{d}}x_{10} {\text{d}}y_{10} {\text{d}}x_{20} {\text{d}}y_{20}$, $k = \frac{2\pi }{\lambda }$ is the wave number with λ being the wavelength of the light, and ρ ₀ is the coherence length of a spherical wave propagating in the turbulent medium and can be expressed as

$$ \rho_{0} = \left( {\frac{3}{{\pi^{2} k^{2} z\int\nolimits_{0}^{\infty } {\kappa^{3} \Upphi_{n} (\kappa ){\text{d}}\kappa } }}} \right)^{{{\raise0.7ex\hbox{$1$} \!\mathord{\left/ {\vphantom {1 2}}\right.\kern-0pt} \!\lower0.7ex\hbox{$2$}}}} . $$

(5)

The model we used for the spatial power spectrum of the refractive index fluctuations of the oceanic water was obtained in [24, 25], as a linearized polynomial of two variables: the temperature fluctuations and the salinity fluctuations. The model is valid under the assumption that the turbulence is isotropic and homogeneous, and hence, we require only specification of the one-dimensional spectrum, which has the form

$$ \Upphi_{n} (\kappa ) = 0.388 \times 10^{ - 8} \varepsilon^{{ - {\raise0.7ex\hbox{$1$} \!\mathord{\left/ {\vphantom {1 3}}\right.\kern-0pt} \!\lower0.7ex\hbox{$3$}}}} \kappa^{{ - {\raise0.7ex\hbox{${11}$} \!\mathord{\left/ {\vphantom {{11} 3}}\right.\kern-0pt} \!\lower0.7ex\hbox{$3$}}}} [1 + 2.35(\kappa \eta )^{{{\raise0.7ex\hbox{$2$} \!\mathord{\left/ {\vphantom {2 3}}\right.\kern-0pt} \!\lower0.7ex\hbox{$3$}}}} ]f(\kappa ,v,\chi_{\text{T}} ), $$

(6)

where ε is the rate of dissipation of turbulent kinetic energy per unit mass of fluid which may vary in range from 10⁻⁴ to 10⁻¹⁰ m²/s³, η = 10⁻³ m being the Kolmogorov micro scale (inner scale), and

$$ f(\kappa ,w,\chi_{\text{T}} ) = \frac{{\chi_{\text{T}} }}{{w^{2} }}\left( {w^{2} e^{{ - A_{\text{T}} \delta }} + e{}^{{ - A_{\text{S}} \delta }} - 2we^{{ - A_{\text{TS}} \delta }} } \right), $$

(7)

where χ _T being the rate of dissipation of mean-square temperature, A _T = 1.863 × 10⁻², $A_{S} \, = 1.9 \times 10^{{ - 4}} ,\;A_{{TS}} \, = \,9.41 \times 10^{{ - 3}}$, and $\delta = 8.284(\kappa \eta )^{{{\raise0.7ex\hbox{$4$} \!\mathord{\left/ {\vphantom {4 3}}\right.\kern-0pt} \!\lower0.7ex\hbox{$3$}}}} + 12.978(\kappa \eta )^{2},$ w being the relative strength of temperature and salinity fluctuations, wherein the ocean water can vary in the interval [−5;0], 0 value corresponding to the case when temperature-driven turbulence dominates and −5 value corresponding to the situation when salinity-driven turbulence prevails.

On substituting from Eq. (3) into Eq. (4) and after letting r ₁ = r ₂ = r, we can obtain the following expressions for the elements of cross-spectral density matrix for radially polarized beam propagating in oceanic turbulence [11]

$$ W_{xx} ({\mathbf{r}},{\mathbf{r}},z) = E_{0}^{2} \frac{{2k^{2} \rho_{0}^{4} \omega_{0}^{6} z^{2} }}{{A_{1}^{2} }}\left[ {\frac{1}{{\rho_{0}^{2} }} + \frac{{k^{2} \rho_{0}^{2} (k^{2} \omega_{0}^{4} + 4z^{2} )x^{2} }}{{2z^{2} A_{1} }}} \right]\exp \left[ { - \frac{{2k^{2} \rho_{0}^{2} \omega_{0}^{2} }}{{A{}_{1}}}{\mathbf{r}}^{2} } \right], $$

(8a)

$$ W_{xy} ({\mathbf{r}},{\mathbf{r}},z) = W_{yx} ({\mathbf{r}},{\mathbf{r}},z) = E_{0}^{2} \frac{{k^{4} \rho_{0}^{6} \omega_{0}^{6} (k^{2} \omega_{0}^{4} + 4z^{2} )xy}}{{A_{1}^{3} }}\exp \left[ { - \frac{{2k^{2} \rho_{0}^{2} \omega_{0}^{2} }}{{A_{1} }}{\mathbf{r}}^{2} } \right], $$

(8b)

$$ W_{yy} ({\mathbf{r}},{\mathbf{r}},z) = E_{0}^{2} \frac{{2k^{2} \rho_{0}^{4} \omega_{0}^{6} z^{2} }}{{A_{1}^{2} }}\left[ {\frac{1}{{\rho_{0}^{2} }} + \frac{{k^{2} \rho_{0}^{2} (k^{2} \omega_{0}^{4} + 4z^{2} )y^{2} }}{{2z^{2} A_{1} }}} \right]\exp \left[ { - \frac{{2k^{2} \rho_{0}^{2} \omega_{0}^{2} }}{{A_{1} }}{\mathbf{r}}^{2} } \right] , $$

(8c)

where $A_{1} = k^{2} \rho_{0}^{2} \omega_{0}^{4} + 4z^{2} (\rho_{0}^{2} + 2\omega_{0}^{2} )$. The spectral density of the beam is defined by the following formula [28]:

$$ S({\mathbf{r}},z) = {\text{Tr}}{\mathop{W}\limits^{\leftrightarrow}}({\mathbf{r}},{\mathbf{r}},z). $$

(9)

On substituting from Eq. (8) into Eq. (9), one can obtain the spectral density of the beam on propagation

$$ S({\mathbf{r}},z) = E_{0}^{2} \frac{{2k^{2} \rho_{0}^{4} \omega_{0}^{6} z^{2} }}{{A_{1}^{2} }}\left[ {\frac{2}{{\rho_{0}^{2} }} + \frac{{k^{2} \rho_{0}^{2} (k^{2} \omega_{0}^{4} + 4z^{2} )(x^{2} + y^{2} )}}{{2z^{2} A_{1} }}} \right]\exp \left[ { - \frac{{2k^{2} \rho_{0}^{2} \omega_{0}^{2} }}{{A{}_{1}}}{\mathbf{r}}^{2} } \right]. $$

(10)

The spectral degree of polarization can be obtained by the expression [29]

$$ P({\mathbf{r}},z;v) = \sqrt {1 - \frac{{4{\text{Det}}[{\mathop{W}\limits^{\leftrightarrow}}({\mathbf{r}},{\mathbf{r}},z)]}}{{{\text{Tr}}[{\mathop{W}\limits^{\leftrightarrow}}({\mathbf{r}},{\mathbf{r}},z)]^{2} }}} , $$

(11)

where Det and Tr stand for determinant and trace of the matrix, respectively.

The mean-squared beam width is a characteristic parameter of beam quality that is defined by [30, 31]

$$ \bar{r}^{2} (z) = \frac{{\int\nolimits_{0}^{2\pi } {\int\nolimits_{0}^{\infty } {r^{2} S({\mathbf{r}},z)r{\text{d}}r{\text{d}}\theta } } }}{{\int\nolimits_{0}^{2\pi } {\int\nolimits_{0}^{\infty } {S({\mathbf{r}},z)r{\text{d}}r{\text{d}} \theta} } }} . $$

(12)

On substituting from Eq. (10) into Eq. (12), one finds

$$ \overline{r}^{2} (z) = \frac{{8z^{2} A_{1} \omega^{2} + 2A_{1} \rho_{0}^{2} (k^{2} \omega^{4} + 4z^{2} )}}{{2\omega^{2} k^{2} \rho_{0}^{2} [8\omega^{2} z^{2} + \rho_{0}^{2} (k^{2} \omega^{4} + 4z^{2} )]}}. $$

(13)

PIB (power in the bucket) is usually used to measure laser power focus ability in the far field. It clearly indicates how much fraction of the total beam power is within a given bucket, and is defined by [32]

$$ {\text{PIB}} = \frac{{\int\nolimits_{0}^{2\pi } {\int\nolimits_{0}^{L} {S({\mathbf{r}},z)r{\text{d}}r{\text{d}}\theta } } }}{{\int\nolimits_{0}^{2\pi } {\int\nolimits_{0}^{\infty } {S({\mathbf{r}},z)r{\text{d}}r{\text{d}}\theta } } }}, $$

(14)

where L is the chosen bucket radius.

On substitution from Eq. (10) into Eq. (14) yields

$$ {\text{PIB}} = \frac{{\frac{{ - A_{1} }}{{\rho_{0}^{2} }}\left( {e^{{\frac{{ - 2k^{2} \rho_{0}^{2} \omega^{2} L}}{{A_{1} }}}} - 1} \right) + \frac{{(k^{2} \omega^{4} + 4z^{2} )A_{1} }}{{8z^{2} \omega^{2} }}\left[ {\left( {\frac{{ - 2k^{2} \rho_{0}^{2} \omega^{2} L}}{{A_{1} }} - 1} \right)e^{{\frac{{ - 2k^{2} \rho_{0}^{2} \omega^{2} L}}{{A_{1} }}}} + 1} \right]}}{{\frac{{A_{1} }}{{\rho_{0}^{2} }} + \frac{{(k^{2} \omega^{4} + 4z^{2} )A_{1} }}{{8z^{2} \omega^{2} }}}} . $$

(15)

3 Numerical results

In this section, we will present some numerical results to show the changes of the radially polarized beam propagation in the oceanic turbulence. The parameters for the following calculations are chosen as ω ₀ = 2 cm, λ = 632.8 nm, η = 10⁻³ m, and ɛ = 10⁻⁷ m²/s^3.

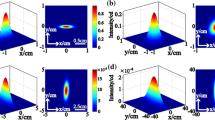
Figure 1 presents the normalized spectral density of the radially polarized beam propagation in oceanic turbulence with several propagation distances for different values of χ _T. It can be found from Fig. 1 that, with the increasing of the propagation distance z, the beam profile will transfer from a doughnut beam profile to Gaussian beam profile, and the larger the rate of dissipation of mean-square temperature χ _T, the faster the beam profile approach to the Gaussian distribution.

Fig. 1

Normalized spectral density S(x, 0, z)/S _max(x, 0, 0) of a radially polarized beam at several propagation distances in oceanic turbulence for two different values of χ _T and with w = −2.5

Now, let us consider the influence of the relative strength of temperature and salinity fluctuations w on the beam profile. In Fig. 2, we present the normalized spectral density of a radially polarized beam propagating in the oceanic turbulence at the certain propagation distance for two different values of w. It is shown that the changes of beam profile approach to a Gaussian distribution more rapidly for larger w. It is known that w being the relative strength of temperature and salinity fluctuations, wherein the ocean water can vary in the interval [−5;0], attaining the upper bound for the maximum temperature-induced optical turbulence. It is evident that the normalized spectral density of a radially polarized beam is most affected when temperature fluctuations in the ocean dominate salinity fluctuations.

Fig. 2

Normalized spectral density S(x, 0, z)/S _max(x, 0, 0) of a radially polarized beam propagating in oceanic turbulence for two different values of w. The other parameters are z = 400 m and χ _T = 10⁻⁹

In Fig. 3, we studied the spectral degree of polarization of a radially polarized beam propagating in the oceanic turbulence at several distances. It is shown that a radially polarized beam changes from a completely polarized beam into a partially polarized one as it propagates in the oceanic turbulence. The on-axis spectral degree of polarization becomes zero on propagation and the width of the dip increases with the increasing of propagation distance.

Fig. 3

Changes in the spectral degree of polarization of a radially polarized beam propagating in oceanic turbulence at several distances a z = 0; b z = 300 m; c z = 500 m; d z = 1,000 m. The other parameters are χ _T = 10⁻⁹ and w = −2.5

Figure 4 presents the spectral degree of polarization of a radially polarized beam propagating through the oceanic turbulence with different parameters (i.e., χ _T, w) of oceanic turbulence. It follows from Fig. 4 that the dip of the spectral degree of polarization increases with a larger χ _T or w.

Fig. 4

Changes in the spectral degree of polarization of a radially polarized beam propagating through the oceanic turbulence with different χ _T and w. a z = 1,000 m, w = −2.5; b z = 1,000 m, χ _T = 10⁻⁹

In the following, we will consider the beam characteristics. Figure 5 presents the relative width $\overline{r} (z)/r_{0}$ of a radially polarized beam propagating through the oceanic turbulence with different χ _T and w. It is shown that the relative width increases with larger value of χ _T and w. In Fig. 6, the changes of PIB of a radially polarized beam propagating through the oceanic turbulence with different χ _T and w are presented. It is found that the PIB decreases with the increasing of χ _T or w.

Fig. 5

Relative width of a radially polarized beam propagating through the oceanic turbulence with different χ _T and w. a w = −2.5; b χ _T = 10⁻⁹

Fig. 6

PIB of a radially polarized beam propagating through the oceanic turbulence with different χ _T and w. a z = 3,000 m, w = −2.5; b z = 3,000 m, χ _T = 10⁻⁸

4 Conclusion

In this manuscript, analytic expressions for the elements of the cross-spectral density matrix for a radially polarized beam propagation in the oceanic turbulence have been derived. The spectral density, the spectral degree of polarization, and the beam quality have been investigated in detail. It is shown that the oceanic turbulence will destroy the radial polarization structure of a radially polarized beam, and a radially polarized beam propagating in oceanic turbulence changes its doughnut beam profile into a Gaussian beam profile as the propagation distance z increases. The beam quality of such a beam on propagation has also been studied. Numerical results are given to show that the beam quality will be destroyed by the oceanic turbulence.