1 Introduction

The theoretical examination of optical wave propagation through turbulence predominantly relies on the extended Huygens-Fresnel principal (Andrews and Phillips 2005; Born and Wolf 1999). In recent years, the study of laser beam propagation through oceanic turbulence has gained significant attention due to its intriguing applications in underwater laser communications and imaging systems (Korotkova 2015; Luo et al. 2018; Hou 2009; Ata and Baykal 2018; Cheng et al. 2016). Researchers have widely investigated the influence of temperature and salinity fluctuations on the propagation of laser beams, which includes the degree of polarization, spreading, and the scintillation index. (Chen et al. 2013; Baykal 2016; Yang et al. 2017). Furthermore, the properties of various beams in an oceanic turbulence have been reported, such as those for radially polarized beams (Tang and Zhao 2013), partially coherent radially polarized doughnut beams (Fu and Zhang 2013), four-petal Gaussian beams (Liu et al. 2017a, b), Gaussian Schell-model vortex beams (Huang et al. 2014), pulsed vortex beams (Benzehoua and Belafhal 2023a), among others.

On the other hand, Casperson and Tover have proposed Hermite-Sinusoidal-Gaussian (HSG) beams as a class of general solutions to the paraxial wave equation (Casperson and Tovar 1998). This class of beams has garnered significant attention that includes a whole family of laser beams characterized by distinct profiles suitable for practical applications (Casperson et al. 1997; Tovar and Casperson 1998; Hricha and Belafhal 2005). Since then, several related studies have analyzed in detail, including Hermite Gaussian, Hermite cosh-Gaussian, vortex Hermite cosh-Gaussian, hollow higher-order cosh-Gaussian, and Generalized Hermite cosh-Gaussian beams propagating through turbulent atmospheres. These studies have explored various aspects, such as average intensity distribution, beam spreading, polarization, angular spread of partially coherent beams, beam propagation factor, scintillation index, and spectral characteristics of pulsed beams (Ji et al. 2008; Ji and Chen 2009; Yuan et al. 2010; Eyyuboglu 2005; Sayan et al. 2020; Hricha et al. 2021; Benzehoua and Belafhal 2023b, c; Saad and Belafhal 2023). Recently, researchers have expanded their interest in beam propagation from turbulent atmospheres to seawater media, specifically ocean water (Hill 1978; Nikishov and Nikishov 2000). In this context, researchers have studied how oceanic turbulence affects the propagation properties of hollow higher-order cosh-Gaussian, Hermite Gaussian, and Hermite cosh-Gaussian beams. These investigations have covered parameters such as intensity distribution, scintillation index, beam quality, effective radius and spectral coherence (Baykal 2020; Wang et al. 2020; Cao 2022; Elmabruk and Bayraktar 2023; Huang et al. 2015; Wu et al. 2023; Zhu et al. 2023). Oceanic turbulence significantly affects the propagation behavior of HSG beam types, which exhibit a rich structure and controllable morphology, potentially enhancing underwater free-space optical communication. Based on these investigations, it is essential to study the evolution properties of GHCGB in oceanic turbulence. The proposed model is a generalized form contains additional parameters compared to their special cases such as a fundamental Gaussian, Cosh-Gaussian, higher-order Cosh-Gaussian, Hollow-Gaussian, Hermite-Gaussian, Hermite cosh-Gaussian and Hollow higher order Cosh Gaussian. Further, the intensity distribution, size, and central dark width can be adjusted by selecting appropriate values of initial beam and oceanic turbulence, allowing for unique possibilities and tailored beam properties for specific applications. The GHCGB has the potential applications in underwater optical wireless communication due to which has the special beam profile. The GHCGB has the potential applications in underwater optical wireless communication due to which has the special beam profile.

The focus of this paper is to explore the evolution properties of the normalized intensity of GHCGB in oceanic turbulence. However, to the best of our knowledge, the received intensity of a GHCGB in oceanic turbulence has not been reported yet. The paper is organized as follows: In Sect. 2, we introduce the source electric field of GHCGB and derive a propagation equation for the received intensity of the beam in oceanic turbulence. In Sect. 3, the influences of source beam parameters and oceanic turbulence parameters on the evolution properties of the received intensity are analyzed with illustrative numerical examples. Finally, the main results obtained are given in the conclusion part.

2 Received intensity of GHCGB propagating through oceanic turbulence

In this Section, we present a theoretical analysis based on the extended Huygens–Fresnel integral for the propagation of a GHCGB in oceanic turbulence. The electric field of a GHCGB at z = 0 in Cartesian coordinates is expressed as follows (Saad and Belafhal 2022)

$$u_{{j,h}}^{{l,n}}\left( {{\rho _x},{\rho _y},z=0} \right)={A_0}\,{\left( {\frac{{{\rho _x}}}{{{\omega _0}}}} \right)^l}\,{\left( {\frac{{{\rho _y}}}{{{\omega _0}}}} \right)^l}{H_j}\left( {\beta {\rho _x}} \right){H_h}\left( {\beta {\rho _y}} \right){\cosh ^n}\left( {\Omega {\rho _x}} \right){\cosh ^n}\left( {\Omega {\rho _y}} \right)\,{e^{ - {{\left( {{\rho _x}^{2}+{\rho _y}^{2}} \right)} \mathord{\left/ {\vphantom {{\left( {{\rho _x}^{2}+{\rho _y}^{2}} \right)} {\omega _{0}^{2}}}} \right. \kern-0pt} {\omega _{0}^{2}}}}}\,,$$
(1)

where ρx and ρy are the coordinates at the source plane, A0 is the amplification factor, with \(\beta ={{\sqrt 2 } \mathord{\left/ {\vphantom {{\sqrt 2 } {{\omega _0}}}} \right. \kern-0pt} {{\omega _0}}}\). The source beam parameters are defined as: \({\omega }_{0}\) is the waist radius of the Gaussian part and l refers to the hollowness parameter and (j, h) are the mode indexes associated with the Hermite polynomials Hj (.) and Hh (.) in the x- and y- directions. n and Ω are the parameters associated to the cosh part. By using the Euler expansion and series transformation (Gradshteyn and Ryzhik 1994), Eq. (1), can be rewritten

$$\begin{aligned} u_{{j,h}}^{{l,n}} \left( {\rho _{x} ,\rho _{y} ,z = 0} \right) = & \frac{{A_{0} {\mkern 1mu} }}{{2^{{2n}} }}\left( {\frac{{\rho _{x} }}{{\omega _{0} }}} \right)^{l} {\mkern 1mu} \left( {\frac{{\rho _{y} }}{{\omega _{0} }}} \right)^{l} {\mkern 1mu} {\mkern 1mu} H_{j} \left( {\beta \rho _{x} } \right){\mkern 1mu} H_{h} \left( {\beta \rho _{y} } \right)\sum\limits_{{m = 0}}^{n} {\sum\limits_{{t = 0}}^{n} {\left( {\begin{array}{*{20}c} n \\ m \\ \end{array} } \right)\left( {\begin{array}{*{20}c} n \\ t \\ \end{array} } \right)} } \exp \left[ {\left( {\alpha _{m}^{2} \delta + \alpha _{t}^{2} \delta } \right)} \right] \\ \times & \exp \left[ { - \left( {\frac{{\rho _{x}^{2} }}{{\omega _{0} }} - \alpha _{m} \sqrt \delta } \right)^{2} } \right]\exp \left[ { - \left( {\frac{{\rho _{y}^{2} }}{{\omega _{0} }} - \alpha _{t} \sqrt \delta } \right)^{2} } \right], \\ \end{aligned}$$
(2)

with \({\alpha _m}=\left( {m - {n \mathord{\left/ {\vphantom {n 2}} \right. \kern-0pt} 2}} \right)\,\,,\,{\alpha _t}=\left( {t - {n \mathord{\left/ {\vphantom {n 2}} \right. \kern-0pt} 2}} \right)\,\) and \(\,\delta =\omega _{0}^{{2\,}}{\Omega ^2}\) is the acentric parameter of cosh-Gaussian beam. At the output plane, with the help of the extended Huygens-Fresnel diffraction integral, the propagation of laser beam in oceanic turbulence along the z-axis can be formulated as (Andrews and Phillips 2005; Born and Wolf 1999)

$$\begin{aligned} \left\langle {I_{{j,h}}^{{l,n}} \left( {r,z} \right)} \right\rangle = & \frac{{k^{2} }}{{4\pi ^{2} z^{2} }}\int\limits_{{ - \infty }}^{\infty } {\int\limits_{{ - \infty }}^{\infty } {\int\limits_{{ - \infty }}^{\infty } {\int\limits_{{ - \infty }}^{\infty } {u_{{j,h}}^{{l,n}} \left( {\rho _{{x1}} ,\rho _{{y1}} ,0} \right)u_{{j,n}}^{{*l,n}} \left( {\rho _{{x2}} ,\rho _{{y2}} ,0} \right)} } } } \\ & \times \exp \left\{ { - \frac{{ik}}{{2z}}\left[ {\left( {\rho _{{x1}} - x} \right)^{2} + \left( {\rho _{{y1}} - y} \right)^{2} + \left( {\rho _{{x2}} - x} \right)^{2} + \left( {\rho _{{y2}} - y} \right)^{2} } \right]} \right\} \\ & \times \left\langle {\exp \left[ {\psi \left( {\rho _{{x1}} ,\rho _{{y1}} ,x,y} \right) + \psi ^{*} \left( {\rho _{{x2}} ,\rho _{{y2}} ,x,y} \right)} \right]u} \right\rangle \rho _{{x1}} d\rho _{{x2}} d\rho _{{y1}} d\rho _{{y2}} , \\ \end{aligned}$$
(3)

where \(r=\left( {x,y} \right)\) are the position vector in the receiver plane, z is the propagation distance, 〈〉refers to ensemble average, \(*\) denotes the complex conjugate and \(k={{2\pi } \mathord{\left/ {\vphantom {{2\pi } \lambda }} \right. \kern-0pt} \lambda }\) is the wave number with \(\lambda\) is the wavelength of the beam. \(\psi\) is the Rytov solution that represents the phase perturbation and the random part of the phase fluctuations induced by the oceanic turbulence. The ensemble average term can be expressed as (Ye et al. 2018)

$$\left\langle {\exp \left[ {\psi \left( {{\rho _{x1}},{\rho _{y1}},x,y} \right)+{\psi ^*}\left( {{\rho _{x2}},{\rho _{y2}},x,y} \right)} \right]\,} \right\rangle =\exp \left\{ { - \frac{1}{{\rho _{0}^{2}}}\left[ {{{\left( {{\rho _{x2}} - {\rho _{x1}}} \right)}^2}+{{\left( {{\rho _{y2}} - {\rho _{y1}}} \right)}^2}} \right]} \right\},$$
(4)

where the coherence length of a spherical wave propagating in oceanic turbulence \({\rho _0}\) can be considered as

$${\rho _0}={\left[ {\frac{{{\pi ^2}{k^2}z}}{3}\int\limits_{0}^{\infty } {dK{K^3}} \Phi \left( K \right)} \right]^{ - 1/2}}$$
(5)

, with K is the spatial frequency, and \(\Phi \left( K \right)\) is the spatial power spectrum of the refractive index fluctuations which for an homogeneous and isotropic turbulent ocean is given by (Nikshov and Nikishov 2000)

$$\begin{gathered} \Phi \left( K \right)=0.388 \times {10^{ - 8}}{\varepsilon ^{ - 11/3}}\frac{{{\chi _T}}}{{{\zeta ^2}}}\left[ {1+2.35{{\left( {k\eta } \right)}^{{2 \mathord{\left/ {\vphantom {2 3}} \right. \kern-0pt} 3}}}} \right] \hfill \\ \,\,\,\,\,\,\,\,\,\,\,\,\,\, \times \left( {{\zeta ^2}\exp \left( { - {A_T}\delta } \right)+\exp \left( { - {A_s}\delta } \right) - 2\zeta \exp \left( { - {A_{TS}}\delta } \right)} \right), \hfill \\ \end{gathered}$$
(6)

where the oceanic turbulence parameters are:

  • \(\varepsilon\) is the rate of dissipation of turbulent kinetic energy per unit mass of fluid, which may vary in the range from \({10^{ - 1}}{m^2}{s^{ - 3}}\,\) to \({10^{ - 10}}{m^2}{s^{ - 3}}\) ,

  • \({\chi _T}\) is the dissipation rate of mean squared temperature taking value in the range from \({10^{ - 4}}{K^2}{S^{ - 1}}\) to \(\,{10^{ - 10}}{K^2}{S^{ - 1}},\)

  • \(\zeta\) represents the relative strength of temperature and salinity fluctuations, which in the ocean water varies in the range from − 5 to 0,

  • \(\eta ={10^{ - 3}}\,\)is the Kolomogorov inner scale, \(\delta =8.284{(K\eta )^{4/3}}+12.978{(K\eta )^2},\)\({A_T}=1.863 \times {10^{ - 2}},\)\({A_S}=1.9 \times {10^{ - 4}}\) and \({A_{TS}}=9.41 \times {10^{ - 3}}\).

Substituting Eqs. (2) and (4) into Eq. (3), and after re-arranging the integrand function, the received intensity can be written via the following expansion

$$\left\langle {I_{{j,h}}^{{l,n}}\left( {x,y,z} \right)} \right\rangle =\frac{{A_{0}^{2}{k^2}}}{{4{\pi ^2}{z^2}{2^{4n}}}}\sum\limits_{{m=0}}^{n} {\sum\limits_{{t=0}}^{n} {\sum\limits_{{m^{\prime}=0}}^{n} {\sum\limits_{{t^{\prime}=0}}^{n} {\left( {_{m}^{n}} \right)} } \left( {_{t}^{n}} \right)\left( {_{{m^{\prime}}}^{n}} \right)} } \left( {_{{t^{\prime}}}^{n}} \right)\,\,\,W_{{m,j}}^{{l,n}}\left( {x,z} \right)W_{{t,h}}^{{l,n}}\left( {y,z} \right),$$
(7)

where

$$\begin{aligned} W_{{m,j}}^{{l,n}} \left( {x,z} \right) = & \int\limits_{{ - \infty }}^{\infty } {\int\limits_{{ - \infty }}^{\infty } {\left( {\rho _{{x1}} } \right)^{l} H_{j} \left( {\beta \rho _{{x1}} } \right)\exp \left[ { - \gamma _{{1x}} \rho _{{x1}}^{2} + 2\left( {Q_{{1x}} + \frac{{\rho _{{x2}} }}{{\rho _{0}^{2} }}} \right)\rho _{{x1}} } \right]} } \\ \times & \left( {\rho _{{x2}} } \right)^{l} H_{j} \left( {\beta \rho _{{x2}} } \right)\exp \left[ { - \gamma _{{2x}} \rho _{{x2}}^{2} + 2\left( {\frac{{\alpha _{{m^{\prime } }} \sqrt \delta }}{{\omega _{0} }} - \frac{{ikx}}{{2z}}} \right)\rho _{{x2}} } \right]d\rho _{{x1}} d\rho _{{x2}} , \\ \end{aligned}$$
(8a)
$$\begin{aligned} W_{{t,h}}^{{l,n}} \left( {y,z} \right) = & \int\limits_{{ - \infty }}^{\infty } {\int\limits_{{ - \infty }}^{\infty } {\left( {\rho _{{y1}} } \right)^{l} H_{h} \left( {\beta \rho _{{y1}} } \right)\exp \left[ { - \gamma _{{1y}} \rho _{{y1}}^{2} + 2\left( {Q_{{1y}} + \frac{{\rho _{{y2}} }}{{\rho _{0}^{2} }}} \right)\rho _{{y1}} } \right]} } \\ \times & \left( {\rho _{{y2}} } \right)^{l} H_{h} \left( {\beta \rho _{{y2}} } \right)\exp \left[ { - \gamma _{{2y}} \rho _{{y2}}^{2} + 2\left( {\frac{{\alpha _{{t^{\prime } }} \sqrt \delta }}{{\omega _{0} }} - \frac{{iky}}{{2z}}} \right)\rho _{{y2}} } \right]d\rho _{{y1}} d\rho _{{y2}} , \\ \end{aligned}$$
(8b)

with

$${\gamma _{1x}}=\frac{1}{{\omega _{0}^{2}}}+\frac{{ik}}{{2z}}+\frac{1}{{\rho _{0}^{2}}},$$
(8c)
$${\gamma _{1y}}=\frac{1}{{\omega _{0}^{2}}}+\frac{{ik}}{{2z}}+\frac{1}{{\rho _{0}^{2}}},$$
(8d)
$${Q_{1x}}=\frac{{{\alpha _m}\sqrt \delta }}{{{\omega _0}}}+\frac{{ikx}}{{2z}},$$
(8e)

and

$${Q_{1y}}=\frac{{{\alpha _t}\sqrt \delta }}{{{\omega _0}}}+\frac{{iky}}{{2z}}.$$
(8f)

By recalling the following equations (Belafhal et al. 2020; Gradshteyn and Ryzhik 1994; Erdelyi et al. 1954; Abramowitz and Stegun, 1970)

$$\int\limits_{{ - \infty }}^{\infty } {x^{l} \;H_{m} \left( {ax} \right){\mkern 1mu} e^{{ - px^{2} + 2qx}} dx} = \frac{1}{{2^{l} }}\sqrt {\frac{\pi }{p}} \exp \left( {\frac{{q^{2} }}{p}} \right)\sum\limits_{{k = 0}}^{{\left[ {m/2} \right]}} {\frac{{\left( { - 1} \right)^{k} m!}}{{k!\left( {m - 2k} \right)!}}} \left( {\frac{\alpha }{{i\sqrt p }}} \right)^{{m + l - 2k}} H_{{m + l - 2k}} \left( {\frac{{iq}}{{\sqrt p }}} \right),\quad with{\mkern 1mu} {\mkern 1mu} \text{Re} \left( p \right) > 0,$$
(9)
$${H_n}\left( {x+y} \right)=\frac{1}{{{2^{{n \mathord{\left/ {\vphantom {n 2}} \right. \kern-0pt} 2}}}}}\sum\limits_{{k=0}}^{n} {\left( {\begin{array}{*{20}{c}} n \\ k \end{array}} \right){H_k}\left( {\sqrt 2 x} \right)\,} {H_{n - k}}\left( {\sqrt 2 y} \right),$$
(10)
$${H_n}\left( x \right)=\sum\limits_{{m=0}}^{{\left[ {{n \mathord{\left/ {\vphantom {n 2}} \right. \kern-0pt} 2}} \right]}} {{{\left( { - 1} \right)}^m}\frac{{n!}}{{m!\left( {n - 2 m} \right)!}}{{\left( {2x} \right)}^{n - 2 m}}} .$$
(11)

After some tedious calculations, we obtain the main analytical expression of the received averaged intensity for the GHCGB propagating in oceanic turbulence as

$$\begin{aligned} \left\langle {I_{{j,h}}^{{l,n}} \left( {x,y,z} \right)} \right\rangle = & \frac{{A_{0}^{2} k^{2} }}{{4z^{2} 2^{{4n + 5L}} \left( {\omega _{0} } \right)^{{4L}} }}\frac{1}{{\sqrt {\gamma _{{1x}} \gamma _{{2x}} \gamma _{{1y}} \gamma _{{2y}} } }} \\ \times & \sum\limits_{{m = 0}}^{n} {\sum\limits_{{m^{\prime } = 0}}^{n} {\sum\limits_{{t = 0}}^{n} {\sum\limits_{{t^{\prime } = 0}}^{n} {\left( {\begin{array}{*{20}c} n \\ m \\ \end{array} } \right)\left( {\begin{array}{*{20}c} n \\ {m^{\prime } } \\ \end{array} } \right)} } } } \left( {\begin{array}{*{20}c} n \\ t \\ \end{array} } \right)\left( {\begin{array}{*{20}c} n \\ {t^{\prime } } \\ \end{array} } \right)\exp \left( {\frac{{Q_{{1x}}^{2} }}{{\gamma _{{1x}} }} + \frac{{Q_{{2x}}^{2} }}{{\gamma _{{2x}} }} + \frac{{Q_{{1y}}^{2} }}{{\gamma _{{1y}} }} + \frac{{Q_{{2y}}^{2} }}{{\gamma _{{2y}} }}} \right) \\ \times & \sum\limits_{{k_{1} = 0}}^{{\left[ {j/2} \right]}} {\sum\limits_{{k_{2} = 0}}^{{\left[ {j/2} \right]}} {\frac{{\left( { - 1} \right)^{{k_{1} + k_{2} }} \left( {j!} \right)^{2} \left( {2\beta } \right)^{{j - 2k_{2} }} }}{{2^{{{{\left( {3j - 2k_{1} - 4k_{2} } \right)} \mathord{\left/ {\vphantom {{\left( {3j - 2k_{1} - 4k_{2} } \right)} 2}} \right. \kern-\nulldelimiterspace} 2}}} k_{1} !k_{2} !\left( {j - 2k_{1} } \right)!\left( {j - 2k_{2} } \right)!}}} } \left( {\frac{\beta }{{i\sqrt {\gamma _{{1x}} } }}} \right)^{{l + j - 2k_{1} }} \\ \times & \sum\limits_{{\nu = 0}}^{{l + j - 2k_{1} }} {\left( {\begin{array}{*{20}c} {l + j - 2k_{1} } \\ \nu \\ \end{array} } \right)H_{v} \left( {\frac{{\sqrt 2 iQ_{{1x}} }}{{\sqrt {\gamma _{{1x}} } }}} \right)} \sum\limits_{{s = 0}}^{{\left[ {l + j - 2k_{1} - \nu /2} \right]}} {\frac{{\left( { - 1} \right)^{s} \left( {l + j - v - 2k} \right)!}}{{s!\left( {l + j - 2k_{1} - v - 2s} \right)!}}} \\ \times & \left( {\frac{{\sqrt 2 }}{{\sqrt {\gamma _{{1x}} \gamma _{{2x}} } \rho _{0}^{2} }}} \right)^{{2L + 2j - 2k_{1} - \nu - 2k_{2} - 2s}} H_{{2L + 2j - 2k_{1} - \nu - 2k_{2} - 2s}} \left( {\frac{{iQ_{{2x}} }}{{\sqrt {\gamma _{{2x}} } }}} \right) \\ \times & \sum\limits_{{p_{1} = 0}}^{{\left[ {h/2} \right]}} {\sum\limits_{{p_{2} = 0}}^{{\left[ {h/2} \right]}} {\mkern 1mu} } {\mkern 1mu} \frac{{\left( { - 1} \right)^{{p_{1} + p_{2} }} \left( {h!} \right)^{2} \left( {2\beta } \right)^{{h - 2p_{2} }} }}{{2^{{{{\left( {3h - 2p_{1} - 4p_{2} } \right)} \mathord{\left/ {\vphantom {{\left( {3h - 2p_{1} - 4p_{2} } \right)} 2}} \right. \kern-\nulldelimiterspace} 2}}} p_{1} !p_{2} !\left( {h - 2p_{1} } \right)!\left( {h - 2p_{2} } \right)!}}{\mkern 1mu} \left( {\frac{\beta }{{i\sqrt {\gamma _{{1y}} } }}} \right)^{{l + h - 2p_{1} }} \\ \times & \sum\limits_{{u = 0}}^{{l + h - 2p_{1} }} {\left( {\begin{array}{*{20}c} {l + h - 2p_{1} } \\ u \\ \end{array} } \right)H_{u} \left( {\frac{{\sqrt 2 {\mkern 1mu} iQ_{{1y}} }}{{\sqrt {\gamma _{{1y}} } }}} \right)} \sum\limits_{{g = 0}}^{{\left[ {l + h - 2p_{1} - u/2} \right]}} {\frac{{\left( { - 1} \right)^{g} \left( {l + h - u - 2p_{1} } \right)!}}{{g!\left( {l + h - 2p_{1} - u - 2g} \right)!}}} \\ \times & \left( {\frac{{\sqrt 2 }}{{\sqrt {\gamma _{{1y}} \gamma _{{2y}} } \rho _{0}^{2} }}} \right)^{{2L + 2h - 2p_{1} - u - 2p_{2} - 2g}} H_{{2L + 2h - 2p_{1} - u - 2p_{2} - 2g}} \left( {\frac{{iQ_{{2y}} }}{{\sqrt {\gamma _{{2y}} } }}} \right), \\ \end{aligned}$$
(12)

where

$${\gamma _{2x}}=\frac{1}{{\omega _{0}^{2}}} - \frac{{ik}}{{2z}}+\frac{1}{{\rho _{0}^{2}}} - \frac{1}{{{\gamma _{1x}}\rho _{0}^{4}}},$$
(13a)
$${\gamma _{2y}}=\frac{1}{{\omega _{0}^{2}}} - \frac{{ik}}{{2z}}+\frac{1}{{\rho _{0}^{2}}} - \frac{1}{{{\gamma _{1y}}\rho _{0}^{4}}},$$
(13b)
$${Q_{2x}}=\frac{{{\alpha _{m^{\prime}}}\sqrt \delta }}{{{\omega _0}}} - \frac{{ikx}}{{2z}}+\frac{{{Q_{1x}}}}{{{\gamma _{1x}}\rho _{0}^{2}}},$$
(13c)

and

$${Q_{2y}}=\frac{{{\alpha _{t^{\prime}}}\sqrt \delta }}{{{\omega _0}}} - \frac{{iky}}{{2z}}+\frac{{{Q_{1y}}}}{{{\gamma _{1y}}\rho _{0}^{2}}}.$$
(13d)

Equation (12) represents the main analytical result of this paper that describes the effect of oceanic turbulence on the evolution properties of the GHCGB beam. Using Eq. (12), we will investigate numerically the received intensity of a GHCGB in oceanic turbulence.

3 Numerical analysis and discussion

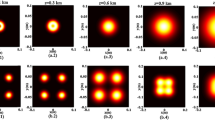
Based on the formula drived above, the evolution properties of a GHCGB propagating through the oceanic turbulence are discussed with numerical examples. Figure 1 presents the normalized average intensity of GHCGB in oceanic turbulence for the different parameter of oceanic turbulence \({\chi _T}\) (the dissipation rate of mean-square temperature parameter\({\chi _T}\)) at several propagation distances. Unless it is specified, the calculation parameters are set as: \(\lambda =417 nm,\,\)\({\omega _0}=0.02\mu m,\,\)\({A_0}=1,\) \({\chi _T}={10^{ - 8}}{K^2}{s^{ - 1}},\,\,\) \(\zeta = - 2.5,\) \(\varepsilon ={10^{ - 7}}{m^2}{s^{ - 3}},\) \(l=1,\,\,\) \(n=2\), \(\,\,j=1,\) \(h=1\) and \(\Omega = 60\;{\text{m}}^{{ - 1}}\).

Fig. 1
figure 1

Normalized average intensity of a GHCGB propagating in oceanic turbulence

Full size image

for different values of \({\chi _T}\) for: (a, b, c) z = 30 m, (d, e, f) z = 100 m, (g ,h, i) z = 180 m, (j, k, l) z = 250 m.

From the plots of Fig. 1, one can see that a beam with small propagation distance can keep its four-petal profile for the first transmission process (see Fig. 1a-c). As the propagation distance increases z = 100 m, the GHCGB also preserves its initial profile with smaller oceanic turbulence parameter \({\chi _T}\) (see Fig. 1d-e) and then the light petals get closer and bond (see Fig. 1f). With further distance increases z = 180 m, the beam can keep its initial profile as \({\chi _T}\) is smaller and finally the beam morphed into a flat-topped profile-like with larger \({\chi _T}\) (see Fig. 1g-i). In the far field at z = 250 m, the beam will lose its first profile and evolves into a Gaussian like beam faster as when \({\chi _T}\)is larger due to the effect of oceanic turbulence (see Fig. 1k-l). Figure 2 illustrates the normalized average intensity of a GHCGB in oceanic turbulence. This intensity is evaluated at several propagation distances for the different parameter of oceanic turbulence \(\varepsilon\).

Fig. 2
figure 2

Normalized average intensity of a GHCGB propagating in oceanic turbulence for different values of

Full size image

\(\varepsilon\) for: (a, b, c) z = 30 m, (d, e, f) z = 100 m, (g ,h, i) z = 180 m, (j, k, l) z = 250 m.

From Fig. 2, one can see that the beam will keep its original four-petal profiles in the near field propagation (see Fig. 2a-c). And as the propagation distance increases z = 100 m, the beam with small oceanic parameter \(\varepsilon\), the light petals become more pronounced (see Fig. 2d), but the beam will lose gradually its initial profiles and become a flat-topped beam with increasing propagation distance z = 180 m and decreasing oceanic parameter \(\varepsilon\) (see Fig. 2g). It is also found that the beam propagating in oceanic turbulence with small parameter \(\varepsilon\) will evolve into a Gauss-like beam rapidly at the far field propagation (see Fig. 2k). This means that the oceanic turbulence becomes stronger for lower oceanic parameter \(\varepsilon\) in the far field.

Figure 3 gives the normalized average intensity of a GHCGB in oceanic turbulence at several propagation distances for different oceanic parameter \(\zeta\) (the ratio of temperature to salinity parameter \(\zeta\)).

Fig. 3
figure 3

Normalized average intensity of a GHCGB propagating in oceanic turbulence for different values of

Full size image

\(\zeta\) for: (a, b, c) z = 30 m, (d, e, f) z = 100 m, (g ,h, i) z = 180 m, (j, k, l) z = 250 m.

From Fig. 3, one can see that the beam with small \(\zeta\) in oceanic turbulence can keep its original intensity profile at short propagation distance (see Fig. 3a-f). But as the propagation distance is further increased, the beam will morph its initial four-petal profile slowly into a flat-topped profile-like with increasing parameter \(\zeta\) (see Fig. 3i). It is also found that, the beam propagating in stronger underwater oceanic turbulence (with larger\(\zeta\)) will evolve gradually into a Gauss-like beam faster at the far field (see Fig. 3j-l).

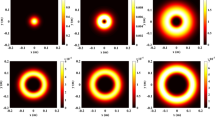
In order to investigate the influence of the cosh parameter \(\Omega\) on the evolution properties of the beam with different parameters of underwater oceanic turbulence (\({\chi _T}\),\(\varepsilon\),\(\zeta\)), the normalized average intensity of a GHCGB propagation through underwater oceanic turbulence at fixed propagation distance z = 200 m is illustrated in Fig. 4.

Fig. 4
figure 4

Normalized intensity distribution in x-direction of a GHCGB propagating in oceanic turbulence

Full size image

for different \({\chi _T},\,\varepsilon\) and \(\zeta\)at z = 200 m, \((a,c,e)\;\Omega = 20\;{\text{m}}^{{ - 1}}\) and \((b,d,f)\;\Omega = 80\;{\text{m}}^{{ - 1}}\).

From the plots of Fig. 4, one can see that a pattern of beam intensity distribution propagating in underwater oceanic turbulence is affected by the cosh parameter \(\Omega\) and the oceanic turbulence parameters. It is also found that a beam with small \(\Omega\) and large \({\chi _T}\) or \(\zeta\), will lose the initial dark hollow center and will cause a faster spreading in underwater oceanic turbulence while the central dark intensity will disappear slowly as when \(\Omega\) is larger. Also, the parameter \(\varepsilon\) will cause the smaller spreading than the parameters \({\chi _T}\) or \(\zeta\)(see Fig. 4c-d). One can conclude from Fig. 4 that the effects of oceanic parameters on the beam properties are different; the oceanic turbulence strength will gradually become stronger with increasing \({\chi _T}\) and \(\zeta\) or decreasing \(\varepsilon\) at the same propagation distance.

Fig. 5
figure 5

Normalized intensity distribution in x-direction of a GHCGB propagating through oceanic turbulence for different beam parameters n, j.and l, at various propagation distances z

Full size image

For comparison, Fig. 5 gives the normalized average intensity of a GHCGB propagating in oceanic turbulence at various propagation distance for the different beam orders (cosh order n, hermite index j and hollowness parameter l). From Fig. 5, one can observe that a GHCGB with small cosh beam order n or Hermite beam index j, propagating through oceanic turbulence will lose its initial dark hollow center rapidly with increasing propagation distance (Fig. 5a and c), and that a beam with large order n or j has a larger central dark hollow (see Fig. 5b and d). The similar evolutions properties are shown for Hermite cosh-Gaussian (Fig. 5e) and GHCGB (Fig. 5f). One can see that the rise speed of the dark hollow center becomes slower for the case of GHCGB with increasing propagation distance (Fig. 5f), this means that a GHCGB can keep its first profile better than the one case of hermit cosh-Gaussian (Fig. 5e). It is clearly seen from Fig. 5e and f that a GHCGB is less perturbed by the oceanic turbulence at a short propagation distance compared to the case of hermit cosh-Gaussian.

Fig. 6
figure 6

illustrates the normalized average intensity of GHCGB propagating in oceanic turbulence for different values of waist radius ω0 and propagation distances z

Full size image

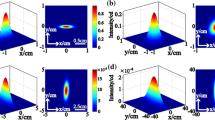
Figure 6  Normalized intensity distribution in x-direction of a GHCGB propagating through oceanic turbulence for different values of waist radius ω0 at various propagation distances z.

One can see that a beam with small waist radius will lose its dark hollow center and will evolve into the Gaussian shape more rapidly with increasing propagation distances. But, a beam with large waist width has a larger dark hollow center, thus increasing the beam waist width is resistant to the influences of oceanic turbulence.

Figure 7 displays the normalized average intensity of a GHCGB for some values of Hermite indexes j and h at different propagation distances z. The symmetry remains unaffected by changing j and h, but altering either j or h causes variations in how the lobes are oriented. For instance, in Fig. 7 (j), there are two double-lobe contours on the left and right sides, indicating that the beam spreads faster along the x-axis than along the y-axis. In contrast, in Fig. 7 (k), the central lobe behaves oppositely to Fig. 7 (j), with double-lobe contours above and below.

Fig. 7
figure 7

Normalized intensity distribution in x-direction of a GHCGB propagating through oceanic turbulence at various propagation distances z, for different hermite indexes j and h

Full size image

(a ,e, i, m) j = 0, h = 0, (b, f, j, n) j = 1, h = 0, (c, g, k, p) j = 0, h = 1, (d, h, i, q) j = 1, h = 1.

Additionally, one can notice that the central lobe patterns become more intense as j and h increase. Moreover, as the propagation distance z increases, the number of lobes decreases and finally the multiple lobes gradually merge into a single lobe in the far field. Furthermore, the diffusion velocity in the x and y directions differs when j and h are unequal. However, when j and h are equal, a GHCGB in oceanic turbulence with larger j and h can maintain its initial shape better than one with smaller j and h.

4 Conclusion

In this work, the evolution of average intensity of a GHCGB in underwater oceanic turbulence is derived by using extended Huygens–Fresnel diffraction integral and discussed with the help of numerical calculations. Then, we have studied the changes in the normalized intensity of a GHCGB in oceanic turbulence by varying the oceanic turbulence parameters and the source field parameters. Our results reveal that the beam can keep its initial intensity profile at short field propagation and will evolve its shape gradually into a Gauss-like beam as the propagation distance increases. It is also found that, the evolution properties of a GHCGB with larger \({\chi _T}\) or \(\zeta\)and smaller \(\varepsilon\) will lose its initial central dark hollow and will evolve into the Gaussian beam rapidly in the far field. While, the oceanic turbulence parameters have different effects on the spreading properties of the beam in oceanic turbulence, one can find that the parameters \(\varepsilon\) will cause the smaller spreading than the parameter \({\chi _T}\) or \(\zeta\) at the same propagation distance. The results obtained in this paper would be helpful to the investigations of oceanic turbulence and their applications in optical underwater communication and imaging systems.