Abstract
In this article, we mainly consider a first-order decoupling penalty method for the 2D/3D time-dependent incompressible magnetohydrodynamic (MHD) equations in a convex domain. This method applies a penalty term to the constraint “divu = 0,” which allows us to transform the saddle point problem into two small problems to solve. The time discretization is based on the backward Euler scheme. Moreover, we derive the optimal error estimate for the penalty method under semi-discretization with the relationship 𝜖 = O(Δt). Finally, we give abundant of numerical tests to verify the theoretical result and the spatial discretization is based on Lagrange finite element.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction
In this article, we consider the following 2D/3D time-dependent incompressible MHD equations:
with the homogeneous boundary conditions and initial conditions
where Ω is a bounded, convex, and open domain in \(\mathbb {R}^{d}(d=2 \text {or} 3)\) with a sufficiently smooth boundary ∂Ω. Here, u is the fluid velocity, B is the magnetic field, p is the hydrodynamic pressure, f denotes the external force term, g is the known applied current with divg = 0, n denotes the outward normal unit vector on ∂Ω, Re is the hydrodynamic Reynolds number, Rm is the magnetic Reynolds number, Sc is the coupling coefficient, and T is the final time.
The incompressible MHD equations mainly describe the dynamic behavior of an electrically conducting fluid under the effect of an imposed magnetic field. It consists of the Navier-Stokes equations for hydrodynamics and Maxwell’s equations for electromagnetism. Its applications involve many branches of physics, such as fusion reactor blankets, liquid metal magnetic pumps, and aluminum electrolysis (see [11, 19, 32]). The detailed information of physical background of the MHD flow, we refer to [12, 20]. In recent years, there have been many research works using finite element method to simulate the MHD equations such as [7, 23, 29,30,31,32,33].
We note that the pressure p does not appear in the incompressible equation, which makes the equations difficult to solve numerically. A popular way to overcome the above difficulty is to relax the incompressibility constraint in an appropriate way. This leads to a number of methods, such as the penalty method, the artificial compressibility method, the pressure stabilization method, and the projection method (see for instance [3,4,5, 25, 26]). As far as we know, the stabilization method was proposed in [3]. Next, a pressure stability analysis for the Stokes problem was given in [2]. For the projection method, it can be traced back to [4, 26]. Then, a consistent projection finite element method for the incompressible MHD equations was discussed in [30]. Convergence analysis of an unconditionally energy stable projection scheme for MHD equations was proposed in [29]. For the artificial compressibility method, it originated in [4, 5, 25, 26]. Next, the artificial compressibility approximation for MHD equations in unbounded domain was given in [8]. For the penalty method, we can refer to [6]. Then, optimal error estimate of the penalty finite element method for the time-dependent Navier-Stokes equations was given in [13]. A penalty finite element method based on the Euler implicit/explicit scheme for the time-dependent Navier-Stokes equations was proposed in [15]. In [22], the authors study iterative methods in penalty finite element discretization for the steady MHD equations. In [7], the authors given a decoupling penalty finite element method for the stationary incompressible MHD equations. It is worth mentioning that the penalty method is the simplest and the most basic of these mentioned above methods.
In this article, we mainly consider the penalty method to solve the time-dependent incompressible MHD equations. The penalty method applied to (1.1) and (1.2) is to approximate the solution (u, p, B) by (u𝜖, p𝜖, B𝜖) satisfying the following penalty system:
with the homogeneous boundary conditions and initial conditions
where \(B(\textbf {u},\textbf {v})=(\textbf {u}\cdot \nabla )\textbf {v} +\frac {1}{2}(\text {div}\textbf {u})\textbf {v}\) is the modified bilinear term, and 0 < 𝜖 < 1 is penalty parameter. The penalty method is a decoupled method, which can easily eliminate the p𝜖 in (1.3) by “divu𝜖 + Re𝜖p𝜖 = 0” to obtain a penalty system containing only (u𝜖, B𝜖), and then directly get the numerical solution of original equations. This idea has been widely used in many fields of computational fluid dynamics (please refer to [7, 13, 15, 18, 21, 22]).
From [7], we know that \(\underset {\epsilon \to 0}{\lim }(\textbf {u}_{\epsilon }, p_{\epsilon }, \textbf {B}_{\epsilon } )=(\textbf {u}, p, \textbf {B})\), the solution of (1.1)–(1.2). The error analysis of the penalty finite element method for the stationary MHD equations is studied in [22,23,24]. For example, the optimal error estimate of the penalty system for the stationary MHD equations is as follows:
where C > 0 is a general positive constant, and ∥⋅∥1 and ∥⋅∥ denote the norm in H1(Ω)d and L2(Ω), respectively. However, there is no literature on the penalty method for time-dependent MHD equations. The purpose of this article is to derive optimal error estimate of the penalty method for the time-dependent MHD equations and its time-discretization. In Theorem 4.1, we derive that the optimal error estimate of the penalty method for time-dependent MHD equations is as follows:
In Theorem 5.1 and (5.17), we derive that the optimal error estimate of the time-discretization scheme of the penalty method for the time-dependent MHD equations is as follows:
where Δt is the time step, tn = nΔt (1 ≤ n ≤ N), \((\textbf {u}_{\epsilon }^{n},p_{\epsilon }^{n},\textbf {B}_{\epsilon }^{n}) \) is an approximation of (u, p, B) at time tn.
The paper is organized as follows. In Section 2, we introduce some notations and preliminary results for the time-dependent penalty MHD equations (1.3) and (1.4). In Section 3, we analyze the error behavior of the linear form for the penalty MHD equations. In Section 4, we consider the penalty method for the MHD equations. In Section 5, we analyze the time-discretized scheme of the penalty MHD equations. In Section 6, we give some numerical tests to verify the theoretical result of the penalty method. Finally, some conclusions are given in Section 7.
2 Preliminaries
In this section, we give some notations. For \(1\leq r\leq \infty \), Lr(Ω) denotes the usual Lebesgue space on Ω with the norm \(\|\cdot \|_{L^{r}}\). In particular, we will denote L2(Ω) norm and L2(Ω) inner product by ∥⋅∥ and (⋅,⋅), respectively. For all non-negative integers k and r, Wk, r(Ω) stands for the standard Sobolev space equipped with the standard Sobolev norm ∥⋅∥k, r. The norm of the space Wk,2(Ω) is represented by ∥⋅∥k. The vector functions and vector spaces will be indicated by boldface type. Now, we introduce the following spaces
and the following trilinear form
Therefore, the trilinear form b(⋅,⋅,⋅) satisfies
Moreover, we have the following two formulas (cf. [22]):
and
which imply that for all B, C ∈W and u ∈X,
Then, we have the following variational formulation of problem (1.1) and (1.2): find (u, p, B) ∈ L2(0, T; X) × L2(0, T;M) × L2(0, T; W) such that for all (v, q, C) ∈X ×M ×W
where divu0 = divB0 = 0 and the variational formulation of (1.3) and (1.4) reads: find (u𝜖, p𝜖, B𝜖) ∈ L2(0, T; X) × L2(0, T;M) × L2(0, T; W) such that for all (v, q, C) ∈X ×M ×W
Moreover, from the variational formulation (2.3), we can get divBt = 0 and divB = 0 (cf. [14, 34]).
We will use the letter C as a general positive constant depending on coefficients of the equations and the domain Ω, which may have different values at its different occurrences. The following two inequalities will be used repeatedly (cf. [21]):
and
Furthermore, we have the following estimates (cf. [9, 28]):
where γ0 (only dependent on Ω) is a positive constant, C0 (only dependent on Ω) is an embedding constant of \(\textbf {H}_{n}^{1}({\Omega })\hookrightarrow \textbf {H}^{1}({\Omega })\) (↪ denotes the continuous embedding), and C1 (only dependent on Ω) is an embedding constant of H1(Ω)↪L4(Ω).
We define A1u = −Δu and \(A_{1\epsilon }\textbf {u}=-{\Delta }\textbf {u}-\frac {1}{\epsilon }\nabla \text {div}\textbf {u}\), which are the operators associated with Navier-Stokes equations and the penalty Navier-Stokes equations. They are the positive self-adjoint operators from \(D(A_{1})=\textbf {H}^{2}({\Omega })\cap \textbf {X} \) onto L2(Ω) and the powers \(A_{1}^{\alpha }\) and \(A_{1\epsilon }^{\alpha }\) \((\alpha \in \mathbb {R})\) are well defined. Similarly, we define the Maxwell’s operator \(A_{2}=P_{H}(\text {curl}\text {curl}-\nabla \text {div}): D(A_{2})\to \tilde {\textbf {H}}\) and also define A2𝜖B = A2B, where \(D(A_{2})=\textbf {H}^{2}({\Omega })\cap \textbf {W} \) and PH is the L2-orthogonal projection. Finally, it is easy to show that (cf. [21, 27])
Furthermore, we have the following lemmas given in [21].
Lemma 2.1
There exists a constant C2 > 0 depending only on Ω and such that for 𝜖 sufficiently small, we have
where H− 2(Ω) is the dual space of H2(Ω) ∩X, ∥⋅∥− 2 is the corresponding norm.
Lemma 2.2
(Gronwall lemma). Let y(t), h(t), g(t), f(t) be nonnegative functions satisfying
Then
Lemma 2.3 (discrete Gronwall lemma)
Let yn, hn, gn, fn be nonnegative series satisfying
Assume Δtgn < 1 for every n. Define \(\sigma =\underset {0 \leq n \leq N}{\max \limits }(1-g^{n}{\Delta } t)^{-1}\), then
In this paper, we assume that the problem (1.1) satisfies the following conditions.
Assumption A1: The initial data \(\textbf {u}_{0}\in \textbf {X}_{0}\cap \textbf {H}^{2}({\Omega })\) and \(\textbf {B}_{0}\in \textbf {W}_{0}\cap \textbf {H}^{2}({\Omega }),\) the external force f, and the applied current g satisfy the bound
Suppose that A1 ensures the existence of a unique strong solution to the problem (2.3) on small time interval [0, T] such that (cf. [20])
by using the smoothing property of the Navier-Stokes equations at t = 0, then (see for instance [16])
Assumption A2: Assume that the boundary of Ω is smooth so that the unique solution (v, q) ∈X ×M of the steady Stokes problem (cf. [14, 34])
for prescribed f ∈L2(Ω) satisfies
and Maxwell’s equations
for the prescribed g ∈L2(Ω) admit a unique solution C ∈W0 which satisfies
where c is a positive constant depending only on Ω, and may take different values at its different places.
Using the operators A1𝜖, A2𝜖, we can rewrite the penalized system (2.4) as
Then, we have
Taking the L2 inner product of the first equation of (2.16) with u𝜖, the second equation with ScB𝜖, and thanks to (2.1), (2.7), we obtain
Due to Lemma 2.1, we have
Combining the above inequality and integrating from 0 to t ≤ T, we get
Taking the L2 inner product of the first equation of (2.16) with A1𝜖u𝜖, the second equation with A2𝜖B𝜖, we obtain
By using Lemma 2.1, (2.5) and (2.9)–(2.13), we get
Combining the above inequalities, we arrive at
Integrating the above inequality over [0, t], using (2.18), (2.10), Lemma 2.1 and the Gronwall lemma, we complete the proof of (2.17).
3 Linearized problem
It is difficult to deal with the nonlinear terms of the MHD equations. Therefore, we derive the penalty errors of its linear form as an intermediate step in the analysis of the nonlinear MHD equations in the next section. Next, we will consider the linear form of MHD equations:
The penalty method applied to (3.1) is
Letting e = u −u𝜖, η = B −B𝜖, ξ = p − p𝜖, and subtracting (3.2) form (3.1), we obtain
We can derive from (3.5) and (3.6) that
Lemma 3.1
Under Assumptions A1 − A2, we have
Proof
Taking the L2 inner product of (3.3) with e, (3.4) with ξ, (3.7) with η, and summing up the three relations, we obtain
Integrating the above inequality from 0 to t ≤ T, thanks to e(0) = 0, η(0) = 0 and (2.14), we have
We now use the standard duality argument. Taking d = 0 and adding Lagrange multiplier ∇d to (3.1) for the third equation, we can get
Then, we have the following variational formulation of the problem (3.10): find (u, p, B, d) ∈ L2(0, T; X) × L2(0, T; M) × L2(0, T; W) × L2(0, T; M) such that
Exchanging \((\textbf {u},p,\textbf {B},d)\leftrightarrow (\textbf {v},q,\textbf {C},s)\), we get
Then, we have
Letting \((\textbf {u},p,\textbf {B},d)\leftrightarrow (\boldsymbol {\omega },\gamma ,\boldsymbol {\phi },k)\), we obtain
Integrating the first equation in (3.11) form 0 to T, we have
By integrating by parts, we get
Taking ω(T) = v(0) = 0, we obtain
Similarly, we can get
Taking \(\tilde {\textbf {f}}=-\textbf {e},\tilde {\textbf {g}}=-\boldsymbol {\eta }\), thanks to ∇k = 0, we get the following dual problem. For any 0 < t ≤ T, we define (ω, γ, ϕ) by
We can derive from (3.14) and (3.15) that
Let us first establish the following inequality:
Taking the L2 inner products of (3.12) with A1ω, (3.16) with A2ϕ, and summing up the two relations, we get
Integrating the above relation from 0 to t, we have
Applying the projection operator PH on (3.12) and (3.16), we derive
From (3.12) and (3.16), we obtain
The proof of (3.17) is thus complete.
Next, taking the L2 inner product of (3.12) with e and (3.14) with η, thanks to (3.3)–(3.5) and divω = 0, we have
Integrating the above relation from 0 to t, thanks to ω(t) = e(0) = 0 and ϕ(t) = η(0) = 0, we obtain
where Cδ is a constant depending on δ only. Due to (3.17) and (3.8), we can choose δ sufficiently small such that
The proof is thus complete. □
Lemma 3.2
Under Assumptions A1 − A2, we have
We can refer to [21] to prove this result.
Lemma 3.3
Under Assumptions A1 − A2, we have
Proof
Let us consider the decomposition (see, for instance, [10])
and v = (−Δ)− 1∇q if −Δv = ∇q and v|∂Ω = 0. It is well known that for p(t) ∈M, there exists a unique \(\boldsymbol {\varphi }(t)\in \textbf {X}_{0}^{\perp }\) such that divφ(t) = p(t) with
Moreover, if pt(t) ∈M, we have divφt(t) = pt(t) with
Taking the L2 inner products of (3.3) with te, (3.4) with tξ, (3.7) with tη, summing up the three relations, and using (3.3), we derive
Using (3.18), we get
Hence, integrating (3.20) from 0 to t, using the above relation, the Cauchy-Schwarz inequality, Lemma 3.1, (3.18), and (3.19), we derive
Next, we take the partial derivative with respect to t on (3.4), we obtain
Taking the L2<< inner product of (3.3) with \(t^{2}\textbf {e}_{t}\), (3.21) with t2ξ, (3.7) with \(t^{2}\boldsymbol {\eta }_{t}\), and summing up the three relations, we obtain
Due to (3.3) and (3.18), we get
Integrating (3.22) and using the Gronwall lemma, we obtain
Finally, we derive from (3.3) that
Therefore, we have
The proof is thus complete. □
To summarize, we prove the following theorem.
Theorem 3.1
Under Assumptions A1 − A2, we have
4 Nonlinear MHD equations
In this section, we transform the nonlinear MHD equations into an intermediate linear equations, and then use the previous result to give an error estimate of the penalty system. Next, let us consider the following intermediate linear equations:
where u and B are the solutions of MHD equations (1.1).
Letting ηu = v −u, ηB = Ψ −B, ηp = q − p, and subtracting (1.1) from (4.1), we obtain
Lemma 4.1
Under Assumptions A1 − A2, we have
Proof
Thanks to Assumption A1 and (2.14), we have f −B(u, u) + SccurlB ×B, g + curl(u ×B) ∈ L2(0, T; L2(Ω)). One the other hand, it can be easily shown that \(t\textbf {u}_{t}\in L^{2}(0,T;\textbf {X}),t\textbf {B}_{t}\in L^{2}(0,T;\textbf {W})\) (cf. [20]). And, since
we have
Then, by applying Lemma 3.1 and Theorem 3.1 to (4.2), we can get Lemma 4.1. □
Next, letting φu = u𝜖 −v, φB = B𝜖 −Ψ, φp = p𝜖 − q, and subtracting (4.1) from (4.2), we get
Since
Theorem 4.1
Under Assumptions A1 − A2, we have the following estimate:
Proof
Taking the L2 inner product of (4.9) with \(A_{1\epsilon }^{-1}\boldsymbol {\varphi }_{\boldsymbol {u}}\) and of (4.9) with \(A_{2\epsilon }^{-1}\boldsymbol {\varphi }_{\boldsymbol {B}}\), summing up the two relations, we get
By using (2.6)–(2.13) and Lemma 2.1, we derive that
Combining the above inequalities, we arrive at
Due to \({{\int \limits }_{0}^{T}}\left (\|\textbf {u}\|_{2}^{2}+\|\textbf {u}_{\epsilon }\|_{2}^{2}+\|\textbf {B}\|_{2}^{2} +\|\textbf {B}_{\epsilon }\|_{2}^{2}\right )dt\leq C\), we can apply the Gronwall lemma, Lemma 4.1, and get
Next, taking L2 the inner products of (4.3) with tφu, (4.4) with tφp, (4.9) with tφB, we derive
Combining the above inequalities, we arrive at
Integrating the above inequality over [0, t], using (4.10), Lemma 4.1, and the Gronwall lemma, we obtain
Then, we take the partial derivative with respect to t of (4.4) to get
Taking the L2 inner products of (4.3) with \(t^{2}\boldsymbol {\varphi }_{ut}\), (4.13) with t2φp, (4.9) with \(t^{2}\boldsymbol {\varphi }_{Bt}\) and adding them up, we get
Using (2.6)–(2.12) and Lemma 4.1, we derive
Combining the above inequalities, we obtain
Integrating over [0, t], using (4.12) and the Gronwall lemma, we get
We have
Due to (4.3) and (4.7), we deduce
By using previous estimates on the above equation, we have
which completes the proof of Theorem 4.1. □
5 Time discretizations of the penalized system
In this part, we give the time-discretization of the penalty system and derive its error estimate. Next, we will give some rules for the solutions of the penalty system.
Lemma 5.1
Suppose \(\text {\textbf {u}}_{0}, \text {\textbf {B}}_{0}\in \text {\textbf {H}}^{2}({\Omega })\) and A1 − A2 are valid. Then the solutions u𝜖, B𝜖 of (2.18) satisfy
Since the proof of (5.1) is standard (cf. [20]), we just need to prove (5.2). Taking the partial derivative with respect to t on (1.3), we have
Taking the L2 inner product of (5.3) with u𝜖t, (5.4) with ScB𝜖t, thanks to (2.1) and (2.7), we obtain
Using Lemma 2.1 and Young’s inequality, we get
Due to (2.6) and Young’s inequality, we have
By using (2.8), (2.12), and Young’s inequality, we have
Combining the above inequalities, we obtain
Since \(\textbf {u}_{\epsilon },\textbf {B}_{\epsilon }\in C(0,T;\textbf {H}^{2}({\Omega }))\), we can show that u𝜖t(0), B𝜖t(0) is well defined (cf. [20]). Hence, integrating over [0, t], using the Gronwall lemma and Lemma 2.1, we derive
By Lemma 2.1, we get \(\|\textbf {u}_{\epsilon t}\|_{L^{2}(0,T;\textbf {H}^{1}({\Omega }))}+ \|\textbf {B}_{\epsilon t}\|_{L^{2}(0,T;\textbf {H}^{1}({\Omega }))}\leq C\). Then by using (2.6), we get
By the same proof, we have
Thus, we get
Then
Taking the L2 inner product of (5.3) with tu𝜖tt, (5.4) with tB𝜖tt, we obtain
Using Schwarz’s inequality, we get
From (2.6), we obtain
By using (2.12) and Young’s inequality, we obtain
Using (2.8)–(2.13), we can derive
Combining the above inequalities, integrating over [0, T], and using Assumption A1 and (5.6), we derive
Let us consider the time discretization of the penalized system (2.16) by the backward Euler scheme
where 0 < Δt < 1 is the time-step size, tn = nΔt, tN = T, \((\textbf {u}_{\epsilon }^{0},\textbf {B}_{\epsilon }^{0})=(\textbf {u}_{0},\textbf {B}_{0})\), and \(d_{t}\textbf {u}_{\epsilon }^{n}=\frac {1}{{\Delta } t}(\textbf {u}_{\epsilon }^{n}-\textbf {u}_{\epsilon }^{n-1})\) for 1 ≤ n ≤ N.
Lemma 5.2
Under the assumption of Lemma 5.1, we have
Proof
Letting \(\boldsymbol {e}_{\boldsymbol {u}}^{n}=\textbf {u}_{\epsilon }(t_{n})-\textbf {u}_{\epsilon }^{n},\boldsymbol {e}_{\boldsymbol {B}}^{n}=\textbf {B}_{\epsilon }(t_{n})-\textbf {B}_{\epsilon }^{n}\) and subtracting (5.6) from (2.18) at t = tn, we get
where
Taking the L2 inner product of (5.7) with \(2{\Delta } t\boldsymbol {e}_{\boldsymbol {u}}^{n}\), (5.8) with \(2S_{c}{\Delta } t\boldsymbol {e}_{\boldsymbol {B}}^{n}\), thanks to (2.1) and (2.7), we obtain
Using the Schwarz inequality, (5.9), and (5.10), we get
We can derive from (2.6) and (5.1) that
Due to (2.8)–(2.11) and (5.1), we have
Combining the above inequalities, we obtain
Summing (5.11) from 1 to m, and using the discrete Gronwall lemma, Lemma 5.1, we derive
Thus,
Taking the L2 inner product of (5.7) with \(2t_{n}{\Delta } t A_{1\epsilon }\boldsymbol {e}_{\boldsymbol {u}}^{n}\), (5.8) with \(2t_{n}{\Delta } tA_{2\epsilon }\boldsymbol {e}_{\boldsymbol {B}}^{n}\), we have
Using Young’s inequality, we can derive
Due to (2.5)–(2.11) and (5.13), we obtain
Combining the above inequalities, we obtain
Taking the summation of (5.14) for n form 1 to m, using the discrete Gronwall lemma and the relation
we get
The proof is thus complete. □
Thus, we have
Finally, combining Theorem 4.1 and Lemma 5.2, we prove the following theorem.
Theorem 5.1
Under the assumption of Lemma 5.1, we have
Taking the L2 inner product of (5.7) with \( 2{t_{n}^{2}}d_{t}\boldsymbol {e}_{\boldsymbol {u}}^{n}{\Delta } t\), (5.8) with \(2{t_{n}^{2}}d_{t}\boldsymbol {e}_{\boldsymbol {B}}^{n}{\Delta } t\), we obtain
Using Young’s inequality, we have
Combining the above inequalities, we obtain
Summing (5.16) from 1 to m and using the discrete Gronwall lemma, we have
From Eq. (5.6) and the available estimates for \(\boldsymbol {e}_{\boldsymbol {u}}^{n},\boldsymbol {e}_{\boldsymbol {B}}^{n}\), we can prove
which is similar to the estimate in the continuous case (see Theorem 4.1).
6 Numerical results
In this section, we present several numerical experiments to illustrate the accuracy and performance of our proposed method. All finite element calculations are carried out by \(({P_{1}^{b}},P_{1},{P_{1}^{b}})\) finite element pair. The penalty parameter 𝜖 is selected as 𝜖 = O(h).
6.1 Accuracy test
This section will test the convergence rates of our proposed penalty finite element method. We set domain Ω = [0,1]2, physical parameters Re = Rm = Sc = 1, and final time T = 1. We prescribe the exact solution (u, p, B) as follows:
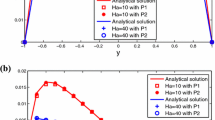
The time step is chosen by Δt = O(h2). The error of velocity, pressure, and magnetic field are presented in Table 1. We observe that the first-order accuracy for \(\|\textbf {u}-\textbf {u}_{\epsilon h}^{n}\|_{1}\), \(\|\textbf {B}-\textbf {B}_{\epsilon h}^{n}\|_{1}\) and the second-order accuracy asymptotically for \(\|\textbf {u}-\textbf {u}_{\epsilon h}^{n}\|\), \(\|\textbf {B}-\textbf {B}_{\epsilon h}^{n}\|\), which agree with the theoretical results. Notice that \(\|p-p_{\epsilon h}^{n}\|\) has faster convergence rate than the theoretical result.
6.2 Island coalescence
Let us consider an example of driving magnetic reconnection, the island coalescence problem. Understanding fast magnetic reconnection is one of the important issues in plasma physics. We set two magnetic islands as the initial conditions of the perturbed Harris sheet magnetic field configuration in the island coalescence problem. The combination of the two magnetic islands produces Lorentz forces, pulling the two islands together. The detailed information of physical background of this issue, we can refer to [31].
In this example, we set Ω = [− 1,1] × [− 0.5,0.5], Re = Rm = 1000, Sc = 1. The source terms are taken as
The initial conditions are set as
Here \(\delta _{1}=-\frac {\gamma }{\pi }\cos \limits (\pi x)\sin \limits (\frac {1}{2}\pi y)\), \(\delta _{2}=\frac {\gamma }{2\pi }\cos \limits (\frac {1}{2}\pi y)\sin \limits (\pi x)\) are perturbations, ζ = 1.0, τ = 0.2, \(\delta =\frac {1}{2\pi }\), and γ = − 0.01. The velocity field u and magnetic field B are periodic boundary conditions on the left and right boundaries, and zeros tangential stress (u2 = 0) and perfect conducting wall (B2 = 0) on the top and bottom boundaries.
We choose \(h=\frac {1}{100}\) and \({\Delta } t=\frac {1}{5000}\). Figure 1 gives the vector field of the magnetic field B and the magnitude of the current density J (J = curlB). We observe the dynamic reconnection behaviors of current density and magnetic island during the coalescence process, and a sharp peak in current density is appeared at the reconnection point. Figure 2 shows the magnitude of pressure at different moments, and we find pressure and magnetic field have the same the coalescence process.
Snapshots of the magnetic field B (in arrows) and the magnitude of the current density J (in colormap) at t = 0.2,0.62,0.7,0.78s
Snapshots of the pressure p at t = 0.2,0.62,0.7,0.78s
6.3 Hydromagnetic Kelvin-Helmholtz instability
The Kelvin-Helmholtz (K-H) instability in sheared flow configuration is an effective mechanism to initiate fluid mixing, momentum and energy transfer, and turbulence development, we can refer to [1]. This question is of great significance when studying various spaces, astrophysical, and geophysical environments involving shear plasma flows. Including the interface between the solar wind and the magnetosphere, coronal streamers moving through the solar wind and so on. Since most astrophysical environments are conductive, related fluids may be magnetized. Therefore, it is important to understand the role of magnetic field in K-H instability. The detailed information of physical background of this issue, we can refer to [32].
In this example, the domain of our calculation is Ω = [0,2] × [0,1]. The initial velocity is u0 = (1.5,0) in the top half domain and u0 = (− 1.5,0) in the bottom half domain. The initial magnetic field is \(\textbf {B}_0=(\tanh (y/\tau ),0)\), where τ = 0.07957747154595 (see [32]). The boundary conditions of velocity u are zero tangential stress (u2 = 0) on the top and bottom boundaries, and periodic boundary conditions on the left and right boundaries. The magnetic field B are B ×n = B0 ×n on the top boundary, B ×n = −B0 ×n on the bottom boundary, and periodic boundary conditions on the left and right boundaries. We set Re = Rm = 1000, Sc = 0.095, \(h=\frac {1}{60}\), \({\Delta } t=\frac {1}{600}\).
Figure 3 shows the contour of the first component B1 of the magnetic field B = (B1, B2) and the velocity u at different moments. We observe the profiles of vortexes and the magnetic field show the typical structure of K-H instability, and it deforms and rotates along with the flow. The magnitude of the pressure p at the time corresponding to B1 is presented in Fig. 4. We find the obtained numerical results are consistent with the experimental results discussed in [33].
The velocity u with the filled contour of B1 that shows the hydromagnetic K-H instability. Snapshots are taken at t = 0.01,2.6,2.8,3s
Snapshots of the pressure p taken at t = 0.01,2.6,2.8,3s
6.4 Flow around a cylinder
This example is about the calculation of the flow around a cylinder, which is a well-known problem in [17]. We set the computational domain as Ω = [0,2.2] × [0,0.41]. A disk of radius 0.05 is placed at (0.2,0.2). We take the initial values u0 = B0 = 0 and the source terms f = g = 0. The velocity u are \(\textbf {u}=\left (\frac {6}{0.41^2}\sin \limits (\frac {\pi t}{8})y(0.41-y),0\right )\) on the left and right boundaries, and no-slip boundary conditions at the other boundaries.
In Fig. 5, we plot the velocity for the MHD equations without magnetic field with Re = 1000. We find that with the increase of time, the two vortices behind the cylinder gradually separated into vortex streets. The numerical results coincide well with the phenomenon in [17]. In order to show the influence of the magnetic field on the fluid, the boundary condition of magnetic field is B ×n = (1,0) ×n. We set Re = 1000, Rm = 1 and change the coupling coefficient Sc to simulate this problem. Figures 6, 7, and 8 describe the plot the velocity at Sc = 0.5,1,100. We find that with the increase of Sc, the magnetic field inhibits the formation of vortex streets.
The velocity u at t = 2,6,7,8s for the MHD equations without magnetic field with Re = 1000
The velocity u at t = 2,6,7,8s with Re = 1000, Rm = 1, Sc = 0.5
The velocity u at t = 2,6,7,8s with Re = 1000, Rm = 1, Sc = 1
The velocity u at t = 2,6,7,8s with Re = 1000, Rm = 1, Sc = 100
6.5 2D-driven cavity flow
In this example, we simulate the 2D-driven cavity flow, we can refer to [31]. Our calculation domain is Ω = [0,1]2. We take the initial values u0 = B0 = 0 and the source terms f = g = 0.
The boundary condition of velocity is u = (1,0) on the top side, and no-flow boundary conditions on the bottom, left, and right sides. The boundary condition of magnetic field is B ×n = (− 1,0) ×n.
We set \(h=\frac {1}{40}\), \({\Delta } t=\frac {1}{400}\), fix Rm = Sc = 1 and change the fluid Reynolds numbers Re or fix Re = Rm = 1 and change the coupling coefficient Sc to simulate this problem. The velocity field u under different fluid Reynolds numbers is presented in Fig. 9. The velocity field u under different coupling coefficient is presented in Fig. 10. We can see the main vortex split into two small vortexes as the fluid Reynolds number increases. The numerical results are similar to the experimental results discussed in [31, 35], which shows that our algorithm is effective.
The streamlines of velocity at Re = 1, 100, 1000
The streamlines of velocity at Sc = 1, 100, 1000
6.6 3D-driven cavity flow
In this example, we test the 3D-driven cavity flow problem, we can refer to [31]. We set a cubic domain Ω = [0,1]3. We take the initial values u0 = B0 = 0 and the source terms f = g = 0. The boundary condition of velocity field is u = (1,0,0) on the top wall, and no-slip boundary conditions on the bottom, front, back, left, and right walls of the domain. The boundary condition of magnetic field is B ×n = (− 1,0,0) ×n on the walls.
We set \(h=\frac {1}{15}\), \({\Delta } t=\frac {1}{150}\), fixed Rm = 1, Sc = 0.1, and change the fluid Reynolds numbers Re to simulate this problem. Figure 11 shows the velocity field u at plane y = 0.5 for fluid Reynolds number Re = 1,100,1000. We find the bigger Re, the vortex becomes larger in the cavity.
The streamlines of velocity at plane y = 0.5 of Re = 1, 100, 1000
7 Conclusions
In this paper, we present the penalty method for the 2D/3D time-dependent MHD equations. The main idea of this method is to decouple the MHD equations into two equations, one is the equation of velocity and magnetic field (u, B), and the other is the equation pressure p. What’s more, we derive the optimal error estimate of the time-discretization of the penalty equations. Several 2D and 3D numerical experiments verify the theoretical result. The fully discrete scheme of the time-dependent MHD equations will be given in our on going work.
Data availability
All data generated or analyzed during this study are included in this published article.
References
Baty, H., Keppens, R., Comte, P.: The two-dimensional magnetohydrodynamic Kelvin-Helmholtz instability: compressibility and large-scale coalescence effects. Phys. Plasmas 10(12), 4661–4674 (2003)
Becker, R., Hansbo, P.: A simple pressure stabilization method for the Stokes equation. Commun. Numer. Methods Eng. 24(11), 1421–1430 (2008)
Brezzi, F., Pitkäranta, J.: On the stabilization of finite element approximations of the Stokes equations. Springer, Wiesbaden (1984)
Chorin, A.: Numerical solution of the Navier-Stokes equations. Math. Comput. 22(104), 745–762 (1968)
Chorin, A.: On the convergence of discrete approximations to the Navier-Stokes equations. Math. Comput. 23(106), 341–353 (1969)
Courant, R.: Variational methods for the solution of problems of equilibrium and vibrations. Bull. Am. Math. Soc. 49, 1–23 (1943)
Deng, J., Si, Z.: A decoupling penalty finite element method for the stationary incompressible magnetohydrodynamics equation. Int. J. Heat Mass Transf. 128, 601–612 (2019)
Donatelli, D.: The artificial compressibility approximation for MHD equations in unbounded domain. J. Hyperbolic Differ. Equ. 10(1), 181–198 (2013)
Dong, X., He, Y., Zhang, Y.: Convergence analysis of three finite element iterative methods for the 2D/3D stationary incompressible magnetohydrodynamics. Comput. Methods Appl. Mech. Eng. 276, 287–311 (2014)
Girault, V., Raviart, P.: Finite element methods for Navier-Stokes equations: theory and algorithms. Springer, Berlin (1987)
Goedbloed, J., Keppens, R., Poedts, S.: Advanced magnetohydrodynamics: with applications to laboratory and astrophysical plasmas. Cambridge University Press, Cambridge (2010)
Gunzburger, M., Meir, A., Peterson, J.: On the existence, uniqueness, and finite element approximation of solutions of the equations of stationary, incompressible magnetohydrodynamics. Math. Comput. 56(194), 523–563 (1991)
He, Y.: Optimal error estimate of the penalty finite element method for the time-dependent Navier-Stokes equations. Math. Comput. 74(251), 1201–1216 (2005)
He, Y.: Unconditional convergence of the Euler semi-implicit scheme for the three-dimensional incompressible MHD equations. IMA J. Numer. Anal. 35(2), 767–801 (2015)
He, Y., Li, J.: A penalty finite element method based on the Euler implicit/explicit scheme for the time-dependent Navier-Stokes equations. J. Comput. Appl. Math. 235(3), 708–725 (2010)
Heywood, J., Rannacher, R.: Finite element approximation of the nonstationary Navier-Stokes problem. I. Regularity of solutions and second order error estimates for spatial discretization. SIAM J. Numer. Anal. 19(2), 275–311 (1982)
John, V.: Reference values for drag and lift of a two-dimensional time-dependent flow around a cylinder. Int. J. Numer. Methods Fluids 44(7), 777–788 (2004)
Lu, X., Lin, P.: Error estimate of the P1 nonconforming finite element method for the penalized unsteady Navier-Stokes equations. Numer. Math. 115(2), 261–287 (2010)
Priest, E., Hood, A.: Advances in solar system magnetohydrodynamics. Cambridge University Press, Cambridge (1991)
Sermange, M., Temam, R.: Some mathematical questions related to the MHD equations. Commun. Pure Appl. Math. 36(4), 635–664 (1983)
Shen, J.: On error estimates of the penalty method for unsteady Navier-Stokes equations. SIAM J. Numer. Anal. 32(2), 386–403 (1995)
Su, H., Feng, X., Huang, P.: Iterative methods in penalty finite element discretization for the steady MHD equations. Comput. Methods Appl. Mech. Eng. 304, 521–545 (2016)
Su, H., Feng, X., Zhao, J.: On two-level Oseen penalty iteration methods for the 2D/3D stationary incompressible magnetohydronamics. J. Sci. Comput. 83(1), 1–30 (2020)
Su, H., Mao, S., Feng, X.: Optimal error estimates of penalty based iterative methods for steady incompressible magnetohydrodynamics equations with different viscosities. J. Sci. Comput. 79(2), 1078–1110 (2019)
Témam, R.: Sur l’approximation de la solution des équations de Navier-Stokes par la méthode des pas fractionnaires (I). Arch. Ration. Mech. Anal. 32(2), 135–153 (1969)
Témam, R.: Sur l’approximation de la solution des équations de Navier-Stokes par la méthode des pas fractionnaires (II). Arch. Ration. Mech. Anal. 33(5), 377–385 (1969)
Yang, J., He, Y.: Stability and error analysis for the first-order Euler implicit/explicit scheme for the 3D MHD equations. Int. J. Comput. Methods 14(2), 1750077 (2017)
Yang, J., He, Y., Zhang, G.: On an efficient second order backward difference Newton scheme for MHD system. J. Math. Anal. Appl. 458(1), 676–714 (2018)
Yang, X., Zhang, G., He, X.: Convergence analysis of an unconditionally energy stable projection scheme for magneto-hydrodynamic equations. Appl. Numer. Math. 136(1), 235–256 (2019)
Yang, Y., Si, Z.: A consistent projection finite element method for the incompressible MHD equations. Appl. Anal. 100(12), 2606–2626 (2021)
Zhang, G., Chen, C.: Uniformly robust preconditioners for incompressible MHD system. J. Comput. Appl. Math. 379, 112914 (2020)
Zhang, G., He, X., Yang, X.: A decoupled, linear and unconditionally energy stable scheme with finite element discretizations for magneto-hydrodynamic equations. J. Sci. Comput. 81(3), 1678–1711 (2019)
Zhang, G., He, X., Yang, X.: Fully decoupled, linear and unconditionally energy stable time discretization scheme for solving the magneto-hydrodynamic equations. J. Comput. Appl. Math. 369, 112636 (2020)
Zhang, G., He, Y.: Decoupled schemes for unsteady MHD equations. I. Time discretization. Numer. Methods for Partial Differ. Equ. 33(3), 956–973 (2017)
Zhang, Q., Su, H., Feng, X.: A partitioned finite element scheme based on gauge-Uzawa method for time-dependent MHD equations. Numer. Algoritm. 78(1), 277–295 (2017)
Acknowledgements
The authors are very much indebted to the referees for their constructive suggestions and insightful comments, which greatly improved the original manuscript of this paper.
Funding
This work is partly supported by the NSF of China (No. 12126361, 12126372, 12061076), Tianshan Youth Project of Xinjiang Province (No. 2017Q079), Scientific Research Plan of Universities in the Autonomous Region (No. XJEDU2020I 001), and Key Laboratory Open Project of Xinjiang Province (No. 2020D04002).
Author information
Authors and Affiliations
Corresponding author
Ethics declarations
Conflict of interest
The authors declare no competing interests.
Additional information
Publisher’s note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Rights and permissions
Springer Nature or its licensor (e.g. a society or other partner) holds exclusive rights to this article under a publishing agreement with the author(s) or other rightsholder(s); author self-archiving of the accepted manuscript version of this article is solely governed by the terms of such publishing agreement and applicable law.
About this article
Cite this article
Shi, K., Feng, X. & Su, H. Optimal error estimate of the penalty method for the 2D/3D time-dependent MHD equations. Numer Algor 93, 1337–1371 (2023). https://doi.org/10.1007/s11075-022-01470-0
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s11075-022-01470-0