Abstract
In the paper we consider the one-level and two-level iterative penalty finite element methods for the steady incompressible magnetohydrodynamic problem based on the iteration of pressure with a factor of penalty parameter. Firstly, the \(\mathbf {H}^1\) and \(\mathbf {L}^2\) error estimates of numerical solutions of one-level iterative penalty finite element method are provided. Secondly, the stability and convergence of two-level iterative penalty finite element method are analyzed. Finally, some numerical results are provided to verify the effectiveness of the developed numerical schemes.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction
In this paper, let \(\Omega \subset R^d(d=2\ \text{ or }\ 3)\) be a convex polygonal/polyhedral domain (see Gunzburger et al. 1991, 2004). We consider the following steady incompressible MHD problem:
subject to the boundary conditions
where \(\mathbf {u}\) is the velocity field, \(\mathbf {B}\) denotes the magnetic field, \(\mathbf {f}\) and \(\mathbf {g}\) are the source terms. \(\mathbf {n}\) is outward normal unit vector of \(\partial \Omega \), p is the hydrodynamic pressure, \(R_e,R_m\) and \(S_c\) are the hydrodynamic Reynolds number, magnetic Reynolds number and coupling number, respectively.
The steady incompressible MHD problem can be used to describe the interaction between a viscous, incompressible, electrically conducting field and an external magnetic field. Namely, the steady incompressible MHD problem is a coupled system, which is composed of Navier–Stokes equations of fluid dynamics and Maxwell’s equations that couple Lorentz’s force with Ohm’s law. We refer to Hughes and Young (1966) and Moreau et al. (1990) for comprehensive accounts of the physical background of MHD problem. Several papers have been devoted to the design and the analysis of numerical schemes for the MHD problem. For example, we can refer to Gunzburger et al. (1991, 2004) for the existence and uniqueness of the solutions, Discacciati (2008) for numerical approximation of the steady MHD problem, Hasler et al. (2004) and Schözau (2004) for the mixed finite element method (FEM), and Dong et al. (2014) and Tao and Zhang (2015) for the iterative method and so on.
The first main difficulty of solving the MHD problem is the nonlinear terms \(\mathbf {u}\cdot \nabla \mathbf {u}, \text{ curl } \mathbf {B}\times \mathbf {B}\) and \(\text{ curl }(\mathbf {u}\times \mathbf {B})\). Two-level method is an efficient numerical scheme for the nonlinear terms, and this method was pioneered by Marion and Xu (1995) and Xu (1996). The main idea of two level method is to find an initial approximation on a coarse mesh firstly, and then to solve a linear problem by using the coarse mesh solution on a fine mesh. It is a good strategy to decrease the computational cost. Therefore, two-level method has been wildly studied in recent years. For example, we can refer to Girault and Lions (2001), He (2003, 2004) and Zhang and Yang (2014) for the research of the Navier–Stokes equations, the nonlinear parabolic problem (Zhang 2013) and the natural convection problem (Zhang et al. 2015a, b). The other main difficulty is that the velocity and the pressure are coupled. Penalty method is a method to overcome this difficulty. Certainly, many researchers have focused on studying penalty method for solving different problems. For example, we can refer to Dai (2007) for the pure Neumann problem, and An and Shi (2015), Gunzburger (1989), He (2005) and Shen (1995) for the incompressible flow. From above mentioned literature, we know that the combination of two-level method and penalty method is quite efficient for solving the nonlinear system. Especially, from the numerical results of An and Shi (2015) and Qiu et al. (2014), we can see that two-level iterative FEM can save much CPU time than one-level iterative FEM with the same convergence order.
In this paper we consider the one-level and two-level iterative penalty FEMs to solve problem (1.1). The penalty parameter \(\varepsilon \ (0<\varepsilon \ll 1)\) is set as a real number. For any positive integer k, which is the number of iteration, the error estimates of the one-level iterative penalty FEM solution \(((\mathbf {u}_{\varepsilon \mu }^k,\mathbf {B}_{\varepsilon \mu }^k),p_{\varepsilon \mu }^k)\) are
and the error estimate of two-level iterative penalty FEM solution \(((\mathbf {u}_\varepsilon ^h,\mathbf {B}_\varepsilon ^h),p_\varepsilon ^h)\) is
Thus, if we choose \(\varepsilon =\mathcal {O}(H)=\mathcal {O}(h^{1/2})\), the one-level and two-level iterative penalty FEMs have the same order as the standard Galerkin FEM (see Dong et al. 2014). While from the point of view of numerical tests, we know that the two-level iterative penalty FEM can save a large amount of computational time than one-level iterative penalty FEM with the same order.
The paper is organized as follows: some notations and basic results of problem (1.1) are recalled in Sect. 2; stability and convergence of iterative penalty FEM are presented in Sect. 3; the stability and convergence of two-level iterative penalty FEM are analyzed in Sect. 4; and some numerical experiments are provided to validate the established theoretical analysis in Sect. 5. Finally, some conclusions are given in the last section.
2 Preliminaries
To gain the variational formulation for the steady incompressible MHD flow, we choose the standard Sobolev space \(H^j(\Omega )=W^{j,2}(\Omega )\) for any nonnegative integer j with norm \(\Vert v\Vert _j=(\sum _{|\gamma |=0}^j \Vert D^\gamma v\Vert _0^2)^{\frac{1}{2}}\). We use the standard Sobolev space \(\mathbf {H}^j(\Omega )=(H^j(\Omega ))^d\) with the corresponding norm \(\Vert \mathbf {v}\Vert _j=(\sum _{i=1}^d \Vert v_i\Vert _j^2)^{\frac{1}{2}}\) (see Adams 1975; Girault and Raviart 1986 for more details). Furthermore, we introduce some spaces as follows.
With the equivalent norms \(\Vert \nabla \mathbf {w}\Vert _0\) and \(\Vert \mathbf {w}\Vert _{\mathbf {H}_0^1(\Omega )}\) of \(\mathbf {X}\), we denote the product space \(\mathbf {W}_{0\mathbf {n}}=\mathbf {X\times W}\) equipped with the usual graph norm \(\mathbf {\Vert (w,\Phi )\Vert }_1,\forall \mathbf {(w,\Phi )\in W}_{0\mathbf {n}}\), where \(\mathbf {\Vert (w,\Phi )\Vert }_i=(\Vert \mathbf {w}\Vert _i^2+\Vert \mathbf {\Phi }\Vert _i^2)^{1/2} (i=0,1,2)\). The dual space of \(\mathbf {H}_0^1(\Omega )\) is denoted as \(\mathbf {H}^{-1}(\Omega )\) which equipped with the norm \(\Vert \cdot \Vert _{-1}\). In addition, the following two formulas
and
imply that
where \((\cdot ,\cdot )_\Omega \) stands for \(L^2\) inner product on the domain \(\Omega \). Define the trilinear term as follows:
With above notations, for \(\mathbf {f}\in \mathbf {H}^1(\Omega ), \mathbf {g}\in L^2(\Omega )^d\), the weak variational formulation of the steady incompressible MHD problem (1.1) reads as: Find \((\mathbf {(u,B)},p)\in \mathbf {W}_{0\mathbf {n}}\times M\) such that
where
Furthermore, we define
The following properties of trilinear form \(a_1(\cdot ,\cdot ,\cdot )\) are useful to obtain the existence and uniqueness of a solution to problem (2.2) and gain the corresponding convergence (Adams 1975; Girault and Raviart 1986):
where \(N>0\) is a constant, \(\gamma _0\) (only dependent on \(\Omega \)) is a positive constant and \(C_0\) (only dependent on \(\Omega \)) is an embedding constant of \(\mathbf {H}^1(\Omega )\hookrightarrow \mathbf {L}^4(\Omega )\) (see Adams 1975) (\(\hookrightarrow \) denotes the continuous embedding), namely
The trilinear form \(A_1(\cdot ,\cdot ,\cdot )\) is skew symmetric with respect to the later two variables, and it satisfies
To obtain the well-posedness of the problem (2.2), we list the coercivity and continuity of \(A_0(\cdot ,\cdot )\) and the continuity of \(A_1(\cdot ,\cdot ,\cdot )\) (see Gunzburger et al. 1991): for all \(\mathbf {(w,\Phi ),(u,B),(v,\Psi )\in W}_{0\mathbf {n}}\) such that
where \(C_1\) (only dependent on \(\Omega \)) is the constant from the following inequality:
\(\sqrt{2}\) and d come from two inequalities as follows:
where d is the dimension of the considered domain \(\Omega \).
Thanks to (2.3)–(2.8), the following properties of \(A_1(\cdot ,\cdot ,\cdot )\) hold (see Lemma 1 of Dong et al. 2014):
Throughout this paper, the letter \(C>0\) denotes different constant at different places, and C is independent of the mesh size \(\mu \) and penalty parameter \(\varepsilon \).
The bilinear form \(d_0(\cdot ,\cdot )\) is continuous on \(\mathbf {W}_{0\mathbf {n}}\times M\), and it satisfies (see Gunzburger et al. 1991):
Moreover, for all \(\mathbf {w\in H}^i(\Omega )\cap \mathbf {X},\ \mathbf {\Phi }\in \mathbf {H}^i(\Omega )\cap \mathbf {W}\ (i=0,1,2),\) we set
We end this section by recalling the following important conclusions.
Theorem 2.1
(See Theorems 1 and 2 of Dong et al. 2014) Suppose that \(R_e, R_m, S_c\), and \(C_1\) satisfy
then problem (2.2) admits a unique solution \(((\mathbf {u,B}),p)\in \mathbf {W}_{0\mathbf {n}}\times M\). Moreover,
Theorem 2.2
(See Theorem 1 of Zhang et al. 2014) Set \(\Omega \) is a convex polygon/polyhedron and \(0<\sigma <1\), if \(\mathbf {f,g\in L}^2(\Omega )\), the solution \((\mathbf {(u,B)},p)\) of problem (2.2) satisfies
3 The stability and convergence of iterative penalty finite element method
3.1 Finite element spaces
Set \(\{\tau _\mu \}\) is a family of triangulations or tetrahedrons of \(\Omega \), and \(\tau _\mu \) is a shape-regular partition of \(\Omega \) with mesh size \(\mu \). The real parameter \(\mu >0\) takes h or \(H(h\ll H)\) tending to 0. The fine grid partition \(\tau _h\) is taken as a mesh refinement generated from the coarse grid \(\tau _H\). Based on the regular partitions \(\tau _h\) and \(\tau _H\), we can construct the conforming finite element spaces \((\mathbf {X}_h,M_h,\mathbf {W}_h)\) and \((\mathbf {X}_H,M_H,\mathbf {W}_H)\subset (\mathbf {X}_h,M_h,\mathbf {W}_h)\). Denote \(\mathbf {W}_{0\mathbf {n}}^\mu =\mathbf {X}_\mu \times \mathbf {W}_\mu \) and assume the finite element spaces \(\mathbf {X}_\mu ,\mathbf {W}_\mu \) and \(M_\mu \) satisfy the following assumptions.
Assumption A1 There are a mapping \(r_\mu \in \mathcal {L}(\mathbf {H}^2(\Omega )\cap \mathbf {V,X}_\mu )\) which satisfies
and an \(L^2\)-orthogonal projection operator \(\rho _\mu :M\rightarrow M_\mu \) which satisfies
and a mapping \(R_\mu \in \mathcal {L}(\mathbf {H}^2(\Omega )\cap \mathbf {V}_\mathbf {n},\mathbf {W}_\mu )\) which satisfies
Assumption A2 Assume that the bilinear form \(d_0(\cdot ,\cdot )\) satisfies the discrete inf-sup condition, namely, there exists a positive constant \(\beta _0\) such that:
There are many finite element spaces satisfying Assumptions A1 and A2 with a convex polygonal or polyhedral domain \(\Omega \). In this paper we choose the stable finite element spaces that have been used traditionally for the Navier–Stokes equations to approximate velocity and pressure. Here, the mini-element is chosen to approximate the velocity and pressure, and those finite element spaces as follows:
where
\(P_1(K)\) is defined as the space of polynomials of degree (the degree \(\le 1\) on K), and \(\hat{b}\) is a bubble function. For the magnetic field approximation space \(\mathbf {W}_\mu \), there is unrestricted. For the sake of convenience, we choose the same finite element space for the magnetic field space as the one for velocity field, i.e., we use \(\mathbf {W}_\mu =(P_{1,\mu }^b)^d \cap \mathbf {W}\) to approximate the magnetic field.
Now we define the discrete form of the divergence-free space \(\mathbf {V}\) as:
Introduce two \(L^2\)-orthogonal projectors \(P_\mu :\mathbf {L}^2(\Omega )\rightarrow \mathbf {V}_\mu \) and \(R_{0\mu }:\mathbf {L}^2(\Omega )\rightarrow \mathbf {W}_\mu \). Define the discrete Stokes operator \(A_{1\mu }=-P_\mu \Delta _\mu \), where \(\Delta _\mu \) is defined by (see Sermane and Temam 1983)
and its corresponding discrete norm is \(\Vert \mathbf {v}_\mu \Vert _{j,\mu }=\Vert A_{1\mu }^{\frac{j}{2}}\mathbf {v}_\mu \Vert _0\) with the order \(j\in R\), in which
Similarly, define the discrete operator \(A_{2\mu }\mathbf {B}_\mu =R_{0\mu }(\nabla _\mu \times \nabla \times \mathbf {B}_{\mu }+\nabla _\mu \nabla \cdot \mathbf {B}_{\mu })\in \mathbf {W}_\mu \) as follows (see He 2015; Sermane and Temam 1983)
and its corresponding discrete norm is \(\Vert \mathbf {B}_\mu \Vert _{j,\mu }=\Vert A_{2\mu }^{\frac{j}{2}}\mathbf {B}_\mu \Vert _0\) with the order \(j\in R\), in which
Moreover, we also introduce some discrete estimates as follows (see Adams 1975; He 2003, 2015)
The Galerkin FEM for problem (2.2) reads as: find \(((\mathbf {u}_\mu ,\mathbf {B}_\mu ),p_\mu )\in \mathbf {W}_{0\mathbf {n}}^\mu \times M_\mu \) such that
Using the similar argument to Theorem 2.1, we can obtain the following conclusions (see Theorems 3 and 4 of Dong et al. 2014).
Theorem 3.1
Under the condition of (2.15) and Assumption A1 , the discrete problem (3.1) admits a unique solution \(((\mathbf {u}_\mu ,\mathbf {B}_\mu ),p_\mu )\in \mathbf {W}_{0\mathbf {n}}^\mu \times M_\mu \), which satisfies
Theorem 3.2
Under the Assumptions A1 and A2 and the condition of (2.15), the solutions of problem (3.1) satisfy
Furthermore, it holds
3.2 Penalty finite element method
The penalty FEM for problem (2.2) is as follows: find \(((\mathbf {u}_{\varepsilon \mu },\mathbf {B}_{\varepsilon \mu }),p_{\varepsilon \mu })\in \mathbf {W}_{0\mathbf {n}}^\mu \times M_\mu \) such that for all \((\mathbf {(v,\Psi )},q)\in \mathbf {W}_{0\mathbf {n}}^\mu \times M_\mu \)
where \(0<\varepsilon \ll 1\) is a penalty parameter. This is the standard penalty FEM for problem (2.2). Now we present the stability and convergence of the standard penalty FEM.
Theorem 3.3
Under the condition of (2.15) and the Assumption A1, the discrete problem (3.5) admits a unique solution \(((\mathbf {u}_{\varepsilon \mu },\mathbf {B}_{\varepsilon \mu }),p_{\varepsilon \mu })\in \mathbf {W}_{0\mathbf {n}}^\mu \times M_\mu \), which satisfies
Furthermore, we have
Proof
Choosing \((\mathbf {v},\mathbf {\Psi })=(\mathbf {u}_{\varepsilon \mu },\mathbf {B}_{\varepsilon \mu })\) and \(q=p_{\varepsilon \mu }\) in (3.5), using (2.11) and (2.9) to get
thus
On the other hand, taking \(q=0\) in (3.5), applying (2.10) and (2.12) to obtain
With the help of (3.7), we have
Thus, the proof is completed.
Theorem 3.4
Let \(\Omega \) be a convex polygonal/polyhedral domain. Under the Assumptions A1, A2 and (2.15), the solution of problem (3.5) satisfies
Proof
Subtracting (3.5) from (2.2), we obtain the following error equation
Taking \((\mathbf {v},\mathbf {\Psi })=(r_\mu \mathbf {u-u}_{\varepsilon \mu },R_\mu \mathbf {B-B}_{\varepsilon \mu })\) and \(q=\rho _\mu p-p_{\varepsilon \mu }\) in (3.8), using (2.9) we have
Due to the Assumption A1, we get
and
Using (2.11) and (2.12) to obtain
Choosing \(q=0\) in (3.8), applying (2.10), (2.12) and Assumption A2, one finds
Substituting (3.13) into (3.12), with the conditions of Theorem 2.1 and (3.6), we obtain
In virtue of the Assumption A1 we have
Applying the triangle inequality to gain
Combining (3.13) with (3.16), the error \(\Vert p-p_{\varepsilon \mu }\Vert _0\) can be bounded by
The proof of Theorem 3.4 is completed.
Next, we consider the relationship between \(((\mathbf {u}_{\varepsilon \mu },\mathbf {B}_{\varepsilon \mu }),p_{\varepsilon \mu })\) and \(((\mathbf {u}_\mu ,\mathbf {B}_\mu ),p_\mu )\) as \(\varepsilon \rightarrow 0\).
Lemma 3.5
Let \(\Omega \) be a convex polygonal/polyhedral domain. Under the Assumptions A1, A2 and (2.15), the solution \(((\mathbf {u}_{\varepsilon \mu },\mathbf {B}_{\varepsilon \mu }),p_{\varepsilon \mu })\) of problem (3.5) converges the solution \(((\mathbf {u}_\mu ,\mathbf {B}_\mu ),p_\mu )\) of problem (3.1) as \(\varepsilon \rightarrow 0\).
Proof
Subtracting (3.5) from (3.1), we obtain the following error equation
Taking \((\mathbf {v},\mathbf {\Psi })=(\mathbf {u}_\mu -\mathbf {u}_{\varepsilon \mu },\mathbf {B}_\mu -\mathbf {B}_{\varepsilon \mu })\) and \(q= p_\mu -p_{\varepsilon \mu }\) in (3.17), using (2.9) we have
Using (2.11) and (2.12) to obtain
Here, \(\min \{R_e^{-1},S_c C_1 R_m^{-1}\}-\sqrt{2}C_0^2\max \{1,\sqrt{2}S_c\}\Vert (\mathbf {u}_\mu ,\mathbf {B}_\mu )\Vert _1\ge \min \{R_e^{-1},S_c C_1 R_m^{-1}\}(1-\sigma )>0\). Choosing \(q=0\) in (3.17), using (2.10), (2.12) and the Assumption A2, one finds
Substituting (3.18) into (3.19), using (3.2) and (3.6) to obtain
thus
Then, from (3.20) we know that \(\Vert p_\mu -p_{\varepsilon \mu }\Vert _0\rightarrow 0\) as \(\varepsilon \rightarrow 0\).
Substituting (3.20) into (3.18) to obtain
From (3.21) we know that \(\Vert (\mathbf {u}_\mu -\mathbf {u}_{\varepsilon \mu },\mathbf {B}_\mu -\mathbf {B}_{\varepsilon \mu })\Vert _1\rightarrow 0\) as \(\varepsilon \rightarrow 0\). Thus the proof is finished.
3.3 Iterative penalty finite element method
The one-level iterative penalty FEM for problem (2.2) reads as:
Step 1 Find \(((\mathbf {u}_{\varepsilon \mu }^0,\mathbf {B}_{\varepsilon \mu }^0),p_{\varepsilon \mu }^0)\in \mathbf {W}_{0\mathbf {n}}^\mu \times M_\mu \) such that for all \((\mathbf {(v,\Psi )},q)\in \mathbf {W}_{0\mathbf {n}}^\mu \times M_\mu \)
Step 2 For \(k=1,2,3,\ldots \), find \(((\mathbf {u}_{\varepsilon \mu }^k,\mathbf {B}_{\varepsilon \mu }^k),p_{\varepsilon \mu }^k)\in \mathbf {W}_{0\mathbf {n}}^\mu \times M_\mu \) such that for all \(\forall (\mathbf {(v,\Psi )},q)\in \mathbf {W}_{0\mathbf {n}}^\mu \times M_\mu \)
From above scheme, we can see that the initial value \(((\mathbf {u}_{\varepsilon \mu }^0,\mathbf {B}_{\varepsilon \mu }^0),p_{\varepsilon \mu }^0)\) of the one-level iterative penalty FEM is gained by Step 1. From Theorems 3.3 and 3.4, we obtain the following conclusion.
Theorem 3.6
Under the conditions of Theorem 3.4, the solution \(((\mathbf {u}_{\varepsilon \mu }^0,\mathbf {B}_{\varepsilon \mu }^0),p_{\varepsilon \mu }^0)\) of the problem (3.22) is unique and satisfies
Furthermore, it holds
Now we study the stability of one-level iterative penalty FEM solution of (3.23).
Theorem 3.7
Under the conditions of Theorem 3.3, suppose that \(((\mathbf {u}_{\varepsilon \mu }^k,\mathbf {B}_{\varepsilon \mu }^k),p_{\varepsilon \mu }^k)\in \mathbf {W}_{0\mathbf {n}}^\mu \times M_\mu \) is the solution of the discrete problem (3.23), then the solution satisfies
Proof
Taking \((\mathbf {v},\mathbf {\Psi })=(\mathbf {u}_{\varepsilon \mu }^k,\mathbf {B}_{\varepsilon \mu }^k)\) and \(q=p_{\varepsilon \mu }^k\) in (3.23), using (2.9), (2.11) and (2.12) to find
Thanks to (3.24), it yields
which implies (3.26). The proof of Theorem 3.7 is completed.
Next, we present the convergence of one-level iterative penalty FEM.
Theorem 3.8
Under the conditions of Theorem 3.4, the solution of problem (3.23) satisfies
Proof
From Theorem 3.6, we know if \(k=0\) (3.27) holds. Then we assume that (3.27) holds for \(k-1\).
From (3.23) and (2.2), we obtain
Taking \((\mathbf {v},\mathbf {\Psi })=(r_\mu \mathbf {u-u}_{\varepsilon \mu }^k,R_\mu \mathbf {B-B}_{\varepsilon \mu }^k)\) and \(q=\rho _\mu p-p_{\varepsilon \mu }^k\) in (3.28), using (2.9) to get
With the Assumption A1, we obtain
and
Using (2.11) and (2.12), one finds
Choosing \(q=0\) in (3.28) and combining (2.10), (2.12) and the Assumption A2 to get
Substituting (3.30) into (3.29), and using (2.16) and (3.26) to gain
Using the Assumption A1 to get
From the triangle inequality we gain
Combining (3.30) with (3.31), the error estimate \(\Vert p-p_{\varepsilon \mu }^k\Vert _0\) can be bounded by
Thus, the proof of Theorem 3.8 is completed.
Next, we present the \(\mathbf {L}^2\) error estimate \(\Vert (\mathbf {u-u}_{\varepsilon \mu }^{k},\mathbf {B-B}_{\varepsilon \mu }^{k})\Vert _0\). To achieve this aim, we consider the following dual problem: find \((\mathbf {(w,\Phi )},s)\in \mathbf {W}_{0\mathbf {n}}\times M\) such that
If the solution of problem (3.33) satisfies \(\mathbf {w}\in \mathbf {H}^2(\Omega )\cap \mathbf {X},\ \mathbf {\Phi }\in \mathbf {H}^2(\Omega )\cap \mathbf {W}\), then we have (see Gunzburger et al. 1991)
Theorem 3.9
Under the conditions of Theorem 3.4, the solution of problem (3.23) satisfies
Proof
Choosing \(\mathbf {(v,\Psi )}=(r_\mu \mathbf {w},R_\mu \mathbf {\Phi })\) and \(q=-\rho _\mu s\) in (3.28), subtracting it from (3.33) with \(\mathbf {(v,\Psi )}=(\mathbf {u-u}_{\varepsilon \mu }^k,\mathbf {B-B}_{\varepsilon \mu }^k)\) and \(q=p_{\varepsilon \mu }^k-p\), we obtain
Applying the conditions of Theorem 2.1, (2.10), (2.12), (3.6) and (3.34), one finds
Thanks to the Theorem 3.8, we have
As a consequence, the desired result is obtained.
4 Two-level iterative penalty finite element method
In this section, we consider the stability and convergence of two-level iterative penalty FEM for the stationary incompressible MHD problem.
The two-level iterative penalty FEM based on Stokes iteration can be described as follows.
Step 1 Find \(((\mathbf {u}_{\varepsilon H}^0,\mathbf {B}_{\varepsilon H}^0),p_{\varepsilon H}^0)\in \mathbf {W}_{0\mathbf {n}}^H\times M_H\) such that for all \((\mathbf {(v,\Psi )},q)\in \mathbf {W}_{0\mathbf {n}}^H \times M_H\)
Step 2 For \(n=1,2,3,\ldots ,k\), find \(((\mathbf {u}_{\varepsilon H}^n,\mathbf {B}_{\varepsilon H}^n),p_{\varepsilon H}^n)\in \mathbf {W}_{0\mathbf {n}}^H\times M_H\) such that for all \((\mathbf {(v,\Psi )},q)\in \mathbf {W}_{0\mathbf {n}}^H \times M_H\)
In step 3, we solve a Stokes iterative MHD problem on fine mesh.
Step 3 Find \(((\mathbf {u}_\varepsilon ^h,\mathbf {B}_\varepsilon ^h),p_\varepsilon ^h)\in \mathbf {W}_{0\mathbf {n}}^h \times M_h\) such that for any \(((\mathbf {v,\Psi }),q)\in \mathbf {W}_{0\mathbf {n}}^h \times M_h\)
Remark 4.1
In our two-level iterative penalty FEM, we adopt the Stokes iteration to treat the nonlinear terms, other iterative schemes, such as the Newton iteration and Oseen iteration, can also be used to treat the nonlinear terms. Here, we omit the analysis of these iterative schemes due to the similar proofs.
Now we present the stability of the two-level iterative penalty FEM.
Theorem 4.2
Under the conditions of Theorem 3.3, the solution \(((\mathbf {u}_\varepsilon ^h,\mathbf {B}_\varepsilon ^h),p_\varepsilon ^h)\) defined by scheme (4.3) satisfies
where k is the number of iterative step.
Proof
Choosing \((\mathbf {v,\Psi })=(\mathbf {u}_\varepsilon ^h,\mathbf {B}_\varepsilon ^h)\) and \(q=p_\varepsilon ^h\) in (4.3), and using (2.11), (2.12), (2.15) and (3.26), we gain
As a consequence one finds
Then the proof is completed.
Theorem 4.3
Under the conditions of Theorem 3.6, the solution \(((\mathbf {u}_\varepsilon ^h,\mathbf {B}_\varepsilon ^h),p_\varepsilon ^h)\) of two-level iterative penalty FEM defined by scheme (4.3) satisfies
Proof
Subtracting (4.3) from (2.2), we have
Taking \((\mathbf {v,\Psi })=(r_h\mathbf {u-u}_\varepsilon ^h,R_h\mathbf {B-B}_\varepsilon ^h)\) and \(q=\rho _h p-p_\varepsilon ^h\) in (4.6), using (2.11),(2.12), (2.13) and (2.14) to gain
Taking \(q=0\) in (4.6), thanks to (2.10), (2.12), (2.13), (2.14) and Assumption A2, one finds
Substituting (4.8) into (4.7) and applying (2.17) we obtain
Using the Theorems 3.8 and 3.9 to obtain
By the triangle inequality and the Assumption A1, it holds
We finish the proof by combining (4.9) with (4.10).
Remark 4.4
If we take \(\varepsilon =\mathcal {O}(H)\) and \(h=\mathcal {O}(H^2)\) for the two-level iterative penalty FEM, we can get the same order of convergence rate as the standard Galerkin FEM, namely, it holds
5 Numerical analysis
In this section, we present some numerical results of one-level and two-level iterative penalty FEMs for incompressible MHD equations. The software FreeFEm++ is used in this numerical experiments (see Hecht et al. 2015). The UMFPACK routine is applied to solve the linear systems arising from the discrete algebraic equations. The mesh consists of triangular elements that are obtained by dividing \(\Omega \) into subsquares of equal size and then drawing the diagonal in each sub-square. The \((P_1b,P_1,P_1b)\) finite element pair is used and the iterative tolerance \(10^{-5}\) is adopted in all numerical tests.
The example is quoted from Tao and Zhang (2015). The steady incompressible MHD equations are defined on a convex domain \(\Omega =[0,1]^2\). The boundary and initial conditions and right-hand side functions \(\mathbf{{f}}\) and \(\mathbf{{g}}\) are selected such that the exact solutions are given by
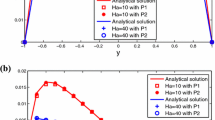
where the components of \(\mathbf{{u}}\) and \(\mathbf{{B}}\) are denoted by \((u_1,u_2)\) and \((B_1,B_2)\) for convenience. Firstly, we choose the parameters \(R_e=R_m=S_c=1\) and \(\varepsilon =0.001\). In all numerical tests, we use several mesh pairs \(1/h=9,16,25,36,49,64,81,100\) and \(H=h^{\frac{1}{2}}\). Comparison of relative errors with different iterations are shown in Tables 1 and 2 for one-level and two-level iterative penalty FEMs respectively. Then we show the relative errors between the exact solution and the numerical solutions obtained from one-level and two-level iterative penalty FEMs in Tables 3 and 4. As observed from Tables 3 and 4, the errors \(\frac{\Vert \mathbf {u-u}_h\Vert _1}{\Vert \mathbf {u}\Vert _1}\), \(\frac{\Vert \mathbf {B-B}_h\Vert _1}{\Vert \mathbf {B}\Vert _1}\), \(\frac{\Vert \mathbf {u-u}_h\Vert _0}{\Vert \mathbf {u}\Vert _0}\) and \(\frac{\Vert \mathbf {B-B}_h\Vert _0}{\Vert \mathbf {B}\Vert _0}\) become smaller and smaller as the mesh is refined. In all tables, the symbol “Iteration” denotes the number of iteration in Step 2 of corresponding method. From these tables, the observations and conclusions are obtained as follows:
-
Based on Tables 1 and 2, the errors of the velocity and magnetic in \(\mathbf {H}^1\)- and \(\mathbf {L}^2\)-norms become smaller as the iteration increasing in both one-level and two-level iterative penalty methods. Especially, when \(k=2\) the results is as good as k takes 3, 4, and 5. Thus we choose the iteration \(k=2\) in following numerical tests.
-
From Table 3, we can see that the optimal numerical convergence orders of one-level iterative penalty FEM are agreed with the ones predicted by the theoretical analysis in Theorems 3.8 and 3.9, namely, \(\mathcal {O}(h)\) for velocity and magnetic in \(\mathbf {H}^1\)-norm and pressure in \(L^2\)-norm, and \(\mathcal {O}(h^2)\) for velocity and magnetic in \(\mathbf {L}^2\)-norm.
-
From Table 4, two-level iterative penalty FEM can achieve the optimal numerical convergence orders of \(\mathcal {O}(h)\) for velocity and magnetic in \(\mathbf {H}^1\)-norm and pressure in \(L^2\)-norm, as proven in Theorem 4.3. Furthermore, we can find that two-level iterative penalty FEM can reach the optimal orders of \(\mathcal {O}(h^2)\) for velocity and magnetic in \(\mathbf {L}^2\)-norm.
-
By comparing the Tables 3 and 4, we can see that two-level iterative penalty FEM significantly takes the least CPU time than the one-level iterative penalty FEM with the same approximation results.
6 Conclusion
In this paper, we present the theoretical analysis of the one-level and two-level iterative penalty FEMs for the steady incompressible MHD problem. The stability and error estimates of these numerical methods are obtained. Numerical experiments are made to show that the one-level and two-level iterative penalty FEMs are valid for solving the incompressible MHD problem, and the numerical results are consistent with the theoretical analysis. Moreover, in our further works we will consider the extensions of the Stokes iteration on fine mesh to other linearization methods, such as the Oseen and Newton iterations, combining the present methods with some stabilization techniques likes subgrid method or variational multiscale method, and solving large Reynolds number MHD problem.
References
Adams RA (1975) Sobolev space. Academic Press, New York
An R, Shi F (2015) Two-level iteration penalty methods for the incompressible flows. Appl Math Model 39:630–641
Dai X (2007) Finite element approximation of the pure Neumann problem using the iterative penalty method. Appl Math Comput 186:1367–1373
Discacciati M (2008) Numerical approximation of a steady MHD problem. Springer, New York
Dong XJ, He YN, Zhang Y (2014) Convergence analysis of three finite element iterative methods for the 2D/3D stationary incompressible magnetohydrodynamics. Comput Methods Appl Mech Eng 276:287–311
Girault V, Lions JL (2001) Two-grid finite element scheme for the steady Navier–Stokes equations in polyhedra. Port Math 58:25–57
Girault V, Raviart PA (1986) Finite element approximation of Navier–Stokes equations. Springer, Berlin
Gunzburger MD (1989) Iterated penalty methods for the Stokes and Navier–Stokes equations. Finite Elem Anal Fluids 1:1040–1045
Gunzburger MD, Meir AJ, Peterson JS (1991) On the existence, uniqueness, and finite element approximation of solutions of the equations of stationary incompressible magnetohydrodynamics. Math Comput 56:523–563
Gunzburger MD, Ladyzhenskaya OA, Peterson JS (2004) On the global unique solvabiity and initial boundary value problems for coupled modified Navier–Stokes and Maxwell equations. J Math Fluid Mech 6:462–482
Hasler U, Schneebeli A, Schözau D (2004) Mixed finite element approximation of incompressible MHD problems based on weighted regularization. Appl Numer Math 51:19–45
He YN (2003) Two-level method based on finite element and Crank–Nicolson extrapolation for the time-dependent Navier–Stokes equations. SIAM J Numer Anal 41:1263–1285
He YN (2004) A two-level finite element Galerkin method for the nonstationary Navier–Stokes equations I: spatial discretization. J Comput Math 22:21–32
He YN (2005) Optimal error estimate of the penalty finite element method for the time-dependent Navier–Stokes equations. Math Comput 74:1201–1216
He YN (2015) Unconditional convergence of the Euler semi-implicit scheme for the 3D incompressible MHD equations. IMA J Numer Anal 35:767–801
Hecht F, Pironneau O, Hyaric A, Ohtsuka K (2015) FreeFem++, version 3.37, 2008. http://www.freefem.org. Accessed 11 May 2015
Hughes WF, Young FJ (1966) The electromagnetics of fluids. Wiley, NewYork
Marion M, Xu JC (1995) Error estimates on a new nonlinear Galerkin method based on two-grid finite elements. SIAM J Numer Anal 32:1170–1184
Moreau R (1990) Magneto-hydrodynamics. Kluwer Academic Publishers, Dordrecht
Qiu HL, Mei LQ, Zhang YM (2014) Iterative penalty methods for the steady Navier–Stokes equations. Appl Math Comput 237:110–119
Schözau D (2004) Mixed finite element methods for stationary incompressible magneto-hydrodynamics. Numer Math 96:771–800
Sermane M, Temam R (1983) Some mathematical questions related to the MHD equations. Commun Pure Appl Math 36(5):635–664
Shen J (1995) On error estimates of the penalty method for unsteady Navier–Stokes equations. SIAM J Numer Anal 32:386–403
Tao ZZ, Zhang T (2015) Stability and convergence of two-level iterative methods for the stationary incompressible magnetohydrodynamics with different Reynolds numbers. J Math Anal Appl 428:627–652
Xu JC (1996) Two-grid discretization techniques for linear and nonlinear PDEs. SIAM J Numer Anal 33:1759–1777
Zhang T (2013) Two grid characteristic finite volume methods for nonlinear parabolic problem. J Comput Math 31:470–487
Zhang GD, He YN, Zhang Y (2014) Streamline diffusion finite element method for stationary incompressible magnetohydrodynamics. Numer Methods Partial Differ Equ 30:1877–1901
Zhang T, Yang JH (2014) Two level finite volume method for the unsteady Navier–Stokes equations based on two local Gauss integrations. J Comput Appl Math 263:377–391
Zhang T, Yuan JY, Si ZY (2015a) Decoupled two grid finite element method for the time-dependent natural convection problem I: spatial discretization. Numer Methods Partial Differ Equ 31(6):2135–2168
Zhang T, Zhao X, Huang PZ (2015b) Decoupled two level finite element methods for the steady natural convection problem. Numer Algorithms 68(4):837–866
Author information
Authors and Affiliations
Corresponding author
Additional information
Communicated by Jorge X. Velasco.
This work was supported by CAPES and CNPq, Brazil (No. 88881.068004/2014.01), the NSF of China (No. 11301157), the Doctor Fund of Henan Polytechnic University (B2012-098) and the Foundation of Distinguished Young Scientists of Henan Polytechnic University (J2015-05).
Rights and permissions
About this article
Cite this article
Deng, J., Tao, Z. & Zhang, T. Iterative penalty finite element methods for the steady incompressible magnetohydrodynamic problem. Comp. Appl. Math. 36, 1637–1657 (2017). https://doi.org/10.1007/s40314-016-0323-y
Received:
Revised:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s40314-016-0323-y