On Two-Level Oseen Penalty Iteration Methods for the 2D/3D Stationary Incompressible Magnetohydronamics

Abstract

This paper studies several decoupled penalty methods to overcome the saddle point system of the steady state 2D/3D incompressible magnetohydronamics (MHD). These approaches combine the Oseen iteration and two-level technique with strong uniqueness condition $0<\frac{\sqrt{2}C_{0}^{2}\max \{1,\sqrt{2}S_{c}\}\Vert {\mathbf{F }}\Vert _{-1}}{(\min \{R_{e}^{-1},S_{c}C_{1}R_{m}^{-1}\})^2}\le 1-\left( \frac{\Vert \mathbf{F }\Vert |_{-1}}{\Vert |\mathbf{F }\Vert _{0}}\right) ^{\frac{1}{2}}<1$ satisfied. For the convenience of implementation, we employ two different simple Lagrange finite element pairs $P_{1}b-P_{1}-P_{1}b$ and $P_{1}-P_{0}-P_{1}$ for velocity field, pressure and magnetic field, respectively. Rigorous analysis of the optimal error estimate and stability are provided. We present comprehensive numerical experiments, which indicate the effectiveness of the proposed methods for both two dimensional and three-dimensional problems.

1 Introduction

The purpose of this work is to devise some decoupled penalty schemes for solving the following 2D/3D stationary incompressible MHD equations:

$$\begin{aligned} \left\{ \begin{array}{lll} -R_e^{-1}\Delta \mathbf{u }+(\mathbf{u }\cdot \nabla )\mathbf{u }+\nabla p-S_c{\mathrm{curl}}\mathbf{B }\times \mathbf{B }=\mathbf{f }, \quad \mathrm{in}~\varvec{\Omega },\\ {\mathrm{div}} \mathbf{u }=0,\quad \mathrm{in}~\Omega ,\\ S_c R_m^{-1}\text{ curl }(\text{ curl }\mathbf{B })-S_c \text{ curl }( \mathbf{u }\times \mathbf{B }) =\mathbf{g }, ~ \text{ in }~\Omega ,\\ {\mathrm{div}} \mathbf{B }=0, \quad \mathrm{in}\Omega .\\ \end{array} \right. \end{aligned}$$

(1)

Here $\Omega$ is a convex polygonal/polyhedral domain in ${\mathbb {R}}^d$, $d=$ 2 or 3, with boundary $\partial \Omega$. $\mathbf{u }$ the velocity of the fluid, p the pressure, $\mathbf{B }$ the magnetic field, $\mathbf{f }$ and $\mathbf{g }$ the external force terms, $R_e$ the hydrodynamic Reynolds number, $R_m$ the magnetic Reynolds number, $S_c$ the coupling number and $\mathbf{n }$ is the outer unit normal of $\partial \Omega$. The system is supplemented with the boundary conditions:

$$\begin{aligned} \left\{ \begin{array}{llll} \mathbf{u }|_{\partial \Omega }=0, ~(\text{ no-slip } \text{ condition }),\\ \mathbf{B }\cdot \mathbf{n }|_{\partial \Omega }=0,\ \ \mathbf{n }\times {\mathrm{curl}}\mathbf{B }|_{\partial \Omega }=0, ~(\text{ perfectly } \text{ wall }),\\ \end{array} \right. \end{aligned}$$

(2)

The incompressible MHD model is a system of PDEs, which are prescribed by the Navier–Stokes equations and coupled with the pre-Maxwell equations. Incompressible MHD has many industrial applications such as metallurgical engineering, electromagnetic pumping, stirring of liquid metals, and measuring flow quantities based on induction [1]. Therefore, it is an important research topic to provide effective numerical methods for solving such flow problem. We refer to [2, 3] for more detailed information of physical background, Furthermore, there are many research works which use finite element methods to simulate the incompressible MHD flows in recent years. We refer to [2, 4,5,6,7,8,9,10,11,12,13,14,15] and many references therein.

The coupled system (1) involves nonlinear terms and the incompressible constraint, which requires much larger numbers of degrees of freedom to resolve numerically. Hence, the Stokes, Newton and Oseen iterative methods are considered for the stationary 2D/3D MHD equations to deal with the nonlinearity in [16,17,18]. And it can be concluded that Stokes iteration and Newton iteration are suitable to small Reynolds number such that the strong uniqueness conditions $0<\sigma :\frac{\sqrt{2}C_{0}^{2}\max \{1,\sqrt{2}S_{c}\}\Vert {\mathbf{F }}\Vert _{-1}}{(\min \{R_{e}^{-1},S_{c}C_{1}R_{m}^{-1}\})^2}\le \frac{2}{5}$ and $0<\sigma \le \frac{5}{11}$ hold, respectively. And the Oseen method is suitable for each Reynolds number such that $0<\sigma <1$ holds.

The penalty method, the pressure stabilization method, the artificial compressibility method and the projection method [19,20,21,22,23,24,25,26], etc. are usually used to handle the incompressible constrain. Besides, we also proposed some decoupling method with Uzawa-type idea for the incompressible MHD equations in [27,28,29]. In this study, we mainly consider the penalty method to decouple the strong-coupled stationary incompressible MHD equations. The penalty method applied to (1) is to approximate the solution $(\mathbf{u },p,\mathbf{B })$ by $(\mathbf{u }_{\epsilon },p_{\epsilon },\mathbf{B }_{\epsilon })$ satisfying the following equations:

$$\begin{aligned} \left\{ \begin{array}{lll} -R_e^{-1}\Delta \mathbf{u }_{\epsilon }+(\mathbf{u }_{\epsilon }\cdot \nabla )\mathbf{u }_{\epsilon } -S_c\text{ curl }\mathbf{B }_{\epsilon }\times \mathbf{B }_{\epsilon } +\nabla p_{\epsilon }=\mathbf{f },\quad \text{ in }~\Omega ,\\ \text{ div } \mathbf{u }_{\epsilon } +R_{e}\epsilon p_{\epsilon }=0,\quad {\mathrm{in}}~\Omega ,\\ S_c R_m^{-1}\text{ curl }(\text{ curl }\mathbf{B }_{\epsilon })-S_c \text{ curl }( \mathbf{u }_{\epsilon }\times \mathbf{B }_{\epsilon }) =\mathbf{g },\quad \text{ in }~\Omega ,\\ {\mathrm{div}} \mathbf{B }_{\epsilon }=0,\quad \mathrm{in}~\Omega ,\\ \end{array} \right. \end{aligned}$$

(3)

with the homogeneous boundary conditions:

$$\begin{aligned} \left\{ \begin{array}{llll} &{}\mathbf{u }_{\epsilon }|_{\partial \Omega }=0, ~(\text{ no-slip } \text{ condition }),\\ &{}\mathbf{B }_{\epsilon }\cdot \mathbf{n }|_{\partial \Omega }=0,\ \ \mathbf{n }\times {\mathrm{curl}}\mathbf{B }_{\epsilon }|_{\partial \Omega }=0, ~(\text{ perfectly } \text{ wall }),\\ \end{array} \right. \end{aligned}$$

(4)

where $0<\epsilon <1$ is penalty parameter.

Although, the penalty method is to decouple $(\mathbf{u} ,\mathbf{B} )$ and p, the resulting system is still large. Two-level scheme, which was put forward by Xu for the nonlinear elliptic boundary value problem in [30, 31] which is efficient to save a large amount of computing time and give reasonable results. Under the strong uniqueness condition $\sigma \le 1-\left( \frac{\Vert \mathbf{F }\Vert |_{-1}}{\Vert |\mathbf{F }\Vert _{0}}\right) ^{\frac{1}{2}}<1$, we focus on the two-level Oseen penalty finite element methods for 2D/3D steady state incompressible MHD equations in this article. And, we mainly explore the finite element space pair $\mathbf{X }_{h}\times \text{ M }_{h}\times \mathbf{W }_{h}$ which does not satisfy the discrete inf-sup condition ($P_{1}-P_{0}-P_{1}$) and the one satisfies the discrete inf-sup condition ($P_{1}b-P_{1}-P_{1}b$). In general, the rigorous analysis shows that the proposed methods can get the optimal accuracy with appropriate relationship between $\epsilon$, H and h. Numerical results confirming theoretical findings are presented for several 2D/3D examples. And we know that, the magnetic variables may have regularity below $H^1$ with the domain $\Omega$ is a non-convex polygon (polyhedron), and the continuous nodal finite element spaces may fail to approximate the singular magnetic solution. Then the magnetic field of our ongoing work is discretized by curl-conforming $N\acute{e}d\acute{e}lec$ elements to deal with the situations of singular magnetic fields.

The paper is organized as follows. In Sect. 2, some basic results are given. Penalty mixed finite element method is given in Sect. 3. Section 4 is devoted to uniform stability and convergence of the two-level penalty iterative methods. Section 5 is reported to show numerical performance and accuracy of our algorithms. Finally, the article is concluded in Sect. 6.

2 Functional Setting of the Stationary MHD Equations

To derive the variational form, we introduce the following spaces

$$\begin{aligned} \mathbf{X }&:=\,\mathbf{H }_{0}^1=\left\{ \mathbf{u }\in H^1(\Omega )^d: \mathbf{u }|_{\partial \Omega }=0\right\} ,\\ \mathbf{W }&:=\,{\mathbf{H }^1_\mathbf{n }}=\left\{ \mathbf{v }\in H^1(\Omega )^d : \mathbf{v }\cdot \mathbf{n }|_{\partial \Omega }=0\right\} ,\\ \mathbf{V }&:=\,\left\{ \mathbf{u }\in \mathbf{X }: \text{ div }\mathbf{u }=0~\text{ in }~\Omega \right\} ,\\ \mathbf{V }_{n}&:=\,\left\{ \mathbf{v }\in \mathbf{W }: \text{ div }\mathbf{v }=0~\text{ in }~\Omega \right\} ,\\ \text{ M }&:=\,L^2_0(\Omega )=\left\{ q\in L^2(\Omega ) : \int _\Omega q d\mathbf{x }=0\right\} . \end{aligned}$$

Throughout this work, space $\mathbf{W }_{0n}=\mathbf{X }\times \mathbf{W }$ equipped with the graph norm $\Vert (\mathbf{v },\mathbf{B })\Vert _1$, where $\Vert (\mathbf{v },\mathbf{B })\Vert _i=(\Vert \mathbf{v }\Vert _i^2+\Vert \mathbf{B }\Vert _i^2)^{\frac{1}{2}}$ for all $\mathbf{v }\in H^i(\Omega )^d\cap \mathbf{X }, \mathbf{B }\in H^i(\Omega )^d\cap \mathbf{W }$$(i=0,1,2)$. And $H^{-1}(\Omega )^d$ is the dual of $\mathbf{X }$ with norm $\Vert \mathbf{f }\Vert _{-1}=\sup _{0\ne \mathbf{w }\in \mathbf{X }}\frac{\langle \mathbf{f },\mathbf{w }\rangle }{\Vert \mathbf{w }\Vert _1},$ where $\langle \cdot ,\cdot \rangle$ denotes duality product. Besides, we set $\Vert \mathbf{F }\Vert _{-1}=\sup _{ (0,0)\ne (\mathbf{v },\varvec{\Psi })\in \mathbf{W }_{0n}}\frac{\langle \mathbf{F },(\mathbf{v },\varvec{\Psi }) \rangle }{\Vert (\mathbf{v },\varvec{\Psi })\Vert _1}$ and $\Vert \mathbf{F }\Vert ^2_{*}=\Vert \mathbf{f} \Vert ^2_{-1}+\Vert \mathbf{g} \Vert ^2_{0}$.

Then, we arrive at an equivalent variational formulation for (1): find $((\mathbf{u },\mathbf{B }),p)\in \mathbf{W }_{0n}\times \text{ M }$ such that

$$\begin{aligned}&A_0((\mathbf{u },\mathbf{B }),(\mathbf{v },\varvec{\Psi }))-d((\mathbf{v },\varvec{\Psi }),p)+ d((\mathbf{u },\mathbf{B }),q) +A_1((\mathbf{u },\mathbf{B }),(\mathbf{u },\mathbf{B }), (\mathbf{v },\varvec{\Psi }))\nonumber \\&\quad =\langle \mathbf{F },(\mathbf{v },\varvec{\Psi })\rangle , \end{aligned}$$

(5)

for all $((\mathbf{v },\varvec{\Psi }),q)\in \mathbf{W }_{0n}\times \text{ M }$ and the variational formulation of (3) reads: find $((\mathbf{u }_{\epsilon },\mathbf{B }_{\epsilon }),p_{\epsilon })\in \mathbf{W }_{0n}\times \text{ M }$ such that for all $((\mathbf{v },\varvec{\Psi }),q)\in \mathbf{W }_{0n}\times \text{ M }$,

$$\begin{aligned} \begin{array}{llll} &{}A_0\left( \left( \mathbf{u }_{\epsilon },\mathbf{B }_{\epsilon }\right) ,\left( \mathbf{v },\varvec{\Psi }\right) \right) -d\left( \left( \mathbf{v },\varvec{\Psi }\right) ,p_{\epsilon }\right) + d\left( \left( \mathbf{u }_{\epsilon },\mathbf{B }_{\epsilon }\right) ,q\right) +A_1\left( \left( \mathbf{u }_{\epsilon },\mathbf{B }_{\epsilon }\right) ,\left( \mathbf{u }_{\epsilon },\mathbf{B }_{\epsilon }\right) , \left( \mathbf{v },\varvec{\Psi }\right) \right) \\ &{}\quad +\,\frac{\epsilon }{\nu _{e}}\left( p_{\epsilon },q\right) =\langle \mathbf{F },\left( \mathbf{v },\varvec{\Psi }\right) \rangle , \end{array}\nonumber \\ \end{aligned}$$

(6)

where $\nu _{e}$ is the reciprocal of $R_{e}$ and

$$\begin{aligned} A_0\left( \left( \mathbf{v },\varvec{\Psi }\right) ,\left( \mathbf{w },\varvec{\Phi }\right) \right)&=a_0\left( \mathbf{v },\mathbf{w }\right) + b_0\left( \varvec{\Psi },\varvec{\Phi }\right) ,\\ a_0\left( \mathbf{v },\mathbf{w }\right)&=R_e^{-1}\left( \nabla \mathbf{v },\nabla \mathbf{w }\right) ,~ b_0\left( \varvec{\Psi },\varvec{\Phi }\right) \\&=S_c R_m^{-1}\left( \text{ curl }\varvec{\Psi },\text{ curl } \varvec{\Phi }\right) +S_c R_m^{-1}\left( \text{ div } \varvec{\Psi },\text{ div }\varvec{\Phi }\right) ,\\ d\left( \left( \mathbf{v },\varvec{\Phi }\right) ,q\right)&=\left( \text{ div } \mathbf{v },q\right) ,~ \langle \mathbf{F },\left( \mathbf{v },\varvec{\Psi }\right) \rangle =\langle \mathbf{f }, \mathbf{v }\rangle +\left( \mathbf{g },\varvec{\Psi }\right) ,\\ A_1\left( \left( \mathbf{u },\mathbf{B }\right) ,\left( \mathbf{v },\varvec{\Psi }\right) ,\left( \mathbf{w },\varvec{\Phi }\right) \right)&=a_1\left( \mathbf{u },\mathbf{v },\mathbf{w }\right) +c\left( \varvec{\Phi },\mathbf{B },\mathbf{v }\right) -c\left( \varvec{\Psi },\mathbf{B },\mathbf{w }\right) ,\\ a_1\left( \mathbf{u },\mathbf{v },\mathbf{w }\right)&=\frac{1}{2}\left( \left( \mathbf{u }\cdot \nabla \right) \mathbf{v },\mathbf{w }\right) -\frac{1}{2}\left( \left( \mathbf{u }\cdot \nabla \right) \mathbf{w }, \mathbf{v }\right) ,~ c\left( \varvec{\Phi },\mathbf{B },\mathbf{v }\right) \\&=S_c\left( \text{ curl }\varvec{\Phi }\times \mathbf{B },\mathbf{v }\right) . \end{aligned}$$

Besides, we need the following properties of $A_0(\cdot ,\cdot )$ and $A_1(\cdot ,\cdot ,\cdot )$ in [2]:   $\forall$$(\mathbf{u },\mathbf{B })$, $(\mathbf{v },\varvec{\Psi })$, $(\mathbf{w },\varvec{\Phi })\in \mathbf{W }_{0n}$, there holds

$$\begin{aligned}&A_0\left( \left( \mathbf{v },\varvec{\Psi }\right) ,\left( \mathbf{w },\varvec{\Phi }\right) \right) \le \max \{R_{e}^{-1},(2+d)S_{c}R_{m}^{-1}\}\Vert \left( \mathbf{v },\varvec{\Psi }\right) \Vert _1\Vert \left( \mathbf{w },\varvec{\Phi }\right) \Vert _1, \end{aligned}$$

(7)

$$\begin{aligned}&A_0\left( \left( \mathbf{v },\varvec{\Psi }\right) ,\left( \mathbf{v },\varvec{\Psi }\right) \right) \ge \min \{R_{e}^{-1},S_{c}C_{1}R_{m}^{-1}\}\Vert \left( \mathbf{v },\varvec{\Psi }\right) \Vert _1^2, \end{aligned}$$

(8)

$$\begin{aligned}&A_1\left( \left( \mathbf{u },\mathbf{B }\right) ,\left( \mathbf{v },\varvec{\Psi }\right) ,\left( \mathbf{w },\varvec{\Phi }\right) \right) \le \sqrt{2}C_{0}^{2}\max \{1,\sqrt{2}S_{c}\}\Vert \left( \mathbf{u },\mathbf{B }\right) \Vert _1 \Vert \left( \mathbf{v },\varvec{\Psi }\right) \Vert _1\Vert \left( \mathbf{w },\varvec{\Phi }\right) \Vert _1, \end{aligned}$$

(9)

$$\begin{aligned}&A_1\left( \left( \mathbf{u },\mathbf{B }\right) ,\left( \mathbf{v },\varvec{\Psi }\right) ,\left( \mathbf{v },\varvec{\Psi }\right) \right) =0, \end{aligned}$$

(10)

$$\begin{aligned}&A_1\left( \left( \mathbf{u },\mathbf{B }\right) ,\left( \mathbf{v },\varvec{\Psi }\right) ,\left( \mathbf{w },\varvec{\Phi }\right) \right) +A_1\left( \left( \mathbf{v },\varvec{\Psi }\right) ,\left( \mathbf{u },\mathbf{B }\right) ,\left( \mathbf{w },\varvec{\Phi }\right) \right) +A_1\left( \left( \mathbf{v },\varvec{\Psi }\right) ,\left( \mathbf{w },\varvec{\Phi }\right) ,\left( \mathbf{u },\mathbf{B }\right) \right) \end{aligned}$$

(11)

$$\begin{aligned}&\le C\sqrt{2}C_{0}^{2}\max \{1,\sqrt{2}S_{c}\}\Vert \left( \mathbf{u },\mathbf{B }\right) \Vert _{1}^{\frac{1}{2}} \Vert \left( \mathbf{u },\mathbf{B }\right) \Vert _{0}^{\frac{1}{2}} \Vert \left( \mathbf{w },\varvec{\Phi }\right) \Vert _{1} \Vert \left( \mathbf{v },\varvec{\Psi }\right) \Vert _{1}. \end{aligned}$$

(12)

And we introduce the properties of trilinear form in [32]:

$$\begin{aligned} \begin{array}{lll} |A_{1}\left( \left( \mathbf{u} ,\mathbf{B} \right) ,\left( \mathbf{v} ,\varvec{\Psi }\right) ,\left( \mathbf{w} ,\varvec{\Phi }\right) \right) | \le C\sqrt{2}C_{0}^{2}\max \{1,\sqrt{2}S_{c}\} \Vert \left( \mathbf{u} ,\mathbf{B} \right) \Vert _{0}\Vert \left( \mathbf{v} ,\varvec{\Psi }\right) \Vert _{2} \Vert \left( \mathbf{w} ,\varvec{\Phi }\right) \Vert _{1},\\ \quad \forall \left( \mathbf{u} ,\mathbf{B} \right) \in L^{2}\left( \Omega \right) ^d\times L^{2}\left( \Omega \right) ^d, \left( \mathbf{w} ,\varvec{\Phi }\right) \in H^{2}\left( \Omega \right) ^{d}\times H^{2}\left( \Omega \right) ^{d}, \left( \mathbf{v} ,\varvec{\Psi }\right) \in \mathbf{W} _{0n}\left( \Omega \right) ,\\ |A_{1}\left( \left( \mathbf{u} ,\mathbf{B} \right) ,\left( \mathbf{v} ,\varvec{\Psi }\right) ,\left( \mathbf{w} ,\varvec{\Phi }\right) \right) | \le C\sqrt{2}C_{0}^{2}\max \{1,\sqrt{2}S_{c}\} \Vert \left( \mathbf{u} ,\mathbf{B} \right) \Vert _{2}\Vert \left( \mathbf{v} ,\varvec{\Psi }\right) \Vert _{1} \Vert \left( \mathbf{w} ,\varvec{\Phi }\right) \Vert _{0},\\ \quad \forall \left( \mathbf{u} ,\mathbf{B} \right) \in H^{2}\left( \Omega \right) ^{d}\times H^{2}\left( \Omega \right) ^{d}, \left( \mathbf{w} ,\varvec{\Phi }\right) \in \mathbf{W} _{0n}\left( \Omega \right) , \left( \mathbf{v} ,\varvec{\Psi }\right) \in L^{2}\left( \Omega \right) ^d\times L^{2}\left( \Omega \right) ^d. \end{array}\nonumber \\ \end{aligned}$$

(13)

For the sake of convenience, C or c (with or without a subscript) will denotes a generic positive constant throughout the paper and denote

$$\begin{aligned} \Vert |\left( \mathbf{w },\varvec{\Phi }\right) \Vert |_{i}= & {} \min \{R_{e}^{-1},S_{c}C_{1}R_{m}^{-1}\}\left( \Vert \mathbf{w }\Vert _{i}^{2}+\Vert \varvec{\Phi }\Vert _{i}^{2}\right) ^{\frac{1}{2}},\\&\forall \quad \mathbf{w } \in H^{i}\left( \Omega \right) ^d\cap \mathbf{X },~\varvec{\Phi }\in H^{i}\left( \Omega \right) ^d\cap \mathbf{W },~i=0,1,2. \end{aligned}$$

Then, we set ${\underline{\gamma }}:=\min \{R_{e}^{-1},S_{c}C_{1}R_{m}^{-1}\},~ {\overline{\gamma }}:=\max \{R_{e}^{-1},(2+d)S_{c}R_{m}^{-1}\},~ N:=\sqrt{2}C_{0}^{2}\max \{1,\sqrt{2}S_{c}\}$ in the following sections.

First, recall the following existence and uniqueness results in [16] for (5) and (6).

Theorem 2.1

Let $\mathbf{f} \in H^{-1}(\Omega )^d$, $\mathbf{g} \in L^{2}(\Omega )^d$ and $R_e$, $R_{m}$ and $S_{c}$ satisfy the uniqueness condition

$$\begin{aligned} 0< \sigma <1, \end{aligned}$$

(14)

the problem (5) admits a unique solution $((\mathbf{u },\mathbf{B }),p)\in \mathbf{W }_{0n}\times {\mathrm{M}}$ such that

$$\begin{aligned} \Vert |(\mathbf{u },\mathbf{B })\Vert |_{1}\le \Vert \mathbf{F }\Vert _{-1}. \end{aligned}$$

(15)

Moreover, suppose that $0< \sigma <1$ and $\mathbf{f },\ \mathbf{g }\in {L}^{2}(\Omega )^d$, then solution $((\mathbf{u },\mathbf{B }),p)$ such that

$$\begin{aligned} \Vert |(\mathbf{u },\mathbf{B })\Vert |_{2}+\Vert p\Vert _{1}\le C\Vert \mathbf{F }\Vert _{0}. \end{aligned}$$

(16)

Theorem 2.2

If $R_e$, $R_{m}$ and $S_{c}$ satisfy the uniqueness condition (14) and $\epsilon c_{0}\le 1$ with $c_{0}>0$, then the problem (6) has a unique solution $((\mathbf{u }_{\epsilon },\mathbf{B }_{\epsilon }),p_{\epsilon })\in \mathbf{W }_{0n}\times {\mathrm{M}}$ which satisfies

$$\begin{aligned} \Vert |(\mathbf{u }_{\epsilon },\mathbf{B }_{\epsilon })\Vert |_{1}\le \Vert \mathbf{F }\Vert _{-1}. \end{aligned}$$

(17)

Then, suppose that $\mathbf{f },\ \mathbf{g }\in L^{2}(\Omega )^d$ and $\epsilon c_{0}\le 1$, solution $((\mathbf{u }_{\epsilon },\mathbf{B }_{\epsilon }),p_{\epsilon })$ of the problem (6) satisfies the following regularity

$$\begin{aligned} \Vert |(\mathbf{u }_{\epsilon },\mathbf{B }_{\epsilon })\Vert |_{2}+\Vert p_{\epsilon }\Vert _{1}\le C\Vert \mathbf{F }\Vert _{0}. \end{aligned}$$

(18)

Theorem 2.3

Under the assumptions of Theorem 2.2, we have the following error bounds

$$\begin{aligned} \Vert |(\mathbf{u }-\mathbf{u }_{\epsilon },\mathbf{B }-\mathbf{B }_{\epsilon })\Vert |_{1}+\Vert p-p_{\epsilon }\Vert _{0}\le C\epsilon \Vert \mathbf{F }\Vert _{0}. \end{aligned}$$

(19)

Proof

Refer to [16] for details. $\square$

3 Penalty Finite Element Galerkin Discretization

Let $\{\tau _\mu \}$ be a family of triangulations or tetrahedrons of $\Omega$ into quasi-uniform finite elements K with ${\bar{\Omega }}=\bigcup _{K\in \tau _{\mu }}K$, mesh size $\mu =h ~or ~ H$. Consider finite element space $\mathbf{X} _{\mu }\subset \mathbf{X}$, $\text{ M }_{\mu }\subset \text{ M }$, $\mathbf{W} _{\mu }\subset \mathbf{W}$ and $(\mathbf{X} _{H},\text{ M }_{H},\mathbf{W} _{H})\subset (\mathbf{X} _{h},\text{ M }_{h},\mathbf{W} _{h})$. $P_{l}(K)$ denote the set of all polynomials on K with order $l\ge 0$ and $\mathbf{W} _{0n}^{\mu }=\text{ X }_{\mu }\times \text{ W }_{\mu }$. Next, we introduce the discrete analogue of space $\mathbf{V}$ as

$$\begin{aligned} \mathbf{V }_{\mu }=\left\{ \mathbf{v }\in \mathbf{X }_{\mu }:d((\mathbf{v },\varvec{\Psi }),q)=0,\forall q\in \text{ M }_{\mu },~\varvec{\Psi }\in \mathbf{W }_{\mu }\right\} . \end{aligned}$$

The discrete Stokes operator ${\mathcal {A}}_{1\mu }=-P_{\mu }\Delta _{\mu }$, and $\Delta _{\mu }$ defined as (see [33])

$$\begin{aligned} -(\Delta _{\mu }\mathbf{u} _{\mu },\mathbf{v} _{\mu })=(\nabla \mathbf{u} _{\mu },\nabla \mathbf{v} _{\mu }), \quad \forall \mathbf{u} _{\mu },\mathbf{v} _{\mu }\in \mathbf{X} _{\mu }, \end{aligned}$$

where $P_{\mu }: L^2(\Omega )^d\rightarrow \mathbf{V} _{\mu }$ defined by $(P_{\mu }\mathbf{u} ,\mathbf{v} _{\mu })=(\mathbf{u} ,\mathbf{v} _{\mu })$ for all $\mathbf{v} _{\mu } \in \mathbf{V} _{\mu }$ and define discrete operator ${\mathcal {A}}_{2\mu }\mathbf{B} _{\mu }=R_{0\mu } (\nabla _{\mu }\times \nabla \times \mathbf{B }_{\mu }+\nabla _{\mu }\nabla \cdot \mathbf{B }_{\mu })\in \mathbf{W} _{\mu }$ as follows (see [34])

$$\begin{aligned} \left( {\mathcal {A}}_{2\mu }\mathbf{B }_{\mu },\varvec{\Psi }\right) = \left( \nabla \times \mathbf{B }_{\mu },\nabla \times \varvec{\Psi }\right) +\left( \nabla \cdot \mathbf{B }_{\mu },\nabla \cdot \varvec{\Psi }\right) ,\quad \forall \mathbf{B }_{\mu },\varvec{\Psi }\in \mathbf{W} _{\mu }, \end{aligned}$$

where $R_{0\mu }: L^2(\Omega )^d\rightarrow \mathbf{W} _{\mu }$ defined by $(R_{0\mu }\mathbf{B} ,\varvec{\Psi }_{\mu })=(\mathbf{B} ,\varvec{\Psi }_{\mu })$ for all $\varvec{\Psi }_{\mu } \in \mathbf{W} _{\mu }$.

The following two finite element pairs are mainly considered to explore the relation between penalty parameter and the algorithms in this article:

$({\mathcal {P}}_{1})$.:

The unstable finite element pair

$$\begin{aligned} \begin{array}{lll} \mathbf{X} _{\mu } =\left\{ \mathbf{u }\in C^{0}({\bar{\Omega }})^d\cap \mathbf{X} : \mathbf{u }|_{K}\in P_{1}(K)^d,~ \forall K \in \tau _{\mu }\right\} ,\\ \text{ M }_{\mu }=\left\{ q\in \text{ M }: q|_{K}\in P_{0}(K),~ \forall K \in \tau _{\mu }\right\} ,\\ \mathbf{W} _{\mu }=\left\{ \mathbf{B }\in C^{0}({\bar{\Omega }})^d\cap \mathbf{W} : \mathbf{B }|_{K}\in P_{1}(K)^d,~ \forall K \in \tau _{\mu }\right\} . \end{array} \end{aligned}$$

$({\mathcal {P}}_{2})$:

. The stable finite element pair

$$\begin{aligned} \begin{array}{lll} \mathbf{X} _{\mu }=\left( P_{1,\mu }^{b}\right) ^d\cap \mathbf{X} ,\\ \text{ M }_{\mu }=\{q\in C^{0}\left( {\bar{\Omega }}\right) \cap \text{ M }: q|_{K}\in P_{1}(K), ~\forall K \in \tau _{\mu }\},\\ \mathbf{W} _{\mu }=\left( P_{1,\mu }^{b}\right) ^d\cap \mathbf{W} , \end{array} \end{aligned}$$

where $P_{1,\mu }^{b}=\{v_{\mu }\in C^{0}({\bar{\Omega }}): v_{\mu }|_{K}\in P_{1}(K)\oplus span\{{\hat{b}}\},~\forall K\in \tau _{\mu }\}$, ${\hat{b}}$ is a bubble function.

The following properties of ${\mathcal {P}}_{1}$ and ${\mathcal {P}}_{2}$ are stated in [9, 22, 32, 34, 35].

Lemma 3.1

The finite element pair ${\mathcal {P}}_{1}$ satisfies the key relation

$$\begin{aligned} \text{ div }\mathbf{X} _{\mu }=\text{ M }_{\mu }. \end{aligned}$$

(20)

Besides, there exists mappings $\pi _{\mu }: H^2(\Omega )^d\cap \mathbf{X} \rightarrow \mathbf{X} _{\mu }$ and $\rho _{\mu }: \text{ M }\rightarrow \text{ M }_{\mu }$ satisfy

$$\begin{aligned} \Vert \nabla (\mathbf{v} -\pi _{\mu }\mathbf{v} )\Vert _{0}\le C \mu \Vert \mathbf{v} \Vert _{2}, \quad \Vert q-\rho _{\mu }q\Vert _{0}\le C \mu \Vert q\Vert _{1}, \end{aligned}$$

(21)

for all $\mathbf{v} \in H^{2}(\Omega )^{d}\cap \mathbf{X}$, $q\in H^{1}(\Omega )\cap \text{ M }$, and a mapping $R_{\mu }:H^{2}(\Omega )^d\cap \mathbf{V} _{n}\rightarrow \mathbf{W} _{\mu }$ satisfy

$$\begin{aligned} \begin{array}{lll} &{}\left( \nabla \times R_{\mu }\mathbf{w} ,\nabla \times \varvec{\Psi }\right) +\left( \nabla \cdot R_{\mu }\mathbf{w} ,\nabla \cdot \varvec{\Psi }\right) = \left( \nabla \times \mathbf{w} ,\nabla \times \varvec{\Psi }\right) +\left( \nabla \cdot \mathbf{w} ,\nabla \cdot \varvec{\Psi }\right) \\ &{}\quad =\left( \nabla \times \mathbf{w} ,\nabla \times \varvec{\Psi }\right) ,\quad \forall \varvec{\Psi }\in \mathbf{W} _{\mu },\\ &{}\qquad \Vert \mathbf{w} -R_{\mu }\mathbf{w} \Vert _{0}+\mu \Vert \mathbf{w} -R_{\mu }\mathbf{w} \Vert _{1}\le C\mu ^2\Vert \mathbf{w} \Vert _{2}, \quad \forall \mathbf{w} \in H^{2}(\Omega )^{d}\cap \mathbf{V} _{n}. \end{array} \end{aligned}$$

(22)

Lemma 3.2

The finite element pair ${\mathcal {P}}_{2}$ satisfies the discrete inf-sup condition

$$\begin{aligned} \sup _{(0,0)\ne (\mathbf{v }_{\mu },\mathbf{B }_{\mu })\in \mathbf{W }_{0n}^{\mu } }\frac{ d((\mathbf{v }_{\mu },\mathbf{B }_{\mu }),q_{\mu })}{\Vert (\mathbf{v }_{\mu },\mathbf{B }_{\mu })\Vert _1}\ge \beta _{0} \Vert q_{\mu }\Vert _0, \quad \forall q_{\mu }\in \text{ M }_{\mu }. \end{aligned}$$

(23)

Besides, there exists mappings $\pi _{\mu }:H^{2}(\Omega )^d\cap \mathbf{X} \rightarrow \mathbf{X} _{\mu }$, $\rho _{\mu }:\text{ M }\rightarrow \text{ M }_{\mu }$ satisfy (21) and

$$\begin{aligned} (\nabla \cdot (\mathbf{v} -\pi _{\mu }\mathbf{v} ),q)=0,~~ \forall q\in \text{ M }_{\mu }. \end{aligned}$$

(24)

And mapping $R_{\mu }: H^{2}(\Omega )^d\cap \mathbf{V} _{n}\rightarrow \mathbf{W} _{\mu }$ satisfies (22).

Then, the penalty finite element discretization of (6) is: find $((\mathbf{u }_{\epsilon \mu },\mathbf{B }_{\epsilon \mu }),p_{\epsilon \mu })\in \mathbf{W} _{0n}^{\mu }\times \text{ M }_{\mu }$ such that

$$\begin{aligned} \begin{array}{lll} &{}A_{0}\left( \left( \mathbf{u }_{\epsilon \mu },\mathbf{B }_{\epsilon \mu }\right) ,\left( \mathbf{v} ,\varvec{\Psi }\right) \right) +A_{1}\left( \left( \mathbf{u }_{\epsilon \mu },\mathbf{B }_{\epsilon \mu }\right) ,\left( \mathbf{u }_{\epsilon \mu },\mathbf{B }_{\epsilon \mu }\right) ,\left( \mathbf{v} ,\varvec{\Psi }\right) \right) -d\left( \left( \mathbf{v} ,\varvec{\Psi }\right) ,p_{\epsilon \mu }\right) \\ &{}\quad +\,d\left( \left( \mathbf{u }_{\epsilon \mu },\mathbf{B }_{\epsilon \mu }\right) ,q\right) \\ &{}\quad +\,\frac{\epsilon }{\nu _{e}}\left( p_{\epsilon \mu },q\right) =\,<\mathbf{F },\left( \mathbf{v} ,\varvec{\Psi }\right) >. \end{array} \end{aligned}$$

(25)

Recalling the following stability and optimal error estimate (see [16]).

Theorem 3.1

Under the assumptions of Theorem 2.2 and if $\text{ X }_{\mu }\times \text{ M }_{\mu }$ satisfies property ${\mathcal {P}}_{k}$, $k=1,2$, then (25) admits a unique solution $((\mathbf{u }_{\epsilon \mu },\mathbf{B }_{\epsilon \mu }),p_{\epsilon \mu })\in \mathbf{W} _{0n}^{\mu }\times \text{ M }_{\mu }$ such that

$$\begin{aligned} \Vert |(\mathbf{u }_{\epsilon \mu },\mathbf{B }_{\epsilon \mu })\Vert |_{1}&\le \Vert \mathbf{F }\Vert _{-1}, ~~ \Vert |({\mathcal {A}}_{1\mu }\mathbf{u} _{\epsilon \mu },{\mathcal {A}}_{2\mu }\mathbf{B} _{\epsilon \mu })\Vert |_{0} \le C\Vert \mathbf{F }\Vert _{0},\\ \Vert p_{\epsilon \mu }\Vert _{0}&\le \left( \frac{\nu _{e}}{\epsilon {\underline{\gamma }}}\right) ^{\frac{1}{2}}\Vert \mathbf{F }\Vert _{-1}, \quad for ~{\mathcal {P}}_{1},\\ \Vert p_{\epsilon \mu }\Vert _{0}&\le C\Vert \mathbf{F }\Vert _{-1}, \quad for~ {\mathcal {P}}_{2}, \end{aligned}$$

Theorem 3.2

Under the assumptions of Theorem 2.2 and if $\text{ X }_{\mu }\times \text{ M }_{\mu }$ satisfies property ${\mathcal {P}}_{k}$, $k=1,2$ and assume that $\mu \le \left( \frac{\Vert \mathbf{F }\Vert _{-1}}{\Vert \mathbf{F }\Vert _{0}}\right) ^{\frac{1}{2}}(1-\sigma )$, then we have the following error estimate

$$\begin{aligned} \begin{array}{lll} &{}\left( 1-\sigma \right) \epsilon ^{\frac{1}{2}}\Vert |\left( \mathbf{u }_{\epsilon }-\mathbf{u }_{\epsilon \mu },\mathbf{B }_{\epsilon }-\mathbf{B }_{\epsilon \mu }\right) \Vert |_{0} +\mu \left( \Vert |\left( \mathbf{u }_{\epsilon }-\mathbf{u }_{\epsilon \mu },\mathbf{B }_{\epsilon }-\mathbf{B }_{\epsilon \mu }\right) \Vert |_{1} +\epsilon ^{\frac{1}{2}}\Vert p_{\epsilon }-p_{\epsilon \mu }\Vert _{0}\right) \\ &{}\quad \le C\epsilon ^{-\frac{1}{2}}\mu ^2\Vert \mathbf{F }\Vert _{0},\\ &{}\left( 1-\sigma \right) \Vert |\left( \mathbf{u }_{\epsilon }-\mathbf{u }_{\epsilon \mu },\mathbf{B }_{\epsilon }-\mathbf{B }_{\epsilon \mu }\right) \Vert |_{0} +\mu \left( \Vert |\left( \mathbf{u }_{\epsilon }-\mathbf{u }_{\epsilon \mu },\mathbf{B }_{\epsilon }-\mathbf{B }_{\epsilon \mu }\right) \Vert |_{1} +\Vert p_{\epsilon }-p_{\epsilon \mu }\Vert _{0}\right) \\ &{}\quad \le C \mu ^2\Vert \mathbf{F }\Vert _{0}, \end{array} \end{aligned}$$

for ${\mathcal {P}}_{1}$ and ${\mathcal {P}}_{2}$, respectively.

Remark 3.1

On account of the important relation (20), the discrete penalty finite element form for ${\mathcal {P}}_{1}$ can be defined as follows

$$\begin{aligned}&A_{0}\left( \left( \mathbf{u }_{\epsilon \mu },\mathbf{B }_{\epsilon \mu }\right) ,\left( \mathbf{v} ,\varvec{\Psi }\right) \right) +A_{1}\left( \left( \mathbf{u }_{\epsilon \mu },\mathbf{B }_{\epsilon \mu }\right) ,\left( \mathbf{u }_{\epsilon \mu },\mathbf{B }_{\epsilon \mu }\right) ,\left( \mathbf{v} ,\varvec{\Psi }\right) \right) +\frac{\nu _{e}}{\epsilon }\left( \text{ div }\mathbf{u} _{\epsilon \mu },\text{ div }\mathbf{v} \right) \\&\quad =\,<\mathbf{F },\left( \mathbf{v} ,\varvec{\Psi }\right) >,\\&\qquad p_{\epsilon \mu }=-\frac{\nu _{e}}{\epsilon }\text{ div }\mathbf{u} _{\epsilon \mu }. \end{aligned}$$

But the finite element space $\mathbf{X} _{h}\times M_{h}$ for ${\mathcal {P}}_{2}$ does not have property (20). Therefore, we have to employ the projection $\rho _{\mu }$ to rewrite the penalty finite element discretization as

$$\begin{aligned}&A_{0}\left( \left( \mathbf{u }_{\epsilon \mu },\mathbf{B }_{\epsilon \mu }\right) ,\left( \mathbf{v} ,\varvec{\Psi }\right) \right) +A_{1}\left( \left( \mathbf{u }_{\epsilon \mu },\mathbf{B }_{\epsilon \mu }\right) ,\left( \mathbf{u }_{\epsilon \mu },\mathbf{B }_{\epsilon \mu }\right) ,\left( \mathbf{v} ,\varvec{\Psi }\right) \right) +\frac{\nu _{e}}{\epsilon }\left( \rho _{\mu }\text{ div }\mathbf{u} _{\epsilon \mu },\rho _{\mu }\text{ div }\mathbf{v} \right) \\&\quad =\,<\mathbf{F },\left( \mathbf{v} ,\varvec{\Psi }\right) >,\\&\qquad p_{\epsilon \mu }=-\frac{\nu _{e}}{\epsilon }\rho _{\mu }\text{ div }\mathbf{u} _{\epsilon \mu }. \end{aligned}$$

Then, the dimension of the stiffness matrix reduces greatly and leads to a relatively small definite positive stiffness matrix. However, it is very difficult to compute $\rho _{\mu }\text{ div }\mathbf{v}$ for the functions in $M_{\mu }$ are globally discontinuous and $\rho _{\mu }$ is a local projection operator, which acting separately element by element (refer to [33] for details).

4 Penalty Iterative Methods for the 2D/3D Stationary MHD Equations

The Oseen iterative methods in penalty idea which based on finite element pair ${\mathcal {P}}_{1}$ and ${\mathcal {P}}_{2}$ and several two-level schemes are introduced as follows.

Method 0 (Oseen iterative method). Find $((\mathbf{u }_{\epsilon \mu }^{n},\mathbf{B }_{\epsilon \mu }^{n}),p_{\epsilon \mu }^{n})\in \mathbf{W} ^{\mu }_{0n}\times \text{ M }_{\mu }$ such that for all $((\mathbf{v} ,\varvec{\Psi }),q)\in \mathbf{W} ^{\mu }_{0n}\times \text{ M }_{\mu }$

$$\begin{aligned} \begin{array}{lll} &{}A_{0}\left( \left( \mathbf{u }_{\epsilon \mu }^n,\mathbf{B }_{\epsilon \mu }^n\right) ,\left( \mathbf{v} ,\varvec{\Psi }\right) \right) -d\left( \left( \mathbf{v} ,\varvec{\Psi }\right) ,p_{\epsilon \mu }^{n}\right) +d\left( \left( \mathbf{u }_{\epsilon \mu }^n,\mathbf{B }_{\epsilon \mu }^n\right) ,q\right) +\frac{\epsilon }{\nu _{e}}\left( p_{\epsilon \mu }^{n},q\right) \\ &{}\quad +\,A_{1}\left( \left( \mathbf{u }_{\epsilon \mu }^{n-1},\mathbf{B }_{\epsilon \mu }^{n-1}\right) ,\left( \mathbf{u }_{\epsilon \mu }^{n},\mathbf{B }_{\epsilon \mu }^{n}\right) ,\left( \mathbf{v} ,\varvec{\Psi }\right) \right) =<\mathbf{F },\left( \mathbf{v} ,\varvec{\Psi }\right) >. \end{array} \end{aligned}$$

(26)

Here, $((\mathbf{u }_{\epsilon \mu }^{0},\mathbf{B }_{\epsilon \mu }^{0}),p_{\epsilon \mu }^{0})$ is defined by the discrete penalty equation:

$$\begin{aligned} \begin{array}{lll} &{}A_{0}\left( \left( \mathbf{u }_{\epsilon \mu }^0,\mathbf{B }_{\epsilon \mu }^0\right) ,\left( \mathbf{v} ,\varvec{\Psi }\right) \right) -d\left( \left( \mathbf{v} ,\varvec{\Psi }\right) ,p_{\epsilon \mu }^{0}\right) \\ &{}\quad +\,d\left( \left( \mathbf{u }_{\epsilon \mu }^0,\mathbf{B }_{\epsilon \mu }^0\right) ,q\right) +\frac{\epsilon }{\nu _{e}}\left( p_{\epsilon \mu }^{0},q\right) =\,<\mathbf{F },\left( \mathbf{v} ,\varvec{\Psi }\right) >, \end{array} \end{aligned}$$

(27)

for all $((\mathbf{v} ,\varvec{\Psi }),q)\in \mathbf{W} ^{\mu }_{0n}\times \text{ M }_{\mu }$.

Based on our previous work [16, 17], we have the following stability estimate of the iterative method.

Theorem 4.1

Under the assumptions of Theorem 3.2 and uniqueness condition $0<\sigma <1$ valid, suppose that ${\mathcal {P}}_{1}$ and ${\mathcal {P}}_{2}$ are valid, then $(\mathbf{u }_{\epsilon \mu }^{m},\mathbf{B }_{\epsilon \mu }^{m})$ and $p_{\epsilon \mu }^{m}$ defined by the Method 0 satisfy

$$\begin{aligned} \begin{array}{lll} \Vert |(\mathbf{u }_{\epsilon \mu }^{m},\mathbf{B }_{\epsilon \mu }^{m})\Vert |_{1}\le \Vert \mathbf{F }\Vert _{-1}, \quad \Vert |({\mathcal {A}}_{1\mu }\mathbf{u }_{\epsilon \mu }^{m},{\mathcal {A}}_{2\mu }\mathbf{B }_{\epsilon \mu }^{m})\Vert |_{1} \le C\Vert \mathbf{F }\Vert _{0},\\ \Vert p_{\epsilon \mu }^{m}\Vert _{0} \le \left( \frac{\nu _{e}}{\epsilon {\underline{\gamma }}}\right) ^{\frac{1}{2}}\ |\mathbf{F }\Vert _{-1},~ for~{\mathcal {P}}_{1},~~~ \Vert p_{\epsilon \mu }^{m}\Vert _{0} \le \beta _{0}^{-1}\left( \frac{{\overline{\gamma }}}{{\underline{\gamma }}}+2\right) \Vert \mathbf{F }\Vert _{-1},~ for~ {\mathcal {P}}_{2}, \end{array} \end{aligned}$$

and satisfy the following error bounds: for ${\mathcal {P}}_{1}$

$$\begin{aligned} \Vert |\left( \mathbf{u }-\mathbf{u }_{\epsilon \mu }^{m},\mathbf{B }-\mathbf{B }_{\epsilon \mu }^{m}\right) \Vert |_{1} \le C\epsilon +\,C\epsilon ^{-\frac{1}{2}}\mu +\sigma ^m\Vert \mathbf{F }\Vert _{-1},\\ \Vert p-p_{\epsilon \mu }^{m}\Vert _{0} \le C\epsilon +\,C\epsilon ^{-1}\mu +\left( \frac{\nu _{e}}{\epsilon {\underline{\gamma }}} \right) ^{\frac{1}{2}}\sigma ^m\Vert \mathbf{F }\Vert _{-1}, \end{aligned}$$

and for ${\mathcal {P}}_{2}$

$$\begin{aligned} \Vert |\left( \mathbf{u }-\mathbf{u }_{\epsilon \mu }^{m},\mathbf{B }-\mathbf{B }_{\epsilon \mu }^{m}\right) \Vert |_{1} \le C\epsilon +C\mu +\sigma ^m\Vert \mathbf{F }\Vert _{-1},\\ \Vert p-p_{\epsilon \mu }^{m}\Vert _{0} \le C\epsilon +C\mu +\beta _{0}^{-1}\left( \frac{{\overline{\gamma }}}{{\underline{\gamma }}}+2\right) \sigma ^m\Vert \mathbf{F }\Vert _{-1}, \end{aligned}$$

for all $m\ge 0$.

4.1 Two-Level Oseen Penalty Iterative Methods

In this section, we consider the two-level Oseen penalty finite element methods under the strong uniqueness condition $\sigma \le 1-\left( \frac{\Vert \mathbf{F }\Vert _{-1}}{\Vert \mathbf{F }\Vert _{0}}\right) ^{\frac{1}{2}}<1$. The methods includes two algorithms: m iteration steps by Oseen technique on the coarse mesh H and once correction by the three corresponding iteration on the fine mesh h.

Method 1.

Step I. Find a coarse grid penalty iterative solution $((\mathbf{u} _{\epsilon H}^m,\mathbf{B} _{\epsilon H}^m),p_{\epsilon H}^{m})\in \mathbf{W} _{0n}^{H}\times \text{ M }_{H}$ such that

$$\begin{aligned} \begin{array}{lll} &{}A_{0}\left( \left( \mathbf{u }_{\epsilon H}^n,\mathbf{B }_{\epsilon H}^n\right) ,\left( \mathbf{v} ,\varvec{\Psi }\right) \right) -d\left( \left( \mathbf{v} ,\varvec{\Psi }\right) ,p_{\epsilon H}^{n}\right) +d\left( \left( \mathbf{u }_{\epsilon H}^n,\mathbf{B }_{\epsilon H}^n\right) ,q\right) +\frac{\epsilon }{\nu _{e}}\left( p_{\epsilon H}^{n},q\right) \\ &{}\quad +\,A_{1}\left( \left( \mathbf{u }_{\epsilon H}^{n-1},\mathbf{B }_{\epsilon H}^{n-1}\right) ,\left( \mathbf{u }_{\epsilon H}^{n},\mathbf{B }_{\epsilon H}^{n}\right) ,\left( \mathbf{v} ,\varvec{\Psi }\right) \right) =<\mathbf{F },\left( \mathbf{v} ,\varvec{\Psi }\right) >. \end{array} \end{aligned}$$

(28)

for $n=1,2,\ldots ,m$, where $((\mathbf{u} _{\epsilon H}^0,\mathbf{B} _{\epsilon H}^0),p_{\epsilon H}^{0})$ is determined by

$$\begin{aligned} \begin{array}{lll} &{}A_{0}\left( \left( \mathbf{u} _{\epsilon H}^{0},\mathbf{B} _{\epsilon H}^{0}\right) ,\left( \mathbf{v} ,\varvec{\Psi }\right) \right) -d\left( \left( \mathbf{v} ,\varvec{\Psi }\right) ,p_{\epsilon H}^{0}\right) +d\left( \left( \mathbf{u} _{\epsilon H}^{0},\mathbf{B} _{\epsilon H}^{0}\right) ,q\right) \\ &{}\quad +\,\frac{\epsilon }{\nu _{e}}\left( p_{\epsilon H}^{0},q\right) =\langle \mathbf{F },\left( \mathbf{v} ,\varvec{\Psi }\right) \rangle , \end{array} \end{aligned}$$

(29)

for all $((\mathbf{v} ,\varvec{\Psi }),q)\in \mathbf{W} _{0n}^{H}\times \text{ M }_{H}$.

Step II. Find a fine grid solution $((\mathbf{u} _{\epsilon mh},\mathbf{B} _{\epsilon mh}),p_{\epsilon mh})\in \mathbf{W} _{0n}^{h}\times \text{ M }_{h}$ defined by the following Stokes correction.

$$\begin{aligned} \begin{array}{lll} &{}A_{0}\left( \left( \mathbf{u} _{\epsilon mh},\mathbf{B} _{\epsilon mh}\right) ,\left( \mathbf{v} ,\varvec{\Psi }\right) \right) -d\left( \left( \mathbf{v} ,\varvec{\Psi }\right) ,p_{\epsilon mh}\right) +d\left( \left( \mathbf{u} _{\epsilon mh},\mathbf{B} _{\epsilon mh}\right) ,q\right) +\frac{\epsilon }{\nu _{e}}\left( p_{\epsilon mh},q\right) \\ &{}\quad =\langle \mathbf{F },\left( \mathbf{v} ,\varvec{\Psi }\right) \rangle - A_{1}\left( \left( \mathbf{u} _{\epsilon H}^{m},\mathbf{u} _{\epsilon H}^{m}\right) , \left( \mathbf{u} _{\epsilon H}^{m},\mathbf{u} _{\epsilon H}^{m}\right) ,\left( \mathbf{v} ,\varvec{\Psi }\right) \right) , \end{array}\nonumber \\ \end{aligned}$$

(30)

for all $((\mathbf{v} ,\varvec{\Psi }),q)\in \mathbf{W} _{0n}^{h}\times \text{ M }_{h}$.

Theorem 4.2

Under the assumptions of Theorem 4.1 and $\sigma \le 1-\left( \frac{\Vert \mathbf{F }\Vert _{-1}}{\Vert \mathbf{F }\Vert _{0}}\right) ^{\frac{1}{2}}<1$, then $((\mathbf{u} _{\epsilon mh},\mathbf{B} _{\epsilon mh}),p_{\epsilon mh})$ provided by Method 1 satisfies the following stability and error estimates:

$$\begin{aligned} \Vert |(\mathbf{u }_{\epsilon mh},\mathbf{B }_{\epsilon mh})\Vert |_{1}\le & {} 2\Vert \mathbf{F }\Vert _{-1},\nonumber \\ \Vert p_{\epsilon mh}\Vert _{0}\le & {} \left( \frac{4\nu _{e}}{\epsilon {\underline{\gamma }}}\right) ^{\frac{1}{2}}\Vert \mathbf{F }\Vert _{-1},~ \textit{for}~{\mathcal {P}}_{1},~~\nonumber \\ \Vert p_{\epsilon mh}\Vert _{0}\le & {} 2\beta _{0}^{-1}\left( \frac{{\overline{\gamma }}}{{\underline{\gamma }}}+1\right) \Vert \mathbf{F }\Vert _{-1}, ~ \textit{for}~{\mathcal {P}}_{2}, \end{aligned}$$

(31)

and satisfy the following error bounds: for ${\mathcal {P}}_{1}$

$$\begin{aligned} \begin{array}{lll} &{}\Vert |\left( \mathbf{u }-\mathbf{u }_{\epsilon mh},\mathbf{B }-\mathbf{B }_{\epsilon mh}\right) \Vert |_{1} \le C\left[ \epsilon + \epsilon ^{-\frac{1}{2}}\left( h+\epsilon ^{-\frac{1}{2}}H^2\left( \frac{\Vert \mathbf{F }\Vert _{0}}{\Vert \mathbf{F }\Vert _{-1}}\right) ^{\frac{1}{2}}\right) \right] \Vert \mathbf{F }\Vert _{0}\\ &{}\quad +\,C\Vert |\left( \mathbf{u} _{\epsilon H}-\mathbf{u} _{\epsilon H}^{m},\mathbf{B} _{\epsilon H}-\mathbf{B} _{\epsilon H}^{m}\right) \Vert |_{1},\\ &{} \Vert p-p_{\epsilon mh}\Vert _{0} \le C\left[ \epsilon + \epsilon ^{-1}\left( h+\epsilon ^{-\frac{1}{2}}H^2\left( \frac{\Vert \mathbf{F }\Vert _{0}}{\Vert \mathbf{F }\Vert _{-1}}\right) ^{\frac{1}{2}}\right) \right] \Vert \mathbf{F }\Vert _{0}\\ &{}\quad +\,C\Vert |\left( \mathbf{u} _{\epsilon H}-\mathbf{u} _{\epsilon H}^{m},\mathbf{B} _{\epsilon H}-\mathbf{B} _{\epsilon H}^{m}\right) \Vert |_{1}, \end{array} \end{aligned}$$

$\epsilon$ and H can be taken as $\epsilon =O(h^{\frac{1}{2}})$, $H^2=O(\epsilon ^{\frac{1}{2}}h)$ and the convergence rate is $O(h^{\frac{1}{2}})$; for ${\mathcal {P}}_{2}$, the optimal error estimates are

$$\begin{aligned} \begin{array}{lll} &{}\Vert |\left( \mathbf{u }-\mathbf{u }_{\epsilon mh},\mathbf{B }-\mathbf{B }_{\epsilon mh}\right) \Vert |_{1} + \Vert p-p_{\epsilon mh}\Vert _{0} \le C\left( \epsilon +h+H^2\left( \frac{\Vert \mathbf{F }\Vert _{0}}{\Vert \mathbf{F }\Vert _{-1}}\right) ^{\frac{1}{2}}\right) \Vert \mathbf{F }\Vert _{0}\\ &{}\quad +\,C\Vert |\left( \mathbf{u} _{\epsilon H}-\mathbf{u} _{\epsilon H}^{m},\mathbf{B} _{\epsilon H}-\mathbf{B} _{\epsilon H}^{m}\right) \Vert |_{1}, \end{array} \end{aligned}$$

$\epsilon$ and H can be taken as $\epsilon =O(h)$, $H^2=O(h)$ and the convergence rate is O(h);

Proof

We can arrive at the stability estimate (31) by setting $(\mathbf{v} ,\varvec{\Psi })=(\mathbf{u }_{\epsilon mh},\mathbf{B }_{\epsilon mh})$ and $q=p_{\epsilon mh}$ in (30) and combining (8)–(10) with (23).

For the error estimate, subtracting (30) from (25) with $\mu =h$ and take $(\mathbf{e} _{h},\mathbf{b} _{h})=(\mathbf{u} _{\epsilon h}-\mathbf{u} _{\epsilon mh},\mathbf{B} _{\epsilon h}-\mathbf{B} _{\epsilon mh})$, $\eta _{h}=p_{\epsilon h}-p_{\epsilon mh}$, we have following error equation

$$\begin{aligned} \begin{array}{lllll} &{}A_{0}\left( \left( \mathbf{e} _{ h},\mathbf{b} _{ h}\right) ,\left( \mathbf{v} ,\varvec{\Psi }\right) \right) -d\left( \left( \mathbf{v} ,\varvec{\Psi }\right) ,\eta _{h}\right) +d\left( \left( \mathbf{e} _{ h},\mathbf{b} _{ h}\right) ,q\right) +\frac{\epsilon }{\nu _{e}}\left( \eta _{h},q\right) \\ &{}\quad +\,A_{1}\left( \left( \mathbf{u} _{\epsilon h}-\mathbf{u} _{\epsilon H},\mathbf{B} _{\epsilon h}-\mathbf{B} _{\epsilon H}\right) ,\left( \mathbf{u} _{\epsilon h},\mathbf{B} _{\epsilon h}\right) ,\left( \mathbf{v} ,\varvec{\Psi }\right) \right) \\ &{}\quad +\,A_{1}\left( \left( \mathbf{u} _{\epsilon H},\mathbf{B} _{\epsilon H}\right) ,\left( \mathbf{u} _{\epsilon h}-\mathbf{u} _{\epsilon H},\mathbf{B} _{\epsilon h}-\mathbf{B} _{\epsilon H}\right) , \left( \mathbf{v} ,\varvec{\Psi }\right) \right) \\ &{}\quad +\,A_{1}\left( \left( \mathbf{u} _{\epsilon H}-\mathbf{u} _{\epsilon H}^{m},\mathbf{B} _{\epsilon H}-\mathbf{u} _{\epsilon H}^{m}\right) ,\left( \mathbf{u} _{\epsilon H},\mathbf{B} _{\epsilon H}\right) ,\left( \mathbf{v} ,\varvec{\Psi }\right) \right) \\ &{}\quad +\,A_{1}\left( \left( \mathbf{u} _{\epsilon H}^m,\mathbf{B} _{\epsilon H}^m\right) ,\left( \mathbf{u} _{\epsilon H}-\mathbf{u} _{\epsilon H}^{m},\mathbf{B} _{\epsilon H}-\mathbf{u} _{\epsilon H}^{m}\right) ,\left( \mathbf{v} ,\varvec{\Psi }\right) \right) =0. \end{array} \end{aligned}$$

(32)

Substituting $(\mathbf{v} ,\varvec{\Psi })=(\mathbf{e} _{h},\mathbf{b} _{h})$, $q=\eta _{h}$ in (32) with (8), (9), (13) and Theorem 3.1, we have

$$\begin{aligned} \begin{array}{lll} &{}\frac{1}{{\underline{\gamma }}} \Vert |\left( \mathbf{e} _{h},\mathbf{b} _{h}\right) \Vert |_{1}^2 +\frac{\epsilon }{\nu _{e}}\Vert \eta _{h}\Vert _{0}^{2}\\ &{}\quad \le \frac{CN}{{\underline{\gamma }}^2} \Vert |\left( \mathbf{u} _{\epsilon h}-\mathbf{u} _{\epsilon H},\mathbf{B} _{\epsilon h}-\mathbf{B} _{\epsilon H}\right) \Vert |_{0} \Big \{\Vert \left( {\mathcal {A}}_{1H}\mathbf{u} _{\epsilon H},{\mathcal {A}}_{2H}\mathbf{B} _{\epsilon H}\right) \Vert _{0}\\ &{}\qquad +\,\Vert \left( {\mathcal {A}}_{1h}\mathbf{u} _{\epsilon h},{\mathcal {A}}_{2h}\mathbf{B} _{\epsilon h}\right) \Vert _{0}\Big \} \Vert |\left( \mathbf{e} _{h},\mathbf{b} _{h}\right) \Vert |_{1}\\ &{}\qquad +\,\frac{N}{{\underline{\gamma }}^3} \Vert |\left( \mathbf{u} _{\epsilon H}-\mathbf{u} _{\epsilon H}^m,\mathbf{B} _{\epsilon H}-\mathbf{B} _{\epsilon H}^m\right) \Vert |_{1} \\ &{}\qquad \Big \{\Vert |\left( \mathbf{u} _{\epsilon H},\mathbf{B} _{\epsilon H}\right) \Vert |_{1} + \Vert |\left( \mathbf{u} _{\epsilon H}^m,\mathbf{B} _{\epsilon H}^m\right) \Vert |_{1}\Big \} \Vert |\left( \mathbf{e} _{h},\mathbf{b} _{h}\right) \Vert |_{1}, \end{array} \end{aligned}$$

(33)

which guarantees that

$$\begin{aligned} \begin{array}{lll} \Vert |\left( \mathbf{e} _{h},\mathbf{b} _{h}\right) \Vert |_{1} \le C\sigma \frac{\Vert \mathbf{F }\Vert _{0}}{\Vert \mathbf{F }\Vert _{-1}} \Vert |\left( \mathbf{u} _{\epsilon h}-\mathbf{u} _{\epsilon H},\mathbf{B} _{\epsilon h}-\mathbf{B} _{\epsilon H}\right) \Vert |_{0} \\ \quad +2\sigma \Vert |\left( \mathbf{u} _{\epsilon H}-\mathbf{u} _{\epsilon H}^m,\mathbf{B} _{\epsilon H}-\mathbf{B} _{\epsilon H}^m\right) \Vert |_{1}. \end{array} \end{aligned}$$

(34)

For ${\mathcal {P}}_{1}$, using Theorems 3.1, 3.2, 4.1 and (34), we derive that

$$\begin{aligned} \begin{array}{lll} \Vert |\left( \mathbf{e} _{h},\mathbf{b} _{h}\right) \Vert |_{1}\le C\left[ \epsilon ^{-1}H^2\left( \frac{\Vert \mathbf{F }\Vert _{0}}{\Vert \mathbf{F }\Vert _{-1}}\right) ^{\frac{1}{2}}\Vert \mathbf{F }\Vert _{0} +\Vert |\left( \mathbf{u} _{\epsilon H}-\mathbf{u} _{\epsilon H}^{m},\mathbf{B} _{\epsilon H}-\mathbf{B} _{\epsilon H}^{m}\right) \Vert |_{1}\right] , \end{array} \end{aligned}$$

(35)

then utilising (33) and Young’s inequality, we deduce

$$\begin{aligned} \begin{array}{lll} \frac{\epsilon }{\nu _{e}}\Vert \eta _{h}\Vert _{0}^{2} \le C\left[ \epsilon ^{-2}H^4\frac{\Vert \mathbf{F }\Vert _{0}}{\Vert \mathbf{F }\Vert _{-1}}\Vert \mathbf{F }\Vert _{0}^2 +\Vert |\left( \mathbf{u} _{\epsilon H}-\mathbf{u} _{\epsilon H}^{m},\mathbf{B} _{\epsilon H}-\mathbf{B} _{\epsilon H}^{m}\right) \Vert |_{1}^2\right] , \end{array} \end{aligned}$$

which we can get the error estimate for ${\mathcal {P}}_{1}$.

Combining Theorems 3.2, 4.1 and (34), the bound for ${\mathcal {P}}_{2}$ is

$$\begin{aligned} \begin{array}{lll} \Vert |\left( \mathbf{e} _{h},\mathbf{b} _{h}\right) \Vert |_{1}\le C\left[ H^2\left( \frac{\Vert \mathbf{F }\Vert _{0}}{\Vert \mathbf{F }\Vert _{-1}}\right) ^{\frac{1}{2}}\Vert \mathbf{F }\Vert _{0} +\Vert |\left( \mathbf{u} _{\epsilon H}-\mathbf{u} _{\epsilon H}^{m},\mathbf{B} _{\epsilon H}-\mathbf{B} _{\epsilon H}^{m}\right) \Vert |_{1}\right] , \end{array} \end{aligned}$$

(36)

and with (23), (34), (7), (36), Theorems 3.2 and 4.1 , we conclude

$$\begin{aligned} \begin{array}{lll} \Vert \eta _{h}\Vert _{0} \le C\beta _{0}^{-1}\left[ H^2\left( \frac{\Vert \mathbf{F }\Vert _{0}}{\Vert \mathbf{F }\Vert _{-1}}\right) ^{\frac{1}{2}}\Vert \mathbf{F }\Vert _{0} +\Vert |\left( \mathbf{u} _{\epsilon H}-\mathbf{u} _{\epsilon H}^{m},\mathbf{B} _{\epsilon H}-\mathbf{B} _{\epsilon H}^{m}\right) \Vert |_{1}\right] . \end{array} \end{aligned}$$

(37)

We can finish the proof by Theorems 2.3, 3.2 and triangle inequality and some simple calculations. $\square$

Method 2.

Step I. Find a coarse grid penalty iterative solution $((\mathbf{u} _{\epsilon H}^m,\mathbf{B} _{\epsilon H}^m),p_{\epsilon H}^{m})\in \mathbf{W} _{0n}^{H}\times \text{ M }_{H}$ such that

$$\begin{aligned} \begin{array}{lll} &{}A_{0}\left( \left( \mathbf{u }_{\epsilon H}^n,\mathbf{B }_{\epsilon H}^n\right) ,\left( \mathbf{v} ,\varvec{\Psi }\right) \right) -d\left( \left( \mathbf{v} ,\varvec{\Psi }\right) ,p_{\epsilon H}^{n}\right) +d\left( \left( \mathbf{u }_{\epsilon H}^n,\mathbf{B }_{\epsilon H}^n\right) ,q\right) +\frac{\epsilon }{\nu _{e}}\left( p_{\epsilon H}^{n},q\right) \\ &{}\quad +\,A_{1}\left( \left( \mathbf{u }_{\epsilon H}^{n-1},\mathbf{B }_{\epsilon H}^{n-1}\right) ,\left( \mathbf{u }_{\epsilon H}^{n},\mathbf{B }_{\epsilon H}^{n}\right) ,\left( \mathbf{v} ,\varvec{\Psi }\right) \right) =<\mathbf{F },\left( \mathbf{v} ,\varvec{\Psi }\right) >. \end{array} \end{aligned}$$

(38)

for $n=1,2,\ldots ,m$, where $((\mathbf{u} _{\epsilon H}^0,\mathbf{B} _{\epsilon H}^0),p_{\epsilon H}^{0})$ is determined by

$$\begin{aligned} \begin{array}{lll} A_{0}\left( \left( \mathbf{u} _{\epsilon H}^{0},\mathbf{B} _{\epsilon H}^{0}\right) ,\left( \mathbf{v} ,\varvec{\Psi }\right) \right) -d\left( \left( \mathbf{v} ,\varvec{\Psi }\right) ,p_{\epsilon H}^{0}\right) +d\left( \left( \mathbf{u} _{\epsilon H}^{0},\mathbf{B} _{\epsilon H}^{0}\right) ,q\right) +\frac{\epsilon }{\nu _{e}}\left( p_{\epsilon H}^{0},q\right) \\ \quad =\langle \mathbf{F },\left( \mathbf{v} ,\varvec{\Psi }\right) \rangle , \end{array} \end{aligned}$$

(39)

for all $((\mathbf{v} ,\varvec{\Psi }),q)\in \mathbf{W} _{0n}^{H}\times \text{ M }_{H}$.

Step II. Find a fine grid solution $((\mathbf{u} _{\epsilon mh},\mathbf{B} _{\epsilon mh}),p_{\epsilon mh})\in \mathbf{W} _{0n}^{h}\times \text{ M }_{h}$ defined by the following Newton correction.

$$\begin{aligned}&A_{0}\left( \left( \mathbf{u }_{\epsilon mh},\mathbf{B }_{\epsilon mh}\right) ,\left( \mathbf{v} ,\varvec{\Psi }\right) \right) -d\left( \left( \mathbf{v} ,\varvec{\Psi }\right) ,p_{\epsilon mh}\right) +d\left( \left( \mathbf{u }_{\epsilon mh},\mathbf{B }_{\epsilon mh}\right) ,q\right) +\frac{\epsilon }{\nu _{e}}\left( p_{\epsilon mh},q\right) \nonumber \\&\qquad +\,A_{1}\left( \left( \mathbf{u }_{\epsilon mh},\mathbf{B }_{\epsilon mh}\right) ,\left( \mathbf{u }_{\epsilon H}^{m},\mathbf{B }_{\epsilon H}^{m}\right) ,\left( \mathbf{v} ,\varvec{\Psi }\right) \right) +A_{1}\left( \left( \mathbf{u }_{\epsilon H}^{m},\mathbf{B }_{\epsilon H}^{m}\right) ,\left( \mathbf{u }_{\epsilon mh},\mathbf{B }_{\epsilon mh}\right) ,\left( \mathbf{v} ,\varvec{\Psi }\right) \right) \nonumber \\&\quad =\,<\mathbf{F },\left( \mathbf{v} ,\varvec{\Psi }\right) >+A_{1}\left( \left( \mathbf{u }_{\epsilon H}^{m},\mathbf{B }_{\epsilon H}^{m}\right) ,\left( \mathbf{u }_{\epsilon H}^{m},\mathbf{B }_{\epsilon H}^{m}\right) ,\left( \mathbf{v} ,\varvec{\Psi }\right) \right) . \end{aligned}$$

(40)

for all $((\mathbf{v} ,\varvec{\Psi }),q)\in \mathbf{W} _{0n}^{h}\times \text{ M }_{h}$.

Theorem 4.3

Under the assumptions of Theorem 4.2, then $((\mathbf{u} _{\epsilon mh},\mathbf{B} _{\epsilon mh}),p_{\epsilon mh})$ provided by Method 2 with Newton Correction satisfies the following stability and error estimates:

$$\begin{aligned} \Vert |\left( \mathbf{u }_{\epsilon mh},\mathbf{B }_{\epsilon mh}\right) \Vert |_{1}&\le 2\Vert \mathbf{F }\Vert _{-1} +\frac{\sigma }{\Vert \mathbf{F }\Vert _{-1}} \Vert |\left( \mathbf{u} _{\epsilon mh}-\mathbf{u} _{\epsilon H}^{m},\mathbf{B} _{\epsilon mh}-\mathbf{B} _{\epsilon H}^{m}\right) \Vert |_{1}^2,\nonumber \\ \Vert p_{\epsilon mh}\Vert _{0}&\le C\left( \frac{\nu _{e}}{{\underline{\gamma }}\epsilon }\right) ^{\frac{1}{2}} \left[ \Vert \mathbf{F }\Vert _{-1} +\Vert |\left( \mathbf{u} _{\epsilon mh}-\mathbf{u} _{\epsilon H}^{m},\mathbf{B} _{\epsilon mh}-\mathbf{B} _{\epsilon H}^{m}\right) \Vert |_{1}^2\right] ,~ \textit{for}~{\mathcal {P}}_{1},\nonumber \\ \Vert p_{\epsilon mh}\Vert _{0}&\le C\left[ \Vert \mathbf{F }\Vert _{-1} +\Vert |\left( \mathbf{u} _{\epsilon mh}-\mathbf{u} _{\epsilon H}^{m},\mathbf{B} _{\epsilon mh}-\mathbf{B} _{\epsilon H}^{m}\right) \Vert |_{1}^2\right] , ~ \textit{for}~{\mathcal {P}}_{2}, \end{aligned}$$

(41)

and $((\mathbf{u} _{\epsilon mh},\mathbf{B} _{\epsilon mh}),p_{\epsilon mh})$ satisfies the following error estimates, for ${\mathcal {P}}_{1}$

$$\begin{aligned} \begin{array}{lll} &{}\Vert |\left( \mathbf{u }-\mathbf{u }_{\epsilon mh},\mathbf{B }-\mathbf{B }_{\epsilon mh}\right) \Vert |_{1} \le C\left[ \epsilon + \epsilon ^{-\frac{1}{2}}\left( h+\epsilon ^{-1}|\ln h|H^3\frac{\Vert \mathbf{F }\Vert _{0}}{\Vert \mathbf{F }\Vert _{-1}}\right) \right] \Vert \mathbf{F }\Vert _{0}\\ &{}\quad +\,C\Vert |\left( \mathbf{u} _{\epsilon H}-\mathbf{u} _{\epsilon H}^{m},\mathbf{B} _{\epsilon H}-\mathbf{B} _{\epsilon H}^{m}\right) \Vert |_{1}^2,\\ &{}\Vert p-p_{\epsilon mh}\Vert _{0} \le C\left[ \epsilon + \epsilon ^{-1}\left( h+\epsilon ^{-1}|\ln h|H^3\frac{\Vert \mathbf{F }\Vert _{0}}{\Vert \mathbf{F }\Vert _{-1}}\right) \right] \Vert \mathbf{F }\Vert _{0}\\ &{}\quad +\,C\Vert |\left( \mathbf{u} _{\epsilon H}-\mathbf{u} _{\epsilon H}^{m},\mathbf{B} _{\epsilon H}-\mathbf{B} _{\epsilon H}^{m}\right) \Vert |_{1}^2, \end{array} \end{aligned}$$

$\epsilon$ and H can be taken as $\epsilon =O(h^{\frac{1}{2}})$, $H^3=O(\epsilon h|\ln h|^{-1})$ and the convergence rate is $O(h^{\frac{1}{2}})$ in the 2D case; for ${\mathcal {P}}_{2}$, the optimal error estimates are

$$\begin{aligned} \begin{array}{lll} \Vert |\left( \mathbf{u }-\mathbf{u }_{\epsilon mh},\mathbf{B }-\mathbf{B }_{\epsilon mh}\right) \Vert |_{1} + \Vert p-p_{\epsilon mh}\Vert _{0} &{}\le C\left[ \epsilon + h+|\ln h|H^3\frac{\Vert \mathbf{F }\Vert _{0}}{\Vert \mathbf{F }\Vert _{-1}}\right] \Vert \mathbf{F }\Vert _{0}\\ &{}\quad +\,C\Vert |\left( \mathbf{u} _{\epsilon H}-\mathbf{u} _{\epsilon H}^{m},\mathbf{B} _{\epsilon H}-\mathbf{B} _{\epsilon H}^{m}\right) \Vert |_{1}^2, \end{array} \end{aligned}$$

$\epsilon$ and H can be taken as $\epsilon =O(h)$, $H^3=O( h|\ln h|^{-1})$ and the convergence rate is O(h) in the 2D case; and for ${\mathcal {P}}_{1}$

$$\begin{aligned} \Vert |\left( \mathbf{u }-\mathbf{u }_{\epsilon mh},\mathbf{B }-\mathbf{B }_{\epsilon mh}\right) \Vert |_{1}\le & {} C\left[ \epsilon + \epsilon ^{-\frac{1}{2}}\left( h+\epsilon ^{-\frac{3}{4}}H^\frac{5}{2}\frac{\Vert \mathbf{F }\Vert _{0}}{\Vert \mathbf{F }\Vert _{-1}}\right) \right] \Vert \mathbf{F }\Vert _{0}\nonumber \\&+\,C\Vert |\left( \mathbf{u} _{\epsilon H}-\mathbf{u} _{\epsilon H}^{m},\mathbf{B} _{\epsilon H}-\mathbf{B} _{\epsilon H}^{m}\right) \Vert |_{1}^2,\\ \Vert p-p_{\epsilon mh}\Vert _{0}\le & {} C\left[ \epsilon + \epsilon ^{-1}\left( h+\epsilon ^{-\frac{3}{4}}H^\frac{5}{2}\frac{\Vert \mathbf{F }\Vert _{0}}{\Vert \mathbf{F }\Vert _{-1}}\right) \right] \Vert \mathbf{F }\Vert _{0}\nonumber \\&+\,C\Vert |\left( \mathbf{u} _{\epsilon H}-\mathbf{u} _{\epsilon H}^{m},\mathbf{B} _{\epsilon H}-\mathbf{B} _{\epsilon H}^{m}\right) \Vert |_{1}^2, \end{aligned}$$

$\epsilon$ and H can be taken as $\epsilon =O(h^{\frac{1}{2}})$, $H^\frac{5}{2}=O(\epsilon ^{\frac{3}{4}} h)$ and the convergence rate is $O(h^{\frac{1}{2}})$ in the 3D case; for ${\mathcal {P}}_{2}$, the optimal error estimates are

$$\begin{aligned} \Vert |\left( \mathbf{u }-\mathbf{u }_{\epsilon mh},\mathbf{B }-\mathbf{B }_{\epsilon mh}\right) \Vert |_{1} + \Vert p-p_{\epsilon mh}\Vert _{0}\le & {} C\left[ \epsilon + h+H^\frac{5}{2}\frac{\Vert \mathbf{F }\Vert _{0}}{\Vert \mathbf{F }\Vert _{-1}}\right] \Vert \mathbf{F }\Vert _{0}\\&+\,C\Vert |\left( \mathbf{u} _{\epsilon H}-\mathbf{u} _{\epsilon H}^{m},\mathbf{B} _{\epsilon H}-\mathbf{B} _{\epsilon H}^{m}\right) \Vert |_{1}^2, \end{aligned}$$

$\epsilon$ and H can be taken as $\epsilon =O(h)$, $H^\frac{5}{2}=O( h)$ and the convergence rate is O(h) in the 3D case.

Proof

By choosing $(\mathbf{v} ,\varvec{\Psi })=(\mathbf{u} _{\epsilon mh},\mathbf{B} _{\epsilon mh})$ and $q=p_{\epsilon mh}$ in (40), we derive that

$$\begin{aligned}&{\underline{\gamma }}\Vert \left( \mathbf{u} _{\epsilon mh},\mathbf{B} _{\epsilon mh}\right) \Vert _{1}^2 +\frac{\epsilon }{\nu _{e}}\Vert p_{\epsilon mh}\Vert _{0}^2 \nonumber \\&\quad \le N\Vert \left( \mathbf{u} _{\epsilon H}^m,\mathbf{B} _{\epsilon H}^m\right) \Vert _{1} \Vert \left( \mathbf{u} _{\epsilon mh}-\mathbf{u} _{\epsilon H}^{m},\mathbf{B} _{\epsilon mh}-\mathbf{B} _{\epsilon H}^{m}\right) \Vert _{1}\Vert \left( \mathbf{u} _{\epsilon mh},\mathbf{B} _{\epsilon mh}\right) \Vert _{1}\nonumber \\&\qquad +\,\Vert \mathbf{F }\Vert _{-1}\Vert \left( \mathbf{u} _{\epsilon mh},\mathbf{B} _{\epsilon mh}\right) \Vert _{1}, \end{aligned}$$

(42)

which combining Young’s inequality guarantees that

$$\begin{aligned} \Vert |\left( \mathbf{u} _{\epsilon mh},\mathbf{B} _{\epsilon mh}\right) \Vert |_{1}\le & {} \frac{N}{{\underline{\gamma }}^2} \Vert |\left( \mathbf{u} _{\epsilon H}^m,\mathbf{B} _{\epsilon H}^m\right) \Vert |_{1} {\Vert |\left( \mathbf{u} _{\epsilon mh}-\mathbf{u} _{\epsilon H}^{m},\mathbf{B} _{\epsilon mh}-\mathbf{B} _{\epsilon H}^{m}\right) \Vert |_{1}} +\Vert \mathbf{F }\Vert _{-1}\nonumber \\\le & {} \left( \frac{1}{4}\sigma +1\right) \Vert \mathbf{F }\Vert _{-1} +\frac{\sigma }{\Vert \mathbf{F }\Vert _{-1}} \Vert |\left( \mathbf{u} _{\epsilon mh}-\mathbf{u} _{\epsilon H}^{m},\mathbf{B} _{\epsilon mh}-\mathbf{B} _{\epsilon H}^{m}\right) \Vert |_{1}^2.\nonumber \\ \end{aligned}$$

(43)

For ${\mathcal {P}}_{1}$, from (42), (43) and Young’s inequality, we have

$$\begin{aligned} \frac{\epsilon }{\nu _{e}}\Vert p_{\epsilon mh}\Vert _{0}^2\le & {} \frac{N}{{\underline{\gamma }}^3} \Vert |\left( \mathbf{u} _{\epsilon H}^m,\mathbf{B} _{\epsilon H}^m\right) \Vert |_{1} {\Vert |\left( \mathbf{u} _{\epsilon mh}-\mathbf{u} _{\epsilon H}^{m},\mathbf{B} _{\epsilon mh}-\mathbf{B} _{\epsilon H}^{m}\right) \Vert |_{1}} \Vert |\left( \mathbf{u} _{\epsilon mh},\mathbf{B} _{\epsilon mh}\right) \Vert |_{1}\nonumber \\&+\, \frac{1}{{\underline{\gamma }}}\Vert \mathbf{F }\Vert _{-1}\Vert |\left( \mathbf{u} _{\epsilon mh},\mathbf{B} _{\epsilon mh}\right) \Vert |_{1}\nonumber \\\le & {} C\frac{1}{{\underline{\gamma }}} {\Vert |\left( \mathbf{u} _{\epsilon mh}-\mathbf{u} _{\epsilon H}^{m},\mathbf{B} _{\epsilon mh}-\mathbf{B} _{\epsilon H}^{m}\right) \Vert |_{1}^4} +C\frac{1}{{\underline{\gamma }}} \Vert \mathbf{F }\Vert _{-1}^2, \end{aligned}$$

(44)

which is that

$$\begin{aligned} \Vert p_{\epsilon mh}\Vert _{0} \le C\left( \frac{\nu _{e}}{\epsilon {\underline{\gamma }}}\right) ^{\frac{1}{2}} \left[ \Vert \mathbf{F }\Vert _{-1} +\Vert |\left( \mathbf{u} _{\epsilon mh}-\mathbf{u} _{\epsilon H}^{m},\mathbf{B} _{\epsilon mh}-\mathbf{B} _{\epsilon H}^{m}\right) \Vert |_{1}^2\right] . \end{aligned}$$

(45)

Apply the similar technique used in Theorem 4.2, we have the following estimate for ${\mathcal {P}}_{2}$

$$\begin{aligned} \Vert p_{\epsilon mh}\Vert _{0}\le & {} \frac{{\overline{\gamma }}}{{\underline{\gamma }}}\Vert |\left( \mathbf{u} _{\epsilon mh},\mathbf{B} _{\epsilon mh}\right) \Vert |_{1} +\frac{N}{{\underline{\gamma }}^2} \Vert |\left( \mathbf{u} _{\epsilon H}^m,\mathbf{B} _{\epsilon H}^m\right) \Vert |_{1} \Vert |\left( \mathbf{u} _{\epsilon mh},\mathbf{B} _{\epsilon mh}\right) \Vert |_{1}\nonumber \\&+\,\frac{N}{{\underline{\gamma }}^2} \Vert |\left( \mathbf{u} _{\epsilon H}^m,\mathbf{B} _{\epsilon H}^m\right) \Vert |_{1} \Vert |\left( \mathbf{u} _{\epsilon mh}-\mathbf{u} _{\epsilon H}^{m},\mathbf{B} _{\epsilon mh}-\mathbf{B} _{\epsilon H}^{m}\right) \Vert |_{1}+\Vert \mathbf{F }\Vert _{-1}\nonumber \\\le & {} C \left[ \Vert \mathbf{F }\Vert _{-1} +\Vert |\left( \mathbf{u} _{\epsilon mh}-\mathbf{u} _{\epsilon H}^{m},\mathbf{B} _{\epsilon mh}-\mathbf{B} _{\epsilon H}^{m}\right) \Vert |_{1}^2\right] . \end{aligned}$$

(46)

Next, we will give the bounds of error estimate.

Subtracting (40) from (25) with $\mu =h$, we have

$$\begin{aligned}&A_{0}\left( \left( \mathbf{e} _{h},\mathbf{b} _{h}\right) ,\left( \mathbf{v} ,\varvec{\Psi }\right) \right) -d\left( \left( \mathbf{v} ,\varvec{\Psi }\right) ,\eta _{h}\right) +d\left( \left( \mathbf{e} _{h},\mathbf{b} _{h}\right) ,q\right) +\frac{\epsilon }{\nu _{e}}\left( \eta _{h},q\right) \nonumber \\&\quad +\,A_{1}\left( \left( \mathbf{u} _{\epsilon H}^{m},\mathbf{B} _{\epsilon H}^{m}\right) ,\left( \mathbf{e} _{h},\mathbf{b} _{h}\right) ,\left( \mathbf{v} ,\varvec{\Psi }\right) \right) +A_{1}\left( \left( \mathbf{e} _{h},\mathbf{b} _{h}\right) ,\left( \mathbf{u} _{\epsilon H}^{m},\mathbf{B} _{\epsilon H}^{m}\right) ,\left( \mathbf{v} ,\varvec{\Psi }\right) \right) \nonumber \\&\quad +\,A_{1}\left( \left( \mathbf{u} _{\epsilon h}-\mathbf{u} _{\epsilon H}^{m},\mathbf{B} _{\epsilon h}-\mathbf{B} _{\epsilon H}^{m}\right) ,\left( \mathbf{u} _{\epsilon h}-\mathbf{u} _{\epsilon H}^{m},\mathbf{B} _{\epsilon h}-\mathbf{B} _{\epsilon H}^{m}\right) ,\left( \mathbf{v} ,\varvec{\Psi }\right) \right) =0. \end{aligned}$$

(47)

Take $(\mathbf{v} ,\varvec{\Psi })=(\mathbf{e} _{h},\mathbf{b} _{h})$, $q=\eta _{h}$ in (47), with (8), (9), (13) and Theorem 3.1, we have

$$\begin{aligned}&\left( 1-\sigma \right) {\underline{\gamma }}\Vert \left( \mathbf{e} _{h},\mathbf{b} _{h}\right) \Vert _{1}^2 +\frac{\epsilon }{\nu _{e}}\Vert \eta _{h}\Vert _{0}^2\nonumber \\&\quad \le CN\Vert \left( \mathbf{u} _{\epsilon h}-\mathbf{u} _{\epsilon H},\mathbf{B} _{\epsilon h}-\mathbf{B} _{\epsilon H}\right) \Vert _{1}^{\frac{3}{2}} \Vert \left( \mathbf{u} _{\epsilon h}-\mathbf{u} _{\epsilon H},\mathbf{B} _{\epsilon h}-\mathbf{B} _{\epsilon H}\right) \Vert _{0}^{\frac{1}{2}}\Vert \left( \mathbf{e} _{h},\mathbf{b} _{h}\right) \Vert _{1}\nonumber \\&\qquad +\,CN\Vert \left( \mathbf{u} _{\epsilon h}-\mathbf{u} _{\epsilon H},\mathbf{B} _{\epsilon h}-\mathbf{B} _{\epsilon H}\right) \Vert _{1}^{\frac{1}{2}} \Vert \left( \mathbf{u} _{\epsilon h}-\mathbf{u} _{\epsilon H},\mathbf{B} _{\epsilon h}-\mathbf{B} _{\epsilon H}\right) \Vert _{0}^{\frac{1}{2}}\nonumber \\&\qquad \times \,\Vert \left( \mathbf{u} _{\epsilon h}-\mathbf{u} _{\epsilon H},\mathbf{B} _{\epsilon h}-\mathbf{B} _{\epsilon H}\right) \Vert _{1} \Vert \left( \mathbf{e} _{h},\mathbf{b} _{h}\right) \Vert _{1}\nonumber \\&\qquad +\,N\Vert \left( \mathbf{u} _{\epsilon h}-\mathbf{u} _{\epsilon H},\mathbf{B} _{\epsilon h}-\mathbf{B} _{\epsilon H}\right) \Vert _{1}^2 \Vert \left( \mathbf{e} _{h},\mathbf{b} _{h}\right) \Vert _{1}, \end{aligned}$$

(48)

which is that

$$\begin{aligned} \Vert |\left( \mathbf{e} _{h},\mathbf{b} _{h}\right) \Vert |_{1}\le & {} \frac{C\sigma }{\Vert \mathbf{F }\Vert _{-1}} \Vert |\left( \mathbf{u} _{\epsilon h}-\mathbf{u} _{\epsilon H},\mathbf{B} _{\epsilon h}-\mathbf{B} _{\epsilon H}\right) \Vert |_{1}^{\frac{3}{2}} \Vert |\left( \mathbf{u} _{\epsilon h}-\mathbf{u} _{\epsilon H},\mathbf{B} _{\epsilon h}-\mathbf{B} _{\epsilon H}\right) \Vert |_{0}^{\frac{1}{2}}\nonumber \\&+\,\frac{C\sigma }{\Vert \mathbf{F }\Vert _{-1}} \Vert |\left( \mathbf{u} _{\epsilon h}-\mathbf{u} _{\epsilon H},\mathbf{B} _{\epsilon h}-\mathbf{B} _{\epsilon H}\right) \Vert |_{1} \Vert |\left( \mathbf{u} _{\epsilon h}-\mathbf{u} _{\epsilon H},\mathbf{B} _{\epsilon h}-\mathbf{B} _{\epsilon H}\right) \Vert |_{0}\nonumber \\&+\,\frac{5}{4}\frac{\sigma }{\Vert \mathbf{F }\Vert _{-1}}\Vert |\left( \mathbf{u} _{\epsilon h}-\mathbf{u} _{\epsilon H}^{m},\mathbf{B} _{\epsilon h}-\mathbf{B} _{\epsilon H}^{m}\right) \Vert |_{1}^2. \end{aligned}$$

(49)

For ${\mathcal {P}}_{1}$, from (49), Theorems 3.2 and 4.1 , we have

$$\begin{aligned} \Vert |\left( \mathbf{e} _{h},\mathbf{b} _{h}\right) \Vert |_{1} \le C\left[ \epsilon ^{-\frac{5}{4}}H^\frac{5}{2}\frac{\Vert \mathbf{F }\Vert _{0}}{\Vert \mathbf{F }\Vert _{-1}}\Vert \mathbf{F }\Vert _{0} +\Vert |\left( \mathbf{u} _{\epsilon H}-\mathbf{u} _{\epsilon H}^{m},\mathbf{B} _{\epsilon H}-\mathbf{B} _{\epsilon H}^{m}\right) \Vert |_{1}^2\right] , \end{aligned}$$

(50)

and with (48) and (50), we have

$$\begin{aligned} \begin{array}{lll} \frac{\epsilon }{\nu _{e}}\Vert \eta _{h}\Vert _{0}^2 &{}\le \frac{C\sigma }{\Vert \mathbf{F }\Vert _{-1}} \Vert |\left( \mathbf{u} _{\epsilon h}-\mathbf{u} _{\epsilon H},\mathbf{B} _{\epsilon h}-\mathbf{B} _{\epsilon H}\right) \Vert |_{1}^{\frac{3}{2}} \Vert |\left( \mathbf{u} _{\epsilon h}-\mathbf{u} _{\epsilon H},\mathbf{B} _{\epsilon h}-\mathbf{B} _{\epsilon H}\right) \Vert |_{0}^{\frac{1}{2}} \Vert |\left( \mathbf{e} _{h},\mathbf{b} _{h}\right) \Vert |_{1}\\ &{}\quad +\,\frac{C\sigma }{\Vert \mathbf{F }\Vert _{-1}} \Vert |\left( \mathbf{u} _{\epsilon h}-\mathbf{u} _{\epsilon H},\mathbf{B} _{\epsilon h}-\mathbf{B} _{\epsilon H}\right) \Vert |_{1} \Vert |\left( \mathbf{u} _{\epsilon h}-\mathbf{u} _{\epsilon H},\mathbf{B} _{\epsilon h}-\mathbf{B} _{\epsilon H}\right) \Vert |_{0}\Vert |\left( \mathbf{e} _{h},\mathbf{b} _{h}\right) \Vert |_{1}\\ &{}\quad +\, \frac{5}{4}\frac{\sigma }{\Vert \mathbf{F }\Vert _{-1}}\Vert |\left( \mathbf{u} _{\epsilon h}-\mathbf{u} _{\epsilon H}^{m},\mathbf{B} _{\epsilon h}-\mathbf{B} _{\epsilon H}^{m}\right) \Vert |_{1}^2\Vert |\left( \mathbf{e} _{h},\mathbf{b} _{h}\right) \Vert |_{1}\\ &{}\le C\epsilon ^{-\frac{5}{2}}H^5\left( \frac{\Vert \mathbf{F }\Vert _{0}}{\Vert \mathbf{F }\Vert _{-1}}\right) ^2\Vert \mathbf{F }\Vert _{0}^2 +C\Vert |\left( \mathbf{u} _{\epsilon H}-\mathbf{u} _{\epsilon H}^{m},\mathbf{B} _{\epsilon H}-\mathbf{B} _{\epsilon H}^{m}\right) \Vert |_{1}^4, \end{array}\nonumber \\ \end{aligned}$$

(51)

with some simple calculations, we complete the proof of the estimate for ${\mathcal {P}}_{1}$.

And for ${\mathcal {P}}_{2}$, from (49), Theorems 3.2 and 4.1, we have

$$\begin{aligned} \begin{array}{lll} \Vert |\left( \mathbf{e} _{h},\mathbf{b} _{h}\right) \Vert |_{1} \le C\left[ H^\frac{5}{2}\frac{\Vert \mathbf{F }\Vert _{0}}{\Vert \mathbf{F }\Vert _{-1}}\Vert \mathbf{F }\Vert _{0} +\Vert |\left( \mathbf{u} _{\epsilon H}-\mathbf{u} _{\epsilon H}^{m},\mathbf{B} _{\epsilon H}-\mathbf{B} _{\epsilon H}^{m}\right) \Vert |_{1}^2\right] , \end{array} \end{aligned}$$

(52)

and with (23), (34), (7), (36), Theorems 3.2 and 4.1, we deduce that

$$\begin{aligned} \begin{array}{lll} \beta _{0}\Vert \eta _{h}\Vert _{0} &{}\le \frac{{\overline{\gamma }}}{{\underline{\gamma }}} \Vert |\left( \mathbf{e} _{h},\mathbf{b} _{h}\right) \Vert |_{1} +\frac{N}{{\underline{\gamma }}^2} \Vert |\left( \mathbf{e} _{h},\mathbf{b} _{h}\right) \Vert |_{1} \Vert |\left( \mathbf{u} _{\epsilon h}^m,\mathbf{B} _{\epsilon h}^m\right) \Vert |_{1}\\ &{}\quad +\,\frac{CN}{{\underline{\gamma }}^2} \Vert |\left( \mathbf{u} _{\epsilon h}-\mathbf{u} _{\epsilon H},\mathbf{B} _{\epsilon h}-\mathbf{B} _{\epsilon H}\right) \Vert |_{1}^{\frac{3}{2}} \Vert |\left( \mathbf{u} _{\epsilon h}-\mathbf{u} _{\epsilon H},\mathbf{B} _{\epsilon h}-\mathbf{B} _{\epsilon H}\right) \Vert |_{0}^{\frac{1}{2}}\\ &{}\quad +\,\frac{CN}{{\underline{\gamma }}^2} \Vert |\left( \mathbf{u} _{\epsilon h}-\mathbf{u} _{\epsilon H},\mathbf{B} _{\epsilon h}-\mathbf{B} _{\epsilon H}\right) \Vert |_{1} \Vert |\left( \mathbf{u} _{\epsilon h}-\mathbf{u} _{\epsilon H},\mathbf{B} _{\epsilon h}-\mathbf{B} _{\epsilon H}\right) \Vert |_{0}\\ &{}\quad +\,\frac{5}{4}\frac{N}{{\underline{\gamma }}^2} \Vert |\left( \mathbf{u} _{\epsilon h}-\mathbf{u} _{\epsilon H},\mathbf{B} _{\epsilon h}-\mathbf{B} _{\epsilon H}\right) \Vert |_{1}^2\\ &{}\le C\left[ H^\frac{5}{2}\frac{\Vert \mathbf{F }\Vert _{0}}{\Vert \mathbf{F }\Vert _{-1}}\Vert \mathbf{F }\Vert _{0} +\Vert |\left( \mathbf{u} _{\epsilon H}-\mathbf{u} _{\epsilon H}^{m},\mathbf{B} _{\epsilon H}-\mathbf{B} _{\epsilon H}^{m}\right) \Vert |_{1}^2\right] . \end{array} \end{aligned}$$

(53)

On the other hand, in the 2D case, applying the inverse inequality

$$\begin{aligned} \Vert v_{\mu }\Vert _{L^{\infty }}\le & {} C|\ln \mu |^{\frac{1}{2}}\Vert v_{\mu }\Vert _{1},~~ \Vert \Psi _{\mu }\Vert _{L^{\infty }}\nonumber \\\le & {} C|\ln \mu |^{\frac{1}{2}}\Vert \Psi _{\mu }\Vert _{1}, ~\forall v_{\mu }\in \mathbf{X }_{\mu },\Psi _{\mu }\in \mathbf{W }_{\mu },\quad \mu =h,H, \end{aligned}$$

(54)

in the estimate of the trilinear term, from (53), Theorems 3.2 and 4.1, we derive that

$$\begin{aligned} \begin{array}{lll} &{}\left( 1-\sigma \right) \Vert |\left( \mathbf{e} _{h},\mathbf{b} _{h}\right) \Vert |_{1} \\ &{}\quad \le \frac{C\sigma }{\Vert \mathbf{F }\Vert _{-1}}|\ln h|^{\frac{1}{2}} \Vert |\left( \mathbf{u} _{\epsilon h}-\mathbf{u} _{\epsilon H},\mathbf{B} _{\epsilon h}-\mathbf{B} _{\epsilon H}\right) \Vert |_{1} \Vert |\left( \mathbf{u} _{\epsilon h}-\mathbf{u} _{\epsilon H},\mathbf{B} _{\epsilon h}-\mathbf{B} _{\epsilon H}\right) \Vert |_{0}\\ &{}\quad \quad +\,\frac{C\sigma }{\Vert \mathbf{F }\Vert _{-1}}\Vert |\left( \mathbf{u} _{\epsilon h}-\mathbf{u} _{\epsilon H},\mathbf{B} _{\epsilon h}-\mathbf{B} _{\epsilon H}\right) \Vert |_{1} \Vert |\left( \mathbf{u} _{\epsilon h}-\mathbf{u} _{\epsilon H},\mathbf{B} _{\epsilon h}-\mathbf{B} _{\epsilon H}\right) \Vert |_{0}\\ &{}\quad \quad +\,\frac{5}{4}\frac{\sigma }{\Vert \mathbf{F }\Vert _{-1}} \Vert |\left( \mathbf{u} _{\epsilon H}-\mathbf{u} _{\epsilon H}^m,\mathbf{B} _{\epsilon H}-\mathbf{B} _{\epsilon H}^m\right) \Vert |_{1}^2. \end{array} \end{aligned}$$

(55)

For ${\mathcal {P}}_{1}$, with (55), Theorems 3.2 and 4.1, we have

$$\begin{aligned} \Vert |\left( \mathbf{e} _{h},\mathbf{b} _{h}\right) \Vert |_{1} \le C\left[ \epsilon ^{-\frac{3}{2}}|\ln h|H^3\frac{\Vert \mathbf{F }\Vert _{0}}{\Vert \mathbf{F }\Vert _{-1}}\Vert \mathbf{F }\Vert _{0} +\Vert |\left( \mathbf{u} _{\epsilon H}-\mathbf{u} _{\epsilon H}^m,\mathbf{B} _{\epsilon H}-\mathbf{B} _{\epsilon H}^m\right) \Vert |_{1}^2 \right] ,\nonumber \\ \end{aligned}$$

(56)

and with (56), we have

$$\begin{aligned} \begin{array}{lll} \frac{\epsilon }{\nu _{e}}\Vert \eta _{h}\Vert _{0}^2 &{}\le \frac{C\sigma }{\Vert \mathbf{F }\Vert _{-1}}|\ln h|^{\frac{1}{2}} \Vert |\left( \mathbf{u} _{\epsilon h}-\mathbf{u} _{\epsilon H},\mathbf{B} _{\epsilon h}-\mathbf{B} _{\epsilon H}\right) \Vert |_{1} \\ &{}\qquad \Vert |\left( \mathbf{u} _{\epsilon h}-\mathbf{u} _{\epsilon H},\mathbf{B} _{\epsilon h}-\mathbf{B} _{\epsilon H}\right) \Vert |_{0}\Vert \left( \mathbf{e} _{h},\mathbf{b} _{h}\right) \Vert _{1}\\ &{}\quad +\,\Vert |\left( \mathbf{u} _{\epsilon h}-\mathbf{u} _{\epsilon H},\mathbf{B} _{\epsilon h}-\mathbf{B} _{\epsilon H}\right) \Vert |_{1} \Vert |\left( \mathbf{u} _{\epsilon h}-\mathbf{u} _{\epsilon H},\mathbf{B} _{\epsilon h}-\mathbf{B} _{\epsilon H}\right) \Vert |_{0}\Vert \left( \mathbf{e} _{h},\mathbf{b} _{h}\right) \Vert _{1}\\ &{}\quad +\,\frac{5}{4}\frac{\sigma }{\Vert \mathbf{F }\Vert _{-1}}|\ln h|^{\frac{1}{2}} \Vert |\left( \mathbf{u} _{\epsilon H}-\mathbf{u} _{\epsilon H}^m,\mathbf{B} _{\epsilon H}-\mathbf{B} _{\epsilon H}^m\right) \Vert |_{1}^2\Vert \left( \mathbf{e} _{h},\mathbf{b} _{h}\right) \Vert _{1}\\ &{}\le C\frac{\Vert \mathbf{F }\Vert _{0}^2}{\Vert \mathbf{F }\Vert _{-1}^2}\Vert \mathbf{F }\Vert _{0}^2|\ln h|\epsilon ^{-3}H^6 +C\Vert |\left( \mathbf{u} _{\epsilon H}-\mathbf{u} _{\epsilon H}^m,\mathbf{B} _{\epsilon H}-\mathbf{B} _{\epsilon H}^m\right) \Vert |_{1}^4, \end{array} \end{aligned}$$

which is that

$$\begin{aligned} \begin{array}{lll} \Vert \eta _{h}\Vert _{0} \le C\left[ |\ln h|\epsilon ^{-2}H^3\frac{\Vert \mathbf{F }\Vert _{0}}{\Vert \mathbf{F }\Vert _{-1}}\Vert \mathbf{F }\Vert _{0} +\Vert |\left( \mathbf{u} _{\epsilon H}-\mathbf{u} _{\epsilon H}^m,\mathbf{B} _{\epsilon H}-\mathbf{B} _{\epsilon H}^m\right) \Vert |_{1}^2\right] . \end{array} \end{aligned}$$

And for ${\mathcal {P}}_{2}$, from Theorems 3.2,  4.1 and (55), we have

$$\begin{aligned} \begin{array}{lll}\Vert |\left( \mathbf{e} _{h},\mathbf{b} _{h}\right) \Vert |_{1} \le C\left[ H^3|\ln h|\frac{\Vert \mathbf{F }\Vert _{0}}{\Vert \mathbf{F }\Vert _{-1}}\Vert \mathbf{F }\Vert _{0} +\Vert |\left( \mathbf{u} _{\epsilon H}-\mathbf{u} _{\epsilon H}^m,\mathbf{B} _{\epsilon H}-\mathbf{B} _{\epsilon H}^m\right) \Vert |_{1}^2 \right] , \end{array} \end{aligned}$$

(57)

and with (23), (7), (57), Theorems 3.2 and 4.1, we deduce that

$$\begin{aligned} \begin{array}{lll} \beta _{0}\Vert \eta _{h}\Vert _{0} &{}\le \max \{R_{e}^{-1},(2+d)S_{c}R_{m}^{-1}\}\Vert \left( \mathbf{e} _{h},\mathbf{b} _{h}\right) \Vert _{1}\\ &{}\quad + \frac{C\sigma }{\Vert \mathbf{F }\Vert _{-1}}|\ln h|^{\frac{1}{2}} \Vert |\left( \mathbf{u} _{\epsilon h}-\mathbf{u} _{\epsilon H},\mathbf{B} _{\epsilon h}-\mathbf{B} _{\epsilon H}\right) \Vert |_{1} \Vert |\left( \mathbf{u} _{\epsilon h}-\mathbf{u} _{\epsilon H},\mathbf{B} _{\epsilon h}-\mathbf{B} _{\epsilon H}\right) \Vert |_{0}\\ &{}\quad + \frac{C\sigma }{\Vert \mathbf{F }\Vert _{-1}}|\ln h|^{\frac{1}{2}}\Vert |\left( \mathbf{u} _{\epsilon h}-\mathbf{u} _{\epsilon H},\mathbf{B} _{\epsilon h}-\mathbf{B} _{\epsilon H}\right) \Vert |_{1} \Vert |\left( \mathbf{u} _{\epsilon h}-\mathbf{u} _{\epsilon H},\mathbf{B} _{\epsilon h}-\mathbf{B} _{\epsilon H}\right) \Vert |_{0}\\ &{}\quad + \frac{5}{4}\frac{\sigma }{\Vert \mathbf{F }\Vert _{-1}}|\ln h|^{\frac{1}{2}} \Vert |\left( \mathbf{u} _{\epsilon H}-\mathbf{u} _{\epsilon H}^m,\mathbf{B} _{\epsilon H}-\mathbf{B} _{\epsilon H}^m\right) \Vert |_{1}^2\\ &{}\le C\left[ H^3|\ln h|\frac{\Vert \mathbf{F }\Vert _{0}}{\Vert \mathbf{F }\Vert _{-1}}\Vert \mathbf{F }\Vert _{0} +\Vert |\left( \mathbf{u} _{\epsilon H}-\mathbf{u} _{\epsilon H}^m,\mathbf{B} _{\epsilon H}-\mathbf{B} _{\epsilon H}^m\right) \Vert |_{1}^2 \right] . \end{array} \end{aligned}$$

Then, we complete the proof. $\square$

Method 3.

Step I. Find a coarse grid penalty iterative solution $((\mathbf{u} _{\epsilon H}^m,\mathbf{B} _{\epsilon H}^m),p_{\epsilon H}^{m})\in \mathbf{W} _{0n}^{H}\times \text{ M }_{H}$ such that

$$\begin{aligned} \begin{array}{lll} &{}A_{0}\left( \left( \mathbf{u }_{\epsilon H}^n,\mathbf{B }_{\epsilon H}^n\right) ,\left( \mathbf{v} ,\varvec{\Psi }\right) \right) -d\left( \left( \mathbf{v} ,\varvec{\Psi }\right) ,p_{\epsilon H}^{n}\right) +d\left( \left( \mathbf{u }_{\epsilon H}^n,\mathbf{B }_{\epsilon H}^n\right) ,q\right) +\frac{\epsilon }{\nu _{e}}\left( p_{\epsilon H}^{n},q\right) \\ &{}\quad +\,A_{1}\left( \left( \mathbf{u }_{\epsilon H}^{n-1},\mathbf{B }_{\epsilon H}^{n-1}\right) ,\left( \mathbf{u }_{\epsilon H}^{n},\mathbf{B }_{\epsilon H}^{n}\right) ,\left( \mathbf{v} ,\varvec{\Psi }\right) \right) =<\mathbf{F },\left( \mathbf{v} ,\varvec{\Psi }\right) >. \end{array} \end{aligned}$$

(58)

for $n=1,2,\ldots ,m$, where $((\mathbf{u} _{\epsilon H}^0,\mathbf{B} _{\epsilon H}^0),p_{\epsilon H}^{0})$ is determined by

$$\begin{aligned} \begin{array}{lll} A_{0}\left( \left( \mathbf{u} _{\epsilon H}^{0},\mathbf{B} _{\epsilon H}^{0}\right) ,\left( \mathbf{v} ,\varvec{\Psi }\right) \right) -d\left( \left( \mathbf{v} ,\varvec{\Psi }\right) ,p_{\epsilon H}^{0}\right) +d\left( \left( \mathbf{u} _{\epsilon H}^{0},\mathbf{B} _{\epsilon H}^{0}\right) ,q\right) +\frac{\epsilon }{\nu _{e}}\left( p_{\epsilon H}^{0},q\right) \\ \quad =\langle \mathbf{F },\left( \mathbf{v} ,\varvec{\Psi }\right) \rangle , \end{array} \end{aligned}$$

(59)

for all $((\mathbf{v} ,\varvec{\Psi }),q)\in \mathbf{W} _{0n}^{H}\times \text{ M }_{H}$.

Step II. Find a fine grid solution $((\mathbf{u} _{\epsilon mh},\mathbf{B} _{\epsilon mh}),p_{\epsilon mh})\in \mathbf{W} _{0n}^{h}\times \text{ M }_{h}$ defined by the following Oseen correction.

$$\begin{aligned} \begin{array}{lll} &{}A_{0}\left( \left( \mathbf{u} _{\epsilon mh},\mathbf{B} _{\epsilon mh}\right) ,\left( \mathbf{v} ,\varvec{\Psi }\right) \right) -d\left( \left( \mathbf{v} ,\varvec{\Psi }\right) ,p_{\epsilon mh}\right) +d\left( \left( \mathbf{u} _{\epsilon mh},\mathbf{B} _{\epsilon mh}\right) ,q\right) +\frac{\epsilon }{\nu _{e}}\left( p_{\epsilon mh},q\right) \\ &{}\quad +\,A_{1}\left( \left( \mathbf{u} _{\epsilon H}^{m},\mathbf{u} _{\epsilon H}^{m}\right) , \left( \mathbf{u} _{\epsilon mh},\mathbf{u} _{\epsilon mh }\right) ,\left( \mathbf{v} ,\varvec{\Psi }\right) \right) =\langle \mathbf{F },\left( \mathbf{v} ,\varvec{\Psi }\right) \rangle , \end{array} \end{aligned}$$

(60)

for all $((\mathbf{v} ,\varvec{\Psi }),q)\in \mathbf{W} _{0n}^{h}\times \text{ M }_{h}$.

Theorem 4.4

Under the assumptions of Theorem 4.2, then $((\mathbf{u} _{\epsilon mh},\mathbf{B} _{\epsilon mh}),p_{\epsilon mh})$ provided by Method 3 satisfies the following stability and error estimates:

$$\begin{aligned} \Vert |\left( \mathbf{u }_{\epsilon mh},\mathbf{B }_{\epsilon mh}\right) \Vert |_{1}\le & {} \Vert \mathbf{F }\Vert _{-1},\nonumber \\ \Vert p_{\epsilon mh}\Vert _{0}\le & {} \left( \frac{\nu _{e}}{\epsilon {\underline{\gamma }}}\right) ^{\frac{1}{2}}\Vert \mathbf{F }\Vert _{-1},~ for~{\mathcal {P}}_{1},~~\nonumber \\ \Vert p_{\epsilon mh}\Vert _{0}\le & {} \beta _{0}^{-1}\left( \frac{{\overline{\gamma }}}{{\underline{\gamma }}}+2\right) \Vert \mathbf{F }\Vert _{-1}, ~ for~{\mathcal {P}}_{2}, \end{aligned}$$

(61)

and satisfy the following bounds:

$$\begin{aligned} \Vert |\left( \mathbf{u }-\mathbf{u }_{\epsilon mh},\mathbf{B }-\mathbf{B }_{\epsilon mh}\right) \Vert |_{1}&\le C\left[ \epsilon + \epsilon ^{-\frac{1}{2}}\left( h+\epsilon ^{-\frac{1}{2}}H^2\left( \frac{\Vert \mathbf{F }\Vert _{0}}{\Vert \mathbf{F }\Vert _{-1}}\right) ^{\frac{1}{2}}\right) \right] \Vert \mathbf{F }\Vert _{0}\\&\quad +C\Vert |\left( \mathbf{u} _{\epsilon H}-\mathbf{u} _{\epsilon H}^{m},\mathbf{B} _{\epsilon H}-\mathbf{B} _{\epsilon H}^{m}\right) \Vert |_{1},\\ \Vert p-p_{\epsilon mh}\Vert _{0}&\le C\left[ \epsilon + \epsilon ^{-1}\left( h+\epsilon ^{-\frac{1}{2}}H^2\left( \frac{\Vert \mathbf{F }\Vert _{0}}{\Vert \mathbf{F }\Vert _{-1}}\right) ^{\frac{1}{2}}\right) \right] \Vert \mathbf{F }\Vert _{0}\\&\quad +C\Vert |\left( \mathbf{u} _{\epsilon H}-\mathbf{u} _{\epsilon H}^{m},\mathbf{B} _{\epsilon H}-\mathbf{B} _{\epsilon H}^{m}\right) \Vert |_{1}, \end{aligned}$$

$\epsilon$ and H can be taken as $\epsilon =O(h^{\frac{1}{2}})$, $H^2=O(\epsilon ^{\frac{1}{2}}h)$ and the convergence rate is $O(h^{\frac{1}{2}})$; for ${\mathcal {P}}_{2}$, the optimal error estimates are

$$\begin{aligned} \begin{array}{lll} \Vert |\left( \mathbf{u }-\mathbf{u }_{\epsilon mh},\mathbf{B }-\mathbf{B }_{\epsilon mh}\right) \Vert |_{1} + \Vert p-p_{\epsilon mh}\Vert _{0} &{}\le C\left( \epsilon +h+H^2\left( \frac{\Vert \mathbf{F }\Vert _{0}}{\Vert \mathbf{F }\Vert _{-1}}\right) ^{\frac{1}{2}}\right) \Vert \mathbf{F }\Vert _{0}\\ &{}\quad +\,C\Vert |\left( \mathbf{u} _{\epsilon H}-\mathbf{u} _{\epsilon H}^{m},\mathbf{B} _{\epsilon H}-\mathbf{B} _{\epsilon H}^{m}\right) \Vert |_{1}, \end{array} \end{aligned}$$

$\epsilon$ and H can be taken as $\epsilon =O(h)$, $H^2=O(h)$ and the convergence rate is O(h);

Proof

We can finish the proof by the similar technique used in Theorem 4.2. $\square$

Besides, from Theorems 4.2, 4.3 and 4.4, the comparison of the proposed schemes can be concluded by:

Remark 4.1

From finite element space discretization point of view, the theoretical results always about the penalty parameter for the methods which based on ${\mathcal {P}}_{1}$ discretization, while the choice of coarse mesh for the methods which based on ${\mathcal {P}}_{2}$ discretization have no relationship with the penalty parameter. The inf-sup condition is the main reason.

Remark 4.2

In terms of convergence rate, Method 1 and Method 3 have linear convergence rate with respect to $\Vert |(\mathbf{u} _{\epsilon H}-\mathbf{u} _{\epsilon H}^{m},\mathbf{B} _{\epsilon H}-\mathbf{B} _{\epsilon H}^{m})\Vert |_{1}$. But Method 2 has the second convergence rate. Besides, the classical iterative solver can be applied to Method 1 for it’s invariant stiffness matrix. However, GMERES is a better choice for Method 2 and 3 for their variable stiffness matrix.

5 Numerical Results

In this section, we present several numerical examples to verify the numerical performance of the above presented methods. The penalty parameter $\epsilon$ is selected as $\epsilon =O(h^{\frac{1}{2}})$ for ${\mathcal {P}}_{1}$ and $\epsilon =O(h)$ for ${\mathcal {P}}_{2}$ based on Theorems 4.2–4.4 in all the following numerical tests. The iterative tolerance is set as $10^{-10}$ for numerical implementations.

5.1 Problems with Smooth Solutions

A smooth solution benchmark problem is presented to verify the convergence performance in the square domain $\Omega =[0,1]^d$, $d=2,3$ in this case. The exact solutions are given by

$$\begin{aligned} \left\{ \begin{array}{llll} u_1=\alpha x^2(x-1)^2y(y-1)(2y-1), ~~~ u_2=\alpha y^2(y-1)^2x(x-1)(2x-1),\\ B_1=\alpha \sin (\pi x)\cos (\pi y), ~~~ B_2=-\alpha \sin (\pi y)\cos (\pi x), \\ p=\alpha (2x-1)(2y-1), \end{array} \right. \end{aligned}$$

for $d=2$ and

$$\begin{aligned} \left\{ \begin{array}{llll} u_1=\alpha (y^4+z), ~~~ u_2=\alpha (x+z^3), ~~~ u_3=\alpha (x^2+y^2),\\ B_1=\alpha \sin (y z), ~~~ B_2=-\alpha \sin (x+z), ~~~ B_3=-\alpha y\sin (x^2), \\ p=\alpha (2x-1)(2y-1)(2z-1), \end{array} \right. \end{aligned}$$

for $d=3$. Here, $\alpha$ is chosen such that $0<\sigma <1$. The body forces $\mathbf{f}$, $\mathbf{g}$ are determined accordingly for any $R_{e}$, $R_{m}$ and $S_{c}$.

Fig. 1

2D $\Vert |(\mathbf{e} ^{m},\mathbf{b} ^{m})\Vert |_{1}$ versus iterative number m by linear-log plots

Fig. 2

3D $\Vert |(\mathbf{e} ^{m},\mathbf{b} ^{m})\Vert |_{1}$ versus iterative number m by linear-log plots

Table 1 Parameters of the investigations (2D)

Table 2 Parameters of the investigations (3D)

Tables 1 and 2 present the value of $\sigma$ with different $\alpha$. And we use the gradually increasing $\alpha$ to modify the value of $\sigma$ in this part. From the detail of numerical analysis of Theorems 4.2–4.4, it is known that $\sigma ^ m$ or $\sigma ^{2m}$ come from the estimates given in Theorem 4.1. And it is difficult to obtain the relations between the error estimates and $\sigma$ for the fast decaying of $\sigma ^ m$ or $\sigma ^{2m}$. In Fig. 1, 2, we can see that there exists a linear relation between $\log (\Vert |(\mathbf{e} ^m,\mathbf{b} ^m)\Vert |)$ and iterative step m, which is consistent with the theoretical analysis.

Table 3 $M_{i}$ with $\epsilon =O(h^{1/2})$ and $\alpha =0.1$ for $P_{1}-P_{0}-P_{1}$ element (2D)

Table 4 $M_{i}$ with $\epsilon =O(h)$ and $\alpha =0.1$ for $P_{1}b-P_{1}-P_{1}b$ element (2D)

Table 5 $M_{i}$ with $\epsilon =O(h^{1/2})$ and $\alpha =0.1$ for $P_{1}-P_{0}-P_{1}$ element (3D)

Table 6 $M_{i}$ with $\epsilon =O(h)$ and $\alpha =0.1$ for $P_{1}b-P_{1}-P_{1}b$ element (3D)

Tables 1, 2, 3, 4, 5 and 6 present the numerical results of relative error and CPU time for uniform refinement. The comparisons indicate that the relative error are almost the same with the same finite element pair for different methods. And the relative errors of $P_{1}b-P_{1}-P_{1}b$ element is smaller than $P_{1}-P_{0}-P_{1}$ one with decrease of mesh size h. The convergence rate investigations are in good agreement with the theoretical analysis in Theorems 4.1–4.4. Specifically, the convergence rate of $\mathbf{B }$ for $P_{1}-P_{0}-P_{1}$ element pair can reach O(h), it is even higher than the theoretical result $O(h^{1/2})$. Furthermore, all the given schemes remain much the same property (i.e. $\text{ div }\mathbf{u }=0$, $\text{ div }\mathbf{B }=0$) as the original equations.

Then, it can be seen clearly that the computational speed of method $M_{1}$ with $P_{1}-P_{0}-P_{1}$ element is fastest and method $M_{2}$ with $P_{1}b-P_{1}-P_{1}b$ element leads to the slowest one. Since, the complexity of the discretization of the nonlinear terms and the order of the finite element pair are the main causes.

Fig. 3

2D relative error for $P_{1}-P_{0}-P_{1}$

Fig. 4

2D relative error for $P_{1}b-P_{1}-P_{1}b$

Fig. 5

3D relative error for $P_{1}-P_{0}-P_{1}$

Fig. 6

3D relative error for $P_{1}b-P_{1}-P_{1}b$

The final issue is to validate the effectiveness of the proposed methods for different parameter $\alpha$. A comparison of Figs. 3, 4, 5 and  6 with gradually increasing $\alpha$ reveal that the precision of $M_{2}$ with $P_{1}b-P_{1}-P_{1}b$ element is best and $M_{1}$ with $P_{1}-P_{0}-P_{1}$ element is the worst. That is to say, method $M_{2}$ with $P_{1}b-P_{1}-P_{1}b$ element has good adaptation for relatively large $\sigma$.

5.2 Hartman Flow

Here we explore both 2D and 3D Hartmann flow with $Ha=\sqrt{R_{e}R_{m}S_{c}}$. For 2D, we treat a steady undirectional flow in the channel $\Omega =[0,10]\times [-1,1]$ under the influence of the transverse magnetic field $B_{0}=(0,1)$. The analytical solutions are:

$$\begin{aligned} \left\{ \begin{array}{lll} \mathbf{u }(x,y)=(u(y),~0),\qquad \mathbf{B }(x,y)=(B(y),~1),\\ p(x,y)=-Gx-S_{c}B^2(y)/2+p_{0}, \end{array} \right. \end{aligned}$$

with

$$\begin{aligned} \begin{array}{lll} u(y)=\frac{R_{e}G}{Ha\cdot \tanh (Ha)} \left( 1-\frac{\cosh (yHa)}{\cosh (Ha)}\right) ,\quad B(y)=\frac{G}{S_{c}}\left( \frac{\sinh (yHa)}{\sinh (Ha)}-y\right) . \end{array} \end{aligned}$$

We impose the following boundary conditions:

$$\begin{aligned} \left\{ \begin{array}{lll} \mathbf{u }=0,~\text{ on } ~~y=\pm 1,\\ \left( p\mathbf{I }-R_{e}^{-1}\nabla \mathbf{u }\right) \mathbf{n }=p_{d}\mathbf{n }, ~ \text{ on }~~ x=0 ~ \text{ and } ~ x=10,\\ \mathbf{n }\times \mathbf{B }=\mathbf{n }\times \mathbf{B }_{d},~\text{ on } ~~\partial \Omega , \end{array} \right. \end{aligned}$$

where $p_{d}(x,y)=p(x,y)$, $p_{0}$ is a constant and $\mathbf{I }$ is identity matrix. Whilst, 3D Hartmann flow in a rectangular duct $\Omega =[0,L]\times [-y_{0},y_{0}]\times [-z_{0},z_{0}]$ with $L=10, y_{0}=2, z_{0}=1$ under the influence of a magnetic field $\mathbf{B} _{d}=(0,1,0)$ has the following form

$$\begin{aligned} \left\{ \begin{array}{lll} \mathbf{u }(x,y,z)=(u(y,z),~0,~0),\quad \mathbf{B }(x,y,z)=(B(y,z),~1,0),\\ p(x,y,z)=-Gx-S_{c}B^2(y,z)/2+p_{0}, \end{array} \right. \end{aligned}$$

with

$$\begin{aligned} \begin{array}{lll} u\left( y,z\right) =-\frac{1}{2}GR_{e}\left( z^2-z_{0}^2\right) +\sum \limits _{i=0}^{+\infty }u_{i}(y)\cos \left( \lambda _{i}z\right) ,\quad B\left( y,z\right) =\sum \limits _{i=0}^{+\infty }b_{i}\left( y\right) \cos \left( \lambda _{i}z\right) , \end{array} \end{aligned}$$

where

$$\begin{aligned} \begin{array}{lll} u_{i}\left( y\right) =A_{i}\cosh \left( p_{1}y\right) +B_{i}\cosh \left( p_{2} y\right) ,\\ b_{i}\left( y\right) =\frac{1}{R_{e}S_{c}}\left( A_{i}\frac{\lambda _{i}^{2}-p_{1}^2}{p_{1}}\sinh \left( p_{1}y\right) +B_{i}\frac{\lambda _{i}^{2}-p_{2}^2}{p_{1}}\sinh \left( p_{2}y\right) \right) ,\\ \lambda _{i}=\frac{\left( 2i+1\right) \pi }{2z_{0}},\quad u_{i}\left( y_{0}\right) =\frac{-2GR_{e}}{\lambda _{i}^{3}z_{0}}\sin \left( \lambda _{i}z_{0}\right) ,\\ p_{1,2}^{2}=\lambda _{i}^2+Ha^2/2\pm Ha\sqrt{\lambda _{i}^2+Ha^2/4},\\ \gamma _{i}=p_{2}\left( \lambda _{i}^2-p_{1}^2\right) \sinh \left( p_{1}y_{0}\right) \cosh \left( p_{2}y_{0}\right) -p_{1}\left( \lambda _{i}^2-p_{2}^2\right) \sinh \left( p_{2}y_{0}\right) \cosh \left( p_{1}y_{0}\right) ,\\ A_{i}=\frac{-p_{1}\left( \lambda _{i}^2-p_{2}^2\right) }{\gamma _{i}}u_{i}\left( y_{0}\right) \sinh \left( p_{2}y_{0}\right) , \quad B_{i}=\frac{-p_{2}\left( \lambda _{i}^2-p_{1}^2\right) }{\gamma _{i}}u_{i}\left( y_{0}\right) \sinh \left( p_{1}y_{0}\right) , \end{array} \end{aligned}$$

the boundary conditions are imposed by

$$\begin{aligned} \left\{ \begin{array}{lll} \mathbf{u }=0,~~\text{ on } ~~y=\pm y_{0}~~ \text{ and } ~~z=\pm z_{0}\\ \left( p\mathbf{I }-R_{e}^{-1}\nabla \mathbf{u }\right) \mathbf{n }=p_{d}\mathbf{n }, ~~\text{ on }~~ x=0 ~~ \text{ and }~~ x=L,\\ \mathbf{n }\times \mathbf{B }=\mathbf{n }\times \mathbf{B }_{d},~~ \text{ on } ~~\partial \Omega . \end{array} \right. \end{aligned}$$

In this part, we only consider the $P_{1}b-P_{1}-P_{1}b$ element for its high precision and take $G=0.1$. The first observation is in the scope of the Hartmann number Ha with the presented methods. From the structure of algorithm $M_{1}$-$M_3$, we observe that the first step of these methods dominate the adaptivity of Hartmann number. Then, we make a comparison with the penalty Newton iteration, Stokes iteration and $M_{0}$, which described in our previous work [16]. And we choose the following three cases to simulate 2D problem:

$$\begin{aligned} \begin{array}{lll} (a)~~ Ha=1:R_e=1,~~R_m=0.1,~~S_{c}=10;\\ (b)~~ Ha=10:R_e=10,~~R_m=1,~~S_{c}=10;\\ (c)~~ Ha=100:R_e=100,~~R_m=1,~~S_{c}=10. \end{array} \end{aligned}$$

and choose the following three cases to simulate 3D problem:

$$\begin{aligned} \begin{array}{lll} (a)~~ Ha=1:R_e=1,~~R_m=0.1,~~S_{c}=10;\\ (b)~~ Ha=10:R_e=10,~~R_m=1,~~S_{c}=10;\\ (c)~~ Ha=5\sqrt{14}:R_e=35,~~R_m=1,~~S_{c}=10. \end{array} \end{aligned}$$

Fig. 7

Iteration convergence error in 2D Hartmann flow for $P_{1}b-P_{1}-P_{1}b$

Fig. 8

Iteration convergence error in 3D Hartmann flow for $P_{1}b-P_{1}-P_{1}b$

As can be seen from Figs. 7 and  8, method $M_{0}$ can deal with relatively large Hartmann number and Stokes iteration is only suitable for small Hartmann number. The primary cause is the limitation of uniqueness condition.

Fig. 9

(2D) Slices along $x=5,-1<y<1$: computed (points) and theoretical (lines)

Fig. 10

(3D) Slices along $x=5,-2<y<2,z=0$: computed (points) and theoretical (lines)

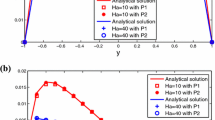
One final observation is in accuracy. Figure 9 depict the analytical solutions of the first component u(y) and B(y) along with numerical ones $u(y_{k})$ and $B(y_{k})$ ($y_{k}=-1+0.1k,~k=0,\ldots ,20$) obtained by scheme $M_{1}-M_{3}$ with $Ha=10$$(R_{e}=5,R_{m}=5,S_{c}=4)$ and $Ha=100$$(R_{e}=100,R_{m}=10,S_{c}=10)$ for the 2D problem. And the analytical solutions of the first component u(y, z) and B(y, z) along with numerical ones $u(y_{k},0)$ and $B(y_{k},0)$ ($y_{k}=-2+0.1k,~k=0,\ldots ,40$) with $Ha=1$$(R_{e}=1,R_{m}=0.1,S_{c}=10)$ and $Ha=10$$(R_{e}=10,R_{m}=1,S_{c}=10)$ for the 3D problem are shown in Fig. 10. It shows that the methods presented in this paper can achieve the desired results for different Hartmann numbers.

5.3 Driven Cavity Flow

In this example, we consider a 2D/3D driven cavity flow which used in fluid dynamics with the implementation domain $\Omega =(-1,1)^{d}, d=2$ and $\Omega =(0,1)^{3}, d=3$, and set the source terms to be zero. The boundary conditions are prescribed as follows:

$$\begin{aligned} \left\{ \begin{array}{lll} \mathbf{u }=0,~~\text{ on }~ x=\pm 1~~\text{ and } ~~y=-1,\\ \mathbf{u }=(1,0),~~\text{ on }~~y=1,\\ \mathbf{n} \times \mathbf{B }=\mathbf{n} \times \mathbf{B }_{D},~~\text{ on }~~\partial \Omega , \end{array} \right. \end{aligned}$$

where $\mathbf{B }_{D}=(1,0)$ for $d=2$;

$$\begin{aligned} \left\{ \begin{array}{lll} \mathbf{u }=0,~~\text{ on }~ x=0, x=1, y=0, y=1~~\text{ and } ~~z=0,\\ \mathbf{u }=(1,0,0),~~\text{ on }~~z=1,\\ \mathbf{n} \times \mathbf{B }=\mathbf{n} \times \mathbf{B }_{D},~~\text{ on }~~\partial \Omega , \end{array} \right. \end{aligned}$$

where $\mathbf{B }_{D}=(1,0,0)$ for $d=3$.

In this subsection, we mainly take a further investigation on the effectiveness for the classical benchmark problem with different parameters. We set $R_{e}\in \{1,5\cdot 10^2,6\cdot 10^3\}$, $R_{m}\in \{10^{-2},1,10\}$, $S_{c}\in \{1,10^3,10^6\}$ and $R_{e}\in \{1,10^2,3\cdot 10^2\}$, $R_{m}\in \{10^{-2},1,20\}$, $S_{c}\in \{1,10^2,5\cdot 10^2\}$ for 2D and 3D case, respectively. And we only consider $M_{2}$ with $P_{1}b-P_{1}-P_{1}b$ element in this part.

Fig. 11

(2D) Comparison results versus $R_{e}$

Fig. 12

(2D) Comparison results versus $R_{m}$

Fig. 13

(2D) Comparison results versus $S_{c}$

Fig. 14

(2D) Numerical streamlines versus $R_{e}$

Fig. 15

((2D) Numerical streamlines versus $R_{m}$

Fig. 16

(2D) Numerical streamlines versus $S_{c}$

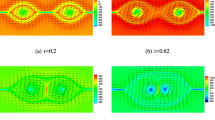
The numerical results of horizontal velocity, pressure and magnetic field distribution at the mid-width for various $R_{e}$, $R_{m}$ and $S_{c}$ are shown in Figs. 11, 12 13, 17, 18 and 19. It shows that the numerical results have an excellent agreement with the standard two-level Oseen iterative method. Figures 14, 15, 16, 20, 21 and 22 describe the numerical streamline of the cavity flow for different hydrodynamic Reynolds numbers, magnetic Reynolds numbers and coupling coefficients. It is observed that the velocity main vortex turns into several small ones and become more complex with the increase of $R_{e}$. And it shows that more resolved vortexes may captured with the increase of $S_{c}$. Besides, the velocity vortex remain almost unchanged for different $R_{m}$.

Fig. 17

(3D) Comparison results versus $R_{e}$

Fig. 18

(3D) Comparison results versus $R_{m}$

Fig. 19

(3D) Comparison results versus $S_{c}$

Fig. 20

(3D) Velocity contour line and vector versus $R_{e}$ along slice y = 0.5

Fig. 21

(3D) Velocity contour line and vector versus $R_{m}$ along slice y = 0.5

Fig. 22

(3D) Velocity contour line and vector versus $S_{c}$ along slice y = 0.5

6 Conclusions

In this paper, we have proposed some two-level Oseen penalty finite element methods with strong uniqueness condition $\sigma \le 1-\left( \frac{\Vert \mathbf{F }\Vert |_{-1}}{\Vert |\mathbf{F }\Vert _{0}}\right) ^{\frac{1}{2}}<1$ for solving the 2D/3D steady incompressible MHD equations. The main advantage of the presented methods is that they can overcome the incompressible constrain and save large amount of computational time. And we give the rigorous analysis of the stability and optimal error estimate for different finite element pair ${\mathcal {P}}_{1}$ and ${\mathcal {P}}_{2}$ under the penalty parameter $\epsilon$. Both 2D/3D numerical results illustrated that Method 3 with $P_{1}b-P_{1}-P_{1}b$ exhibits good performance in terms of adaptability for large $\sigma$ and high precision. A further study about the 2D/3D non stationary incompressible MHD equations in this direction is in progress.