Integrating automatic order determination with response prediction error minimization for nonlinear subspace identification in structural dynamics

Abstract

The singular value decomposition order determination method used in nonlinear subspace identification may encounter challenges due to the noise in signals, resulting in the omission of modes or the occurrence of spurious mode. Additionally, the lack of an iterative process in the nonlinear subspace identification, which primarily relies on matrix operations, will lead to suboptimal solutions. To address these challenges, an improved framework for nonlinear subspaces identification is proposed in this paper. False modes are eliminated through data preprocessing and modal stability criteria, followed by the clustering of stable modes using the Density-Based Spatial Clustering of Applications with Noise algorithm for automatic order determination; Simultaneously, an iterative optimization approach based on response prediction error minimization is introduced to enhance the accuracy of the state-space model estimation results. The effectiveness of proposed method is validated through two simulation cases and one experimental verification. The results show that the clustering algorithm effectively distinguishes real modes from false ones and achieves automatic system order determination across various SNR conditions. The iterative optimization process notably enhances state-space model estimation accuracy. Compared to original nonlinear subspace identification, proposed method significantly improves identification accuracy.

1 Introduction

Nonlinear system identification refers to determining the mathematical model of a nonlinear dynamical system from input and output data [1,2,3]. Accurate dynamic models play a crucial role in various fields such as vibration isolation, structural optimization, and damage identification [4,5,6]. Several papers have reviewed the development history and major methods of nonlinear system identification [7,8,9].

In recent years, many nonlinear system identification methods have been proposed and developed [10,11,12]. One notable method is the Nonlinear Subspace Identification (NSI) introduced by Marchesiello and Garibaldi [13, 14]. This method combines nonlinear feedback interpretation with the classical subspace identification framework, showcasing strong effectiveness and robustness, making it one of the classic approaches in nonlinear system identification [15,16,17]. Anastasio et al. [18] integrated NSI with the harmonic balance method, utilizing this enhanced approach to identify and analyze periodically excited dynamic systems to investigate the stability of system periodic solutions, showcasing promising prospects for applications in rotating machinery such as rotors. Zhu et al. [19] applied NSI to the aerodynamics domain, enabling systematic identification and analysis of the nonlinear airfoil-store system, demonstrating its robustness and flexibility across various wind speeds. Liu et al. [20] combined NSI with the Krotov method to establish a nonlinear Hammerstein model for multivariate molten iron quality, addressing the control issues encountered in the blast furnace ironmaking process.

However, NSI still faces significant challenges, notably in accurately determining the system order, a crucial aspect of the method. In NSI method, the system order is determined using Singular Value Decomposition (SVD), where the number of singular values before the largest difference between adjacent singular values corresponds to the system order [13]. But the higher-order singular values of the Hankel matrix are often susceptible to noise, hindering the clear detection of singular value jumps and accurate system order determination, leading to mode omission or pseudo-mode phenomena [21, 22]. To address this challenge, numerous scholars have conducted research [23,24,25]. Among these efforts, the introduction of stability diagram techniques has provided a novel approach to determining system order [26, 27]. Zhou et al. [28] proposed a stability diagram method that combines Monte Carlo techniques, effectively distinguishing between system modes and spurious modes caused by noise, thereby accurately determining the system’s order. The application of clustering techniques also supports the automatic determination of system order [29, 30]. Bakir [31] introduced the modal phase collinearity index to remove false modal poles, followed by hierarchical clustering to group real modes into large clusters. Zhang et al. [32] proposed an algorithm utilizing fast-density peak clustering, enabling the automatic determination of system modal parameters without requiring user intervention.

Moreover, the NSI method suffers from the limitation that its computed identification results might not always represent the optimal solution, thereby compromising the accuracy of the identification process [13]. To address this issue, Wei et al. [33] introduced an enhanced NSI method that integrates the prediction error method (PEM) to re-estimate the coefficient matrix within the state-space representation. This refinement step occurs after obtaining the initial system model through the NSI method. The enhanced approach has demonstrated significantly improved recognition accuracy, especially in challenging and noisy environments, surpassing the performance of the conventional NSI method.

This paper addresses the issues above by proposing an improved framework for nonlinear subspace identification. Through the amalgamation of the Density-Based Spatial Clustering of Applications with Noise (DBSCAN) clustering algorithm and the stabilization graph method, automatic determination of system order is achieved. Before ordering, eliminate false modes and erroneous estimates caused by noise through data preprocessing and modal stability criteria, thereby enhancing the algorithm’s robustness to noise and improving computational efficiency. At the same time, an iterative optimization algorithm based on response prediction error minimization is introduced in the process of estimating the state-space model, ensuring that the obtained state-space matrices are all optimal solutions, further enhancing the identification accuracy. Finally, the feasibility of the proposed method is validated through two multi-degree-of-freedom simulation cases, complemented by experimental verification on a multilayer building with nonlinear characteristics.

2 Theoretical basis

2.1 Automatic order determination

NSI is a nonlinear system identification method that establishes a relationship between the underlying frequency response function and nonlinear parameters. Appendix A offers a succinct introduction to the NSI method. Estimating the state-space model constitutes the central aspect of the NSI method. For a nonlinear system with N degrees of freedom, the state-space model can be represented as follows:

$$ \begin{gathered} \dot{\varvec{x}}\left( t \right) = {\mathbf{A}}_{c} {\varvec{x}}\left( t \right) + {\mathbf{B}}_{c} {\varvec{u}}\left( t \right) \hfill \\ {\varvec{y}}\left( t \right) = {\mathbf{C}}{\varvec{x}}\left( t \right) + {\mathbf{D}}{\varvec{u}}\left( t \right) \hfill \\ \left\{ \begin{gathered} {\mathbf{A}}_{c} = \left[ {\begin{array}{*{20}c} {\mathbf{0}} & {\mathbf{I}} \\ { - {\mathbf{M}}^{ - 1} {\mathbf{K}}} & { - {\mathbf{M}}^{ - 1} {\mathbf{C}}_{v} } \\ \end{array} } \right],{\mathbf{B}}_{c} = \left[ {\begin{array}{*{20}c} {\mathbf{0}} & {\mathbf{0}} & \cdots & {\mathbf{0}} \\ {{\mathbf{M}}^{ - 1} } & {\theta_{1} {\mathbf{M}}^{ - 1} {\varvec{L}}_{1} } & \cdots & {\theta_{p} {\mathbf{M}}^{ - 1} {\varvec{L}}_{p} } \\ \end{array} } \right] \hfill \\ {\varvec{C}} = \left[ {\begin{array}{*{20}c} {{\mathbf{I}}_{N \times N} } & {{\mathbf{0}}_{N \times N} } \\ \end{array} } \right],{\mathbf{D}} = \left[ {\begin{array}{*{20}c} {{\mathbf{0}}_{N \times N} } & {{\mathbf{0}}_{N \times 1} } & \cdots & {{\mathbf{0}}_{N \times 1} } \\ \end{array} } \right] \hfill \\ \end{gathered} \right. \hfill \\ \end{gathered} $$

(1)

The continuous time state-space model can be discretized using a sampling interval Δt, with the relationship between the continuous time and discrete time models expressed as:

$$ {\mathbf{A}} = e^{{{\mathbf{A}}_{c} \Delta t}} ,{\mathbf{B}} = \left( {e^{{{\mathbf{A}}_{c} \Delta t}} - {\mathbf{I}}} \right){\mathbf{A}}_{c}^{ - 1} {\mathbf{B}}_{c} $$

(2)

In Eq. (1), A_c represents the dynamical system matrix, B_c represents the input matrix, C represents the output matrix, and D represents the direct feedthrough matrix. The mass matrix M, stiffness matrix K, and damping matrix C_v constitute the underlying linear components, while local nonlinear factors are governed by position vector L_i and nonlinear parameter θ_i. The output y(t) is a q-dimensional column vector, where t denotes time. The input u(t) is an m-dimensional column vector, and the system order, denoted by the dimension of the state vector x(t), is n.

As mentioned in the introduction, NSI methods determine the system order n through singular value decomposition, which is susceptible to noise interference. The following section introduces an improved method to address automatic order determination in noisy environments.

2.1.1 Data preprocessing

After each NSI run, matrices A, B, C, and D are identified. The system matrix A contains modal information and the system order n can be determined by the stable modal parameter count.

The number of identifiable modal parameters varies with different orders of A. Initially, the system order is changed from a small value n_min, to a sufficiently large value n_max and NSI is performed separately for each. Assuming R identifications are conducted during this process, performing eigenvalue decomposition on the R identified A matrices yields R_n complex eigenvalues. The eigenvalues are represented by the vector λ = [λ₁, λ₂, …, λ_Rn]^T and the eigenvectors by the matrix Φ = [ϕ₁, ϕ₂, …, ϕ_Rn]. To match the modal shape measured from the sensor, each complex eigenvector is multiplied by the output matrix C associated with the identification, and the resulting matrix is still denoted by Φ. The modal frequency and damping ratios of the system can be obtained from λ, and the modal shapes can be obtained from Φ.

During the process, noise can introduce errors in the decomposition of matrix A. Hence, some evidently incorrect decomposition outcomes should be eliminated. Specifically, the correct eigenvalues should possess the following properties:

• 1. The real part of the eigenvalues is directly linked to the damping ratio. It is crucial for this real part to be non-negative, as negative values would not make physical sense.

• 2. The eigenvalues need to belong to the complex number field, indicating that their imaginary parts should not be zero.

• 3. The eigenvalues always appear as complex conjugate pairs. This property reflects the inherent symmetry of the system and should be maintained throughout the decomposition process.

These properties can be expressed mathematically:

$$ \left\{ \begin{gathered} {\text{Re}} \left( {\lambda_{i} } \right) > 0 \hfill \\ {\text{Im}} \left( {\lambda_{i} } \right) \ne 0 \hfill \\ \lambda_{j} = \lambda_{i}^{ * } \hfill \\ \end{gathered} \right. $$

(3)

According to Eq. (3), any eigenvalue λ_i and its corresponding eigenvector ϕ_i that do not satisfy any of the three conditions are eliminated. For each pair of complex conjugate modes, only one eigenvalue and one eigenvector are retained. Consequently, the correct eigenvalue decomposition is obtained, consisting of the remaining R_r eigenvalues and eigenvectors denoted by λ_r = [λ₁, λ₂, …, λ_Rr]^T and Φ = [ϕ₁, ϕ₂, …, ϕ_Rr] respectively.

This data preprocessing operation effectively eliminates numerous erroneous estimates, resulting in an improved quality of analysis. Moreover, the computational workload of the algorithm is significantly reduced as a result.

2.1.2 Mode stability criteria

After removing erroneous estimates, stable modes are determined by specifying modal stability criteria.

The vectors f ∈ ℝ^Rr and ζ ∈ ℝ^Rr are introduced to capture the frequency and damping ratio from the eigenvalue vector λ_r, respectively. Consider a pair of identified modes characterized by their respective frequency, damping ratio, and mode shape vector, denoted as f_i, ζ_i and ϕ_i for one mode, and f_j, ζ_j and ϕ_j for the other mode. For the quantitative assessment of the correlation between these modes, the following calculation criteria are introduced:

$$ \begin{gathered} \Delta f_{ij} = \frac{{\left| {f_{i} - f_{j} } \right|}}{{f_{j} }} \hfill \\ \Delta \zeta_{ij} = \frac{{\left| {\zeta_{i} - \zeta_{j} } \right|}}{{\zeta_{j} }} \hfill \\ {\text{MAC}}_{ij} = {\text{MAC}}\left( {\varvec{\phi}_{i} ,\varvec{\phi}_{j} } \right) \hfill \\ \end{gathered} $$

(4)

where MAC is defined as the mode confidence criterion, it quantifies the correlation between the identified mode shape ϕ_i and ϕ_j. MAC is calculated using the formula |ϕ_i^Tφ_j|²/(ϕ_i^Tϕ_i)∙(φ_j^Tφ_j), with values ranging from 0 to 1. MAC value closer to 1 indicates a stronger correlation, suggesting that the identified two modes are of the same order. Conversely, MAC value of 0 indicates no relationship between the modes.

Equation (4) indicate the degree of similarity between the two modes. Define a matrix Δ where the elements in the matrix Δ are represented as:

$$ \Delta_{ij} = \left\{ {\begin{array}{*{20}l} {1,} \hfill & {\Delta f_{ij} \le \varepsilon_{f} ,\Delta \zeta_{j} \le \varepsilon_{\zeta } ,1 - MAC_{lj} \le \varepsilon_{{{\text{MAC}}}} } \hfill \\ {0,} \hfill & {{\text{else}}} \hfill \\ \end{array} } \right. $$

(5)

where ε_f, ε_ζ, and ε_MAC represent custom tolerances for frequencies, damping ratios, and mode shapes, respectively, all pertaining to modes of the same order. In this paper, the tolerance values were determined as follows: ε_f = 0.01, ε_ζ = 0.04, ε_MAC = 0.05.

When Δ_ij = 1, it signifies that the i_th and j_th modes belong to the same mode order. Consequently, by performing a statistical analysis on the j_th column of the matrix Δ, the count of modes belonging to the same mode order as the j_th mode can be determined. Define a new vector z to represent the statistical result of all modes, whose elements are integers, and the element values can be expressed as:

$$ z_{j} = \left\{ {\begin{array}{*{20}l} { - 1 + \sum\limits_{i = 1}^{{{\text{Nr}}}} {\Delta_{ij} } ,} \hfill & {\zeta_{j} \in \left[ {0,\zeta_{\max } } \right]} \hfill \\ {0,} \hfill & {\zeta_{j} \notin \left[ {0,\zeta_{\max } } \right]} \hfill \\ \end{array} } \right. $$

(6)

where ζ_max is the maximum value of the estimated value of the mode damping ratio of the structure, which can be assumed to be 0.1–0.2 depending on the structural characteristics.

By utilizing the vector z, stable and spurious modes can be distinguished. A significant coefficient z_j in z indicates that R_r modes possess comparable frequencies, damping ratios, and mode shapes to the j_th mode, thus suggesting its stability. Conversely, a smaller z_j value indicates sporadic recognition of the mode, rendering it unsuitable for classification as stable. To identify a set of stable modes rather than noisy modes, it is essential to establish a minimum number of similar modes, z_min. The selection of z_min should not be excessively large, as it may inadvertently eliminate low-frequency stable modes, albeit enhancing the reliability of false mode detection. Conversely, opting for a smaller z_min value effectively removes most noise modes without compromising low-frequency modes. In this study, the value of z_min is established as the smallest integer greater than or equal to 0.3 times R.

To determine the desired number of stable modes, a new binary vector s = [s₁, s₂, …, s_Rr] is derived from the vector z. Here, s_j takes a value of either 0 or 1, for all j = 1, 2, …, R_r. If z_j is greater than or equal to z_min, s_j is set to 1, indicating the j_th mode as stable and thus retained. Conversely, if s_j is assigned a value of 0, it signifies that the j_th mode is considered noise and subsequently discarded.

Calculating the non-zero terms in s yields P stable modes. At this point, vector f, ζ, and matrix Φ become:

$$ {\varvec{f}} = \left[ {\begin{array}{*{20}c} {f_{1} } \\ {f_{2} } \\ \vdots \\ {f_{P} } \\ \end{array} } \right],\varvec{\zeta} = \left[ {\begin{array}{*{20}c} {\zeta_{1} } \\ {\zeta_{2} } \\ \vdots \\ {\zeta_{P} } \\ \end{array} } \right],{{\varvec{\Phi}}} = \left[ {\begin{array}{*{20}c} {{\varvec{\phi}}_{1} } & {{\varvec{\phi}}_{2} } & \cdots & {{\varvec{\phi}}_{P} } \\ \end{array} } \right] $$

(7)

Clearly, many components of the obtained vectors f and ζ, as well as the corresponding columns in matrix Φ, are highly like each other, representing information about the same-order modes. Therefore, the number of clusters for determining stable modes can be identified through clustering, thereby achieving automatic determination of the system order.

2.1.3 Determining system order using DBSCAN

The DBSCAN clustering algorithm [34, 35] is employed to determine the system order. This algorithm operates on the premise that each point within a cluster must have a minimum number of neighboring points (MinPts) within a specified radius e, and the density within this neighborhood should surpass a certain threshold. The process involves iteratively examining whether the mode quantity associated with any of the P modes corresponds to the representative of a specific cluster. The algorithm terminates when all P modes are assigned to clusters or rejected as outliers.

In mode clustering, a set of integers {a₁, a₂, …, a_g} represents the positions of cluster elements within the vectors f, ζ, and matrix Φ, where the dimension of the cluster is denoted by g. Thus, for the i_th cluster, denoted as C_i with a dimension of g_i, a set of integers {a₁, a₂, …, a_gi} is employed for representation. The modal information within cluster C_i are expressed as C_if = {f_a1, f_a2, …, f_agi}, C_iζ = {ζ_a1, ζ_a2, …, ζ_agi}, C_iϕ = {ϕ_a1, ϕ_a2, … ϕ_agi}, respectively. The mean values of these sets are f_Ci, ζ_Ci, and ϕ_Ci, representing the centroid coordinates of cluster C_i.

To do clustering, first define a vector p = [1, 2, …, P]^T and v = [v₁, v₂, …, v_p]^T, the elements of v are a random permutation of the elements in p. At the beginning, each element of the vector v is marked as "not accessed".

In the q_th step, assuming that l clusters have already been identified, each cluster contains a different number of modal parameters. The q_th element v_q in v is used to compute the distance d(v_q) between the q_th modal parameter and the rest of the modal parameters. The distance calculation is performed using the Euclidean distance measure. Subsequently, a new modal set S_q is created, containing K_q modes that all within a radius distance e of the modal corresponding to v_q.Based on the minimum number of points MinPts, a new cluster C_l+1 can be initialized.

$$ K_{q} \ge {\text{MinPts}} \Rightarrow C_{l + 1} = \left\{ {v_{q} } \right\} $$

(8)

Alternatively, this point can be classified as an outlier or noise mode and subsequently assigned to cluster C₀, which is specifically designated as the outlier cluster:

$$ K_{q} < {\text{MinPts}} \Rightarrow C_{0} = C_{0} \cup \left\{ {v_{q} } \right\} $$

(9)

If the mode corresponding to v_q is identified as an outlier or noise mode, the next "not accessed" element in vector v is considered. In case the new cluster C_l+1 has been initialized, the set S_q consisting of all points within the vicinity of e is examined. Each point is then reassigned either to the new C_l+1 cluster or to a predefined cluster C_i.

The iterative process continues until all elements of vector v are marked as "accessed," resulting in the completion of the clustering. Consequently, every point in vector p will be assigned to a mode class or an outlier class.

The DBSCAN algorithm needs to select two parameters: the neighborhood distance e, and the minimum number of points MinPts to form a dense area. In general, for datasets with high noise levels and large datasets, larger MinPts values are usually better to form more significant clusters; For the threshold distance e, if the value selected is too small, a large part of the data cannot be correctly clustered. In the follow-up study of this paper, MinPts was set as MinPts = ln(P) and e was set as 0.01.

2.2 Iterative optimization of state-space matrices

Automatic determination of system order relies on estimating the system matrix A in the state-space model. Likewise, NSI for nonlinear parameter identification is grounded in state-space model estimation. Nevertheless, NSI lacks nonlinear optimization methods, resulting in its numerical procedures (e.g., projection, QR decomposition, SVD decomposition) being non-iterative and thus yielding suboptimal solutions for the state-space model. To further enhance the identification performance of the proposed method, an iterative optimization method based on response prediction error minimization is integrated into the framework.

The predicted value of the output y of the system can be determined iteratively by Eq. (1).

$$ \begin{gathered} \hat{\varvec{y}}_{{\varvec{k}}} = {\mathbf{CA}}^{k} {\varvec{x}}_{0} + {\mathbf{CA}}^{k - 1} {\mathbf{B}}{\varvec{u}}_{0} + \ldots + {\mathbf{CAB}}{\varvec{u}}_{k - 2} \\ + {\mathbf{CB}}{\varvec{u}}_{k - 1} + {\mathbf{D}}{\varvec{u}}_{k} \\ \end{gathered} $$

(10)

Then the error between the measured output and the predicted output can be expressed as:

$$ {\varvec{\varepsilon}}_{k} = {\varvec{y}}_{k} - \hat{\varvec{y}}_{k} $$

(11)

The error matrix can be further determined:

$$ {{\varvec{\Delta}}}{\varvec{\varepsilon}} = \left[ {\begin{array}{*{20}c} {{\varvec{\varepsilon}}_{k} } & {{\varvec{\varepsilon}}_{k + 1} } & \cdots & {{\varvec{\varepsilon}}_{k + sh} } \\ \end{array} } \right] $$

(12)

where sh is the number of selected output samples.

Different models have different error criterion functions. Here the function is set as:

$$ {\mathbf{J}} = h\left( {\frac{1}{sh}\det ({{\varvec{\Delta}}}{\varvec{\varepsilon}}^{T} {{\varvec{\Delta}}}{\varvec{\varepsilon}})} \right) $$

(13)

where det (·) represents the determinant of the computed matrix (·) and h(·) represents a scalar monotonically increasing function.

Optimal estimates for the state-space matrices A, B, C, and D are obtained by solving a minimization problem

$$ \left\{ {{\mathbf{A}},{\mathbf{B}},{\mathbf{C}},{\mathbf{D}}} \right\} = \mathop {\arg \min }\limits_{{{\mathbf{A}},{\mathbf{B}},{\mathbf{C}},{\mathbf{D}}}} \left( {\mathbf{J}} \right), $$

(14)

several established methods can be used for this purpose, such as the steepest descent method, the Gauss–Newton method, or the Levenberg–Marquardt algorithm. In this study, the Levenberg–Marquardt algorithm was chosen for its ability to quickly converge to an optimal solution.

After obtaining the optimal matrix estimation, the parameter identification is completed according to Eq. (15).

$$ {\mathbf{H}}_{{\mathbf{E}}} \left( \omega \right) = {\mathbf{D}} + {\mathbf{C}}(i\omega {\mathbf{I}} - {\mathbf{A}}_{{\mathbf{c}}} )^{ - 1} {\mathbf{B}}_{{\mathbf{c}}} = \left[ {\begin{array}{*{20}c} {{\mathbf{H}}\left( \omega \right)} & {\theta_{1} {\varvec{L}}_{1} {\mathbf{H}}\left( \omega \right)} & {...} & {\theta_{p} {\varvec{L}}_{p} {\mathbf{H}}\left( \omega \right)} \\ \end{array} } \right] $$

(15)

2.3 Algorithm implementation process

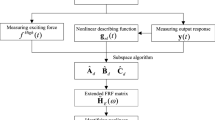
Figure 1 summarizes the proposed method in this paper. Specifically, the main steps include:

• 1. Perform eigenvalue decomposition of the system matrix A for different orders and store the complex eigenvalues and eigenvectors in vectors λ and Φ, respectively.

• 2. Preprocess the data and eliminate incorrect eigenvalues and eigenvectors using Eq. (3);.

• 3. Calculate the modal parameters using the eigenvalues and eigenvectors, and compute the matrix Δ based on the stability criterion in Eq. (4).

• 4. Determine the minimum number of similar modes z_min, create a binary vector s, and select which modes to retain to eliminate noise modes and keep only the stable modes.

• 5. Apply the DBSCAN algorithm to cluster the stable modes, with the number of clusters representing the mode system order.

• 6. Identify the state matrix A, B, C, and D of the system after determining the system order.

• 7. Predict the measured response using the state matrix based on Eq. (10) and determine the error criterion function.

• 8. Solve the optimized A, B, C, and D in Eq. (14) using a nonlinear optimization algorithm.

• 9. Identify the nonlinear parameters using the optimized matrix.

Fig. 1

Improved framework for nonlinear subspace identification

3 Simulation cases

3.1 Four degrees of freedom system

Consider a four-degree-of-freedom system with cubic stiffness nonlinearity. The schematic of this system is depicted in Fig. 2, while its pertinent physical parameters are delineated in Table 1. The nonlinear restoring force operative within the system can be expressed as:

$$ f_{nl} = k_{n} x_{2}^{3} $$

(16)

Fig. 2

Four-degree-of-freedom nonlinear systems

Table 1 Four-degree-of-freedom nonlinear system parameters

At t = 0 s, a zero-mean Gaussian random force (r.m.s = 500 N) is applied to DOF 2 to simulate the forced response of the system at a sampling frequency f_s = 1000 Hz and a total simulation time of 10 s. The fourth-order Runge–Kutta time integration scheme was used to obtain the time response history of the system, the response data length was 10⁴, and a zero-mean Gaussian white noise with SNR = 20 dB was added to each analog output.

The NSI method determines the system order through singular value decomposition. If the signal is noise-free, as shown in Fig. 3a, the singular value decomposition yields clear jumps in singular values at the 8th order, allowing for the determination of the system order. However, in the presence of noise, depicted in Fig. 3b, no significant singular value jumps are apparent, rendering the NSI method inadequate for system order determination.

Fig. 3

Singular values of the skew projection matrix

Using the automated order determination method introduced in Sect. 2.1, the system order was initially varied from 2 to 200, and the eigenvalues and eigenvectors of the system matrix A were extracted respectively. Throughout this process, a total of 10,100 complex eigenvalues and eigenvectors were obtained. The system mode parameters estimated from all eigenvalues and eigenvectors are illustrated in Fig. 4a and b. These figures exhibit numerous false modes generated by noise, such as damping ratio values exceeding 100% at low frequencies in Fig. 4b.

Fig. 4

Modal parameter estimation results

Subsequently, the 10,100 modes were preprocessed and assessed for modal stability using the principles outlined in Eq. (3)–(6). Throughout this process, numerous false modes and erroneous estimations were eliminated, reducing the total number of stable modes to 525. The stable modal results are illustrated in Fig. 4c and d, where Fig. 4c displays four stable frequency axes, and Fig. 4d shows clusters of four modal damping ratios.

The DBSCAN clustering algorithm was employed to cluster the 525 frequency and damping data points obtained in the preceding step. The modal clustering results are illustrated in Fig. 5. During the grouping process facilitated by DBSCAN, a total of four clusters were identified within the stable modes, as shown in Fig. 5a. The distribution of modes in each cluster is depicted in Fig. 5b, and more fourth-order modes are identified. Particularly noteworthy is the algorithm’s efficacy in distinguishing closely aligned second and third-order modes. Regarding the clustering results, the system order is determined to be 4 × 2 = 8.

Fig. 5

Modal clustering results

Once the system order is determined, the A, B, C, and D matrices in the state-space model can be readily established. The frequency response curve H₂₂ is estimated directly using Eq. (15), as depicted by the red dashed line in Fig. 6. The directly estimated results exhibit considerable deviations from the theoretical values, particularly at the peaks. Subsequently, by optimizing the A, B, C, and D matrices based on the principles outlined in Sect. 2.3, the optimized estimated frequency response curve is represented by the blue dashed line in Fig. 6. The optimized results demonstrate a higher level of consistency with the theoretical values.

Fig. 6

Frequency response curve H₂₂

Figure 7 presents the identification results of nonlinear parameters in the form of histograms. Figure 7a displays the identification results directly obtained through NSI method, while Fig. 7b illustrates the identification results of proposed method. It can be observed that the parameter results obtained directly from identification exhibit greater dispersion, whereas the results from proposed method are more concentrated and closer to the theoretical values. The identification results, determined by taking the average, are shown in Table 2. Evidently, the proposed method significantly enhances the accuracy of parameter identification in noisy environments. In this case study, the error of the optimized estimation results is reduced by approximately 20%.

Fig. 7

Histograms of nonlinear parameters identified

Table 2 Nonlinear parameter identification values and errors

The simulation case was then replicated under different noise levels, and the outcomes of parameter identification errors are depicted in Fig. 8. From the figure, it can be observed that under low noise intensity conditions, the proposed method exhibits a slight improvement in identification accuracy. However, as the noise level increases, a significant discrepancy in accuracy between the NSI method and the proposed method emerges, with the gap widening as the noise level rises.

Fig. 8

Recognition results under different intensity noise

3.2 Complex multi-degree-of-freedom example

To further verify the recognition performance of the algorithm in complex structures, consider a complex multi-degree-of-freedom system as shown in Fig. 9 where nonlinearity consists of cubic stiffness between degrees of freedom 2 and 5, Coulomb friction at degrees of freedom 6, in the form of:

$$ f_{nl1} = k_{n} \left( {x_{2} - x_{5} } \right)^{3} ,f_{nl2} = c_{n} {\text{sgn}} \left( {\dot{x}_{6} } \right) $$

(17)

Fig. 9

Complex multi-degree-of-freedom systems

Detailed values for the physical and nonlinear parameters of the system are shown in Table 3. At t = 0 s, a zero-mean Gaussian random force (r.m.s = 30 N) is applied to DOF 1 to simulate the forced response of the system at a sampling frequency f_s = 1000 Hz and a total simulation time of 10 s. The response is calculated using the fourth-order Runge–Kutta algorithm, adding zero-mean white Gaussian noise with SNR = 20 dB to each analog output.

Table 3 Complex multi-degree-of-freedom systems parameters

The system order was increased from 2 to 220, and the modal parameters of the system were estimated by extracting the eigenvalues and eigenvectors of the system matrix A, as shown in Fig. 10. Like the four-degree-of-freedom case, without data preprocessing and modal stability criterion, Fig. 10a and b exhibits numerous spurious frequency axes and inaccurate damping ratios. The identification results in Fig. 10c and d show significant improvement, revealing six stable frequency axes and a more concentrated relationship between frequency and damping ratios. However, unlike the four-degree-of-freedom case, there are still some erroneous estimation points at high frequencies.

Fig. 10

Modal parameter estimation results

Figure 11 depicts the clustering outcomes of the DNSCAN algorithm for stable mode frequency and damping. Six normal clusters and one outlier cluster are discernible. The elements within the normal clusters exhibit a balanced distribution, whereas the outlier cluster comprises only a few elements, signifying their outlier status. By disregarding the outlier cluster, the system order can be established as 6 × 2 = 12.

Fig. 11

Modal clustering results

Similar to Sect. 3.1, once the system order is determined, the A, B, C, and D matrices can be estimated within the state-space framework. By incorporating the estimated A, B, C, and D matrices into the optimization algorithm detailed in Sect. 2.3, the frequency response curve H₂₁ is estimated, as depicted in Fig. 12. The estimated frequency response curve demonstrates a strong alignment with the theoretical values.

Fig. 12

Frequency response curve H₂₁

Figure 13 presents parameter identification results in the form of a statistical histogram. From the graph, it is evident that both the nonlinear stiffness parameters and damping parameters are concentrated near their theoretical values.

Fig. 13

Histograms of nonlinear parameters identified

Table 4 summarizes the parameter identification results by averaging. The results indicate that despite the complexity of the nonlinear system, this method maintains a commendable level of identification accuracy.

Table 4 Nonlinear parameter identification results and errors

4 Experimental verification

An experimental investigation was undertaken to explore the practical application of the methodology proposed in this paper to real structures. The experimental dataset was generously provided by Prof. Stefano Marchesiello [36, 37] from the Department of Mechanics and Aerospace at Politecnico di Torino, Italy.

The test object used in the study is a five-story structure consisting of five aluminum laminates interconnected by thin steel beams. The schematic representation of the structure is shown in Fig. 14. By simplifying the frame structure as a 5-degree-of-freedom system, it can be assumed that the vertical thin steel beams contribute primarily to the bending stiffness. Table 5 provides the essential physical parameters of the structure.

Fig. 14

multilayer nonlinear structure

Table 5 Physical parameters of the test device

The fifth layer of the structure is equipped with a thin tension metal wire that exhibits nonlinear stiffness when subjected to significant oscillations. The total restoring force exerted by the wire can be represented as the sum of a linear stiffness force k_lx₅ and a cubic nonlinear stiffness force k_n x₅³. This nonlinear term in the system can be expressed as:

$$ f_{nl} = k_{n} x_{5} \left( t \right)^{3} $$

(18)

In the second layer of the structure, an electric shaker applies a random external force with an r.m.s. value of 20.89 N. Each layer is equipped with an acceleration sensor to obtain displacement signals by integrating the acceleration response. Figure 15 illustrates the inputs and responses for the second layer.

Fig. 15

Excitation and displacement response for layer 2

When applying the NSI method to all displacement and excitation signals, the singular value decomposition results in Fig. 16 are similar to the simulation cases. Noise components in the signals disrupt the decomposition, resulting in several singular value spikes. Consequently, determining the system order based on singular values becomes unfeasible.

Fig. 16

Singular value distribution

System orders, ranging from 2 to 200 in even increments, were employed, and the NSI method was executed individually. Eigenvalue decomposition of the recognized system matrix A generated a total of 10,100 eigenvalues and eigenvectors from 100 identifications. Subsequently, by employing data preprocessing and modal stability criteria to eliminate spurious modes and erroneous estimations, the modal identification results transition from Fig. 17a and b to Fig. 17c and d. In Fig. 17c and d, five frequency axes and five modal damping ratio points are evident. However, unlike the simulation cases, the first frequency axis appears sparse, indicating a potential occurrence of excessive denoising.

Fig. 17

System mode identification results

In Fig. 18, observe the frequency-damping clustering outcomes. These results reveal the presence of five distinct clusters within the stable modes, with the fifth cluster corresponding to the recognition of the first-order mode. Notably, the elements in this cluster are notably lower, approximately 1/6 to 1/7 compared to those in the other clusters, indicating relatively unstable recognition. Based on this clustering outcome, the automatic determination of the system order can be established as 5 × 2 = 10.

Fig. 18

Modal clustering results

In reference [36], modal parameters of the structure were estimated using low-level excitation, with the first five modal frequencies depicted by the blue dashed lines in Fig. 19. It can be observed from Fig. 19 that the peaks of the frequency response curves estimated by the proposed method are closer to the natural frequencies, indicating higher credibility compared to the directly estimated results.

Fig. 19

Frequency response curves

The real part of the identified nonlinear parameters at each frequency is shown in Fig. 20. Taking the mean value of the real part in the range of 0 ~ 30 Hz as the final identification result, the value of k_n obtained from NSI method is 3.80 × 10⁷ N/m³, and the value of k_n obtained from proposed method is 5.78 × 10⁷ N/m³.

Fig. 20

Real part of the identified nonlinear parameters

Since an accurate nonlinear restoring force model cannot be determined, the identification results are evaluated by reconstructing responses. The response is reconstructed using the identified state-space model, and the reconstructed response is shown in Fig. 21.

Fig. 21

Reconstructed displacement response

The fitting between the response signal and the measured signal is evaluated using the R-squared coefficient. A higher R-squared coefficient, closer to 1, indicates a better accuracy of response reconstruction and consequently a better identification result of the system. The results of the R-squared coefficient are presented in Table 6, where it’s clear that for each response, the R-squared coefficients obtained from NSI method are lower than the proposed method. The lowest R-squared coefficient obtained from NSI method is 48.72%, and the highest is 57.35%, whereas all optimized R-squared coefficients obtained from proposed method exceed 60%.

Table 6 R-squared coefficient

5 Conclusions

This paper presents an improved framework for nonlinear subspace identification. The proposed method utilizes the DBSCAN algorithm for cluster analysis of stable modes, enabling automatic determination of system order and enhancing the estimation accuracy of the state-space model through an iterative optimization algorithm based on response prediction error minimization. These measures effectively improve the accuracy of nonlinear parameter identification. The effectiveness of this method is demonstrated through simulation studies involving two multi-degree-of-freedom systems and experimental validation on a multilayer building with nonlinear characteristics.

The main conclusions of this paper are as follows:

• 1. Through data preprocessing and modal stability criteria, a significant number of false modes and erroneous estimates induced by noise can be eliminated. Results from two numerical examples demonstrate that over 90% of the erroneous estimates are eliminated through this process.

• 2. In noisy environments, the NSI method of determining system order via singular value decomposition in subspace methods may fail. The DBSCAN clustering algorithm introduced in this paper effectively automates the determination of system order.

• 3. The response prediction error minimization method optimizes the identification results of system matrices. Compared to NSI methods, the proposed approach exhibits strong noise resistance. Simulation results indicate that under SNR = 20 dB, the parameter identification accuracy of the method surpasses NSI methods by over 20%. Experimental results also show that the method achieves approximately 10% higher fidelity in reconstructing responses compared to NSI methods.

Despite these promising results, there are several limitations to the proposed method that warrant further investigation:

• 1. The current methodology cannot be applied to systems with inherent time delays. Time-delay systems introduce additional complexity into the model, which requires specialized techniques to accurately capture the delay dynamics.

• 2. Another limitation of the proposed method is its inability to perform real-time identification. This issue arises from the construction of the Hankel matrix in subspace identification methods. Future work might overcome this limitation by integrating the proposed approach with real-time identification techniques such as recursive subspace methods.

Appendix

The dynamic control equations for an N-degree-of-freedom mechanical structure with localized nonlinearity can be formulated as follows:

$$ {\textbf{M}}\ddot{\varvec{q}}\left( t \right) + {\mathbf{C}}_{v} \dot{\varvec{q}}\left( t \right) + {\textbf{K}}\varvec{q}\left( t \right) + \user2{f}_{{nl}} \left( t \right) = \varvec{f}\left( t \right) $$

(A.1)

where ${\textbf{M}}{\ddot{\varvec{q}}}\left( t \right)$ represents the inertial force with M denoting the mass matrix and $\ddot{\varvec{q}} (t)$(t) indicating the acceleration at time t. C_v$\dot{\varvec{q}} (t)$ denotes the damping dissipative force, with C_v as the damping matrix, and $\dot{\varvec{q}}$(t) representing velocity. Kq(t) signifies the elastic force, with K as the stiffness matrix, and q(t) denoting displacement. These forces, damping dissipative and elastic, are linear restorative components within the system. f_nl(t) characterizes the non-linear restorative force within the system, which depends on displacement and velocity and can be expressed as the sum of p forces:

$$ {\varvec{f}}_{nl} \left( t \right) = \sum\limits_{i = 1}^{p} {\theta_{i} {\varvec{L}}_{i} g_{i} \left( t \right)} $$

(A.2)

where g_i(t) signifies the functional form of the i_th nonlinear elastic or damping force, L_i represents the force location, and θ_i denotes the stiffness and damping coefficients of the i_th non-linear force, which are the parameters to be identified in this study.

Moving the nonlinear terms to the right-hand side results in:

$$ {\mathbf{M}} \ddot{\varvec{q}}\left( t \right) + {\mathbf{C}}_{v} \dot{\varvec{q}}\left( t \right) + {\mathbf{K}}\dot{\varvec{q}}\left( t \right) = {\varvec{f}}\left( t \right) - \sum\limits_{i = 1}^{p} {\theta_{i} {\varvec{L}}_{i} g_{i} \left( t \right)} = {\varvec{f}}\left( t \right) - {\varvec{f}}_{nl} \left( t \right) $$

(A.3)

Equation (A.3) considers nonlinearity as internal feedback forces applied to the underlying linear system. Consequently, the measured output of a non-linear system can be seen as the result of the combined action of external force f(t) and internal feedback force f_nl(t) on the underlying linear system.

The state-space representation of Eq. (A.3) for the defined state vector x(t) = [q(t) $\dot{q}$(t)]^T, input vector u(t) = [f(t) -g₁(t) … -g_p(t)]^T, and output vector y(t) = q(t) can be expressed as follows:

$$ \begin{gathered} \dot{\varvec{x}}\left( t \right) = {\varvec{A}}_{c} \varvec{x}\left( t \right) + {\textbf{B}}_{c} \varvec{u}\left( t \right) \hfill \\ \varvec{y}\left( t \right) = {\textbf{C}}\varvec{x}\left( t \right) + {\textbf{D}}\varvec{u}\left( t \right) \hfill \\ \end{gathered} $$

(A.4)

where A_c, B_c, C, D, respectively, denote the system matrices and can be expressed as follows:

$$ \left\{ \begin{gathered} {\mathbf{A}}_{c} = \left[ {\begin{array}{*{20}c} {\mathbf{0}} & {\mathbf{I}} \\ { - {\mathbf{M}}^{ - 1} {\mathbf{K}}} & { - {\mathbf{M}}^{ - 1} {\mathbf{C}}_{v} } \\ \end{array} } \right],{\mathbf{B}}_{c} = \left[ {\begin{array}{*{20}c} {\mathbf{0}} & {\mathbf{0}} & \cdots & {\mathbf{0}} \\ {{\mathbf{M}}^{ - 1} } & {\theta_{1} {\mathbf{M}}^{ - 1} {\varvec{L}}_{1} } & \cdots & {\theta_{p} {\mathbf{M}}^{ - 1} {\varvec{L}}_{p} } \\ \end{array} } \right] \hfill \\ {\varvec{C}} = \left[ {\begin{array}{*{20}c} {{\mathbf{I}}_{N \times N} } & {{\mathbf{0}}_{N \times N} } \\ \end{array} } \right],{\mathbf{D}} = \left[ {\begin{array}{*{20}c} {{\mathbf{0}}_{N \times N} } & {{\mathbf{0}}_{N \times 1} } & \cdots & {{\mathbf{0}}_{N \times 1} } \\ \end{array} } \right] \hfill \\ \end{gathered} \right. $$

(A.5)

where I denotes the unit matrix.

It is possible to transform the continuous-time state-space model into a discrete-time model. Given a sampling interval Δt, the relationship between the continuous-time and discrete-time state-space models are as follows:

$$ {\mathbf{A}} = e^{{{\mathbf{A}}_{c} \Delta t}} ,{\mathbf{B}} = \left( {e^{{{\mathbf{A}}_{c} \Delta t}} - {\mathbf{I}}} \right){\mathbf{A}}_{c}^{ - 1} {\mathbf{B}}_{c} $$

(A.6)

The Fourier transform of Eq. (A.4) yields the extended frequency response function matrix:

$$ {\mathbf{H}}_{E} = {\mathbf{D}} + {\mathbf{C}}\left( {i\omega {\mathbf{I}} - {\mathbf{A}}_{c} } \right)^{ - 1} {\mathbf{B}}_{c} $$

(A.7)

where i denotes the unit imaginary number, i = ${\sqrt{-{1}}}$.

Defining the Matrix:

$$ {\mathbf{N}} = \left[ {\begin{array}{*{20}c} {{\mathbf{N}}_{11} } & {{\mathbf{N}}_{12} } \\ {{\mathbf{N}}_{21} } & {{\mathbf{N}}_{22} } \\ \end{array} } \right] = i\omega {\mathbf{I}} - {\mathbf{A}}_{c} ,{\mathbf{P}} = \left[ {\begin{array}{*{20}c} {{\mathbf{P}}_{11} } & {{\mathbf{P}}_{12} } \\ {{\mathbf{P}}_{21} } & {{\mathbf{P}}_{22} } \\ \end{array} } \right] = \left( {i\omega {\mathbf{I}} - {\mathbf{A}}_{c} } \right)^{ - 1} $$

(A.8)

Substituting Eq. (A.8) into Eq. (A.7) yields:

$$ {\mathbf{H}}_{E} \left( \omega \right) = {\mathbf{P}}_{12} \left[ {\begin{array}{*{20}c} {{\mathbf{M}}^{ - 1} } & {\theta_{1} {\mathbf{M}}^{ - 1} {\varvec{L}}_{1} } & \cdots & {\theta_{p} {\mathbf{M}}^{ - 1} {\varvec{L}}_{p} } \\ \end{array} } \right] $$

(A.9)

This is obtained according to the chunked matrix inversion rule:

$$ {\mathbf{P}}_{12} = - {\mathbf{N}}_{11}^{ - 1} {\mathbf{N}}_{12} \left( {{\mathbf{N}}_{22} - {\mathbf{N}}_{21} {\mathbf{N}}_{11}^{ - 1} {\mathbf{N}}_{12} } \right)^{ - 1} = \left( {{\mathbf{K}} + i\omega {\mathbf{C}}_{v} - \omega^{2} {\mathbf{M}}} \right)^{ - 1} {\mathbf{M}} = {\mathbf{H}}^{ - 1} \left( \omega \right){\mathbf{M}} $$

(A.10)

Thus, Eq. (A.7) can finally be expressed as:

$$ {\mathbf{H}}_{E} \left( \omega \right) = \left[ {\begin{array}{*{20}c} {{\mathbf{H}}\left( \omega \right)} & {\theta_{1} {\varvec{L}}_{1} {\mathbf{H}}\left( \omega \right)} & \cdots & {\theta_{p} {\varvec{L}}_{p} {\mathbf{H}}\left( \omega \right)} \\ \end{array} } \right] $$

(A.11)

where H(ω) is the underlying linear system frequency response function.

From Eq. (A.11), it is evident that nonlinear parameters can be obtained by calculating the extended frequency response function H_E(ω). Considering the presence of the imaginary unit i, identified nonlinear parameters are complex quantities associated with frequency. At each frequency ω, the real part represents the parameter estimate, ideally having a zero imaginary component. However, the presence of noise and nonlinear modeling errors can introduce non-zero imaginary components.