1 Introduction

In practice, most mechanical systems are significantly affected by nonlinearity, with rotor systems being particularly significant [1]. In the process of studying the nonlinear characteristics and diagnosing faults of rotor systems, regardless of the research scheme adopted, the first step is to study the modeling methods of rotor systems [2,3,4]. One of the most commonly used modeling methods for rotor systems is the finite element method. Ren et al. [5] analyzed the stability and Hopf instability of the periodic motion of the complex rotor-bearing system with coupled faults. Mereles et al. [6] achieved finite element analysis of a high-dimensional rotor foundation system with bearing oil film as the nonlinear source. Briend et al. [7] analyzed the dynamic instability caused by imbalanced mass, support rotation, the coupling between both phenomena by Timoshenko beam elements.

However, as modern machinery becomes increasingly complex and traditional methods become inadequate [8], more and more scholars are paying attention to data-driven models. This method is called system identification, and its numerical model can be established just by measuring the input and output data of the system, making it possible to model very complex systems. In the 1980s, Billings proposed a Nonlinear Auto-Regressive with eXogenous inputs (NARX) model based on the Volterra series model [9]. The most common method for building NARX models is the Forward Regression Orthogonal Least Square (FROLS) algorithm [10]. Asgari et al. [11] established and validated the NARX model for heavy-duty single shaft gas turbines. Fravolini et al. [12] completed robust fault detection of the air data system by NARX model.

In general, NARX model identification always chooses random signals as system inputs because random signals contain more information in the frequency domain, which can ensure the accuracy of modeling results. However, the excitation force used to identify rotor systems is usually generated by an unbalanced mass on the rotor, which is a harmonic excitation [13]. Ma et al. [14] used the sweep signal generated during the acceleration process as input signals to establish the NARX model. Long Jin et al. [15] proposed a time-domain swept frequency modeling method for rotor bearing systems, which improves the reliability of modeling by incorporating system input and output data at different speeds into calculations. This algorithm is similar to the Extended Forward Orthogonal Regression (EFOR) algorithm for parameter dependent NARX modelling [16], except that the relevant parameter is speed. Luo Zhong et al. proposed a frequency domain sweeping modeling method [17, 18] for rotor systems, which also integrates information from multiple rotational speeds to improve the success rate of identification.

The above studies have all focused on the selection of important model terms, but the number of model terms in the NARX model is also crucial. In traditional methods, the determination of the number of model terms relies on the Error Reduction Rate (ERR) criterion, just like the selection of terms. The ERR value of one model term reflects the accuracy of this term's one step ahead accuracy [19]. It only focuses on the contribution rates of one model term, without evaluating the accuracy of the NARX model itself. As a result, when using traditional methods to identify rotor systems, the identification models often lack accuracy or even fail due to overfitting or underfitting.

Based on the above analysis, in this paper, the Model Prediction Output (MPO) error is used as the basis for determining the number of model terms. The proposed method is based on the speed-dependent EFOR algorithm, in which the selected model terms are used as a sub-model to calculate its MPO error during the iteration process. After iterating to a certain extent, the sub-model with the smallest is selected as the identification result. In this way, the problem of poor model accuracy or divergence due to overfitting or underfitting can be effectively avoided, and it can be ensured that the identified model will be the optimal model that can be obtained. Simulations and experiments on the rotor system demonstrate the feasibility of the proposed method. The work provides an important basis for the analytical study and fault diagnosis of the nonlinear rotor system.

This paper is organized as follows. Section 2 briefly introduces the traditional EFOR algorithm; Sect. 3 uses a rotor system with a rub-impact fault as a numerical case to illustrate the problems of EFOR algorithm based on AERR criterion in practice; Sect. 4 introduces the proposed improved EFOR algorithm based on MPO and analyzes its advantages over traditional algorithms; In Sect. 5, the effectiveness of the proposed method is verified using the numerical examples proposed earlier; An experimental application of the proposed method is presented in Sect. 6; Sect. 7 summarizes the conclusion.

2 Speed dependent EFOR algorithm

Considering the input and output data of the rotor system at multiple speeds through the speed-dependent EFOR algorithm can provide more information for system identification. This can improve the reliability of rotor system NARX model identification to some extent.

A polynomial structured speed dependent NARX model can be represented as:

$$ \begin{aligned} y(t) & = \theta_{0} (\omega ) + \sum\limits_{{i_{1} = 1}}^{n} {\theta_{{i_{1} }} (\omega )x_{{i_{1} }} (t) + } \sum\limits_{{i_{1} = 1}}^{n} {\sum\limits_{{i_{2} = i_{1} }}^{n} {\theta_{{i_{1} i_{2} }} (\omega )x_{{i_{1} }} (t)x_{{i_{2} }} (t)} + ...} \\ & \quad + \sum\limits_{{i_{1} = 1}}^{n} {...\sum\limits_{{i_{l} = i_{l - 1} }}^{n} {\theta_{{i_{1} i_{2} ...i_{l} }} (\omega )x_{{i_{1} }} (t)...x_{{i_{l} }} (t)} } \\ \end{aligned} $$
(1)

where θi is the model structure coefficient; l is the highest order of the nonlinear system polynomial;n = ny + nu, ny and nu are the maximum time delay of the system output sequence and input sequence, respectively; xm(t) is the delay term of the input sequence and output sequence:

$$ x_{m} (t) = \left\{ {\begin{array}{*{20}l} {y(t - m)} \hfill & {1 \le m \le n_{y} } \hfill \\ {u(t - (m - n_{y} ))} \hfill & {n_{y} + 1 \le m \le n_{y} + n_{u} } \hfill \\ \end{array} } \right. $$
(2)

Assuming that there are R different rotational speeds separately driving the system, R pairs of input–output dataset will be generated. To enable the modeling process to contain all rotational speed information, a candidate terms dictionary is established for each pair of input–output datasets:

$$ \begin{aligned} P_{r} & = \left[ {p_{r,1} ,p_{r,2} ,...,p_{r,M} } \right] \\ & = \left[ {\begin{array}{*{20}l} {p_{r,1} (k)} \hfill & {p_{r,2} (k)} \hfill & \ldots \hfill & {p_{r,M} (k)} \hfill \\ {p_{r,1} (k + 1)} \hfill & {p_{r,2} (k + 1)} \hfill & \ldots \hfill & {p_{r,M} (k + 1)} \hfill \\ \vdots \hfill & \vdots \hfill & \ddots \hfill & \vdots \hfill \\ {p_{r,1} (N)} \hfill & {p_{r,2} (N)} \hfill & \ldots \hfill & {p_{r,M} (N)} \hfill \\ \end{array} } \right] \\ \end{aligned} $$
(3)

where pr,m(t),(t = k,k + 1,…,N) is the sampling value of the model term pr,m at time t. One of model terms pr,m is composed of elements or combinations of products between elements in a vector [x1(t),x2(t),…,xm(t)]. And it can be calculated that there are a total of M = (n + l)!/(n!l!) candidate model terms. P is a matrix composed of model terms. The subscript r represents the corresponding r-th excitation speed.

In order to avoid the interference caused by the mutual coupling between various regression terms to the subsequent calculation, it is necessary to orthogonalize the candidate dictionary according to Schmidt orthogonalization method[20].

Assuming the iteration proceeds to step n, for m ≠ li,i = 1,2,…,n, calculate:

$$ w^{(n)}_{r,m} = p_{r,m} - \sum\limits_{j = 1}^{n - 1} {\frac{{\left\langle {p_{r,m} ,w_{r,i} } \right\rangle }}{{\left\langle {w_{r,i} ,w_{r,i} } \right\rangle }}} w_{j} ,\,\,\,m = 1,2,...,M $$
(4)
$$ g^{(n)}_{r,m} = \frac{{\left\langle {y_{r} ,w^{(n)}_{r,m} } \right\rangle }}{{\left\langle {w^{(n)}_{r,m} ,w^{(n)}_{r,m} } \right\rangle }},\,\,\,m = 1,2,...,M $$
(5)
$$ AERR^{(n)}_{m} = \frac{1}{R}\sum\limits_{l = 1}^{R} {\frac{{g_{l,m}^{(n)2} \left\langle {w^{(n)}_{r,m} ,w^{(n)}_{r,m} } \right\rangle }}{{\left\langle {y_{r} ,y_{r} } \right\rangle }}} \times 100\% $$
(6)
$$ l_{n} = \arg \max \{ m|AERR^{(n)}_{m} \} ,\,\,\,1 \le m \le M $$
(7)

where \(\left\langle { \cdot , \cdot } \right\rangle\) represents the inner product of a vector.

Let wr,n = wr,ln, gr,n = gr,ln, AERRn = AERR(n)ln.

The above is the method for selecting important model term in one step iteration. How to terminate iterations is another key issue and the focus of this study.

For traditional methods, when calculating to step M0, if the Error to Signal Ratio (ESR) meets the following conditions, the iteration terminates:

$$ ESR = 1 - \sum\limits_{m}^{{M_{0} }} {AERR_{m} \le \rho } $$
(8)

where ρ is called the error threshold, which is a very small value that needs to be selected based on experience. Ideally, the size of the ρ value directly determines the length and accuracy of the model. However, due to the characteristics of rotor systems, this approach often fails to achieve the desired results in model identification for rotor systems. This will be reflected in the numerical examples that follow.

Finally, through inverse Schmidt orthogonalization, the NARX model of the rotor system with a unified model structure can be obtained:

$$ y(k) = \sum\limits_{m}^{{M_{0} }} {\theta_{m} (\omega )} p_{m} (k) $$
(9)
$$ \theta_{m} (\omega ) = \sum\limits_{n = 0}^{N} {\beta_{m,n} \omega^{n} } $$
(10)

where θm(ω) is the coefficient of the model term corresponding to the speed, which can be determined by the least squares method based on the coefficient matrix θr,m and the speed vector ω = [ω1,ω2,…,ωR].

3 Problem statement

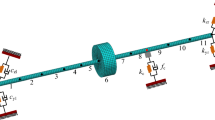
In this section, a single disk rotor system with rubbing faults is selected for study. The principle diagram of friction is shown in Fig. 1, and the schematic diagram of the finite element model is shown in Fig. 2.where O1 represents the center of the stationary rotor; O2 represents the center of the rotor when rub occurs; O3 represents the center of the rotor if no rub occurs; U represents the amount of deformation between the rotor and stator when rub occurs; δ0 represents the initial clearance between the rotor and stator; ω is the rotational speed of the rotor; kr and λ are the contact stiffness and friction coefficient between the rotor and stator, respectively.

Fig. 1
figure 1

Schematic diagram of the rotor rub–impact

Full size image
Fig. 2
figure 2

Schematic diagram of single disk rotor system with rotor rub-impact

Full size image

The entire rotor system is divided into 11 shaft segments, totaling 12 nodes. The disk has a diameter of 70mm and is located on the 6th shaft segment. Two rolling bearings are located at both ends of the shaft, and the friction fault occurred on the 8th shaft segment. Here, the motion of the rolling element inside the bearing is ignored and represented by equivalent stiffness and damping.

The shaft segment is simulated using Timoshenko beam elements. In the Timoshenko beam element, each element has two nodes, and each node has 4 degrees of freedom. The generalized coordinates of the beam element are represented as:

$$ q = \left( {x_{A} ,y_{A} ,\theta_{{x_{A} }} ,\theta_{{Y_{A} }} ,x_{B} ,y_{B} ,\theta_{{x_{B} }} ,\theta_{{Y_{B} }} } \right)^{T} $$
(11)

Due to the short duration of the collision in the rotor system, it can be approximated that a linear deformation occurs between the stator and rotor, i.e., the friction is proportional to the normal force at the point of contact. As shown in Fig. 1, FN represents the normal frictional force, FT represents the tangential frictional force, and its specific expression is as follows:

$$ \left\{ {\begin{array}{*{20}l} {F_{N} = 0} \hfill & {r < \delta_{0} } \hfill \\ {F_{N} = (r - \delta_{0} )k_{r} } \hfill & {r \ge \delta_{0} } \hfill \\ {F_{T} = \lambda F_{N} } \hfill & {} \hfill \\ \end{array} } \right. $$
(12)

In the Cartesian coordinate system, the rubbing force can also be expressed as:

$$ \left\{ \begin{gathered} F_{x} (x,y) \hfill \\ Fy(x,y) \hfill \\ \end{gathered} \right\} = - H(r - \delta_{0} )\frac{{\left( {r - \delta_{0} } \right)k_{r} }}{r}\left( {\begin{array}{*{20}c} 1 & { - \lambda } \\ \lambda & 1 \\ \end{array} } \right)\left\{ \begin{gathered} x \hfill \\ y \hfill \\ \end{gathered} \right\} $$
(13)

In the equation, \(r = \sqrt {x^{2} + y^{2} }\) represents the radial displacement of the rotor, H(·) is the Heaviside function, defined as:

$$ H(x) = \left\{ {\begin{array}{*{20}c} {1,} & {x \ge 0} \\ {0,} & {x < 0} \\ \end{array} } \right. $$
(14)

Therefore, the dynamic equation of a rub-impact rotor can be expressed as:

$$ \left\{ {\begin{array}{*{20}l} {M\ddot{x} + (C + G)\dot{x} + Kx = F_{Ux} + F_{x} (x,y)} \hfill \\ {M\ddot{y} + (C + G)\dot{y} + Ky = F_{Uy} + F_{y} (x,y)} \hfill \\ \end{array} } \right. $$
(15)

where M is the mass matrix, C is the damping matrix, G is the gyro matrix, and K is the stiffness matrix of the rotor system; FUx,FUy,Fx(x,y),Fy(x,y) are the unbalanced force vectors and friction force vectors along the x and y directions, respectively.

Assume excitation speed ω ∈ [1200:1400]rpm, the difference between adjacent two excitation speeds is dω = 10rpm. Therefore, there are a total of 21 different input–output data sets. In this study, the friction clearance is set δ0 = 140μm. The rotor simulation result at 1300 rpm is shown in Fig. 3

Fig. 3
figure 3

Simulation results of rubbing rotor, ω = 1300rpm

Full size image

To simulate the actual application, 50 dB Gaussian white noise is added to the output signal. Now, the EFOR algorithm is used to find the top ten important model terms without considering the iteration termination problem, and the results are shown in Table 1:

Table 1 The top 10 model terms identified by the EFOR algorithm
Full size table

It can be seen that the AERR values are very small for each model term except for the first one. The identification results are therefore extremely sensitive to changes in ρ values. In the traditional approach, the selection of the ρ value needs to be done empirically. This makes it very difficult in practice to build the optimal NARX model.

For example, two NARX models are built with 8 and 9 model terms respectively. When verifying speed ω = 1300rpm, the two models are shown in Table 2:

Table 2 NARX model with 8 and 9 terms
Full size table

The ESR values of these two NARX models are 0.00799% and 0.00779%, respectively. According to the AERR criterion, the fitting accuracy of these two models should exceed 99.99%, and there should be no significant difference between the two models. However, the MPO validation results for these two models suggest otherwise:

Obviously, although the ESR values of the two NARX models are small enough, their MPO validation results are not ideal and cannot fit the original signal at all. Even the NARX model with 8 model terms are divergent.

Furthermore, although the NARX model with 9 model terms as shown in Fig. 4b is convergent, this is the validation result at 1300rpm. As shown in Fig. 5, the model does not converge when the validation speed is 1250rpm:

Fig. 4
figure 4

MPO validation results: a Model predicted output of the NARX model with 8 terms. b Model predicted output of the NARX model with 9 terms

Full size image
Fig. 5
figure 5

Model predicted output of the NARX model with 9 terms when ω = 1250rpm

Full size image

In summary, a sufficiently small ESR value sometime cannot guarantee a sufficiently high model fitting accuracy. This is one of the major reasons why there are often failed results in NARX model identification of rotor systems.

4 EFOR algorithm based on model prediction output

Through the aforementioned analysis, it is found that the traditional EFOR algorithm has the problem of difficulty in obtaining the optimal NARX model. The main reason is that the AERR criterion cannot reflect the overall fitting accuracy of the NARX model. Based on this judgment, an improved EFOR algorithm based on MPO error is introduced in this section.

In order to avoid the absolute value difference caused by the signal amplitude, this paper introduces the Normalized Mean Square Error (NMSE) to evaluate the MPO validation results of each sub-model [21, 22]:

$$ NMSE{ = }\frac{{\sum\limits_{t = 1}^{N} {\left[ {y_{NARX} (t) - y(t)} \right]} }}{{\sum\limits_{t = 1}^{N} {\left[ {y_{NARX} (t)} \right]}^{2} }} $$
(16)

where yNARX(t) represents the predicted output of the target NARX model, and y(t) represents the actual output of the sampled system.

Due to the differences in the results of NARX models at different excitation speeds, it is necessary to conduct MPO validation for all excitation speeds and calculate the Average NMSE (ANMSE) values during modeling.

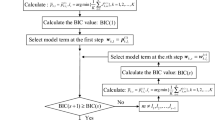
The EFOR identification algorithm based on MPO is shown in Fig. 6, which can be summarized as follows:

  1. 1

    Parameter settings: Set the maximum input delay nu, the maximum output delay ny, the highest order l of the model, and the maximum number of model terms Mmax. To ensure that the computation is not too complex, Mmax should not be too large, and to ensure a sufficiently accurate NARX model can be obtained, Mmax should also not be too small.

  2. 2

    Select model terms: Significant model terms were selected stepwise based on the AERR criterion. For each new model term, all the selected model terms are formed into a sub-model, and the sub-model is validated by MPO and its ANMSE value is calculated. Until the number of selected model terms reaches Mmax.

  3. 3

    Select the optimal model: First, all sub-models that diverged at certain RPMs were excluded. Then, the MPO errors of the remaining sub-models are calculated at different excitation speeds. Finally, the submodel with the smallest ANMSE value is selected as the final identification result.

Fig. 6
figure 6

The flowchart of the identification process with the EFOR algorithm based on MPO

Full size image

Compared with traditional algorithms, the EFOR algorithm based on MPO has the following advantages:

  1. 1

    As the iteration progresses, the ESR value of the current model always decreases. But MPO error is not. This means that ANMSE can better reflect the fitting error of the current model than ESR.

  2. 2

    The MPO validation results are used to select the optimal potential identification results, which solves the problem of overfitting or underfitting that often occurs in traditional methods.

  3. 3

    The identification process no longer relies on a priori knowledge, which effectively reduces the dependence on specialized knowledge for NARX modeling and improves the practicality and efficiency of NARX model identification.

5 Numerical case study

As mentioned earlier, assume excitation speed ω ∈ [1200:1400]rpm, the difference between adjacent two excitation speeds is dω = 10rpm, and the friction clearance is set δ0 = 140μm. Set the identification parameters: the maximum delay of input and output is nu = ny = 4, the highest order of the model l = 4, and the maximum number of terms of the model Mmax = 22. The model identification of the rotor finite element model established in Sect. 3 is carried out using the MPO-based EFOR algorithm, and the results are shown in Table 3 and Fig. 7.

Table 3 Modeling results of EFOR algorithm based on MPO
Full size table
Fig. 7
figure 7

MPO validation results of NARX model when ω = 1300rpm

Full size image

The NARX model with 19 model terms is the best NARX model among all potential identification results. The ANMSE value of this optimal model is 8.5755 × 10–4, and the total AERR is 99.9956%. This NARX model can be represented as:

$$ y(k) = \theta_{1} (\omega )y(k - 1) + \theta_{2} (\omega )y(k - 2) + ... + \theta_{19} (\omega )u(k - 3)^{2} u(k - 4)y(k - 3) $$
(17)

From Table 3, it can be seen that the NARX sub-models containing 6 to 15 model terms all diverge, and in fact, most of them are not able to maintain convergence at all excitation speeds. While the other non-optimal sub-models are convergent, they are all also significantly less accurate than the optimal sub-model. These suboptimal NARX models are easily obtained if conventional methods are used.

For example, if the traditional method is used for modeling, and ρ = 6 × 10–5 is set, then the NARX model obtained from the identification will contain 13 model terms. This model is dispersive at the validation rotational speed of 1300 rpm as shown in Fig. 8.

Fig. 8
figure 8

MPO validation results of NARX model identified by traditional method, ρ = 6 × 10–5

Full size image

Alternatively, setting ρ = 5 × 10–5, the obtained model contains 17 model terms, and its MPO validation error ANMSE value is 3.7620 × 10–3. This model is a relatively easy to obtain identification result, but still has a certain accuracy gap compared with the optimal model. The comparison of the MPO validation results of this model with the optimal model is shown in Fig. 9.

Fig. 9
figure 9

MPO validation of suboptimal model and optimal model

Full size image

In contrast, the NARX model built with the proposed method can fit the signal characteristics of the rotor system well.

6 Experiment

In order to obtain the displacement response data required to identify the NARX model of the rotor friction system at various speeds, a rotor test bench is constructed as shown in Fig. 10. The required harmonic excitation in the experiment is achieved by the imbalance added to the disk. Adjust the rotor speed through a speed controller, measure the vibration displacement response of the rotor in the vertical direction through an eddy current sensor, collect the sensor voltage signal through the NI-9234 acquisition card, and finally save the experimental data through the Labview software program. The severity of friction in the experiment is controlled by adjusting the number of feed turns of the friction bolt.

Fig. 10
figure 10

Rotor fixed point rubbing fault test bench

Full size image

By turning the knob of the speed controller, the displacement response of the rubbing rotor was measured at 10 different speeds between 1500 and 1700rpm. An input signal with a speed of ω = 1605rpm was used to validate the identified model. The identification results are shown in Tables 4 and 5. The predicted outputs are compared to the real output in both the time and frequency domains, as shown in Fig. 11.

Table 4 identification results (ω = 1605rpm)
Full size table
Fig. 11
figure 11

Comparison of the responses of the rotor system in the horizontal direction (ω = 1605rpm): a in the time-domain; b in the frequency-domain

Full size image
Table 5 NMSE values of identified model under different rotational speed conditions
Full size table

The MPO validation results show good agreement between the model outputs and the actual signals. The proposed method effectively avoids suboptimal and divergent potential identification results and yields the optimal NARX model that may be obtained.

7 Conclusions

Considering that the NARX model identification method has the problem of unsuccessful identification for rotor systems, an improved EFOR identification algorithm based on the rotational speed related EFOR algorithm is proposed in this study. Compared with the original EFOR algorithm, the improved algorithm checks all possible identification results based on the MPO error during the iteration process, and outputs the optimal NARX model among them. This not only effectively solves the problem of identification failure, but also avoids the poor model accuracy due to overfitting or underfitting, and ensures the accuracy and reliability of NARX model identification.

Both numerical simulations and experimental studies demonstrate the effectiveness and reliability of the proposed method. The results show that the improved EFOR algorithm successfully avoids the failure model and suboptimal model and obtains the optimal results when the identification is performed for rotor systems. More importantly, this process is done automatically by the algorithm without additional manual adjustment. The results of this study show the promise of the improved EFOR algorithm for system analysis and diagnosis in engineering practice.