Online system identification using fractional-order Hammerstein model with noise cancellation

Abstract

Slow convergence and low accuracy are two main drawbacks in nonlinear system identification methods. It becomes more complicated when time delay and noises are considered. In this paper, considering a fractional-order Hammerstein model, an online identification method is proposed. A combination of an evolutionary optimization method and recursive least square algorithm is used to estimate the system parameters and orders in the presence of unknown noises. Finally, simulation results are taken to prove the effectiveness of the proposed algorithm.

1 Introduction

Previously, standard systems as well as standard control systems, regardless of reality, were all considered to be integer-order systems. Recent researches, however, have shown that some of real-world systems are fractional order. In recent years, an increasing number of real-time physical systems have been better described by fractional-order differential equations (FODEs) than classical integer-order models. So, researchers and engineers are increasingly using fractional-order dynamical models to model real physical systems.

Identifying of the mathematical model of the system is very important in analyzing the properties of the system as well as designing a suitable controller for the system. System identification is a standard tool for modeling unknown systems whose main purpose is to determine the structure and parameters of the mathematical model of the system to reproduce the dynamic behavior of the system. This process becomes more difficult when physical systems are described by FODE instead of integer-order models. In this regard, the high complexity and lack of sufficient mathematical tools had led to little attention to fractional-order (FO) dynamical systems in theory and practice [1, 2]. But today, however, with the growth of computers and their ability to compute complex integrals and FO derivatives, this problem has been somewhat solved and fractional calculations have become an attractive research topic in the scientific and industrial communities. In recent decades, due to this growth, along with the theoretical research of fractional integrals and derivatives [3, 4], the use of fractional operators in various fields has been significantly developed.

Fractional calculus has been introduced in various fields of science and engineering [5, 6], including identification of thermal systems [7], identification of biological tissues [8], image processing [9], signal processing [10], path planning [11], path tracking [12], robotics [13], mechanical damping [14], battery [15], control theory and its applications [16, 17], mechanics [18], diffusion [19]. Also, systems with long-memory transient characteristics and independent frequency domain [14, 20, 21], transmission and distribution lines, electromechanical processes, dielectric polarization, viscoelastic materials such as polymers and rubbers, relaxation phenomena of organic dielectric materials, flexible structures, traffic in information networks and biological systems [7, 19, 22,23,24,25,26,27,28,29], colored noise, chaos [30], controllers [31], etc., can be modeled more appropriately by FO models than integer-order models. This confirms the fact that a significant number of real systems are generally fractional. Although for many of them, the degree of fractionality is very low. Thus, the application of fractional calculus has become the focus of international academic research, and the identification of such fractional-order systems has aroused growing interest in the scientific community. Although FO models are more suitable for describing dynamic systems than integer-order models, they require suitable methods for analytical or numerical calculations of FODEs [3, 4].

The aim of this paper is presenting a new online method for identifying nonlinear systems which offers two features simultaneously: increasing accuracy and decreasing computations. For this purpose, a nonlinear system identification based on FO Hammerstein model has been considered. The proposed method uses recursive identification algorithm with the ability of online identification.

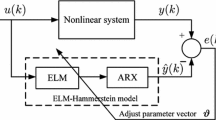
The reason for using the Hammerstein model (Fig. 1) is that this model does not require a lot of basic information from the system, which makes identifying using process data relatively easier. The motivation for using fractional calculations in system identification is to preserve the features and phenomena ignored by integer-order models by FO models, as well as the fact that the dynamic behavior of an increasing number of real processes can be more accurately expressed using fractional models.

Fig. 1

Single-input–single-output Hammerstein model structure

In the FO Hammerstein model identification using input/output data, all unknown system parameters include:

• 1. The coefficients of numerators and denominators of the transfer function and fractional degrees in the linear dynamics part.

• 2. Bezir–Bernstein polynomial (BBP) coefficients or radial basis function neural network (RBFNN) parameters including centers, widths and connection weights in the nonlinear static part are estimated. The recursive method in identification is based on updating unknown parameters by adding new input/output data using a recursive optimization algorithm. In this paper, recursive least square (RLS) algorithm is used for this purpose.

The fractional Hammerstein model is developed to identify multi-input–single-output (MISO) nonlinear systems with the following structure (Fig. 2). It is clear that the identification of MISO systems has many practical applications and it can be generalized to multi-input–multi-output (MIMO) systems.

Fig. 2

MISO Hammerstein model structure

Modeling the behavior of the nonlinear static part is a major challenge in the Hammerstein model. In this paper, two methods are used to represent this part:

• 1. Bezier–Bernstein polynomials: From the point of numerical analysis view, although different types of polynomial functions can be used to estimate the function, in [32] it is shown that Bernstein basic functions are the best and most stable basic functions against other polynomial basic functions.

• 2. Artificial neural network: An important advantage of using artificial neural network is overcoming limitations such as slow convergence and complexity of the structure [33].

Weaknesses and limitations of existing methods of identifying the Hammerstein model, which has become a motivation to present a new method, can be mentioned as follows:

• 1. Limited to the proportional fractional orders [34,35,36,37,38,39,40,41]

• 2. Assuming the fractional orders as known [34,35,36, 39, 40]

• 3. Disqualification for online identification due to computational complexity [34,35,36,37,38,39,40,41]

• 4. High estimation errors [34,35,36,37,38,39,40,41]

• 5. Not to consider time delays especially in online mode [34,35,36,37,38,39,40,41,42,43,44,45,46,47]

• 6. Lack of generality of the presented models. For example, most methods are only applicable to nonlinear systems that have quasi-linear properties [37, 38];

• 7. Inability in system identification in the presence of noises [43,44,45,46,47,48].

In this paper, a recursive method that is generalized to online identification will be used and the Hammerstein model will be considered with the following features:

• 1. The linear part transfer function is considered as a fractional order, which, in addition to more accurate identification of the system, allows the reduction of the number of parameters as a feature of FO systems.

• 2. Due to the BBP properties and RBFNN in more accurate modeling of nonlinear dynamics, these two functions are used to represent the nonlinear part of the Hammerstein model.

• 3. The FO Hammerstein model is developed in MISO mode.

• 4. According to the use of the recursive method and other mentioned features, the proposed identification method is generalized to the online mode.

2 Mathematical background

2.1 Fractional-order models

A continuous-time FO dynamical system can be expressed by a FODE as follows [27, 49]:

$$ \begin{aligned} & H(D^{{\alpha _{0} \alpha _{1} \cdots \alpha _{n} }} )y(t) = G(D^{{\beta _{0} \beta _{1} \cdots \beta _{n} }} )u(t), \\ & H(D^{{\alpha _{0} \alpha _{1} \cdots \alpha _{n} }} ) = \sum\limits_{{k = 0}}^{n} {a_{k} D^{{\alpha _{k} }} } , \\ & G(D^{{\beta _{0} \beta _{1} \cdots \beta _{n} }} ) = \sum\limits_{{k = 0}}^{m} {b_{k} D^{{\beta _{k} }} } \\ \end{aligned} $$

(1)

where $a_{k} ,b_{k} \in {\mathbf{\mathbb{R}}}$. In explicit form:

$$ \begin{aligned} & a_{n} D^{{\alpha _{n} }} y(t) + a_{{n - 1}} D^{{\alpha _{{n - 1}} }} y(t) + \cdots + a_{0} D^{{\alpha _{0} }} y(t) \\ & \quad = b_{m} D^{{\beta _{m} }} u(t) + b_{{m - 1}} D^{{\beta _{{m - 1}} }} u(t) + \cdots + b_{0} D^{{\beta _{0} }} u(t) \\ \end{aligned} $$

(2)

By applying the Laplace transform with zero initial conditions, the input–output representation of the FO system can be obtained in the form of a transfer function:

$$ G(s) = \frac{Y(s)}{{U(s)}} = \frac{{b_{m} s^{{\beta_{m} }} + b_{m - 1} s^{{\beta_{m - 1} }} + \cdots + b_{0} s^{{\beta_{0} }} }}{{a_{n} s^{{\alpha_{n} }} + a_{n - 1} s^{{\alpha_{n - 1} }} + \cdots + a_{0} s^{{\alpha_{0} }} }} $$

(3)

2.2 The structure of Hammerstein model

As mentioned, the MISO Hammerstein model consists of a linear static subsystem and a linear dynamic part. In general, the system is modeled as follows:

$$ \begin{aligned} & y(t) + \sum\limits_{{i = 1}}^{n} {a_{i} D^{{\alpha _{i} }} y(t)} = \sum\limits_{{j = 0}}^{m} {b_{j} D^{{\beta _{j} }} (w_{1} (t) + \ldots + w_{r} (t))} \\ & w_{k} (t) = f(u_{k} (t)) \\ \end{aligned} $$

(4)

where $y(t)$ is the output of the system and $u_{k} (t),k = 1,2, \ldots ,r$ specifies the inputs, and $w_{k} (t),k = 1,2, \ldots ,r$ are the outputs of the nonlinear part and the input to the dynamic one, and $n,m$ are the input and output delays for the linear subsystem.

In this paper, for the linear dynamics part, the FO transfer function is used as follows:

$$ G(s) = \frac{B(s)}{{A(s)}} = \frac{{b_{m} s^{{\beta_{m} }} + \cdots + b_{1} s^{{\beta_{1} }} + b_{0} s^{{\beta_{0} }} }}{{1 + a_{n} s^{{\alpha_{n} }} + \cdots + a_{1} s^{{\alpha_{1} }} }} $$

(5)

where $a_{1} , \ldots ,a_{n} ,b_{0} , \ldots ,b_{m} \in R$ are coefficients and $\alpha_{1} , \ldots ,\alpha_{n} ,\beta_{0} , \ldots ,\beta_{m} \in R$ are fractional orders. The corresponding FODE is shown as follows:

$$ \begin{aligned} & a_{n} D^{{\alpha _{n} }} y(t) + a_{{n - 1}} D^{{\alpha _{{n - 1}} }} y(t) + \cdots + a_{0} D^{{\alpha _{0} }} y(t) \\ & \quad = b_{m} D^{{\beta _{m} }} u(t) + b_{{m - 1}} D^{{\beta _{{m - 1}} }} u(t) + \cdots + b_{0} D^{{\beta _{0} }} u(t) \\ \end{aligned} $$

(6)

In the considered fractional-order transfer function, there is no proportional order constraint.

In order to use the output estimation method, Eq. (6) must be written in the regression form:

$$ y(t) = - \sum\limits_{i = 1}^{n} {a_{i} D^{{\alpha_{i} }} y(t)} + \sum\limits_{j = 0}^{m} {b_{j} D^{{\beta_{j} }} w(t)} $$

(7)

In this paper, three different structures are considered for the nonlinear static part:

2.2.1 Bezier–Bernstein polynomials

Reference [32] has shown that among the various types of polynomial functions for estimating a function, Bernstein's basic functions are the best and most stable of the basic functions against other polynomial basic functions. Therefore, the first method considered for modeling the nonlinear static part is the use of BBP functions. In 1912, S.N. Bernstein introduced the following polynomials for a function defined on the interval [1, 0] [50]:

$$ B_{n} f(t) = \sum\limits_{i = 0}^{n} {\left( {\begin{array}{*{20}c} n \\ i \\ \end{array} } \right)t^{i} (1 - t)^{n - i} f(\frac{i}{n})} \;n{ = 1,2,} \ldots \, $$

(8)

Bernstein’s polynomials can be defined on an interval [a, b] by the following equation [50]:

$$ B_{i,n} (t) = \left( {\begin{array}{*{20}c} n \\ i \\ \end{array} } \right)\frac{{\left( {t - a} \right)^{i} (b - t)^{n - i} }}{{\left( {b - a} \right)^{n} }}\; \, i{ = 0,1,2,} \ldots {,}n \, $$

(9)

These polynomials can be used to estimate any continuous function in the interval [a, b] and have the following properties [50]:

$$ \sum\limits_{i = 0}^{n} {B_{i,n} (t)} = 1 $$

(10)

A general Bezier curve of degree n, defined by n + 1 vertices, can be expressed as follows [50]:

$$ B(t) = \sum\limits_{i = 0}^{n} {a_{i} B_{i,n} (t)} \;t \in \left[ {a,b} \right] $$

(11)

where $a_{i}$ defines the $i{\text{th}}$ vertex and provides information about the shape of the B-curve. Bezier extended the idea of estimating a function to the estimation of a polygon in which n + 1 vertices of a polygon are estimated by Bernstein’s basis. As a result, it was called the Bezier–Bernstein polynomial curve.

The Bezier–Bernstein polynomial used for the nonlinear static part in this paper is considered in the following form:

$$ f\left( {u(t)} \right) = \sum\limits_{j = 0}^{{\text{d}}} {\delta_{j} B_{j,d} (x(u(t)))} $$

(12)

where $j,{\text{d}}$ are non-negative integers, $\delta_{j}$ are weights that must be specified, $x(u(t)$ converts the input change interval to the interval [1, 0] ($x \in \left[ {0,1} \right]$), and $B_{{j,{\text{d}}}} (.)$ are the BBPs with the following definition:

$$ B_{{j,{\text{d}}}} (x) = \left( {\begin{array}{*{20}c} {\text{d}} \\ j \\ \end{array} } \right)x^{j} \left( {1 - x} \right)^{{{\text{d}} - j}} $$

(13)

The number of Bernstein univariate polynomials of degree d is d + 1.

In [40], a formula for Bernstein polynomials defined in interval [a, b] is given as follows:

$$ \begin{aligned} & B_{{j,{\text{d}}}} (x) = \left( {\begin{array}{*{20}c} {\text{d}} \\ j \\ \end{array} } \right)\frac{{(x - a)^{j} \left( {b - x} \right)^{{{\text{d}} - j}} }}{{(b - a)^{{\text{d}}} }}\quad {\text{ }}j{\text{ = 0,1,}} \ldots {\text{,d}}\quad {\text{ }}a \le x \le b{\text{ }} \\ & \quad {\text{, }}a{\text{ = min(}}u{\text{(}}t{\text{)), }}b{\text{ = max(}}u{\text{(}}t{\text{))}} \\ \end{aligned} $$

(14)

With this definition, the relation (12) can be written as follows:

$$ f\left( {u(t)} \right) = \sum\limits_{j = 0}^{{\text{d}}} {\delta_{j} B_{{j,{\text{d}}}} (u(t))} $$

(15)

Using BBPs to represent the nonlinear part, we have in relation (4):

$$ w_{k} \left( t \right) = f_{k} \left( {u_{k} \left( t \right)} \right) = \sum\limits_{i = 0}^{{\text{d}}} {\delta_{k\,i} B}_{k\;i,d} \left( {u_{k} \left( t \right)} \right) $$

(16)

$B_{{k\;i,{\text{d}}}} \left( {u_{k} \left( t \right)} \right),i = 0, \ldots ,{\text{d}},k = 1, \ldots ,r$ are BBPs related to kth input and $\delta_{k\;i} ,i = 0,1, \ldots ,{\text{d}},k = 1, \ldots ,r$ are related weights to be determined.

2.2.2 Radial basis function neural network (RBFNN)

In this case, the identification of the fractional-order Hammerstein model with RBFNN in the nonlinear static part and the fractional-order transfer function in the linear dynamic part is investigated.

The two advantages of using a RBFNN for the structure of a nonlinear gain function are the ability to quickly modify modeling during changes in process dynamics and to overcome constraints such as slow convergence and structural complexity [33]. In fact, the ability of Hammerstein models in nonlinear dynamics modeling with relatively simpler models is combined with the ability of more accurately and simpler system estimation using fractional-order transfer functions. As a result, the problems of inadequacy for online identification and high estimation error in existing methods are eliminated. Also, due to RBFNN capabilities for estimating functions, its use in this paper, by increasing the accuracy of nonlinear part estimation, affects the reduction of estimation error. In this case, the output of the nonlinear part and the input to the linear part are obtained from the following relation:

$$ w_{k} (t) = f_{k} \left( {u_{k} (t)} \right) = \omega_{0k} + \sum\limits_{h = 1}^{M} {\omega_{hk} \phi_{hk} (u_{k} (t))} $$

(17)

$\phi_{hk} (.),h = 1, \ldots ,M,k = 1, \ldots ,r$ are the Gaussian functions of hth hidden node related to kth input and $\omega_{hk} (.),h = 1, \ldots ,M,k = 1, \ldots ,r$ are the connection weights from hth hidden node to the output related to kth input which should be identified. M is the number of radial basis neural network functions.

$$ \phi_{hk} (u_{k} (t)) = \exp \left\{ { - \left( {{{\left\| {u_{k} (t) - c_{hk} } \right\|^{2} } \mathord{\left/ {\vphantom {{\left\| {u_{k} (t) - c_{hk} } \right\|^{2} } {{\text{d}}_{hk}^{2} }}} \right. \kern-0pt} {{\text{d}}_{hk}^{2} }}} \right)} \right\} $$

(18)

$c_{hk} ,{\text{d}}_{hk} ,h = 1, \ldots ,M,k = 1, \ldots ,r$ are the centers and widths of the hth RBF hidden unit associated with the kth input and $\left\| . \right\|$ defines the Euclidean norm.

2.2.3 Modified radial basis function neural network (MRBFNN)

RBFNNs consist of only one layer of activation functions that are radially symmetric. In the standard form, the number RBFNN parameters increases exponentially with increasing the number of inputs. In the modified RBFNN, the centers and widths of Gaussian functions are concentrated in a single adjustable point instead of different points, and only different weights are used. Also, in RBFNN, the number of hidden nodes is equal to the number of sampled training data. But in the MRFNN, the number of hidden nodes is limited and selectable. These two features significantly reduce the number of unknown parameters in the identification process. In this case, the Gaussian functions associated with kth input are no longer dependent on the hidden nodes and have a constant center and width for each input. They are as follows:

$$ \phi_{k} (u_{k} (t)) = \exp \left\{ { - \left( {{{\left\| {u_{k} (t) - c_{k} } \right\|^{2} } \mathord{\left/ {\vphantom {{\left\| {u_{k} (t) - c_{k} } \right\|^{2} } {d_{k}^{2} }}} \right. \kern-0pt} {d_{k}^{2} }}} \right)} \right\} $$

(19)

That is, $\phi_{hk} (.)$ Gaussian functions have the same centers and widths and are simplified to $\phi_{k} (.),k = 1, \ldots ,r$.

3 System identification algorithms

In the proposed identification method, the modified genetic algorithm (MGA) [51] is applied to identify fractional orders and time delays in the dynamic part and to identify the centers and widths of RBF units (Eqs. 17–19) in the nonlinear part as well as the production of initial estimations for the coefficients of the fractional-order transfer function, BBP weights (Eq. 16) and NN weights (Eqs. 17–19).

GA with an innovative strategy is called as modified genetic algorithm (MGA). Comparing with the classic GA in which the best solutions or chromosomes are selected and transferred to the next generation, the best characteristics or properties are selected and transferred to the next generation in MGA. It is inspired from artificial genetic operation in some agronomic products that the best properties of different types by genetic manipulation are transferred to the new product. In this algorithm, the crossover is performed exchanging the best genes between the chromosomes [51].

The crossover step is the main difference between the classic GA and MGA. In MGA, after selection the best chromosomes, the genes are changed between them. The aim of continuing this process is finding the best genes instead of the best chromosomes. The artificial parents are generated with the best genes and putting them together. Better solutions, escaping from local optima and faster convergence are some of the advantages of MGA which are very vital in the online identification process. These advantages will be illustrated by examples [51].

For the identification process, a part of the input/output data is used to obtain all the unknown parameters using MGA. In the next step, using these initial estimations, the recursive least squares (RLS) algorithm is used to update and optimize them using the rest of data. The effective combination of these two algorithms provides the ability to track the nonlinear time-variable behavior of the system. The proposed online system identification structure is shown in Fig. 3.

Fig. 3

Online system identification block diagram

3.1 MISO Hammerstein model using BBPs

Considering Eq. (15), Eq. (7) becomes:

$$ y(t) = - \sum\limits_{i = 1}^{n} {a_{i} D^{{\alpha_{i} }} y(t)} + \sum\limits_{j = 0}^{m} {b_{j} D^{{\beta_{j} }} \left( {\sum\limits_{l = 0}^{{\text{d}}} {\delta_{l} B_{{l,{\text{d}}}} (u(t))} } \right)} $$

(20)

Equation (20) for MISO mode can be written in the following form:

$$ \begin{aligned} y(t) & = - \sum\limits_{{i = 1}}^{n} {a_{i} D^{{\alpha _{i} }} y(t)} + \\ & \quad + \sum\limits_{{j1 = 0}}^{{m_{1} }} {b_{{j1}} D^{{\beta _{{j1}} }} \left( {\sum\limits_{{l = 0}}^{{\text{d}}} {\delta _{l} B_{{l,{\text{d}}}} (u_{1} (t))} } \right)} + ... + \sum\limits_{{jr = 0}}^{{m_{r} }} {b_{{jr}} D^{{\beta _{{jr}} }} \left( {\sum\limits_{{l = 0}}^{{\text{d}}} {\delta _{l} B_{{l,{\text{d}}}} (u_{r} (t))} } \right)} \\ \end{aligned} $$

(21)

According to Eq. (9), in the general case, for BBP of d degree, we have:

$$ y(t) = - \sum\limits_{i = 1}^{n} {a_{i} D^{{\alpha_{i} }} y(t)} + \sum\limits_{j1 = 1}^{{m_{1} }} {b_{j1} D^{{\beta_{j1} }} \sum\limits_{l1 = 0}^{{\text{d}}} {h_{l1} u^{l1} } } + ... + \sum\limits_{jr = 1}^{{m_{r} }} {b_{jr} D^{{\beta_{jr} }} \sum\limits_{lr = 0}^{{\text{d}}} {h_{lr} u^{lr} } } $$

(22)

Using Grunwald–Letnikov estimation:

$$ \begin{aligned} y(k + 1) & = - \sum\limits_{{i = 1}}^{n} {a^{\prime}_{i} Y_{i} (k)} \\ & \quad + \sum\limits_{{j = 0}}^{m} {\left( {\sum\limits_{{l = 0}}^{{\text{d}}} {b1^{\prime}_{{jl}} (F1_{{jl}} (k))} + ... + \sum\limits_{{l = 0}}^{{\text{d}}} {br^{\prime}_{{jl}} (Fr_{{jl}} (k))} } \right)} \\ \end{aligned} $$

(23)

where

$$ a^{\prime}_{i} = \frac{{\frac{{a_{i} }}{{h^{{\alpha_{i} }} }}}}{{1 + \sum\limits_{k = 1}^{n} {\frac{{a_{k} }}{{h^{{\alpha_{k} }} }}} }}, \, bv^{\prime}_{jl} = \frac{{\frac{{b_{j} h_{lv} }}{{h^{{\beta_{j} }} }}}}{{1 + \sum\limits_{k = 1}^{n} {\frac{{a_{k} }}{{h^{{\alpha_{k} }} }}} }} \, \begin{array}{*{20}c} {{1} \le {\text{i}} \le n{, 1} \le {\text{j}} \le m,{ 0} \le {\text{l}} \le {\text{d,}}} \\ {1 \le v \le r} \\ \end{array} \, $$

(24)

$$ \begin{gathered} Y_{i} (k) = \sum\limits_{j = 1}^{N} {\left( { - 1} \right)^{j} \left( {\begin{array}{*{20}c} {\alpha_{i} } \\ j \\ \end{array} } \right)y(k + 1 - j)} , \, \hfill \\ {\text{Fv}}_{jl} (k) = \sum\limits_{i = 0}^{N} {\left( { - 1} \right)^{i} \left( {\begin{array}{*{20}c} {\beta_{i} } \\ {jv} \\ \end{array} } \right)\left( {u_{v} (k + 1 - i)} \right)^{l} } {\text{ F1}} \le {\text{Fv}} \le F{\text{r}} \hfill \\ \end{gathered} $$

(25)

If we consider the measured data $u(t)$ and $y^{*} (t) = y(t) + p(t)$ where $p(t)$ is the disturbance signal, Eqs. (3–43) can be rewritten as follows:

$$ \begin{gathered} y^{*} (k + 1) = - \sum\limits_{i = 1}^{n} {a^{\prime}_{i} Y_{i}^{*} (k)} + \hfill \\ \, + \sum\limits_{j = 0}^{{m_{1} }} {\sum\limits_{l = 0}^{{\text{d}}} {b1^{\prime}_{jl} (F1_{jl} (k))} } + ... + \sum\limits_{j = 0}^{{m_{r} }} {\sum\limits_{l = 0}^{{\text{d}}} {br^{\prime}_{jl} (Fr_{jl} (k))} } + e(k + 1) \hfill \\ \end{gathered} $$

(26)

while

$$ Y_{i}^{*} (k) = \sum\limits_{j = 1}^{N} {\left( { - 1} \right)^{j} \left( {\begin{array}{*{20}c} {\alpha_{i} } \\ j \\ \end{array} } \right)y^{*} (k + 1 - j)} $$

(27)

$$ e(k + 1) = p(k + 1) + \sum\limits_{i = 1}^{n} {a^{\prime}_{i} \sum\limits_{j = 1}^{N} {\left( { - 1} \right)^{j} \left( {\begin{array}{*{20}c} {\alpha_{i} } \\ j \\ \end{array} } \right)p(k + 1 - j)} } $$

(28)

Equation (26) is linear with respect to coefficients and can be expressed as follows:

$$ y(k + 1) = \theta^{T} \phi (k) + e(k + 1) $$

(29)

which:

$$ \theta = \left[ {a^{\prime}_{1} , \ldots ,a^{\prime}_{n} ,b1^{\prime}_{00} , \ldots ,b1^{\prime}_{0d} ,...,b1^{\prime}_{{m_{1} 0}} , \ldots ,b1^{\prime}_{md} ,...,br^{\prime}_{00} , \ldots ,br^{\prime}_{0d} ,...,br^{\prime}_{m0} , \ldots ,br^{\prime}_{md} } \right]^{T} $$

(30)

$$ \begin{gathered} \phi (k) = \left[ { - Y_{1}^{*} (k), \ldots , - Y_{n}^{*} (k),F1_{00} (k), \ldots ,F1_{0d} (k), \ldots ,F1_{m0} (k), \ldots } \right., \hfill \\ \left. { \, F1_{md} (k), \ldots ,Fr_{00} (k), \ldots ,Fr_{0d} (k), \ldots ,Fr_{m0} (k), \ldots ,Fr_{md} (k)} \right]^{T} \hfill \\ \end{gathered} $$

(31)

The estimation vector $\hat{\theta }_{k}$ is obtained by minimizing the following quadratic least squares criterion:

$$ \hat{\theta }_{k} = \arg \min_{\theta } \frac{1}{k}\sum\limits_{i = 1}^{k} {\left[ {y(i) - \hat{y}(i,\theta )} \right]^{2} } $$

(32)

The solution to this problem can be obtained by the least squares estimation:

$$ \hat{\theta }_{k} = \left[ {\sum\limits_{i = 1}^{k} {\phi (i - 1)\phi^{T} (i - 1)} } \right]^{ - 1} \sum\limits_{i = 1}^{k} {\phi (i - 1)y(i)} $$

(33)

provided that there is the inverse $\left[ {\sum\limits_{i = 1}^{k} {\phi (i - 1)\phi^{T} (i - 1)} } \right]^{ - 1}$.

In order to provide the online identification possibility, the recursive algorithms are required. For this purpose, a recursive version of Eq. (33) is proposed, which can be written as follows:

$$ \left\{ {\begin{array}{*{20}c} {\hat{\theta }_{k + 1} = \hat{\theta }_{k} + G_{k} \phi (k)\varepsilon (k + 1)} \\ {G_{k + 1} = G_{k} - \frac{{G_{k} \phi (k)\phi^{T} (k)G_{k} }}{{1 + \phi^{T} (k)G_{k} \phi (k)}}} \\ {\varepsilon (k + 1) = \frac{{y(k + 1) - \hat{\theta }_{k}^{T} \phi (k)}}{{1 + \phi^{T} (k)G_{k} \phi (k)}}} \\ \end{array} } \right. $$

(34)

where the initial value of the adaptation gain matrix $G_{k}$ is generally selected as:

$$ G_{0} = \frac{1}{\gamma }I;{ 0 < }\gamma \ll 1 $$

(35)

For static systems with slow-varying parameters, a forgetting factor $\lambda {, 0 < }\lambda < 1$ can be considered. Therefore, the RLS algorithm is converted as:

$$ \left\{ \begin{gathered} \hat{\theta }_{k + 1} = \hat{\theta }_{k} + G_{k} \phi (k)\varepsilon (k + 1) \hfill \\ G_{k + 1} = \frac{1}{\lambda }\left[ {G_{k} - \frac{{G_{k} \phi (k)\phi^{T} (k)G_{k} }}{{\lambda + \phi^{T} (k)G_{k} \phi (k)}}} \right] \hfill \\ \varepsilon (k + 1) = \frac{{y(k + 1) - \hat{\theta }_{k}^{T} \phi (k)}}{{1 + \phi^{T} (k)G_{k} \phi (k)}} \hfill \\ \end{gathered} \right. $$

(36)

Using this recursive algorithm, the coefficients $a^{\prime}_{i} ,bv^{\prime}_{jl}$ are determined; then, the values of $a_{i} ,b_{j}$ can be obtained using Eq. (24). Finally, Eq. (23) is used to obtain the estimated output values. The convergence of RLS algorithm in the reference [51] has been proven.

3.2 MISO Hammerstein model using RBFNN

As mentioned, in order to increase the accuracy of system dynamics investigation, time-delay information must be considered in practical processes or systems identification. In this case, the system is considered with time delays in the inputs. It is modeled as follows:

$$ \begin{gathered} y(t) + \sum\limits_{i = 1}^{n} {a_{i} D^{{\alpha_{i} }} y(t)} = \sum\limits_{j = 0}^{m} {b_{j} D^{{\beta_{j} }} (w_{1} (t - \gamma_{1} ) + \ldots + w_{r} (t - \gamma_{r} ))} \hfill \\ w_{k} (t - \gamma_{k} ) = f(u_{k} (t - \gamma_{k} )) \hfill \\ \end{gathered} $$

(37)

where $y(t)$ is system output, $w_{k} (t),k = 1,2, \ldots ,r$ are RBFNN outputs and the inputs to the linear dynamics section. $\gamma_{k} ,k = 1,2, \ldots ,r$ are time delays and $n,m$ are the input and output delays for the linear subsystem. Nonlinear static functions in this case are considered as follows:

$$ w_{k} (t - \gamma_{k} ) = f_{k} \left( {u_{k} (t - \gamma_{k} )} \right) = \omega_{0k} + \sum\limits_{h = 1}^{M} {\omega_{hk} \phi_{hk} (u_{k} (t - \gamma_{k} ))} $$

(38)

which $u_{1} ,u_{2} , \ldots ,u_{r}$ define inputs. As shown in the following equation, $\phi_{hk} (.),h = 1, \ldots ,M,k = 1, \ldots ,r$ are Gaussian functions related to kth input. Also, $\omega_{hk} (.),h = 1, \ldots ,M,k = 1, \ldots ,r$ are the connection weights from hth hidden node to the output and related to the kth input that must be determined. M is the number of RBFs.

$$ \phi_{hk} (u_{k} (t)) = \exp \left\{ { - \left( {{{\left\| {u_{k} (t) - c_{hk} } \right\|^{2} } \mathord{\left/ {\vphantom {{\left\| {u_{k} (t) - c_{hk} } \right\|^{2} } {{\text{d}}_{hk}^{2} }}} \right. \kern-0pt} {{\text{d}}_{hk}^{2} }}} \right)} \right\} $$

(39)

$c_{hk} ,{\text{d}}_{hk} ,h = 1, \ldots ,M,k = 1, \ldots ,r$ are the centers and widths of the hth RBF hidden unit associated with kth input. $\left\| . \right\|$ defines the Euclidean norm.

Also, the linear subsystem is considered as follows:

$$ G(s) = \frac{B(s)}{{A(s)}} = \frac{{b_{m} s^{{\beta_{m} }} + \cdots + b_{1} s^{{\beta_{1} }} + b_{0} s^{{\beta_{0} }} }}{{1 + a_{n} s^{{\alpha_{n} }} + \cdots + a_{1} s^{{\alpha_{1} }} }} $$

(40)

which $a_{1} , \ldots ,a_{n} ,b_{0} , \ldots ,b_{m} \in R$ are coefficients and $\alpha_{1} , \ldots ,\alpha_{n} ,\beta_{0} , \ldots ,\beta_{m} \in R$ are the fractional orders.

Considering Eqs. (38) to (40), the input–output relationship is equal to:

$$ \begin{gathered} y(t) = - \sum\limits_{i = 1}^{n} {a_{i} D^{{\alpha_{i} }} y(t)} + \sum\limits_{j = 0}^{m} {b_{j} D^{{\beta_{j} }} \left( {\sum\limits_{k = 1}^{r} {\sum\limits_{h = 0}^{M} {\left( {\omega_{hk} \phi_{hk} (u_{k} (t - \gamma ))} \right)} } } \right)} = \hfill \\ \quad \quad - \sum\limits_{i = 1}^{n} {a_{i} D^{{\alpha_{i} }} y(t)} + \sum\limits_{j = 0}^{m} {b_{j} D^{{\beta_{j} }} \left( {\omega_{01} \phi_{01} (u_{1} (t - \gamma )) + \ldots } \right.} \hfill \\ { + }\omega_{M1} \phi_{M1} (u_{1} (t - \gamma )) + \ldots + \omega_{0r} \phi_{0r} (u_{r} (t - \gamma )) + \ldots \left. { + \omega_{Mr} \phi_{Mr} (u_{r} (t - \gamma ))} \right) \hfill \\ \end{gathered} $$

(41)

If the measured inputs and outputs are $u(t)$ and $y^{*} (t) = y(t) + q(t)$, respectively, which $q(t)$ is a random Gaussian noise with zero mean and $\sigma^{2}$ variance, Eq. (41) is rewritten as follows:

$$ \begin{gathered} y^{*} (t) = - \sum\limits_{i = 1}^{n} {a_{i} D^{{\alpha_{i} }} y^{*} (t)} + \sum\limits_{j = 0}^{m} {b_{j} D^{{\beta_{j} }} \left( {\sum\limits_{k = 1}^{r} {\sum\limits_{h = 0}^{M} {\left( {\omega_{hk} \phi_{hk} (u_{k} (t - \gamma_{k} ))} \right)} } } \right)} = \hfill \\ = - \sum\limits_{i = 1}^{n} {a_{i} D^{{\alpha_{i} }} y^{*} (t)} + \sum\limits_{j = 0}^{m} {b_{j} D^{{\beta_{j} }} \left( {\omega_{01} \phi_{01} (u_{1} (t - \gamma_{1} )) + \ldots + } \right.} \hfill \\ \, + \omega_{M1} \phi_{M1} (u_{1} (t - \gamma_{1} )) + \ldots + \omega_{0r} \phi_{0r} (u_{r} (t - \gamma_{r} )) + \ldots \left. { + \omega_{Mr} \phi_{Mr} (u_{r} (t - \gamma_{r} ))} \right) + q(t) \hfill \\ \end{gathered} $$

(42)

Unknown parameters are divided into two subcategories: The first subset includes time delays $\gamma_{k} ,k = 1,2, \ldots ,r$, fractional orders $\alpha_{1} , \ldots ,\alpha_{n} ,\beta_{0} , \ldots ,\beta_{m}$, and centers and widths of RBF units ${\text{d}}_{hk} ,c_{hk} ,h = 0, \ldots ,M,k = 1, \ldots ,r$. And the second category includes the coefficients of the transfer function $a_{1} , \ldots ,a_{n} ,b_{0} , \ldots ,b_{m}$ and the connection weights $\omega_{hk} \left( \cdot \right),h = 1, \ldots ,M,k = 1, \ldots ,r$ from the jth hidden node to the output. In this paper, input/output data are divided into two parts. The first part is used to obtain both sets of unknown parameters using MGA. Then, using these estimations, RLS algorithm uses the I/O data second part to update and optimize the second subcategory of unknown parameters.

The standard RLS algorithm needs to set initial values for unknown parameters. In the standard method, these initial values are calculated using the batch least squares algorithm from multiple prototypes. In this method, the regressors dimension of the known parameters determines the number of samples required to determine the unique solution. In this paper, MGA is used for this task.

In order to use the output error estimation method, the input–output relationship (41) must be written in regression form:

$$ y(t) = z^{T} (t)\theta + v(t) $$

(43)

where $z$ is known parameters including input–output data:

$$ z(t) = \left[ {z_{a}^{T} (t),z_{{b_{0} }}^{T} (t),z_{{b_{1} }}^{T} (t), \ldots ,z_{{b_{r} }}^{T} (t),1} \right]^{T} $$

(44)

$$ z_{a} (t) = \left[ { - D^{{\alpha_{1} }} y^{*} (t), - D^{{\alpha_{2} }} y^{*} (t), \ldots , - D^{{\alpha_{n} }} y^{*} (t)} \right]^{T} $$

(45)

$$ z_{{b_{j} }} (t) = \left[ {D^{{\beta_{j} }} \phi_{1} (u_{1} (t - \gamma )),D^{{\beta_{j} }} \phi_{2} (u_{2} (t - \gamma )),} \right.\left. { \ldots ,D^{{\beta_{j} }} \phi_{r} (u_{r} (t - \gamma ))} \right] $$

(46)

That:

$$ \phi_{k} (u_{k} (t - \gamma )) = [\phi_{0k} (u_{k} (t - \gamma )), \ldots ,\phi_{Mk} (u_{k} (t - \gamma ))],k = 1, \ldots ,r $$

(47)

And $\theta$ shows unknown parameters:

$$ \theta = \left[ {\theta_{a}^{T} ,\theta_{{b_{0} }}^{T} ,\theta_{{b_{1} }}^{T} , \ldots ,\theta_{{b_{r} }}^{T} ,\theta_{{\omega_{0} }} } \right]^{T} $$

(48)

Including:

$$ \theta_{a} = \left[ {a_{1} ,a_{2} , \ldots ,a_{n} } \right]^{T} $$

(49)

$$ \theta_{{b_{j} }} = \left[ {\theta_{{b_{j,1} }} ,\theta_{{b_{j,2} }} , \ldots ,\theta_{{b_{j,M} }} } \right]^{T} = \left[ {b_{j} \omega_{1} ,b_{j} \omega_{2} , \ldots ,b_{j} \omega_{M} } \right]^{T} $$

(50)

$$ \theta_{{\omega_{0} }} = \left[ {b_{r} \omega_{0} } \right] $$

(51)

Which in (50):

$$ \omega_{h} = \left[ {\omega_{h1} ,\omega_{h2} , \ldots ,\omega_{hr} } \right],h = 1, \ldots ,M $$

(52)

Provided that $\left[ {\sum\limits_{i = 1}^{k} {z(i - 1)z^{T} (i - 1)} } \right]^{ - 1}$ has a definable value, solving this problem using the LS estimation is:

$$ \hat{\theta }_{k} = \left[ {\sum\limits_{i = 1}^{k} {z(i - 1)z^{T} (i - 1)} } \right]^{ - 1} \sum\limits_{i = 1}^{k} {z(i - 1)y(i)} $$

(53)

When the parameters matrix $z$ is singular or poorly conditioned, its inverse calculation will be very difficult. To avoid the problem of inverse calculation in online identification, the recursive version of Eq. (53) is written as follows [51].

$$ \left\{ {\begin{array}{*{20}c} \begin{gathered} \hat{\theta }(k) = \hat{\theta }(k - 1) + L(k)\varepsilon (k) \hfill \\ \varepsilon (k) = y(k) - z^{T} (k)\hat{\theta }(k - 1) \hfill \\ \end{gathered} \\ {P(k) = P(k - 1) - \frac{{P(k - 1)z(k)z^{T} (k)P(k - 1)}}{{1 + z^{T} (k)P(k - 1)z(k)}}} \\ {L(k) = \frac{P(k - 1)z(k)}{{1 + z^{T} (k)P(k - 1)z(k)}}} \\ \end{array} } \right. $$

(54)

In general, the initial value of the adaptation gain matrix P is selected as follows [51]:

$$ P_{0} = \frac{1}{\eta }I;{ 0 < }\eta \ll 1 $$

(55)

Without losing the generality, we assume that $\hat{b}_{r} (k) = 1$:

$$ \left\{ {\begin{array}{*{20}c} {\hat{\theta }_{{b_{r} }} (k) = \left[ {\hat{\omega }_{1} (k),\hat{\omega }_{2} (k),...,\hat{\omega }_{M} (k)} \right]^{T} } \\ {\hat{\theta }_{{\omega_{0} }} (k) = \hat{\omega }_{0} (k)} \\ \end{array} } \right. $$

(56)

The unknown coefficients $a_{i} ,i = 1,...,n$ are obtained directly from $\hat{\theta }_{a}$. The $b_{j} {, 0} \le j \le m \,$ values are calculated using linear least squares, assuming $\hat{b}_{r} (k) = 1$ as the following:

$$ \hat{b}_{j} (k) = {{\sum\limits_{h = 1}^{M} {\hat{\theta }_{{b_{r,h} }} (k)\hat{\theta }_{{b_{j,h} }} (k)} } \mathord{\left/ {\vphantom {{\sum\limits_{h = 1}^{M} {\hat{\theta }_{{b_{r,h} }} (k)\hat{\theta }_{{b_{j,h} }} (k)} } {\sum\limits_{h = 1}^{M} {\hat{\theta }_{{b_{r,h} }}^{2} (k)} }}} \right. \kern-0pt} {\sum\limits_{h = 1}^{M} {\hat{\theta }_{{b_{r,h} }}^{2} (k)} }} \, ,j = 0,1, \ldots ,m - 1 $$

(57)

3.3 MISO Hammerstein model using MRBFNN

In this case, Eq. (41) is modified as:

$$ \begin{gathered} y(t) = - \sum\limits_{i = 1}^{n} {a_{i} D^{{\alpha_{i} }} y(t)} + \sum\limits_{j = 0}^{m} {b_{j} D^{{\beta_{j} }} \left( {\sum\limits_{k = 1}^{r} {\sum\limits_{h = 0}^{M} {\left( {\omega_{hk} \phi_{k} (u_{k} (t - \gamma_{k} ))} \right)} } } \right)} \hfill \\ \quad \quad = - \sum\limits_{i = 1}^{n} {a_{i} D^{{\alpha_{i} }} y(t)} + \sum\limits_{j = 0}^{m} {b_{j} D^{{\beta_{j} }} \left( {\omega_{01} \phi_{1} (u_{1} (t - \gamma_{1} )) + \ldots } \right.} \hfill \\ \, \quad { + }\omega_{M1} \phi_{1} (u_{1} (t - \gamma_{1} )) + \ldots + \omega_{0r} \phi_{r} (u_{r} (t - \gamma_{r} )) + \ldots \left. { + \omega_{Mr} \phi_{r} (u_{r} (t - \gamma_{r} ))} \right) \hfill \\ \, \quad = - \sum\limits_{i = 1}^{n} {a_{i} D^{{\alpha_{i} }} y(t)} + \sum\limits_{j = 0}^{m} {b_{j} D^{{\beta_{j} }} \left( {(\omega_{01} + \ldots + \omega_{M1} )\phi_{1} (u_{1} (t - \gamma_{1} )) + \ldots } \right.} \hfill \\ \, + \left. {(\omega_{0r} + ... + \omega_{Mr} )\phi_{r} (u_{r} (t - \gamma_{r} ))} \right) \hfill \\ \, \quad = - \sum\limits_{i = 1}^{n} {a_{i} D^{{\alpha_{i} }} y(t)} + \sum\limits_{j = 0}^{m} {b_{j} D^{{\beta_{j} }} \left( {\Omega_{1} \phi_{1} (u_{1} (t - \gamma_{1} )) + \ldots } \right.} + \left. {\Omega_{r} \phi_{r} (u_{r} (t - \gamma_{r} ))} \right) \hfill \\ \end{gathered} $$

(58)

If the measured inputs and outputs are $u(t)$ and $y^{*} (t) = y(t) + q(t)$, respectively, which $q(t)$ is a random Gaussian noise with zero mean and $\sigma^{2}$ variance, Eq. (58) is rewritten as follows:

$$ \begin{gathered} y^{*} (t) = - \sum\limits_{i = 1}^{n} {a_{i} D^{{\alpha_{i} }} y^{*} (t)} + \sum\limits_{j = 0}^{m} {b_{j} D^{{\beta_{j} }} \left( {\sum\limits_{k = 1}^{r} {\sum\limits_{h = 0}^{M} {\left( {\omega_{hk} \phi_{hk} (u_{k} (t - \gamma_{k} ))} \right)} } } \right)} \hfill \\ \quad \quad = - \sum\limits_{i = 1}^{n} {a_{i} D^{{\alpha_{i} }} y^{*} (t)} + \sum\limits_{j = 0}^{m} {b_{j} D^{{\beta_{j} }} \left( {\omega_{01} \phi_{01} (u_{1} (t - \gamma_{1} )) + \ldots } \right.} \hfill \\ \, + \quad \omega_{M1} \phi_{M1} (u_{1} (t - \gamma_{1} )) + \ldots + \omega_{0r} \phi_{0r} (u_{r} (t - \gamma_{r} )) + \ldots \left. { + \omega_{Mr} \phi_{Mr} (u_{r} (t - \gamma_{r} ))} \right) + q(t) \hfill \\ \end{gathered} $$

(59)

And the relation (46) is modified as:

$$ z_{{b_{j} }} (t) = \left[ {D^{{\beta_{j} }} \phi_{1} (u_{1} (t - \gamma )),D^{{\beta_{j} }} \phi_{2} (u_{2} (t - \gamma )), \ldots ,\left. {D^{{\beta_{j} }} \phi_{r} (u_{r} (t - \gamma ))} \right]^{T} } \right. $$

(60)

In this case, time delays $\gamma_{k} ,k = 1,2, \ldots ,r$, fractional orders $\alpha_{1} , \ldots ,\alpha_{n} ,\beta_{0} , \ldots ,\beta_{m}$, and centers and widths of RBF units $d_{hk} ,c_{hk} ,h = 0, \ldots ,M,k = 1, \ldots ,r$ are identified using MGA. And an initial estimation for the coefficients of the transfer function $a_{1} , \ldots ,a_{n} ,b_{0} , \ldots ,b_{m}$ and the connection weights from the jth hidden node to the output $\omega_{hk} \left( \cdot \right),h = 1, \ldots ,M,k = 1, \ldots ,r$ are obtained using this evolutionary algorithm. Then, these estimations are updated and optimized using RLS algorithm.

In comparison with classic RBFNN which the number of unknown parameters is equal to $3M + 1$ (i.e., $c_{hk} ,d_{hk} ,\omega_{hk} ,\gamma_{k}$ and $h = 1, \ldots ,M$ where M is the data samples number), their number in modified RBFNN is equal to 4 (i.e. $d_{k} ,c_{k} ,\Omega_{k} ,\gamma_{k}$).

4 Simulation results

The main reason for using the recursive method is the ability to generalize to online identification. In order to demonstrate the ability of online identification, two examples have been considered:

• 1. Hammerstein model with piecewise nonlinear characteristic such as dead-zone characteristic [52]

• 2. Continuous-time linear parameter-varying (CT LPV) nonlinear benchmark system [53]

Both systems have been identified online using all three presented structures. One hundred samples were used to estimate the prototype. Then, by adding any input/output data in online mode, the model is updated using RLS. In the online mode, the MGA is executed only once at the beginning of the detection process and then only the LS algorithm is executed recursively. Therefore, all that is required in each instance is the recursive formula of the LS algorithm.

In addition, it is considered a case in which with adding each input / output data, MGA runs in a small number of generations, i.e., 15 generations. In this case, the MGA updates all the unknown parameters in each sampling starting from the best chromosome of the last run in the previous sampling (instead of starting from random chromosomes). Then, RLS goes one step further and updates the connection coefficients and weights.

4.1 Hammerstein model with piecewise nonlinear characteristic

In this Hammerstein model, the recursive relation forms the linear dynamic part:

$$ y(k) = 1.6961y(k - 1) - 0.8651y(k - 2) + 0.5895h(k - 1) + 0.4701h(k - 2) $$

(61)

And the discrete nonlinear part is described by the following equation:

$$ N(u) = \left\{ {\begin{array}{*{20}c} {u + 0.28} & {u \le - 0.28} \\ 0 & { - 0.28 \le u \le 0.28} \\ {u - 0.28} & {u \ge 0.28} \\ \end{array} } \right. $$

(62)

Actual output and estimated output in the last sample (using 200 sampled data) for the Hammerstein model with Bezier–Bernstein polynomials in Fig. 4, for the Hammerstein model with RBFNN in Fig. 5 and with MRBFNN, is shown in Fig. 6. The corresponding estimation error using the three nonlinear functions Bezier–Bernstein, RBFNN and MRBFNN is presented in Figs. 7, 8 and 9, respectively.

Fig. 4

The actual (blue line) and estimated (red dashed line) outputs using Bezier–Bernstein polynomial—Example 1. (Color figure online)

Fig. 5

The actual (blue line) and estimated (red dashed line) outputs using RBFNN—Example 1. (Color figure online)

Fig. 6

The actual (blue line) and estimated (red dashed line) outputs using MRBFNN—Example 1. (Color figure online)

Fig. 7

The estimation error using BBP—Example 1

Fig. 8

The estimation error using RBFNN—Example 1

Fig. 9

The estimation error using MRBFNN—Example 1

In order to compare the estimation accuracy of three different structures, the changes of estimation error during the identification process (in different samples) in these three structures are shown in Figs. 10, 11 and 12, and the values of these errors are given in Table 1.

Fig. 10

The MSE estimation error with high noise using three different structures—Example 1

Fig. 11

The RMS estimation error with high noise using three different structures—Example 1

Fig. 12

The $\delta$ estimation error with high noise using three different structures—Example 1

Table 1 The estimation error comparison between three presented structures—Example 1

The comparison of the estimation errors in Table 1 and corresponding Figs. 10, 11 to 12 shows the superiority of identification accuracy using the MRBFNN in Hammerstein model over the two other structures.

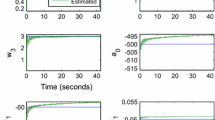
Also, in order to compare the parameters convergence speed in three different structures, the variations of the identified parameters for the Hammerstein model with Bezier–Bernstein polynomials in Figs. 13 and 14, for the Hammerstein model with RBFNN in Figs. 15, 16 and 17 and for the Hammerstein model with MRBFNN are presented in Figs. 18, 19 and 20. The comparison of the figures shows that the identification process of the Hammerstein model with MRBFNN has the highest convergence speed due to the smaller number of unknown parameters identified between the three proposed structures.

Fig. 13

The estimation of transfer function coefficients and fractional orders using BBP—Example 1

Fig. 14

The estimation of polynomial weights using BBP—Example 1

Fig. 15

The estimation of transfer function coefficients and fractional orders using RBFNN—Example 1

Fig. 16

The estimation of NN weights using RBFNN—Example 1

Fig. 17

The estimation of NN centers and widths using RBFNN—Example 1

Fig. 18

The estimation of transfer function coefficients and fractional orders using MRBFNN—Example 1

Fig. 19

The estimation of NN weights using MRBFNN—Example 1

Fig. 20

The estimation of NN centers and widths using MRBFNN—Example 1

4.2 Continuous-time linear parameter-varying (CT LPV) nonlinear benchmark system

The second system is a benchmark problem proposed by Rao and Garnier in [54]. This problem is inspired by the "moving pole" parameter-varying system, a fourth-order system with non-minimum phase freezing dynamics and complex poles pair dependent to $p$ parameter. This system is defined as follows:

$$ \left\{ \begin{gathered} A_{0} (d,p)\chi_{0} (t) = B_{0} (d,p)u(t) \hfill \\ y(t) = \chi_{0} (t) + v_{0} (t) \hfill \\ \end{gathered} \right. $$

(63)

where the $d$ operator is a time derivative, $p$ is a time-dependent programming variable, $A_{0}$ and $B_{0}$ are polynomials of $d$ with coefficients $a_{i}^{0}$ and $b_{i}^{0}$. These coefficients are functions of $p$; $v_{0}$ is a process with semi-static noise with limited and unrelated spectral density as follows:

$$ v_{0} (t) = H_{0} (q)e_{0} (t) = \frac{{C_{0} \left( {q^{ - 1} } \right)}}{{D_{0} \left( {q^{ - 1} } \right)}}e_{0} (t) $$

(64)

The $e_{0} (t)$ is a white noise process with a mean of zero, $q^{ - 1}$ is the backward time shift operator, $C_{0}$ and $D_{0}$ are polynomials with constant coefficients. The values of the parameters used in this paper are as follows [53]:

$$ \left\{ \begin{gathered} A_{0} (d,p) = d^{4} + a_{1}^{0} (p)d^{3} + a_{2}^{0} (p)d^{2} + a_{3}^{0} (p)d + a_{4}^{0} (p) \hfill \\ B_{0} (d,p) = b_{0}^{0} (p)d + b_{1}^{0} (p) \hfill \\ H_{0} (q) = \frac{1}{{1 - q^{ - 1} + 0.2q^{ - 2} }} \hfill \\ \end{gathered} \right. $$

(65)

For coefficients:

$$ \begin{array}{*{20}c} {a_{1}^{0} (p) = 5 + 0.25p} & {a_{2}^{0} (p) = 408 + 3p + 0.25p^{2} } \\ {a_{3}^{0} (p) = 416 + 108p + p^{2} } & {a_{4}^{0} (p) = 1600 + 800p + 100p^{2} } \\ {b_{0}^{0} (p) = - 6400 - 3200p - 400p^{2} } & {b_{1}^{0} (p) = 1600 + 800p + 100p^{2} } \\ \end{array} $$

(66)

The input signal is a uniform distribution sequence in the interval $[ - 1,1]$, $p$ is selected as $p(t) = \sin (\pi t)$, and the sampling time is $1{\text{ms}}$.

Actual output and estimated output in the last sample (using 500 sampled data) for the Hammerstein model with Buzzer–Bernstein polynomials are shown in Fig. 21, for the Hammerstein model with RBFNN in Fig. 22 and for the MRBFNN in Fig. 23. The corresponding estimation error using the three nonlinear functions Bezier–Bernstein, RBFNN and MRBFNN is presented in Figs. 24, 25 and 26, respectively.

Fig. 21

The actual (blue line) and estimated (red dashed line) outputs using BBP—example 2. (Color figure online)

Fig. 22

The actual (blue line) and estimated (red dashed line) outputs using RBFNN—example 2. (Color figure online)

Fig. 23

The actual (blue line) and estimated (red dashed line) outputs using MRBFNN—example 2. (Color figure online)

Fig. 24

The estimation error using BBP—Example 2

Fig. 25

The estimation error using RBFNN—Example 2

Fig. 26

The estimation error using MRBFNN—Example 2

In order to compare the accuracy of estimation with three different structures, the variations of estimation error during the identification process (in different samples) in these three structures are shown in Figs. 27, 28 and 29 and the values of these errors are given in Table 2.

Fig. 27

The MSE estimation error with high noise using three different structures—Example 2

Fig. 28

The RMS estimation error with high noise using three different structures—Example 2

Fig. 29

The $\delta$ estimation error with high noise using three different structures—Example 2

Table 2 The estimation error comparison between three presented structures—Example 2

The comparison of the results of estimation errors in Table 2 and the corresponding Figs. 26, 27 and 28 shows the superiority of identification accuracy in the Hammerstein model using the MRBFNN compared to the Hammerstein model with the classic RBFNN.

Also, in order to compare the convergence velocity of the parameters in three different structures, the variations of the identified parameters for Hammerstein model with Bezier–Bernstein polynomials are presented in Figs. 30 and 31, for Hammerstein model with RBFNN in Figs. 32, 33 and 34 and for the Hammerstein model with MRBFNN in Figs. 35, 36 and 37. The comparison of the figures shows that the process of identifying the Hammerstein model with MRBFNN has the highest convergence speed between the three proposed structures, due to the smaller number of unknown parameters identified.

Fig. 30

The estimation of transfer function coefficients and fractional orders using BBP—Example 2

Fig. 31

The estimation of polynomial weights using BBP—Example 2

Fig. 32

The estimation of transfer function coefficients and fractional orders using RBFNN—Example 2

Fig. 33

The estimation of NN weights using RBFNN—Example 2

Fig. 34

The estimation of NN centers and widths using RBFNN—Example 2

Fig. 35

The estimation of transfer function coefficients and fractional orders using MRBFNN—Example 2

Fig. 36

The estimation of NN weights using MRBFNN—Example 2

Fig. 37

The estimation of NN centers and widths using RBFNN—Example 2

5 Conclusion

In this paper, a numerical example and a benchmark problem were introduced to evaluate the accuracy of the proposed online identification method. Then, each of the three proposed structures was used to identify these systems and the results were presented. These results confirm the ability of the proposed method to accurately identify the system and eliminate noise. A comparison is made between the online identification of the three proposed structures in terms of convergence speed and estimation accuracy, which shows the relative superiority of accuracy using the modified one. This comparison shows that using the Hammerstein model with the MRBFNN, the accuracy of estimation and the speed of convergence of the parameters in the online mode increase compared to the use of the classical NN. The estimation accuracy of the modified NN in the first example is 63.05% higher than the Bezier–Bernstein polynomial and 18.7% lower in the second example. Considering the speed of convergence of the modified NN compared to the use of Bezier–Bernstein polynomials, the use of the Hammerstein structure with the modified NN is recommended.