1 Introduction

Identification of nonlinear vibrating systems has attracted a wide attention in recent years for the extensive existence of nonlinearities in engineering structures, such as high-speed flexible rotors, satellite antennas, and flexible robots. Significant progress has been performed in this issue, and a variety of identification approaches have been proposed in recent years. A significant summary can be found in [1]. Several common algorithms include the restoring force surface method [2, 3], the Volterra series [4, 5], the Kalman-filter-based method [6], the reverse path method [7,8,9], the subspace identification, and its subsequent developments [10,11,12]. Those algorithms are routinely used for experimental modal analysis, damage detection, and structural health monitoring [13,14,15].

Among the significant progress in the nonlinear system identification, a crucial contribution was proposed by Adams and Allemang [16]. They regarded the nonlinearity as an internal feedback force to the linear dynamic system. Based on this, the linear and nonlinear parts of the system can be naturally decoupled. Recently, this feedback idea has been exploited for developing a nonlinear extension of the stochastic subspace identification method (SSIM) [11, 17]. This nonlinear subspace identification method (NSIM) converts the nonlinear system to the form of state-space equations, and the system state matrices are estimated by the SSIM. The FRFs of the underlying linear system and the nonlinear parameter to be identified are then calculated. This method avoids an intractable issue of the reverse path method which is the relatively large correlation of the signals around the natural frequencies of the underlying linear system. Lacy and Bernstein [11] extended the subspace method to identify a kind of multi-input multi-output nonlinear time-varying systems with nonlinear in measured data and linear in unmeasured states. Marchesiello and Garibaldi [18] adopted the NSIM to experimentally investigate a scaled multi-story building with a local clearance-type nonlinearities. Results showed a good performance of the NSIM on mechanical system with a general set of nonlinear terms. Noël and Kerschen [10] introduced a frequency-domain subspace-based method for nonlinear system identification which was an equivalent form of the time-domain NSIM in the frequency domain. Noël et al. [19] identified the SmallSat spacecraft with the time- and frequency-domain nonlinear subspace identification techniques. A closer inspection of the identified coefficients revealed that the estimated results by the frequency-domain method exhibited larger frequency variations than that by the time-domain one. Gandino et al. [20] proposed a complete input–output covariance-driven identification method which did not suffer from the memory limitation problems and was suitable for the case of large data sets. Zhang et al. [21] divided the identified nonlinear system into an underlying linear part and a local nonlinear part and proposed a two-stage time-domain subspace method which was more accurate and reliable than the single-stage method. In light of the effectiveness and robustness of subspace methods, those nonlinear subspace approaches open completely new horizons for identification of nonlinear dynamic systems.

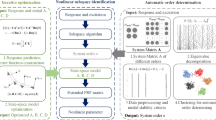
The identification process of a NSIM consists of two basic steps. The first one is to find the estimates of the extended observability matrix by making a projection of certain subspaces. The second one is to obtain the system state matrices from the extended observability matrix. Obviously, the NSIM does not involve nonlinear optimization techniques. It means that they are fast and accurate due to non-iterative operation and no problems in terms of parameterization. However, the price to be paid is that the estimated results by the NSIM are not the optimal solutions. This may result in the reduced accuracy of the identified results for the identification of the nonlinear coefficients and the FRFs of the underlying linear system. To solve this shortcoming, an improved NSIM named as a nonlinear subspace-prediction error method (NSPEM) is developed here. The proposed NSPEM uses the prediction error method (PEM) to reestimate the identified system matrices of the state-space model after determining a good initial estimate of the system model with the help of the SSIM. The PEM clearly optimizes an objective function using a full parameterization of the state-space model with regularization which will obtain the optimal identification results in the least square sense. Therefore, the proposed method may be more accurate and reliable when applying for identification of the nonlinear vibrating structures and performs more robustly in a noisy environment.

The paper is organized as follows. In Sect. 2, the state-space model of the nonlinear vibrating structures is derived by introducing the internal feedback idea. Section 3 illustrates the proposed NSPEM in detail. This method consists of three steps, i.e., estimation of the extended observability matrix, estimation of the system state matrices, and estimation of the nonlinear coefficients and the FRFs of the underlying linear systems. Then, by taking a six DOF discrete mass-spring-damper system and a cantilever beam structure with local nonlinearities as examples, estimations of the nonlinear coefficients and the FRFs of the underlying linear systems are computed numerically in Sect. 4. The identified results are compared with that by the NSIM, and the effects of different noise levels on the identified results are also considered. Finally, Sect. 5 gives a brief conclusion.

2 State-space model of nonlinear systems

The governing equation of a p degree-of-freedom (DOF) dynamic system with lumped nonlinear stiffness and dampers [10, 17, 21] can be represented as

$$\begin{aligned}&{} \mathbf{M}\ddot{{\varvec{z}}}\left( t\right) +\mathbf{C}\dot{{\varvec{z}}}\left( t\right) +\mathbf{K}{\varvec{z}}\left( t\right) \nonumber \\&\quad +\sum _{i=1}^h {\mu _i g_i \left( t\right) {\varvec{L}}_i } ={\varvec{L}}_f F\left( t\right) , \end{aligned}$$
(1)

where M, K, and C are the mass, damping, and stiffness matrices, respectively. \({\varvec{z}}(t)\) is the generalized displacement response vector, and F(t) is the external excitation force which should be persistent excitation such as random excitation and swept frequency excitation. A Gaussian white noise is used in this study. The nonlinear terms are expressed by the sum of h components in which the component depends on the nonlinear function \(\mu _{i}g_{i}(t)\). Some types of nonlinearities, such as Coulomb friction, clearance, and quadratic damping, can be specified by the base function \(g_{i}(t)\) which is assumed to be known. \(\mu _{i}\) is the unknown nonlinear coefficient. \({\varvec{L}}_{i}\) and \({\varvec{L}}_{f}\) are, respectively, the vectors of Boolean values indicating the locations of the nonlinear element and the excitation. The item \({\varvec{L}}_{i}\) can be determined from the nonlinear location identification.

Fig. 1
figure 1

Feedback description of nonlinear mechanical systems

Full size image

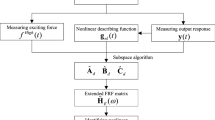
By moving the nonlinear components of Eq. (1) to the right side of the equation, the original system can be considered as being subjected to the external excitation \({\varvec{F}}_{ex}(t)\) and the internal feedback forces \({\varvec{F}}_{nl}(t)\) which is caused by the nonlinearities [16] (Fig. 1).

$$\begin{aligned}&{} \mathbf{M}\ddot{{\varvec{z}}}\left( t\right) +\mathbf{C}\dot{{\varvec{z}}}\left( t\right) +\mathbf{K}{\varvec{z}}\left( t\right) \nonumber \\&\quad ={\varvec{L}}_f F\left( t\right) -\sum _{i=1}^h {\mu _i g_i \left( t \right) {\varvec{L}}_i } \nonumber \\&\quad ={\varvec{F}}_{{\textit{ex}}} \left( t\right) +{\varvec{F}}_{{\textit{nl}}} \left( t\right) . \end{aligned}$$
(2)

Then, the continuous-time state-space formulation of Eq. (1) can be expressed as

$$\begin{aligned}&\left[ {{\begin{array}{ll} {\dot{{\varvec{z}}}} \\ {\ddot{{\varvec{z}}}} \\ \end{array} }} \right] =\left[ {{\begin{array}{ll} {{\varvec{0}}_{p\times p} } &{}\quad {{\varvec{I}}_{p\times p} } \\ {-\mathbf{M}^{-1}{} \mathbf{K}} &{}\quad {-\mathbf{M}^{-1}{} \mathbf{C}} \\ \end{array} }} \right] \left[ {{\begin{array}{ll} {\varvec{z}} \\ {\dot{{\varvec{z}}}} \\ \end{array} }} \right] \nonumber \\&\qquad \qquad \!+\left[ {{\begin{array}{llll} {\mathbf{0}_{p\times 1} } &{}\quad {\mathbf{0}_{p\times 1} } &{}\quad \cdots &{}\quad {\mathbf{0}_{p\times 1} } \\ {\mathbf{M}^{-1}{\varvec{L}}_f } &{}\quad {\mathbf{M}^{-1}\mu _1 {\varvec{L}}_1 } &{}\quad \cdots &{}\quad {\mathbf{M}^{-1}\mu _h {\varvec{L}}_h } \\ \end{array} }}\right] \nonumber \\&\qquad \qquad \!\times \,\left[ {{\begin{array}{lllll} {F\left( t \right) } \\ {-g_1 \left( t \right) } \\ \vdots \\ {-g_h \left( t \right) } \\ \end{array} }} \right] \end{aligned}$$
(3)
$$\begin{aligned}&{\varvec{y}}=\left[ {{\begin{array}{ll} {\mathbf{I}_{p\times p} } &{}\quad {\mathbf{0}_{p\times p} } \\ \end{array} }} \right] \left[ {{\begin{array}{ll} {\varvec{z}} \\ {\dot{{\varvec{z}}}} \\ \end{array} }} \right] , \end{aligned}$$
(4)

where \({\varvec{y}}={{\varvec{z}}}\) is the output vector. 0 and I denote zero and identity matrices, respectively.

It is assumed that external excitation force and displacements are measured. Defining the input vector \({\varvec{u}}=\left[ {{\begin{array}{llll} {F\left( t \right) } &{}\quad {-g_1 \left( t \right) } &{}\quad \cdots &{}{-g_h \left( t \right) } \\ \end{array} }} \right] ^{T}\) and the state vector \({\varvec{x}}=\left[ {{\begin{array}{lll} {\varvec{z}} &{}\quad {\dot{{\varvec{z}}}} \\ \end{array} }} \right] ^{T}\), Eqs. (3) and (4) can be rewritten as

$$\begin{aligned} \left\{ {{\begin{array}{l} {\dot{{\varvec{x}}}=\mathbf{A}_c {\varvec{x}}+\mathbf{B}_c {\varvec{u}}} \\ {{\varvec{y}}=\mathbf{C}_c {\varvec{x}}} \\ \end{array} }},\right. \end{aligned}$$
(5)

where the subscript c denotes continuous-time state space. \(\mathbf{A}_c \in R^{n\times n}\), \(\mathbf{B}_c \in R^{n\times q}\), and \(\mathbf{C}_c \in R^{p\times n}\) stand for the state, input, and output matrices, respectively. \(n=2p\) and \(q=h+1\). The state-space matrices and the physical-space matrices have the relations as follows

$$\begin{aligned} \left\{ {{\begin{array}{ll} {{\mathbf{A}}_c =\left[ {{\begin{array}{ll} {{\varvec{0}}_{p\times p} } &{}\quad {{\mathbf{I}}_{p\times p} } \\ {-\mathbf{M}^{-1}{} \mathbf{K}} &{}\quad {-\mathbf{M}^{-1}{} \mathbf{C}} \\ \end{array} }} \right] } \\ {\mathbf{B}_c =\left[ {{\begin{array}{llll} {\mathbf{0}_{p\times 1} } &{}\quad {\mathbf{0}_{p\times 1} } &{}\quad \cdots &{}\quad {\mathbf{0}_{p\times 1} } \\ {\mathbf{M}^{-1}{\varvec{L}}_f } &{}\quad {\mathbf{M}^{-1}\mu _1 {\varvec{L}}_1 } &{}\quad \cdots &{}\quad {{\mathbf{M}}^{-1}\mu _h {\varvec{L}}_h } \\ \end{array} }} \right] } \\ {\mathbf{C}_c =\left[ {{\begin{array}{ll} {\mathbf{I}_{p\times p} } &{}\quad {\mathbf{0}_{p\times p} } \\ \end{array} }} \right] } \\ \end{array}}}.\right. \end{aligned}$$
(6)

3 Nonlinear subspace-prediction error method

For nonlinear system identification, the classical identification procedure includes three steps, i.e., detection, characterization, and parameter estimation. After the nonlinear behavior is detected, the nonlinear system can be featured. That means, the location vectors and base functions of all nonlinearities [\({\varvec{L}}_{i}\) and \(g_{i}(t)\) in Eq. (1)] are determined. Then, the parameter of the selected nonlinear model can be identified using the employed identification algorithms.

The proposed approach targets the estimation of the nonlinear coefficients and the FRFs of the underlying linear system. Given F(t), \({{\varvec{z}}}(t)\), \(g_{i}(t)\), \({{\varvec{L}}}_{i}\) and \({{\varvec{L}}}_{f}\), the proposed NSPEM firstly estimates the extended observability matrix using the matrix projection and the singular value decomposition algorithm. Then, the three system matrices \(\mathbf{A}_{c}\), \(\mathbf{B}_{c}\), and \(\mathbf{C}_{c}\) can be determined from the estimated extended observability matrix. Those identified system matrices are then reestimated by the PEM to obtain the optimal solutions. The estimation of the nonlinear coefficients and FRFs of the underlying linear system is subsequently obtained by the conversion from state space to physical space.

3.1 Estimation of the extended observability matrix

The SSIM is an identification method for discrete-time state-space models. Therefore, the continuous-time state-space model described in Eq. (5) should be transformed into a discrete-time one under the zero-order hold assumption. The zero-order hold assumption supposes that the input vector \({{\varvec{u}}}\) is constant during one sample period. The transformation between the continuous-time state-space model and the discrete-time one can be represented as

$$\begin{aligned} \left\{ {{\begin{array}{l} {\mathbf{A}_d =e^{\mathbf{A}_c \Delta t}} \\ {\mathbf{B}_d =\left( {e^{\mathbf{A}_c \Delta t}-\mathbf{I}} \right) \mathbf{A}_c^{-1} \mathbf{B}_c } \\ {\mathbf{C}_d =\mathbf{C}_c } \\ \end{array} }} \right. , \end{aligned}$$
(7)

where subscript d denotes discrete-time state space. \(\Delta t\) is the one sample period. \(\mathbf{A}_d \in R^{n\times n}\), \(\mathbf{B}_d \in R^{n\times q}\), and \(\mathbf{C}_d \in R^{L\times n}\) are the matrices to be identified of the discrete-time state-space model, respectively.

The identified discrete-time state-space model can be expressed as

$$\begin{aligned} \left\{ {{\begin{array}{l} {{\varvec{x}}_{k+1} =\mathbf{A}_d {\varvec{x}}_k +\mathbf{B}_d {\varvec{u}}_k +{\varvec{w}}_k } \\ {{\varvec{y}}_k =\mathbf{C}_d {\varvec{x}}_k +{\varvec{v}}_k } \\ \end{array} }},\right. \end{aligned}$$
(8)

where \({\varvec{x}}_k \in R^{n}\), \({\varvec{u}}_k \in R^{q}\), and \({\varvec{y}}_k \in R^{L}\) are the state vector, the input vector, and the output vector at the discrete time \(t_{k}\), respectively. \({\varvec{w}}_k \in R^{n}\) and \({\varvec{v}}_k \in R^{L}\), respectively, denote the process noise and the output measurement noise at the discrete time \(t_{k}\) and are all assumed to be zero-mean white noises.

By iterating Eq. (8), one can obtain

$$\begin{aligned} {\varvec{y}}_k= & {} \mathbf{C}_d \mathbf{A}_d^{k-1} {\varvec{x}}_1 +\mathbf{C}_d \mathbf{A}_d^{k-2} \mathbf{B}_d {\varvec{u}}_1 +\mathbf{C}_d \mathbf{A}_d^{k-3} \mathbf{B}_d {\varvec{u}}_2 +\cdots \nonumber \\&+\,\mathbf{C}_d \mathbf{B}_d {\varvec{u}}_{k-1} +\mathbf{C}_d {\mathbf{A}}_d^{k-2} {\varvec{w}}_1 +\mathbf{C}_d \mathbf{A}_d^{k-3} {\varvec{w}}_2 +\cdots \nonumber \\&+\,\mathbf{C}_d {\varvec{w}}_{k-1} +{\varvec{v}}_k. \end{aligned}$$
(9)

Then, an input–output matrix equation can be assembled as

$$\begin{aligned} \mathbf{Y}={\varvec{\Gamma }} \mathbf{X}+{\varvec{\Xi }} _r^d \mathbf{U}+{\varvec{\Xi }} _r^s \mathbf{W}+\mathbf{V}, \end{aligned}$$
(10)

where \({\varvec{\Gamma }}\) denotes the extended observability matrix. \({\varvec{\Xi }}_r^d \) and \({\varvec{\Xi }}_r^s\) are the deterministic and stochastic lower block triangular Toeplitz matrices of the unknown system, respectively. They are defined as

$$\begin{aligned} {\varvec{\Gamma }}= & {} \left[ {{\begin{array}{l} {\mathbf{C}_d } \\ {\mathbf{C}_d \mathbf{A}_d } \\ \vdots \\ {\mathbf{C}_d \mathbf{A}_d^r } \\ \end{array} }} \right] \end{aligned}$$
(11)
$$\begin{aligned} {\varvec{\Xi }} _r^d= & {} \left[ {{\begin{array}{lllll} \mathbf{0} &{}\quad \mathbf{0} &{}\quad \mathbf{0} &{}\quad \cdots &{}\quad \mathbf{0} \\ {\mathbf{C}_d \mathbf{B}_d } &{}\quad \mathbf{0} &{}\quad \mathbf{0} &{}\quad \cdots &{}\quad \mathbf{0} \\ {\mathbf{C}_d \mathbf{A}_d \mathbf{B}_d } &{}\quad {\mathbf{C}_d \mathbf{B}_d } &{}\quad \mathbf{0} &{}\quad \cdots &{}\quad \mathbf{0} \\ \vdots &{}\quad \vdots &{}\quad \vdots &{}\quad \ddots &{}\quad \vdots \\ {\mathbf{C}_d \mathbf{A}_d^{r-2} \mathbf{B}_d } &{}\quad {\mathbf{C}_d \mathbf{A}_d^{r-3} \mathbf{B}_d } &{}\quad {\mathbf{C}_d \mathbf{A}_d^{r-4} \mathbf{B}_d } &{}\quad \cdots &{}\quad \mathbf{0} \\ \end{array} }} \right] \nonumber \\\end{aligned}$$
(12)
$$\begin{aligned} {\varvec{\Xi }} _r^s= & {} \left[ {{\begin{array}{lllll} \mathbf{0} &{}\quad \mathbf{0} &{}\quad \cdots &{}\quad \mathbf{0} &{}\quad \mathbf{0} \\ {\mathbf{C}_d } &{}\quad \mathbf{0} &{}\quad \cdots &{}\quad \mathbf{0} &{}\quad \mathbf{0} \\ {\mathbf{C}_d \mathbf{A}_d } &{}\quad {\mathbf{C}_d \mathbf{B}_d } &{}\quad \cdots &{}\quad \mathbf{0} &{}\quad \mathbf{0} \\ \vdots &{}\quad \vdots &{}\quad \ddots &{}\quad \vdots &{}\quad \vdots \\ {\mathbf{C}_d \mathbf{A}_d^{r-2} } &{}\quad {\mathbf{C}_d \mathbf{A}_d^{r-3} } &{}\quad \cdots &{}\quad {\mathbf{C}_d } &{}\quad \mathbf{0} \\ \end{array} }} \right] \end{aligned}$$
(13)
$$\begin{aligned} \mathbf{Y}= & {} \left[ {{\begin{array}{lllll} {{\varvec{y}}_1 } &{}\quad \cdots &{}\quad {{\varvec{y}}_k } &{}\quad \cdots &{}\quad {{\varvec{y}}_L } \\ {{\varvec{y}}_2 } &{}\quad \cdots &{}\quad {{\varvec{y}}_{k+1} } &{}\quad \cdots &{}\quad {{\varvec{y}}_{L+1} } \\ \vdots &{}\quad \vdots &{}\quad \vdots &{}\quad \vdots &{}\quad \vdots \\ {{\varvec{y}}_r } &{}\quad \cdots &{}\quad {{\varvec{y}}_{k+r-1} } &{}\quad \cdots &{}\quad {{\varvec{y}}_{L+r-1} } \\ \end{array} }} \right] \end{aligned}$$
(14)
$$\begin{aligned} \mathbf{X}= & {} \left[ {{\begin{array}{lllll} {{\varvec{x}}_1 } &{}\quad \cdots &{}\quad {{\varvec{x}}_k } &{}\quad \cdots &{}\quad {{\varvec{x}}_L } \\ {{\varvec{x}}_2 } &{}\quad \cdots &{}\quad {{\varvec{x}}_{k+1} } &{}\quad \cdots &{}\quad {{\varvec{x}}_{L+1} } \\ \vdots &{}\quad \vdots &{}\quad \vdots &{}\quad \vdots &{}\quad \vdots \\ {{\varvec{x}}_r } &{}\quad \cdots &{}\quad {{\varvec{x}}_{k+r-1} } &{}\quad \cdots &{}\quad {{\varvec{x}}_{L+r-1} } \\ \end{array} }} \right] \end{aligned}$$
(15)
$$\begin{aligned} \mathbf{U}= & {} \left[ {{\begin{array}{lllll} {{\varvec{u}}_1 } &{}\quad \cdots &{}\quad {{\varvec{u}}_k } &{}\quad \cdots &{}\quad {{\varvec{u}}_L } \\ {{\varvec{u}}_2 } &{}\quad \cdots &{}\quad {{\varvec{u}}_{k+1} } &{}\quad \cdots &{}\quad {{\varvec{u}}_{L+1} } \\ \vdots &{}\quad \vdots &{}\quad \vdots &{}\quad \vdots &{}\quad \vdots \\ {{\varvec{u}}_r } &{}\quad \cdots &{}\quad {{\varvec{u}}_{k+r-1} } &{}\quad \cdots &{}\quad {{\varvec{u}}_{L+r-1} } \\ \end{array} }} \right] \end{aligned}$$
(16)
$$\begin{aligned} \mathbf{W}= & {} \left[ {{\begin{array}{lllll} {{\varvec{w}}_1 } &{}\quad \cdots &{}\quad {{\varvec{w}}_k } &{}\quad \cdots &{}\quad {{\varvec{w}}_L } \\ {{\varvec{w}}_2 } &{}\quad \cdots &{}\quad {{\varvec{w}}_{k+1} } &{}\quad \cdots &{}\quad {{\varvec{w}}_{L+1} } \\ \vdots &{}\quad \vdots &{}\quad \vdots &{}\quad \vdots &{}\quad \vdots \\ {{\varvec{w}}_r } &{}\quad \cdots &{}\quad {{\varvec{w}}_{k+r-1} } &{}\quad \cdots &{}\quad {{\varvec{w}}_{L+r-1} } \\ \end{array} }} \right] \end{aligned}$$
(17)
$$\begin{aligned} \mathbf{V}= & {} \left[ {{\begin{array}{lllll} {{\varvec{v}}_1 } &{}\quad \cdots &{}\quad {{\varvec{v}}_k } &{}\quad \cdots &{}\quad {{\varvec{v}}_L } \\ {{\varvec{v}}_2 } &{}\quad \cdots &{}\quad {{\varvec{v}}_{k+1} } &{}\quad \cdots &{}\quad {{\varvec{v}}_{L+1} } \\ \vdots &{}\quad \vdots &{}\quad \vdots &{}\quad \vdots &{}\quad \vdots \\ {{\varvec{v}}_r } &{}\quad \cdots &{}\quad {{\varvec{v}}_{k+r-1} } &{}\quad \cdots &{}\quad {{\varvec{v}}_{L+r-1} } \\ \end{array} }} \right] \end{aligned}$$
(18)

in which L and r are the user-defined integers which satisfy the relationships \(r>2n\) and \(L\gg 2n\). Equation (10) includes the state vector item \({\varvec{\Gamma }}{} \mathbf{X}\), the input vector item \({\varvec{\Xi }}_r^d \mathbf{U}\), the process noise item \({\varvec{\Xi }} _r^s \mathbf{W}\), and the measurement noise item \(\mathbf{V}\).

Additionally, defining a projection matrix \({\varvec{\Pi }} _{\mathbf{U}^{T}}^\bot \)

$$\begin{aligned} {\varvec{\Pi }} _{{\mathbf{U}}^{T}}^\bot =\mathbf{I}-\mathbf{U}^{T}\left( {\mathbf{UU}^{T}} \right) ^{-1}{} \mathbf{U} \end{aligned}$$
(19)

and post-multiplying this projection matrix, Eq. (10) becomes

$$\begin{aligned} \mathbf{Y}{\varvec{\Pi }} _{{\mathbf{U}}^{T}}^\bot ={\varvec{\Gamma }} \mathbf{X}{\varvec{\Pi }} _{\mathbf{U}^{T}}^\bot +{\varvec{\Xi }} _r^d \mathbf{U}{\varvec{\Pi }}_{{\mathbf{U}}^{T}}^\bot +{\varvec{\Xi }}_r^s \mathbf{W}{\varvec{\Pi }}_{\mathbf{U}^{T}}^\bot +\mathbf{V}{\varvec{\Pi }}_{\mathbf{U}^{T}}^\bot . \end{aligned}$$
(20)

By taking into account the property of projection matrix \((\mathbf{U}{\varvec{\Pi }} _{{\mathbf{U}}^{T}}^\bot =\mathbf{0})\), one can obtain

$$\begin{aligned} \mathbf{Y}{\varvec{\Pi }} _{\mathbf{U}^{T}}^\bot ={\varvec{\Gamma }} \mathbf{X}{\varvec{\Pi }} _{\mathbf{U}^{T}}^\bot +{\varvec{\Xi }} _r^s \mathbf{W}{\varvec{\Pi }} _{\mathbf{U}^{T}}^\bot +\mathbf{V}{\varvec{\Pi }} _{\mathbf{U}^{T}}^\bot . \end{aligned}$$
(21)

A matrix \(\mathbf{P}\) can be constructed based on instrumental variables technique

$$\begin{aligned} \mathbf{P}=\left[ {\mathbf{U}_p^T ,\quad \mathbf{Y}_p^T } \right] ^{T}, \end{aligned}$$
(22)

where \(\mathbf{U}_{p}\) and \(\mathbf{Y}_{p}\) have the similar forms with the matrices U and Y. Because the noise items \({\varvec{w}}_{k}\) and \({\varvec{v}}_{k}\) are all assumed to be white noise and are uncorrelated with the input vector \({\varvec{u}}_{k}\), the matrix \(\mathbf{P}^{T}\) have the relationship of \(\left( {{\varvec{\Xi }}_r^s \mathbf{W}+\mathbf{V}} \right) {\varvec{\Pi }} _{\mathbf{U}^{T}}^\bot \mathbf{P}^{T}=\mathbf{0}\).

By post-multiplying the matrix \(\mathbf{P}^{T}\), Eq. (21) becomes

$$\begin{aligned} \mathbf{Y}{\varvec{\Pi }} _{\mathbf{U}^{T}}^\bot \mathbf{P}^{T}={\varvec{\Gamma }} \mathbf{X}{\varvec{\Pi }} _{\mathbf{U}^{T}}^\bot \mathbf{P}^{T}. \end{aligned}$$
(23)

Then, based on the singular value decomposition, one can obtain the estimated observability matrix \({\varvec{\Gamma }}^{e}\)

$$\begin{aligned} \left\{ {{\begin{array}{l} {\mathbf{H}_1 \mathbf{Y}{\varvec{\Pi }} _{\mathbf{U}^{T}}^\bot \mathbf{P}^{T}{} \mathbf{H}_2 =\mathbf{H}_1 {\varvec{\Gamma }} \mathbf{X}{\varvec{\Pi }} _{\mathbf{U}^{T}}^\bot \mathbf{P}^{T}{} \mathbf{H}_2 =\mathbf{QSV}^{T}} \\ {\mathbf{QSV}^{T}\approx \bar{{\mathbf{Q}}}\bar{{\mathbf{S}}}\bar{{\mathbf{V}}}^{T}=\bar{{\mathbf{Q}}}\left[ {{\begin{array}{llll} {\sigma _1 } &{}\quad \cdots &{}\quad 0 \\ \vdots &{}\quad \ddots &{}\quad \vdots \\ 0 &{}\quad \cdots &{}\quad {\sigma _s } \\ \end{array} }} \right] \bar{{\mathbf{V}}}^{T}} \\ {{\varvec{\Gamma }} ={\varvec{\Gamma }} ^{e}{} \mathbf{T}=\mathbf{H}_1^{-1} \bar{{\mathbf{Q}}}{} \mathbf{T}} \\ \end{array}}},\right. \end{aligned}$$
(24)

where two full-rank matrices \(\mathbf{H}_{1}\) and \(\mathbf{H}_{2}\) are respectively pre-multiplied and post-multiplied to Eq. (23) for improving the accuracy of the singular value decomposition. S is the diagonal matrix in singular value decomposition, and its diagonal elements are the calculated singular values \(\left( {{\begin{array}{lll} {\sigma _1 } &{}\quad \cdots &{}\quad {\sigma _s } \\ \end{array} }} \right) \). \(\bar{{\mathbf{Q}}}\) is the matrix by removing some columns from the matrix Q based on their corresponding diagonal elements in S.

It is shown that \({\varvec{\Gamma }} \) and \(\mathbf{Y}{\varvec{\Pi }} _{\mathbf{U}^{T}}^\bot \mathbf{P}^{T}\) have the same column space based on the rank analysis. Therefore, the column space of the estimated observability matrix \({\varvec{\Gamma }}^{e}\) is the same as that of the true observability matrix \({\varvec{\Gamma }}\) through the singular value decomposition. And \({\varvec{\Gamma }}\) can be obtained by post-multiplying a nonsingular matrix T.

3.2 Estimation of the system state matrices

After the estimation of the extended observability matrix, the next step is to identify the system state matrices. This computation process should yield accurate estimations while preserving an acceptable computation time. In this section, a new strategy to estimate \(\mathbf{A}_{d}\), \(\mathbf{B}_{d}\), and \(\mathbf{C}_{d}\) is presented. First, those three system matrices \(\mathbf{A}_{d}\), \(\mathbf{B}_{d}\), and \(\mathbf{C}_{d}\) are calculated from the estimated extended observability matrix. Then, an alternative scheme with the help of the PEM is suggested to reestimate the system matrices. It is mainly because the estimated results with the NSIM are not the optimal solutions which may result in the decrease in the identified accuracy. The PEM uses a full parameterization of the state-space model to optimize an objective function for obtaining the optimal solutions in the least square sense.

It is a common way to exploit the shifted structure of \({\varvec{\Gamma }} ^{e}\) to estimate \(\mathbf{A}_d^e \) and \(\mathbf{C}_d^e \) in which \(\mathbf{A}_d^e \) and \(\mathbf{C}_d^e \) represent the estimates of the \(\mathbf{A}_{d}\) and \(\mathbf{C}_{d}\) [22, 23]. The shift property can be written as

$$\begin{aligned} \underline{{\varvec{\Gamma }}}^{e}{} \mathbf{A}_d^e =\bar{{{\varvec{\Gamma }} }}^{e}, \end{aligned}$$
(25)

where \({\underline{\varvec{\Gamma }} }^{e}\) and \(\bar{{{\varvec{\Gamma }} }}^{e}\) denote the matrices by removing the first and the last h rows from \({\varvec{\Gamma }}^{e}\), respectively. Then, \(\mathbf{A}_d^e \) can be obtained by the equations of the overdetermined systems

$$\begin{aligned} \mathbf{A}_d^e ={\underline{\varvec{\Gamma }} }^{e+}\bar{{{\varvec{\Gamma }} }}^{e}, \end{aligned}$$
(26)

where \({\underline{\varvec{\Gamma }}}^{e+}\) is the pseudo-inverse of \({\underline{\varvec{\Gamma }}}^{e}\). Based on the definition of the extended observability matrix Eq. (11), \(\mathbf{C}_d^e \) can be obtained by

$$\begin{aligned} \mathbf{C}_d^e ={\varvec{\Gamma }} ^{e}\left( {1:h,:} \right) , \end{aligned}$$
(27)

where \(\left( {1:h,:} \right) \) denotes the first h lines of the \({\varvec{\Gamma }}^{e}\).

After the system matrices \(\mathbf{A}_d^e \) and \(\mathbf{C}_d^e \) are determined, the matrices \(\mathbf{B}_d^e \) are usually estimated by the linear regression equation from Eq. (8) [17, 21]. Iterating Eq. (8), one can obtain

$$\begin{aligned} {\varvec{y}}_k= & {} \mathbf{C}_d {\varvec{x}}_k +{\varvec{v}}_k =\mathbf{C}_d \left( {\mathbf{A}_d {\varvec{x}}_{k-1} +\mathbf{B}_d {\varvec{u}}_{k\hbox {-}1} +{\varvec{w}}_{k-1} } \right) +{\varvec{v}}_k\nonumber \\= & {} \ldots \nonumber \\= & {} \mathbf{C}_d \mathbf{A}_d ^{k-1}{\varvec{x}}_1 +\sum _{i=1}^{k-1} {\left( {\mathbf{C}_d \mathbf{A}_d ^{k-i-1}{} \mathbf{B}_d {\varvec{u}}_i } \right) } \nonumber \\&+\,{\varvec{Noise}}\left( {{\varvec{w}}_1 ,\ldots ,{\varvec{w}}_{k-1} ,{\varvec{v}}_k } \right) \nonumber \\= & {} \mathbf{C}_d \mathbf{A}_d ^{k-1}{\varvec{x}}_1 +\sum _{i=1}^{k-1} {\left( {{\varvec{u}}_i ^{T}\otimes \left( {\mathbf{C}_d \mathbf{A}_d ^{k-i-1}} \right) } \right) } \hbox {vec}(\mathbf{B}_d )\nonumber \\&+\,{\varvec{Noise}}\left( {{\varvec{w}}_1 ,\ldots ,{\varvec{w}}_{k-1} ,{\varvec{v}}_k } \right) \nonumber \\= & {} \left[ {{\begin{array}{ll} {\mathbf{C}_d \mathbf{A}_d ^{k-1}} &{}\quad {\sum \limits _{i=1}^{k-1} {\left( {{\varvec{u}}_i ^{T}\otimes \left( {\mathbf{C}_d \mathbf{A}_d ^{k-i-1}} \right) } \right) } } \\ \end{array} }} \right] \left[ {{\begin{array}{l} {{\varvec{x}}_1 } \\ {\hbox {vec}(\mathbf{B}_d )} \\ \end{array} }} \right] \nonumber \\&+\,{{\varvec{Noise}}}\left( {{\varvec{w}}_1 ,\ldots ,{\varvec{w}}_{k-1} ,{\varvec{v}}_k } \right) , \end{aligned}$$
(28)

where \({{{\varvec{Noise}}}}\left( {{\varvec{w}}_1 ,\ldots ,{\varvec{w}}_{k-1} ,{\varvec{v}}_k } \right) \) is the residual term of the system which is the sum of all the process noise and the output measurement noise. \(\otimes \) denotes the Kronecker multiplier. \(\hbox {vec}(\mathbf{B}_d )\) stands for the column vectors obtained by the rearrangement of each column of the matrices \(\mathbf{B}_d^e \) from left to right, respectively. Then, \(\mathbf{B}_d^e\) can be estimated by solving a linear regression equation with the help of the least square method. It should be noted that the relationships of the estimated matrices and the true ones are as follows

$$\begin{aligned} \left\{ {{\begin{array}{l} {\mathbf{A}_d^e =\mathbf{TA}_d \mathbf{T}^{-1}} \\ {\mathbf{B}_d^e =\mathbf{TB}_d } \\ {\mathbf{C}_d^e =\mathbf{C}_d \mathbf{T}^{-1}} \\ \end{array} }} \right. \end{aligned}$$
(29)

The algorithm described above rapidly gives an initial model of the identified system. Then, the PEM [24] is applied by using a full parameterization of the state-space model in which \({\varvec{\theta }}\) is the parameter vector consisted of the elements of the system matrices \(\mathbf{A}_d^e \), \(\mathbf{B}_d^e \), and \(\mathbf{C}_d^e \). The one-step ahead prediction error defined as

$$\begin{aligned} {\varvec{\varepsilon }} _k ={\varvec{y}}_k -\hat{{{\varvec{y}}}}_k \end{aligned}$$
(30)

is minimized to find the optimal system parameters in which \(\hat{{{\varvec{y}}}}_k \) is the one-step ahead prediction of the output. For the discrete-time state-space model of Eq. (8), the \(\hat{{{\varvec{y}}}}_k \) can be described as follows:

$$\begin{aligned} \hat{{{\varvec{y}}}}_k= & {} \mathbf{C}_d^e \mathbf{A}_d^{e {(k-1)}}\hat{{{\varvec{x}}}}_1 \nonumber \\&+\,\mathbf{C}_d^e \mathbf{A}_d^{e {(k-2)}}{} \mathbf{B}_d^e \hat{{{\varvec{u}}}}_1 +\mathbf{C}_d^e \mathbf{A}_d^{e {(k-3)}}{} \mathbf{B}_d^e \hat{{{\varvec{u}}}}_2 +\cdots \nonumber \\&+\,\mathbf{C}_d^e \mathbf{B}_d^e \hat{{{\varvec{u}}}}_{k-1} +\mathbf{C}_d^e \mathbf{A}_d^{e {(k-2)}}{\varvec{w}}_1 \nonumber \\&+\,\mathbf{C}_d^e \mathbf{A}_d^{e {(k-3)}}{\varvec{w}}_2 +\cdots \nonumber \\&+\,\mathbf{C}_d^e {\varvec{w}}_{k-1} +{\varvec{v}}_k. \end{aligned}$$
(31)

The criterion functions \(J_N \left( {\varvec{\theta }} \right) \) has to be determined first to implement the PEM. The function \(J_N \left( {\varvec{\theta }} \right) \) is generally chosen as

$$\begin{aligned} J_N \left( {\varvec{\theta }} \right) =h\left( {R_N \left( {\varvec{\theta }} \right) } \right) , \end{aligned}$$
(32)

where \(h(\cdot )\) represents a scalar monotonically increasing function. \(R_N \left( {\varvec{\theta }} \right) \) denotes the sample covariance matrix of the prediction errors and is defined as

$$\begin{aligned} R_N \left( {\varvec{\theta }} \right) =\frac{1}{N}\sum _{t=1}^N {\varepsilon \left( {t,{\varvec{\theta }} } \right) \varepsilon ^{T}\left( {t,{\varvec{\theta }} } \right) }. \end{aligned}$$
(33)

Then, the estimation of the parameter vector \({\varvec{\theta }}\) is obtained by minimizing the criterion function \(J_N \left( {\varvec{\theta }}\right) \)

$$\begin{aligned} {\varvec{\theta }} _N^e =\mathrm{arg}\mathop {\min }\limits _\theta \left( {J_N \left( {\varvec{\theta }} \right) } \right) . \end{aligned}$$
(34)

In general, the predictors nonlinearly rely on the parameters. Therefore, the solution is obtained through the iteration process as follows

$$\begin{aligned} \tilde{{\varvec{\theta }} }_N^{(i+1)} =\tilde{{\varvec{\theta }} }_N^{(i)} -\eta _N^{(i)} \left( {R_N^{(i)} } \right) ^{-1}J_N^{\prime } \left( {\tilde{{\varvec{\theta }} }^{(i)}} \right) , \end{aligned}$$
(35)

where \(\tilde{\theta }^{(i)}\) is the ith iteration and \(R_N^{(i)} \) is the matrix determining the search direction. \(J_N^{\prime } \left( {\tilde{{\varvec{\theta }} }^{(i)}} \right) \) denotes the gradient of the criterion function relating to the parameter vector. \(\eta _N^{(i)} \) stands for the step size and should be carefully chosen to ensure that the current value of the criterion function is no larger than that of the previous one. Several numerical algorithms, such as the Newton–Raphson algorithm or the Gauss–Newton algorithm, can be used for this iteration process. Finally, the system state matrices of the continuous-time state-space model \(\mathbf{A}_{c}\), \(\mathbf{B}_{c}\), and \(\mathbf{C}_{c}\) can be obtained by the relationships of Eq. (7).

3.3 Estimation of nonlinear coefficients and FRFs of the underlying linear systems

Once the system model \(\mathbf{A}_{c}\), \(\mathbf{B}_{c}\), and \(\mathbf{C}_{c}\) have been estimated, the final step is to estimate the nonlinear coefficients and the FRFs of the underlying linear system. The main calculated process is based on the extended FRF which contains nonlinear terms in the model [17]. By taking Fourier transform of Eq. (5), an extended FRF of the system is obtained

$$\begin{aligned} \mathbf{H}_{{\textit{ex}}} \left( \omega \right) =\mathbf{C}_c \left( {i\omega \mathbf{I}-\mathbf{A}_c } \right) ^{-1}{} \mathbf{B}_c. \end{aligned}$$
(36)

Defining two matrices

$$\begin{aligned} \mathbf{N}= & {} \left[ {{\begin{array}{ll} {\mathbf{N}_{11} }&{}\quad {\mathbf{N}_{12} } \\ {\mathbf{N}_{21} }&{}\quad {\mathbf{N}_{22} } \\ \end{array} }} \right] = i\omega \mathbf{I}-\left[ {{\begin{array}{cc} {\mathbf{0}_{n\times n} }&{}\quad {\mathbf{I}_{n\times n} } \\ {-\mathbf{M}^{-1}{} \mathbf{K}}&{}\quad {-\mathbf{M}^{-1}{} \mathbf{C}} \\ \end{array} }} \right] \end{aligned}$$
(37)
$$\begin{aligned} \mathbf{P}= & {} \left[ {{\begin{array}{ll} {\mathbf{P}_{11} }&{}\quad {\mathbf{P}_{12} } \\ {\mathbf{P}_{21} }&{}\quad {\mathbf{P}_{22} } \\ \end{array} }} \right] =\left( {i\omega \mathbf{I}-\left[ {{\begin{array}{cc} {\mathbf{0}_{n\times n} }&{}\quad {\mathbf{I}_{n\times n} } \\ {-\mathbf{M}^{-1}{} \mathbf{K}}&{}\quad {-\mathbf{M}^{-1}{} \mathbf{C}} \\ \end{array} }} \right] } \right) ^{-1}\nonumber \\ \end{aligned}$$
(38)

and taking into account Eq. (6), \(\mathbf{H}_{{\textit{ex}}} \left( \omega \right) \) can be derived as

$$\begin{aligned}&{} \mathbf{H}_{{\textit{ex}}} \left( \omega \right) \nonumber \\&\quad =\left[ {{\begin{array}{ll} {\mathbf{I}_{p\times p} }&{}\quad {\mathbf{0}_{p\times p} } \nonumber \\ \end{array} }} \right] \left[ {{\begin{array}{ll} {\mathbf{P}_{11} }&{}\quad {\mathbf{P}_{12} } \\ {\mathbf{P}_{21} }&{}\quad {\mathbf{P}_{22} } \\ \end{array} }} \right] \nonumber \\&\qquad \left[ {{\begin{array}{cclc} {\mathbf{0}_{p\times 1} }&{}\quad {\mathbf{0}_{p\times 1} }&{}\quad {\cdots }&{}\quad {\mathbf{0}_{p\times 1} } \\ {\mathbf{M}^{-1}{\varvec{L}}_f }&{}\quad {\mathbf{M}^{-1}\mu _1 {\varvec{L}}_1 }&{}\quad {\cdots }&{}\quad {\mathbf{M}^{-1}\mu _h {\varvec{L}}_h } \\ \end{array} }} \right] \nonumber \\&\quad =\left[ {{\begin{array}{ll} {\mathbf{P}_{11} }&{}\quad {\mathbf{P}_{12} } \\ \end{array} }} \right] \left[ {{\begin{array}{cclc} {\mathbf{0}_{p\times 1} }&{}\quad {\mathbf{0}_{p\times 1} }&{}\quad {\ldots }&{}\quad {\mathbf{0}_{p\times 1} } \\ {\mathbf{M}^{-1}{\varvec{L}}_f }&{}\quad {\mathbf{M}^{-1}\mu _1 {\varvec{L}}_1 }&{}\quad {\ldots }&{}\quad {\mathbf{M}^{-1}\mu _h {\varvec{L}}_h } \\ \end{array} }} \right] \nonumber \\&\quad =\mathbf{P}_{12} \left[ {{\begin{array}{cclc} {\mathbf{M}^{-1}{\varvec{L}}_f }&{}\quad {\mathbf{M}^{-1}\mu _1 {\varvec{L}}_1 }&{}\quad {\ldots }&{}\quad {\mathbf{M}^{-1}\mu _h {\varvec{L}}_h } \\ \end{array} }} \right] . \end{aligned}$$
(39)

Based on the block matrix inversion rule, \(\mathbf{P}_{12}\) can be obtained by

$$\begin{aligned} \mathbf{P}_{12}= & {} -\,\mathbf{N}_{11}^{-1} \mathbf{N}_{12} \left( {\mathbf{N}_{22} -\mathbf{N}_{21} \mathbf{N}_{11}^{-1} \mathbf{N}_{12} } \right) ^{-1} \nonumber \\= & {} \left( {\mathbf{K}+i\omega \mathbf{C}-\omega ^{2}{} \mathbf{M}} \right) ^{-1}{} \mathbf{M}. \end{aligned}$$
(40)

Therefore, \(\mathbf{H}_{{\textit{ex}}} \left( \omega \right) \) can be rewritten as

$$\begin{aligned}&{} \mathbf{H}_{ex} \left( \omega \right) \nonumber \\&\quad = \mathbf{P}_{12} \left[ {{\begin{array}{llll} {\mathbf{M}^{-1}{\varvec{L}}_f }&{}\quad {\mathbf{M}^{-1}\mu _1 {\varvec{L}}_1 }&{}\quad {\ldots }&{}\quad {\mathbf{M}^{-1}\mu _h {\varvec{L}}_h } \\ \end{array}}} \right] \nonumber \\&\quad =\left( {\mathbf{K}+i\omega \mathbf{C}-\omega ^{2}{} \mathbf{M}} \right) ^{-1}\left[ {{\begin{array}{llll} {{\varvec{L}}_f }&{}\quad {\mu _1 {\varvec{L}}_1 }&{}\quad {\ldots }&{}\quad {\mu _h {\varvec{L}}_h }\nonumber \\ \end{array} }} \right] . \\ \end{aligned}$$
(41)

where the item \(\left( {\mathbf{K}+i\omega \mathbf{C}-\omega ^{2}{} \mathbf{M}} \right) ^{-1}\) describes the dynamic features of the underlying linear system and the item \(\left[ {{\begin{array}{llll} {{\varvec{L}}_f }&{}\quad {\mu _1 {\varvec{L}}_1 }&{}\quad {\ldots }&{}\quad {\mu _h {\varvec{L}}_h } \\ \end{array} }} \right] \) includes the nonlinear coefficients to be identified. With the hypothesis that the FRF of the underlying linear system \(\left( {\mathbf{K}+i\omega \mathbf{C}-\omega ^{2}{} \mathbf{M}} \right) ^{-1}\) is a symmetric matrix, the nonlinear coefficients \(\mu _{i}\) and the FRF of the underlying linear system can be obtained from Eq. (41).

In order to demonstrate the calculating process for estimating the nonlinear coefficients and the FRFs of the underlying linear system, a two DOF dynamic system with one local nonlinear stiffness is considered as

$$\begin{aligned} \mathbf{M}\ddot{{\varvec{z}}}\left( t \right) +\mathbf{C}\dot{{\varvec{z}}}\left( t \right) +\mathbf{K}{\varvec{z}}\left( t\right) +k_n g_1 \left( t\right) {\varvec{L}}_1 ={\varvec{L}}_f F\left( t \right) , \end{aligned}$$
(42)

where \(k_{n}\) is the local nonlinear stiffness to be identified. \({\varvec{z}}(t)\) is the displacement response vector of the system, and \({\varvec{z}}\left( t \right) =\left[ {{\varvec{z}}_1 \left( t \right) {\varvec{z}}_2 \left( t \right) } \right] ^{T}\). \(g_{1}(t)\) denotes the base function of nonlinear component which is

$$\begin{aligned} g_1 \left( t \right) ={\varvec{z}}_1^3 \left( t \right) . \end{aligned}$$
(43)
Fig. 2
figure 2

Overview of the NSPEM

Full size image

\({\varvec{L}}_{1}\) and \({\varvec{L}}_{f}\) are the location vectors of the nonlinear element and the excitation, respectively. They can be assumed as

$$\begin{aligned} {\varvec{L}}_f =\left[ {{\begin{array}{ll} 0 &{}\quad 1 \\ \end{array} }} \right] ^{T}, \quad {\varvec{L}}_1 =\left[ {{\begin{array}{ll} 1 &{}\quad 0 \\ \end{array} }} \right] ^{T}. \end{aligned}$$
(44)

After the system models \(\mathbf{A}_{c}\), \(\mathbf{B}_{c}\), and \(\mathbf{C}_{c}\) are estimated, the extended FRF of the system \(\mathbf{H}_{{\textit{ex}}2} \left( \omega \right) \) can be obtained and one has the following relationship based on Eq. (41)

$$\begin{aligned} \mathbf{H}_{{\textit{ex}}2} \left( \omega \right)= & {} \left[ {{\begin{array}{ll} {\mathbf{H}_{{\textit{ex}}11} } &{}\quad {\mathbf{H}_{{\textit{ex}}12} } \\ {\mathbf{H}_{{\textit{ex}}21} } &{}\quad {\mathbf{H}_{{\textit{ex}}22} } \\ \end{array} }} \right] \nonumber \\= & {} \mathbf{H}\left( \omega \right) \left[ {{\begin{array}{ll} {{\varvec{L}}_f } &{}\quad {k_n {\varvec{L}}_1 } \\ \end{array} }} \right] \nonumber \\= & {} \mathbf{H}\left( \omega \right) \left[ {{\begin{array}{ll} 0 &{}\quad {k_n } \\ 1 &{}\quad 0 \\ \end{array} }} \right] =\left[ {{\begin{array}{ll} {\mathbf{H}_{12} } &{}\quad {k_n \mathbf{H}_{11} } \\ {\mathbf{H}_{22} } &{}\quad {k_n \mathbf{H}_{21} } \\ \end{array} }} \right] ,\nonumber \\ \end{aligned}$$
(45)

where \(\mathbf{H}\left( \omega \right) \) represents the FRF of the underlying linear system and is expressed as

$$\begin{aligned} \mathbf{H}\left( \omega \right) =\left[ {{\begin{array}{ll} {\mathbf{H}_{11} } &{}\quad {\mathbf{H}_{12} } \\ {\mathbf{H}_{21} } &{}\quad {\mathbf{H}_{22} } \\ \end{array} }} \right] . \end{aligned}$$
(46)

Taking into account \(\mathbf{H}_{12}=\mathbf{H}_{21}\), the nonlinear coefficient \(k_{n}\) can be obtained by

$$\begin{aligned} k_n =\frac{k_n \mathbf{H}_{21} }{\mathbf{H}_{21} }=\frac{k_n \mathbf{H}_{21} }{\mathbf{H}_{12} }=\frac{\mathbf{H}_{ex22} }{\mathbf{H}_{ex11} }. \end{aligned}$$
(47)

The FRF of the underlying linear system can be calculated by

$$\begin{aligned} \left\{ {{\begin{array}{l} {\mathbf{H}_{12} =\mathbf{H}_{ex11} } \\ {\mathbf{H}_{22} =\mathbf{H}_{ex21} } \\ \end{array} }} \right. . \end{aligned}$$
(48)

To summarize, Fig. 2 presents an overview of the NSPEM.

Fig. 3
figure 3

Six DOF mass-spring-damper system with one local nonlinearity

Full size image

4 Numerical simulations

4.1 A six DOF discrete mass-spring-damper system

As shown in Fig. 3, a six DOF mass-spring-damper system with one local nonlinearity is considered. The system parameters are set as \(k_{i} = 3\times 10^{4}\,\hbox {Nm}^{-1}\), \(c_{i} = 5\times 10^{-5} \times k_{i}\,\hbox {Nsm}^{-1}\), and \(m_{i} = 1\,\hbox {kg}\,(i = 1,{\ldots },6)\). The nonlinearity in the system is located between the \(x_{1}\) and the ground. The expression of the nonlinearity is written as

$$\begin{aligned} f_{Nd1} =k_{nd} x_1^3, \end{aligned}$$
(49)

where \(k_{nd}\) is the nonlinear coefficient with the value of \(10^{13}\,\hbox {Nm}^{-3}\). \(x_{i}\) (\(i = 1,{\ldots },6)\) is the displacement response and obtained by the fourth-order Runge–Kutta algorithm with the sample frequency of 2000 Hz. The excitation \(F_\mathrm{ind}\) on node six is chosen as a zero-mean white Gaussian noise whose root-mean-square (RMS) value is 1 N.

Fig. 4
figure 4

Estimated FRF \((\hbox {H}_{16})\) of the six DOF discrete mass-spring-damper system and theoretical FRF \((\hbox {H}_{16})\) of its underlying linear system

Full size image

Figure 4 gives the estimated FRF\((\hbox {H}_{16})\) by the typical linear technique \(\hbox {H}_{1}\) estimator. The theoretical FRF\((\hbox {H}_{16})\) of its underlying linear system is also plotted. It is noted that there are obvious differences of those two FRFs, indicating the existence of nonlinearities.

Fig. 5
figure 5

Histograms of the estimated nonlinear coefficient \(k_{nd}\) by a the proposed method and b the NSIM under the 20 dB noise

Full size image

In order to illustrate the performance of the proposed method under different levels of noise environment, all the simulated responses are contaminated by different levels of noises with the SNR = 20, 40, 60 dB in sequence. And each group of numerical experiments consists of 100 times simulation calculation by the Monte Carlo method. Figure 5 compares the estimated nonlinear coefficient by the proposed method and the NSIM under a 20-dB noise environment. The results show that the distribution of estimated nonlinear coefficient obtained by the proposed method is more concentrated than that obtained by the NSIM. Table 1 lists the means and variances of the estimated results under different levels of noises. Note that the mean values obtained by the proposed method are more accurate than those results calculated by the NSIM. The variance values obtained by the proposed method are smaller than those calculated by the NSIM under the same level of noise. It is mainly because that the NSPEM obtains the parameter estimate with the help of the PEM which can give the optimal identification results in the least square sense. Figure 6 plots the estimated FRF \((\hbox {H}_{16})\) of the underlying linear system using the proposed method under the 20-dB noise. It is noted that the estimated FRF of the underlying linear system is in good agreement with the theoretical values.

Table 1 Comparison of the estimated nonlinear coefficients by the proposed method and the NSIM under different levels of noises (the six DOF discrete mass-spring-damper system)
Full size table
Fig. 6
figure 6

Estimated FRF (\(\hbox {H}_{16})\) of the underlying linear system for the six DOF discrete mass-spring-damper system under the 20 dB noise

Full size image

4.2 A cantilever beam structure

A cantilever beam with two local nonlinearities depicted in Fig. 7 is carried out in this subsection. The beam is modeled by the finite element method [25] with Euler beam unit, while the first three modes between 0 and 300 Hz are discussed herein. The density and elasticity modulus of the beam are 7800 \(\hbox {kgm}^{-3}\) and 2.06e11 Pa, respectively. The length, height, and width of the beam are 0.2, 0.01, and 0.005 m, respectively.

Fig. 7
figure 7

Cantilever beam structure with two local nonlinearities

Full size image

The dynamic equation of the cantilever beam can be expressed as

$$\begin{aligned} \mathbf{M}\ddot{{\varvec{x}}}+\mathbf{C}\dot{{\varvec{x}}}+\mathbf{K}{\varvec{x}}={\varvec{F}}+{\varvec{F}}_n, \end{aligned}$$
(50)

where

$$\begin{aligned}&{\varvec{F}}=\left[ {0,0,0,0,F_{in} ,0} \right] ^{T} \end{aligned}$$
(51)
$$\begin{aligned}&{\varvec{F}}_n =\left[ {0,0,-F_{Nc1} ,0,-F_{Nc2} ,0} \right] \end{aligned}$$
(52)
$$\begin{aligned}&{\varvec{x}}=\left[ {x_1 ,\theta _1 ,x_2 ,\theta _2 ,x_3 ,\theta _3 } \right] ^{T}. \end{aligned}$$
(53)

\(x_{i}\,(i = 1,{\ldots },6)\) is the displacement response of the corresponding node, and \(\theta _{i}\) (\(i=1,2,3\)) is the angular displacement of the corresponding node of the beam. M, K, and C denote the mass, stiffness, and damping matrices, respectively. \(\hbox {C}=\mathbf{U}^{-\mathrm{T}}\hbox {diag}(2\zeta _{i}\omega _{i})\mathbf{U}^{-1}\) in which \(\zeta _{i}\,(i = 1,\ldots ,N)\) denotes the modal damping ratios and is assumed to be 0.2%. The natural frequencies \(\omega _{i}\) and the orthonormalized modal matrix U can be calculated by the eignvalue problem of the underlying linear system. The excitation \(F_{{\textit{in}}}\) is subjected to the \(x_{3}\) and also chosen as a zero-mean white Gaussian noise whose RMS value is 1 N. The two nonlinearity internal feedback forces of the system \(F_{{\textit{Nc}}1}\) and \(F_{{\textit{Nc}}2}\) are expressed as

$$\begin{aligned} \left\{ {{\begin{array}{l} {F_{{\textit{Nc}}1} =k_{{\textit{nc}}1} x_3 \left| {x_3 } \right| } \\ {F_{{\textit{Nc}}2} =k_{{\textit{nc}}2} x_5^3 } \\ \end{array} }} \right. , \end{aligned}$$
(54)

where \(k_{{\textit{nc}}1} = 10^{7}\,\hbox {Nm}^{-1}\), \(k_{{\textit{nc}}2} = 8\times 10^{8}\,\hbox {Nm}^{-1}\) are the nonlinear coefficients of the forces. The system response is obtained by the fourth-order Runge–Kutta algorithm with the sample frequency of 10 kHz.

Fig. 8
figure 8

Estimated FRF \((\hbox {H}_{15})\) of the cantilever beam structure and theoretical FRF \((\hbox {H}_{15})\) of its underlying linear system

Full size image
Fig. 9
figure 9

Histograms of the estimated nonlinear coefficient \(k_{nc1}\) by a the proposed method and b the NSIM under the 20 dB noise

Full size image
Fig. 10
figure 10

Histograms of the estimated nonlinear coefficient \(k_{nc2}\) by a the proposed method and b the NSIM under the 20 dB noise

Full size image

The estimated and theoretical values of the FRF \((\hbox {H}_{15})\) of the underlying linear system are given in Fig. 8. Results show that those two FRFs have obvious differences, implying that the nonlinearities are present. To make a comparison between the proposed method and the NSIM, the identified nonlinear coefficients \(k_{nc1}\) and \(k_{nc2}\) of the cantilever beam structure between these two methods under a 20-dB noise environment are plotted in Figs. 9 and  10. The numerical experiments also consist of 100 times simulation calculation by the Monte Carlo method. From the results, one can see that the distribution of the estimated nonlinear coefficients calculated by the proposed method is more concentrated than that calculated by the NSIM. More specifically, the mean and variance of the estimated results for the cantilever beam structure under different levels of noises (SNR \(=\) 20, 40, 60 dB) are listed in Table 2. It can be seen that the mean values obtained by the proposed method are more accurate than those values obtained by the NSIM. The variance values by the proposed method are much smaller than those by the NSIM under the same level of noise. This is mainly because that the PEM clearly optimize an objective function and the NSPEM provides a more suitable way to determine the estimate of the state-space model. Figure 11 gives the estimated FRF \((\hbox {H}_{15})\) of the underlying linear system using the proposed method under the 20-dB noise. It is also shown that the estimated FRF of the underlying linear system is in good consistency with the theoretical one, verifying the accurate of the NSPEM.

Table 2 Comparison of the estimated nonlinear coefficients by the proposed method and the NSIM under different levels of noises (the cantilever beam structure)
Full size table
Fig. 11
figure 11

Estimated FRF (\(\hbox {H}_{15})\) of the underlying linear system for the cantilever beam structure under the 20 dB noise

Full size image

5 Conclusions

In this study, a new time-domain subspace identification approach named as the nonlinear subspace-prediction error method (NSPEM) is proposed for nonlinear system identifications. One of the major shortcomings of the nonlinear subspace identification method (NSIM) is that the estimated results generated by the NSIM are not the optimal solutions, leading to the decrease in the identified accuracy. To solve this shortcoming, an improved NSIM has been suggested in this paper. The proposed NSPEM utilizes the prediction error approach (PEM) to reestimate those estimated coefficient matrices of the state-space model after obtaining an initial system model with the application of the NSIM. The PEM employs a full parameterization of the state-space model with regularization to obtain the optimal identification results in the least square sense. Both the original NSIM and the proposed method have been used to identify the nonlinear vibrating structures, i.e., a six DOF discrete mass-spring-damper system with one local nonlinearity and a cantilever beam structure with two local nonlinearities. The results show that the proposed method has better identification results than the NSIM under a noise environment. It is confirmed that the proposed NSPEM is a promising tool for identifying nonlinear vibrating structures.