An improved approach for frequency-domain nonlinear identification through feedback of the outputs by using separation strategy

Abstract

This paper focuses on the problem of nonlinear system identification by proposing an improved approach for existing frequency-domain nonlinear identification through feedback of the outputs (NIFO) method via separation strategy. Suitable excitation level is difficult to select for the existing NIFO method, and coupling errors are usually caused by the large differences in the numerical magnitude between the excitation forces and the nonlinear description functions when both of them are simultaneously considered as an input vector. In this work, a nonlinear separation identification through feedback of the outputs (NSIFO) method is proposed to avoid the limitation of the selection range of the excitation level and reduce coupling errors of the existing NIFO method. The proposed method needs two excitation tests including the low-level excitation test and the high-level excitation test. The underlying linear frequency response function matrix is firstly identified under low-level excitation, and only nonlinear description functions are considered as an input to identify nonlinear parameters under high-level excitation by using separation strategy. Two numerical structural examples and a three-story experimental structure are, respectively, used to validate the effectiveness and feasibility of the proposed method via a comparative study focused on the identification of nonlinear systems. Numerical and experimental identification results finally demonstrate the superior achievable accuracy and stability of the proposed method compared to the existing NIFO method.

1 Introduction

Nonlinear systems exist widely in the real world, and their intrinsic nonlinear behavior is usually inevitable in engineering practices. For example, freeplay nonlinearity is inevitable for deployable structures due to the factors such as mismachining tolerance, assembly errors and abrasion [1,2,3]. Friction nonlinearity caused by contact and sliding between bodies with respect to each other exists widely in mechanical systems [4,5,6]. With the practical need of engineering applications, more and more researchers pay attention to the identification of nonlinear systems. Kerschen et al. [7] and Noël et al. [8] reviewed the research progress of nonlinear system identification in structural dynamics over the past decades and presented a critical survey of parameter estimation methods including linearization, time-domain, frequency-domain, time–frequency analysis, nonlinear modal analysis, black-box modeling and model updating methods. In recent years, frequency-domain methods have been widely used in parameter estimation of nonlinear systems. The reason is that processing data in the frequency domain can sometimes provide the possibility to focus on easier calculations and more intuitive interpretation [7]. In addition, frequency-domain processing can make it easier to focus on a specific frequency range, which can substantially reduce the computational burden involved in identification and thus accurately calculate a great number of nonlinear parameters [8].

In the frequency domain, the nonlinear identification through feedback of the outputs (NIFO) method was pointed out as a promising method in Ref. [7, 8]. Adams and Allemang completed the early research of the NIFO method. In 1999, Adams and Allemang [9] introduced a new and important perspective of nonlinearity as internal feedback forces that act together with the external excitation forces to generate the response of a nonlinear system and derived a new matrix formula of frequency response functions (FRFs) by introducing the dynamic equation of the nonlinear system in the frequency domain. Based on the frequency response relationships proposed in the previous article, they further proposed a new method of characterizing nonlinear structural dynamic systems in Ref. [10]. Thereafter, Adams and Allemang [11] developed the NIFO method by using internal feedback to consider the nonlinearity and viewing the nonlinear term as the additional excitation applied to the underlying linear system. In 2006, Spottswood and Allemang [12] extended the NIFO method to estimate nonlinear parameters by using experimental data in the reduced order space, and the nonlinear parameters are used in the assembly of reduced order models as a means of the predictive research before the formal experiments. Considering that the NIFO method treats the nonlinear forces as feedback inputs so that the inputs are larger than the outputs, Haroon and Adams [13] developed an modified H₂ algorithm with stronger robustness based on the NIFO method, which makes the amount of inputs equal to the amount of outputs by adding the correlated outputs equal in number to the nonlinear feedback forces to the original output vector of the system. Furthermore, Haroon et al. [14] developed a nonlinear system identification method in the absence of input measurements by coupling the NIFO and restoring force surface (RFS) methods, which was used to identify a cantilever beam system with adjustable clearance and contact stiffness in Ref. [15].

On the one hand, the NIFO method has the advantages of simultaneous estimation of underlying linear FRFs and multiple nonlinear parameters in a single step [11]. Besides, the linear and nonlinear parameters are naturally decoupled by feedback formulation, and the method is able to estimate nonlinear parameters at unforced as well as forced degrees-of-freedom (DOFs) with good adjustment and computational efficiency [11]. The NIFO method has been applied to a vehicle suspension system in Ref. [16] and has shown good capability of encoding frequency dependence in the parameters. On the other hand, the NIFO method also has some limitations. For instance, a priori form of the nonlinearity has to be specified before using this method [16]. The root mean square (RMS) value of Gaussian random excitation needs to be specified in order to ensure that the nonlinear factor is weak to medium [11], and the selection of the excitation RMS value has great influence on the identification results of underlying linear FRFs and nonlinear parameters.

In addition to the NIFO method mentioned above, several nonlinear identification methods have been recently developed based on the idea of treating nonlinear forces as feedback inputs [8], such as time-domain subspace method [17] and frequency-domain subspace method [18]. Regarding these methods based on the feedback perspective, the excitation forces (corresponding to the linear part) and the nonlinear description functions (corresponding to the nonlinear part) are simultaneously considered as an input vector, which may result in coupling errors due to large numerical magnitude differences in case the nonlinear feedbacks are not properly scaled. Furthermore, it is difficult to choose an appropriate excitation level to obtain accurate identification results. In order to reduce the coupling errors, Liu et al. [19] proposed a separation strategy by, respectively, identifying the underlying linear FRFs under low-level excitation and nonlinear parameters under high-level excitation in two steps and enhanced the capability of the time-domain subspace method by implementing the separation strategy. Besides, a two-stage time domain method was proposed to identify the linear part and the nonlinear part by conducting two tests under low-level excitation and high-level excitation to alleviate possible numerical problems [20]. This work aims to propose an improved NIFO method by using the idea of the separation strategy, in order to reduce the coupling errors, avoid the limitation of the selection range of the excitation level, and improve the identification accuracy of the existing NIFO method.

The paper begins by reviewing the existing NIFO method in Sect. 2 and proposing a novel improved NIFO method via separation strategy in Sect. 3. The proposed method is numerically validated by identification of two nonlinear structural systems in Sect. 4. In Sect. 5, a three-story experimental structure with clearance nonlinearity is built to conduct identification experiments and further validate the capability of the proposed method. Section 6 summarizes the study.

2 Existing NIFO method

As a frequency-domain method for nonlinear system identification, the existing NIFO method is able to identify FRFs of the underlying linear system and nonlinear parameters in one step by treating the nonlinearity term as the feedback forces [11]. Before proposing the improved NIFO method via separation strategy, we begin by reviewing the existing NIFO method in this section.

The equation of motion of a structural system with $h$ DOFs with general localized nonlinear structure can be expressed in the following form

$$ {\varvec{M}}\ddot{\varvec{z}}(t) + {\varvec{C}}_{v} \dot{\varvec{z}}(t) + {\varvec{Kz}}(t) + \sum\limits_{j = 1}^{p} {\mu_{j} {\varvec{L}}_{nj} } g_{j} (t) = {\varvec{f}}(t) = {\varvec{L}}_{f} {\varvec{F}}(t) $$

(1)

where ${\varvec{M}}$, ${\varvec{C}}_{v}$ and ${\varvec{K}}$ are, respectively, the mass, viscous damping and stiffness matrices. ${\varvec{z}}(t)$, $\dot{\varvec{z}}(t)$ and ${\ddot{z}}(t)$ denote, respectively, the displacement, velocity and acceleration vectors, and ${\varvec{f}}(t)$ is the force vector, both of dimension $h$. ${\varvec{F}}(t)$ is the external excitation, and ${\varvec{L}}_{f}$ is the location vector of the external excitation. The nonlinear term $\sum\nolimits_{j = 1}^{p} {\mu_{j} {\varvec{L}}_{nj} } g_{j} (t)$ is expressed as the sum of $p$ components and each of them depending on the scalar nonlinear function $g_{j} (t)$, which indicates the type of the nonlinearity, through a location vector ${\varvec{L}}_{nj}$, which indicates the location of the nonlinear element. ${\varvec{L}}_{f}$ and ${\varvec{L}}_{nj}$ are constants whose values are  −1, 0 and 1. $\mu_{j} g_{j} (t)$ is the local nonlinearity and $\mu_{j}$ is the nonlinear parameter to-be-identified.

By moving the nonlinear term to the right-hand side of (1), we have

$$ {\varvec{M}}\ddot{\varvec{z}}(t) + {\varvec{C}}_{v} \dot{\varvec{z}}(t) + {\varvec{Kz}}(t) = {\varvec{L}}_{f} {\varvec{F}}(t) - \sum\limits_{j = 1}^{p} {\mu_{j} {\varvec{L}}_{nj} } g_{j} (t) = {\varvec{f}}(t) + {\varvec{f}}_{nl} (t) $$

(2)

Equation (2) represents the idea of the NIFO method, that is, the nonlinear term is viewed as the underlying additional excitation [11]. In other words, the measured outputs of a nonlinear system can be regarded as outputs produced by a underlying linear model of the system acted together with the external excitation forces ${\varvec{f}}(t)$ and the internal feedback forces ${\varvec{f}}_{nl} (t)$.

The frequency-domain version of (2) is obtained by taking the following Fourier transforms

$$ ({\varvec{K}} + i\omega {\varvec{C}}_{v} - \omega^{2} {\varvec{M}}){\varvec{Z}}(\omega ) = {\varvec{F}}(\omega ) - \sum\limits_{j = 1}^{p} {\mu_{j} {\varvec{L}}_{nj} {\varvec{G}}_{j} (\omega ) = {\varvec{F}}(\omega ) + {\varvec{F}}_{nl} (\omega )} $$

(3)

where ${\text{i}} = \sqrt { - 1}$. In this equation, capital letters denote Fourier transforms, and the Fourier transform can transform time-domain data into frequency-domain data, i.e., ${\varvec{Z}}(\omega ) = {\mathcal{F}}({\varvec{z}}(t))$, ${\varvec{F}}(\omega ) = {\mathcal{F}}({\varvec{f}}(t))$, ${\varvec{F}}_{nl} (\omega ) = {\mathcal{F}}({\varvec{f}}_{nl} (t))$ and ${\varvec{G}}_{j} (\omega ) = {\mathcal{F}}(g_{j} (t ))$.

The underlying linear FRF matrix is

$$ {\varvec{H}}_{L} (\omega ) = ({\varvec{K}} + i\omega {\varvec{C}}_{v} - \omega^{2} {\varvec{M}})^{ - 1} $$

(4)

Equation (3) can be rewritten into

$$ {\varvec{B}}_{L} (\omega ){\varvec{Z}}(\omega ) = {\varvec{F}}(\omega ) - \mathop \sum \limits_{{j = {1}}}^{p} \mu_{j} {\varvec{L}}_{nj} {\varvec{G}}_{j} (\omega ) = {\varvec{F}}(\omega ) + {\varvec{F}}_{nl} (\omega ) $$

(5)

where ${\varvec{B}}_{L} (\omega )$ is the linear impedance matrix.

Multiplying both sides of (5) on the left by the underlying linear FRF matrix ${\varvec{H}}_{L} (\omega )$, and separating the measured and unmeasured quantities, we have the set of linear equations at each frequency as follows

$$ {\varvec{Z}}(\omega ) = \left[ {{\varvec{H}}_{L} (\omega ){\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\varvec{H}}_{L} (\omega )\mu_{1} {\varvec{L}}_{n1} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\varvec{H}}_{L} (\omega )\mu_{2} {\varvec{L}}_{n2} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} \cdots {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\varvec{H}}_{L} (\omega )\mu_{p} {\varvec{L}}_{np} } \right]\left\{ {\begin{array}{*{20}c} {{\varvec{F}}(\omega )} \\ { - \left( {\begin{array}{*{20}c} {{\varvec{G}}_{1} (\omega )} \\ {{\varvec{G}}_{2} (\omega )} \\ \vdots \\ {{\varvec{G}}_{p} (\omega )} \\ \end{array} } \right)} \\ \end{array} } \right\} $$

(6)

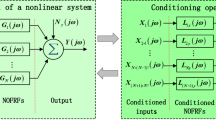
Equation (6) is similar to a multiple input multiple output (MIMO) linear model in the frequency domain, which is the kernel equation of the NIFO method. It follows that the NIFO method has the ability to handle multiple nonlinearities simultaneously. Therefore, the extended input vector of the MIMO system becomes

$$ {\varvec{F}}_{E} (\omega ) = \left[ {\begin{array}{*{20}c} {{\varvec{F}}(\omega )} & { - {\varvec{G}}_{1} (\omega )} & { - {\varvec{G}}_{2} (\omega )} & \cdots & { - {\varvec{G}}_{p} (\omega )} \\ \end{array} } \right]^{{\text{T}}} $$

(7)

The extended FRF matrix of the MIMO system becomes

$$ {\varvec{H}}_{E} (\omega ) = \left[ {{\varvec{H}}_{L} (\omega ){\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\varvec{H}}_{L} (\omega )\mu_{1} {\varvec{L}}_{n1} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\varvec{H}}_{L} (\omega )\mu_{2} {\varvec{L}}_{n2} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} \cdots {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\varvec{H}}_{L} (\omega )\mu_{p} {\varvec{L}}_{np} } \right] $$

(8)

Equation (6) at each frequency can be written as

$$ {\varvec{Z}}(\omega ) = {\varvec{H}}_{E} (\omega ){\varvec{F}}_{E} (\omega ) $$

(9)

By running the measurement $N_{avg}$ repeatedly or dividing a measurement into $N_{avg}$ parts [17], Eq. (9) can be assembled as

$$ \left[ {\begin{array}{*{20}c} {{\varvec{Z}}^{1} (\omega )} & {{\varvec{Z}}^{2} (\omega )} & \cdots & {{\varvec{Z}}^{{N_{avg} }} (\omega )} \\ \end{array} } \right] = {\varvec{H}}_{E} (\omega ) \cdot \left[ {\begin{array}{*{20}c} {{\varvec{F}}_{E}^{1} (\omega )} & {{\varvec{F}}_{E}^{2} (\omega )} & \cdots & {{\varvec{F}}_{E}^{{N_{avg} }} (\omega )} \\ \end{array} } \right] $$

(10)

By solving the set of equations using the best least-squares estimate, ${\varvec{H}}_{E} (\omega )$ can be obtained

$$ {\varvec{H}}_{E} (\omega ) = \left[ {\begin{array}{*{20}c} {{\varvec{Z}}^{1} (\omega )} & {{\varvec{Z}}^{2} (\omega )} & \cdots & {{\varvec{Z}}^{{N_{avg} }} (\omega )} \\ \end{array} } \right] \cdot \left[ {\begin{array}{*{20}c} {{\varvec{F}}_{E}^{1} (\omega )} & {{\varvec{F}}_{E}^{2} (\omega )} & \cdots & {{\varvec{F}}_{E}^{{N_{avg} }} (\omega )} \\ \end{array} } \right]^{\dag } $$

(11)

where the symbol † denotes pseudoinverse.

Once ${\varvec{H}}_{E} (\omega )$ has been estimated, the underlying linear FRF matrix ${\varvec{H}}_{L} (\omega )$ and nonlinear parameter $\mu_{j}$ can be obtained from Eq. (8) according to the reciprocity of the linear FRF matrix. The existing NIFO method needs to select the input level so that the nonlinear factor is weak to medium [11], resulting in a limited selection of the input range. In case the nonlinear factor is relatively weak, FRFs of the underlying linear system may be well identified at the price of poor identification accuracy of nonlinear parameters. Stronger nonlinear factor helps to better identify nonlinear parameters, but it does this at the expense of reducing the identification accuracy of the underlying linear FRFs. The reason is that the coupling errors occur in the calculation process when the numerical magnitude of the excitation forces and the nonlinear description functions differ greatly [19]. It also means that if the selection of the input level is not appropriate, the identification results of the underlying linear FRFs and nonlinear parameters cannot be guaranteed simultaneously. Therefore, it is usually not easy to implement this method when dealing with nonlinear system identification of real structures.

3 Improved NIFO method via separation strategy

In order to overcome the deficiency of the existing NIFO method, a novel improved NIFO method via separation strategy, referred to as nonlinear separation identification through feedback of the outputs (NSIFO) method, is proposed in this section. The key idea of the separation strategy is to identify the underlying linear FRFs and nonlinear parameters separately [19, 21,22,23]: Firstly, the underlying linear FRF matrix is identified under low-level excitation, as the weaker the nonlinearity caused by the excitation, the closer the frequency response recognition is to the true value. Generally, this is valid for stiffness nonlinearity as the corresponding nonlinear behavior is weaker for low-amplitude motions, but not for the nonlinearity dominated by low-level excitation, such as friction nonlinearity. Secondly, the nonlinear parameters are identified under high-level excitation, as larger applied forces are necessary to well excite the nonlinearity of the system. By using the separation strategy, the coupling errors can be reduced and hence, the proposed NSIFO method is able to achieve superior accuracy than the existing NIFO method, even if the numerical magnitude of the inputs and the nonlinear description functions differ greatly.

The proposed NSIFO method needs to conduct two tests of low-level excitation and high-level excitation, respectively. Firstly, low-level excitation is applied to the nonlinear system to obtain the underlying linear FRF matrix. Secondly, high-level excitation is applied to the same nonlinear system and its response is divided into linear response parts and nonlinear response parts by using the separation strategy. The nonlinear system can be viewed as the combination of the nonlinear part and underlying linear part. According to the principle of nonlinear identification through outputs feedback, the excitation forces and feedback forces in the extended input vector can be regarded as acting on the underlying linear system simultaneously [19].

Equation (6) can be rewritten as

$$ \begin{aligned} {\varvec{Z}}_{{{\text{high}}}} (\omega ) = & \underbrace {{{\varvec{H}}_{L} (\omega ){\varvec{F}}_{{{\text{high}}}} (\omega )}}_{{{\varvec{Z}}_{L} (\omega )}} + \underbrace {{{\varvec{H}}_{L} (\omega )\mu_{1} {\varvec{L}}_{n1} \cdot ( - {\varvec{G}}_{1} (\omega )) + {\varvec{H}}_{L} (\omega )\mu_{2} {\varvec{L}}_{n2} \cdot ( - {\varvec{G}}_{2} (\omega )) + \cdots + {\varvec{H}}_{L} (\omega )\mu_{p} {\varvec{L}}_{np} \cdot ( - {\varvec{G}}_{p} (\omega ))}}_{{{\varvec{Z}}_{{{\text{NL}}}} (\omega )}} \\ = & {\varvec{Z}}_{L} (\omega ) + {\varvec{Z}}_{{{\text{NL}}}} (\omega ) \\ \end{aligned} $$

(12)

According to (12), the output response in frequency domain can be regarded as the linear response ${\varvec{Z}}_{L} (\omega )$ caused by the action of the excitation forces and the nonlinear response ${\varvec{Z}}_{NL} (\omega )$ caused by the action of the feedback forces.

The implementation of proposed NSIFO method can be divided into three steps:

Firstly, the underlying linear FRF matrix ${\varvec{H}}_{L} (\omega )$ of a nonlinear system is obtained by using linear estimation methods and the linear response part of the nonlinear system is calculated. In this work, the underlying linear FRF matrix ${\varvec{H}}_{L} (\omega )$ is obtained by the linear least squares approach under low-level excitation, as follows

$$ {\varvec{H}}_{L} (\omega ){\kern 1pt} = {\varvec{Z}}_{low} (\omega ){\varvec{F}}_{low} (\omega )^{\dag } $$

(13)

For the underlying linear system, ${\varvec{H}}_{L} (\omega )$ is only related to the intrinsic characteristics of the system itself (such as mass, damping, stiffness matrices). It also means that ${\varvec{H}}_{L} (\omega )$ is an invariant matrix regardless of the type and level of excitation. The response of the nonlinear system under high-level excitation is separated into two parts: the linear response part caused by the excitation forces and the nonlinear response part caused by the feedback forces. Once ${\varvec{H}}_{L} (\omega )$ is known, the linear response part of the nonlinear system can be calculated by the following general frequency-domain linear model

$$ {\varvec{Z}}_{L} (\omega ) = {\varvec{H}}_{L} (\omega ){\kern 1pt} {\varvec{F}}_{high} (\omega ) $$

(14)

Secondly, once the linear response part ${\varvec{Z}}_{L} (\omega )$ of the nonlinear system has been obtained, the nonlinear response part ${\varvec{Z}}_{NL} (\omega )$ can be computed as follows

$$ {\varvec{Z}}_{NL} (\omega ) = {\varvec{Z}}_{high} (\omega ) - {\varvec{Z}}_{L} (\omega ) $$

(15)

Finally, the nonlinear parameters are estimated by using the existing NIFO method. The nonlinear describing functions and the nonlinear response part become new extended input and output vector, respectively. Accordingly, the kernel equation of the NIFO method can be rewritten as

$$ {\varvec{Z}}_{NL} (\omega ) = \left[ {{\varvec{H}}_{L} (\omega )\mu_{1} {\varvec{L}}_{n1} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\varvec{H}}_{L} (\omega )\mu_{2} {\varvec{L}}_{n2} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} \cdots {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\varvec{H}}_{L} (\omega )\mu_{p} {\varvec{L}}_{np} } \right]\left\{ { - \left( {\begin{array}{*{20}c} {{\varvec{G}}_{1} (\omega )} \\ {{\varvec{G}}_{2} (\omega )} \\ \vdots \\ {{\varvec{G}}_{p} (\omega )} \\ \end{array} } \right)} \right\} $$

(16)

As a result, the new extended input vector becomes

$$ \tilde{{F}}_{E} (\omega ) = \left[ {\begin{array}{*{20}c} { - {\varvec{G}}_{1} (\omega )} & { - {\varvec{G}}_{2} (\omega )} & \cdots & { - {\varvec{G}}_{p} (\omega )} \\ \end{array} } \right]^{{\text{T}}} $$

(17)

The new extended FRF matrix becomes

$$ \begin{aligned} \tilde{{H}}_{E} (\omega )& = \left[ {\begin{array}{*{20}c} {{\varvec{H}}_{L} (\omega )\mu_{1} {\varvec{L}}_{n1} } & {{\varvec{H}}_{L} (\omega )\mu_{2} {\varvec{L}}_{n2} } & \cdots & {{\varvec{H}}_{L} (\omega )\mu_{p} {\varvec{L}}_{np} } \\ \end{array} } \right] \hfill \\ {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} \\ &= {\varvec{H}}_{L} (\omega )\left[ {\begin{array}{*{20}c} {\mu_{1} {\varvec{L}}_{n1} } & {\mu_{2} {\varvec{L}}_{n2} } & \cdots & {\mu_{p} {\varvec{L}}_{np} } \\ \end{array} } \right] \hfill \\ \end{aligned} $$

(18)

By solving the set of equations using the best least-squares estimate, $\tilde{{H}}_{E} (\omega )$ can be estimated by

$$ \tilde{{H}}_{E} (\omega ) = {\varvec{Z}}_{NL} (\omega ) \cdot \tilde{{F}}_{E} (\omega )^{\dag } $$

(19)

Similar to the existing NIFO method, once the extended FRF matrix $\tilde{{H}}_{E} (\omega )$ has been estimated, nonlinear parameters can be finally identified.

As given by (11), the existing NIFO method involves only one matrix inversion operation, and the proposed NSIFO method needs to perform the similar matrix inversion operation twice, as given by (13) and (19). However, the computational complexity of the NSIFO method is lower, as the dimensionalities of the input vectors in (13) and (19) are, respectively, ${\varvec{F}}_{low} (\omega ) \in {\mathbb{R}}^{h \times 1}$ and $\tilde{{F}}_{E} (\omega ) \in {\mathbb{R}}^{p \times 1}$, which are smaller than ${\varvec{F}}_{E} (\omega ) \in {\mathbb{R}}^{(h + p) \times 1}$ in (11). The reason is that the excitation forces and nonlinear description functions are, respectively, used as the input vector in (13) and (19), but they are simultaneously considered as the input vector in (11).

As mentioned in the previous sections, the main steps of the existing NIFO method are summarized in Fig. 1. It can be found that the existing NIFO method consists of only one step and the high-level excitation is directly used to arouse the nonlinear factors. As a contrast, Fig. 2 shows the main steps of the proposed NSIFO method. It can be seen that the new method includes two steps, namely low-level excitation test and high-level excitation test. The separation strategy of the NSIFO method divides the nonlinear response into the linear response part and nonlinear response part and is able to reduce the coupling errors when a large magnitude difference is caused by simultaneously processing the excitation forces and the nonlinear forces [19]. In other words, the selection of the input level is no longer strictly limited, and the proposed NSIFO method is able to achieve superior accuracy by using the separation strategy.

Fig. 1

Flow diagram of the existing NIFO method

Fig. 2

Flow diagram of the proposed NSIFO method

It should be further stressed that the first step of proposed NSIFO method is to obtain the linear response part of the nonlinear system, while the key of obtaining the linear response part is to obtain the underlying linear FRF matrix. Both finite element analysis and vibration testing on the dynamic system can be utilized to obtain characteristic matrices of underlying linear system, but these methods may be difficult to apply in practice due to some factors, such as modeling errors, the coupling relationship of components and so on [19]. Fortunately, the nonlinear factor is usually weak enough under low-level excitation for some nonlinear types, and the nonlinear system can be regarded as an underlying linear system to calculate the underlying linear FRF matrix. In particular, the dynamic behavior of the system is linear when the nonlinearity is a clearance type and the excitation is small enough, in case the maximum displacement at the nonlinear position is less than the clearance value.

4 Numerical validation

4.1 Example 1: three DOFs structure with clearance nonlinearity

As a common nonlinear phenomenon, clearance exists widely in many mechanical structures. The presence of clearance changes the normal dynamic response and may lead to difficulties in predicting the dynamic response and result in low precision and short lifetime in engineering structures. Therefore, it is very critical to identify the clearance value and the relevant nonlinear parameters, which is also a necessary condition to eliminate and control the clearance [24]. In this section, a numerical example with clearance nonlinearity is used to illustrate the procedure and performance of the proposed NSIFO method.

A three DOFs structure with clearance nonlinearity is shown in Fig. 3, whose dynamic equation can be described as follows

$$ {\varvec{M}}\ddot{\varvec{z}}(t) + {\varvec{C}}_{v} \dot{{z}}(t) + {\varvec{Kz}}(t) + \mu {\varvec{L}}_{n} g(t) = {\varvec{f}}(t) = {\varvec{L}}_{f} {\varvec{F}}(t) $$

(20)

where ${\varvec{M}}$, ${\varvec{C}}_{v}$ and ${\varvec{K}}$ are, respectively, the mass, viscous damping and stiffness matrices of the three DOFs structure. ${\varvec{z}}(t)$,$\dot{{z}}(t)$ and ${\ddot{z}}(t)$ denote, respectively, the displacement, velocity and acceleration vectors, and ${\varvec{f}}(t)$ is the force vector. ${\varvec{F}}(t)$ is the external excitation, and ${\varvec{L}}_{f} { = }\left[ {\begin{array}{*{20}c} {0} & {1} & {0} \\ \end{array} } \right]^{{\text{T}}}$ is the location of the external excitation.

Fig. 3

A three DOFs structure with clearance nonlinearity

The nonlinear force vector ${\varvec{f}}_{nl} (t)$ is described by

$$ {\varvec{f}}_{nl} (t) = \mu {\varvec{L}}_{n} g(t) = k_{c} \left[ {\begin{array}{*{20}c} 0 \\ 1 \\ 0 \\ \end{array} } \right]g(t) $$

(21)

where $\mu = k_{c}$ is contact stiffness of clearance nonlinearity, ${\varvec{L}}_{n} { = }\left[ {\begin{array}{*{20}c} {0} & {1} & {0} \\ \end{array} } \right]^{{\text{T}}}$ is the location of the clearance nonlinearity, and $g(t)$ is the nonlinear description function.

The clearance nonlinear description function can be defined as

$$ g(t) = \left\{ {\begin{array}{*{20}l} {z_{2} (t) - d_{c} ,} \hfill & {z_{2} (t) > d_{c} } \hfill \\ {0,} \hfill & {z_{2} (t) \le d_{c} } \hfill \\ \end{array} } \right. $$

(22)

where $d_{c}$ is clearance value.

The above numerical system is utilized to verify the reliability of the proposed NSIFO method. System parameters are summarized in Table 1. By numerical integration of the equation of motion using the Runge–Kutta method with a time step of $\Delta t{ = 10}^{{ - {3}}} {\text{s}}$, response samples with the length of 10⁵ are generated after a total time of $T{\text{ = 100s}}$ with zero-mean Gaussian random excitation being the input.

Table 1 System parameters of the numerical example

On the one hand, the low-level and high-level excitation cannot be described quantitatively from the perspective of method derivation. But, the most important principle for choosing excitation magnitude is that nonlinearity should be weak enough under low-level excitation and well excited under high-level excitation. On the other hand, the excitation magnitude can be reasonably chosen on a case by case basis. For example, the dynamic behavior of the numerical system is linear when the nonlinearity is a clearance type and the excitation is small enough. In such case, the excitation magnitude can be easily determined by comparing the maximum displacement at the nonlinear position and the clearance value. The maximum displacement at the nonlinear position should be smaller than the clearance value under low-level excitation, so as to obtain the underlying linear FRFs with good accuracy. In contrast, the maximum displacement at the nonlinear position should exceed the clearance value under high-level excitation to well arouse the clearance nonlinearity.

The displacement responses of the numerical example are, respectively, obtained under high-level excitation and low-level excitation and denoted by the blue-solid and green-dotted lines, as shown in Fig. 4, where the red-dashed line is the position of the clearance value. As we can see from Fig. 4, the displacement response under low-level excitation is small and within the range of clearance, which means the system is linear without any nonlinear factors. In case high-level excitation is applied, the displacement response exceeds the clearance, and the nonlinear factor of the system is aroused.

Fig. 4

Displacement responses at the clearance position under high-level excitation and low-level excitation

Regarding the above nonlinear system with clearance, parameters to-be-identified include clearance value and contact stiffness, and the identification of clearance value is the premise of identifying contact stiffness. The accuracy of clearance value identification is very important, because a small error in clearance value identification will lead to a large error in contact stiffness identification [24]. At present, many methods for clearance identification have been developed, including the derivative plot of probability density function (DPPDF) method [24], the trilinear function method [17] and the RFS method [15], etc. In this section, the DPPDF method is used to estimate the clearance value, as this method can avoid the cumbersome and repeated procedure of determining nonlinear description functions. Li et al. [24] indicated that the distribution of response around the clearance value is unique due to the presence of the clearance; hence, concavity or convexity exists near the clearance value in the probability density function (PDF) plot. The concavity or convexity in the PDF plot is hard to directly estimate the exact clearance value. But by taking the second derivative of the PDF, the clearance value can be determined by choosing the horizontal axis value of the turning point. As shown in Fig. 5, the clearance value of the numerical example is identified as $\hat{d}_{c} = 0.0009656\;{\text{m}}$ with the error of 3.4% based on the displacement response at the clearance location under high-level excitation. Generally, the DPPDF method can further improve the accuracy of the identified clearance value by adjusting the sampling frequency and the excitation forces [24]. If there is no prior information about the nonlinear description function, the polynomial method [25] and the spline adaptive nonlinear identification method [26, 27] may be referred.

Fig. 5

The second derivative plot of the PDF of the displacement response at the clearance location

The excitation and response signals are divided into $N_{avg}$ segments with the overlap of each segment being 91%, which helps to decrease the random error in the estimates when using the data that is attenuated due to the windowing technique [11]. And then, the time-domain data are converted to the frequency domain by fast Fourier transform. The RMS values of the high-level excitation force and low-level excitation force are, respectively, 14.4750 N and 0.5136 N. The H₁ estimation method is directly utilized to calculate the FRFs of the numerical example under high-level excitation and low-level excitation, respectively. The FRF $H_{{{3}3}}$ curve of the numerical example is represented by blue-solid and green-dotted lines, respectively, as shown in Fig. 6, where the red-dashed line represents the true underlying linear FRF $H_{{{3}3}}$ curve. The first subscript of $H_{{{3}3}}$ represents the location of the measured displacement, and the second subscript represents the location of the applied excitation force. It can be seen that the estimated FRF curve is distorted with the increase in nonlinear factors under high-level excitation. However, the estimated FRF curve is almost identical to the true underlying linear FRF curve under low-level excitation, as the displacement response is smaller than the clearance value and the system can still be regarded as a linear system without nonlinear behavior.

Fig. 6

The FRF H₃₃ curve of the first example under high-level excitation and low-level excitation

The existing NIFO method and the proposed NSIFO method are used to estimate the underlying linear FRFs and nonlinear parameters. Regarding the existing NIFO method, the excitation force and the nonlinear description function are simultaneously processed as the input vector and their RMS values are, respectively, 14.4750 N and ${3}{\text{.2037}} \times {10}^{{ - 5}}$ m. It can be found that the two numerical magnitudes differ greatly and larger coupling errors may be caused in the identification progress. Figures 7 and 8 show the whole and local plots of the underlying linear FRF curve of the numerical example identified by the NIFO and NSIFO method, respectively. It can be observed that the identification results of the two methods approximately coincide with the true values except for the peak positions. But the identification results of the NSIFO method are much closer to the true values and evidently better than those of the NIFO method at the peaks, which indicate that the proposed NSIFO method is able to achieve superior identification accuracy of underlying linear FRFs. It should be noted that direct outputs of both NIFO and NSIFO method are the underlying linear FRFs instead of the underlying modal parameters. Currently, there are many well-known methods (such as least squares complex frequency domain method) to extract modal parameters from FRFs, which is beyond the scope of this work. As we know, better estimation of the underlying linear FRFs by the NSIFO method than the NIFO method means better estimation of the underlying modal parameters, because the procedure from FRFs to modal parameters for the two methods is same.

Fig. 7

The underlying linear FRF H₃₃ curve of the first example: NIFO estimate (blue-solid line), NSIFO estimate (green-dotted line) and true underlying linear FRF (red-dashed line)

Fig. 8

The underlying linear FRF H₂₃ curve of the first example: NIFO estimate (blue-solid line), NSIFO estimate (green-dotted line) and true underlying linear FRF (red-dashed line)

The real and imaginary parts of contact stiffness identified by the NIFO and NSIFO method are, respectively, shown in Fig. 9. Real and imaginary parts come from the identification methodology, which gives the nonlinear parameters essentially as a ratio between FRFs. As we know, the contact stiffness in the numerical system is constant with the true value of $k_{c} = 10^{6} {\text{N/m}}$, which means the estimated real part should be close to the true value and the estimated imaginary part should be close to zero. The nonlinear parameter $\mu$ of the numerical example is constant and should not change with the frequency. Evidently, the identified value by the proposed NSIFO method is significantly smoother than its counterpart by the NIFO method. In order to quantify the accuracy of contact stiffness identification results, the evaluation index of errors is introduced as

$$ {\text{Error}} = 100 \times \frac{{\left( {\hat{k}_{c} - \overline{k}_{c} } \right)}}{{\overline{k}_{c} }}\% $$

(23)

where $\hat{k}_{c}$ represents estimated value of contact stiffness of clearance nonlinearity, $\overline{k}_{c}$ represents the true value in the numerical example. The estimation errors of the contact stiffness are displayed in Fig. 10, which further demonstrate that the proposed NSIFO method is able to achieve better accuracy in identifying nonlinear parameters.

Fig. 9

Real and imaginary parts of the estimated contact stiffness $k_{c}$ of the first example: NIFO estimate (blue-solid line), NSIFO estimate (green-dotted line) and true value (red-dashed line)

Fig. 10

Estimation errors of the contact stiffness $k_{c}$: NIFO estimate (blue-solid line), NSIFO estimate (green-dotted line)

In addition, the mean value and standard deviation of the real part of contact stiffness identified by the NIFO method are 1.0036 × 10⁶ N/m and 1.2023 × 10⁵ N/m in Fig. 9, where the mean value and standard deviation of the real part of contact stiffness identified by the NSIFO method are 1.0011 × 10⁶ N/m and 1.5743 × 10⁴ N/m. Although the mean values of the estimates by the two methods are relatively close, the standard deviation of the estimates by the NSIFO method is significantly smaller than the NIFO method. In other words, the estimates by the NSIFO method have smaller fluctuation and variance. Figure 11 illustrates the clearance nonlinear characteristic curves reconstructed based on mean values of the real part of contact stiffness, which indicate that both methods can reconstruct the accurate nonlinear characteristics, but the proposed NSIFO method may have better accuracy and higher stability by taking the smaller variance of the contact stiffness estimates into consideration.

Fig. 11

Reconstruction of the clearance nonlinear characteristic curve: NIFO estimate (blue circles), NSIFO estimate (green crosses) and true value (red dots)

The performance of the proposed NSIFO method is further illustrated by considering the noise effects. Displacement responses are here contaminated by noise with the signal-to-noise ratio (SNR) being 40 dB. The NIFO and NSIFO method is, respectively, used to identify the nonlinear system based on data contaminated by noise. Figures 12 and 13 show the estimated underlying linear FRF $H_{{{3}3}}$ curve and real and imaginary parts of contact stiffness of the numerical example with noise contamination, respectively. Compared to the identification results in Figs. 7 and 9, both the NIFO and NSIFO methods obtain worse results after adding noise to the displacement responses. However, the enhanced capability of the proposed NSIFO method is also validated in such case, as it can achieve much better identification results than the existing NIFO method.

Fig. 12

The underlying linear FRF H₃₃ curve of the first example with noise contamination: NIFO estimate (blue-solid line), NSIFO estimate (green-dotted line) and true underlying linear FRF (red-dashed line)

Fig. 13

Real and imaginary parts of the estimated contact stiffness $k_{c}$ of the first example with noise contamination: NIFO estimate (blue-solid line), NSIFO estimate (green-dotted line) and true value (red-dashed line)

4.2 Example 2: three DOFs structure with clearance and cubic stiffness nonlinearity

In this section, clearance and cubic stiffness nonlinearity are simultaneously included in the nonlinear numerical example. The performance of the proposed NSIFO method is here illustrated when the system has multiple sources of nonlinearity.

A three DOFs structure with clearance and cubic stiffness nonlinearity is shown in Fig. 14, whose dynamic equation can be described as follows

$$ {\varvec{M}}\ddot{\varvec{z}}(t) + {\varvec{C}}_{v} \dot{{z}}(t) + {\varvec{Kz}}(t) + \mu_{1} {\varvec{L}}_{{n_{1} }} g_{1} (t) + \mu_{2} {\varvec{L}}_{{n_{2} }} g_{2} (t) = {\varvec{f}}(t) = {\varvec{L}}_{f} {\varvec{F}}(t) $$

(24)

where $\mu_{1} = k_{c}$ is contact stiffness of clearance nonlinearity, ${\varvec{L}}_{{n_{1} }} { = }\left[ {\begin{array}{*{20}c} {0} & {1} & {0} \\ \end{array} } \right]^{{\text{T}}}$ is the location of the clearance nonlinearity, and $g_{1} (t)$ is the clearance nonlinear description function; $\mu_{2} = k_{n}$ is stiffness of cubic nonlinearity, ${\varvec{L}}_{{n_{2} }} { = }\left[ {\begin{array}{*{20}c} {0} & 0 & {1} \\ \end{array} } \right]^{{\text{T}}}$ is the location of the cubic nonlinearity, and $g_{2} (t)$ is the cubic nonlinear description function.

Fig. 14

A three DOFs structure with clearance and cubic stiffness nonlinearity

The nonlinear force vectors ${\varvec{f}}_{{nl_{1} }} (t)$ and ${\varvec{f}}_{{nl_{2} }} (t)$ are, respectively, described by

$$ \mu_{1} {\varvec{L}}_{{n_{1} }} g_{1} (t) = k_{c} \left[ {\begin{array}{*{20}c} 0 \\ 1 \\ 0 \\ \end{array} } \right]\left\{ {\begin{array}{*{20}l} {z_{2} (t) - d_{c} ,} \hfill & {z_{2} (t) > d_{c} } \hfill \\ {0,} \hfill & {z_{2} (t) \le d_{c} } \hfill \\ \end{array} } \right.,\;\;\mu_{2} {\varvec{L}}_{{n_{2} }} g_{2} (t) = k_{n} \left[ {\begin{array}{*{20}c} 0 \\ 0 \\ 1 \\ \end{array} } \right]z_{3}^{2} (t) $$

(25)

As given by Table 1, the system parameters are the same as the first example in Sect. 4.1 and the value of the cubic stiffness is $k_{n} = 5 \times 10^{6} {\text{N/m}}^{3}$. Figure 15 shows the estimated underlying linear FRF $H_{{{3}3}}$ curve of the numerical example identified by the NIFO and NSIFO method, against their true counterpart. It can be observed that the identification results of the NSIFO method are much closer to the true values and evidently better than those of the NIFO method at the peak positions, which indicate that the proposed NSIFO is able to achieve superior identification accuracy of underlying linear FRFs for system with multiple sources of nonlinearity.

Fig. 15

The underlying linear FRF H₃₃ curve of the second example: NIFO estimate (blue-solid line), NSIFO estimate (green-dotted line) and true underlying linear FRF (red-dashed line)

The real and imaginary parts of contact stiffness and cubic stiffness identified by the NIFO and NSIFO method are, respectively, shown in Figs. 16 and 17. For both contact stiffness and cubic stiffness, the identified values by the proposed NSIFO method are better than their counterparts by the NIFO method. Their estimation errors are, respectively, displayed in Figs. 18 and 19, which further demonstrates that the proposed NSIFO method is able to achieve better accuracy in identifying nonlinear parameters. Different nonlinear characteristic curves are, respectively, reconstructed based on mean values of the real part of contact stiffness and cubic stiffness, as shown in Figs. 20 and 21.

Fig. 16

Real and imaginary parts of the estimated contact stiffness $k_{c}$ of the second example: NIFO estimate (blue-solid line), NSIFO estimate (green-dotted line) and true value (red-dashed line)

Fig. 17

Real and imaginary parts of the estimated cubic stiffness $k_{n}$ of the second example: NIFO estimate (blue-solid line), NSIFO estimate (green-dotted line) and true value (red-dashed line)

Fig. 18

Estimation errors of the contact stiffness $k_{c}$: NIFO estimate (blue-solid line), NSIFO estimate (green-dotted line)

Fig. 19

Estimation errors of the cubic stiffness $k_{n}$: NIFO estimate (blue-solid line), NSIFO estimate (green-dotted line)

Fig. 20

Reconstruction of the clearance nonlinear characteristic curve: NIFO estimate (blue circles), NSIFO estimate (green crosses) and true value (red dots)

Fig. 21

Reconstruction of the cubic nonlinear characteristic curve: NIFO estimate (blue circles), NSIFO estimate (green crosses) and true value (red dots)

Displacement responses are here contaminated by noise with the SNR being 40 dB. The NIFO and NSIFO method is, respectively, used to identify the nonlinear system based on data contaminated by noise. Figure 22 shows the estimated underlying linear FRF $H_{33}$ curve of the numerical example with noise contamination, which indicates that the identification results of the proposed NSIFO method are superior to the NIFO method. The estimated real and imaginary parts of contact stiffness and cubic stiffness of the numerical example with noise contamination are shown in Figs. 23 and 24, respectively. Compared to the identification results in Figs. 16 and 17, both the NIFO and NSIFO methods obtain worse results after adding noise to the displacement responses, but the proposed NSIFO method seems to achieve much better identification results than the existing NIFO method in the low frequency range.

Fig. 22

The underlying linear FRF H₃₃ curve of the second example with noise contamination: NIFO estimate (blue-solid line), NSIFO estimate (green-dotted line) and true underlying linear FRF (red-dashed line)

Fig. 23

Real and imaginary parts of the estimated contact stiffness $k_{c}$ of the second example with noise contamination: NIFO estimate (blue-solid line), NSIFO estimate (green-dotted line) and true value (red-dashed line)

Fig. 24

Real and imaginary parts of the estimated cubic stiffness $k_{n}$ of the second example with noise contamination: NIFO estimate (blue-solid line), NSIFO estimate (green-dotted line) and true value (red-dashed line)

5 Experimental validation

In this section, a three-story experimental structure with clearance nonlinearity is built to validate the proposed NSIFO method by identifying its underlying linear FRFs and nonlinear characteristics of the clearance. Figures 25 and 26, respectively, illustrate the schematic diagram and experimental setup of the three-story structure with clearance nonlinearity. An exciter is arranged in the first floor, and the clearance is arranged in the second floor. In this experiment, the zero-mean Gaussian random excitation is generated and applied to the first floor of the structure, and in the meantime three eddy current sensors are used to measure the displacement response of each floor, as shown in Fig. 26.

Fig. 25

Schematic diagram of the three-story structure with clearance nonlinearity

Fig. 26

Experimental setup of the three-story structure with clearance nonlinearity

Obviously, the nonlinear behavior of the system can be aroused, in case the positive displacement of the second floor exceeds the clearance value under relatively larger excitation. In other words, the selection of the excitation level depends on whether enough clearance nonlinear factors are aroused. In this section, high-level excitation test and low-level excitation test are, respectively, conducted, with the RMS values of the high-level excitation force and low-level excitation force being 6.0462 N and 1.2814 N. Force and displacement signals are measured and sampled at 10³ Hz, producing 10⁵ sample-long versions of vibration signals after a total time of 100 s. Figure 27 illustrates the excitation force and displacement response at the clearance location under high-level excitation, respectively. The clearance nonlinear factor is observed from Fig. 27, where positive values of the displacement signal are obviously truncated.

Fig. 27

The excitation force and displacement response at the clearance location

Based on the measured excitation force and displacement response signals, the existing NIFO method and the proposed NSIFO method are, respectively, used to identify the underlying linear FRFs and nonlinear characteristics of the clearance. First of all, the DPPDF method is used to identify the clearance value of the experimental structure by considering 10⁵ response samples under high-level excitation. The DPPDF result is shown in Fig. 28, and the clearance is identified with the value of 0.0002117 m by choosing the horizontal axis value of the turning point. And then, the time-domain data are converted to the frequency domain by fast Fourier transform, and the existing NIFO method and the proposed NSIFO method are used to identify the underlying linear FRFs and the contact stiffness based on the identified clearance value.

Fig. 28

The DPPDF result at the clearance location

The RMS values of the high-level excitation force and the nonlinear description function are 6.0462 N and ${7}{\text{.0959}} \times {10}^{ - 6}$ m, respectively. It can be found that the two numerical magnitudes differ greatly and larger coupling errors may be caused for the existing NIFO method. Figures 29 and 30 display the underlying linear FRF $H_{{{3}3}}$ and $H_{{{2}3}}$ curve of the three-story experimental structure identified by the NIFO, NSIFO method and their baseline counterparts by linear H₁ estimation method, respectively. Evidently, the identification results of the proposed NSIFO method are superior to the existing NIFO method, especially around peak positions, which demonstrates that the proposed method is able to achieve better identification accuracy of the underlying linear FRFs.

Fig. 29

The underlying linear FRF H₃₃ curve of the three-story experimental structure: NIFO estimate (blue-solid line), NSIFO estimate (green-dotted line) and baseline underlying linear FRF (red-dashed line)

Fig. 30

The underlying linear FRF H₂₃ curve of the three-story experimental structure: NIFO estimate (blue-solid line), NSIFO estimate (green-dotted line) and baseline underlying linear FRF (red-dashed line)

Figure 31 shows the real and imaginary parts of the estimated contact stiffness $k_{c}$. The imaginary parts are almost zero, and the real parts can be regarded as the contact stiffness. Obviously, the identification results of the NSIFO method exhibit smaller fluctuations and are much smoother than its counterparts by the NIFO method. Note that the peak protruding at 18.92 Hz is the anti-resonant frequency, while the peak protruding at 50 Hz is due to the influence of alternating current frequency for the identification results of the NSIFO method.

Fig. 31

Real and imaginary parts of the estimated contact stiffness $k_{c}$ of the three-story experimental structure: NIFO estimate (blue-solid line), NSIFO estimate (green-dotted line)

Additionally, the mean value and standard deviation of the real part of contact stiffness identified by the NIFO method are 3.1132 × 10⁵ N/m and 2.5462 × 10⁵ N/m in Fig. 31, where the mean value and standard deviation of the real part of contact stiffness identified by the NSIFO method are 3.3281 × 10⁵ N/m and 1.5406 × 10⁵ N/m. Compared to the existing NIFO method, the proposed NSIFO has a smaller standard deviation with smaller fluctuations by inspecting the results above. The reconstruction of the clearance nonlinear characteristic curve is shown in Fig. 32 by using Eq. (21). Note that mean values of the identification results by the two methods are, respectively, selected as the contact stiffness of clearance nonlinearity. Both methods can obtain similar nonlinear characteristics, but from the perspective of the smaller standard deviation, the proposed NSIFO method has the capability of better accuracy and higher stability.

Fig. 32

Reconstruction of the clearance nonlinear characteristic curve: NIFO estimate (blue circles), NSIFO estimate (green crosses)

6 Conclusions

In this work, a novel improved approach for frequency-domain nonlinear identification through feedback of the outputs by using separation strategy is proposed. The underlying linear FRFs of a nonlinear system are identified under low-level excitation, and its nonlinear parameters are identified under high-level excitation. Compared to the existing NIFO method, the proposed NSIFO method is able to avoid the limitation of the selection range of the excitation level and reduce coupling errors caused by the large differences in the numerical magnitude between the excitation forces and the nonlinear description functions when both of them are simultaneously considered as an input vector. Numerical and experimental identification results further demonstrate the superior achievable accuracy and stability of the proposed method for identification of nonlinear systems.

It should be noted that the proposed method in this paper is suitable for the stiffness nonlinearity, but not for the nonlinearity dominated by low-level excitation, such as friction nonlinearity. In such cases, the nonlinear factors caused by the forces under low-level excitation may affect the underlying linear system and cannot be ignored. Fortunately, the proposed method is still applicable if the underlying linear system can be obtained in advance by using other methods instead of the estimation manner used in this paper.