Abstract
To describe the particular mechanical behaviors of beams with both uniform and non-uniform cross sections, such as the bidirectional bending, torsion-bending coupling, the torsion-related warping, the cross-sectional stretch, and Wagner effects, a series of efficient higher-order beam elements (HOBEs) is proposed in the frame of the absolute nodal coordinate formulation (ANCF). In the proposed HOBEs, a new mixed kinematic description of beam elements is introduced via the warping functions and slope vectors. Compared with the existing HOBEs using Lagrange polynomials, the additional degrees of freedom per element proposed to accurately describe the warping deformation are dramatically reduced. Moreover, the tremendous Von-Mises stress on the cross sections in the existing HOBEs does not occur in the proposed new HOBEs. Compared with the classical nonlinear finite elements formulations, the complete 3D strain state with the higher-order terms allows the cross-sectional stretch and avoids the expensive calculations of the extra warping and Wagner strain measures and their derivatives. Moreover, the transverse integration allows an arbitrary section shape to vary along the beam axial direction. Thus, these new HOBEs benefit from the efficient warping description in the classical FE and inherit the advantages of 3D-continuum theory in the ANCF. In addition, the shear locking is alleviated due to the ability to capture the non-uniform distribution of shear stress, and the Poisson locking is addressed via the enhanced continuum mechanics approach. Finally, the proposed HOBEs are validated and compared using statics and dynamics undergoing complex significant deformations on various benchmarks, FEs, commercial codes, and experimental data.
Similar content being viewed by others
Explore related subjects
Discover the latest articles, news and stories from top researchers in related subjects.Avoid common mistakes on your manuscript.
1 Introduction
The thin-walled beams, non-uniform beams, small slenderness ratio beams, and pre-twisted beams have been extensively used in engineering. Under the assumption that the cross section of a beam keeps planar, the classic Euler–Bernoulli beam model and the Timoshenko beam model fail to capture specific deformation patterns [1,2,3,4,5,6,7,8,9,10,11,12,13,14,15,16,17,18,19,20,21,22,23,24,25,26,27,28,29,30] of the overhead beams, such as the bidirectional bending [28], torsion-related warping [8,9,10,11,12,13,14,15,16,17,18,19, 26, 27], bending-related warping [19], cross-sectional stretch [13, 14, 25] (the so-called transverse extension in [13] and cross section contraction in [14]), and Wagner effects [10,11,12,13,14,15,16,17,18] in particular. Wagner effects [4] include Wagner moment and Wagner strains (the quadratic torsion curvature), which play an important role in analyzing large nonlinear torsion consisting of warping and torsional resistance phenomenon that occurs with twist rotation. Under the small strain assumption, most existing commercial codes of finite element (FE) formulations do not account for Wagner effects [9]. Thus, they cannot predict a beam’s structural behavior correctly under significant torsional actions [9, 25]. Besides, in some FE formulations implemented codes, the cross-sectional stretch cannot be captured because the transverse strains are identically equal to zeros [25].
Many methods have been proposed to remove the above limitations of classical beam theories [30]. The shear correction factors [1,2,3] are introduced to measure the effective transverse shear strains, straightforwardly accounting for the shear stress of non-uniform distributed along the cross section. Although the shear correction factors can improve the global response of a lower-order (or planar) beam model, such as bidirectional bending [31,32,33,34], they cannot capture the out-of-plane warping. There is a vast of works about improving the description of the cross-sectional deformation via the warping function [8,9,10,11,12,13,14,15,16,17,18,19] and the higher-order beam element (HOBE) theory [22,23,24,25,26,27,28,29]. In the geometrically exact beam formulation (GEBF) proposed by Simo [5] and Simo and Vu-Quoc [6], early work in [8] suggested introducing the warping function into the kinematics. It combined two extra warping strain measures to account for the warping effects. For the nonlinear torsion of thin-walled beams, the small strain assumption does not hold, and thus, the nonlinear Wagner effects [4] are increasingly significant and must be considered in the GEBF-based works [10,11,12,13,14]. The Wagner effects induce an apparent axial shortening at the beam free end, accompanied by a cross section stretch [17]. Based on the 1D-continuum theory [16], most GEBF neglected the cross-sectional stretch [5,6,7,8,9,10,11,12], just to name a few. Recently, works [13, 14] also allowed the cross-sectional stretch via polynomial ansatz functions and deformation modes, respectively, but resulted in additional DOFs due to the stretch. However, little effort has been devoted to the non-uniform cross-sectional deformation. A comprehensive historical overview is given in the latest work [16]. The absolute nodal coordinate formulation (ANCF) proposed by Shabana [35] is based on the 3D-continuum theory and considers the high-order strain, namely the cross-sectional stretch [25] and Wagner effects are considered inherently. Furthermore, the ANCF is applicable for cross-sectional deformation of the non-uniform beam, since the cross-sectional shapes can vary along the beam axial direction by changing the upper and lower limit functions of sections. Thus, the complete 3D strain state in the ANCF element level benefits from a nonlinear 3D FE analysis. The existing ANCF [24,25,26,27,28,29] uses higher orders of the cross-sectional displacement field and transverse derivatives to capture the deformation and coupling among different modes, such as warping [26, 27], warping-stretch coupling [25], and bidirectional bending [28]. Moreover, one can get an insight into other nonlinear FE formulations of uniform cross-sectional deformation, e.g., the generalized beam theory (GBT) [20] via the deformation modes in [17], and generalized strain beam formulation [21] via extra warping and Wagner strain measures in [18] (similar to GEBF [8,9,10,11,12,13,14]).
The nonlinear FE beam formulations of GEBF and ANCF are promising to handle complex dynamics of flexible multibody systems (FMBS) undergoing large deformations and overall rotations. Although the ANCF benefits from the complete 3D strain state, the original fully parameterized beam elements [35] suffer from serious numerical problems of shear locking and Poisson locking and are not accurate enough in the large deformation [24, 26, 29, 31, 36,37,38,39]. In general, the simulation accuracy and efficiency depend on the geometric description to define the kinematic description. The locking arises here due to a linear transverse interpolation but a cubic axial interpolation for the displacement field, which violates some continuity conditions at the element interface and induces rigid shear strains [29, 31]. As reported in [39], shear locking effectively suppresses the antisymmetric bending mode. The Poisson locking that arises here due to the linear transverse model cannot satisfy the required linear Hooke’s law, resulting in a stiff bending response [26, 29, 31]. The numerical stiffing phenomenon of shear locking results in a slow convergence rate [29]. It can be alleviated via dense mesh, while the Poisson locking may lead to a wrong result regardless of the number of beam elements used [26, 29, 31].
Locking is a commonly stiffing phenomenon in most FE formulations [16, 22, 29, 30, 40]. The works [29, 40] also give a comprehensive historical overview of the locking alleviation techniques for classical FE and ANCF, respectively. In the ANCF, early works about locking alleviation are to use the mixed formulation [36], the cross-sectional HOBEs [24], the modified constitutive law, the Veubeke–Hu–Washizu principle [41], and Hellinger–Reissner principle [42]. Most of the locking alleviation techniques for ANCF are inspired by the vast locking alleviation techniques successfully used in classical FE, then refined and used by many researchers [25,26,27,28,29, 31,32,33, 43,44,45,46,47]. The methodology of the mixed formulation [36] calculates the stiffness via the structural mechanic for bending, twisting, shear, axial extension, and later with cross-sectional stretch [43]. Matikainen et al. [24] reported that the trapezoidal cross-sectional mode helps mitigate the locking in the fully parameterized beam elements, essentially a cross-sectional HOBE theory. Later, the trapezoidal cross-sectional mode was also successfully used to mitigate the locking in the fully parameterized plate element [44]. The modified constitutive law includes the enhanced continuum mechanics approach (CMA) [28, 31, 33, 36, 43], the strain split method (SSM) [29, 46, 47], and the shear scaling factors (a split technique of stiffness matrix) [45]. The first two methodologies have significantly improved the bending behavior of ANCF beam elements. Gerstmayr et al. [36] proposed the enhanced CMA, a technique of split elastic tensor with a selectively reduced integration, and considered the Poisson effect only on the beam axis. The roots of the enhanced CMA lie in the concept of selectively reduced integration in GEBF [6] to handle the well-known over-stiff solutions due to shear locking. Recently, Patel and Shabana [29] proposed the SSM, a technique of split strain tensor of uncoupled with a full integration procedure [29, 46, 47]. Although the existing HOBEs [24,25,26,27,28,29] slightly differ in warping description and locking alleviation, they are computationally expensive due to the use of Lagrange polynomials on the beam sections (e.g., the cubic element 34X3c [28] with 120DOFs and biquadratic element B4 [26] with 96DOFs).
For the FMBS dynamics, the most time-consuming computation is for the nonlinear terms [48], mostly of high dimensions. In terms of the number of unknowns to be solved in a set of differential–algebraic equations (DAEs), a reduced-order model (ROM) using energy equivalence can significantly reduce the computational effort. The proper orthogonal decomposition (POD) is a classical method to reduce the DOFs of the large-scale numerical simulation for a complex nonlinear system in many fields. It has also been used in the FMBS modeled by ANCF, which is required to pre-simulate with the prior knowledge of run-time load [49, 50] to obtain an appropriate ROM to verify its solution over the same period [51,52,53]. Thus, the POD model is only the optimal approximation to the prior training data within the period as mentioned above, rather than the partial differential equations for the original system. However, many works reported that the POD model lacks robustness due to a significantly low accuracy when the system parameters change [54,55,56,57,58,59,60]. It can fail in a broad scope of parameters [59], especially for the FMBS. On the contrary, if the POD model is reconstructed when loading conditions change [61], the expensive time spent on training makes the POD model lose its significance in the sense of model order reduction [59]. On the other hand, the component mode synthesis (CMS) model, such as Craig–Bampton (C–B) method [62], is an optimal approximation to the partial differential equations for the structures, and no prior knowledge of pre-simulation under run-time load is required. The CMS has also been successfully used in many problems, such as flexible aircraft control [49], contacts and frictions [63, 64], and slewing flexible beam [65]. Many CMS-related works about LOBEs were trying to address the difficulty facing the large nonlinear deformation in the FMBS, such as the FFRF [61, 66,67,68,69,70], the ANCF [33, 50, 71], and the GEBF [72]. For an FMBS, the challenge in establishing a high-robust and high-precision ROM is caused by the large deformation resulting from overall rotation and its coupling deformation, distinguished from the structural dynamics do not experience the overall rotation. Therefore, the ability to capture the dynamic response of high-speed rotation under 3D loading is an index to evaluate many order reduction techniques. To the authors’ best knowledge, the model order reduction based on successive linearizations can sufficiently address the case of 72 rad/s in [33]. Although there are minor works to reduce the HOBE-based model, it is increasingly urgent since the HOBEs can accurately describe the cross-sectional deformation but are time-consuming due to many DOFs, as mentioned above.
This study proposes a mixed kinematic description of beam elements via the slope vectors and warping functions in a complete 3D strain state undergoing large deformations and overall rotations. Thus, the new HOBEs for ANCF can obtain the cross-sectional deformations (such as warping, stretch and Wagner effects) even with non-uniform variation section and large torsion in a compact strain expression. The six entries of the Green–Lagrange strain tensor depend on the mixed kinematic description, avoiding the expensive calculations of the extra warping and Wagner strain measures and their derivatives [8,9,10,11,12]. Moreover, an accurately warping function helps the proposed HOBEs account for the non-uniform distribution of shear stress, eliminating the need to modify the shear energy. To describe the warping deformations, unlike the existing HOBEs [24,25,26,27,28,29] using Lagrange polynomials, the proposed HOBEs are interpolated via the warping functions to reduce the element DOFs significantly. To capture the geometries of non-uniform beams, unlike some conventional FE formulations using dense mesh, the new HOBEs only need sparse elements with smaller DOFs because the cross-sectional shapes can vary along the beam axial direction. Thus, these new elements inherit the advantages of 3D-continuum theory and benefit from the efficient description of warping in the GEBF.
The remaining part of this paper is organized as follows. Firstly, based on the ANCF, a series of new HOBEs interpolated with the slope vectors and warping functions is proposed as a novel technique in Sect. 2. The governing equations in the FMBs are depicted in Sect. 3. In Sect. 4, the computation complexity in terms of the number of unknowns is analyzed in detail to highlight the benefits of new HOBEs. In the static numerical examples in Sects. 5.1 and 5.2, the frequency, deformation, Von-Mises stress distribution, and torsional limit of the new HOBEs and their ROMs are compared among the GEBF, commercial codes, and experimental data, respectively. In Sect. 5.3, a dynamic numerical example is presented to demonstrate the importance of the consideration of warping in the nonlinear bending-torsion coupled dynamics. Finally, some concluding remarks are made in Sect. 6.
2 The ANCF model contains warping
2.1 Kinematic description
Let \({\mathbf{r}} = {\mathbf{r}}(x,y,z,t) \in {\mathbb{R}}^{3}\) denote the global position vector of an arbitrary point on the beam element at time t. According to the work by Sugiyama et al. [73], a planar beam configuration can be described by the global position vector \({\mathbf{r}}^{c}\) of the centroid line and a linear polynomial interpolation of the cross section. Thus, r can be described by the material frame x–y-z defined in the element coordinate system as follows,
where \({\mathbf{r}}^{c}\) is a interpolation function of quadratic [31,32,33, 43] or cubic [28, 35, 38] polynomial. \({\mathbf{r}}_{,y} = \partial {\mathbf{r}}/\partial y \in {\mathbb{R}}^{3}\) and \({\mathbf{r}}_{,z} = \partial {\mathbf{r}}/\partial z \in {\mathbb{R}}^{3}\) are the transverse slope vectors (or first-order directional derivatives). The elements with displacement field given by Eq. (1) with linear transverse interpolation are the lower-order beam elements (LOBEs). Importantly, the transverse slope vectors \({\mathbf{r}}_{,y}\) and \({\mathbf{r}}_{,z}\) are no longer orthogonal unit vectors and can induce parallelogram deformation [74] and stretch deformation. Thus, the kinematic description Eq. (1) relaxes the assumption of a rigid cross section.
The slope vectors in Eq. (1) can be interpolated over all p nodes of an element
where \({\mathbf{r}}_{i,\alpha }^{{}} = {{\partial {\mathbf{r}}_{i} } \mathord{\left/ {\vphantom {{\partial {\mathbf{r}}_{i} } {\partial \alpha }}} \right. \kern-\nulldelimiterspace} {\partial \alpha }} = {\mathbf{r}}_{,\alpha }^{{}} \left( {x_{i} ,t} \right)\), \(\alpha = y,z\), represents the directional derivative of node i, which constitutes the beam’s nodal coordinates. \(f_{i} \left( x \right)\) is the parameter function for the local coordinate x and will be discussed separately for each classical element [28, 35, 43, 75].
Substituting Eq. (2) into Eq. (1) yields
Using the slope vectors instead of rotation angle makes no singular problem but results in locking problems [26, 29, 31, 37,38,39, 41,42,43] in the ANCF. An immense amount of methods on locking alleviation in the ANCF [24,25,26,27,28,29, 31, 33, 36, 43,44,45,46,47] were proposed for various locking mechanisms. As stated in the introduction, the shear locking and Poisson locking arise due to the linear transverse model and lead to excessive torsional stiffness and bending stiffness.
The warping displacement field \({\overline{\mathbf{X}}}\) is the cross-sectional deviation of the deformed beam from a plane surface, which can be described via an enriched displacement field. This enriched displacement field motivates the development of HOBEs to expand the cross section kinematics and overcome the planar beam theories’ limitations. The limitations are elaborated in the introduction [1,2,3,4,5,6,7,8,9,10,11,12,13,14,15,16,17,18,19,20,21,22,23,24,25,26,27,28,29,30]. The warping displacement field \({\overline{\mathbf{X}}}\) is superposed on the LOBE’s (or planar beam’s) field described by Eq. (1), yielding the global position vector of an arbitrary point on a beam as follows,
Obviously, when \({\overline{\mathbf{X}}} = {\mathbf{0}}_{3 \times 1}\) holds, the beam cross section deforms as a planar surface and Eq. (4) will degenerate to Eq. (1).
In the existing HOBEs [24,25,26,27,28,29] of ANCF, \({\overline{\mathbf{X}}}\) can be described with the higher-order interpolation as
where \({\mathcal{O}}(\alpha \beta )\), \({\mathcal{O}}(\alpha \beta \gamma )\) and \({\mathcal{O}}(\alpha \beta \gamma \tau )\), respectively, denote the functions of second-order, third-order, fourth-order directional derivatives in the transverse directions, and \(\alpha ,\beta ,\gamma ,\tau = y,\;z\).
Orzechowski and Shabana [27] proposed a two-node HOBE, which covers quadratic interpolation in the transverse directions. A quadratic element allows the cross-sectional deviation from a plane surface to be equal to \({\overline{\mathbf{X}}}{ = }{\mathcal{O}}(\alpha \beta )\), which can be written more explicitly with a complete polynomial over p nodes,
where \({\mathbf{r}}_{,\alpha \beta }^{{}} = {{\partial {\mathbf{r}}_{{}}^{2} } \mathord{\left/ {\vphantom {{\partial {\mathbf{r}}_{{}}^{2} } {\left( {\partial \alpha \partial \beta } \right)}}} \right. \kern-\nulldelimiterspace} {\left( {\partial \alpha \partial \beta } \right)}} \in {\mathbb{R}}^{3}\) is the curvature vector [27] (or second-order directional derivatives). Compared with the LOBEs, \({\mathbf{r}}_{i,\alpha \beta }^{{}} = {{\partial {\mathbf{r}}_{i}^{2} } \mathord{\left/ {\vphantom {{\partial {\mathbf{r}}_{i}^{2} } {\left( {\partial \alpha \partial \beta } \right)}}} \right. \kern-\nulldelimiterspace} {\left( {\partial \alpha \partial \beta } \right)}}\,{ = }\,{\mathbf{r}}_{,\alpha \beta }^{{}} \left( {x_{i} ,t} \right) \in {\mathbb{R}}^{3}\) is the additional nodal coordinates in the quadratic elements.
Similarly, a cubic element allows the cross-sectional deviation from a plane surface to be equal to \({\overline{\mathbf{X}}}{ = }{\mathcal{O}}(\alpha \beta ){ + }{\mathcal{O}}(\alpha \beta \gamma )\), where
where \({\mathbf{r}}_{,\alpha \beta \gamma }^{{}} = {{\partial {\mathbf{r}}_{{}}^{3} } \mathord{\left/ {\vphantom {{\partial {\mathbf{r}}_{{}}^{3} } {\left( {\partial \alpha \partial \beta \partial \gamma } \right)}}} \right. \kern-\nulldelimiterspace} {\left( {\partial \alpha \partial \beta \partial \gamma } \right)}} \in {\mathbb{R}}^{3}\) and \({\mathbf{r}}_{i,\alpha \beta \gamma }^{{}} = {{\partial {\mathbf{r}}_{i}^{3} } \mathord{\left/ {\vphantom {{\partial {\mathbf{r}}_{i}^{3} } {\left( {\partial \alpha \partial \beta \partial \gamma } \right)}}} \right. \kern-\nulldelimiterspace} {\left( {\partial \alpha \partial \beta \partial \gamma } \right)}}{ = }{\mathbf{r}}_{,\alpha \beta r}^{{}} \left( {x_{i} ,t} \right) \in {\mathbb{R}}^{3}\). Compared with the LOBEs, \({\mathbf{r}}_{i,\alpha \beta }^{{}}\) and \({\mathbf{r}}_{i,\alpha \beta \gamma }^{{}}\) are the additional nodal coordinates in the cubic elements. Moreover, the higher-order representation of the cross-sectional deformation can ensure the smoothness and continuity of the cross section at the element interface [27,28,29]. Thus, the HOBEs can alleviate shear locking as well as capture the warping displacement. By increasing the order of polynomials in Eq. (5), the existing HOBEs [24,25,26,27,28,29] can improve the prediction of deformation but sharply increase the element DOFs [26, 28] and computation time [26].
In general, the accuracy and efficiency of the numerical solution depend on the geometric description used to define the FE displacement field. Early work [8] suggested introducing the Saint–Venant warping function into the kinematics of the GEBF, which is a finite formulation of 1D-continuum theory [16] and neglects the cross-sectional stretch. Inspired by this, a mixed kinematic description of beam elements is proposed by introducing the warping function into the kinematics of ANCF, a finite formulation of 3D-continuum theory. When the beam twist along the central axis x, \({\overline{\mathbf{X}}}\) can be described as
where \(\omega\) is the warping function. r,ω represents the angle of twist to the x-the tangent of the beam’s axial line, which allows for describing distortional deformations of the cross section. For a beam without pre-torsion, the initial value of \({{\varvec{\uptheta}}}\left( {x,t} \right) = \left[ {\begin{array}{*{20}c} 0 & 0 & 0 \\ \end{array} } \right]^{{\text{T}}}\) is a null vector. The ability to capture cross-sectional warping is the main difference between LOBEs (planar beams) and HOBEs. From this point of view, the proposed new elements are essentially HOBEs. Substituting Eq. (8) into Eq. (4), one can get the displacement field for the proposed new HOBEs.
Similar to Eq. (2), the vector \({\mathbf{r}}_{,\omega } \left( {x,t} \right)\) in Eq. (8) for ANCF can be also interpolated over all p nodes as
where \({\mathbf{r}}_{i,\omega } = {{\partial {\mathbf{r}}_{i} } \mathord{\left/ {\vphantom {{\partial {\mathbf{r}}_{i} } {\partial \omega }}} \right. \kern-\nulldelimiterspace} {\partial \omega }} = {\mathbf{r}}_{,\omega } \left( {x_{i} ,t} \right)\) is the additional nodal coordinates compared with the LOBEs. Furthermore, the warping displacement field \({\overline{\mathbf{X}}}\) can be further cast as
The comparisons related to different transverse interpolation approaches are shown in Table 1. For the sake of readability, the element naming conventions used in the works by Orzechowski and Shabana [27] and by Ebel et al. [28] are still adopted in this study. Four classical LOBEs described by Eq. (1) are given in the first column, which are the essential elements to construct the HOBEs. By increasing the order of polynomials in Eq. (5), the existing HOBEs [24,25,26,27,28,29] can improve the deformation prediction, especially for the cross sections. Thus, the additional DOFs per element will sharply increase to 9p, 21p, and 36p in the quadratic, cubic and biquadratic beam elements, respectively. However, this will lead to a high computational cost for the existing HOBEs to obtain a correct analysis, as reported in [26]. However, the warping displacement field described by Eq. (8) in the new HOBEs differs from the field described by Eq. (5) in the existing HOBEs. The element names supplemented by the letter “ω” represent the proposed new HOBEs interpolated with the warping function, as shown in Eq. (8). In the new elements, \({\mathbf{r}}_{i,\omega } \left( {x,t} \right)\) is the additional nodal coordinates, which indicates only 3p additional DOFs per element are needed to capture the warping deformation. Thus, compared with the existing HOBEs in the ANCF, the proposed new HOBEs sharply reduce the element DOFs and will be carefully studied via two-node, three-node, and four-node beam elements in this study.
For the existing method of creating HOBEs via Eq. (5), to capture the bending-torsion coupling in the Princeton beam experiment, a cubic beam element 34X3 needs to be designed, as reported in [28]. Moreover, to capture the warping displacement of a square beam under the pure torsion, a biquadratic beam element B4 needs to be designed as reported in [26]. Thus, in the following Sects. 5.1 and 5.2, the performance of the proposed new HOBEs will be tested compared with 34X3 and B4.
Using the displacement field given by Eqs. (1) and (4), the global position vector r can be further expressed as follows,
where e is the vector of element nodal coordinates and S is matrix of dimensionless shape functions of element.
For an HOBE, the shape function matrix is divided into two parts, one is related to the essential LOBE, and the other is related to the superposed warping. The matrix of shape functions of the proposed HOBEs possess the following structure,
where “ ⊗ ” denotes the Kronecker product, I is a 3 × 3 identity matrix, \(N^{{\text{E}}}\) is the element DOFs, and \({\mathbf{s}}_{i}^{{{\text{LOBE}}}}\) forms the row vector of shape functions of a LOBE. Table 2 gives the schematic, defined vector e and the corresponding shape function matrix S of each element. Moreover, the warping-related shape functions can be written as
where \(\xi\), \(\eta\), and \(\zeta\) are the dimensionless element coordinates. The warping function \(\omega\) of sectional shape is given in Appendix B, and can be substituted into Table 2 to get the specific expressions of S. This is crucial for a successful interpolation. The shape functions of LOBEs and their dimensionless parameter functions \(f_{i} \left( \xi \right)\) are also provided in Table 2 (see the box).
2.1.1 The proposed two-node beam elements: BE24-ω
The classical LOBE BE24, also called the fully parameterized beam element of ANCF, was originally proposed by Yakoub and Shabana [35]. The position of an arbitrary point on the BE24 is defined using the displacement field given by Eq. (1), and the position of the centroid line is interpolated using cubic Hermite polynomials. Based on BE24, the BE24-ω is proposed using the warping displacement field given by Eq. (8). As displayed in Table 2, the vector of element nodal coordinates is defined as \({\mathbf{e}} = \left[ {{\mathbf{e}}_{1}^{{\text{T}}} \;\;{\mathbf{e}}_{2}^{{\text{T}}} \;} \right]^{{\text{T}}} \in {\mathbb{R}}^{30}\), where \({\mathbf{e}}_{i}^{{\text{T}}} { = }\left[ {{\mathbf{r}}_{i}^{{\text{T}}} \;\;{\mathbf{r}}_{i,x}^{{\text{T}}} \;\;{\mathbf{r}}_{i,y}^{{\text{T}}} \;\;{\mathbf{r}}_{i,z}^{{\text{T}}} \;\;{\mathbf{r}}_{i,\omega }^{{\text{T}}} } \right]\), \(i{ = }1,\;2\). Thus,
For the LOBE BE24 [35], \({\mathbf{s}}_{i}^{{{\text{BE24}}}} { = }[S_{i} \;\;S_{i,1} \;\;S_{i,2} \;\;S_{i,3} \;]\) (see Table 2). The subscripts “1,” “2,” and “3” represent the shape functions accordingly multiplied by the directional derivatives in the x, y, and z directions at node i. For example, \(S_{i,2} {\mathbf{I}}\) is multiplied by the directional derivatives \({\mathbf{r}}_{i,y}^{{}}\) at node i. Moreover, l is the length of the beam element of undeformed in Table 2.
According to the work by Ebel et al. [28], the beam elements have the same number of vectors per node can be noted with four digits abcd, a denotes the dimension of an element, b denotes the nodes per element, c denotes the number of vectors per node, and d always takes the value 3 for the same polynomial basis. Thus, the BE24 was also called 3243 in [24].
2.1.2 The proposed three-node beam elements: MGD30-ω and 3333-ω
Ren [75] proposed a C1-continuous LOBE, whose position of the centroid line is interpolated with cubic Hermite polynomials. It is a gradient-deficient beam element without the longitudinal slope vector only in the middle node. Thus, the above-mentioned naming convention via four digits is not suited for the element proposed by Ren [75]. For the convenience of readability, it is named as MGD30 in this study. As shown in Table 2, based on the MGD30, a new HOBE noted as MGD30-ω is proposed using the displacement field given by Eq. (8) to account for the cross-sectional warping. The vector of element nodal coordinates is defined as \(\;{\mathbf{e}} = \left[ {{\mathbf{e}}_{1}^{{\text{T}}} \;\;{\mathbf{e}}_{2}^{{\text{T}}} \;\;{\mathbf{e}}_{3}^{{\text{T}}} } \right]^{{\text{T}}} \in {\mathbb{R}}^{39}\), where \({\mathbf{e}}_{1}^{{\text{T}}} { = }\left[ {{\mathbf{r}}_{1}^{{\text{T}}} \;\;{\mathbf{r}}_{1,x}^{{\text{T}}} \;\;{\mathbf{r}}_{1,y}^{{\text{T}}} \;\;{\mathbf{r}}_{1,z}^{{\text{T}}} \;\;{\mathbf{r}}_{1,\omega }^{{\text{T}}} } \right]\), \({\mathbf{e}}_{2}^{{\text{T}}} { = }\left[ {{\mathbf{r}}_{2,y}^{{\text{T}}} \;\;{\mathbf{r}}_{2,z}^{{\text{T}}} \;\;{\mathbf{r}}_{2,\omega }^{{\text{T}}} } \right]\), and \({\mathbf{e}}_{3}^{{\text{T}}} { = }\left[ {{\mathbf{r}}_{3}^{{\text{T}}} \;\;{\mathbf{r}}_{3,x}^{{\text{T}}} \;\;{\mathbf{r}}_{3,y}^{{\text{T}}} \;\;{\mathbf{r}}_{3,z}^{{\text{T}}} \;\;{\mathbf{r}}_{3,\omega }^{{\text{T}}} } \right]\). Thus,
In the LOBE MGD30 [75],\({\mathbf{s}}_{1}^{{{\text{MGD30}}}} { = }\left[ {S_{1} \;S_{1,1} \;S_{1,2} \;S_{1,3} } \right]\), \({\mathbf{s}}_{2}^{{{\text{MGD30}}}} { = }\left[ {S_{2,2} \;S_{2,3} } \right]\), \({\mathbf{s}}_{3}^{{{\text{MGD30}}}} { = }\left[ {S_{3} \;S_{3,1} \;S_{3,2} \;S_{3,3} } \right]\) (see Table 2).
Nachbagauer [43] originally proposed the LOBE 3333, and the position of the beam’s centroid line is interpolated by quadratic polynomials. It is a gradient-deficient beam element without longitudinal slope vector in each node. As shown in Table 2, similarly to the interpolation of warping function of Eq. (8), a new HOBE 3333-ω is proposed. The vector of element nodal coordinates is defined as \({\mathbf{e}}{ = }\left[ {{\mathbf{e}}_{1}^{{\text{T}}} \;\;{\mathbf{e}}_{2}^{{\text{T}}} \;\;{\mathbf{e}}_{3}^{{\text{T}}} } \right]^{{\text{T}}} \in {\mathbb{R}}^{36}\), where \({\mathbf{e}}_{i}^{{\text{T}}} { = }\left[ {{\mathbf{r}}_{i}^{{\text{T}}} \;{\mathbf{r}}_{i,y}^{{\text{T}}} \;\;{\mathbf{r}}_{i,z}^{{\text{T}}} \;\;{\mathbf{r}}_{i,\omega }^{{\text{T}}} } \right]\), \(i{ = }1,\;2,\;3\). Thus,
In the LOBE 3333 [43], \({\mathbf{s}}_{i}^{3333} { = }\left[ {S_{i} \;\;S_{i,2} \;\;S_{i,3} } \right]\) (see Table 2).
2.1.3 The proposed four-node beam elements: 3433-ω
The LOBE 3433 was originally proposed in the work of Ebel et al. [28]; however, the element shape functions were not provided. Thus, in this study, a new four-node beam element also named 3433 is proposed using the displacement field given by Eq. (3). As shown in Table 2, based on the proposed LOBE 3433, a new HOBE 3433-ω is proposed using the displacement field given by Eq. (8). The vector \({\mathbf{e}} \in {\mathbb{R}}^{48}\) of element nodal coordinates is defined as \(\;{\mathbf{e}} = \left[ {{\mathbf{e}}_{1}^{{\text{T}}} \;\;{\mathbf{e}}_{2}^{{\text{T}}} } \right.\;\;\;\left. {{\mathbf{e}}_{3}^{{\text{T}}} \;\;{\mathbf{e}}_{4}^{{\text{T}}} } \right]^{{\text{T}}} ,\) where \({\mathbf{e}}_{i}^{{\text{T}}} { = }\left[ {{\mathbf{r}}_{i}^{{\text{T}}} \;\;{\mathbf{r}}_{i,y}^{{\text{T}}} \;\;{\mathbf{r}}_{i,z}^{{\text{T}}} \;\;{\mathbf{r}}_{i,\omega }^{{\text{T}}} } \right]\), \(i{ = }1,\;2,\;3,\;4\). Thus,
In the LOBE 3433 [28], \({\mathbf{s}}_{i}^{3433} { = }[S_{i} \;\;S_{i,2} \;\;S_{i,3} \;]\) (see Table 2).
The existing HOBEs whose displacement fields are given by Eq. (5), such as BE42 and 34X3, are defined in Appendix A. In addition, there are many other HOBEs reported in works by Matikainen et al. [24] and Ebel et al. [28].
The parameter functions for the two-node, three-node, and four-node HOBEs in Table 2 reproduce a linear, quadratic, and cubic interpolation of rotations, which can address constant [37, 43], linear, and quadratic interpolation of curvatures, respectively. Thus, multiple-node beam elements are intended to be used for large deformation problems and can improve the rate of convergence even with a rougher mesh. However, the HOBEs are not yet eliminating locking. Moreover, their performances are also dependent on the constitutive model used [29] and will be demonstrated in the following Sect. 2.3.
2.2 The constant element mass matrix
The element kinetic energy T.E can be calculated from the following volume integral
where \(\int_{V} {\rho {\mathbf{S}}^{{\text{T}}} {\mathbf{S}}} dV\) is the constant element mass matrix M, and S is the matrix of shape functions associated with the proposed elements, as shown in Table 2.
2.3 Computation of element elastic forces
Gerstmayr et al. [36] originally proposed the enhanced CMA to alleviate the excessive bending stiffness due to the Poisson coupling among the axial and transverse deformations. The enhanced CMA combines a split elastic tensor and a selective integration procedure. For a isotropic linear elastic beam, the fourth-order elastic tensor \({\mathbf{\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle\thicksim}$}}{E} }}{ = 2}G\left( {{\mathbf{I}}_{4} + \tfrac{\nu }{1 - 2\nu }{\mathbf{I}} \otimes {\mathbf{I}}} \right)\) is split into two parts \({\mathbf{\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle\thicksim}$}}{E} }}{ = }{\mathbf{\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle\thicksim}$}}{E} }}^{0} { + }{\mathbf{\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle\thicksim}$}}{E} }}^{\nu }\), where \({\mathbf{\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle\thicksim}$}}{E} }}^{\nu }\) accounts for the Poisson effect only on the beam axis with the selective integration procedure and \({\mathbf{\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle\thicksim}$}}{E} }}^{0}\) does not include the Poisson’s ratio ν with a full integration procedure. \(G = {E \mathord{\left/ {\vphantom {E {\left( {2\left( {1 + \nu } \right)} \right)}}} \right. \kern-\nulldelimiterspace} {\left( {2\left( {1 + \nu } \right)} \right)}}\) is the shear modulus, E is the Young’s modulus, and I4 is the fourth-order identity tensor.
The entries of \({\mathbf{\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle\thicksim}$}}{E} }}^{\nu }\) and \({\mathbf{\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle\thicksim}$}}{E} }}^{0}\) can be given by
where \(\gamma = {{E\nu } \mathord{\left/ {\vphantom {{E\nu } {\left( {\left( {1 + \nu } \right)\left( {1 - 2\nu } \right)} \right)}}} \right. \kern-\nulldelimiterspace} {\left( {\left( {1 + \nu } \right)\left( {1 - 2\nu } \right)} \right)}}\) is the constant Lamé coefficient. \(k_{2}\) and \(k_{3}\) are the shear correction factors account for the distribution of the shear stress along the cross section. In fact, a warping function helps the proposed HOBEs account for the non-uniform distribution of shear stress, and thus relax the need for a shear correction factors, i.e., \(k_{2} = k_{3} = 1\). The shear correction factors were also eliminated because the HOBE theory in [76] can correctly account for the parabolic shear stress distribution on the cross section. In contrast to the standard CMA with 21 nonzero entries for \({\mathbf{\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle\thicksim}$}}{E} }}\), there are 9 nonzero entries for \({\mathbf{\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle\thicksim}$}}{E} }}^{\nu }\) and 15 nonzero entries for \({\mathbf{\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle\thicksim}$}}{E} }}^{0}\).
The split elastic tensor results in a split form of the second Piola–Kirchhoff stress \({{\varvec{\upsigma}}}\), leading to
where \({{\varvec{\upvarepsilon}}} = {{\left( {{\mathbf{F}}^{{\text{T}}} {\mathbf{F}} - {\mathbf{I}}} \right)} \mathord{\left/ {\vphantom {{\left( {{\mathbf{F}}^{{\text{T}}} {\mathbf{F}} - {\mathbf{I}}} \right)} 2}} \right. \kern-\nulldelimiterspace} 2}\) is the symmetric Green–Lagrange strain tensor and F is the deformation gradient tensor. By using the chain rule and the mapping between the deformed configuration r and the initial configuration r0, the deformation gradient tensor reads
where the vector \({{\varvec{\upbeta}}} = \left[ {\begin{array}{*{20}c} x & y & z \\ \end{array} } \right]^{{\text{T}}}\) is defined in the element local coordinate system and e0 is the vector of initial generalized coordinates. And \({\mathbf{s}}_{,\beta }^{\left( j \right)} = {{\partial {\mathbf{s}}_{{}}^{\left( j \right)} } \mathord{\left/ {\vphantom {{\partial {\mathbf{s}}_{{}}^{\left( j \right)} } {\partial \beta }}} \right. \kern-\nulldelimiterspace} {\partial \beta }}\), where \({\mathbf{s}}_{{}}^{\left( j \right)} \in {\mathbb{R}}^{{N^{{\text{E}}} }}\) is the j-th row of S, j = 1, 2, 3. For example, the explicit form for \({\mathbf{S}}^{{{\text{MGD30}} - \omega }} \in {\mathbb{R}}^{3 \times 39}\) is equal to
When a flexible body experience a rigid-body rotation, the stress and deformation measures should remain constant to satisfy the objectivity requirement, which is essential in analyzing large deformations. According to the book by Shabana [77], let the orthogonal matrix R describe an arbitrary rigid-body rotation, \({\mathbf{F}}_{0}\) and \({\mathbf{F}}\) be the deformation gradient tensor on the continuous body before and after the rigid-body rotation, respectively. Thus, \({\mathbf{F}} = {\mathbf{RF}}_{0}\), and
At this point, the Green–Lagrange strain tensor remains constant during the rigid-body rotation. While in the GEBF, the interpolation of the rotation variables spoils the objectivity of the strain measures with respect to a rigid-body rotation [7].
Next, to illustrate the effect of the kinematic description on the strain tensor, a beam of the straight and undistorted initial configuration is considered since its identity element Jacobian \({\mathbf{J}}_{0}^{{}} = {\mathbf{I}}\) in Eq. (22) makes the analysis simpler. Now let \({\mathbf{F}}\) be the deformation gradient tensor after deformation, thus
where \({\mathbf{S}}_{xx} = \sum\limits_{j = 1}^{3} {{\mathbf{s}}_{{{,}x}}^{{\left( j \right){\text{T}}}} {\mathbf{s}}_{{{,}x}}^{\left( j \right)} }\), \({\mathbf{S}}_{yy} = \sum\nolimits_{j = 1}^{3} {{\mathbf{s}}_{{{,}y}}^{{\left( j \right){\text{T}}}} {\mathbf{s}}_{,y}^{\left( j \right)} }\), \({\mathbf{S}}_{zz} = \sum\nolimits_{j = 1}^{3} {{\mathbf{s}}_{{{,}z}}^{{\left( j \right){\text{T}}}} {\mathbf{s}}_{,z}^{\left( j \right)} }\), \({\mathbf{S}}_{xy} = \sum\nolimits_{j = 1}^{3} {{\mathbf{s}}_{{{,}x}}^{{\left( j \right){\text{T}}}} {\mathbf{s}}_{,y}^{\left( j \right)} }\), \({\mathbf{S}}_{xz} = \sum\nolimits_{j = 1}^{3} {{\mathbf{s}}_{{{,}x}}^{{\left( j \right){\text{T}}}} {\mathbf{s}}_{,z}^{\left( j \right)} }\), \({\mathbf{S}}_{yz} = \sum\nolimits_{j = 1}^{3} {{\mathbf{s}}_{{{,}y}}^{{\left( j \right){\text{T}}}} {\mathbf{s}}_{,z}^{\left( j \right)} }\). The general expression Eq. (25) can both express the strain tensor in the LOBEs and the proposed HOBEs. For example, for the LOBE MGD30, the shape function is \({\mathbf{S}}^{{{\text{MGD30}}}} \in {\mathbb{R}}^{3 \times 30}\), and \({\mathbf{S}}_{xx}^{{{\text{MGD30}}}} = \sum\nolimits_{j = 1}^{3} {{\mathbf{s}}_{{{,}x}}^{{\left( j \right){\text{T}}}} {\mathbf{s}}_{{{,}x}}^{\left( j \right)} } \in {\mathbb{R}}^{30 \times 30}\) in Eq. (25). For the proposed HOBE MGD30-ω, the shape function is \({\mathbf{S}}^{{{\text{MGD30}} - \omega }} \in {\mathbb{R}}^{3 \times 39}\) (as shown in Eq. 23), and \({\mathbf{S}}_{xx}^{{{\text{MGD30}} - \omega }} = \sum\nolimits_{j = 1}^{3} {{\mathbf{s}}_{{{,}x}}^{{\left( j \right){\text{T}}}} {\mathbf{s}}_{{{,}x}}^{\left( j \right)} } \in {\mathbb{R}}^{39 \times 39}\) in Eq. (25). Obviously, warping effects are considered in the Green–Lagrange strain tensor in the proposed HOBEs. This is totally different from [8,9,10,11,12,13,14,15,16,17,18], where extra strain measures need to be defined to capture the warping effects. The following statements in Tables 3 and 5 will point out the differences brought out by the proposed HOBEs and how the warping-related entries affect the components in the Green–Lagrange strain tensor.
Compared with the existing HOBEs for ANCF, the superior improvement is that the new elements can accurately predict the cross-sectional deformations with much smaller DOFs, as elaborated in Table 1. Next, the comparisons among the LOBEs for ANCF and other classical FE formulations in the strain measure level are made below.
The main differences in the strain values between the LOBEs and proposed HOBEs come from the contribution of the warping function. As demonstrated in Eq. (13), \(S_{i}^{\omega } = \omega \left( {\eta ,\zeta } \right)f_{i} \left( \xi \right),\;\;i{ = }1 \cdots p\). Compared with the LOBEs, the improvements in the HOBEs yields:
-
(1)
In the LOBEs, for the strains \(\varepsilon_{yy}\) and \(\varepsilon_{zz}\), e.g.,\(\varepsilon_{yy} = \frac{1}{2}{\mathbf{e}}^{{\text{T}}} {\mathbf{S}}_{yy} {\mathbf{e}} = \frac{1}{2}\left( {{\mathbf{e}}^{{\text{T}}} \left( {\sum\limits_{j = 1}^{3} {{\mathbf{s}}_{{{,}y}}^{{\left( j \right){\text{T}}}} {\mathbf{s}}_{,y}^{\left( j \right)} } } \right){\mathbf{e}} - 1} \right)\), the constant entry of \({\mathbf{s}}_{,y}^{\left( j \right)}\) from Table 2 yields a constant \(\varepsilon_{yy}\) at a given x. A similar conclusion of the LOBE (TDBE12, which is a degenerate case of space beam BE24 in plane problem) can also be found in [25]. And some works [26, 29] believed that the Poisson locking arose here because the constant strains \(\varepsilon_{yy}\) and \(\varepsilon_{zz}\) cannot satisfy the required linear Hooke’s law. While in the proposed HOBEs, the warping-related entry \({{\partial S_{i}^{\omega } } \mathord{\left/ {\vphantom {{\partial S_{i}^{\omega } } {\partial y}}} \right. \kern-\nulldelimiterspace} {\partial y}} = f_{i} \left( \xi \right){{\partial \omega } \mathord{\left/ {\vphantom {{\partial \omega } {\partial y}}} \right. \kern-\nulldelimiterspace} {\partial y}}\) of \({\mathbf{s}}_{,y}^{\left( j \right)}\) yields the strain \(\varepsilon_{yy}\) to be a quadratic function with respect to \({{\partial \omega } \mathord{\left/ {\vphantom {{\partial \omega } {\partial y}}} \right. \kern-\nulldelimiterspace} {\partial y}}\) (\(\ne\) constant), as shown in Table 3. Therefore, the Poisson locking can be moderately alleviated, same reason to the existing HOBEs [24,25,26,27,28,29]. What is more, for a two-ends-fixed beam under upper and lower surface-pressure case in [26], the cross-sectional boundaries are distorted with in-plane warping [78, 79] and cross-sectional extension in the HOBEs. As shown in Table 3, the nonlinear strains \(\varepsilon_{yy}\) and \(\varepsilon_{zz}\) in the HOBEs cause nonlinear stretch combining with in-plane warping [78, 79] and cross-sectional extension, while the constant strains \(\varepsilon_{yy}\) and \(\varepsilon_{zz}\) in the LOBEs only cause constant stretch (or cross-sectional extension). However, the cross-sectional extension is neglected in [78, 79], it is effective for locking alleviation and crucial for a correct analysis, as reported in [17].
-
(2)
In the LOBEs (e.g., [28, 35, 43, 75]), for the shear strains \(\varepsilon_{xy}\) and \(\varepsilon_{xz}\), e.g.,\(\varepsilon_{xy} = \frac{1}{2}{\mathbf{e}}^{{\text{T}}} {\mathbf{S}}_{xy} {\mathbf{e}} = \frac{1}{2}{\mathbf{e}}^{{\text{T}}} \left( {\sum\limits_{i = 1}^{3} {{\mathbf{s}}_{{{,}x}}^{{\left( j \right){\text{T}}}} {\mathbf{s}}_{,y}^{\left( j \right)} } } \right){\mathbf{e}}\), the product of linear entry of \({\mathbf{s}}_{,x}^{\left( j \right)}\) from Table 2 and constant entry of \({\mathbf{s}}_{,y}^{\left( j \right)}\) yields a linear shear strain \(\varepsilon_{xy}\). Thus, the cross-sectional shape of a LOBE keeps planar but no longer restricts normal to the beam’s neutral axis. The linear transverse models (or LOBEs) lead to the linear distribution of the shear strains. Therefore, the shear energy is modified with correction factors [1,2,3] to improve the accuracy of mechanical response. While in the HOBEs, the product of nonlinear entry \({{\partial S_{i}^{\omega } } \mathord{\left/ {\vphantom {{\partial S_{i}^{\omega } } {\partial x}}} \right. \kern-\nulldelimiterspace} {\partial x}} = \omega {{\partial f_{i} \left( \xi \right)} \mathord{\left/ {\vphantom {{\partial f_{i} \left( \xi \right)} {\partial x}}} \right. \kern-\nulldelimiterspace} {\partial x}}\) of \({\mathbf{s}}_{,x}^{\left( j \right)}\) and linear or nonlinear entry \({{\partial S_{i}^{\omega } } \mathord{\left/ {\vphantom {{\partial S_{i}^{\omega } } {\partial y}}} \right. \kern-\nulldelimiterspace} {\partial y}} = f_{i} \left( \xi \right){{\partial \omega } \mathord{\left/ {\vphantom {{\partial \omega } {\partial y}}} \right. \kern-\nulldelimiterspace} {\partial y}}\) of \({\mathbf{s}}_{,y}^{\left( j \right)}\) yields a nonlinear shear strain \(\varepsilon_{xy}\), as shown in Table 3. Therefore, the cross-sectional shape will warp out of their original plane surfaces. In practice, even a tiny cross-sectional warping can significantly contribute to the torsional response (see following Sect. 5.4).
The new HOBEs significantly benefit from fully considering the Green–Lagrange strains, i.e., a complete 3D Green–Lagrange strain state with the higher-order terms. Compared with the classical FE formulation, the ANCF gets the Wagner effects and cross-sectional stretch in a straightforward and compact manner. As shown in Table 4, considering a complete 3D Green–Lagrange strain brings advantages in two aspects:
-
(1)
In the classical FE formulations, such as the GEBF [5,6,7,8] and GBT [20], the higher-order terms of y and z in \(\varepsilon_{xx}\) [9,10,11,12,13,14, 17, 18]) are ignored under the small strain assumption. However, when the thin-walled beam experiences a moderate torque, the small strain assumption is no longer hold and the increasing nonlinear Wagner effects should be considered for correct results [9,10,11,12,13,14, 17, 18]). While in the ANCF, the higher-order terms in \(\varepsilon_{xx} = \frac{1}{2}{\mathbf{e}}^{{\text{T}}} {\mathbf{S}}_{xx} {\mathbf{e}} = \frac{1}{2}\left( {{\mathbf{e}}^{{\text{T}}} \left( {\sum\limits_{j = 1}^{3} {{\mathbf{s}}_{{{,}x}}^{{\left( j \right){\text{T}}}} {\mathbf{s}}_{{{,}x}}^{\left( j \right)} } } \right){\mathbf{e}} - 1} \right)\) are considered always, such as the warping-related entry \({{\partial S_{i}^{\omega } } \mathord{\left/ {\vphantom {{\partial S_{i}^{\omega } } {\partial x}}} \right. \kern-\nulldelimiterspace} {\partial x}} = \omega {{\partial f_{i} \left( \xi \right)} \mathord{\left/ {\vphantom {{\partial f_{i} \left( \xi \right)} {\partial x}}} \right. \kern-\nulldelimiterspace} {\partial x}}\) of \({\mathbf{s}}_{,x}^{\left( j \right)}\) in the proposed HOBEs, which avoids the expensive calculations of the extra warping and Wagner strain measures and their derivatives [8,9,10,11,12,13,14].
-
(2)
In some FE formulations based on the 1D-continuum theory, such as the GEBF [5,6,7,8,9,10,11,12] and the generalized strain beam formulation-based work [18], the cross-sectional stretch is neglected directly. Although the cross-sectional stretch often makes a relatively small contribution to the overall mechanical response, it is effective for locking alleviation and crucial for a correct analysis, as reported in [17]. After considering Wagner effects in [9,10,11,12,13,14], the GEBF [14] has been further refined via more GBT cross-sectional stretch modes to obrain a more flexible behavior. While in the ANCF based on the 3D-continuum theory, the cross-sectional stretch is always considered. This complete 3D-continuum theory-based ANCF allows the cross-sectional shape to vary along the beam axial direction, while the cross-sectional shape in the 1D-continuum theory-based formulations is often unchanged and constant. Moreover, in contrast to GBT modes [17] of uncoupled, many ANCF modes are stretch coupled modes [42, 73, 74] and the important effect of coupled modes in a large deformation case has been discussed in [42] for LOBEs. And it will also be discussed for the proposed HOBEs in the flowing Sect. 5.2.
In this study, the strain energy is given in terms of the energy-conjugate pair consisting of the Piola–Kirchhoff stress and the Green–Lagrange strain tensor. And the split strain subdivides the element elastic energy \(U^{\rm E}\) into two components, as
where T and W are the element thickness and width, respectively. The integral of an irregular section is usually divided into several independent integrals of regular sections; more details are given in Appendix C.
An alternative strain energy formulation can be further developed via the so-called structural mechanics formulation via generalized 3D strain measures, i.e., axial strain, shear strain, torsional strain, bending strain, cross-sectional stretch strain, and two extra warping strain measures. These two extra strain measures are conjugating to stress measures of bi-shear and bi-moment [8]. In GEBF, the way to simply the 3D Green–Lagrange strain tensor to the generalized 1D strain measures under the small train assumption can be found in [12]. The strain energy based on the elastic linear approach and obtained with respect to the relationships of all the kinematic modes can be found in [28, 36, 42, 43] only for LOBEs and existing HOBEs. However, the coupled modes to correctly predict the large deformation will be missing in this so-called structural mechanics formulation [42]. It is interesting to improve the so-called structural mechanics formulation to get a clear mechanical power expression via the vector of resultant forces and their conjugate strain measures, but it is beyond the scope of this study.
The entry in the vector of element elastic force [33] is
where \(H_{ta} = {{J_{0}^{ - 1} \partial S_{t} } \mathord{\left/ {\vphantom {{J_{0}^{ - 1} \partial S_{t} } {\partial \beta_{a} }}} \right. \kern-\nulldelimiterspace} {\partial \beta_{a} }}\) and \(H_{ta} = {{\partial S_{t} } \mathord{\left/ {\vphantom {{\partial S_{t} } {\partial \beta_{a} }}} \right. \kern-\nulldelimiterspace} {\partial \beta_{a} }}\) in a straight and undistorted reference configuration. \(\delta_{bc}\) is the Kronecker delta function, \(a,b,c,d,m,n = 1,2,3\), \(t,k,f,v = 1,2, \ldots ,{{N^{{\text{E}}} } \mathord{\left/ {\vphantom {{N^{{\text{E}}} } 3}} \right. \kern-\nulldelimiterspace} 3}\), \(i = 1,2 \cdots N^{E}\).
The entry in the tangent stiffness matrix or the Jacobian matrix of element elastic force [33] is
where \(j = 1,2 \cdots N^{E}\) and Eq. (28) is symmetric and nonlinear. The integral terms in Eqs. (27) and (28) are invariant quantities to be done in the pre-processing when computing at any state of deformation.
According to the work by Ebel et al. [28], the element names supplemented by the letter “c” throughout this study indicate the full elasticity-based elements (based on the CMA), such as the element MGD30c-ω (defined in Sect. 2.1.2). To prevent Poisson locking, elements here apply the enhanced CMA elaborated in this Sect. The element names supplemented by the letter “s” denote the elements using the structural mechanics to prevent Poisson locking, such as the element 3333 s (see Sect. 2.1.2).
3 The governing equations of the FMBs
The governing equations in the FMBs are a set of differential–algebraic equations (DAEs) of index-3 as follows,
where M is the constant mass matrix, e is the vector of generalized coordinates, FE is the vector of smooth nonlinear elastic forces, \({{\varvec{\uplambda}}}\) is the vector of Lagrange multipliers, \({\mathbf{C}} \in {\mathbb{R}}^{{n^{c} }}\) is the vector of smooth holonomic constrains, nc is the number of constraint equations, \({\mathbf{C}}_{{\mathbf{e}}}^{{\text{T}}} \in {\mathbb{R}}^{{n \times n^{c} }}\) is the Jacobian of vector C, and the over-dot denotes time derivative. Q is the vector of external forces and usually depends on position and velocity generalized vectors, which can stand for friction, aerodynamic and damping forces, etc. Thus, the first row of Eq. (29) are the dynamic equilibrium equations of the system, the second row of Eq. (29) are the nc kinematic constraints for the mechanical joints of the system.
4 Analysis of computational complexity
To highlight the advantages of using warping function over Lagrange polynomials in the HOBEs, the computation complexity \({\mathcal{O}}\left( {n^{m} } \right)\) in one Newton–Raphson iteration method is analyzed. For a relatively fair estimation with the same level for calculations, the beam modeled with the two-node, three-node, and four-node LOBEs is meshing into 38, 24, and 16 elements (around 588 DOFs). Compared with the existing HOBEs using Lagrange polynomials to describe the warping deformation in Eq. (5), the proposed new HOBEs can reduce the model DOFs using warping function in Eq. (8). For example, for the two-node HOBEs, the proposed B24-ω, respectively, reduces the model DOFs from 819 (B42 [26, 27, 29]) and 1872 (B4 [26]) to 585. For the three-node HOBEs, the proposed 3333-ω reduces the model DOFs from 882 (3363 [28]) to 588. For the four-node HOBEs, the proposed 3433-ω extremely reduces the model DOFs from 1470 (34X3 [28]) to 588. Same meshes ne for the proposed p-node HOBEs will be numerically tested in the following Princeton beam.
For statics problems as shown in Table 5, the computational cost estimation in one Newton–Raphson iteration is consistent with the model DOFs. Thus, the computational complexities are \({\mathcal{O}}\left( n \right)\) and \({\mathcal{O}}\left( {n_{t} + n_{b} } \right)\) in the FOM and ROM, respectively. And \(n \gg n_{t} + n_{b}\) always holds. For dynamics problems, the computational complexity is \({\mathcal{O}}\left( {n + n^{c} } \right)\) for solving the DAEs described by Eq. (29). Table 5 indicates the potential of time reduction when the proposed HOBEs are used. In the following numerical examples, the accuracy and efficiency of the proposed HOBEs will be tested comprehensively.
5 Case studies
5.1 Princeton beam experiment
The Princeton beam has served as a benchmark to assess the accuracy of the beam formulations in many studies [28, 31,32,33,34]. It is subjected to actions of combined axial compressive, large biaxial bending, and bending-torsion coupled under vertical loading. The condensed adaptive CMS algorithm recently proposed by the authors [33], based on the FE model of the LOBE 3333c with shear correction factors, has been validated by the Princeton beam. It indicates that the CMS based on the successively local linearizations [71] can describe the nonlinear curve in space and capture such significant nonlinear multi-coupling problems. An interesting phenomenon is that the tip force in one direction decreases but the displacement increases, mainly caused by the coupling of bending-torsion. As reported in [28], among the proposed elements with the ability to describe the non-uniform shear stress on the cross section, only the above 34X3c can capture this coupling phenomenon when k2 = k3 = 1. However, the accuracy and efficacy of the numerical solution depend on the geometric description defined by the kinematic description. Therefore, a comparative study is first made based on the Princeton beam to test the performance of the new HOBEs whose displacement field is constructed by the warping function.
As shown in Fig. 1, X–Y-Z is the inertial frame, and x–y-z is the material frame attached at the beam end. Under a tip load P, the free end tip orientation of the cantilever beam is defined as \(\theta\). Thus, the free end tip twist can be written as \(\phi = \theta - \left. \theta \right|_{P = 0}\). The free end tip deflection along the vectors y and z is denoted as \(u_{2}\) and \(u_{3}\), respectively. The applied tip load P is varied from 0 to 90 degrees.
Results in Figs. 2, 3, and 4 show the 11 predictions for the 4 proposed HOBEs (BE24c-ω, 3333c-ω, 3433c-ω, and MGD30c-ω), 2 existing HOBEs (BE42c and 34X3c), 2 LOBEs (3333c and MGD30c), ANSYS BEAM188, ANSYS SOLID95, and GEBF of Bauchau et al. [32] under 3 loading cases, as well as the error bar (MGD30c-ω vs. experiment [80]). The 3 loading cases are P1 = 4.448 N, P2 = 8.896 N, and P3 = 13.345 N, respectively. As mentioned above, the Princeton beam meshes ne the same as the p-node elements in Table 5.
As shown in Fig. 2, the LOBEs 3333c and MGD30c fail to predict the bending-torsion coupling under P3 = 13.345 N, i.e., the tip force in z direction decreases but the corresponding displacement |u3| increases. This coupling phenomenon arises because the planar beam elements cannot describe the non-uniform distributed shear stress when k2 = k3 = 1. The 6 curves of 3333c-ω, 3433c-ω, MGD30c-ω, ANSYS BEAM188, ANSYS SOLID95, and the GEBF [32] agree well with each other, and are close to the experimental data [80], but the curves of BE24c-ω, 34X3c, and BE42c deviate a little from the above curves. In Fig. 3, the displacement prediction |u2| in the y direction of the 11 elements and the experimental data [80] agree well with each other.
As shown in Fig. 4, the differences among the 11 elements and the experimental data [80] are apparent in the twist angle predictions. The number of curves close to the experimental data [80] is reduced from 6 to 4, because the 2 curves of ANSYS cannot predict the behavior under significant torsional actions correctly [9, 25]. The 2 curves of BE24c-ω and ANSYS SOLID95 deviate a little from the above 4 closed curves. The 3 curves of BE42c, 34X3c, and ANSYS BEAM188 differ far from the above 4 closed curves. Similarly, the LOBEs 3333c and MGD30c completely fail to predict the twist angle. The curves of LOBE BE24c are close to the curves of 3333c and MGD30c, which are not plot in Figs. 2, 3, and 4 so as not to affect the observation of other curves. These results demonstrate that a warping function helps the proposed HOBEs account for the non-uniform distribution of shear stress, and thus relax the need for a shear correction factors.
The Von-Mises stress obtained from the proposed MGD30c-ω is slightly smaller than that from ANSYS SOLID95 under P3 = 13.345 N at three loading angles, as shown in Fig. 5. It is worth noting that all these results of ANCF are obtained when k2 = k3 = 1. Although using shear correction factors can improve the performance of LOBEs straightforward [31,32,33,34], it cannot capture the cross-sectional warping, as shown in Fig. 6. The end-sectional Von-Mises stress (Pa) contour modeled by the proposed is still slightly smaller than that from ANSYS SOLID95, and it distributes more uniformly. Although the existing HOBEs can improve the global response by increasing Lagrange polynomials’ order, they cause increasingly tremendous Von-Mises stress on the end section. The warping shape differs from each other when modeling by different transverse interpolations.
The computation time of the Princeton beam under the 3 loading cases (21 computing cases) is shown in Table 6. Most of the time spent in the pre-processing is to calculate the invariant quantities in Eqs. (27) and (28) to compute force and stiffnesses at any state of deformation. The solving time is to solve the equations of nonlinear static equilibrium in the Newton–Raphson iteration. The time consumed for the 34X3c is taken as the standard one, i.e., \(T_{3}^{s} = 1779.89s\). Simulations show that the total time consumed for the BE24c-ω, MGD30c-ω, and 3333c-ω is all, respectively, smaller than \(T_{3}^{s} \%\). The 34X3c is still time-consuming even when ne = 1, because T1 = 1734.26 s and T2 = 0.81 s. The proposed BE24c-ω, 3333c-ω, 3433c-ω, and MGD30c-ω all are more accurate and extremely time-saving than the existing HOBEs 34X3c in this benchmark test.
The displacement u3 (m) with an increasing mesh (P = 13.345 N and \(\theta { = }30^{{\text{o}}}\)) is shown in Table 7. The relative error in the last column is \(\Delta { = }\left| {{{\left( {u - u_{s} } \right)} \mathord{\left/ {\vphantom {{\left( {u - u_{s} } \right)} {u_{s} }}} \right. \kern-\nulldelimiterspace} {u_{s} }}} \right| \times 100\%\), where u is the final results of the elements used when ne = 48, and us is the standard results of experiment [80]. To avoid locking, the mixed formulation 3333 s [28] uses the structural mechanics to calculate the stiffness and thus yields an error of 0.75%. As expected, the LOBEs 3333c and MGD30c poorly overestimate the stiffness since they both miss the warping deformation and the shear correction factor. The results of 3333 s, 3333c-ω, MGD30c-ω, and 3433c-ω yield an error smaller than 1%. And the results of BE24c-ω, ANSYS BEAM188, and ANSYS SOLID95 yield an error between 1% and 1.5%. The result of 34X3c derived in this study final agrees well with that of the 34X3c of Ebel et al. [28] when ne = 48, and is closer to the experiment date [80] with a rough meshing. Under a rough mesh ne = 1 or 4, the MGD30c-ω, 34X3c, 3433c-ω, ANSYS BEAM188, and 3333 s exhibit significant locking alleviation.
5.2 Uniform and non-uniform cross section cantilever beam under torsion
This example aims to evaluate the proposed new HOBEs, mainly MGD30c-ω, under pure twisting conditions. As shown in Fig. 7, four beams of uniform and non-uniform cross sections are subjected to an imposed torsion at its free end, respectively. In Fig. 7a, the I-section cantilever beam has been investigated in the GEBF [10,11,12, 17] to analyze Wagner effects [4] on the thin-walled beams and will be served as a benchmark problem here. To capture the geometries of beams with non-uniform cross section, some classical FE formulations have to use dense mesh because the cross-sectional shapes cannot change along the element length. However, dense mesh are often too computationally expensive to be practical in a large-scale engineering system. In the ANCF, the cross-sectional shapes can vary along the element length via changing the upper and lower limits of cross-sectional integral terms instead of dense mesh. In Fig. 7d, the tapered cantilever has been investigated in the ANCF/FFR SSM [46] about the first bending frequency and will be served as a benchmark problem in this study. To better compare with existing works, the Young's modulus E = 210 GPa for I-section cantilever beam is set the same with [10], while E = 1 GPa for the rest four cantilevers is set the same with [46]. For the five studied cantilever beams, the length, density, and Poisson’s ratio are L = 2 m, ρ = 7850 kg/m3, and \(\nu\) = 0.3, respectively.
As stated below Eq. (26) and Appendix C, the I-section in Fig. 7a is divided into three rectangular regions, and the hollow cross section in Fig. 7c, d is divided into four rectangular regions. Many works [10,11,12] of GEBF use the warping function and shear correction factor to improve its performance, mainly because the inadequacy of the assumed warping displacement field for the I-section beam in detecting cross-sectional modes [17]. In this study, BE24c-ω and MGD30c-ω (k2 = k3 = 0.3868 [2]) are discussed, and two quadratic elements BE24c-ω-II and MGD30c-ω-II (k2 = k3 = 1) with more cross-sectional modes are also discussed comparatively. Please see Appendix B2 for more details of the element MGD30c-ω-II.
Table 8 compares the first in-plane (X–Z plane) bending frequency of the cantilevers modeled by the proposed HOBEs, ANCF/FFR SSM (modeled by BE24) in [46], and commercial codes accordingly. It is worth noting that the results not supplemented with parentheses “()” are divided into neelements by default, and the commercial solid elements need to be finely meshed to obtain the correct solutions. For the I-section and hollow tapered cantilever beams, the frequencies of the proposed HOBEs are slightly higher than the commercial codes. Compared with the frequency of MGD30c-ω, the frequency of MGD30c-ω-II is smaller because more cross-sectional modes make the system more flexible. For the square, hollow rectangular and tapered cantilever beams, the frequencies of MGD30c-ω agree well with those of commercial codes. Besides, the beams modeled by MGD30c-ω get the correct solutions via a minimal mesh, significantly reducing the computational burden. For the tapered beam, the frequency of MGD30c-ω converges faster than the ANCF/FFR SSM in [46].
In Fig. 8, the results of different FEs with an increasing torque Mx for the I-section cantilever are presented. The GBT [20] is widely used in assessing the structural behavior of thin-walled prismatic bars via deformation modes (shape functions). In Fig. 8a, the GBT displayed a slightly more flexible response than GEBF, because the cross-sectional in-plane modes are considered in GBT [17] but neglected in GEBF [10]. Recently, the GEBF-based work [14] has been refined by adding more kinematic DOFs via the deformation modes of the GBT, leading to more flexible behavior. While the cross-sectional in-plane modes are always considered in the ANCF as a 3D-continuum theory, three conclusions can be drawn:
-
(1)
Fefferred to [81], the linear rotation angle is \(\theta = {{M_{x} L} \mathord{\left/ {\vphantom {{M_{x} L} {\left( {GI_{t} } \right)}}} \right. \kern-\nulldelimiterspace} {\left( {GI_{t} } \right)}}\), where \(I_{t} = \left( {\left( {H - 2T_{{{\text{flange}}}} } \right)W_{{{\text{web}}}}^{3} + 2W_{{{\text{flange}}}} T_{{{\text{flange}}}}^{3} } \right){\eta \mathord{\left/ {\vphantom {\eta 3}} \right. \kern-\nulldelimiterspace} 3}\), and \(\eta = 1.2\) for the I-section. The geometric parameters are shown in Fig. 7a, thus \(\theta = {{M_{x} L} \mathord{\left/ {\vphantom {{M_{x} L} {\left( {GI_{t} } \right)}}} \right. \kern-\nulldelimiterspace} {\left( {GI_{t} } \right)}} = {{{7}{\text{.198}}M_{x} } \mathord{\left/ {\vphantom {{{7}{\text{.198}}M_{x} } {10^{5} }}} \right. \kern-\nulldelimiterspace} {10^{5} }}\). Literature [10] pointed out that the nonlinear Wagner effects increase crucial when the tip end rotation angle \(\theta > \pi /12\). And the linear and nonlinear results only match well when the nonlinear Wagner effects are not significant \(\theta \le \pi /12\). When \(M_{x} = 3.637{\text{kNm}}\), the corresponding \(\theta = 15^{{\text{o}}}\) in the linear analytical results [81] and \(\theta = 14.2^{{\text{o}}}\) in the proposed MGD30c-ω. As shown in Fig. 10a, the curves of proposed elements agree well throughout the whole range \(\theta \in \left[ {\begin{array}{*{20}c} 0 & {\pi /2} \\ \end{array} } \right]\) in [10] to demonstrate the correctness of the proposed elements in the linear (\(\theta \le \pi /12\)) and nonlinear rotation (\(\theta > \pi /12\)) problems.
-
(2)
The results of BE24c-ω and MGD30c-ω are close to [10, 17] only when \(\theta \le \pi /2\). When \(\theta > \pi /2\), the results of BE24c-ω and MGD30c-ω become rigid and differ from [10, 17] apparently. Moreover, considering more cross-sectional modes (e.g., warping and stretch), the results of BE24c-ω-II and MGD30c-ω-II are more flexible. Especially, the results of MGD30c-ω-II and GBT coincide throughout the load range considered in [17]. Although the contributions of cross-sectional stretch are relatively small, they are crucial for the correct analysis, especially in the large nonlinear analysis.
-
(3)
As demonstrated above, considering the full effects of Green–Lagrange strains in the ANCF, the continuity of displacement field is always satisfied. Thus, the maximum rotation θ for the proposed HOBEs can exceed 16 radians, as depicted in Fig. 8. In contrast, the maximum rotation θ is approximately 5 radians in GBT [17], even smaller in GEBF [10,11,12] and commercial FE codes (1.75π and 0.7π accordingly for ABAQUS C3D8I and ANSYS SOLID95).
In Fig. 8b, a nonlinear axial shortening phenomenon occurs at the free end accounting for Wagner effects. In the ANCF, Wagner effects are captured entirely with the full consideration of the Green–Lagrange strain tensor (more detailed discussions as shown below Eq. 25). However, most existing commercial FE codes do not consider Wagner effects, leading to an inaccurate structural behavior under significant nonlinear torsional actions [9, 25]. For example, the results of ne(= 2300) ABAQUS C3D8I (solid elements) are more rigid than [10, 17]. In addition, for the proposed HOBEs, although the element DOFs are reduced significantly, it is still significant to construct the ROM. As shown in Fig. 8, the ROM named CMS-MGD30c-ω-II with \(n_{t} =\) 250 modes can fully capture the large nonlinear torsional behavior of the FOM (495 DOFs), exhibiting high robustness when \(M_{x} \in \left[ {0\;\;8000} \right]\) kNm.
The modal analysis is made for a single MGD30c-ω-II element of I-section, and some partial mode shapes are depicted in Fig. 9. On the one hand, mode shapes in the first row are the common modes of MGD30c and MGD30c-ω-II. They can only describe the planar section during deforming, including the stretch, and thus belong to the lower-order part of MGD30c-ω-II. On the other hand, mode shapes in the second and third rows are unique in the MGD30c-ω-II and belong to its higher-order part to describe a complex cross-sectional deformation, especially the warping. As it can be seen, mode 5 is the torsional mode, modes 37 and 40 are the warping shear modes, and modes 43, 44, and 45 are the in-plane shear modes (the so-called local plate modes in [17]). It is worth mentioning that the full consideration of the Green–Lagrange strain tensor leads to many cross-sectional stretch coupled modes, which is a typical characteristic of ANCF. For example, mode 7 couples the axial extension and cross-sectional stretch significantly, similar to modes 9 and 12. Mode 17 couples the warping shear and transverse stretch, similar to mode 50. Mode 25 couples the warping shear, axial extension, and transverse stretch. The cross-sectional stretch coupled modes may benefit the ROM using not many modes (or DOFs) to predict the large deformation correctly, especially in the cases where the cross-sectional stretch is crucial. For example, to maintain the accuracy over a medium nonlinear torsion range \(\theta \in \left[ {0\;\;5} \right]\), there are only \(n_{t} =\) 120 mostly coupled modes in the ANCF but 726 uncoupled modes (a lot of cross-sectional stretch modes) in GBT [17]. The important effect of coupled modes to correctly predict the large deformation has been discussed in [42] for LOBEs. In addition, the modes must increase to 250 if the nonlinear torsion range expands as \(\theta \in \left[ {0\;\;16} \right]\).
As shown in Fig. 10, the results of the ROM and FOM are closely matched in all three cantilever beams. The ROM discards the modes with minimal contributions, thus showing a slightly rigid behavior than the FOM near the maximum torque, only observed in the enlarged view. As shown in Fig. 10a, similarly, the torsional response of ABAQUS C3D8I (ne = 1600) shows a slightly rigid behavior compared with MGD30c-ω (ne = 20), and diverges around a small torque of 9 kNm. In Fig. 10c, the modes can be reduced gradually to \(n_{t} =\) 120 modes when \(\theta \in \left[ {0\;\;2} \right]\). Although not shown, the conclusions related with the ROM of Fig. 10a, c are applied to the other cantilever beams studied. The linear results are fefferred to [81], and the geometric parameters are shown in Fig. 7b, e. In the square cantilever, \(\theta = {{M_{x} L} \mathord{\left/ {\vphantom {{M_{x} L} {GI_{t} }}} \right. \kern-\nulldelimiterspace} {GI_{t} }}\), where \(I_{t} = \beta HW^{3}\), and \(\beta = 0.1406\). Thus, \(\theta = {{{3}{\text{.688}}M_{x} } \mathord{\left/ {\vphantom {{{3}{\text{.688}}M_{x} } {10^{4} }}} \right. \kern-\nulldelimiterspace} {10^{4} }}\). In the closed thin-walled cantilever, \(\theta = {{M_{x} LS} \mathord{\left/ {\vphantom {{M_{x} LS} {4GAT}}} \right. \kern-\nulldelimiterspace} {4GAT}}\), where \(S\) and \(A\) are the center line length of the wall section and area bounded by wall section, respectively. Thus, \(\theta = {{{1}{\text{.2406}}M_{x} } \mathord{\left/ {\vphantom {{{1}{\text{.2406}}M_{x} } {10^{3} }}} \right. \kern-\nulldelimiterspace} {10^{3} }}\). The nonlinear Wagner effects increase sharply at a small rotation angle in the thin-walled box cantilever in Fig. 10d, while increase slowly in the other three cantilevers and can be neglected at least when \(\theta \le \pi\).
The torsional configurations of the cantilever beams are depicted in Fig. 11, and θ represents the free end rotation angle. The visible axial shortening at the free end is due to Wagner effects. When θ = 360°, although the cross sections warp out of their original plane surfaces, the cross-sectional stretch is not obvious and the cross-sectional projections almost retain their original shapes on the section view. The cross-sectional stretch is visible in Fig. 11b (θ = 2160°) and Fig. 11d (θ = 1260°). Although the stretch affection is not significant in distorting the local cross-sectional shape, it cannot be neglected due to the global response, as discussed in Fig. 8a.
The Von-Mises stress (Pa) contour, cross-sectional shape after warping (θ = 540°), and the corresponding rigid shape of each beam are shown in Fig. 12. When θ increases, the cross-sectional projections no longer retain their original shapes on the YZ view and will be slightly different due to the cross-sectional stretch and shear. The distorted boundary of the cross section deviates visibly from the original/rigid shape in Fig. 12a, d. The cross-sectional straight boundaries in Fig. 12a are distorted as curve boundaries due to the nonlinear strains εyy and εzz in the proposed HOBEs, as stated below Table 3. The difference between the rigid shape, planar shape in Eq. (1) and cross-sectional shape after warping in Eqs. (4) and (8) can be understood in Fig. 9d. The two adjacent edges of the rectangle are no longer perpendicular to each other in the planar shape. As stated in the beginning of Sect. 2, the ANCF LOBEs in Eq. (1) relax the assumption of a rigid cross section, and induce parallelogram [74] and strech deformations. The maximum deviation of the cross section after warping from a plane surface is almost up to 80 mm, 7 mm, 15 mm, and 25 mm in the I-section, square, hollow rectangular, and thin-walled box cantilevers, respectively.
The Von-Mises stress (Pa) contours of twist beams and cross sections are plot in Tables 9 and 10; some conclusions are drawn:
-
(1)
For the I-section cantilever (see Table 9), although the tip end rotations of MGD30c-ω and ANSYS SOLID95 agree well at a same torque, the web’s Von-Mises stress of MGD30c-ω is much smaller. In comparison, concering more cross-sectional modes, MGD30c-ω-II agrees well with ANSYS SOLID95 in the predictions of tip end rotation and Von-Mises stress distribution.
-
(2)
For the square cantilever (see Table 9), only B4 can capture the torsional-warping shape accurately among the HOBEs proposed in [26], but it caused tremendous end-sectional Von-Mises stress. In contrast, the MGD30c-ω can accurately capture the Von-Mises stress and torsional-warping shape with low computational burdens, which improves the accuracy and efficiency of existing HOBEs [26]. It is worthy to mention that although the free-locking LOBEs do not generate tremendous end-sectional Von-Mises stress, they generate wrong distributed Von-Mises stress on the side in the square cantilever under torsion [26].
-
(3)
The linear analytic solution for square cantilever and thin-walled box cantilever has been given below Fig. 10. For the square cantilever, when \(M_{x} = 10{\text{kNm}}\), \(\theta \approx { 211}{\text{.3}}^{{\text{o}}}\) in the linear analytic solution, which agrees well with the ANSYS SOLID95 \(\theta \approx { 210}^{{\text{o}}}\) and the proposed MGD30c-ω \(\theta \approx { 212}^{{\text{o}}}\). For the closed thin-walled cantilever, when \(M_{x} = 0.8{\text{kNm}}\), \(\theta \approx { 45}{\text{.8}}^{{\text{o}}}\) in the linear analytic solution [81], which only agrees well with the proposed MGD30c-ω \(\theta \approx { 46}^{{\text{o}}}\) and much smaller than the ANSYS SOLID95 \(\theta \approx { 60}^{{\text{o}}}\). For the thin-walled box cantilever experiencing linear rotations, the proposed MGD30c-ω performs better than ANSYS SOLID95.
-
(4)
For the cantilevers, although the proposed HOBEs are meshed much rougher than ANSYS SOLID95 (8 vs. 1261 FE and 20 vs. hundreds FE, respectively), their Von-Mises stress contours are basically in good agreement in both the qualitative and quantitative aspects. Unfortunately, the ANSYS SOLID95 code gradually diverges after reaching the provided rotation angles in Table 9, far from the prediction of the proposed HOBEs with considerable rotation angles presented in Table 10. In the ANCF, the excellent torsional capacity benefits from the full consideration of the Green–Lagrange strain tensor.
-
(5)
For each symmetric cross section as presented in Tables 9 and 10, the sectional contours of the free end are symmetric under a pure torsion.
5.3 The dynamics of an unbalanced shaft
The numerical example of the rotating hollow circular shaft with an unbalanced disk has been served as a benchmark in the nonlinear dynamic analysis [32,33,34]. As shown in Fig. 13, a rigid disk is attached to the shaft at its mid-span and above the shaft axis by an offset d and some geometry data and material parameters are also listed here. In the shaft, the end C is connected to the rigid ground via a cylindrical joint, while the end O is driven by a revolute joint at angular speed \(\Omega \left( t \right)\), yields
where A1 = 0.8, A2 = 1.2, T1 = 0.5 s, T2 = 1 s, T3 = 1.25 s, and \(\omega = 60{\text{rad/s}}\).
The results of the lateral oscillations of the hollow circular shaft passing through the critical speeds are shown in Fig. 15. The isogeometric analysis (IGA) [82] uses a spline interpolation in the FE. While the Dymore [32] (GEBF-based FMBS code) and the ANCF discretize the continuum using traditional methods by sharing end nodes. The shear energy is modified in the LOBEs-based works [32, 34], and the Dymore [32] serves as the reference solution here. Three following conclusions are obtained: (i) The results of C-MGD30c (k2 = k3 = 0.5306 [2]) show the best agreement with [32], while the results of IGA in [34] show a relatively large error after t = 1 s. (ii) Once the FEs do not modify the shear energy, the error of LOBE, i.e., MGD30c (k2 = k3 = 1), increases visually after 1.8 s. However, the results of the HOBE, i.e., MGD30c-ω (k2 = k3 = 1), and the Dymore in [32] match closely. This result again demonstrates that it is unnecessary to modify the shear energy if the HOBE can well capture the non-uniform distribution of the shear stress. (iii) However, the results of 34X3c deviate the farthest from [32]. Similarly, the 34X3c was compared with ANSYS BEAM189 in [83] via a solid circular shaft, and their results did not match well. These results again demonstrate that it is unnecessary to modify the shear energy if the HOBE can well capture the non-uniform distribution of the shear stress.
In Fig. 15, the Von-Mises stress contours show that strong forces can be observed in the middle and at both ends of each shaft, as expected. The Von-Mises stress contours of MGD30c (k2 = k3 = 0.5306), MGD30c (k2 = k3 = 1) and MGD30c-ω (k2 = k3 = 1) match well, except for the cross section since only the MGD30c-ω (k2 = k3 = 1) can capture the non-distributed sheer stress of the unbalanced shaft. While the cross-sectional Von-Mises stress is minimal for the planar beams and excessively large for HOBE 34X3c. The application of the higher-order Lagrange polynomials to describe the cross-sectional deformation can cause tremendous Von-Mises stress, which has also been reported for B4 in [26] (as demonstrated in Sect. 5.2 for the square cantilever).
The computation time of the unbalanced shaft is shown in Table 11. The time consumed for the 34X3c is taken as the standard one, i.e., \(T_{3}^{s} = 21830{\text{s}}\). Compared with the propossed MGD30c-ω and the existing HOBE 34X3c, (i) the pre-processing time consumed is reduced to 1.35% (233 s vs. 17217 s), (ii) the solving time consumed is reduced to 38.78% (1789s vs. 4613 s), and (iii) the total time consumed is reduced to 9.26% (2022s vs. 21830 s). Again, the proposed MGD30c-ω is more accurate and extremely time-saving than the existing HOBE 34X3c in this benchmark test.
6 Conclusion
Existing high-order beam elements (HOBEs) for ANCF require cubic (34X3c [28]) and biquadratic (B4 [26]) Lagrange polynomials to accurately predict the benchmarks of bidirectional bending and cross-sectional warping, respectively. An existing p-node (low-order beam element) LOBE usually only has 9p, 10p or 12p DOFs per element, while the additional DOFs increase to 21p and 36p in the cubic and biquadratic HOBEs, respectively. It is very time-consuming to increase the accuracy by only increasing the interpolation order in the HOBEs. What is worse, the existing HOBEs with accurate deformation responses cause tremendous Von-Mises stress on the end-section.
Inspired by the GEBF [8], a new mixed kinematic description of beam elements is introduced via the slope vectors and warping functions. To alleviate the element locking and preserve the coupled modes, the strain energy formulation is derived via the enhanced continuum mechanic approach. In contrast to the classical FE (based on 1D-continuum theory) [8], the new ANCF HOBEs (based on 3D-continuum theory) capture the out-of-plane warping, nonlinear cross-sectional stretch, and nonlinear Wagner effects of uniform and non-uniform beams straightforwardly. While for the strain energy formulation obtained with respect to the relationships of all the kinematic modes [28, 36, 42, 43], the coupled modes to correctly predict the large deformation will be missing [42].
The accuracy and efficiency of the proposed HOBEs are examined on various benchmarks, FE formulations, commercial codes, and experimental data. Conclusions are drawn as follows from these challenging benchmarks:
-
(1)
In contrast to [26, 28], the additional DOFs per element proposed to describe the out-of-plane warping can be significantly reduced to 3p. Thus, the efficiency is promoted by one or even two orders of magnitude than the existing 34X3c and B4.
-
(2)
The distribution and accuracy of Von-Mises stress in the proposed HOBEs are significantly improved compared with the existing HOBEs and LOBEs, which matches well with the results from commercial ANSYS SOLID95 codes.
-
(3)
In a significant torsion, the stretch is often crucial for obtaining correct results and the coupled modes make the reduced-order model reserve fewer modes compared with the classical FE formulations [17].
-
(4)
The proposed HOBEs exhibit excellent agreements with the standard results in all the provided challenging benchmarks, and MGD30c-ω can be the first choice in simulation. Moreover, a complete 3D strain state without a small strain assumption is helped to expand the torsional range.
-
(5)
The ANCF LOBEs relax the assumption of a rigid cross section, and parallelogram and stretch deformations are allowed. In addition, the locking-free LOBEs are accurate enough in some benchmarks where the warping and Von-Mises stress in a twisting condition are unconcerned. The existing HOBEs are accurate enough in some benchmarks where the computational efficiency and end-sectional Von-Mises stress are unconcerned.
The proposed HOBEs will be used to study the reduced-order model of dynamic systems of composite structures or folded wings in aviation in future research.
Availability of data and materials
The datasets generated during the current study are available from the corresponding author on reasonable request.
References
Timoshenko, S.P., Goodier, J.N.: Theory of Elasticity. McGraw-Hill, New York (1970)
Cowper, G.R.: The shear coefficient in Timoshenko’s beam theory. J. Appl. Mech. 33(2), 335–340 (1966)
Popescu, B., Hodges, D.H.: On asymptotically correct Timoshenko-like anisotropic beam theory. Int. J. Solids Struct. 37(3), 535–558 (2000)
Wagner, H.: Verdrehung und knickung von offenen profilen (Torsion and buckling of open sections). In: NACA Tech, Washington, DC, Memorandum No. 807 (1936)
Simo, J.C.: A finite strain beam formulation. The three-dimensional dynamic problem. Part I. Comput. Methods Appl. Mech. Eng. 49(1), 55–70 (1985)
Simo, J.C., Vu-Quoc, L.: On the dynamics of flexible beams under large overall motions—the plane case: part II. J. Appl. Mech. 53(4), 855–863 (1986)
Jelenic, G., Crisfield, M.A.: Geometrically exact 3D beam theory: implementation of a strain-invariant finite element for statics and dynamics. Comput. Methods Appl. Mech. Eng. 171(1–2), 141–171 (1999)
Simo, J.C., Vu-Quoc, L.A.: Geometrically-exact rod model incorporating shear and torsion-warping deformation. Int. J. Solid Struct. 27(3), 371–393 (1991)
Pi, Y.L., Bradford, M.A., Uy, B.: A spatially curved-beam element with warping and Wagner effects. Int. J. Numer. Methods Eng. 63(9), 1342–1369 (2005)
Manta, D., Goncalves, R.: A geometrically exact Kirchhoff beam model including torsion warping. Comput. Struct. 177, 192–203 (2016)
Goncalves, R.: A shell-like stress resultant approach for elastoplastic geometrically exact thin-walled beam finite elements. Thin-Walled Struct. 103, 263–272 (2016)
Rong, J., Wu, Z., Liu, C., Brüls, O.: Geometrically exact thin-walled beam including warping formulated on the special Euclidean group SE(3). Comput. Methods Appl. Mech. Eng. 369, 113062 (2020)
Wackerfuss, J., Gruttmann, F.: A nonlinear Hu-Washizu variational formulation and related finite-element implementation for spatial beams with arbitrary moderate thick cross-sections. Comput. Methods Appl. Mech. Eng. 200(17–20), 1671–1690 (2011)
Peres, N., Gonalves, R., Camotim, D.: A geometrically exact beam finite element for curved thin-walled bars with deformable cross-section. Comput. Methods Appl. Mech. Eng. 381(3), 113804 (2021)
Han, S., Bauchau, O.A.: Nonlinear, three-dimensional beam theory for dynamic analysis. Multibody Syst. Dyn. 41, 173–200 (2017)
Meier, C., Popp, A., Wall, W.A.: Geometrically exact finite element formulations for slender beams: Kirchhoff-Love theory versus Simo-Reissner theory. Arch. Computat. Methods Eng. 26(1), 163–243 (2019)
Duan, L., Zhao, J.: A geometrically exact cross-section deformable thin-walled beam finite element based on generalized beam theory. Comput. Struct. 218, 32–59 (2019)
Jonker, J.B.: Three-dimensional beam element for pre- and post-buckling analysis of thin-walled beams in multibody systems. Multibody Syst. Dyn. 52(1), 59–93 (2021)
Arora, A., Kumar, A., Steinmann, P.: A computational approach to obtain nonlinearly elastic constitutive relations of special Cosserat rods. Comput. Methods Appl. Mech. Eng. 350, 295–314 (2019)
Schardt, R.: Verallgemeinerte Technische Biegetheorie. Springer, Berlin (1989)
Besseling, J.F.: Non-linear theory for elastic beams and rods and its finite element representation. Comput. Methods Appl. Mech. Eng. 31(2), 205–222 (1982)
Eisenberger, M.: An exact higher-order beam element. Comput. Struct. 81(3), 147–152 (2003)
Corre, G.: Higher-order elastoplastic beam models. Ph.D. Thesis, Universite Paris-Est (2018)
Matikainen, M.K., Dmitrochenko, O., Mikkola, A.: Beam elements with trapezoidal cross section deformation modes based on the absolute nodal coordinate formulation. In: International Conference of Numerical Analysis and Applied Mathematics, Rhodes, Greece (2010)
Li, P., Gantoi, F.M., Shabana, A.A.: Higher-order representation of the beam cross-sectional deformation in large displacement finite element analysis. J. Sound Vib. 330(26), 6495–6508 (2011)
Shen, Z., Li, P., Liu, C., Hu, G.: A finite element beam model including cross-section distortion in the absolute nodal coordinate formulation. Nonlinear Dyn. 77(3), 1019–1033 (2014)
Orzechowski, G., Shabana, A.A.: Analysis of warping deformation modes using higher-order ANCF beam element. J. Sound Vib. 363, 428–445 (2016)
Ebel, H., Matikainen, M.K., Hurskainen, V.V., Mikkola, A.: Higher-order beam elements based on the absolute nodal coordinate formulation for three-dimensional elasticity. Nonlinear Dyn. 88(2), 1075–1091 (2017)
Patel, M., Shabana, A.A.: Locking alleviation in the large displacement analysis of beam elements: the strain split method. Acta. Mech. 229, 2923–2946 (2018)
Carrera, E., Giunta, G., Petrolo, M.: Beam Structures: Classical and Advanced Theories. Wiley, New York (2011)
Bauchau, O.A., Han, S., Mikkola, A., Matikainen, M.K., Gruber, P.: Experimental validation of flexible multibody dynamics beam formulations. Multibody Syst. Dyn. 34(4), 373–389 (2015)
Bauchau, O.A., Betsch, P., Cardona, A., Gerstmayr, J., Jonker, B., Masarati, P., Sonneville, V.: Validation of flexible multibody dynamics beam formulations using benchmark problems. Multibody Syst. Dyn. 37(1), 29–48 (2016)
Tang, Y., Hu, H., Tian, Q.: A condensed algorithm for adaptive component mode synthesis of viscoelastic flexible multibody dynamics. Int. J. Numer. Methods Eng. 122(2), 609–637 (2021)
Tasora, A., Benatti, S., Mangoni, D., Garziera, R.: A geometrically exact isogeometric beam for large displacements and contacts. Comput. Methods Appl. Mech. Engrg. 358, 112635 (2020)
Yakoub, R.Y., Shabana, A.A.: Three dimensional absolute nodal coordinate formulation for beam elements: implementation and applications. J. Mech. Des. 123(4), 614–621 (2001)
Gerstmayr, J., Matikainen, M.K., Mikkola, A.: A geometrically exact beam element based on the absolute nodal coordinate formulation. Multibody Syst. Dyn. 20, 359–384 (2008)
Romero, I.: A comparison of finite elements for nonlinear beams: the absolute nodal coordinate and geometrically exact formulations. Multibody Syst. Dyn. 20(1), 51–68 (2008)
Bauchau, O.A., Han, S., Mikkola, A., Matikainen, M.K.: Comparison of the absolute nodal coordinate and geometrically exact formulations for beams. Multibody Syst. Dyn. 32(1), 67–85 (2014)
Schwab, A.L., Merjaard, J.P.: Comparison of three-dimensional flexible beam elements for dynamic analysis: classical finite element formulation and absolute nodal coordinate formulation. J. Comput. Nonlin. Dyn. 5(1), 11010 (2010)
Nachbagauer, K.: State of the art of ANCF elements regarding geometric description, interpolation strategies, definition of elastic forces, validation and the locking phenomenon in comparison with proposed beam finite elements. Arch. Computat. Methods Eng. 21(3), 293–319 (2014)
Schwab, A.L., Meijaard, J.P.: Comparison of three-dimensional flexible beam elements for dynamic analysis: finite element method and absolute nodal coordinate formulation. In: Proceedings of ASME International Design Engineering Technical Conferences and Computer and Information in Engineering Conference, Long Beach, CA (2005)
Hussein, B.A., Sugiyama, H., Shabana, A.A.: Coupled deformation modes in the large deformation finite-element analysis: problem definition. J Comput Nonlinear Dyn. 2(2), 146–154 (2007)
Nachbagauer, K., Gruber, P., Gerstmayr, J.: A 3D shear deformable finite element based on the absolute nodal coordinate formulation. Multibody Syst. Dyn. 28, 77–96 (2013)
Matikainen, M.K., Valkeapää, A.I., Mikkola, A., Schwab, A.L.: A study of moderately thick quadrilateral plate elements based on the absolute nodal coordinate formulation. Multibody Syst. Dyn. 31(3), 309–338 (2014)
Carpenter, N., Belytschko, T., Stolarski, H.: Locking and shear scaling factors in C0 bending elements. Comput. Struct. 22(1), 39–52 (1986)
Tinsley, B., Shabana, A.A.: Convergence characteristics of geometrically-accurate spatial finite elements. J. Comput. Nonlin. Dyn. 16(1), 011006 (2021)
Shabana, A.A., Xu, L.: Rotation-based finite elements: reference-configuration geometry and motion description. Acta Mech. Sin. 37(1), 105–126 (2021)
Negrut, D., Rampalli, R., Ottarsson, G., Sajdak, A.: On an implementation of the Hilber-Hughes-Taylor method in the context of index 3 differential-algebraic equations of multibody dynamics. J. Comput. Nonlin. Dyn. 2(1), 73–85 (2007)
Wang, Y., Wynn, A., Palacios, R.: Nonlinear modal aeroservoelastic analysis framework for flexible aircraft. AIAA J. 54(10), 3075–3090 (2016)
Tian, Q., Lan, P., Yu, Z.: Model-order reduction of flexible multibody dynamics via free-interface component mode synthesis method. J. Comput. Nonlin. Dyn. 15(10), 101008 (2020)
Luo, K., Hu, H., Liu, C., Tian, Q.: Model order reduction for dynamic simulation of a flexible multibody system via absolute nodal coordinate formulation. Comput. Methods Appl. Mech. Eng. 324, 573–594 (2017)
Kim, E., Kim, H., Cho, M.: Model order reduction of multibody system dynamics based on stiffness evaluation in the absolute nodal coordinate formulation. Nonlinear Dyn. 87(3), 1901–1915 (2017)
Hou, Y., Liu, C., Hu, H.: Component-level proper orthogonal decomposition for flexible multibody systems. Comput. Methods Appl. Mech. Eng. 361, 112690 (2020)
Amsallem, D., Farhat, C.: On the stability of reduced-order linearized computational fluid dynamics models based on POD and Galerkin Projection: descriptor vs non-descriptor forms. In: Reduced-Order Methods for Modeling and Computational Reduction. Springer, Cham, Switzerland (2014)
Lieu, T., Farhat, C., Lesoinne, M.: Reduced-order fluid/structure modeling of a complete aircraft configuration. Comput. Methods Appl. Mech. Eng. 195(41–43), 5730–5742 (2006)
Amabili, M., Sarkar, A., Paidoussis, M.P.: Chaotic vibrations of circular cylindrical shells: galerkin versus reduced-order models via the proper orthogonal decomposition method. J. Sound Vib. 290(3–5), 736–762 (2006)
Amabili, M., Touzé, C.: Reduced-order models for nonlinear vibrations of fluid-filled circular cylindrical shells: Comparison of POD and asymptotic nonlinear normal modes methods. J. Fluid Struct. 23(6), 885–903 (2007)
Epureanu, B.I.: A parametric analysis of reduced order models of viscous flows in turbomachinery. J. Fluid Struct. 17(7), 971–982 (2003)
Jin, Y., Lu, K., Hou, L., Chen, Y.: An adaptive proper orthogonal decomposition method for model order reduction of multi-disc rotor system. J. Sound Vib. 411, 210–231 (2017)
Lu, K., Jin, Y., Chen, Y., Yang, Y., Lei, H., Zhang, Z., Li, Z., Fu, C.: Review for order reduction based on proper orthogonal decomposition and outlooks of applications in mechanical systems. Mech. Syst. Signal Pr. 123, 264–297 (2019)
Jeong, Y.M., Kim, J.S.: On the stable mode selection for efficient component mode synthesis of geometrically nonlinear beams. J. Mech. Sci. Tech. 34(7), 2961–2973 (2020)
Bampton, M.C.C., Craig, J.R.R.: Coupling of substructures for dynamic analyses. AIAA J. 6(7), 1313–1319 (1968)
Pichler, F., Witteveen, W., Fischer, P.: A complete strategy for efficient and accurate multibody dynamics of flexible structures with large lap joints considering contact and friction. Multibody Syst. Dyn. 40(4), 407–436 (2016)
Ziegler, P., Kazaz, L., Eberhard, P.: Achieving high-precision transient local contact behaviour without introducing unphysical dynamics. Mech. Mach. Theory 148, 103785 (2020)
Patalano, S., Furnari, A.M., Vitolo, F., Dion, J.-L., Plateaux, R., Renaud, F.: A critical exposition of model order reduction techniques: application to a slewing flexible beam. Arch. Comput. Methods Eng. 28(1), 31–52 (2021)
Yoo, H.H., Ryan, R.R., Scott, R.A.: Dynamics of flexible beams undergoing overall motions. J. Sound Vib. 181(2), 261–278 (1995)
Liu, Z., Hong, J., Liu, J.: Complete geometric nonlinear formulation for rigid-flexible coupling dynamics. J. Cent. South Univ. Technol. 16(1), 119–124 (2009)
Slaats, P.M.A., Jongh, J.D., Sauren, A.A.H.J.: Model reduction tools for nonlinear structural dynamics. Comput. Struct. 54(6), 1155–1171 (1995)
Vizzaccaro, A., Givois, A., Longobardi, P., Shen, Y., Deü, J.F., Salles, L., Touzé, C., Thomas, O.: Non-intrusive reduced-order modelling for the dynamics of geometrically nonlinear flat structures using three-dimensional finite elements. Comput. Mech. 66(6), 1293–1319 (2020)
Wu, L., Tiso, P., Tatsis, K., Chatzi, E., Keulen, F.: A modal derivatives enhanced Rubin substructuring method for geometrically nonlinear multibody systems. Multibody Syst. Dyn. 45(1), 57–85 (2019)
Tang, Y., Hu, H., Tian, Q.: Model order reduction based on successive linearizations for flexible multibody dynamics. Int. J. Numer. Methods Eng. 118(3), 159–180 (2019)
Sonneville, V., Scapolan, M., Shan, M.H., Bauchau, O.A.: Modal reduction procedures for flexible multibody dynamics. Multibody Syst. Dyn. 51(4), 377–418 (2021)
Sugiyama, H., Gerstmayr, J., Shabana, A.A.: Deformation modes in the finite element absolute nodal coordinate formulation. J. Sound Vib. 298(4–5), 1129–1149 (2006)
Sopanen, J.T., Mikkola, A.M.: Description of elastic forces in absolute nodal coordinate formulation. Nonlinear Dyn. 34(1–2), 53–74 (2003)
Ren, H.: A simple absolute nodal coordinate formulation for thin beams with large deformations and large rotations. J. Comput. Nonlin. Dyn. 10(6), 061005 (2015)
Heyliger, P.R., Reddy, J.N.: A higher-order beam finite element for bending and vibration problems. J. Sound Vib. 126(2), 309–326 (1988)
Shabana, A.A.: Computational Continuum Mechanics. the, 3rd edn. Wiley, New York (2018)
Mazor, D., Rand, O.: The influence of the in-plane warping on the behavior of thin-walled beams. Thin-Walled Struct. 37(4), 363–390 (2000)
Rand, O.: In-plane warping effects in thin-walled box beams. AIAA J 38(3), 542–544 (2000)
Dowell, E.H., Traybar, J.J.: An experimental study of the nonlinear stiffness of a rotor blade undergoing flap, lag, and twist deformations. In: Aerospace and mechanical science report, Princeton University, Memorandum No. 1194–1257 (1975)
Gere, J.M., Timoshenko, S.P.: Mechanics of Materials, the, 2nd edn. Van Nostrand Reinhold, New York (1984)
Hughes, T.J.R., Cottrell, J.A., Bazilevs, Y.: Isogeometric analysis: CAD, finite elements, NURBS, exact geometry and mesh refinement. Comput. Methods Appl. Mech. Eng. 194(39–41), 4135–4195 (2005)
Bozorgmehri, B., Hurskainen, V.V., Matikainen, M.K., Mikkola, A.: Dynamic analysis of rotating shafts using the absolute nodal coordinate formulation. J. Sound Vib. 453, 214–236 (2019)
Chandra, R., Stemple, A.D., Chopra, I.: Thin-walled composite beams under bending, torsional, and extensional loads. J. Aircraft 27(7), 619–626 (1990)
Chung, J., Hulbert, G.M.: A time integration algorithm for structural dynamics with improved numerical dissipation: the generalized-α method. J. Appl. Mech. 60(2), 371–375 (1993)
Acknowledgements
This work was supported in part by the National Natural Science Foundation of China under the Grants 11832005 and 12125201. The ABAQUS results in Sect. 4.2 provided by professor Yunqing Zhang from Huazhong University of Science and Technology and the Nastran results in Table 8 provided by Songhao Shi from Nanjing University of Aeronautics and Astronautics are greatly appreciated.
Author information
Authors and Affiliations
Corresponding author
Ethics declarations
Conflict of interest
The authors declare that they have no conflict of interest.
Additional information
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Appendices
Appendix
The existing HOBEs
The existing HOBEs (e.g., B42 [26, 27, 29], 3363 [28], 34X3 [28], and B4 [26]) introduced here are the complete polynomial based on Pascal's triangle. And some existing HOBEs with incomplete polynomial can be found in the works by Matikainen et al. [24] and Ebel et al. [28], just to name a few.
The quadratic beam element BE42
To test the performance of locking alleviation, the higher-order BE42 was studied by the standard CMA [26, 27] and subsequently studied by the strain split method [29]. Compared with the BE24, the main improvement in the BE42 is using the displacement field given by Eq. (5) with quadratic interpolation in the transverse directions. As shown in Table 1, the BE42 possess three additional directional derivatives for each node of the two-node to describe the cross-sectional warping. As displayed in Table 2, the vector of element nodal coordinates is defined as \({\mathbf{e}} = \left[ {{\mathbf{e}}_{1}^{{\text{T}}} \;\;{\mathbf{e}}_{2}^{{\text{T}}} \;} \right]^{{\text{T}}} \in {\mathbb{R}}^{42}\). Thus
What is more, the beam element BE42 studied in [26, 27, 29] is also the beam element 3273 studied in [28].
The cubic beam element 34X3
As shown in Table 2, the beam element 34X3 is proposed using the displacement field given by Eq. (5) considering cubic interpolation in the transverse directions. The vector of nodal coordinates is defined as \(\;{\mathbf{e}} = \left[ {{\mathbf{e}}_{1}^{{\text{T}}} \;\;{\mathbf{e}}_{2}^{{\text{T}}} } \right.\;\;\;\left. {{\mathbf{e}}_{3}^{{\text{T}}} \;\;{\mathbf{e}}_{4}^{{\text{T}}} } \right]^{{\text{T}}} \in {\mathbb{R}}^{120}\), where \({\mathbf{e}}_{I}^{{\text{T}}} = \left[ {{\mathbf{r}}_{I}^{{\text{T}}} \;{\mathbf{r}}_{I,y}^{{\text{T}}} \;{\mathbf{r}}_{I,z}^{{\text{T}}} \;{\mathbf{r}}_{I,yy}^{{\text{T}}} \;{\mathbf{r}}_{I,yz}^{{\text{T}}} \;{\mathbf{r}}_{I,zz}^{{\text{T}}} \;{\mathbf{r}}_{I,yyy}^{{\text{T}}} \;{\mathbf{r}}_{I,yyz}^{{\text{T}}} \;{\mathbf{r}}_{I,yzz}^{{\text{T}}} \;{\mathbf{r}}_{I,zzz}^{{\text{T}}} } \right]\;\), \(i = 1,\;2,\;3,\;4\). Thus,
Warping
5.1 Rectangular beam
Assuming that the warping function of the rectangular cross section takes the form of the product of hyperbolic and sine functions as follows [11],
where \(c_{n} = ( - 1)^{{{{\left( {n + 1} \right)} \mathord{\left/ {\vphantom {{\left( {n + 1} \right)} 2}} \right. \kern-\nulldelimiterspace} 2}}} \frac{{8H^{2} }}{{n^{3} {\uppi }^{3} \cosh \left( {{{n{\uppi }W} \mathord{\left/ {\vphantom {{n{\uppi }W} {\left( {2H} \right)}}} \right. \kern-\nulldelimiterspace} {\left( {2H} \right)}}} \right)}}\), H and W are the height and width. For a square beam, H = W holds in Eq. (33).
I-section beam
The approximate warping function for the I-section is assumed as follows [10,11,12, 17],
where \(\overline{h} = H - T_{{{\text{flange}}}}\) is the distance between the mid-lines of the flanges and displayed in Fig. 7.
In the I-section beam, the top flange, web, and bottom flange have their own warping functions. Thus, the warping-related function \(\overline{S}\) can be written as the following compact form,
where \(\overline{z}_{{{\text{top}}\;{\text{flange}}}} = z - \overline{h}\), \(\overline{z}_{{{\text{web}}}} = - z\) and \(\overline{z}_{{{\text{botton}}\;{\text{flange}}}} = z + \overline{h}\).
In the previous works [10,11,12], the shear-related energy part is modified by the approximate warping function of Eq. (34) and the shear correction factors. However, a so-called “geometrically exact cross section deformable thin-walled beam” in [17] was proposed via more cross-sectional modes than [10,11,12]. As a result, it can get a more detailed description of the cross-sectional deformation and thus lead to a more flexible torsion response. Similarly, in this study, BE24c-ω and MGD30c-ω are examined with k2 = k3 = 0.3868 [2]. Moreover, to get more cross-sectional modes, the quadratic elements BE24c-ω-II and MGD30c-ω-II are also examined without shear energy correction. The dimensionless shape functions related with the additional nodal coordinates \({\mathbf{r}}_{{i,y^{2} }}\), \({\mathbf{r}}_{i,yz}\), \({\mathbf{r}}_{{i,z^{2} }}\), \({\mathbf{r}}_{{i,y^{3} }}\), \({\mathbf{r}}_{{i,y^{2} z}}\), \({\mathbf{r}}_{{i,yz^{2} }}\), and \({\mathbf{r}}_{{i,z^{3} }}\) are depicted in Table
12, same rules with the BE24c-ω-II.
Hollow rectangular beam
According to the work of Chandra et al. [84], the warping function for the hollow rectangular beam in Fig. 7c is assumed to be
Tapered beam
In the tapered beam of a linearly varying cross section height, the upper and lower limits of integral terms for the initial configuration are linear functions of the axial generalized coordinates [47]. That is, \(z_{u} = {H \mathord{\left/ {\vphantom {H 2}} \right. \kern-\nulldelimiterspace} 2} + k_{s} x\) and \(z_{l} = - {H \mathord{\left/ {\vphantom {H 2}} \right. \kern-\nulldelimiterspace} 2} - k_{s} x\), where l, H, and ks are the length, height, and slope of beam element, respectively. Thus,
It is worth noting that the nonlinear functions of x for the upper and lower integral limits in Eq. (37) can account for the beam configuration of a nonlinearly varying cross section height.
Substituting Eq. (37) into Eq. (33) to get the warping function of the tapered beam when n = 1 as follows.
The integral of an irregular section
The integral of an irregular section is usually divided into n independent integrals of regular sections. Thus, the element elastic energy \(U^{\rm E}\) in Eq. (26) can be rewritten as.
I-section beam
The I-section is divided into n = 3 rectangular regions to integrate independently, and the subscript i = 1, i = 2, and i = 3 in Eq. (39) represents the web, up flange, and bottom flange, respectively. \(T_{1} = H - 2T_{flange}\),\(\;W_{1} = W_{web}\), \(T_{2} = T_{3} = T_{flange}\), and \(\;W_{2} = \;W_{3} = W_{flange}\)
Hollow rectangular beam
The hollow rectangular is divided into n = 4 rectangular regions to integrate independently, and the subscript i = 1, i = 2, i = 3, and i = 4 in Eq. (39) represents the top, bottom, left, and right rectangular regions. \(T_{1} = T_{2} = T_{3} = T_{4} = T\),\(\;W_{1} = W_{2} = W\), and \(\;W_{3} = \;W_{4} = H - 2T\).
Rights and permissions
About this article
Cite this article
Tang, Y., Tian, Q. & Hu, H. Efficient modeling and order reduction of new 3D beam elements with warping via absolute nodal coordinate formulation. Nonlinear Dyn 109, 2319–2354 (2022). https://doi.org/10.1007/s11071-022-07547-8
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s11071-022-07547-8



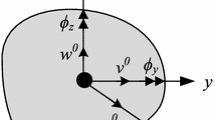















 IGA (Tasora et al.) [
IGA (Tasora et al.) [ Dymore [
Dymore [ MGD30c (k2 = k3 = 0.5306)
MGD30c (k2 = k3 = 0.5306)  MGD30c (k2 = k3 = 1)
MGD30c (k2 = k3 = 1)  MGD30c-ω (k2 = k3 = 1)
MGD30c-ω (k2 = k3 = 1)  34X3c (k2 = k3 = 1)
34X3c (k2 = k3 = 1)