Refined sectional analysis with shear center prediction for nonhomogeneous anisotropic beams with nonuniform warping

Abstract

A two-dimensional (2D) finite element (FE) sectional analysis system is developed for nonhomogeneous anisotropic beams established on a refined displacement-based elasticity theory. The classical effects due to elastic couplings, and nonclassical effects pertaining to three-dimensional (3D) warping displacements are incorporated in the formulation. The formulation allows for a generalized refined model with 12 × 12 stiffness matrix which subsequently encapsulates the Timoshenko model, Vlasov model for restrained torsion, and refined model for fully nonuniform warping (NUW). In addition, the shear center and tension center offsets are computed as cross-sectional properties based on the extended Trefftz’ theory for anisotropic beams. The accuracy of the sectional analysis is substantiated for isotropic as well as anisotropic, closed and open section beams with and without end restraints. The results indicate reliable predictions of the elastic properties for isotropic as well as anisotropic beams compared with the analytical solution, 3D FE solution, and other state-of-the-art methods. The static behavior of the beams is shown to be significantly influenced by the NUW effects especially in the vicinity of beam boundaries.

1 Introduction

With the advances in composites technology, the elastic properties of beams can be tailored to achieve desired stiffness and strength which are required to adjust the static and dynamic characteristics. Beams are slender structures typically with the axial (lengthwise) dimension much larger than the sectional ones [1]. They are widely used in civil, mechanical and aerospace engineering fields for modeling aircraft wings, and helicopter/wind turbine blades, and bridge structures. In the past decades, significant efforts have been made in the analysis methodology of straight and prismatic, nonhomogeneous anisotropic beams. The full 3D analysis of the layered anisotropic beams is a cumbersome task requiring elaborate modeling and large computation time. For the simplified and efficient modeling of 3D beams, the analysis is generally decomposed into a local 2D cross-sectional level and a global one-dimensional (1D) beam level, referred to as the dimensional reduction [1]. The need for accurate modeling and analysis of layered composite beam sections have led to the development of various sophisticated theories. The modeling of both the classical effects (elastic couplings), and nonclassical effects such as the warping displacements and the warping restraints is essential for accurate determination of the sectional elastic properties of composite beams [2]. The 3D displacements, strains, and stresses can also be systematically recovered using the sectional elastic constants computed from sectional analysis followed by internal loads computation from 1D beam analysis [1]. Furthermore, the cross-sectional analysis integrated with a 1D beam analysis can be exploited for the structural optimization which can drastically reduce the required computation time compared to that of full 3D beams.

There are various approaches available in the literature for the modeling of complex beam sections. Primarily, they can be categorized into two: a shell-wall based analytical approach and a FE analysis-based method. In the former approach, the walls of the beam section are idealized as contour of the mid-walls modeled into thin shells. This approach offers closed-form analysis solution for anisotropic beams with thin-walled and moderately thick-walled configurations. However, the model is limited to simple shell-wall type beam cross-sections. In the latter approach, the cross-section is discretized into 2D FEs. This approach is more suited to nonhomogeneous sections with arbitrary geometry and material distributions.

The analytical-based methods have an extensive history including Rehfield et al. [3], Chandra et al. [4], Smith and Chopra [5], Chandra and Chopra [6], and Jung et al. [2]. An appropriate approximation of the shell-wall displacement field was assumed to determine the strain energy and the cross-sectional stiffness matrix of composite beams and blades. Berdichevsky et al. [7] and Badir et al. [8] developed a systematic approach to refine the displacement approximations through a variational asymptotic method. They analyzed thin-walled composite beams with open and closed cross-sections. Volovoi and Hodges [9] proposed a linear, asymptotically consistent theory for anisotropic thin-walled beams. They studied the effect of in-plane (hoop) bending moment also known as in-plane shear for special cases of elastically-coupled composite box beams. Jung et al. [2] presented a mixed force-displacement approach along with the effects of shell-wall thickness, transverse shear, hoop moment, and torsional warping restraint to obtain the cross-sectional stiffness properties.

The FE analysis-based approach has been followed by a relatively few researchers. The seminal work done by Giavotto et al. [10] laid the foundation of the linear FE cross-sectional analysis based on the anisotropic beam theory. They modeled the in-plane and the out-of-plane warping displacements using a generalized Saint-Venant (SV) beam theory. They proposed the concept of central solutions to determine the cross-sectional uniform warping field and stiffness coefficients while the end effects were represented through eigenmodes called as extremity solutions. They obtained diffusion lengths of a box beam and a rectangular homogeneous beam, however, the effect on 1D static behavior using those eigenmodes as well as the influence on open section composite beams was not studied. Borri and Merlini [11] and Borri et al. [12] later extended this theory for nonlinear analysis, and subsequently for initially curved and twisted beams. Cesnik and Hodges [13] proposed a FE cross-sectional analysis called variational asymptotic beam sectional analysis (VABS) based on the work of Berdichevsky [14] to model complex anisotropic beams with initial twist and curvature. A slightly different version of VABS was later reported by Yu et al. [15, 16]. They realized the generalized Timoshenko and Vlasov theories through the asymptotic expansion of the strain energy derived in terms of slenderness ratio as a reference parameter. Recently, the previous expression of the strain energy transformation in the variational asymptotic formulation was corrected by Yu et al. [17] which showed a considerable influence on the composite beams with circumferentially uniform stiffness layup as well as for the beams with initial twist and curvature. Kim and Kim [18] adopted an asymptotic method along with a mixed variational approach to develop a Rankine–Timoshenko–Vlasov theory which resulted in improved correlation for composite box and I-section beams.

The beams are categorized into closed and open section beams based on the geometric shape. The warping restraints at the boundaries can have noticeable impact on the behavior of open section beams. Generally, the extended Vlasov’s theory Vlasov [19] is considered to be sufficient to model the behavior of open section beams which takes into account the influence of torsional warping restraint. Chandra and Chopra [20] studied experimentally and analytically the effect of torsional restraint on the composite I-beams. The analytical solution was obtained using a shell-wall based beam theory. Jung and Lee [21] followed a mixed force-displacement approach and used a shell-wall based formulation to obtain the torsional warping related stiffness coefficients. A $7\times 7$ matrix was formulated including the transverse shear and torsional restraint effects. Yu et al. [16] extended the variational asymptotic method in VABS to compute the generalized $5\times 5$ Vlasov stiffness matrix through reduction procedure from $6\times 6$ Timoshenko like stiffness matrix with reference to the generalized shear center. It needs to be emphasized that the modeling of full NUW (such as shear, bending, and extension) due to boundary restraints is lacking in the earlier works. The fully clamped boundary constraints restrict the out-of-plane shear deformations inducing additional axial stresses. The Poisson’s effect (sectional in-plane distortion) due to bending and/or extension vanishes under the presence of boundary constraints. Since the deformations may be coupled due to geometric or material couplings, the ramifications of the restraints on the global behavior may be noteworthy, especially for the anisotropic beams.

The accurate prediction of shear center location is crucial for the practical application of beams, particularly in the comprehensive analysis of helicopter/wind turbine rotor blades where the diagonal elastic stiffnesses are normally used along with the locations of the shear center and tension center to decouple the stiffness terms. However, the shear center must be used with caution for cases with nonzero elastic couplings between bending–torsion and extension–torsion for anisotropic materials. Kosmatka and Dong [22] recognized a SV semi-inverse method to predict the location of shear center for homogeneous anisotropic beams. Yu et al. [23] used the shear coupling stiffness coefficients from the $6\times 6$ stiffness matrix in the FE cross-sectional analysis VABS to predict the shear center location. Lee [24] presented a shell-wall based analytical approach to compute the shear center of thin-walled composite beams. In the present formulation, Trefftz’ theory of isotropic beams [25, 26] is extended to a generalized form for nonhomogeneous anisotropic beams to estimate the shear center offset. An important feature of the Trefftz’ theory is that the shear center is independent of the material properties for isotropic beams.

The present study focuses on the development of a versatile FE sectional analysis for nonhomogeneous anisotropic beams with NUW. To the authors’ knowledge, the effects of full NUW have not yet been studied in the previous works. The formulation is established from the displacement-based anisotropic elasticity theory. The unique features of present formulation are: (1) the effects of classical elastic couplings and nonclassical 3D warping displacements (which include contributions from extension, shear, torsion, and bending) are modeled in generic form; (2) the nonuniform 3D warping which induces secondary stresses due to boundary restraints is incorporated; (3) the resulting $12\times 12$ sectional stiffness matrix represents generalized Timoshenko model for bending and shear, generalized Vlasov model for restrained torsion, and refined model for full NUW; (4) the shear and tension center offsets are derived as cross-sectional properties based on the extended Trefftz’ definition for anisotropic beams; and (5) in addition, the elastic as well as inertial properties are computed with reference to the user defined axis, and transformed to the sectional offsets such as shear center, tension center, mass center, and principal bending and inertial axes. This provides the user with freedom to choose any reference for the global 1D beam analysis. The recovery of sectional strains and stresses can be performed under given loading conditions or given generalized strains. Several isotropic as well as composite open and closed beam sections are analyzed to demonstrate the performance of the present analysis.

2 Theory

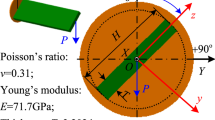
The theoretical foundation is based on the anisotropic elasticity theory that incorporates the effects of NUW. The derivations of shear center and tension center offsets are presented based on an extended Trefftz’ theory for anisotropic beams. The sectional inertial properties are systematically obtained from the 3D kinetic energy. The schematic of the beam section is shown in Fig. 1 where x-axis passes through the beam reference line, and y- and z-axes form the beam cross-sectional plane.

Fig. 1

Schematic of the beam section

2.1 Assumptions

The present formulation is established on the following assumptions:

• (A1) The beam is considered to be straight and prismatic.

• (A2) The material is assumed to be linearly elastic.

• (A3) The formulation is valid for small and linear strains at the beam sectional level.

2.2 Material constitutive relations

From the generalized Hooke’s law, the linear elastic stress–strain relation for anisotropic material is given by

$$\begin{aligned} \sigma _m = \mathbf {C}_m \varepsilon _m \end{aligned}$$

(1)

where $\sigma _m$ is the stress vector, $\varepsilon _m$ is the strain vector, and $\mathbf {C}_m$ is the material elastic constants matrix in the material coordinate system. The matrix $\mathbf {C}_m$ is fully populated for generally anisotropic materials.

The material constitutive relations in beam coordinate system can be obtained by rotational transformations through the fiber orientation $\theta _3$ and layer orientation $\theta _1$ of anisotropic materials, as shown in Fig. 2. These can then be expressed as

$$\begin{aligned} \sigma =\mathbf {C} \varepsilon \end{aligned}$$

(2)

where the stress vector $\sigma$ and strain vector $\varepsilon$ are defined as

$$\begin{aligned}&\sigma = \lfloor \begin{array}{cccccc} \sigma _{xx}&\sigma _{xy}&\sigma _{xz}&\sigma _{yy}&\sigma _{zz}&\sigma _{yz} \end{array} \rfloor ^T \nonumber \\&\varepsilon = \lfloor \begin{array}{cccccc} \varepsilon _{xx}&\varepsilon _{xy}&\varepsilon _{xz}&\varepsilon _{yy}&\varepsilon _{zz}&\varepsilon _{yz} \end{array} \rfloor ^T \end{aligned}$$

(3)

Fig. 2

Material orientations with reference to beam coordinate system xyz. a Fiber orientation $\theta _3$ b Layer orientation $\theta _1$

2.3 Kinematics

The position vector of an arbitrary material point located on the undeformed beam is denoted by ${\mathbf {x}}=\left\lfloor \begin{array}{ccc} x&y&z \end{array} \right\rfloor ^T$.

2.3.1 Displacements

The position vector ${\mathbf {X}}$ of an arbitrary material point on the section of the deformed beam is defined as

$$\begin{aligned} {\mathbf {X}} = {\mathbf {x}} + {\mathbf {u}} \end{aligned}$$

(4)

where ${\mathbf {u}}=\left\lfloor \begin{array}{ccc} u&v&w \end{array} \right\rfloor ^T$ represents the displacement of an arbitrary material point on the section, and defined as the sum of the roto-translational displacements ${\mathbf {u}}_{1D}$ of the beam reference line and the sectional warping displacements $\varPsi$, as given by

$$\begin{aligned} {\mathbf {u}} = {\mathbf {u}}_{1D} + \varPsi \end{aligned}$$

(5)

where,

$$\begin{aligned} {\mathbf {u}}_{1D}&= \mathbf {B} {\mathbf {q}}, \quad \varPsi = \left\lfloor \begin{array}{ccc} \psi _x&\psi _y&\psi _z \end{array} \right\rfloor ^T \nonumber \\ {\mathbf {q}}&= \left\lfloor \begin{array}{cccccc} u^0&v^0&w^0&\phi _x&\phi _y&\phi _z \end{array} \right\rfloor ^T, \quad \mathbf {B} = \left[ \begin{array}{cccccc} 1 & 0 & 0 & 0 & z & -y \\ 0 & 1 & 0 & -z & 0 & 0 \\ 0 & 0 & 1 & y & 0 & 0 \end{array} \right] \end{aligned}$$

(6)

where $u^0, v^0, w^0$ represent the translations, and $\phi _x, \phi _y, \phi _z$ denote the rotations of the beam section. These translations and rotations are obtained from the elastic analysis of 1D beam, and can be viewed as the rigid motion of the beam section.

2.3.2 Warping constraints

The warping field is six times redundant as defined in Eq. (5). It can be conveniently considered that 1D beam displacement field describes an average behavior of the cross-section in terms of rigid translations and rotations. The 1D displacement vector ${\mathbf {u}}_{1D}$ thus represents the average deformation of the cross-section. The first three constraints for the warping can then be obtained as

$$\begin{aligned} \int _A \psi _i(x,y,z)\,dA = 0, \quad (i=x,y,z) \end{aligned}$$

(7)

The next three constraints are obtained by averaging the local rotations about x-, y-, and z-axes as given by

$$\begin{aligned}&\int _A \left[ \psi _{z,y}(x,y,z)-\psi _{y,z}(x,y,z) \right] \,dA = 0 \end{aligned}$$

(8a)

$$\begin{aligned}&\int _A \left[ \psi _{x,z}(x,y,z)-\psi _{z,x}(x,y,z) \right] \,dA = 0 \end{aligned}$$

(8b)

$$\begin{aligned}&\int _A \left[ \psi _{y,x}(x,y,z)-\psi _{x,y}(x,y,z) \right] \,dA = 0 \end{aligned}$$

(8c)

where $(\cdot )_{,x}$, $(\cdot )_{,y}$ and $(\cdot )_{,z}$ indicate the derivatives with respect to x, y, and z, respectively.

The constraints can be written in compact form as

$$\begin{aligned} \int _A \mathscr {D}_w \varPsi \,dA = \mathbf {0} \end{aligned}$$

(9)

where $\mathscr {D}_w$ is the operator matrix defined as

$$\begin{aligned} \mathscr {D}_w = \left[ \begin{array}{ccc} 1 & 0 & 0 \\ 0 & 1 & 0 \\ 0 & 0 & 1 \\ 0 & -\partial _z & \partial _y \\ \partial _z & 0 & -\partial _x \\ -\partial _y & \partial _x & 0 \end{array} \right] \end{aligned}$$

(10)

where $\partial _x,\partial _y,\partial _z$ represent the derivatives with respect to x, y, and z, respectively.

2.3.3 Strains

With the assumption of small strains and small local rotation, the 3D strains $\varepsilon$ can be expressed in terms of displacements as

$$\begin{aligned} \varepsilon = \mathscr {L}_s {\mathbf {u}} + \mathscr {L}_b {\mathbf {u}}' \end{aligned}$$

(11)

where $(\cdot )'$ indicates derivative with respect to x, and $\mathscr {L}_s$ and $\mathscr {L}_b$ are the operator matrices defined as

$$\begin{aligned} \mathscr {L}_s = \left[ \begin{array}{ccc} 0 & 0 & 0 \\ \partial _y & 0 & 0 \\ \partial _z & 0 & 0 \\ 0 & \partial _y & 0 \\ 0 & 0 & \partial _z \\ 0 & \partial _z & \partial _y \end{array} \right] , \quad \mathscr {L}_b = \left[ \begin{array}{ccc} 1 & 0 & 0 \\ 0 & 1 & 0 \\ 0 & 0 & 1 \\ 0 & 0 & 0 \\ 0 & 0 & 0 \\ 0 & 0 & 0 \end{array} \right] \end{aligned}$$

(12)

Substitution of displacements from Eq. (5) results in

$$\begin{aligned} \varepsilon = \mathscr {L}_s \mathbf {B} {\mathbf {q}} + \mathscr {L}_b \mathbf {B} {\mathbf {q}}' + \mathscr {L}_s \varPsi + \mathscr {L}_b \varPsi ' \end{aligned}$$

(13)

The generalized strain measures $\varGamma$ can be defined in terms of ${\mathbf {q}}$ as

$$\begin{aligned} \varGamma = \left\lfloor \begin{array}{cccccc} \gamma _x&\gamma _y&\gamma _z&\kappa _x&\kappa _y&\kappa _z \end{array} \right\rfloor ^T= \mathbf {T} {\mathbf {q}} + {\mathbf {q}}' \end{aligned}$$

(14)

where $\gamma _x$ is the extensional strain, $\gamma _y,\gamma _z$ are the transverse shear strains, $\kappa _x$ is the rate of twist (or twist curvature), $\kappa _y,\kappa _z$ are the bending curvatures, and the matrix $\mathbf {T}$ is given by

$$\begin{aligned} \mathbf {T} = \left[ \begin{array}{cccccc} 0 & 0 & 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 & 0 & -1 \\ 0 & 0 & 0 & 0 & 1 & 0 \\ 0 & 0 & 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 & 0 & 0 \end{array} \right] \end{aligned}$$

(15)

Using the above relation for 1D generalized strain measures, the strains from Eq. (13) result into

$$\begin{aligned} \varepsilon = \mathscr {L}_b \mathbf {B} \varGamma + \mathscr {L}_s \varPsi + \mathscr {L}_b \varPsi ' \end{aligned}$$

(16)

2.3.4 Discretization of warping displacements

The warping displacements can be discretized using isoparametric shape functions as

$$\begin{aligned} \varPsi (x,y,z) = {\mathbf {N}}(y,z) \varLambda (x) \end{aligned}$$

(17)

where $\mathbf {N}$ represents the matrix of FE shape functions, and $\varLambda$ represents the nodal values of warping displacements.

The warping constraints in Eq. (9) can be discretized using Eq. (17) as

$$\begin{aligned} \int _A \mathscr {D}_w \mathbf {N} \varLambda \,dA = \left( \int _A \mathscr {D}_w \mathbf {N} \,dA \right) \varLambda = \mathbf {D} \varLambda = \varLambda ^T \mathbf {D}^T = \mathbf {0} \end{aligned}$$

(18)

where $\mathbf {D}$ denotes the discretized warping constraints matrix.

2.4 Governing equations

2.4.1 Sectional strain energy

The strain energy per unit length of the beam (sectional strain energy) $U_s$ can be obtained as

$$\begin{aligned} U_s = \frac{1}{2} \int _A \varepsilon ^T \sigma \,dA = \frac{1}{2} \int _A \varepsilon ^T \mathbf {C} \varepsilon \,dA \end{aligned}$$

(19)

The first variation of the sectional strain energy is given by

$$\begin{aligned} \delta U_s = \int _A \delta \varepsilon ^T \mathbf {C} \varepsilon \,dA \end{aligned}$$

(20)

Substituting the strain-displacement relations from Eq. (16) and using discretized warping displacements from Eq. (17), the variation of the sectional strain energy can be obtained in compact form as

$$\begin{aligned} \delta U_s = \left\{ \begin{array}{c} \delta \varLambda ' \\ \delta \varLambda \\ \delta \varGamma \end{array} \right\} ^T \left[ \begin{array}{ccc} \mathbf {A} & \mathbf {E} & \mathbf {G} \\ \mathbf {E}^T & \mathbf {H} & \mathbf {Q} \\ \mathbf {G}^T & \mathbf {Q}^T & \mathbf {R} \end{array} \right] \left\{ \begin{array}{c} \varLambda ' \\ \varLambda \\ \varGamma \end{array} \right\} \end{aligned}$$

(21)

where,

$$\begin{aligned} \mathbf {A}&= \int _A \left( \mathscr {L}_b \mathbf {N} \right) ^T \mathbf {C} \left( \mathscr {L}_b \mathbf {N} \right) \,dA \nonumber \\ \mathbf {E}&= \int _A \left( \mathscr {L}_b \mathbf {N} \right) ^T \mathbf {C} \left( \mathscr {L}_s \mathbf {N} \right) \,dA \nonumber \\ \mathbf {G}&= \int _A \left( \mathscr {L}_b \mathbf {N} \right) ^T \mathbf {C} \left( \mathscr {L}_b \mathbf {B} \right) \,dA \\ \mathbf {H}&= \int _A \left( \mathscr {L}_s \mathbf {N} \right) ^T \mathbf {C} \left( \mathscr {L}_s \mathbf {N} \right) \,dA \nonumber \\ \mathbf {Q}&= \int _A \left( \mathscr {L}_s \mathbf {N} \right) ^T \mathbf {C} \left( \mathscr {L}_b \mathbf {B} \right) \,dA \nonumber \\ \mathbf {R}&= \int _A \left( \mathscr {L}_b \mathbf {B} \right) ^T \mathbf {C} \left( \mathscr {L}_b \mathbf {B} \right) \,dA \nonumber \end{aligned}$$

(22)

The matrices $\mathbf {A}$, $\mathbf {E}$, $\mathbf {G}$, $\mathbf {H}$, $\mathbf {Q}$, and $\mathbf {R}$ describe the effects related to geometric and material couplings of the beam section.

2.4.2 External work

The sectional stress resultants ${\mathbf {F}}$ for SV warping can be obtained from the tractions ${\mathbf {p}}$ acting on the section as given by

$$\begin{aligned} {\mathbf {F}} = \int _A \mathbf {B}^T {\mathbf {p}}\,dA \end{aligned}$$

(23)

with

$$\begin{aligned} {\mathbf {F}} = \left\lfloor \begin{array}{cccccc} F_x&F_y&F_z&M_x&M_y&M_z \end{array} \right\rfloor ^T, \quad {\mathbf {p}} = \left\lfloor \begin{array}{ccc} \sigma _{xx}&\sigma _{xy}&\sigma _{xz} \end{array} \right\rfloor ^T \end{aligned}$$

(24)

where $F_x$ is the extensional force, $F_y$ and $F_z$ are the transverse shear forces, $M_x$ is the torsional moment, and $M_y$ and $M_z$ are the bending moments.

Neglecting the surface and body forces, the external work per unit length of the beam $W_s$ due to the tractions ${\mathbf {p}}$ is given by

$$\begin{aligned} W_s = \int _A \left( {\mathbf {u}}^T {\mathbf {p}} \right) '\,dA \end{aligned}$$

(25)

Substituting Eqs. (5) and (6) and using the stress resultants from Eq. (23), the external work can be expressed as

$$\begin{aligned} W_s = \left[ {\mathbf {q}}^{\prime T} {\mathbf {F}} + {\mathbf {q}}^T {\mathbf {F}}' \right] + \int _A \left[ \varPsi ^{\prime T} {\mathbf {p}} + \varPsi ^T {\mathbf {p}}' \right] \,dA \end{aligned}$$

(26)

The first bracketed term in the above equation is independent of warping displacements and depends only on the rigid displacements of the section. The first variation of external work $\delta W_s$ can be obtained as

$$\begin{aligned} \delta W_s&= \left[ \delta \left( \mathbf {T} {\mathbf {q}} + {\mathbf {q}}' \right) ^T {\mathbf {F}} + \delta {\mathbf {q}}^T \left( {\mathbf {F}}' - \mathbf {T}^T {\mathbf {F}}\right) \right] \nonumber \\&\quad + \int _A \left[ \delta \varPsi ^{\prime T} {\mathbf {p}} + \delta \varPsi ^T {\mathbf {p}}' \right] \,dA \end{aligned}$$

(27)

Using the definition of $\varGamma$ from Eq. (14) and substituting the discretized warping displacements from Eq. (17), the variation of external work can be expressed as

$$\begin{aligned} \delta W_s = \left\{ \begin{array}{c} \delta \varLambda ' \\ \delta \varLambda \\ \delta \varGamma \end{array} \right\} ^T \left\{ \begin{array}{c} \mathbf {P} \\ \mathbf {P}' \\ {\mathbf {F}} \end{array} \right\} + \delta {\mathbf {q}}^T \left( {\mathbf {F}}' - \mathbf {T}^T {\mathbf {F}}\right) \end{aligned}$$

(28)

where,

$$\begin{aligned} \mathbf {P} = \int _A \mathbf {N}^T {\mathbf {p}} \,dA, \quad \mathbf {P}' = \int _A \mathbf {N}^T {\mathbf {p}}' \,dA \end{aligned}$$

(29)

2.4.3 Energy principle

According to the principle of virtual work, the variation of the total energy is stated as

$$\begin{aligned} \delta \varPi = \delta U_s - \delta W_s = 0 \end{aligned}$$

(30)

Substituting Eqs. (21) and (28) in the above equation, energy principle for a unit beam length can be formulated as

$$\begin{aligned}&\left\{ \begin{array}{c} \delta \varLambda ' \\ \delta \varLambda \\ \delta \varGamma \end{array} \right\} ^T \left[ \begin{array}{ccc} \mathbf {A} & \mathbf {E} & \mathbf {G} \\ \mathbf {E}^T & \mathbf {H} & \mathbf {Q} \\ \mathbf {G}^T & \mathbf {Q}^T & \mathbf {R} \end{array} \right] \left\{ \begin{array}{c} \varLambda ' \\ \varLambda \\ \varGamma \end{array} \right\} = \left\{ \begin{array}{c} \delta \varLambda ' \\ \delta \varLambda \\ \delta \varGamma \end{array} \right\} ^T \left\{ \begin{array}{c} \mathbf {P} \\ \mathbf {P}' \\ {\mathbf {F}} \end{array} \right\} \nonumber \\&\qquad + \delta {\mathbf {q}}^T \left( {\mathbf {F}}' - \mathbf {T}^T {\mathbf {F}}\right) \end{aligned}$$

(31)

For arbitrary $\delta \varLambda$, $\delta \varLambda '$, $\delta \varGamma$, and $\delta {\mathbf {q}}$, the above equation results in the following set of equilibrium equations,

$$\begin{aligned} \mathbf {A} \varLambda ' + \mathbf {E} \varLambda + \mathbf {G} \varGamma&= \mathbf {P} \end{aligned}$$

(32a)

$$\begin{aligned} \mathbf {E}^T \varLambda ' + \mathbf {H} \varLambda + \mathbf {Q} \varGamma&= \mathbf {P}' \end{aligned}$$

(32b)

$$\begin{aligned} \mathbf {G}^T \varLambda ' + \mathbf {Q}^T \varLambda + \mathbf {R} \varGamma&= {\mathbf {F}} \end{aligned}$$

(32c)

$$\begin{aligned} {\mathbf {F}}'&= \mathbf {T}^T {\mathbf {F}} \end{aligned}$$

(32d)

Differentiating the first equation with respect to x, and combining first two equations, the equilibrium equations are reduced into

$$\begin{aligned} \mathbf {A} \varLambda '' + \left( \mathbf {E} - \mathbf {E}^T \right) \varLambda ' + \mathbf {G} \varGamma ' - \mathbf {H} \varLambda - \mathbf {Q} \varGamma&= \mathbf {0} \end{aligned}$$

(33a)

$$\begin{aligned} \mathbf {G}^T \varLambda ' + \mathbf {Q}^T \varLambda + \mathbf {R} \varGamma&= {\mathbf {F}} \end{aligned}$$

(33b)

$$\begin{aligned} {\mathbf {F}}'&= \mathbf {T}^T {\mathbf {F}} \end{aligned}$$

(33c)

Differentiating the above set of equations with respect to x,

$$\begin{aligned} \mathbf {A} \varLambda ''' + \left( \mathbf {E} - \mathbf {E}^T \right) \varLambda '' + \mathbf {G} \varGamma '' - \mathbf {H} \varLambda ' - \mathbf {Q} \varGamma '&= \mathbf {0} \end{aligned}$$

(34a)

$$\begin{aligned} \mathbf {G}^T \varLambda '' + \mathbf {Q}^T \varLambda ' + \mathbf {R} \varGamma ' = {\mathbf {F}}'&= \mathbf {T}^T {\mathbf {F}} \end{aligned}$$

(34b)

$$\begin{aligned} {\mathbf {F}}'' = \mathbf {T}^T {\mathbf {F}}' = \mathbf {T}^T \mathbf {T}^T {\mathbf {F}}&= \mathbf {0} \end{aligned}$$

(34c)

Note that the second and higher derivatives of $\varLambda$ and $\varGamma$ vanish which leads to the following set of equilibrium equations,

$$\begin{aligned}&\left[ \begin{array}{cc} \mathbf {H} & \mathbf {Q} \\ \mathbf {Q}^T & \mathbf {R} \end{array} \right] \left\{ \begin{array}{c} \varLambda ' \\ \varGamma ' \end{array} \right\} = \left\{ \begin{array}{c} \mathbf {0} \\ \mathbf {T}^T {\mathbf {F}} \end{array} \right\} \end{aligned}$$

(35a)

$$\begin{aligned}&\left[ \begin{array}{cc} \mathbf {H} & \mathbf {Q} \\ \mathbf {Q}^T & \mathbf {R} \end{array} \right] \left\{ \begin{array}{c} \varLambda \\ \varGamma \end{array} \right\} = \left[ \begin{array}{cc} \mathbf {E} - \mathbf {E}^T & \mathbf {G} \\ -\mathbf {G}^T & \mathbf {0} \end{array} \right] \left\{ \begin{array}{c} \varLambda ' \\ \varGamma ' \end{array} \right\} + \left\{ \begin{array}{c} \mathbf {0} \\ {\mathbf {F}} \end{array} \right\} \end{aligned}$$

(35b)

Note that the matrices $\mathbf {A}$ and $\mathbf {E}$ are not present in the above equations which implies that they do not affect the warping solution. These will however be required for the resolution of beam stiffness matrix described in the later section.

2.5 Warping solution

At the global 1D level, the SV warping displacements $(\varLambda )$ can be conveniently assumed to have contributions from sectional stress resultants ${\mathbf {F}}$ (which are linearly proportional to the generalized strain measures and their derivatives), and therefore can be expressed as

$$\begin{aligned} \varLambda = {\tilde{\varLambda}} {\mathbf {F}}, \quad {\varLambda '} = {{\tilde{\varLambda }}}' {\mathbf {F}}, \quad \varGamma = {\tilde{\varGamma }} {\mathbf {F}}, \quad {\varGamma '} = {\tilde{\varGamma }}' {\mathbf {F}} \end{aligned}$$

(36)

where ${{\tilde{\varLambda }}}$ (a $3n\times 6$ matrix, n is the total number of nodes) and ${\tilde{\varGamma }}$ (a 6 × 6 matrix) are the coefficient matrices which correspond to the contributions of each stress resultant in $\varLambda$ and $\varGamma$, respectively. The terms with $(\cdot )'$ indicate the coefficients corresponding to the derivatives of generalized strain measures present in the sectional stress resultants. The coefficient matrices ${\tilde{\varGamma }}$ and ${\tilde{\varGamma }}'$ are constant over the beam section. Note that in the classical Timoshenko beam theory, only the out-of-plane transverse shear deformations are modeled and their distribution is assumed to be linear over the section. On the contrary, the present formulation makes no such assumption, and both the out-of-plane and in-plane warping displacements are discretized in a very general manner leading to a generic nonlinear distribution of sectional warping over the beam section. The warping displacements can thus appropriately characterize any elastic couplings present in the section which may be crucial, especially for composite beams.

The above approximation of warping displacements can be applied to the equilibrium equations obtained in Eq. (35). With the inclusion of warping constraints from Eq. (18), this leads to

$$\begin{aligned} \left[ \begin{array}{ccc} \mathbf {H} & \mathbf {Q} & \mathbf {D}^T \\ \mathbf {Q}^T & \mathbf {R} & \mathbf {0} \\ \mathbf {D} & \mathbf {0} & \mathbf {0} \end{array} \right] \left[ \begin{array}{c} {{\tilde{\varLambda }}}' \\ {\tilde{\varGamma }}' \\ \varTheta ' \end{array} \right]&= \left[ \begin{array}{c} \mathbf {0} \\ \mathbf {T}^T \\ \mathbf {0} \end{array} \right] \end{aligned}$$

(37a)

$$\begin{aligned} \left[ \begin{array}{ccc} \mathbf {H} & \mathbf {Q} & \mathbf {D}^T \\ \mathbf {Q}^T & \mathbf {R} & \mathbf {0} \\ \mathbf {D} & \mathbf {0} & \mathbf {0} \end{array} \right] \left[ \begin{array}{c} {{\tilde{\varLambda }}} \\ {\tilde{\varGamma }} \\ \varTheta \end{array} \right]&= \left[ \begin{array}{ccc} \mathbf {E} - \mathbf {E}^T & \mathbf {G} & \mathbf {0} \\ -\mathbf {G}^T & \mathbf {0} & \mathbf {0} \\ \mathbf {0} & \mathbf {0} & \mathbf {0} \end{array} \right] \left[ \begin{array}{c} {{\tilde{\varLambda }}}' \\ {\tilde{\varGamma }}' \\ \varTheta ' \end{array} \right] + \left[ \begin{array}{c} \mathbf {0} \\ \mathbf {I}_6 \\ \mathbf {0} \end{array} \right] \end{aligned}$$

(37b)

where $\mathbf {I}_6$ is a $6\times 6$ identity matrix, and $\varTheta '$ and $\varTheta$ are the Lagrange multipliers corresponding to the warping constraints. The structure of the matrix on the left hand side is sparse and symmetric which can be solved using any available sparse direct or iterative solver.

2.6 Generalized Timoshenko like sectional stiffness matrix

The generalized Timoshenko like $6\times 6$ stiffness matrix is constituted using the SV warping which is assumed as uniform along the beam axis. With the known warping solution from Eq. (37), the strain energy variation $(\delta U_s)$ from Eq. (21) becomes

$$\begin{aligned} \delta U_s = \delta {\mathbf {F}}^T \left[ \begin{array}{c} {{\tilde{\varLambda }}}' \\ {{\tilde{\varLambda }}} \\ {\tilde{\varGamma }} \end{array} \right] ^T \left[ \begin{array}{ccc} \mathbf {A} & \mathbf {E} & \mathbf {G} \\ \mathbf {E}^T & \mathbf {H} & \mathbf {Q} \\ \mathbf {G}^T & \mathbf {Q}^T & \mathbf {R} \end{array} \right] \left[ \begin{array}{c} {{\tilde{\varLambda }}}' \\ {{\tilde{\varLambda }}} \\ {\tilde{\varGamma }} \end{array} \right] {\mathbf {F}} \end{aligned}$$

(38)

The variation of the external work can be restated in terms of Timoshenko like sectional flexibility matrix $\mathbf {S}$ as

$$\begin{aligned} \delta W_s = \delta \varGamma ^T {\mathbf {F}} = \delta {\mathbf {F}}^T \mathbf {S} {\mathbf {F}} \end{aligned}$$

(39)

where $\mathbf {S}$ can be determined using energy principle defined in Eq. (30), as given by

$$\begin{aligned} \mathbf {S} = \left[ \begin{array}{c} {{\tilde{\varLambda }}}' \\ {{\tilde{\varLambda }}} \\ {\tilde{\varGamma }} \end{array} \right] ^T \left[ \begin{array}{ccc} \mathbf {A} & \mathbf {E} & \mathbf {G} \\ \mathbf {E}^T & \mathbf {H} & \mathbf {Q} \\ \mathbf {G}^T & \mathbf {Q}^T & \mathbf {R} \end{array} \right] \left[ \begin{array}{c} {{\tilde{\varLambda }}}' \\ {{\tilde{\varLambda }}} \\ {\tilde{\varGamma }} \end{array} \right] \end{aligned}$$

(40)

The generalized Timoshenko like stiffness matrix $\mathbf {K}$ can be computed by inverting the flexibility matrix, which is given by

$$\begin{aligned} \mathbf {K} = \mathbf {S}^{-1} \end{aligned}$$

(41)

The above stiffness matrix $\mathbf {K}$ takes into account the effects of elastic couplings, transverse shear, and Poisson deformation. For the case of general anisotropic beams, the $6\times 6$ stiffness matrix may be fully populated. It is noted that the initial development of the governing equations and the resolution of warping displacements follow the central solutions of Giavotto et al. [10]. With regard to the NUW model (extremity solutions), the present formulation differs from [10] in that the NUW is described by introducing the warping moments (bimoments) and the warping derivatives $(\varLambda ')$ expressed in terms of nonzero derivatives of generalized strain measures $(\varGamma ')$. A refined $12\times 12$ sectional stiffness matrix is subsequently obtained from the strain energy expression through the static condensation. Detailed description on NUW is presented in the next section.

2.7 Nonuniform warping and refined sectional stiffness matrix

In the generalized SV beam approach, the beam sections are allowed to warp freely while the end effects due to boundary conditions are neglected. However, under the presence of boundary constraints, additional internal loads and subsequently the secondary stresses are induced to prevent the section from warping leading to a nonuniform distribution of warping displacements along the beam span. These effects are pronounced near the restraint region which decay along the beam axis. Giavotto et al. [10] treat the end effects through the eigenmodes called as extremity solutions. These eigenmodes are obtained by solving a homogeneous equation where an exponential decay is assumed along the beam axis. The approach requires that the short wavelength modes should be selected to represent the end effects. A different approach is adopted in the present formulation where the sectional bimoments (warping moments) are introduced analogous to the Vlasov’s restrained torsion theory [19] to model NUW. Six bimoments are defined corresponding to the nonuniform extension, shear, bending, and torsion. The effects of torsional restraint are known to be significant for open section and thin-walled closed section composite beams [3, 20]. In addition, the effects of shear restraints cannot be neglected, especially for open section and thin-walled closed section composite beams, since the transverse shear also involves a short wavelength characteristic. Furthermore, the Poisson’s effect due to extension and/or bending diminishes at the restrained boundaries. The beam behavior becomes even more complicated in the presence of elastic couplings where additional warping related couplings appear. These nonuniform effects of warping are taken into account in the present formulation to capture the global behavior of the beam accurately and to recover the stresses of the structure.

Similar to the Vlasov beam theory, the sectional bimoments ${\mathbf {F}}_w$ are defined as

$$\begin{aligned} {\mathbf {F}}_w = \left\lfloor \begin{array}{cccccc} P_x&P_y&P_z&Q_x&Q_y&Q_z \end{array} \right\rfloor ^T \end{aligned}$$

(42)

where $P_x$ represents extensional bimoment, $P_y$ and $P_z$ shear bimoments, $Q_x$ torsional bimoment, and $Q_y$ and $Q_z$ bending bimoments, respectively.

Neglecting the distributed external loads, the linear force equilibrium equations Eq. (32) for the refined model can be modified as

$$\begin{aligned} {\mathbf {F}}' - \mathbf {T}^T {\mathbf {F}} - {\mathbf {F}}''_w+ \mathbf {T}^T {\mathbf {F}}'_w = \mathbf {0} \end{aligned}$$

(43)

The sectional stress resultants ${\mathbf {F}}_r$ for the refined model are then defined as

$$\begin{aligned} {\mathbf {F}}_r = \left\lfloor \begin{array}{cc} \mathbf {F}^T&\mathbf {F}_w^T \end{array} \right\rfloor ^T \end{aligned}$$

(44)

The generalized strain measures $\varGamma _r$ with NUW are defined as

$$\begin{aligned} \varGamma _r = \left\lfloor \begin{array}{cc} \varGamma ^T&\varGamma ^{\prime T}\end{array} \right\rfloor ^T \end{aligned}$$

(45)

where the nonzero derivatives of generalized strains $(\varGamma ')$ describe the effect of NUW due to end restraints.

The variation of the sectional strain energy for the NUW case can be expressed through the superposition of warping-dependent terms on the generalized Timoshenko (or SV) model. This can be stated as

$$\begin{aligned} \delta U_s = \delta U_s^{GT} + \delta U_s^{NUW} \end{aligned}$$

(46)

where $\delta U_s^{GT}$ is the contribution from generalized Timoshenko model, and $\delta U_s^{NUW}$ is the contribution from NUW, respectively given by

$$\begin{aligned} \delta U_s^{GT} =&\, \delta \varGamma ^T \mathbf {K} \varGamma \end{aligned}$$

(47)

$$\begin{aligned} \delta U_s^{NUW} =&\,\, \left\{ \begin{array}{c} \delta \varLambda ' \\ \delta \varLambda \end{array} \right\} ^T \left[ \begin{array}{cc} \mathbf {A} & \mathbf {E} \\ \mathbf {E}^T & \mathbf {H} \end{array} \right] \left\{ \begin{array}{c} \varLambda ' \\ \varLambda \end{array} \right\} + \left\{ \begin{array}{c} \delta \varLambda ' \\ \delta \varLambda \end{array} \right\} ^T \left[ \begin{array}{cc} \mathbf {G} \\ \mathbf {Q} \end{array} \right] \varGamma \nonumber \\&+\,\, \delta \varGamma ^T \left[ \begin{array}{cc} \mathbf {G} \\ \mathbf {Q} \end{array} \right] ^T \left\{ \begin{array}{c} \varLambda ' \\ \varLambda \end{array} \right\} \end{aligned}$$

(48)

For the NUW model, only the derivatives of warping displacements $(\varLambda ')$ will be needed to represent the nonuniform variation along the beam span. Note that the warping displacements are already incorporated in the generalized Timoshenko model. Following this, the expression for the variation of warping-dependent strain energy can be reduced using a static condensation procedure as

$$\begin{aligned} \delta U_s^{NUW} =&\, \delta \varLambda ^{\prime T} \left( \mathbf {A} - \mathbf {E} \mathbf {H}^+ \mathbf {E}^T \right) \varLambda ' + \delta \varLambda ^{\prime T} \left( \mathbf {G} - \mathbf {E} \mathbf {H}^+ \mathbf {Q} \right) \varGamma \nonumber \\&+\, \delta \varGamma ^T \left( \mathbf {G} - \mathbf {E} \mathbf {H}^+ \mathbf {Q} \right) ^T \varLambda ' \end{aligned}$$

(49)

where the superscript ‘+’ indicates the Moore–Penrose pseudoinverse of matrix H since the latter may be badly scaled or singular.

For the refined model with NUW, the nodal warping displacements $(\varLambda )$ and their derivatives $(\varLambda ')$ can be expressed in terms of generalized strain measures $(\varGamma )$ using Timoshenko like stiffness matrix from Eq. (41), which implies

$$\begin{aligned}&\varLambda = {\widehat{\varLambda }} \varGamma , \quad \varLambda ' = {\widehat{\varLambda }} \varGamma ', \quad {\widehat{\varLambda }} = {\tilde{\varLambda }} {\mathbf {K}} \end{aligned}$$

(50)

where ${\widehat{\varLambda }}$ is a $3n\times 6$ matrix containing the warping coefficients (which change only in magnitude with reference to ${\tilde{\varLambda }}$) corresponding to the generalized strain measures.

Using the above relations, the variation of the total sectional strain energy $(\delta U_s)$ from Eq. (21) is transformed to

$$\begin{aligned} \delta U_s = \left\{ \begin{array}{c} \delta \varGamma \\ \delta \varGamma ' \end{array} \right\} ^T \left[ \begin{array}{cc} \mathbf {K} & \mathbf {K}_{ab} \\ \mathbf {K}_{ab}^T & \mathbf {K}_{bb} \end{array} \right] \left\{ \begin{array}{c} \varGamma \\ \varGamma ' \end{array} \right\} \end{aligned}$$

(51)

where,

$$\begin{aligned} \mathbf {K}_{ab}&= \left( \mathbf {G} - \mathbf {E} \mathbf {H}^{+} \mathbf {Q} \right) ^T {\widehat{\varLambda }} \nonumber \\ \mathbf {K}_{bb}&= {\widehat{\varLambda }}^T \left( \mathbf {A} - \mathbf {E} \mathbf {H}^{+} \mathbf {E}^T \right) {\widehat{\varLambda }} \end{aligned}$$

(52)

where $\mathbf {K}_{ab}$ and $\mathbf {K}_{bb}$ are $6\times 6$ matrices.

The variation of external work for the refined model can be expressed as

$$\begin{aligned} \delta W_s = \delta \varGamma _r^T {\mathbf {F}}_r = \delta \varGamma _r^T \mathbf {K}_r \varGamma _r \end{aligned}$$

(53)

where $\mathbf {K}_r$ is a $12\times 12$ stiffness matrix which can be determined using the principle of virtual work defined in Eq. (30), as given by

$$\begin{aligned} \mathbf {K}_r = \left[ \begin{array}{cc} \mathbf {K} & \mathbf {K}_{ab} \\ \mathbf {K}_{ab}^T & \mathbf {K}_{bb} \end{array} \right] \end{aligned}$$

(54)

where $\mathbf {K}_{bb}$ consists of the direct warping stiffnesses due to extension, shear, bending and torsion, and $\mathbf {K}_{ab}$ contains the couplings between generalized Timoshenko and direct warping stiffnesses. These additional stiffness coefficients are resulted from NUW effect which is prominent near the restraints.

The sectional flexibility matrix $\mathbf {S}_r$ can be obtained by inverting the stiffness matrix $\mathbf {K}_r$ as

$$\begin{aligned} \mathbf {S}_r = \mathbf {K}_r^{-1} \end{aligned}$$

(55)

The $12\times 12$ sectional stiffness matrix $\mathbf {K}_r$ represents a refined form including the effects of nonuniform 3D warping. The present model describes the Timoshenko like theory (includes transverse shear), Vlasov like theory (restrained torsion), and refined theory for fully restrained warping. The formulation also takes into account the Poisson effect due to in-plane warping. In addition to the generalized Timoshenko stiffness coefficients, the present refined model includes direct warping stiffness constants for extension, shear, torsion, and bending, along with the related coupling stiffness coefficients.

2.8 Shear center

The shear center is defined as a point on the cross-section at which the application of transverse shear forces produces no torsional deformation. The shear center is considered as a cross-sectional property computed using the Trefftz’ definition of the torsion-free flexure [25]. However, it must be remarked that for the composite beams with bending–torsion coupling, twist can still be induced due to the indirect bending moments. For such cases, it is recommended to use fully coupled elastic stiffness matrix. For beams with no bending–torsion coupling, the shear center can be used to fully decouple the torsional and transverse shear deformations.

Consider a beam subjected to a torsional moment $M_x^t$. The cross-sectional strain energy due to pure torsion is given by

$$\begin{aligned} U_s^t = \frac{1}{2} S_{44} \left( M_x^t\right) ^2 \end{aligned}$$

(56)

where $S_{44}$ is the torsional flexibility coefficient.

If the beam is subjected to transverse shear forces $F_y$ and $F_z$, the cross-sectional flexural strain energy is expressed as

$$\begin{aligned} U_s^f = \frac{1}{2} \left\{ \begin{array}{c} F_y \\ F_z \\ M_x^f \end{array} \right\} ^T \left[ \begin{array}{ccc} S_{22} & S_{23} & S_{24} \\ S_{23} & S_{33} & S_{34} \\ S_{24} & S_{34} & S_{44} \end{array} \right] \left\{ \begin{array}{c} F_y \\ F_z \\ M_x^f \end{array} \right\} \end{aligned}$$

(57)

where $M_x^f$ is the torsional moment induced due to transverse shear forces as given by

$$\begin{aligned} M_x^f = y_{sc} F_z - z_{sc} F_y \end{aligned}$$

(58)

where $(y_{sc},z_{sc})$ is the location of the shear center.

If the beam is subjected to pure torsion and then to transverse shear forces without removing the torsional moment, the total cross-sectional strain energy is given by

$$\begin{aligned} U_s =\, \frac{1}{2} \left\{ \begin{array}{c} F_y \\ F_z \\ M_x^t+M_x^f \end{array} \right\} ^T \left[ \begin{array}{ccc} S_{22} & S_{23} & S_{24} \\ S_{23} & S_{33} & S_{34} \\ S_{24} & S_{34} & S_{44} \end{array} \right] \left\{ \begin{array}{c} F_y \\ F_z \\ M_x^t+M_x^f \end{array} \right\} \end{aligned}$$

(59)

By the Trefftz’ definition, the transverse shear forces do not induce any torsion at the shear center. This implies that the total cross-sectional strain energy can be obtained by summing up the torsional and flexural contributions. The residual term from the summation of torsional and flexural strain energy must be equal to zero. This implies

$$\begin{aligned} U_s - \left( U_s^t + U_s^f\right) = 0 \end{aligned}$$

(60)

For nonzero $F_y$, $F_z$, and $M_x^t$, the location of the shear center can then be obtained as

$$\begin{aligned} y_{sc} = -\frac{S_{34}}{S_{44}}, \quad z_{sc} = \frac{S_{24}}{S_{44}} \end{aligned}$$

(61)

2.9 Tension center and principal bending axes

The tension center (neutral axis) is defined as a point on the cross-section at which the application of extensional force does not produce any bending moments. Similar to the Trefftz’ definition for the shear center, the definition of bending-free extension can be used to locate the tension center.

Following the similar procedure described in the determination of the shear center, the location of the tension center can be obtained as

$$\begin{aligned} y_{tc} = \frac{S_{16}S_{55}-S_{15}S_{56}}{S_{55}S_{66}-S_{56}^2}, \quad z_{tc} = -\frac{S_{15}S_{66}-S_{16}S_{56}}{S_{55}S_{66}-S_{56}^2} \end{aligned}$$

(62)

At the principal bending axes, the bending–bending coupling vanishes implying $\overline{S}_{56}=0$. The rotational transformation of bending-bending flexibility submatrix by the principal bending axes orientation $\theta _b$ would result in zero off-diagonal components. This can be stated in mathematical form as

$$\begin{aligned} \left[ \begin{array}{cc} c & s \\ -s & c \end{array} \right] \left[ \begin{array}{cc} S_{55} & S_{56} \\ S_{56} & S_{66} \end{array} \right] \left[ \begin{array}{cc} c & s \\ -s & c \end{array} \right] ^T = \left[ \begin{array}{cc} \overline{S}_{55} & \overline{S}_{56} \\ \overline{S}_{56} & \overline{S}_{66} \end{array} \right] \end{aligned}$$

(63)

where $c\equiv \cos \theta _b$ and $s\equiv \sin \theta _b$. By equating the off-diagonal coupling term $\overline{S}_{56}$ to zero, the principal bending axes orientation is computed as

$$\begin{aligned} \theta _b = \frac{1}{2} {{\mathrm{atan}}}\frac{-2 S_{56} }{ S_{66}-S_{55} } \end{aligned}$$

(64)

Note that if the origin of the principal bending axes is located at the tension center, both extension–bending and bending–bending couplings will vanish.

2.10 Recovery analysis

For the recovery of 3D displacements, strains, and stresses, 1D generalized strain measures $(\varGamma )$ and their derivatives $(\varGamma ')$ are needed which can be computed from the 1D beam analysis based on the relevant stiffness model. The warping displacements can be determined using Eq. (36). The 3D displacements of the beam can be recovered using Eq. (5) and the known warping solution. The 3D strains can be calculated based on Eq. (16) which require derivatives of 1D generalized strain measures. Generally, it is useful to express strain measures in terms of stress resultants using the flexibility matrix $\mathbf {S}$ (or $\mathbf {S}_r$). For the refined model, however, the bimoments and their derivatives are not readily available. In such cases, the derivatives of strain measures must be determined from 1D beam analysis with additional variables and boundary conditions.

For the simplified models such as Timoshenko or Euler–Bernoulli, the derivative of stress resultants can be resolved using 1D equilibrium equations as

$$\begin{aligned} {\mathbf {F}}' = \mathbf {T}^T {\mathbf {F}} - {\mathbf {f}} \end{aligned}$$

(65)

where ${\mathbf {f}}$ represents the contributions from 1D applied distributed loads and inertial loads, given as

$$\begin{aligned} {\mathbf {f}} = \left\lfloor \begin{array}{cccccc} f_x&f_y&f_z&m_x&m_y&m_z \end{array} \right\rfloor ^T \end{aligned}$$

(66)

The subsequent derivatives of stress resultants can be expressed as

$$\begin{aligned}&{\mathbf {F}}'' = \mathbf {T}^T {\mathbf {F}}' - {\mathbf {f}}' = \mathbf {T}^T {\mathbf {f}} - {\mathbf {f}}' \end{aligned}$$

(67)

$$\begin{aligned}&{\mathbf {F}}''' = \mathbf {T}^T {\mathbf {f}}' - {\mathbf {f}}'' \end{aligned}$$

(68)

The above quantities ${\mathbf {F}}$, ${\mathbf {f}}$, ${\mathbf {f}}'$, and ${\mathbf {f}}''$ can thus be used to compute the generalized strain measures, and consequently the 3D strains and stresses of the beam. The recovery relations for stresses in the beam coordinate system can be determined from Eq. (2). The strains and stresses in the material coordinate system, which may be required for the failure analysis, can be obtained by the transformation from beam to material coordinate system. The strains and stresses are calculated at the numerical integration points for the recovery and failure analyses, and at the element centroids for visualization in both the beam and material coordinate systems.

2.11 Cross-sectional inertial properties

The sectional mass per unit length, sectional mass moments of inertia, and mass center offset constitute the inertial properties which are required for the 1D global dynamic analysis of beams. To compute the inertial properties, the 3D kinetic energy needs to be resolved first. The velocity vector ${\mathbf {V}}$ of an arbitrary point on the section can be obtained by taking time derivative of Eq. (4) as

$$\begin{aligned} {\mathbf {V}} = \dot{{\mathbf {X}}} = \dot{{\mathbf {x}}} + \dot{{\mathbf {u}}} = \dot{{\mathbf {x}}} + \mathbf {B} \dot{{\mathbf {q}}} + \dot{\varPsi } \end{aligned}$$

(69)

where $\dot{(\cdot )}$ indicates the derivative with respect to time. Defining the velocity field $\tilde{{\mathbf {V}}}$ as

$$\begin{aligned} \tilde{{\mathbf {V}}} = \left\lfloor \begin{array}{cccccc} V_x&V_y&V_z&\omega _x&\omega _y&\omega _z \end{array} \right\rfloor ^T \end{aligned}$$

(70)

where $V_x,V_y,V_z$ are the velocities, and $\omega _x,\omega _y,\omega _z$ are the angular velocities of an arbitrary point on the section. This leads to

$$\begin{aligned} {\mathbf {V}} = \mathbf {B} \tilde{{\mathbf {V}}} + \dot{\varPsi } \end{aligned}$$

(71)

The 3D kinetic energy $K_{3D}$ is given by

$$\begin{aligned} K_{3D}&= \frac{1}{2} \int _l \int _A \rho {\mathbf {V}}^T {\mathbf {V}} \,dA\,dx = \frac{1}{2} \int _l \int _A \rho \tilde{{\mathbf {V}}}^T \mathbf {B}^T \mathbf {B} \tilde{{\mathbf {V}}} \,dA\,dx \nonumber \\&\quad + \frac{1}{2} \int _l \int _A \rho \left( \tilde{{\mathbf {V}}}^T \mathbf {B}^T \dot{\varPsi } + \dot{\varPsi }^T \dot{\varPsi } \right) \,dA\,dx \end{aligned}$$

(72)

Dropping the warping related terms, the 1D kinetic energy $K_{1D}$ per unit length of the beam can be reduced to

$$\begin{aligned} K_{1D} = \frac{1}{2} \tilde{{\mathbf {V}}}^T \left( \int _A \rho \mathbf {B}^T \mathbf {B} \,dA \right) \tilde{{\mathbf {V}}} = \frac{1}{2} \tilde{{\mathbf {V}}}^T \mathbf {M} \tilde{{\mathbf {V}}} \end{aligned}$$

(73)

where $\mathbf {M}$ is the $6\times 6$ sectional mass matrix computed as

$$\begin{aligned} \mathbf {M} = \left[ \begin{array}{cccccc} m & 0 & 0 & 0 & m z_{mc} & -m y_{mc} \\ 0 & m & 0 & -m z_{mc} & 0 & 0 \\ 0 & 0 & m & m y_{mc} & 0 & 0 \\ 0 & -m z_{mc} & m y_{mc} & I_{yy}+I_{zz} & 0 & 0 \\ m z_{mc} & 0 & 0 & 0 & I_{yy} & -I_{yz} \\ -m y_{mc} & 0 & 0 & 0 & -I_{yz} & I_{zz} \end{array} \right] \end{aligned}$$

(74)

where m is the mass per unit length, $(y_{mc},z_{mc})$ is the location of mass center, $m y_{mc}$ and $m z_{mc}$ are the first mass moments of inertia, $I_{yy}$ and $I_{zz}$ are the second mass moments of inertia, and $I_{yz}$ is the product of mass moment of inertia, defined respectively as

$$\begin{aligned}&m = \int _A \rho \,dA, \quad m y_{mc}= \int _A \rho y\,dA, \quad m z_{mc}= \int _A \rho z\,dA \nonumber \\&I_{yy} = \int _A \rho z^2\,dA, \quad I_{zz} = \int _A \rho y^2\,dA, \quad I_{yz} = \int _A \rho yz\,dA \end{aligned}$$

(75)

3 Finite element implementation

The formulation is implemented in a FE analysis code written in Fortran 90. The flowchart of the implementation is presented in Fig. 3. The beam cross-section is first discretized into FEs, and the material properties are provided as input. For the orthotropic or anisotropic materials, the fiber angles (or ply angles) are also given as inputs. The four different isoparametric elements are implemented to perform the cross-sectional discretization: linear 3-node (T3) and quadratic 6-node (T6) triangular elements, and linear 4-node (Q4) and quadratic 8-node (Q8) quadrilateral elements. The $C^0$-continuous Lagrange interpolation functions are used for the FE discretization. The analysis is capable of handling mixed or hybrid mesh consisting of multiple types of elements which may be desired for the accurate modeling of beams with complex geometries. The warping coefficients matrices are computed first using the equilibrium equations given by Eq. (37). These are then used to determine the $12\times 12$ refined sectional stiffness matrix using Eq. (54), and eventually the locations of shear and tension center offsets are calculated using Eqs. (61) and (62), respectively. The cross-sectional mass and inertial properties are computed via numerical integration using Gauss quadrature scheme. The sectional stiffness matrix and inertial properties are then transformed to the desired sectional offsets such as shear center, tension center, and mass center. The stiffness matrix and inertial properties can be used to perform 1D beam analysis to compute the generalized strains. These can then be used to recover the 3D displacements, strains, and stresses of the beam section. Once the strains and stresses are determined, the failure analysis for isotropic as well as anisotropic materials can be performed.

Fig. 3

Flowchart for the present sectional analysis

4 Comparison with other theories

As compared to the seminal work done by Giavotto et al. [10], SV solutions for warping displacements in the present theory are similar to the central solutions. The warping constraints are however applied in a different manner. In Giavotto et al. [10], warping constraints are imposed by eliminating six degrees of freedom from the discretized model. However, in the present formulation, the average sectional translations and rotations are assumed to be zero, defined in Eq. (9). To compute the warping solution, these constraints are then imposed using Lagrange multipliers as given in Eq. (37). Furthermore, the effects of fully restrained warping (extension, shear, bending, and torsion) are lacking in the former which may yield significant errors in the cases of open section and thin-walled closed section beams. The warping restraint effects are modeled in the present formulation through additional bimoments as sectional loads which induce secondary stresses to prevent the section from warping. The sectional analysis code VABS by Cesnik and Hodges [13] describes the generalized Timoshenko like modeling i.e., includes the effects of transverse shear deformations, however, neglecting the effect of restraints. In a more recent work by Yu et al. [16], the sectional analysis VABS is updated to model the torsional restraint using generalized Vlasov theory. However, the shear as well as the other warping contributions are modeled as uniform thus neglecting the effect of boundary restraints. The present theory encapsulates the effects of transverse shear deformations in 3D warping as well as full NUW in the presence of restraints. The experimental study carried out by Chandra and Chopra [20] clearly indicates the impact of torsional warping restraints for composite I-beams with bending–torsion couplings. The effect of in-plane shear (without restraints) was shown to significantly affect the torsional stiffness of thin-walled composite box beams in Yu et al. [17, 23]. As confirmed by Rehfield et al. [3], the fully restrained warping can have considerable impact on the behavior of composite beams with open or thin-walled closed sections. It should be noted that the NUW effects may have only marginal improvement in the 3D displacements, however, these impact the strain and stress recovery at or near the boundary restraint regions significantly. This can be verified from the strain expression given in Eq. (16) and NUW approximation from Eq. (50), where the presence of the derivatives of generalized strains can be noted (these are neglected in the SV solutions for uniform warping). It is remarked that the computation of stresses and strains is imperative during the design process as well as the structural lifecycle to correctly predict the material failure. Several numerical examples are presented in the later section to demonstrate the effects of NUW near the boundary constraints. Furthermore, the prediction of generalized shear and tension center offsets as cross-sectional properties is presented using extended Trefftz’ theory for anisotropic beams. In general, for elastically coupled composite beams, the actual position may vary over the beam length depending on the bending–torsion coupling. In case of negligible bending–torsion coupling, the shear center can be used to simplify the analysis by decoupling shear and torsion to evaluate the global beam behavior.

5 Numerical results and discussion

The efficacy of the present sectional analysis is evaluated for a number of benchmark beam section cases. The accuracy of shear center prediction is examined for open and closed beam sections. The detailed elastic and inertial properties including the classical and nonclassical elastic couplings are presented for several beam sections with arbitrary geometry and material properties. These include a highly heterogeneous section, an isotropic blade-like section, and a composite thin-walled box section beam. For the highly heterogeneous section and the isotropic blade-like section, the structural properties are computed with reference to the shear center with axes parallel to the user defined coordinate system while the inertial properties are computed with reference to the principal inertial axes positioned at the mass center. The elastic stiffness results are supported by the warping displacement modes for the sections with or without elastic couplings. The effects of NUW (or restrained warping) are investigated for anisotropic thin strips with elastic couplings, orthotropic strip, anisotropic I-section, and thin-walled composite box section beams. The predicted results are compared with the analytical, 3D FE analysis, and/or experimental data available in the literature.

5.1 Shear center locations

The first example is an equilateral triangular section [27] with unit sides as shown in Fig. 4. The Poisson ratio is $\nu =0.3$. For the present analysis, the section was discretized with 12 Q8 elements and 49 nodes, whereas 36 boundary elements were used by Friedman and Kosmatka [27]. Table 1 shows the comparison of the present results with the exact solution and those of Friedman and Kosmatka [27]. The present prediction correlates well with the exact value where the z-location of shear center is slightly better than that of Friedman and Kosmatka [27]. It is noted that the latter uses the boundary element method to estimate the shear center location.

Fig. 4

Triangular section

Table 1 Shear center location of triangular section

The second example is an isotropic channel section [23] with varying aspect ratio b / t, as shown in Fig. 5. The section has an equal height and width b while the wall thickness t is varied from very thin to very thick. The elasticity solution from thin-walled beam theory is given by [23]

$$\begin{aligned} \frac{e}{b} = \frac{1}{3} - \frac{1}{12}\left( \frac{t}{b} \right) ^2 + \left( \frac{5}{3} \left( \frac{t}{b} \right) ^2 + \frac{7}{3}\right) ^{-1} \end{aligned}$$

(76)

The shear center location (e) is normalized by the thin-walled elasticity solution which approaches unity with the increase in the aspect ratio (b / t). Figure 6 shows the comparison of normalized shear center with varying aspect ratios. It is interesting to note that the present results are almost identical to those obtained by VABS [23] where the shear center location is computed through stiffness coefficients determined using an asymptotic approach. It is seen from Fig. 6 that with the increase in the aspect ratio, the predicted shear center approaches the thin-walled elasticity solution.

Fig. 5

Isotropic channel section with origin at centroid

Fig. 6

Shear center location of channel section with varying aspect ratio

5.2 Sectional elastic and inertial properties

5.2.1 Highly heterogeneous section

To assess the complete set of section properties, a highly heterogeneous isotropic section [28] shown in Fig. 7 is considered next. The section consists of an asymmetric C-channel profile having real material properties and the remaining portion of the section with dummy material properties having a substantially low value. The mechanical properties of the real material are: $E=206.843\,\hbox {GPa}$, $\nu =0.49$ and $\rho =1068.69\, \hbox {kg/m}^{3}$ whereas that of the dummy material are $10^{-12}$ times smaller than those of the real material, except for the Poisson ratio which remains the same. For the present analysis, the section is discretized using 3056 Q8 elements and 9895 nodes.

Fig. 7

Highly heterogeneous section

Table 2 presents the comparison of section properties obtained using the present analysis with the analytical solution, and with those from PreComp [28] and VABS [28]. The elastic constants (stiffnesses) are computed at Euler–Bernoulli level ($4\times 4$ stiffness matrix) for the present example. It is seen that the present results are nearly identical to the analytical solution. The maximum deviation of the present results relative to the analytical solution is 1.74 % for the cross-bending stiffness $(K_{34})$ while VABS shows a difference of 2.09 %. It is noted that PreComp shows significantly large deviations for both the elastic constants and inertial properties with a maximum value of 473.42 % reported in $I_{zz}$. The present estimations of inertial properties which include mass (m), mass moments of inertia $(I_{yy},I_{zz})$, and mass center $(y_{mc},z_{mc})$ match exactly with the analytical solution and perform slightly better than those of VABS.

Table 2 Comparison of sectional properties of highly heterogeneous section. (1–extension; 3,4–bending)

5.2.2 Isotropic blade-like section

The section was studied by Chen et al. [28] which resembles a complex geometry of thin-walled rotor blade, as shown in Fig. 8. The material properties are the same as that of the highly heterogeneous section. The cross-section is discretized with 10 segments through the thickness and 120 segments along the circumference leading to a total of 1200 Q8 elements and 3840 nodes.

Fig. 8

Isotropic blade-like section

The sectional properties predicted by PreComp [28], VABS [28], CROSTAB [28], 3D FE analysis ANSYS [28] and the present analysis are compared with the analytical solution in Table 3. The section stiffnesses ($EA,EI_y,EI_z,GJ$, and $K_{14}$) obtained from the present code are nearly identical to those of VABS and ANSYS. The location of shear center is predicted close to that of ANSYS solution and VABS. The analytical results of chordwise bending $(EI_z)$, extension–torsion coupling $(K_{14})$ and shear center $(y_{sc})$ show large deviations from ANSYS predictions. The reason for the discrepancy is that the analytical approach is based on the thin-walled beam theory which may not adequately represent the section geometry, particularly near the trailing edge. The inertial properties which include the sectional mass per unit length and sectional mass moments of inertia are accurately predicted by the present analysis as they match exactly with the analytical and ANSYS solutions. It is observed that the predictions of mass center $(y_{mc})$ and tension center $(y_{tc})$ offsets are slightly better than VABS despite the same number of elements. Note that PreComp and CROSTAB fail to predict most of the section properties correctly.

Table 3 Comparison of sectional properties of isotropic blade-like section

5.3 Effects of nonuniform warping

Several examples are studied to identify the influence of NUW on the static response of composite beams with solid, and thin-walled open and closed sections. The convergence behavior of the stiffness coefficients with the number of beam FEs is also investigated for anisotropic thin strips. The NUW effect is demonstrated with varying slenderness ratios (defined as length-to-width ratio) and represented in terms of diffusion length which is defined (similar to that of [10] or boundary layer zone of [3]) as the beam axial location where the nonuniform static response decays to 5 % of that at the extreme boundary.

5.3.1 Anisotropic thin strips with elastic couplings

The anisotropic thin strips exhibiting bending–torsion and extension–torsion couplings were studied experimentally and theoretically by Minguet and Dugundji [29]. The sections were analyzed later by Hodges et al. [30] and more recently by Morandini et al. [31]. The strips are made of AS4/3501-6 graphite-epoxy with properties as $E_{11}=142.0\,\hbox {GPa}$, $E_{22}=E_{33}=9.8\,\hbox {GPa}$, $G_{12}=G_{13}=6.0\,\hbox {GPa}$, $G_{23}=3.447\,\hbox {GPa}$, $\nu _{12}=\nu _{13}=0.30$, and $\nu _{23}=0.34$. Two types of strips are considered: (a) the first strip is 30.023 mm wide and 1.4712 mm thick with a layup of $[45^{\circ }/0^{\circ }]_{3s}$ exhibiting a bending–torsion coupling; (b) the second strip is 30.023 mm wide and 1.9215 mm thick having a layup of $[20^{\circ }/-70^{\circ }/-70^{\circ }/20^{\circ }]_{2a}$ which exhibits an extension–torsion coupling. The computed warping deformation and stiffness coefficients may be dependent on mesh refinements and therefore, a convergence study is necessary. The rectangular solid section is modeled using 12 elements through the thickness (1 for each composite layer) while the number of elements along the width is varied. Figure 9 shows the comparison of the relative error (with respect to the converged value) for the stiffness coefficients obtained using Q4 and Q8 elements. It is indicated that the torsional stiffness $(K_{44})$, bending–torsion coupling stiffness $(K_{45})$, bending–shear warping coupling stiffness $(K_{68})$, extensional warping stiffness $(K_{77})$, extensional warping–shear warping coupling stiffness $(K_{78})$, shear warping stiffness $(K_{99})$ and bending warping stiffness $(K_{12,12})$ show relatively large errors with Q4 elements while Q8 elements converge rather quickly. A maximum error of 1.24 % is obtained with 120 Q8 elements for the shear warping stiffness $(K_{99})$ and therefore Q8 elements are utilized in the following validation examples. The bending–torsion coupled strip is modeled using 120 Q8 elements whereas the extension–torsion coupled strip is modeled using 160 Q8 elements.

Fig. 9

Convergence of stiffness coefficients with number of elements for bending–torsion coupled anisotropic thin strip. Q4 and Q8 denote 4- and 8-node quadrilateral elements, respectively. (1—extension; 2—shear; 4—torsion; 5,6—bending; 7—extensional warping; 8,9—shear warping; 10—torsional warping; 12—bending warping)

Tables 4 and 5 present the comparison of stiffness coefficients for the bending–torsion and extension–torsion coupled strips, respectively. The predicted results are compared with those obtained by Minguet and Dugundji [29], Hodges et al. [30], and Morandini et al. [31]. Minguet and Dugundji [29] used the classical lamination theory (CLT) to compute the sectional stiffnesses. Hodges et al. [30] used a FE based section analysis called nonhomogeneous anisotropic beam section analysis (NABSA) which is developed based from the theory of Giavotto et al. [10]. Morandini et al. [31] employed the generalized eigenvector approach to compute the sectional stiffness matrix. The stiffness coefficients for the bending–torsion coupled strip obtained by the present analysis show excellent correlation with those of Hodges et al. [30] and Morandini et al. [31] where the maximum difference of -0.58 % is noted for shear stiffness $(K_{33})$ in comparison to NABSA. For the extension–torsion coupled strip, the stiffness coefficients show an excellent agreement with those of Hodges et al. [30] and Morandini et al. [31], except the shear stiffness $K_{33}$ and shear–bending coupling stiffness $K_{36}$ where deviations of −3.6 and −2.7 % are recorded, respectively. It is worth mentioning that Morandini et al. [31] show a deviation of 6.8 % for the shear–bending coupling stiffness $K_{36}$ compared to Hodges et al. [30]. The stiffness coefficients corresponding to CLT [29] show significantly large variations compared to the other state-of-the-art predictions.

Table 4 Comparison of stiffness coefficients for the bending–torsion coupled anisotropic thin strip

The warping stiffness coefficients are also presented in Tables 4 and 5 which can be used to model the influence of NUW. At the beam boundary constraint, the warping deformation is prevented leading to internal loads (represented by bimoments) which in turn result into higher stresses. The SV solutions corresponding to uniform (or free) warping become invalid near the boundary region. The warping stiffness coefficients can accurately determine the stresses at these locations. These effects decay along the beam length towards the free boundary. Table 4 presents the additional nonzero stiffness coefficients corresponding to NUW for the bending–torsion coupled anisotropic strip. The nonclassical stiffness coefficients for refined model include extensional warping stiffness $(K_{77})$, extensional warping–shear warping coupling stiffness $(K_{78})$, shear warping stiffnesses $(K_{88},K_{99})$, shear warping–torsional warping coupling stiffness $(K_{9,10})$, torsional warping stiffness $(K_{10,10})$, torsional warping–bending warping coupling stiffnesses $(K_{10,11},K_{10,12})$, and bending warping stiffnesses $(K_{11,11},K_{12,12})$. The warping related stiffnesses for extension–torsion coupled anisotropic strip are also presented in Table 5. Note that the couplings between shear warping and torsional warping $(K_{8,10}, K_{9,10})$ are negligible for the extension–torsion couple strip. It should be remarked that the computation of warping stiffness constants along with NUW is the unique feature of the present analysis and all relevant warping stiffness values are provided in Tables 4 and 5.

Table 5 Comparison of stiffness coefficients for the extension–torsion coupled anisotropic thin strip

5.3.2 Orthotropic thin strip

An orthotropic thin strip studied by Yu et al. [16] is introduced to investigate the effect of warping restraint. The strip is 0.762 mm thick and 24.206 mm wide, and consists of a single layer of orthotropic material with properties as: $E_{11}=141.9631\,\hbox {GPa}$, $E_{22}=E_{33}=9.7906\,\hbox {GPa}$, $G_{12}=G_{13}=5.9984\,\hbox {GPa}$, $G_{23}=4.7988\,\hbox {GPa}$, $\nu _{12}=\nu _{13}=\nu _{23}=0.42$. The fiber angle of the orthotropic layer is 0$^{\circ }$. The section does not possess any elastic couplings. The section is discretized using 60 segments along the width and 2 segments through the thickness resulting in a total of 120 Q8 elements and 485 nodes.

Table 6 presents the stiffness coefficients where the torsional $(K_{44})$ and torsional warping $(K_{10,10})$ stiffnesses obtained by the present analysis are compared with VABS [16]. The correlation is excellent for torsional stiffness $(K_{44})$ albeit a slight deviation of 1.95 % is recorded in the torsional warping stiffness. In Table 6, the other nonzero stiffness coefficients including the warping stiffnesses representing the NUW effect are also presented for reference purpose. The bending warping stiffnesses are found to be negligible and are therefore not reported here.

Table 6 Comparison of stiffness coefficients for thin orthotropic strip

The NUW effects related to the torsional and shear restraints on the static response of a cantilever beam under various sectional loadings are investigated in the following subsections. The beam length (L) is considered to be 0.254 m for the torsional case. For the shear restraint, the slenderness ratio (length-to-width ratio L/b) is varied to investigate the end effects.

Torsional restraint The beam is subjected to a force couple ($F_c=4.448$ N) at the tip end resulting in a torsional moment $(\overline{M}_x)$ of 0.108 Nm [16]. The boundary conditions at the clamped end of the beam are: $\phi _x(0)=0$, $\phi '_x(0)=0$, $Q_x(L)=0$. Assuming small rotations, the equilibrium equation for the torsion can be extracted from Eq. (43) as

$$\begin{aligned} M'_x - Q''_x = 0 \end{aligned}$$

(77)

The analytical solution for twist angle $\phi _x$ can then be obtained as

$$\begin{aligned} \phi _x(x)&= \frac{\beta _x}{\alpha _x} \left[ x - \frac{1}{\sqrt{\alpha _x}} \sinh (\sqrt{\alpha _x} x) \right. \nonumber \\&\left. \qquad + \frac{1}{\sqrt{\alpha _x}} \tanh (\sqrt{\alpha _x} L) \left[ \cosh (\sqrt{\alpha _x} x) - 1 \right] \right] \end{aligned}$$

(78)

where,

$$\begin{aligned} \alpha _x = K_{44}/K_{10,10}, \quad \beta _x = \overline{M}_x/K_{10,10} \end{aligned}$$

(79)

Figure 10 shows the variation of twist angle and twist rate along the beam length. The predicted response is compared with that of ABAQUS 3D FE solution [16] and VABS [16]. The response corresponding to VABS is reproduced using the stiffness coefficients given in Table 6. The SV solutions (for uniform warping) obtained by the present analysis are also provided as reference. It can be seen in Fig. 10 that the present results match exactly with the ABAQUS 3D FE solution and those obtained by VABS. Both predictions on the twist rate $(\phi '_x)$ eventually converge to the SV solution towards the free end of the beam with diffusion length as 20.21 %, as can be seen in Fig. 10b. It is clear from Fig. 10a that the SV solutions are certainly not valid for open section anisotropic beams where a difference of 7.23 % is observed in the tip twist angle as compared to the present results with NUW effect. Note that the twist rate (see Fig. 10b) obtained using SV beam theory remains constant which fails to capture the secondary loads (and subsequently secondary stresses) at the clamped end of the beam. In addition to the torsional warping, the influence of warping restraints associated with the shear deformation is examined in the next subsection. It should be noted that this has never been addressed in the literature.

Fig. 10

Twist response of orthotropic thin strip under a tip torsional moment. a Twist angle $\phi _x$ b Twist rate $\phi '_x$

Shear restraint The flap shear response is computed to show the effect of nonuniform shear warping for beams with varying slenderness ratio (L / b). A flap shear force $(\overline{F}_z)$ of 4.448 N is applied at the beam tip. The boundary conditions at the clamped end of the beam are: $\gamma _z(0)=0$, $P_z(L)=0$. Assuming small rotations, the equilibrium equation for flap shear can be obtained from Eq. (43) as

$$\begin{aligned} F'_z - P''_z = 0 \end{aligned}$$

(80)

The 1D analytical solution for flap shear strain $\gamma _z$ can then be obtained as

$$\begin{aligned} \gamma _z(x)&= \frac{\beta _z}{\alpha _z} \left[ 1 - \cosh (\sqrt{\alpha _z} x) \right. \nonumber \\&\left. \quad + \tanh (\sqrt{\alpha _z} L) \sinh (\sqrt{\alpha _z} x) \right] \end{aligned}$$

(81)

where,

$$\begin{aligned} \alpha _z = K_{33}/\overline{K}_{99}, \quad \beta _z = \overline{F}_z/\overline{K}_{99}, \quad \overline{K}_{99} = K_{99}-K_{59}^2/K_{55} \end{aligned}$$

(82)

Figure 11 shows the variation of flap shear strain $(\gamma _z)$ and its derivative $(\gamma '_z)$ along the nondimensional beam length. The effect on the response is examined for varying slenderness ratio (L / b). The SV solution with uniform shear warping is also presented which indicates a constant value for the flap shear strain and subsequently zero value for its derivative. It can be noted from Fig. 11 that near the clamped end the NUW provides a realistic solution. As the slenderness ratio is increased from 2 to 15, the NUW effect dissipates rapidly and the response approaches SV solution away from the clamped end of the beam. The diffusion length for the beam with the slenderness ratio $L/b=10$ is 6.83 % which decreases at higher slenderness ratios. For short beams $(L/b=2,5)$, the response shows significantly large deviations and decays slowly towards the beam tip. The variation of the derivative of flap shear strain also shows a similar behavior with the decrease in the slenderness ratio. This effect has been neglected even in the state-of-the-art research and requires adequate modeling for the reliable beam response. The nonuniform distribution of $\gamma _z$ and $\gamma '_z$ leads to additional loads and stresses in the affected region which can have considerable impact especially for highly coupled beams. An accurate determination of shear response and secondary stresses, thus cannot be guaranteed with the SV approach.

Fig. 11

Flap shear strain and its derivative for orthotropic thin strip under a tip shear force. a Flap shear strain $\gamma _z$ b Derivative of flap shear strain $\gamma '_z$

5.3.3 Anisotropic I-section beam

An anisotropic I-section beam [16] shown in Fig. 12 is investigated next. The material properties are the same as those used for the orthotropic thin strip in the previous section. The top and bottom flanges have a mirror image layup of $[(0^{\circ }/90^{\circ })_2/(90^{\circ }/0^{\circ }) /15^{\circ }_2]_T$, and the web has a symmetric layup of $[(0^{\circ }/90^{\circ })_2]_s$. This section exhibits bending–torsion and extension–shear couplings. A little extension–bending coupling is also present. The section is discretized with 390 Q8 elements leading to a total of 1513 nodes.

Fig. 12

Anisotropic I-section beam

Figure 13 shows the warping displacement modes for the anisotropic I-beam. The extension–shear coupling can be clearly seen in Fig. 13a. The effect of bending–torsion coupling on the bending deformation is visible in Fig. 13e. The bending deformation due to an extension–bending coupling is shown as exaggerated view in Fig. 13f. These warping modes evidently describe the classical as well as nonclassical elastic couplings present in the anisotropic I-section beam.

Fig. 13

Warping modes of anisotropic I-section beam (not to scale). a Extension $(\gamma _x)$ b Shear $(\gamma _y)$ c Shear $(\gamma _z)$ d Torsion $(\kappa _x)$ e Bending $(\kappa _y)$ f Bending $(\kappa _z)$

Table 7 shows the comparison of the effective torsional stiffness and the warping stiffness with those obtained by VABS [16], and Kim and Kim [18]. The effective torsional stiffness is computed by taking into account the bending–torsion coupling, given as $\overline{K}_{44} = K_{44} - K_{45}^2/K_{55}$. The effective torsional stiffness obtained using the present analysis is very close to that of VABS with a difference of 1.33 % while the value reported by Kim and Kim [18] shows a deviation of 3.71 %. The torsional warping stiffness from the present analysis is lower by 6.85 % compared to VABS whereas Kim and Kim [18] report a higher value by 4.13 %. Note that the formulation developed by Kim and Kim [18] has much resemblance to that of VABS, both using the asymptotic methods, though the reason for the discrepancy in the values is unknown. The deviations in the present analysis are attributed to the dissimilarities in the treatment of warping restraints which result in a lower warping stiffness.

Table 7 Comparison of stiffness coefficients for the anisotropic I-section beam

In addition to torsion related stiffnesses, Table 7 presents other non-negligible stiffness coefficients which include extensional stiffness $(K_{11})$, extension–shear coupling stiffness $(K_{12})$, shear stiffnesses $(K_{22},K_{33})$, bending stiffnesses $(K_{55},K_{66})$, extensional warping stiffness $(K_{77})$, shear warping stiffnesses $(K_{88},K_{99})$, and bending warping stiffnesses $(K_{10,10},K_{10,11})$. Furthermore, nonclassical elastic couplings exist between bending-extensional warping $(K_{67})$, bending-shear warping $(K_{59},K_{68})$, and extensional warping-shear warping $(K_{78})$. The warping restraints can have considerable influence near the boundary constraint region as a result of these nonzero warping stiffnesses. The effects of NUW due to torsion and shear are investigated next.

Torsional restraint The effect of torsional warping restraint on the twist response of a cantilever beam is examined next. The beam length (L) is 0.254 m. The beam is subjected to a force couple at the tip resulting in a torsional moment $(\overline{M}_x)$ of 0.113 Nm. The boundary conditions are the same as those defined for the orthotropic thin strip in the previous section. The twist angle along the beam length is computed analytically using Eq. (78), where the constants $\alpha _x$ and $\beta _x$ are given as

$$\begin{aligned}&\alpha _x = \overline{K}_{44}/K_{10,10}, \qquad \beta _x = \overline{M}_x/K_{10,10} \nonumber \\&\overline{K}_{44} = K_{44} - K_{45}^2/K_{55} \end{aligned}$$

(83)

Figure 14 shows the comparison of twist angle $(\phi _x)$ and twist rate $(\phi '_x)$ obtained by the present analysis with the 3D FE solution from ABAQUS [16], and those obtained by VABS [16] and Kim and Kim [18]. The SV solution obtained using the present analysis is also provided as a reference. As can be seen, the present results are in excellent agreement with the 3D FE solutions of ABAQUS. The predictions by VABS or Kim and Kim [18] are slightly underpredicted which can be explained by the higher torsional warping stiffness reported by both methods. It should be remarked that the SV solutions show a striking difference compared to those obtained using the nonuniform torsional warping. The nonuniform torsional effect does not dissipate at all and is therefore inevitable for open section composite beams.

Fig. 14

Twist response of anisotropic I-section beam under a tip torsional moment. a Twist angle $\phi _x$ b Twist rate $\phi '_x$

Shear restraint The effect of nonuniform shear is studied for anisotropic I-section beams with various slenderness ratios. A shear force $\overline{F}_z=4.448$ N is applied at the free tip of the beam. The boundary conditions are the same as that for the orthotropic strip in the previous section. The 1D linear analytical solution can be computed using Eq. (81) with constants $\alpha _z$ and $\beta _z$ defined in Eq. (82). The computed flap shear strain $(\gamma _z)$ and its derivative $(\gamma '_z)$ are shown in Fig. 15. The SV solutions are also presented for the reference. The diffusion length for $L/b=10$ is found to be 30.42 %. The derivative of the shear strain $(\gamma '_z)$ is nonzero for the nonuniform case and decays at around one-third of the beam length with $L/b=10$. Although a similar trend is observed compared to the orthotropic thin strip, the shear restraint effect becomes more pronounced for anisotropic I-section beams as evidenced by the higher values of the diffusion length.

The variations of the diffusion length with slenderness ratios for nonuniform torsion and shear are presented in Fig. 16. It is observed that the nonuniform torsion does not dissipate for slenderness ratios less than 30. Even for beams with higher slenderness ratios, the diffusion length is considerably larger and cannot be neglected. For the nonuniform shear, the diffusion length is greater than 10 % for slenderness ratios less than 30. Thus, the nonuniform shear effect is non-negligible near the clamped boundary for beams with low slenderness ratios (L / b). The nonuniform shear is not as dominant as the nonuniform torsion for anisotropic I-section beams, nevertheless, the effects are substantial which apparently cannot be neglected.

Fig. 15

Flap shear strain and its derivative for anisotropic I-section beam under a tip shear force. a Flap shear strain $\gamma _z$ b Derivative of flap shear strain $\gamma '_z$

Fig. 16

Diffusion length for nonuniform torsion and shear of anisotropic I-section beam

5.3.4 Thin-walled composite box section beam

The thin-walled composite box section beam was originally studied by Chandra and Chopra [6], and subsequently by Popescu and Hodges [32], Jung et al. [2], and Yu et al. [17]. The schematic of the beam is presented in Fig. 17 which has a circumferentially uniform stiffness layup of $[15^{\circ }]_6$. The outer width and height of the box section are 24.206 mm (0.953 in) and 13.462 mm (0.53 in), respectively, with a wall thickness of 0.762 mm (0.03 in). The ply thickness is 0.127 mm (0.005 in) for each of the walls. The beam is made of AS4/3501-6 graphite-epoxy material with properties same as those of the orthotropic thin strip, except the Poisson ratios given as: $\nu _{12}=\nu _{13}=0.30$, and $\nu _{23}=0.34$. The beam exhibits extension–torsion and shear–bending couplings.

Fig. 17

Thin-walled composite box section

Each of the warping displacement modes computed using the present analysis are shown in Fig. 18. The elastically-coupled behavior of the box section is captured nicely as can be seen in the plots. The influence of extension–torsion coupling on the extension mode is clearly visible in Fig. 18a which results in an out-of-plane deformation under an extensional action. The shear–bending coupling can be noted in Fig. 18b,c,e, and f. The shear modes indicate in-plane distortion due to the bending moments while the bending modes show out-of-plane deformation due to the shear forces.

Fig. 18

Warping modes of thin-walled composite box section beam (not to scale). a Extension $(\gamma _x)$ b Shear $(\gamma _y)$ c Shear $(\gamma _z)$ d Torsion $(\kappa _x)$ e Bending $(\kappa _y)$ f Bending $(\kappa _z)$

The comparison of nonzero stiffnesses for the composite box beam is presented in Table 8. The correct prediction of these warping modes is crucial to estimate the accurate elastically-coupled stiffness coefficients. The nonzero stiffness coefficients predicted from the present analysis are compared with those obtained by NABSA [32], Jung et al. [2], and VABS [32]. NABSA is a FE code based on the theory developed by Giavotto et al. [10]. Jung et al. [2] used an analytical mixed force-displacement approach implemented in a shell-wall based sectional analysis. For NABSA, the beam is modeled with 216 Q8 elements, whereas for VABS and the present analysis 360 Q8 elements are used. The present results indicate excellent correlation with those of VABS and NABSA. Since Jung et al. [2] used an analytical contour based approach which cannot adequately represent the corners of the box section, the deviations up to 3.79 % are reported in the stiffness coefficients compared to NABSA. Note that the present analysis, being a general FE sectional analysis, can accurately represent the geometry and material distribution of any arbitrary beam section. Additionally, the nonzero warping stiffnesses from the present analysis are also reported in Table 8. These warping stiffnesses may result in nonuniform beam behavior near the boundary restraints as discussed in the following text.

Table 8 Comparison of nonzero stiffnesses for the thin-walled composite box section

The effect of torsional warping restraints for isotropic beams may be negligible, however, neglecting these effects for composite beams may result in significant errors as reported by Rehfield et al. [3]. The influence of nonuniform torsion and shear is explored for thin-walled composite box section beams with varying slenderness ratio (L / b). The 1D analytical solutions for torsion and shear are computed using Eqs. (78) and (81) where the constants $\alpha _z$ and $\beta _z$ are defined in Eq. (82), and $\alpha _x$ and $\beta _x$ are given as

$$\alpha _x = \overline{K}_{44}/K_{10,10}, \quad \beta _x = \overline{M}_x/K_{10,10} \quad \overline{K}_{44} = K_{44} - K_{14}^2/K_{11}$$

(84)

Figure 19 shows the variation of diffusion length with slenderness ratios corresponding to the nonuniform torsion and shear. The nonuniform shear is more prominent than the nonuniform torsion as the diffusion length is greater than 10 % for slenderness ratio less than 20. The nonuniform torsional effect decays rapidly even for short beams. For highly slender beams $(L/b>60)$, the NUW effects can be neglected without significant loss of accuracy. The composite box beams show larger influence of shear restraint compared to the orthotropic thin strip but lower than that of anisotropic I-section. The impact of nonuniform shear for thin-walled composite box beams is important and should be modeled correctly to predict the beam displacements and stresses.

Fig. 19

Diffusion length for nonuniform torsion and shear of composite box section beam

6 Conclusions and recommendations

A refined FE sectional analysis system is developed for nonhomogeneous anisotropic beams with NUW using the displacement-based elasticity theory. The analysis is applicable to beams with arbitrary geometric layout and material properties. The influences of 3D warping and stresses are modeled which include the nonclassical transverse shear and Poisson deformations of the beam in a generic manner. The accuracy of predicted sectional properties is investigated for beams with simple to complex isotropic and anisotropic sections. The following conclusions are deduced from the present study:

• 1. The refined beam model is formulated which takes into account NUW effects related to end restraints leading to a $12\times 12$ sectional stiffness matrix. The generalized Timoshenko stiffness, direct warping stiffness, and the coupling stiffness coefficients are consistently incorporated into the stiffness matrix.

• 2. The various kinds of triangular and quadrilateral shape elements are implemented in the FE sectional analysis for the accurate treatment of arbitrary section profiles with complex geometries and the versatility of the FE modeling procedures.

• 3. In order to predict the shear center location, the Trefftz’ theory is systematically extended for anisotropic beams and has been verified for simple homogeneous as well as complex nonhomogeneous isotropic sections.

• 4. The predicted beam elastic properties which include stiffness coefficients and sectional offsets (shear center and tension center) are obtained for the isotropic and composite beams where an excellent correlation is achieved in comparison with the analytical and/or 3D FE solutions.

• 5. An excellent correlation is achieved for the inertial properties, which include mass, mass moments of inertia, and mass center, compared with other state-of-the-art methods.

• 6. The NUW effects are examined for several open section beams with or without elastic couplings. The response under torsional warping restraint is validated with the 3D FE solution and other state-of-the-art methods. The influence of shear warping restraint is demonstrated for solid, open, and closed section beams with varying slenderness ratios. It is noted that the effects are non-negligible and must be modeled correctly for an accurate prediction of beam response, strains, and stresses. It is revealed that the torsional restraint effect is prominent for thin strips and open section beams whereas the shear restraint effect is more pronounced for thin-walled closed box section beams. Furthermore, the nonuniform shear response decays slowly while the nonuniform torsion response may not decay at all for composite beams with low slenderness ratios.

The current validations confirm the reliable predictions of the sectional properties of isotropic and anisotropic beams, such as helicopter or wind turbine blade applications. The present analysis can describe the beam behavior accurately and offers an efficient alternative to the high cost 3D FE analyses.