Enhanced Beam Formulations with Cross-Section Warping Under Large Displacements

Abstract

This work investigates the capabilities of two different approaches for the analysis of thin-walled structures, both based on enriched beam theories that include out-of-plane cross-section warping, being the in-plane deformations neglected.

First approach relies on a three-dimensional beam finite element based on a four-field mixed formulation, where cross-section warping displacement is introduced as additional independent field to the standard rigid-body displacements, strains, and stresses and is interpolated with the definition of specific shape functions: along the element axis and over the general cross-section. Geometric nonlinearity is included through a corotational approach that considers the coupling between axial and torsional stress/strain components, known as Wagner effect. As opposed to the first approach, a simpler but coarse descriptor of warping displacement field is adopted in the second approach, assuming a priori the warping profile over the cross-section. By adopting nonlinear hyperelastic relations, generalized cross-section constitutive responses are portrayed, accounting for Wagner term. Geometric nonlinearity is also included. In this case, the nonlinear equilibrium equations of the enriched beam model are solved through a finite difference technique.

For selected specimens, modal decompositions and step-by-step incremental analyses are conducted under small and large displacements, comparing the results obtained with both models with analytic solutions and numerical outcomes. Advantages and disadvantages of each approach are discussed, aiming at supplying the reliability ranges of the two models and depict new potential research lines based on a suitable ‘combination’ of the relevant formulations.

1 Introduction

Beam models are commonly used for the analysis of large scale structures because of their computational efficiency in reproducing the structural response. However, most beam formulations used in engineering practice are based on the assumption of rigid body cross-section and fail in correctly describing the response of thin-walled structures, especially when elements with open cross-sections are considered. Indeed, the mechanical behavior of thin-walled beams is significantly influenced by cross-section warping, which causes multi-axial stress/strain interaction and leads to complex nonlinear responses, even under ordinary load conditions [1]. Moreover, due to their slenderness and low torsional stiffness, instability phenomena are generally dominant in such structural elements.

Starting from the pioneering work by Vlasov [2], many authors have proposed enriched formulations that extend classic beam theories, aiming at capturing warping deformations of the cross-section. Among them, thin-walled beam models derived from enriched three-dimensional continua have been proposed by Crespo da Silva [3], Simo and Vu-Quoc [4], Ascione and Feo [5], Di Egidio, Luongo and Vestroni [6]; other authors, as Vlasov [2] and Møllmann [7] adopt a two-dimensional support. Direct one-dimensional models are also available, e.g. those proposed by Epstein [8] and Rizzi and Tatone [9]. A comprehensive review on thin-walled beam modeling approaches for dynamic analyses is reported in [10], while peculiar aspects concerning the design of this kind of elements is discussed in [11]. However, many of these formulations are based on specific kinematic and/or constitutive assumptions that limit their range of application and prevent generalization to complex case studies.

This work explores two different approaches proposed by the authors: the first relies on a three-dimensional beam finite element formulation [12,13,14], whereas the second is a one-dimensional model endowed with a coarse scalar descriptor of the warping displacement field [15]. The purpose of the paper is to move a step forward in the knowledge through direct comparisons of the two beam models. Modal decompositions and incremental analyses are conducted under small and large displacements, comparing the results obtained for both models and showing their relevant advantages and disadvantages. A reliability analysis of the two modeling approaches is provided, together with the recognition of new potential research lines intended to combine the relevant details of the two formulations.

2 Mixed 3D Beam Finite Element

The main aspects of the 3D beam FE formulation presented in [14] are recalled in the following. Considering a dynamic framework where the effects of inertia forces are included, the beam formulation accounts for out-of-plane cross-section warping by introducing an additional independent displacement field. Geometric nonlinearities are included by means of the corotational formulation proposed in [13] that accounts for the second order Wagner term and, thus, couples the axial and torsional strain components of the beam.

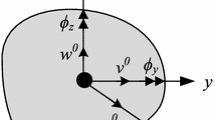
The rigid displacement $\mathbf {u}_r(x,y,z)$ at the cross-section material point m, classically considered in Euler-Bernoulli and Timoshenko beam formulations, is enriched by adding to it the out-of-plane warping field $\mathbf {u}_w(x,y,z)$ (Fig. 1), being these two enforced to be orthogonal. The resulting displacement $\mathbf {u}_m(x,y,z)$ is expressed as:

$$\begin{aligned} \mathbf {u}_m(x,y,z) = \mathbf {u}_r(x,y,z) + \mathbf {u}_w(x,y,z)\,. \end{aligned}$$

(1)

Vector $\mathbf {u}_w(x,y,z)= \begin{Bmatrix} u_w(x,y,z)&0&0 \end{Bmatrix}^T$ contains only the out-of-plane component directed along the beam axis x.

Fig. 1.

Warping displacement representation and interpolation scheme.

To interpolate the warping displacement field $u_w(x,y,z)$, 1D and 2D Lagrange polynomials, $N_{i}(x)$ and $M_{j}(y,z)$, are used along the beam axis x and over the cross-section (y, z), respectively, thus resulting:

$$\begin{aligned} u_{w}(x,y,z) = \sum _{i=1}^{n_{w}}N_{i}(x)\,\mathbf {M}(y,z)\,\mathbf {u}_{w\,i}\,\,, \end{aligned}$$

(2)

where vector $\mathbf {u}_{w\,i}$ collects the $m_{w}$ warping DOFs $u_{w\,ij}$ located on the i-th cross-section and $\mathbf {M}(y,z)$ is a row vector containing the corresponding shape functions $M_{j}(y,z)$. Although a variable number $n_{w}$ of warping interpolation cross-sections can be adopted along the beam axis x, here $n_{w}=2$ is selected and the two warping interpolation cross-sections are placed at the beam end nodes I and J.

The warping DOFs $u_{w\,ij}$ defined on the cross-section at node I and J and collected in the vectors $\mathbf {u}_{wI}$ and $\mathbf {u}_{wJ}$ are added to the standard kinematic translational, $\mathbf {u}_{J}$ and $\mathbf {u}_{J}$, and rotational, $\varvec{\varphi }_{I}$ and $\varvec{\varphi }_{J}$, DOFs, as shown in Fig. 2(a). Then, the two vectors $\mathbf {u}_{wI}$ and $\mathbf {u}_{wJ}$ are added to the element global displacement vector, that is expressed as:

$$\begin{aligned} \widetilde{\mathbf {u}}=\begin{Bmatrix} \mathbf {u}_{I}^{T}&\varvec{\varphi }_{I}^{T}&\mathbf {u}_{J}^{T}&\varvec{\varphi }_{J}^{T}&\mathbf {u}_{wI}^{T}&\mathbf {u}_{wJ}^{T}\end{Bmatrix}^{T} = \begin{Bmatrix} \mathbf {u}\\ \mathbf {u}_{w}\end{Bmatrix}\,. \end{aligned}$$

(3)

The kinematic equations resulting from the corotational approach are used to perform the geometric transformation of the standard element DOFs in $\mathbf {u}$ from the global to local reference system in Fig. 2(b) [13]. Hence, by removing the element rigid body motions, the basic reference system is defined and the six deformation displacement vector is derived, resulting as $\mathbf {v}= \left\{ u_{xJ} \quad \theta _{zI} \quad \theta _{zJ} \quad \theta _{xJ} \quad \theta _{yI} \quad \theta _{yJ} \right\} ^{T}$.

Fig. 2.

Finite element (a) global and (b) basic reference system and nodal displacement variables.

In this system, an equilibrated approach is considered so that the generalized section stress vector $\mathbf {s}(x)$ is expressed as function of the basic forces $\mathbf {q}$ work-conjugate to $\mathbf {v}$, as:

$$\begin{aligned} \mathbf {s}(x)=\mathbf {b}(x)\,\mathbf {q} + \mathbf {s}_q(x)\,, \end{aligned}$$

(4)

with $\mathbf {s}_q(x)$ containing the generalized section stresses due to distributed loads $\mathbf {q}_s(x)$ and $\mathbf {b}(x)$ being the equilibrium matrix. Vector $\mathbf {s}(x)$ collects the axial stress N(x), bending moments $M_{z}(x)$ and $M_{y}(x)$, torsional moment $M_{x}(x)$ and shear stresses $T_{y}(x)$ and $T_{z}(x)$. The generalized section strain vector $\mathbf {e}(x)$, containing axial strain $\varepsilon _{G}(x)$, flexural curvatures $\chi _{z}(x)$ and $\chi _{y}(x)$, torsional curvature $\chi _{x}(x)$ and shear strains $\gamma _{y}(x)$ and $\gamma _{z}(x)$, is related to the section stresses $\mathbf {s}(x)$ by means of the incremental generalized section constitutive law, that is:

$$\begin{aligned} \Delta \mathbf {e}(x)=\mathbf {k}_{ss}^{-1}(x)\,\Delta \mathbf {s}(x)\,, \end{aligned}$$

(5)

with $\Delta \star$ denoting the increment of variable $\star$ and $\mathbf {k}_{ss}(x)$ being the cross-section tangent stiffness matrix.

Moreover, section compatibility conditions relate the generalized cross-section strains $\mathbf {e}(x)$ to the generalized cross-section displacements $\mathbf {u}_s(x)$, defined as:

$$\begin{aligned} \mathbf {u}_s(x)= \begin{Bmatrix} u(x)&v(x)&w(x)&\theta _x(x)&\theta _y(x)&\theta _z(x) \end{Bmatrix}^{T}\,, \end{aligned}$$

(6)

where u(x), v(x) and w(x) are the rigid translations and $\theta _x(x)$, $\theta _y(x)$ and $\theta _z(x)$ the rigid rotations.

The element governing equations are derived by enforcing the stationarity of the following four-field extended Lagrangian functional $\mathcal {L}$:

$$\begin{aligned} \mathcal {L}(\mathbf {u}_{s},\mathbf {e},\mathbf {s},u_{w},\dot{\mathbf {u}}_{s},\dot{u}_{w}) = T(\dot{\mathbf {u}}_{s},\dot{u}_{w}) - \Pi (\mathbf {u}_{s},\mathbf {e},\mathbf {s},u_{w})\, \end{aligned}$$

(7)

with respect to the independent fields $\mathbf {u}_{s}(x)$, $\mathbf {e}(x)$, $\mathbf {s}(x)$ and $u_{w}(x,y,z)$, where T and $\Pi$ are the kinetic and internal potential energy, respectively. Then, the nonlinear material constitutive law, the weak form of the element compatibility and equilibrium and the section equilibrium conditions related to the warping are accordingly obtained. The detailed formulation and numerical validation can be found in [12,13,14, 16].

3 Direct 1D Beam Model

The beam model proposed in [15] is based on a direct one-dimensional continuum, enriched with a scalar measure coarsely describing the warping displacement field. Vlasov’s notions of bi-moment and bi-shear are considered and field equations are geometrically exact. Hence, non-trivial equilibrium paths of open thin-walled beams can be suitably attained. Here, symbols and notations adopted in [15] are modified according to those presented in the previous section for the 3D beam FE.

In the reference shape of the beam, the centroidal center axis is straight and parallel to the x-axis of an orthogonal Cartesian system. The latter is arranged according to a right-handed unit basis $(\mathbf{a}_x,\mathbf{a}_y,\mathbf{a}_z)$, with $\mathbf{a}_y,\mathbf{a}_z$ parallel to the cross-section principal axes of inertia. The current shape of the beam is described through fields that only depend on the abscissa along the beam axis. Kinematics of the beam axis is described by introducing the vector displacement field $\mathbf{u}_o(x)=\tilde{\mathbf{r}}_o(x)-\mathbf{r}_o(x)$, being $\mathbf{r}_o(x)$ and $\tilde{\mathbf{r}}_o(x)$ the position vector of given points in the reference and current shape, respectively. A proper orthogonal tensor field $\mathbf{R}(x)$ characterizes the cross-section rotation from reference to current shape, leading to the current basis $\tilde{\mathbf{a}}_i(x)=\mathbf{R}(x)\mathbf{a}_i$. A coarse scalar descriptor $\xi (x)$ is then superimposed to $\mathbf{u}_o(x)$ to describe the cross-section warping.

By comparing the current and reference shapes and subtracting the rigid transformations, three strain measures are obtained ($i,j,k=x,y,z$):

$$\begin{aligned} {\left\{ \begin{array}{ll} &{}\mathbf{\epsilon }(x)=\tilde{\mathbf{r}}_o'-\mathbf{R}(x) \mathbf{r_o}'(x)=\tilde{\mathbf{r}}_o'-\tilde{\mathbf{a}}_x=\varepsilon _G(x)\tilde{\mathbf{a}}_x(x)+\gamma _y(x)\tilde{\mathbf{a}}_y(x)+\gamma _z(x)\tilde{\mathbf{a}}_z(x)\\ &{}\mathbf{E}(x)=\mathbf{R}'(x)\mathbf{R}^\top (x)=\epsilon _ {ijh}\chi _i(x)\tilde{\mathbf{a}}_j(x)\wedge \tilde{\mathbf{a}}_h(x)\\ &{}\xi (x) \end{array}\right. }\,\,, \end{aligned}$$

(8)

where the prime stands for derivation with respect to the abscissa x and $\epsilon _{ijh}$ is the permutation (Levi-Civita) operator. Equation (8) includes: elongation $\varepsilon _G(x)$ of the beam axis, shear strains $\gamma _y(x),\gamma _z(x)$ between the beam axis and the two principal axes of inertia, torsional curvature $\chi _x(x)$, bending curvatures $\chi _y(x),\chi _z(x)$ and warping $\xi (x)$. This latter is related to the torsional curvature $\chi _x(x)$ by the following condition:

$$\begin{aligned} \xi (x)=\eta \chi _x(x)\Rightarrow \xi '(x)=\eta \chi _x'(x)\,, \end{aligned}$$

(9)

being $\eta$ a real constant. Therefore, balance equations of forces and couples and the auxiliary equation for bi-shear and bi-moment are obtained by balancing external and internal powers. Assuming that the internal power derives from an inner Green-like energy, nonlinear hyperelastic constitutive relations can be derived, keeping into account the coupling terms (extension-torsion-warping, shear-torsion, shear-shear and flexural-torsion couplings). More details on the governing equations are reported in [15].

Solution is provided by a numerical in-house code based on a centered finite difference technique. The stability of (non-trivial) equilibrium positions is studied according to Ljapounov’s theory by superposing small perturbations, while the non-standard eigenvalue problem is solved by standard numerical codes. Both conservative and non-conservative loadings, either stationary and non-stationary, can be included in the balance equations. Hence, the model and the proposed numerical technique may be used to analyze (non-trivial) equilibrium of thin-walled beams and detect static (a.k.a. buckling or divergence) and dynamic instabilities (a.k.a. flutter or Hopf bifurcation).

The proposed approach was numerically validated in [15, 17], confirming the reliability of the implemented technique and providing a quantitative measure of warping effects and pre-critical equilibrium path on critical loadings. Experimental validations are reported in [18, 19].

4 Applications and Comparisons

A simply supported beam, loaded at both ends by bending couples, is considered. The supports prevent torsional rotations and displacements of the axis, except for the axial displacement at the end on the right-hand side. Warping is free. Figure 3 shows the selected case study, with a sketch of the nonlinear equilibrium configurations of the beam axis x, ranging from 0 to the length L.

Fig. 3.

Case study.

Two different steel cross-sections are considered: IPE 200 (I-shape, doubly symmetric) and L$200{\times }100{\times }10$ (L-shape, non-symmetric). The cross-section dimensions are reported in Fig. 4, where o is the centroid, c the shear center and $y,\,z$ the central principal axes.

Fig. 4.

Cross-sections adopted in the simulations (values in mm).

Beam data are summarized in Table 1, being (with $i,j=y,z$): L the beam length, E the Young’s modulus, $\nu$ the Poisson ratio, $\rho$ the mass density, A and $A_i$ the area and shear shape modified areas, $J_t$ the Saint-Venant’s torsional inertia, $I_i$ the central principal moments of inertia, $y_{c}$ and $z_{c}$ the coordinates of the shear center c, $A_{ij}$ the mixed shear shape modified areas, $I_c$ the polar moment of inertia (with respect to the shear centre c), $I_{fi}$ the flexural-torsional constants and ${\varGamma }$ the warping inertia.

Table 1. Beam data and main characteristics of the cross-sections (on the top), and properties due to warping and non-symmetry (on the bottom); dash stands for zero.

The comparison of the two beam models investigate the free frequencies of the unloaded beams and the force-displacement path. The latter aims at implicitly detecting instabilities phenomena as deviations of the force-displacement path obtained by introducing small imperfections in the initial configuration. Unlike the instability analyses developed as eigenvalues problem, this approach better reveals the effectiveness of the two models in describing actual beam element behaviors under large displacements.

4.1 Computational Details for the Mixed 3D Beam FE

The evaluation of the beam cross-section response through the mixed 3D FE approach is obtained by introducing a fiber discretization [12, 20]. Linear elastic material behavior is considered in this work and fibers are distributed over the cross-section according to 2D Gauss-Legendre quadrature rule. Hence, the integrals defined over the cross-section area to compute the resultant stresses and stiffness matrices are evaluated in exact form. In particular, the cross-section is subdivided into rectangular patches and a $2 \times 2$ fiber grid is defined in each patch (blue dots in Fig. 5).

Round-shape fillets between webs and flanges can significantly increase the torsional stiffness of open cross-sections [17]. In the 3D FE model, fillets are included as additional fibers with area equal to $(1 - \pi /4)\,r^2$ and monitoring points located at a distance $\delta _\text {f} = \frac{5/6 - \pi /4}{1 - \pi /4}\,r$ from web and flange edges (i.e., at the fillet centroid indicated with the green dot in Fig. 5), being r the radius of the fillet external edge.

Fig. 5.

Schematic of fiber discretization (mixed 3D beam FE) for the I-shaped cross-section.

4.2 Results

Table 2 shows the comparison of the first six circular frequencies. As reference values, analytic solutions (row ‘a. Analytic’) [21] are considered for the doubly symmetric IPE 200, whereas a finite element solution based on shell elements (rows ‘a. Shell FE’) is used for the non-symmetric L$200{\times }100{\times }10$. The latter was computed with the software SAP2000 [22].

Both mixed 3D and direct 1D beam model were implemented in MATLAB [23]. The results of the mixed 3D FE are collected for two cases: neglecting (row ‘b. Mixed 3D FE (n.f.)’) and considering (row ‘c. Mixed 3D FE’) the round-shape fillets. The results provided by the 1D model are shown in row ‘d. Direct 1D’.

All meshes adopted in the numerical simulations (cases ‘a. Shell FE’, ‘b. Mixed 3D FE (n.f.)’, ‘c. Mixed 3D FE’ and ‘d. Direct 1D’) consider an equally-spaced discretization. The number of elements was determined through a mesh refinement procedure, that is by progressively reducing the element size until the variation observed for the first six frequency values resulted lower than 5‰. The discrepancies between reference (‘a’) and adopted (‘b’, ‘c’ and ‘d’) models are measured evaluating the percentage differences $\Delta _{ab},\,\Delta _{ac},\,\Delta _{ad}$ that are reported in the same table.

Table 2. Comparison of the first six circular frequencies [rad/s].

The percentage errors obtained for the doubly symmetric cross-section show that, when fillets are properly modeled, both mixed 3D and direct 1D beam models are able to correctly evaluate the first six frequencies. Therefore, in this case, given its simplicity and lower computational effort, the adoption of the direct 1D model appears more convenient than that of the mixed 3D FE. By contrast, when the L-shape non-symmetric cross-section is considered, the mixed 3D FE is still in good agreement with the reference solution, whereas the direct 1D model is able to capture only the first and third frequencies.

Moreover, since there is only one fillet instead of four, for this section geometry their effect is less prominent than for the I-shaped beam. However, the model without fillets seems to better reproduce the reference solution than the model endowed with. This occurs because the shell model accounts for the fillets in an approximate way by increasing the element thickness in correspondence of web and flange intersections. This issue needs to be further investigated, for instance by employing brick finite element models. However, it is out of the purposes of the present paper and does not affect the results discussed above.

Step-by-step incremental analyses are developed imposing the following end bending couples:

$$\begin{aligned} \mathbf{m} = H \, \bar{M} \mathbf{a}_y + H\, M \mathbf{a}_z, \qquad \text {with}\quad H=\left\{ -1,+1\right\} \text { in } x=\left\{ 0,L\right\} , \end{aligned}$$

(10)

where $\bar{M}=0.50$ kNm plays the role of the small imperfection and M is the evolutionary parameter. For the I-shaped cross-section, when imperfections are neglected, the following analytic solution holds for the critical values of M, when couples are applied in the symmetry plane [24]:

$$\begin{aligned} {M_{n}=\pm n\frac{\pi }{L}\sqrt{EI_yGJ_t\Big (1+\frac{n^2\pi ^2}{L^2}\frac{E{{\varGamma }}}{GJ_t}\Big )}\qquad n\in \mathbb {N}\,,}\end{aligned}$$

(11)

being $G=E/(2(1+\nu ))$ the shear modulus. For $n=1$, the first critical value provided by Eq. (11) is obtained, resulting equal to $M_1=28.15$ kNm. For the non-symmetric L$200{\times }100{\times }10$ cross-section, the first critical value provided by the FE analysis is $M_1=23.23$ kNm.

Fig. 6.

Load-displacement paths with ‘small’ imperfections.

Load-displacement paths provided by mixed 3D and direct 1D model are reported in Fig. 6, with the magnitude of the end couples in the vertical axis and the displacement along z in the horizontal axis. Results are shown for ‘small’ (top) and ‘large’ (bottom) displacement amplitudes, for I-(left) and L-(right) shaped cross-section. In the plots, the effect of the ‘small’ imperfection is clearly appreciable, as non-zero displacement occurs for $M=0$. For both section geometries the initial imperfection is about $L/1000 = 5$ mm.

For ‘small’ displacement amplitudes (plots on the top), both models are able to detect the onset of the instability phenomena of the beams. The values indicated by the models are in agreement with the critical loads provided by the analytic solution (for the I-shaped cross-section) and by the shell FE model (for the L-shaped cross-section), although for the L-shape section the mixed 3D FE slightly overestimates the critical load magnitude. Indeed, as this model adopts a corotational approach, geometric nonlinearities are not described in exact form and coupling between torsion and shear-flexural deformations, that is predominant for non-symmetric sections, is not perfectly captured. However, as observed for the vibration frequencies, for the L-shape section the mixed 3D FE solution seems to be closer to the reference results when fillets are neglected (blue dashed curves). By contrast, for the I-shape section, this assumption leads to significant underestimation of the critical load magnitude.

Similar comments hold true when ‘large’ displacement amplitudes (plots on the bottom) are considered, but in these cases the direct 1D model moves from the stable equilibrium path to the unstable one. This result is related to the nonlinear solver used in the finite difference procedure, which is based on the Levenberg-Marquardt algorithm (a.k.a. the damped least-squares method): even assuming the previous step solution as initial guess for the solver and also reducing the loading step, the algorithm jumps to local minima which minimize the amplitudes of displacement fields. Aiming at removing these transitions, other types of nonlinear solvers and forcing techniques for the present algorithm are under investigation.

5 Conclusions

Two different approaches for the analysis of thin-walled beams were analyzed and compared. Both approaches are based on enriched beam theories including out-of-plane cross-section warping. The first consists in a three-dimensional beam finite element based on a four-field mixed formulation, while the second is a direct one-dimensional model where a coarse descriptor of the warping displacement field is introduced.

A simply supported beam has been chosen as paradigmatic case study to show the capabilities of the approaches. Two analyses were performed: a modal decomposition of the unloaded beam and a static incremental analysis. The latter was performed introducing a small imperfection on the initial shape and allowed to detect the onset of instabilities and investigate the numerical accuracy of the approaches under large displacements.

Analyses were developed considering two steel cross-sections: a doubly symmetric IPE 200 and a non-symmetric L$200{\times }100{\times }10$. The simulations showed that for the doubly-symmetric cross-section the two approaches are both reliable in modal decomposition and results are close to the analytic solution; in this case the direct 1D model is simpler to implement and could be advantageously preferred to the mixed 3D FE. On the contrary, as shown by the comparison with the shell model, for the non-symmetric cross-section the mixed 3D approach was found superior in describing the free dynamic response of the beam. Referring to step-by-step incremental analyses, both approaches have proven effective to detect the onset of instabilities, although the corotational approach adopted for the mixed 3D FE slightly overestimates the critical load magnitude for the non-symmetric L-shape section. When large displacements are considered, the mixed 3D FE has proven robust in following the stable path, whereas the direct 1D one fell off to unstable paths.

Considering the advantages and disadvantages of each approach, new potential developments, based on suitable combinations of the two formulations, can be depicted. As first enhancement, for symmetric cross-sections the direct 1D model can be adopted to achieve eligible inner constraints for the mixed 3D approach, thus reducing its computational effort. The nonlinear solver used in the direct 1D model may be improved to prevent transitions among more equilibrium paths. The corotational approach used in the mixed 3D FE can be revised to improve the description of beams undergoing large displacements and endowed with non-symmetric cross-sections.