A finite element beam model including cross-section distortion in the absolute nodal coordinate formulation

Abstract

A new class of beam finite elements is proposed in a three-dimensional fully parameterized absolute nodal coordinate formulation, in which the distortion of the beam cross section can be characterized. The linear, second-order, third-order, and fourth-order models of beam cross section are proposed based on the Pascal triangle polynomials. It is shown that Poisson locking can be eliminated with the proposed higher-order beam models, and the warping displacement of a square beam is well described in the fourth-order beam model. The accuracy of the proposed beam elements and the influence of cross-section distortion on structure deformation and dynamics are examined through several numerical examples. We find that the proposed higher-order models can capture more accurately the structure deformation such as cross-section distortion including warping, compared to the existing beam models in the absolute nodal coordinate formulation.

1 Introduction

The absolute nodal coordinate formulation (ANCF) is proposed by Shabana in 1996 [1] as a non-incremental finite element method in flexible multibody dynamics. Global position and gradient vectors are selected as the nodal coordinates, which leads to a constant mass matrix, i.e., centrifugal and Coriolis inertia forces are eliminated in the equation of motion. Therefore, it is more advantageous to simulate a deformable body with a large deformation and motion. Berzeri and Shabana [2] have formulated the position vector of neutral axis of a two-dimensional beam element with the absolute nodal coordinate formulation, the beam is considered as an elastic line similar to Euler–Bernoulli beam model, and thus, the deformation of beam cross section is not considered. For fully parameterized finite elements in the absolute nodal coordinate formulation, Omar and Shabana [3] have proposed a position vector of a two-dimensional shear deformable beam, which is analogous to Timoshenko beam model. Shabana and Yakoub [4] have introduced a 3-dimensional beam element, which is able to consider transverse shear deformation across beam cross section. In addition, other position vectors, which are higher order along neutral axis of beam and linear along cross section of beam, are lately provided by Gerstmayr and Shabana [5]. Kerkkänen et al. [6] proposed a linear two-dimensional shear deformable beam element, in which a linear polynomial is used along the neutral axis of the beam. With the help of these fully parameterized position vectors, the deformation of beam cross section can be described. However, the beam cross section remains plane and its boundaries are still straight due to the assumed linear variation of in-plane displacement or transverse coordinates in the position vectors during deformation. To circumvent this problem, recently, Li et al. [7] developed a two-dimensional higher-order representation for deformation of beam cross section and the assumption of planar cross section is relaxed using a quadratic variation along the transverse direction in the position vector, however, the beam cross-section distortion is not examined in their numerical studies for the higher-order beam element. Therefore, we can see that characterization of beam cross-section distortion in the absolute nodal coordinate formulation is far from complete; this is the objective of this paper. In fact, many higher-order beam theories not formulated in the absolute nodal coordinate formulation have been proposed to consider beam cross-section distortion, for example, by Manjunatha and Kant [8], Vinayak et al. [9], and Matsunage [10]. In addition, these theories are frequently applied to analyze dynamic response of composite beams [11–13].

In this study, fully parameterized position vectors are proposed in the absolute nodal coordinate formulation to consider distortion of beam cross section. Inspired by the unified formulation proposed by Carrera et al. [14], linear, second-order, third-order, and fourth-order models for a 3-dimensional beam are proposed, in which the transverse coordinates of the beam are given by the polynomials like Pascal triangle to characterize the cross-section deformation or distortion and these beam position vectors will be expressed in a unified way. In equations of motion, the elastic forces of the beam elements are formulated by a three-dimensional continuum mechanics approach; therefore, three-dimensional beam models are in fact considered as a mechanical solid with coupled axis, shear, bending, and torsion deformations. However, the continuum mechanics approach may lead to Poisson locking problem since the assumed displacement in a linear model cannot provide the required relations among normal strains due to Poisson’s effect. This problem can be removed using second-order or third-order beam models, which are denoted as higher-order beam model in the following. The physical reason for removing Poisson locking problem is due to more accurate description of beam cross-section deformation and this is fundamentally different from the existing methods: such as the selective reduced integration [15, 16], the zero Poisson’s ratio assumption [17], and the neglecting Poisson effect [6].

The paper is arranged as the following: global position, gradient vectors, and shape functions of the proposed beam models are explained in Sect. 2. The continuum mechanics approach is employed to formulate elastic force of a general laminated composite beam, and this is given in Sect. 3. Several numerical examples are provided to validate and illustrate the proposed models in Sect.  4. Finally, some conclusions are given in Sect. 5.

2 Linear and higher-order beam models

2.1 Position vectors of a spatial beam element

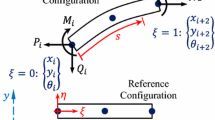
As shown in Fig. 1, a beam in structural mechanics is idealized as a 1-dimensional object based on its centerline. Thus, in a global coordinate system XYZ, the position vector of any point on the beam can be written in a unified way as

$$\begin{aligned} \mathbf{r}\left( {x,y,z,t} \right) =\sum _{i=1}^n {f_i } \left( {y,z} \right) \mathbf{u}_i \left( {x,t} \right) \end{aligned}$$

(1)

where $x,\, y$, and $z$ are the coordinates in a local coordinate system xyz, $t$ is the time, the vector $\mathbf{u}_i$, which can be the position or gradient vector, is a parameter vector of the beam centerline, $f$, which is a function associated with the transverse coordinates $y$ and $z$, is used to describe deformation of beam cross section, and $n$ is the number of expansion terms.

Fig. 1

Position vector of any point and parameter vector of the centerline on a beam

In this paper, the function $f$ is approximated by means of Pascal triangle polynomials. Following the idea proposed by Olshevskiy et al. [18], and Dmitrochenko and Mikkola [19], the position vector of any point on the beam is given by

$$\begin{aligned} \mathbf{r}=\sum _{i=1}^{{\left( {N+1} \right) \left( {N+2} \right) }/2} {f_{i,\alpha } } \left( {y,z} \right) \mathbf{u}_i \left( {x,t} \right) \end{aligned}$$

(2)

where the subscript $\alpha$ is the order of Pascal triangle, as shown in Fig. 2, and $N$ is the order of the beam model, which is the maximum value of the $\alpha$, that is, $\alpha =0\cdots N$.

Fig. 2

Pascal triangle with its zeroth-order, first-order, second-order, and third-order terms

In the following, linear ($N=1$), second-order ($N=2$), and third-order ($N=3$) approximations will be mainly discussed, and in the case of $N > 1$, the beam model is called higher-order beam model in the following.

2.2 Absolute nodal coordinate formulation of beam element

Based on the beam models in Sect. 2.1, in the frame of the absolute coordinate system (XYZ), the displacement field of the beam is approximated using discretization and interpolation techniques of finite element method, as shown in Fig. 3.

Fig. 3

Beam element in the local element coordinate system xyz

The parameter vector of beam centerline is approximated by the following polynomials with respect of $x$

$$\begin{aligned} \mathbf{u}_i \left( {x,t} \right) =\sum _{j=0}^m {x^{j}\mathbf{d}_{j,i} \left( t \right) } \end{aligned}$$

(3)

where the superscript $j$ is the power of $x$, and the vector $\mathbf{d}_{j,i}$ is only associated with time $t$ in dynamic analysis.

For a beam element with two nodes, the vector $\mathbf{d}_{j,i}$ is derived in terms of the selected position and gradient vectors of the beam centerline. In the following, the parameter vector $\mathbf{u}_1$, representing the position and the slope of the beam centerline, is given by

$$\begin{aligned} \mathbf{u}_1 =\mathbf{d}_{0,1} +x\mathbf{d}_{1,1} +x^{2}\mathbf{d}_{2,1} +x^{3}\mathbf{d}_{3,1} \end{aligned}$$

(4)

which is a cubic interpolation polynomial and the other parameter vectors $\mathbf{u}_i \left( {i=2,\ldots ,n} \right)$, which are connected with the beam cross section, are given by cubic and first-order interpolation polynomials, respectively. Here, the parameter vector using the cubic polynomial is named as the model A and is written as

$$\begin{aligned} \mathbf{u}_i =\mathbf{d}_{0,i} +x\mathbf{d}_{1,i} +x^{2}\mathbf{d}_{2,i} +x^{3}\mathbf{d}_{3,i} \quad \left( {i=2,\ldots ,n} \right) . \end{aligned}$$

(5)

The model A is proposed to keep the same order on $x$ between the parameter vector $\mathbf{u}_1$ and the parameter vectors $\mathbf{u}_i \left( {i=2,\ldots ,n} \right)$. In addition, the parameter vector with the first-order polynomial is called the model B, and it is written as

$$\begin{aligned} \mathbf{u}_i =\mathbf{d}_{0,i} +x\mathbf{d}_{1,i} \quad \left( {i=2,\ldots ,n} \right) . \end{aligned}$$

(6)

Based on the proposed parameter vectors (Eqs. (4) and (5)), the nodal coordinates $\mathbf{e}_{p}$ of the node $p$ are given by

$$\begin{aligned} \mathbf{e}_p&= \left[ \mathbf{r}_{p}^\mathrm{T} ,\frac{\partial \mathbf{r}_{p}^\mathrm{T} }{\partial x},\frac{\partial \mathbf{r}_{p}^\mathrm{T} }{\partial f_{2,1} },\frac{\partial ^{2}\mathbf{r}_{p}^\mathrm{T} }{\partial x\partial f_{2,1} },\,\ldots \,,\right. \nonumber \\&\quad \left. \frac{\partial ^{N}\mathbf{r}_{p}^\mathrm{T} }{\partial f_{{\left( {N+1} \right) \left( {N+2} \right) }/2,N} },\frac{\partial ^{N+1}\mathbf{r}_{p}^\mathrm{T} }{\partial x\partial f_{{\left( {N+1} \right) \left( {N+2} \right) }/2,N} } \right] ^\mathrm{T}\nonumber \\ \end{aligned}$$

(7)

which is called in the following as the model $\mathbf{A}N$, and the degrees of freedom are ($N+1)(N+2)$. Here, for example,${\partial ^{4}\mathbf{r}_p }/{\partial x\partial f_{8,3}}$ of the partial derivatives means ${\partial ^{4}\mathbf{r}_p }/{\partial x\partial y^{2}\partial z}$.

In addition, the nodal coordinates of the node $p$ are also given based on Eqs. (4) and (6)

$$\begin{aligned} \mathbf{e}_p =\left[ {\mathbf{r}_{p}^\mathrm{T} ,\frac{\partial \mathbf{r}_{p}^\mathrm{T} }{\partial x},\frac{\partial \mathbf{r}_{p}^\mathrm{T} }{\partial f_{2,1} },\,\ldots \,,\frac{\partial ^{N}\mathbf{r}_{p}^\mathrm{T} }{\partial f_{{\left( {N+1} \right) \left( {N+2} \right) }/2,N} }} \right] ^\mathrm{T}\nonumber \\ \end{aligned}$$

(8)

which is called as the model $\mathbf{B}N$, and its degrees of freedom are ($N+1)(N+2)/2+1$.

Here, we can see that the model B1 is the same as the proposed 3-dimensional beam element by Shabana and Yakoub [4]. In these nodal coordinates (Eqs. (7) and (8)), $\mathbf{r}_{p}$ is the position vector of the node $p$, and the gradient vectors ${\partial \mathbf{r}_p }/{\partial x},\, {\partial \mathbf{r}_p }/{\partial f_{2,1} }$, and ${\partial \mathbf{r}_p }/{\partial f_{3,1} }$ are the slope coordinates of the node $p$ on the beam centerline. The other gradient vectors, which are the second, third, and fourth derivatives of the position vector with respect to the transverse coordinates $y$ and $z$, characterize distortion of beam cross section. However, a clear and simple physical interpretation of these higher-order derivatives is not straightforward, and some of them are illustrated in Fig. 4. If the beam is straight at an initial configuration, the slope coordinates will be a unit vector, and the other higher-order derivatives will be a null vector.

Fig. 4

The configuration of a beam element using the beam model A2

The element shape function matrices can be derived in terms of the assumed position vectors in Eq. (2) and the selected nodal coordinates in Eqs. (7) and (8). It is easily found that the element shape function matrices can be composed of basic shape function matrices. For the model A, the basic shape function matrices are written as

$$\begin{aligned} S_{1\mathrm{{A}}}&= \left[ {{\begin{array}{l@{\quad }l@{\quad }l@{\quad }l@{\quad }l@{\quad }l} {s_1 } &{} 0 &{} 0 &{} {s_2 } &{} 0 &{} 0 \\ 0 &{} {s_1 } &{} 0 &{} 0 &{} {s_2 } &{} 0 \\ 0 &{} 0 &{} {s_1 } &{} 0 &{} 0 &{} {s_2 } \\ \end{array} }} \right] ,\nonumber \\ S_{2\mathrm{{A}}}&= \left[ {{\begin{array}{l@{\quad }l@{\quad }l@{\quad }l@{\quad }l@{\quad }l} {s_3 } &{} 0 &{} 0 &{} {s_4 } &{} 0 &{} 0 \\ 0 &{} {s_3 } &{} 0 &{} 0 &{} {s_4 } &{} 0 \\ 0 &{} 0 &{} {s_3 } &{} 0 &{} 0 &{} {s_4 } \\ \end{array} }} \right] \end{aligned}$$

(9)

where $s_1 =1-3\xi ^{2}+2\xi ^{3},\, s_2 =l\left( {\xi -2\xi ^{2}+\xi ^{3}} \right) , s_3 =3\xi ^{2}-2\xi ^{3},\, s_4 =l\left( {-\xi ^{2}+\xi ^{3}} \right)$, and $\xi =x/l,\, l$ is the length of the beam element.

For the model B, the basic shape function matrices are given by

$$\begin{aligned} S_{1\mathrm{{B}}} =\left[ {{\begin{array}{l@{\quad }l@{\quad }l} {s_5 }&{} 0&{} 0 \\ 0&{} {s_5 }&{} 0 \\ 0&{} 0&{} {s_5 } \\ \end{array} }} \right] ,\,S_{2\mathrm{{B}}} =\left[ {{\begin{array}{l@{\quad }l@{\quad }l} {s_6 }&{} 0&{} 0 \\ 0&{} {s_6 }&{} 0 \\ 0&{} 0&{} {s_6 } \\ \end{array} }} \right] \end{aligned}$$

(10)

where $s_5 =1-\xi ,\, s_6 =\xi$.

With help of the basic shape function matrices in Eq. (9) for the beam model $\mathbf{A}N$, the element shape function matrix is given by

$$\begin{aligned} \mathbf{S}&= \left[ f_{1,0} {{\varvec{S}}}_\mathrm{1A} ,\,\ldots \,,f_{{\left( {N+1} \right) \left( {N+2} \right) }/2,N} {{\varvec{S}}}_\mathrm{1A} ,\,\right. \nonumber \\&\quad \left. f_{1,0}{{\varvec{S}}}_\mathrm{2A} ,\,\ldots \,,f_{{\left( {N+1} \right) \left( {N+2} \right) }/2,N} {{\varvec{S}}}_\mathrm{2A} \right] \end{aligned}$$

(11)

For the beam model $\mathbf{B}N$, the element shape function matrix is given by means of the Eqs. (9) and (10), leading to

$$\begin{aligned} \mathbf{S}&= \left[ {\varvec{S}}_\mathrm{1A} ,f_{2,1} {\varvec{S}}_\mathrm{1B} ,\,\ldots \,,f_{{\left( {N+1} \right) \left( {N+2} \right) }/2,N} {\varvec{S}}_\mathrm{1B} ,\,\right. \nonumber \\&\quad \left. {\varvec{S}}_\mathrm{2A} ,f_{2,1} {\varvec{S}}_\mathrm{2B} ,\,\ldots \,,f_{{\left( {N+1} \right) \left( {N+2} \right) }/2,N} {\varvec{S}}_\mathrm{2B} \right] .\nonumber \\ \end{aligned}$$

(12)

Therefore, in the proposed beam models, the global position vector r of an arbitrary point in the proposed elements can be written as

$$\begin{aligned} \mathbf{r}\left( {x,y,z,t} \right) =\mathbf{S}\left( {x,y,z} \right) \mathbf{e}\left( t \right) \end{aligned}$$

(13)

in which the position vector is separated by the space variable S and the time variable e. Additionally, for deriving efficient formulations of evaluating the elastic force and its Jacobian, the position vector r can be again written as [5]

$$\begin{aligned} \mathbf{r}\left( {x,y,z,t} \right) ={\bar{\mathbf{e}}}\left( t \right) {\bar{\mathbf{S}}}\left( {x,y,z} \right) \end{aligned}$$

(14)

where ${\bar{\mathbf{S}}}$ is the condensed shape function, and is given by

$$\begin{aligned} {\bar{\mathbf{S}}}=\left[ \begin{array}{llll} {s_1 }&{} {s_2 }&{} \cdots &{} {s_{D/3} }\\ \end{array} \right] ^\mathrm{T} \end{aligned}$$

(15)

where $D$ is the number of the degree of freedom of the nodal coordinate for a beam element, and it is equal to 2($N$+1)($N$+2) in the model $\mathbf{A}N$, and ($N$+1)($N$+2)+2 in the model $\mathbf{B}N$, respectively. In addition, the rearranged nodal coordinate is written as

$$\begin{aligned} {\bar{\mathbf{e}}}=\left[ {{\begin{array}{l@{\quad }l@{\quad }l@{\quad }l} {e_1 } &{} {e_4 } &{} \cdots &{} {e_{D-2} } \\ {e_2 } &{} {e_5 } &{} \cdots &{} {e_{D-1} } \\ {e_3 } &{} {e_6 } &{} \cdots &{} {e_D } \\ \end{array} }} \right] . \end{aligned}$$

(16)

3 Equations of motion

The governing equations are derived by means of the virtual displacement. For the different beam models, the virtual displacement of any point can be written as $\delta \mathbf{r}=\mathbf{S}\delta \mathbf{e}$. In addition, the Hamilton’s principle is applied as [20]

$$\begin{aligned} 0=\int _0^t {\left( {\delta U+\delta W-\delta T} \right) } \hbox { d}t \end{aligned}$$

(17)

where $\delta U,\, \delta W$, and $\delta T$ are the virtual strain energy, virtual work done by external applied force, and the virtual kinetic energy, respectively.

3.1 Formulations of elastic force and its Jacobian

For a general laminated composite beam, the virtual strain energy is given by

$$\begin{aligned} \delta U=\sum _{g=1}^G {\int _{V^{\left( g \right) }} {\left( {{\bar{\mathbf{C}}}^{\left( g \right) }{\varvec{\varepsilon }}} \right) \cdot \delta {\varvec{\varepsilon }} \hbox { d}V^{\left( g \right) }} } \end{aligned}$$

(18)

where $G$ is the number of ply, ${\bar{\mathbf{C}}}^{\left( g \right) }$ is the elastic matrix for the $g$th ply in the element coordinate system, it is related to Young’s modulus, Poisson’s ratio, and shear modulus [21], and $V$ is the volume.

Additionally, the strain vector ${\varvec{\varepsilon }}$ can be derived from the deformation gradient [22]

$$\begin{aligned} \mathbf{J}=\frac{\partial \mathbf{r}}{\partial \mathbf{r}_0 }=\frac{\partial \mathbf{r}}{\partial \mathbf{x}}\left( {\frac{\partial \mathbf{r}_0 }{\partial \mathbf{x}}} \right) ^{-1}={\bar{\mathbf{e}}}\frac{\partial {\bar{\mathbf{S}}}}{\partial \mathbf{x}}\left( {\frac{\partial \mathbf{r}_0 }{\partial \mathbf{x}}} \right) ^{-1} \end{aligned}$$

(19)

where $\mathbf{r}_0$ is the position vector of a point at a reference time $t_0$ and $\mathbf{x}=[x,\, y,\, z]^\mathrm{T}$. Thus, the column $i$ of the matrix J is given by

$$\begin{aligned} \mathbf{J}^{i}={\bar{\mathbf{e}}}\frac{\partial {\bar{\mathbf{S}}}}{\partial \mathbf{x}}\left( {\frac{\partial \mathbf{r}_0 }{\partial \mathbf{x}}^{-1}} \right) ^{i}={\bar{\mathbf{e}}}\,\mathbf{B}^{i} \end{aligned}$$

(20)

where the superscript $i$ represents one column of the matrix. With the deformation gradient in Eq. (20), the strain is then written as [23]

$$\begin{aligned} \varepsilon&= \left[ {{\begin{array}{l} {\varepsilon _{xx} } \\ {\varepsilon _{yy} } \\ {\varepsilon _{zz} } \\ {\gamma _{xy} } \\ {\gamma _{yz} } \\ {\gamma _{xz} } \\ \end{array} }} \right] =\frac{1}{2}\left[ {{\begin{array}{l} {\mathbf{J}^{1}\cdot \mathbf{J}^{1}-1} \\ {\mathbf{J}^{2}\cdot \mathbf{J}^{2}-1} \\ {\mathbf{J}^{3}\cdot \mathbf{J}^{3}-1} \\ {2\mathbf{J}^{1}\cdot \mathbf{J}^{2}} \\ {2\mathbf{J}^{2}\cdot \mathbf{J}^{3}} \\ {2\mathbf{J}^{1}\cdot \mathbf{J}^{3}} \\ \end{array} }} \right] \nonumber \\&= \frac{\bar{{e}}_{ij} \bar{{e}}_{ik} }{2}\left[ {{\begin{array}{l} {B_j^1 B_k^1 } \\ {B_j^2 B_k^2 } \\ {B_j^3 B_k^3 } \\ {2B_j^1 B_k^2 } \\ {2B_j^2 B_k^3 } \\ {2B_j^1 B_k^3 } \\ \end{array} }} \right] -\frac{1}{2}\left[ {{\begin{array}{l} 1 \\ 1 \\ 1 \\ 0 \\ 0 \\ 0 \\ \end{array} }} \right] \end{aligned}$$

(21)

where $\varepsilon$ is the normal strain and $\gamma$ is the engineering shear strain. In the matrix ${\bar{\mathbf{e}}}$, the subscript $i$ refers to the row number, and the subscripts $j$ and $k$ are related to columns. In the column vector $\mathbf{B}^{i}$, the subscripts $j$ and $k$ refer to the row number. Their values are $i=1\cdots 3,\, j=1\cdots D/3$ and $k=1\cdots D/3$, respectively. The elastic force is obtained directly from the virtual strain energy, which is given by

$$\begin{aligned} \mathbf{Q}\left( \mathbf{e} \right) =\sum _{g=1}^G {\int _{V^{\left( g \right) }} {\frac{\partial {\varvec{\varepsilon }}}{\partial \mathbf{e}}^{\hbox {T}}{\bar{\mathbf{C}}}^{\left( g \right) }{\varvec{\varepsilon }} \hbox { d}V^{\left( g \right) }} } \end{aligned}$$

(22)

where the $m$th row of $\left( {{\partial {\varvec{\varepsilon }} }/{\partial \mathbf{e}}} \right) ^{\hbox {T}}$ is

$$\begin{aligned} \left( {\frac{\partial {\varvec{\varepsilon }}}{\partial \mathbf{e}}^{\hbox {T}}} \right) _m =\bar{{e}}_{ij} \left[ {{\begin{array}{c} {B_j^1 B_k^1 } \\ {B_j^2 B_k^2 } \\ {B_j^3 B_k^3 } \\ {B_j^1 B_k^2 +B_j^2 B_k^1 } \\ {B_j^2 B_k^3 +B_j^3 B_k^2 } \\ {B_j^1 B_k^3 +B_j^3 B_k^1 } \\ \end{array} }} \right] ^{\hbox {T}} \end{aligned}$$

(23)

where $m=i+3(k-1)$. The Jacobian of the elastic force is given by

$$\begin{aligned} \frac{{\partial {\mathbf {Q}}}}{{\partial {\mathbf {e}}}}&= \sum \limits _{{g = 1}}^{G} \int _{{V^{{\left( g \right) }} }} \sum \limits _{{w = 1}}^{6} {\left( {\frac{{\partial {{\varvec{\varepsilon }} }}}{{\partial {\mathbf {e}}}}_{w} } \right) ^{{\text {T}}} {{\bar{\mathbf C}}}_{w}^{{\left( g \right) }} \frac{{\partial {\varvec{\varepsilon }}}}{{\partial {\mathbf {e}}}}}\nonumber \\&+ \sum \limits _{{w = 1}}^{6} {{{\bar{\mathbf C}}}_{w}^{{\left( g \right) }} {\varvec{\varepsilon }}\frac{{\partial \left( {\frac{{\partial {\varvec{\varepsilon }}}}{{\partial {\mathbf {e}}}}_{w} } \right) ^{{\text {T}}} }}{{\partial {\mathbf {e}}}}} {\text { d}}V^{{\left( g \right) }} \end{aligned}$$

(24)

where the subscript $w$ refers to the row number of the matrices ${{{\bar{\mathbf C}}}^{(g)}}$ and ${\frac{\partial {\varvec{\varepsilon }}}{\partial {\mathbf {e}}}}$

Additionally, in Eq. (24), the $m$th row of the $n$th column of the second derivative of the strain with respect to the nodal coordinate is written as

$$\begin{aligned} \frac{\partial \left( {\frac{\partial {\varvec{\varepsilon }}}{\partial \mathbf{e}}_w } \right) ^{\hbox {T}}}{\partial \mathbf{e}}_{mn} =\left[ {{\begin{array}{c} {\left. {B_j^1 B_k^1 } \right| _{w=1} } \\ {\left. {B_j^2 B_k^2 } \right| _{w=2} } \\ {\left. {B_j^3 B_k^3 } \right| _{w=3} } \\ {\left. {B_j^1 B_k^2 +B_j^2 B_k^1 } \right| _{w=4} } \\ {\left. {B_j^2 B_k^3 +B_j^3 B_k^2 } \right| _{w=5} } \\ {\left. {B_j^1 B_k^3 +B_j^3 B_k^1 } \right| _{w=6} } \\ \end{array} }} \right] \end{aligned}$$

(25)

where $m=i+3(k-1),\, n=i+3(j-1)$.

By means of Eqs. (21), (23), and (25), the integrals in Eqs. (22) and (24) can be computed without operating on the nodal coordinates; therefore, they are calculated only once in the following evaluation of the elastic force and its Jacobian.

3.2 Equilibrium equation of the system

The equilibrium equation of the system can be written as

$$\begin{aligned} \mathbf{M}{\ddot{\mathbf{e}}}+\mathbf{Q}\left( \mathbf{e} \right) +\mathbf{F}\left( \mathbf{e} \right) =\mathbf{0} \end{aligned}$$

(26)

where M is a constant mass matrix, and F is the generalized external force matrix, such as gravity force and external moment [24].

For a constrained mechanical system, the equilibrium equation of the system can be written as [25]

$$\begin{aligned} \left\{ {{\begin{array}{l} \mathbf{M}{\ddot{\mathbf{e}}}+{\varvec{\Phi }}_\mathbf{e} ^{\hbox {T}}{\varvec{\lambda }}=-\mathbf{Q}-\mathbf{F} \\ {{\varvec{\Phi }}(\mathbf{e},t)=\mathbf{0}} \\ \end{array} }} \right. \end{aligned}$$

(27)

where ${\varvec{\Phi }}$ is the constraint equation, ${\varvec{\Phi }}_{\mathbf{e}}$ is the Jacobian of the constraint, and ${\varvec{\lambda }}$ is the Lagrange multipliers.

Finally, the equilibrium equation is solved by means of the generalized-$\alpha$ method [26, 27] and the integration scheme of this method uses the following procedures

$$\begin{aligned} \mathbf{e}_{t+\Delta t}&= \mathbf{e}_t {+}\Delta t{\dot{\mathbf{e}}}_t {+}\Delta t^{2}\left( {\frac{1}{2}{-}\beta } \right) \mathbf{a}_t {+}\Delta t^{2}\beta \mathbf{a}_{t+\Delta t} \end{aligned}$$

(28)

$$\begin{aligned} {\dot{\mathbf{e}}}_{t+\Delta t}&= {\dot{\mathbf{e}}}_t +\Delta t\left( {1-\eta } \right) \mathbf{a}_t +\Delta t\eta \mathbf{a}_{t+\Delta t} \end{aligned}$$

(29)

where $\Delta t$ is time increment, a is an auxiliary variable, and

$$\begin{aligned} \beta =\frac{1}{4}\left( {\eta +\frac{1}{2}} \right) ^{2}, \quad \eta =\frac{1}{2}-\frac{\rho _\infty -1}{\rho _\infty +1} \end{aligned}$$

(30)

where $\rho _\infty$ is the spectral radius.

4 Numerical examples

In this section, several numerical examples are provided to validate the proposed beam models and to illustrate their prediction capacity.

4.1 Poisson locking

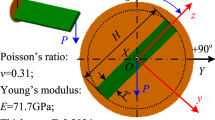
Consider a cantilevered beam with a square cross section and an external force $F$ along $Z$-direction is applied at the center point of the unsupported end cross section, as shown in Fig. 5.

Fig. 5

Cantilevered beam with an end force loading

Geometry properties of the beam are: the length is $L=2\hbox { m}$, and the height is $h=0.2\hbox { m}$. The beam is made of an isotropic material, and its material properties are: Young’s modulus $E=69\hbox { GPa}$, and Poisson’s ratio $\nu =0.33$. The externally applied force is $F=50\hbox { N}$. In Table 1, the displacements along $Z$-direction of the end center point with different discretization are given and compared with the different beam models. Here, the results obtained using the beam element Beam188 and solid element Solid45 of the commercial software ANSYS are also given to validate the proposed models. Additionally, using Euler-Bernoulli and Timoshenko beam theories [28], the $Z$-displacements are $-1.4493\times 10^{-5}$ and $-1.4608\times 10^{-5}\,\mathrm{{m}}$, respectively. Obviously, it is seen in Table 1 that the models A1 and B1 cannot give the correct result due to Poisson locking. However, with the higher-order beam models, the Poisson locking problem can be eliminated. Poisson locking phenomenon is believed to arise from the fact that the assumed displacement field in a linear beam model cannot satisfy the required linear Hooke’s law, i.e., $\varepsilon _{yy} \propto \nu \varepsilon _{xx}$ and $\varepsilon _{zz} \propto \nu \varepsilon _{xx}$ for isotropic materials. To be more specific, in the proposed linear beam model, the position vector is

$$\begin{aligned} \mathbf{r}=\mathbf{u}_1 \left( x \right) +y\mathbf{u}_2 \left( x \right) +z\mathbf{u}_3 \left( x \right) \end{aligned}$$

(31)

and the normal strains can be written as [29]

$$\begin{aligned} \begin{array}{l} \varepsilon _{xx} =\frac{1}{2}\left( {\left| {\frac{\partial \mathbf{u}_1 }{\partial x}+y\frac{\partial \mathbf{u}_2 }{\partial x}+z\frac{\partial \mathbf{u}_3 }{\partial x}} \right| ^{2}-1} \right) \\ \varepsilon _{yy} =\frac{1}{2}\left( {\left| {\mathbf{u}_2 } \right| ^{2}-1} \right) \\ \varepsilon _{yy} =\frac{1}{2}\left( {\left| {\mathbf{u}_3 } \right| ^{2}-1} \right) \\ \end{array} \end{aligned}$$

(32)

It is clear that the relations $\varepsilon _{yy} \propto \nu \varepsilon _{xx}$ and $\varepsilon _{zz} \propto \nu \varepsilon _{xx}$ cannot be satisfied due to the constant distributions of $\varepsilon _{yy}$ and $\varepsilon _{zz}$ across the beam cross section. However, in the proposed second-order beam model, the transverse normal strains are

$$\begin{aligned} \begin{array}{l} \varepsilon _{yy} =\frac{1}{2}\left( {\left| {\mathbf{u}_2 +2y\mathbf{u}_4 +z\mathbf{u}_5 } \right| ^{2}-1} \right) \\ \varepsilon _{zz} =\frac{1}{2}\left( {\left| {\mathbf{u}_3 +y\mathbf{u}_5 +2z\mathbf{u}_6 } \right| ^{2}-1} \right) \\ \end{array} \end{aligned}$$

(33)

In this case, the linear Hooke’s law can be satisfied; thus, Poisson locking is eliminated by means of the proposed higher-order beam models.

Table 1 $Z$-displacement of the end center point: $u_{z}\times 10^{5}\,\mathrm{{m}}$

4.2 Cross-section distortion

A two-ends-fixed beam with a square cross section is subjected to pressures on the upper and lower surfaces, as shown in Fig. 6. This problem is examined to study the distortion of beam cross section. The geometry and material properties of the beam are: $L=0.5\,\mathrm{{m}}$, $h=0.05\,\mathrm{{m}},\, E=30\,\hbox { MPa},\, \nu =0.33$, and the pressure loadings are $F_1 =F_2 =5\cos \left( {{\pi Z}/h} \right) \hbox { MPa}$.

Fig. 6

Two-ends-fixed beam with pressure loadings on the surfaces

In Fig. 7, the cross-section deformations at $X=L/2$ are shown for the different models. The element Solid186 is adopted for the finite element simulation, and the number of elements is $20\times 20\times 200$. For the beam models, the number of elements is 40, which is checked to be sufficient for convergence. As can be seen in this figure, for the model A1, the boundaries of the beam cross section remain straight during deformation. However, with the model A3 and finite element method with the element Solid186, the cross section is distorted, and they agree well with each other. The predictions by the model B are not shown here, since they are almost the same as the predictions by the model A for the corresponding order.

Fig. 7

Cross-section deformation of a two-ends-fixed beam at $X=L/2$

In addition, Fig. 8 shows the distribution of normal stress $\sigma _{yy}$ in the cross section at $X=L/2$. The results of the model A3 and the finite element method with the element Solid186 agree well, except the regions around the four corners. We also emphasize that the degree of freedom in the proposed beam model is much less than that for finite element method with solid elements.

Fig. 8

Normal stress $\sigma _{yy}$ (Pa) in the cross section at $X=L/2$

4.3 Laminated composite beam

Consider a simply supported beam composed of graphite fabric-carbon matrix layers is subjected to uniformly distributed loading, as shown in Fig. 9. The geometry of the beam is: length $L=10\hbox { m}$, and height $h=0.1\hbox { m}$. The material properties of the orthotropic composite layer are: Young’s moduli $E_{11}=173.06$ GPa, $E_{22}=33.10$ GPa, and $E_{33}=5.17$ GPa in 1, 2, and 3 material directions, respectively; shear moduli $G_{12}=9.38$ GPa, $G_{23}=3.24$ GPa, $G_{13}=8.30$ GPa; Poisson’s ratios $\nu _{12}=0.036,\, \nu _{23}=0.171,\, \nu _{13}=0.250$ [21]. The load $F$ is 1000 Pa.

Fig. 9

Simply supported laminated composite beam

For the lay-up [$0^\circ /90^{\circ }/0^{\circ }/90^{\circ }$], the comparison of transverse displacement, obtained using the model B (40 elements) and finite element method ANSYS (Shell181, $4\times 400$ elements), is shown in Fig. 10(a) and there is no significant difference for the considered models. However, for the lay-up [$-45^{\circ }/45^{\circ }/-45^{\circ }/45^{\circ }$], as shown in Fig. 10(b), the difference between linear model (B1) and higher-order models (B2 and B3) is significant, and the prediction by the higher-order models agrees well with that by the element Shell181.

Fig. 10

Transverse displacements of the laminated beam under uniformly distributed load

4.4 Warping displacement

Consider a cantilevered beam with a square cross section and a concentrated torque $M_{x}$ is applied at the unsupported end of the beam, as shown in Fig. 11.

Fig. 11

Cantilever beam with concentrated torque

The cantilever beam has a length $L=2\hbox { m}$ and a height $h=0.2\hbox { m}$, Young’s modulus $E=69$ GPa, Poisson’s ratio $\nu =0.33$, and the applied torque $M_{x}=50\hbox { KN.m.}$ The number of elements is 40 for the beam models. In this section, the axial displacement $u_{x}$, which is also called the warping displacement, is calculated for the cantilever beam with a concentrated torque, and the results obtained using model B are shown in Fig. 12.

Fig. 12

Warping displacement $u_{x}$ (m) of the cross section at $X=L$

However, the results in Fig. 12 show that the even with higher-order models up to the third order, the prediction cannot converge to the analytical solution, which is given by [30]

$$\begin{aligned} u_x =\theta \left( x \right) \omega ^{*}\left( {y,z} \right) \end{aligned}$$

(34)

where $\theta$ is the angle of twist with respect to $x$ and $\omega ^{*}$ is the warping function.

Figure 13a, b show the analytical result and the result obtained using the model B4, respectively; it is found that they agree with each other very well. The position vector of the model B4 can be easily expressed with the unified formulas proposed previously,

$$\begin{aligned} \mathbf{r}&= \underbrace{\mathbf{u}_1 }_{\alpha =0}+\underbrace{y\mathbf{u}_2 +z\mathbf{u}_3 }_{\alpha =1}+\underbrace{y^{2}\mathbf{u}_4 +yz\mathbf{u}_5 +z^{2}\mathbf{u}_6 }_{\alpha =2} \nonumber \\&+\underbrace{y^{3}\mathbf{u}_7 +y^{2}z\mathbf{u}_8 +yz^{2}\mathbf{u}_9 +z^{3}\mathbf{u}_{10} }_{\alpha =3} \nonumber \\&+\underbrace{y^{4}\mathbf{u}_{11} +y^{3}z\mathbf{u}_{12} +y^{2}z^{2}\mathbf{u}_{13} +yz^{3}\mathbf{u}_{14} +z^{4}\mathbf{u}_{15} }_{\alpha =4}\nonumber \\ \end{aligned}$$

(35)

from which the corresponding nodal coordinates and element shape function matrices can be obtained using the same rule as shown in Eqs. (8) and (12).

Fig. 13

Warping displacement $u_{x}$ (m) on the cross section $X=L$

4.5 Large twisted beam

In this section, a cantilever beam under a large torque (Fig. 11) is studied to further show the capability of the model B4. The problem of a largely twisted beam has been previously reported [16, 31, 32], in which the torsional angle and Von Mises stress are mainly analyzed. In the current study, the geometry and material properties of the beam are: $L=2\hbox { m},\, h=0.2\hbox { m},\, E=69\hbox { GPa},\, \nu =0.33$, and the torsional moment is $M_x ={\pi Eh^{4}}/{12L\left( {1+\nu } \right) }$ which will result in 180 deg twist of the beam according to the structural mechanics [16], and the number of elements is 40. The twisted angles are predicted to be 180.44 deg (B1), 220.41 deg (B4), and 210.23 deg (Beam188) by the proposed models and ANSYS, respectively. The beam is twisted approximately to 180 deg in the model B1; this is because the assumed approximate rigid cross section in the model B1 is similar to that in the structural mechanics. In addition, in Fig. 14, the predicted deformed configuration and the contour of Von Mises stress of the twisted beam are shown using the models B1, B4, and finite element method (ANSYS) and we can see that the difference between predictions by the model B1 and the model B4 is significant. However, the predicted results by the model B4 and by the element Beam188 agree well except for the free end cross section. In addition, the stress-focusing effect on the free end cross section can be obtained by the model B4, as shown in Fig. 14(b). The formulation of the generalized external force vector F (Eq. (26)) due to a moment $M_{x}$ can be found in the reference [24].

Fig. 14

Configuration and contour of Von Mises stress (GPa) of a twisted beam

4.6 Natural frequency

Eigen frequency analysis is also performed to validate the proposed models for structural dynamics analysis. With the beam models, the natural frequency and the associated mode shapes of a free beam can be obtained by solving the following equation [33]

$$\begin{aligned} \left( {\mathbf{K}_T -\omega ^{2}\mathbf{M}} \right) {\varvec{\phi }} =\mathbf{0} \end{aligned}$$

(36)

where $\omega$ are natural frequency, ${\varvec{\phi }}$ are the normal modes of the system, and $\mathbf{K}_{T}$ is the tangential stiffness matrix of the system

$$\begin{aligned} \mathbf{K}_T =\frac{\partial \mathbf{Q}\left( \mathbf{e} \right) }{\partial \mathbf{e}} \end{aligned}$$

(37)

which is a function of the general nodal coordinates e defined at the initial configuration.

The examined beam is square in cross section and made of an isotropic material, in which length is $L=0.4\,{ m}$, height is $h=0.02\hbox { m}$, Young’s modulus is $E=70\,\hbox { MPa}$, Poisson’s ratio is $\nu =0.3$ and $\nu =0$, and the mass density is $\rho =1250\,{ kg/m}^{3}$. The predicted frequencies are shown in Tables 2 and 3 for $\nu =0.3$ and $\nu =0$, respectively. In Tables 2 and 3, the numbers of elements in the proposed beam models and the element Beam188 are 40, and there are $10\times 10\times 100$ elements in the analysis with the element Solid45. Since the first six frequencies concern with rigid motions, they are not included in the following discussions. In the case of the models A1 and B1 (linear model) for $\nu =0.3$ (Table 2), the first three bending frequencies are obviously larger than those predicted by the other models, due to the Poisson locking. However, in Table 2, the bending frequencies predicted by the proposed models except for the models A1 and B1 are in good agreement. In Table 3 ($\nu =0$), the bending frequencies predicted by all the models have no significant difference due to $\nu =0$ or suppression of Poisson effect. Furthermore, for the axial frequencies, there is no significant difference for the considered models due to the fact that they are less related to the deformation of the beam cross section. However, the predicted torsion frequencies using the higher-order beam models except the model B4 are larger than the results obtained by finite element method with the element Beam188 and element Solid45.

Table 2 Natural frequencies (Hz) of a free beam for $\nu =0.3$

Table 3 Natural frequencies (Hz) of the free beam for $\nu =0$

4.7 Transient analysis of a falling soft beam

Consider an isotropic square beam clamped at one end falls down under its gravity load, as illustrated in Fig. 15. The beam has a length $L=0.35\hbox { m}$ and a height $h=0.01\hbox { m}$. The material properties are: mass density $\rho =2150\hbox { kg/m}^{3}$, Young’s modulus $E=7$ MPa, Poisson’s ratio $\nu =0.33$, and gravity acceleration is $9.81\hbox { m/s}^{2}$.

Fig. 15

Fall down of a clamed cantilever beam under its gravity

The predicted position variations versus time of the beam by the proposed beam models are illustrated in Fig. 16(a–d) at different time instants, and the number of elements is 40, which is checked to be sufficient for convergence, and the time step-size $\mathrm{{\Delta }} t$ is 0.01 s and the spectral radius $\rho _\infty$ is 0.8. It is seen that higher-order models can give more accurate predictions compared to the linear one; it is also confirmed by Fig. 16(d), which shows the $Z$-displacement of the tip point of the beam as function of time predicted by different models. In Fig. 16, only the result of the model B2 is shown since the results obtained by the other higher-order models are similar with those by the model B2.

Fig. 16

Dynamic responses of a falling soft beam

Figure 17 show the distribution of axial normal stress $\sigma _{xx}$ of the beam at $t=0.45\hbox { s}$ for the models A2 and B2, respectively. The 10 beam elements are adopted to more clearly illustrate stress discontinuity here. As can be seen clearly in Fig. 17(b), in the case of the model B2, the stress distribution is discontinuous due to the linear interpolation in the parameter vectors of the beam cross section (Eq. (6)). With the model A2, however, the stress is continuous due to the interpolation by cubic polynomials in the parameter vectors (Eq.(5)), as shown in Fig. 17(a).

Fig. 17

Distribution of axial normal stress $\sigma _{xx}$(Pa)

In Fig. 18, the energy balance of the falling soft beam is examined with the model B2 and it is seen that the total energy is conserved during the motion of the beam. The results obtained by the other higher-order models are similar with those by the model B2, and they are not reported.

Fig. 18

Energy balance of a falling soft beam

To compare the computational efficiency for the different beam models, the time of computation using the Intel i3, 2.93 GHz, and 4 GB of RAM is shown in Table 4. The pre-processing mainly includes the calculation of some constant matrices, such as the mass matrix and the integrals in the elastic force and its Jacobian, and the solving time is the time used to solve Eq. (27) by means of the constant matrices in the pre-processing. In addition, total number of iterations for evaluating the elastic force Q and total number of addition and multiplication operations (arithmetic operations) for evaluating the elastic force and its Jacobian are also shown.

Table 4 Computation time of the falling soft beam

5 Conclusions

When a beam is subjected to a large deformation, the distortion of its cross section may become significant. To characterize this distortion with the absolute nodal coordinate formulation, several higher-order models for a beam element are proposed, and their position vectors are expressed in a unified way. The proposed models in fact consider a beam as a solid by means of the cross-section function $f$ and the parameter vectors; therefore, more deformation modes can be captured. It is shown that Poisson locking problem can be prevented by means of the higher-order beam models with the high-order polynomials in the displacement approximation. Through a number of numerical examples, we find that the model B2 is more efficient to investigate

most of static and dynamic problems. However, the fourth-order beam model should be adopted in the case of large warping displacements of a beam with square cross section.