Nonlinear, three-dimensional beam theory for dynamic analysis

Abstract

For beams undergoing large motions but small strains, the displacement field can be decomposed into an arbitrarily large rigid-section motion and a warping field. When applying beam theory to dynamic problems, it is customary to assume that all inertial effects associated with warping are negligible. This paper examines this assumption in details. It is shown that inertial forces affect the beam’s dynamic response in two manners: (1) warping motion induces inertial forces directly, and (2) secondary warping arises that alters the beam’s constitutive laws. Numerical examples demonstrate the range of validity of the proposed approach for beams made of both homogeneous isotropic and heterogeneous anisotropic materials. For low-frequency warping, it is shown that inertial forces associated with warping and secondary warping resulting from inertial forces are negligible. To examine the dynamic behavior of beams over a wider range of frequencies, their dispersion curves, natural vibration frequencies, and mode shapes are evaluated using both one- and three-dimensional models; good correlation is observed between the two models. Applications of the proposed beam theory to multibody problems are also presented; here again, good correlation is observed between the prediction of beam models and of full three-dimensional analysis.

1 Introduction

A beam is defined as a structure having one of its dimensions much larger than the other two. The generally curved axis of the beam is defined along that longer dimension and the cross-section slides along this axis. The cross-section’s geometric and physical properties are assumed to be uniform along the beam’s span. Numerous components found in flexible multibody systems are beam-like structures: linkages, transmission shafts, robotic arms, etc. Aeronautical structures such as aircraft wings or helicopter rotor and wind turbine blades are often treated as beams.

Beam theories approximate three-dimensional beam-like structures with one-dimensional models, while retaining, to the extent possible, an accurate representation of the local three-dimensional stress and strain fields over the cross-section. Classical beam theories are based on kinematic assumptions: for instance, the Timoshenko beam theory is based on the rigid cross-section assumption [1]. When dealing with flexible multibody systems, beams undergo large motion, calling for a more accurate kinematic description. Reissner [2] and Simo [3, 4] developed the geometrically exact beam theory, which is also based on the rigid cross-section assumption. In many applications, however, beams are complex build-up structures presenting elaborate sectional geometries. In addition, laminated composite materials have found increased use in many applications, leading to heterogeneous, highly anisotropic structures. Furthermore, the beam’s axis may also be initially curved. For such constructions, cross-section out-of-plane and in-plane warping have been shown [5–11] to alter stress distributions and sectional stiffness properties significantly.

A rigorous beam theory should provide exact solutions for Saint-Venant’s problem [12, 13], that is, three-dimensional equilibrium should be satisfied at every point of the beam except near its two ends. Numerous authors have attempted to solve Saint-Venant’s problem [14–20], but the work of Giavotto et al. [21] is a milestone because their approach is applicable to realistic engineering problems: based on a two-dimensional finite element analysis of the cross-section, the beam’s sectional stiffness properties are evaluated and local, three-dimensional stress fields are recovered for anisotropic beams of arbitrary geometric configurations. Two types of solutions were identified: the central solutions, which are the solutions of Saint-Venant’s problem, and the extremity solutions, which decay exponentially away from the beam’s ends. The decay rates of the extremity solutions provide a quantification of Saint-Venant’s principle. The same semidiscretization procedure was also adopted by Borri et al. [5], Hodges [22, 23], Dong et al. [24], and El Fatmi and Zenzri [25] to solve complex beam problems.

Zhong [17, 26] introduced the Hamiltonian formulation for elasticity and developed novel analytical techniques based on Hamiltonian formalism. Based on this formulation, Bauchau and Han [8] have shown that the central solutions are exact solutions of three-dimensional elasticity and exist for uniform beams of general cross-sectional shape made of anisotropic materials. The same is true for initially curved and twisted beams undergoing large motion but small strains [9]. Saint-Venant’s problem deals with infinitely long, uniform beams undergoing small strain deformation and subjected to loading at their end sections only. Beams must be very long and loaded at their ends only to allow the effect of the end solutions to vanish, leaving the central solutions as exact solutions of the problem. The proposed approach provides a comprehensive analysis methodology for evaluating the dynamic response of beams within the framework of multibody dynamics. Starting with the three-dimensional equations of elasticity, a rigorous procedure based on Hamilton’s formulation produces one-dimensional, beam-like equations. Once these equations are solved, local, three-dimensional strain and stress fields are recovered.

The overall process is depicted in Fig. 1. The process starts with a linear, two-dimensional analysis of the cross-section (box 1 of Fig. 1). This step, called “sectional analysis,” evaluates the sectional compliance and mass matrices. Given the distribution of material properties and geometry of the cross-section, the sectional analysis provides the beam’s $6\times 6$ sectional compliance and mass matrices. These sectional matrices take into account the three-dimensional deformation of the beam’s cross-section stemming from complex sectional geometries, material heterogeneity, and initial curvature of the reference line.

Fig. 1

Integration of sectional analysis with multibody dynamic analysis

The second step of the process is a one-dimensional nonlinear analysis of the geometrically exact beam problem (box 2 of Fig. 1). Typically, this analysis is performed via a finite element discretization of the beam and time integration of the resulting discrete equations. At the end of this process, time histories of the stress resultants are available for the entire duration of the simulation. The sectional compliance and mass matrices obtained from the sectional analysis are inputs to this process. The final step of the process is the recovery of local three-dimensional strain and stress fields (box 3 of Fig. 1). The recovery relationships are provided by the sectional analysis.

In summary, for small strain problems, the nonlinear three-dimensional elasticity problem splits into two simpler problems: the linear sectional analysis problem and the nonlinear geometrically exact beam problem. As illustrated in Fig. 1, the sectional analysis is both a pre- and post-processor for the beam analysis and is run once only, prior to the nonlinear beam analysis.

Whereas the strategy has been applied to dynamic problems, little attention has been devoted to inertial effects. The goal of this paper is to assess the range of validity of the proposed beam theory when applied to dynamics problems. For static problems, the proposed approach provides exact solutions of three-dimensional elasticity for uniform beams of arbitrary geometric configuration and made of anisotropic composite materials. Yet, the performance of these models in the dynamic regime has not been assessed.

Han and Bauchau [27] have investigated the problem of beams subjected to distributed loads and have shown that these loads induce additional warping, called “secondary warping,” that affect the beam’s stiffness characteristics and local stress fields. In accordance with d’Alembert’s principle, inertial forces can be considered to be a type of externally applied loading, and hence, they give rise to secondary warping. Consequently, when applying the proposed beam theory to dynamic problems, two issues must be addressed: (1) what is the warping field induced by inertial forces? (see the lower dashed ellipse of Fig. 1), and (2) what is the effect of the secondary warping induced by the distributed inertial forces on the beam’s sectional stiffness and three-dimensional stress distributions? (see the upper dashed ellipse of Fig. 1). This paper examines beams undergoing low-frequency warping. Given this limitation, it will be shown that the inertial forces associated with warping and the secondary warping induced by inertial forces are both negligible.

This paper is organized as follows: the kinematics and governing equations of dynamic beam problems are presented in Sects. 2 and 3, respectively. The construction of a projective transformation is discussed in Sect. 4 and leads to the reduced, beam-like equations presented in Sect. 5. To illustrate the results, the linear problem is presented in Sect. 6, and three-dimensional stress recovery relations are discussed in Sect. 7. Integration of the proposed sectional analysis with multibody dynamic analysis is summarized in Sect. 8. Finally, numerical examples are presented in Sect. 9.

2 Kinematics of the problem

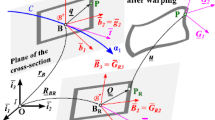
Figure 2 depicts the reference and deformed configurations of a naturally curved and twisted beam. The beam is generated by sliding its cross-section $\mathcal{A}$ along reference lines $\mathcal{C}_{0}$ and $\mathcal{C}$ of the reference and deformed configurations, respectively.

Fig. 2

Configuration of a curved beam

In the reference configuration, the reference line $\mathcal{C}_{0}$ is defined by parametric equation $\mathbf{{r}}_{B0} (\alpha_{1})$, where $\mathbf{{r}}_{B0}$ is the position vector of point B with respect to the origin of the reference frame $\mathcal{F}_{I} = [ \mathbf{O}, \mathcal{I}= (\mathbf{{i}}_{1}, \mathbf{{i}}_{2}, \mathbf{{i}}_{3}) ]$, and $\alpha_{1}$ is the arc-length coordinate along the curve $\mathcal{C}_{0}$. The cross-section is defined by the frame $\mathcal{F}_{0} = [ \mathbf{B}_{0}, \mathcal{B}_{0} = (\mathbf{{b}}_{10}, \mathbf{{b}}_{20}, \mathbf{{b}}_{30}) ]$. The plane of the cross-section is determined by two mutually orthogonal unit vectors $\mathbf{{b}}_{20}$ and $\mathbf{{b}}_{30}$.

In the deformed configuration, the parametric equation of the reference line $\mathcal{C}$ becomes $\mathbf{{r}}_{B} (\alpha_{1})$. Typically, the material plane of the cross-section is now distorted and warped. For convenience, a fictitious plane of the cross-section is introduced, which is determined by two mutually orthogonal unit vectors $\mathbf{{b}}_{2}$ and $\mathbf{{b}}_{3}$, as depicted in Fig. 2. The fictitious rigid cross-section is defined by the frame $\mathcal{F}_{R} = [ \mathbf{B}, \mathcal{B}_{R} = (\mathbf{{b}}_{1}, \mathbf{{b}}_{2}, \mathbf{{b}}_{3}) ]$, and the displacement field over the cross-section is decomposed into an arbitrarily large rigid-section motion and an arbitrary warping field.

The following motion tensors [28] are defined to represent the finite rigid-body motion from the frame $\mathcal{F}_{I}$ to $\mathcal{F}_{0}$ and $\mathcal{F}_{R}$, respectively:

$$\begin{aligned} {\mathbf{{C}}}_{0} (\mathbf{{r}}_{B0}, \mathbf{{R}}_{0}) &= \left[\textstyle\begin{array}{c@{\quad}c} {\mathbf{{R}}}_{0} & \tilde{\mathbf{{r}}}_{B0} {\mathbf{{R}}}_{0} \\ \mathbf{{O}}& {\mathbf{{R}}}_{0} \end{array}\displaystyle \right] , \end{aligned}$$

(1a)

$$\begin{aligned} \mathbf{{C}}_{R} (\mathbf{{r}}_{B}, \mathbf{{R}}) &= \left[\textstyle\begin{array}{c@{\quad}c} {\mathbf{{R}}}& \tilde{\mathbf{{r}}}_{B} {\mathbf{{R}}}\\ \mathbf{{O}}& {\mathbf{{R}}} \end{array}\displaystyle \right] , \end{aligned}$$

(1b)

where $\mathbf{{R}}_{0}$ and $\mathbf{{R}}$ are the rotation tensors that bring the basis ℐ to $\mathcal{B}_{0}$ and $\mathcal{B} _{R}$, respectively. The beam’s generalized curvature tensor in its initial and deformed configurations are

$$\begin{aligned} \tilde{\boldsymbol{\kappa }}_{0} &= \mathbf{{C}}_{0}^{-1} {\mathbf{{C}}}_{0}' = \left[\textstyle\begin{array}{c@{\quad}c} \tilde{\mathbf{{k}}}_{0} & \tilde{\mathbf{{t}}}_{0} \\ \mathbf{{O}}& \tilde{\mathbf{{k}}}_{0} \end{array}\displaystyle \right] , \end{aligned}$$

(2a)

$$\begin{aligned} \tilde{\boldsymbol{\kappa }}_{R} &= \mathbf{{C}}_{R}^{-1} {\mathbf{{C}}}_{R}' = \left[\textstyle\begin{array}{c@{\quad}c} \tilde{\mathbf{{k}}}& \tilde{\mathbf{{t}}}\\ \mathbf{{O}}& \tilde{\mathbf{{k}}} \end{array}\displaystyle \right] , \end{aligned}$$

(2b)

where the notation $(\cdot )'$ indicates a derivative with respect to $\alpha_{1}$. The notation $\tilde{(\cdot )}$ indicates the $3\times 3$ skew-symmetric matrix constructed from the components of vector $(\cdot )$ of size $3\times 1$. When applied to a vector of size $6\times 1$, the same notation indicates the upper-triangular matrix defined by Eqs. (2a)–(2b). The notation $\mathrm{axial}(\cdot )$ indicates the vector form of a $3\times 3$ skew-symmetric matrix $\tilde{(\cdot )}$. The curvature vectors associated with rotation fields $\mathbf{{R}}_{0} ( \alpha_{1})$ and $\mathbf{{R}}(\alpha_{1})$ are $\mathbf{{k}}_{0} = \mathrm{axial}(\mathbf{{R}}_{0}^{T} {\mathbf{{R}}}_{0}^{\prime })$ and $\mathbf{{k}}= \mathrm{axial}(\mathbf{{R}}^{T} {\mathbf{{R}}}^{\prime })$, respectively; the components of the tangent vectors to the reference lines in the reference and fictitious rigid configurations are $\mathbf{{t}}_{0} = \mathbf{{r}}_{B0}'$ and $\mathbf{{t}}= \mathbf{{r}}_{B}'$, respectively. The notation $\mathcal{A}\mathrm{xial}(\cdot )$ indicates the vector form of the $6\times 6$ upper-triangular matrix shown in Eqs. (2a)–(2b). The generalized curvature vectors in the reference and deformed configurations are denoted ${\boldsymbol{\kappa }}_{0} = \mathcal{A}\mathrm{xial}(\mathbf{{C}}_{0}^{-1} {\mathbf{{C}}}_{0}^{\prime }) = \{ \mathbf{{k}}_{0}^{T}, \mathbf{{t}}_{0}^{T} \}^{T}$ and ${\boldsymbol{\kappa }}_{R} = \mathcal{A}\mathrm{xial}(\mathbf{{C}}_{R}^{-1} {\mathbf{{C}}}_{R}^{\prime }) = \{\mathbf{{k}}^{T}, \mathbf{{t}}^{T}\}^{T}$, respectively.

For dynamic problems, the motion tensor $\mathbf{{C}}_{R}$ is a function of time $t$. The components of the beam’s generalized velocity vector, resolved in material basis, are

$$ \tilde{\boldsymbol{\upsilon }}_{R} = \mathbf{{C}}_{R}^{-1} \dot{\mathbf{{C}}}_{R} = \left[\textstyle\begin{array}{c@{\quad}c} {\boldsymbol{\omega }}& \tilde{\mathbf{{v}}} \\ \mathbf{{O}}& \tilde{\boldsymbol{\omega }} \end{array}\displaystyle \right] ,\quad {\boldsymbol{\upsilon }}_{R} = \mathcal{A}\mathrm{xial}\bigl(\mathbf{{C}}_{R}^{-1} \dot{\mathbf{{C}}}_{R}\bigr) = \begin{Bmatrix} {\mathbf{{R}}}^{T} \dot{\mathbf{{r}}}_{B} \\ \mathrm{axial}\bigl(\mathbf{{R}}^{T} \dot{\mathbf{{R}}}\bigr) \end{Bmatrix} = \begin{Bmatrix} {\mathbf{{v}}} \\ {\boldsymbol{\omega }} \end{Bmatrix} , $$

(3)

where the notation $\dot{(\cdot )}$ indicates a derivative with respect to time. The velocity vector ${\boldsymbol{\upsilon }}_{R}$ combines the velocity vector $\mathbf{{v}}$ of the cross-section’s reference point and its angular velocity ${\boldsymbol{\omega }}= \mathrm{axial}(\mathbf{{R}}^{T} \dot{\mathbf{{R}}})$, both resolved in material basis ℬ.

2.1 Acceleration components

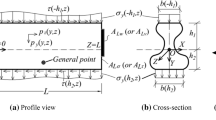
Let $\alpha_{2}$ and $\alpha_{3}$ denote the in-plane material coordinates along the directions of unit vectors $\mathbf{{b}}_{20}$ and $\mathbf{{b}}_{30}$, respectively. The position vector of an arbitrary material point $\mathbf{P}$ of the beam in its reference configuration becomes

$$ {\mathbf{{r}}}_{0} (\alpha_{1}, \alpha_{2}, \alpha_{3}) = \mathbf{{r}}_{B0} ( \alpha_{1}) + \mathbf{{R}}_{0} (\alpha_{1}) \mathbf{{q}}, $$

(4)

where the vector $\mathbf{{q}}= \{ 0, \alpha_{2}, \alpha_{3} \}^{T}$. After deformation, the position vector of a material point becomes

$$ {\mathbf{{r}}}(\alpha_{1}, \alpha_{2}, \alpha_{3},t) = \mathbf{{r}}_{B}(\alpha _{1},t) + \mathbf{{R}} (\alpha_{1},t) \bigl[ {\mathbf{{q}}}+ \mathbf{{w}}( \alpha _{1}, \alpha_{2}, \alpha_{3},t) \bigr] , $$

(5)

where $\mathbf{{w}}$ is the warping field with its components resolved in basis ℬ denoted $w_{i}$, that is, $\mathbf{{w}}= w_{1} {\mathbf{{b}}}_{1} + w_{2} {\mathbf{{b}}}_{2} + w_{3} {\mathbf{{b}}}_{3}$.

The velocity vector of the point P becomes

$$ \dot{\mathbf{{r}}} = \dot{\mathbf{{r}}}_{B} + \mathbf{{R}} \bigl[ \tilde{\boldsymbol{\omega }}( \mathbf{{q}}+ \mathbf{{w}}) + \dot{ \mathbf{{w}}} \bigr] = \mathbf{{R}} \bigl[ {\mathbf{{v}}}+ \dot{\mathbf{{w}}} + \tilde{\boldsymbol{\omega }}( \mathbf{{q}}+ \mathbf{{w}}) \bigr] . $$

(6)

Taking the second time derivative yields the components of the acceleration vector, resolved in the material basis, as

$$\begin{aligned} {\mathbf{{a}}}= \mathbf{{R}}^{T} \ddot{ \mathbf{{r}}} = & \dot{\mathbf{{v}}} - \tilde{\mathbf{{q}}}\dot{{\boldsymbol{\omega }}} + \tilde{\boldsymbol{\omega }} {\mathbf{{v}}}+ \tilde{\boldsymbol{\omega }}\tilde{\boldsymbol{\omega }} {\mathbf{{q}}} + \ddot{\mathbf{{w}}} + 2 \tilde{\boldsymbol{\omega }}\dot{\mathbf{{w}}} + ( \dot{ \tilde{\boldsymbol{\omega }}} + \tilde{\boldsymbol{\omega }}\tilde{\boldsymbol{\omega }}) \mathbf{{w}}. \end{aligned}$$

(7)

The first line of this equation lists the acceleration terms stemming from the rigid-section motion, and the second line those originating from warping deformation; hence, the warping induced inertial forces are $\mathbf{{f}}_{W}^{I} = \rho [\ddot{\mathbf{{w}}} + 2 \tilde{\boldsymbol{\omega }} \dot{\mathbf{{w}}} + ( \dot{\tilde{\boldsymbol{\omega }}} + \tilde{\boldsymbol{\omega }} \tilde{\boldsymbol{\omega }}) \mathbf{{w}}]$, where $\rho$ is the material density.

Textbooks on vibration establish that the frequency of beam bending vibrations is $\varOmega_{n}^{2} \propto n^{4} H / (m L^{4})$, where $n$ is the mode number, $L$ the beam’s length, $H$ its bending stiffness, and $m$ its mass per unit span. If $a$ is a representative dimension of the cross-section, then these quantities can be estimated as $H \propto E a^{4}$ and $m = \rho a^{2}$. Furthermore, $\lambda _{n} = L / n$ is a good estimate of the wave length of the associated vibration mode shape, leading to $\varOmega_{n}^{2} \propto E a^{2} / ( \rho \lambda_{n}^{4})$. If the beam is vibrating at this frequency, then $\| {\mathbf{{f}}}_{W}^{I} \| \approx \rho \varOmega_{n}^{2} (1 + \| {\boldsymbol{\omega }} \| / \varOmega_{n} )^{2} \| {\mathbf{{w}}}\| \approx \rho \varOmega_{n}^{2} \| {\mathbf{{w}}}\|$, where the norm of the angular velocity vector is assumed to be of the same order of magnitude as the vibration frequency to obtain the last result. Finally, the norm of the inertial force vector can be estimated as $\| {\mathbf{{f}}}_{W}^{I} \| \approx (a / \lambda_{n})^{4} E \| {\mathbf{{w}}}\| / a^{2}$. For beams undergoing torsional vibration, a similar reasoning yields $\varOmega_{n}^{2} \propto E / (\rho \lambda_{n}^{2})$, leading to $\| {\mathbf{{f}}}_{W}^{I} \| \approx (a / \lambda_{n})^{2} E \| {\mathbf{{w}}}\| / a^{2}$.

The warping induced strains are estimated as $\epsilon_{W} \approx \| {\mathbf{{w}}}\| / a$, the corresponding stresses as $\sigma_{W} = E \epsilon_{W}$, and stress gradients as $\nabla \sigma_{W} = \sigma _{W} / a$. This leads to $\| {\mathbf{{f}}}_{W}^{I} \| \approx (a / \lambda _{n})^{4} \nabla \sigma_{W}$ and $\| {\mathbf{{f}}}_{W}^{I} \| \approx (a / \lambda_{n})^{2} \nabla \sigma_{W}$ for beam undergoing bending and torsional vibrations, respectively. Clearly, for low-frequency vibrations, $\lambda_{n} \gg a$, and hence, $\| {\mathbf{{f}}}_{W}^{I} \| \ll \nabla \sigma_{W}$. Because the dynamic equilibrium condition states that $\nabla \sigma _{W} + \| {\mathbf{{f}}}_{W}^{I} \| + \mbox{rigid-section motion-induced inertial} \ \mbox{forces} = 0$, the warping-induced inertial forces can be neglected.

In summary, for beams undergoing low-frequency vibration, defined as vibration for which $\lambda_{n} \gg a$, the warping-induced inertial forces can be neglected. The low-frequency assumption is not an additional one. Indeed, even for static problems, beam theory is valid only if stresses vary slowly along its span. Clearly, beam theory can only predict accurately low-frequency modes, and for such modes, the warping-induced inertial forces are negligible. For high-frequency vibration, a three-dimensional elasticity model should be used, and warping-induced inertial forces should be included. Finally, it should be noted that in many practical applications, structures respond in their lowest-frequency modes only; little vibratory energy is associated with the high-frequency modes, which can be neglected altogether.

When the warping-induced inertial forces are negligible, the acceleration vector in Eq. (7) reduces to

$$ {\mathbf{{a}}}\approx \dot{\mathbf{{v}}} - \tilde{\mathbf{{q}}} \dot{{\boldsymbol{\omega }}} + \tilde{\boldsymbol{\omega }} {\mathbf{{v}}}+ \tilde{\boldsymbol{\omega }} \tilde{\boldsymbol{\omega }} {\mathbf{{q}}}= \mathbf{{z}} \dot{{\boldsymbol{\upsilon }}}_{R} + {\boldsymbol{\psi }} {\boldsymbol{\varOmega }}_{R} = {\boldsymbol{\pi }} \mathbf{{a}}_{R}. $$

(8)

The matrix $\mathbf{{z}}= [ {\mathbf{{I}}}, - \tilde{\mathbf{{q}}} ]$, the matrix ${\boldsymbol{\pi }}= [ {\mathbf{{z}}}, {\boldsymbol{\psi }}]$, and the following quantities were defined:

$$ {\boldsymbol{\psi }}= \left[\textstyle\begin{array}{c@{\quad}c@{\quad}c@{\quad}c@{\quad}c@{\quad}c@{\quad}c@{\quad}c} 1 & 0 & 0 & 0 & 0 & 0 & \alpha_{3} & \alpha_{2} \\ 0 & 1 & 0 & - \alpha_{2} & 0 & \alpha_{3} & 0 & 0 \\ 0 & 0 & 1 & 0 & - \alpha_{3} & \alpha_{2} & 0 & 0 \end{array}\displaystyle \right] ,\qquad \mathbf{{a}}_{R} = \left\{\textstyle\begin{array}{c} \dot{{\boldsymbol{\upsilon }}}_{R} \\ {\boldsymbol{\varOmega }}_{R} \end{array}\displaystyle \right\} . $$

(9)

Let $v_{i}$ and $\omega_{i}$, $i = 1,2,3$, denote the $i$th components of velocity of the cross-section’s reference point and its angular velocity $\mathbf{{v}}$ and ${\boldsymbol{\omega }}$, respectively. The array ${\boldsymbol{\varOmega }}_{R}^{T} = \{ v_{3}\omega_{2} - v_{2} \omega_{3}, v _{1} \omega_{3} - v_{3} \omega_{1}, v_{2} \omega_{1} - v_{1} \omega _{2}, \omega_{1}^{2} + \omega_{3}^{2}, \omega_{1}^{2} + \omega_{2} ^{2}, \omega_{2} \omega_{3}, \omega_{1} \omega_{3}, \omega_{1} \omega _{2} \}$ and array $\mathbf{{a}}_{R}$ collects all components related to the acceleration of the rigid section.

2.2 Strain components

Because sectional warping generates strains that are of the same order as those due to rigid-section motion, warping effects must to be taken into account when evaluating the strain field. Assuming small warping and strain components, the Green–Lagrange strain tensor reduces to

$$ {\boldsymbol{\gamma }}\approx {\mathbf{{A}}} \mathbf{{w}}^{\prime } + \mathbf{{B}} \mathbf{{w}}+ \mathbf{{z}} {\boldsymbol{\varepsilon }}_{R}, $$

(10)

where ${\boldsymbol{\varepsilon }}_{R}$ stores the beam’s sectional strains due to the fictitious rigid cross-section motion

$$ {\boldsymbol{\varepsilon }}_{R} = {\boldsymbol{\kappa }}_{R} - {\boldsymbol{\kappa }}_{0}. $$

(11)

These sectional strain measures are identical to those derived by Reissner [2] and Simo [3].

Let $t_{i0}$ and $k_{i0}$ denote the $i$th components of the tangent and curvature vectors $\mathbf{{t}}_{0}$ and $\mathbf{{k}}_{0}$, respectively. In Eq. (10), the following differential operators were defined:

$$ {\mathbf{{A}}}= \frac{1}{\sqrt{g}} \left[\textstyle\begin{array}{c} {\mathbf{{I}}} \\ \mathbf{{O}} \end{array}\displaystyle \right] ,\qquad \mathbf{{B}}= \left[\textstyle\begin{array}{c} {\mathbf{{D}}}_{O} \\ \mathbf{{D}}_{I} \end{array}\displaystyle \right] , $$

(12)

where the scalar $\sqrt{g} = t_{10} - k_{30} \alpha_{2} + k_{20} \alpha_{3}$ is the determinant of the metric tensor in the reference configuration. In Eq. (12), differential operators $\mathbf{{D}}_{O}$ and $\mathbf{{D}}_{I}$ were defined as

$$ {\mathbf{{D}}}_{O} = \left[\textstyle\begin{array}{c@{\quad}c@{\quad}c} d & - k_{30} & k_{20} \\ k_{30} + \sqrt{g} \frac{\partial }{\partial \alpha_{2}} & d & - k_{10} \\ - k_{20} + \sqrt{g} \frac{\partial }{\partial \alpha_{3}} & k_{10} & d \end{array}\displaystyle \right] ,\quad\quad \mathbf{{D}}_{I} = \left[\textstyle\begin{array}{c@{\quad}c@{\quad}c} 0 & \sqrt{g} \frac{\partial }{\partial \alpha_{2}} & 0 \\ 0 & 0 & \sqrt{g} \frac{\partial }{\partial \alpha_{3}} \\ 0 & \sqrt{g} \frac{\partial }{\partial \alpha_{3}} & \sqrt{g} \frac{\partial }{\partial \alpha_{2}} \end{array}\displaystyle \right] , $$

(13)

where the scalar $d = - (t_{20} - k_{10} \alpha_{3}) \partial (\cdot ) / \partial \alpha_{2} - (t_{30} + k_{10}\alpha_{3})\partial (\cdot ) / \partial \alpha_{3}$. A more detailed derivation of the strain components is given by Han and Bauchau [9].

2.3 Semidiscretization of the warping field

The following semidiscretization of the displacement field is performed:

$$ {\mathbf{{w}}}(\alpha_{1}, \alpha_{2}, \alpha_{3}) = \mathbf{{N}}(\alpha_{2}, \alpha_{3}) {\hat{\mathbf{{w}}}}(\alpha_{1}), $$

(14)

where the matrix $\mathbf{{N}}(\alpha_{2}, \alpha_{3})$ stores the two-dimensional shape functions used in the discretization, and the array ${\hat{\mathbf{{w}}}}(\alpha_{1})$ stores the nodal values of the displacement field. The notation $\hat{(\cdot )}$ indicates the nodal quantities of the discretized variables. Let $\ell$ be the number of nodes used to discretize the beam’s cross-section, and $n = 3 \ell$ be the total number of degrees of freedom. Introducing this discretization into Eq. (6) and (10) yields the components of the acceleration vector and strain tensor as

$$\begin{aligned} {\mathbf{{a}}} &= \mathbf{{N}} {\boldsymbol{\varPi }} \mathbf{{a}}_{R}, \end{aligned}$$

(15a)

$$\begin{aligned} {\boldsymbol{\gamma }} &= \mathbf{{A}} \mathbf{{N}} {\hat{\mathbf{{w}}}}' + \mathbf{{B}} \mathbf{{N}} {\hat{\mathbf{{w}}}}+ \mathbf{{N}} \mathbf{{Z}} {\boldsymbol{\varepsilon }} _{R}, \end{aligned}$$

(15b)

where the matrices $\mathbf{{Z}}$ and ${\boldsymbol{\varPi }}$ stack the rows of the matrices $\mathbf{{z}}$ and ${\boldsymbol{\pi }}$, respectively, for each of the nodes over the cross-section.

3 Governing equations

The beam’s governing equations will be derived based on the Hamiltonian formalism. The inertial forces are derived in Sect. 3.1, followed by the investigation of strain energy of the system in Sect. 3.2, and, finally, governing equations are obtained.

3.1 Inertial forces

The beam is assumed to be made of linearly elastic anisotropic materials. The cross-sectional distribution of materials is arbitrary but remains uniform along the beam’s span. In view of Eq. (15a), the nodal inertial forces are

$$ {\mathbf{{f}}}_{I} = - \int_{\mathcal{A}} {\mathbf{{N}}}^{T} {\mathbf{{N}}} {\boldsymbol{ \varPi }} \mathbf{{a}}_{R} \rho \sqrt{g} \,\mathrm{d}\mathcal{A}= - {{ \mathbb{M}}} {\boldsymbol{\varPi }} \mathbf{{a}}_{R} = { - \mathbf{{m}} \dot{{\boldsymbol{\upsilon }}}_{R} + \tilde{\boldsymbol{\upsilon }}_{R}^{T}{\mathbf{{m}}} {\boldsymbol{\upsilon }}_{R},} $$

(16)

where $\rho$ is the mass density of the material, and the mass matrix, of size $n \times n$, is ${{ \mathbb{M}}}= \int_{\mathcal{A}} \rho {\mathbf{{N}}}^{T} {\mathbf{{N}}} \sqrt{g} \,\mathrm{d}\mathcal{A}$. Because the inertial effects due to warping are ignored, the beam’s sectional mass matrix $\mathbf{{m}}$, of size $6\times 6$, becomes

$$ {\mathbf{{m}}}= \mathbf{{Z}}^{T} {{{ \mathbb{M}}}} \mathbf{{Z}}. $$

(17)

Due to the nature of the problem, matrix $\mathbf{{m}}$ is of the following structure:

$$ {\mathbf{{m}}}= \left[\textstyle\begin{array}{c@{\quad}c@{\quad}c@{\quad}c@{\quad}c@{\quad}c} m_{00} & 0 & 0 & 0 & m_{00} \alpha_{3m} & - m_{00} \alpha_{2m} \\ 0 & m_{00} & 0 & - m_{00} \alpha_{3m} & 0 & 0 \\ 0 & 0 & m_{00} & m_{00} \alpha_{2m} &0 & 0 \\ 0 & - m_{00} \alpha_{3m} & m_{00} \alpha_{2m} & m_{11} & 0 & 0 \\ m_{00} \alpha_{3m} & 0 & 0 &0 & m_{22} & - m_{23} \\ - m_{00} \alpha_{2m} & 0 & 0 &0 & - m_{23} & m_{33} \end{array}\displaystyle \right] . $$

(18)

The sectional mass per unit span is $m_{00} = \int_{\mathcal{A}} \rho \sqrt{g} \,\mathrm{d}\mathcal{A}$; the coordinates of the sectional center of mass with respect to the reference point are $m_{00} \alpha_{2m} = \int_{\mathcal{A}} \rho \alpha_{2} \sqrt{g}\, \mathrm{d}\mathcal{A}$ and $m_{00} \alpha_{3m} = \int_{\mathcal{A}} \rho \alpha_{3} \sqrt{g} \,\mathrm{d}\mathcal{A}$; the sectional mass moments of inertia per unit span about unit vectors $\mathbf{{b}}_{2}$ and $\mathbf{{b}}_{3}$ are $m_{22} = \int_{\mathcal{A}} \rho \alpha_{3}^{2} \sqrt{g} \,\mathrm{d}\mathcal{A}$ and $m_{33} = \int_{\mathcal{A}} \rho \alpha_{2}^{2} \sqrt{g} \,\mathrm{d}\mathcal{A}$, respectively; the sectional cross-product of inertia per unit span is $m_{23} = \int_{\mathcal{A}} \rho \alpha_{2} \alpha_{3} \sqrt{g} \,\mathrm{d} \mathcal{A}$; finally, the polar moment of inertia per unit span is $m_{11} = m_{22} + m_{33}$. The following identity is used to yield the last equality in Eq. (16):

$$ - \tilde{\boldsymbol{\upsilon }}_{R}^{T}{ \mathbf{{m}}} {\boldsymbol{\upsilon }}_{R} = \mathbf{{Z}}^{T} \mathrm{diag} ( \tilde{\boldsymbol{\omega }} ) {{ \mathbb{M}}} \mathbf{{Z}}= {\boldsymbol{ \varPsi }} {\boldsymbol{\varOmega }}. $$

(19)

3.2 Strain energy

The strain energy density of the beam is

$$ L = \frac{1}{2} \int_{\mathcal{A}} {\boldsymbol{\gamma }}^{T} {\mathbf{{D}}} {\boldsymbol{ \gamma }} \sqrt{g} \,\mathrm{d}\mathcal{A}, $$

(20)

where the components of the $6\times 6$ material stiffness matrix resolved in the material basis are denoted as $\mathbf{{D}}$. Introducing the discretized components of the strain tensor given by Eq. (15b), the strain energy density becomes

$$ L = \frac{1}{2} \bigl( \mathbf{{Z}} {\boldsymbol{ \varepsilon }}+ {\hat{\mathbf{{w}}}} ^{\prime } \bigr) \bigl[ {\mathbf{{M}}} \bigl( \mathbf{{Z}} {\boldsymbol{\varepsilon }}+ {\hat{\mathbf{{w}}}}^{\prime } \bigr) + \mathbf{{C}} ^{T} {\hat{\mathbf{{w}}}} \bigr] + \frac{1}{2} {\hat{\mathbf{{w}}}}^{T} \bigl[ {\mathbf{{C}}} \bigl( \mathbf{{Z}} {\boldsymbol{\varepsilon }}+ {\hat{\mathbf{{w}}}}^{\prime } \bigr) + \mathbf{{E}} {\hat{\mathbf{{w}}}} \bigr] . $$

(21)

The matrices $\mathbf{{M}}$, $\mathbf{{C}}$, and $\mathbf{{E}}$, each of size $n \times n$, are

$$\begin{aligned} {\mathbf{{M}}} & = \int_{\mathcal{A}} (\mathbf{{A}} \mathbf{{N}})^{T} { \mathbf{{D}}}(\mathbf{{A}} \mathbf{{N}}) \sqrt{g} \,\mathrm{d}\mathcal{A}, \end{aligned}$$

(22a)

$$\begin{aligned} \mathbf{{C}} & = \int_{\mathcal{A}} (\mathbf{{A}} \mathbf{{N}})^{T} { \mathbf{{D}}}(\mathbf{{B}} \mathbf{{N}}) \sqrt{g} \,\mathrm{d}\mathcal{A}, \end{aligned}$$

(22b)

$$\begin{aligned} \mathbf{{E}} & = \int_{\mathcal{A}} (\mathbf{{B}} \mathbf{{N}})^{T} { \mathbf{{D}}}(\mathbf{{B}} \mathbf{{N}}) \sqrt{g} \,\mathrm{d}\mathcal{A}. \end{aligned}$$

(22c)

Given the distribution of material stiffness properties, these matrices can be evaluated by integration over the cross-section.

3.3 Governing equations

For this problem, the strain energy density is also the Lagrangian of the system. The nodal forces are introduced:

$$ {\hat{\mathbf{{p}}}}= \frac{\partial L}{\partial ( {\hat{\mathbf{{w}}}}' + \mathbf{{Z}} {\boldsymbol{\varepsilon }}_{R} ) } = \mathbf{{M}} \bigl( { \hat{\mathbf{{w}}}}' + \mathbf{{Z}} {\boldsymbol{\varepsilon }}_{R} \bigr) + \mathbf{{C}}^{T} {\hat{\mathbf{{w}}}}. $$

(23)

The nodal displacements and forces are dual variables in Hamilton’s formalism. The Hamiltonian of the system, denoted $H$, is defined via Legendre’s transformation [29] as $H = \hat{\mathbf{{p}}} ^{T} (\mathbf{{Z}} {\boldsymbol{\varepsilon }}_{R} + {\hat{\mathbf{{w}}}}') - L$, and tedious algebra reveals that $H = - 1/2\ \hat{\mathbf{{x}}}^{T} (\mathbf{{J}} \mathbf{{H}}) \hat{\mathbf{{x}}}$, where the array $\hat{\mathbf{{x}}}$ stores the nodal displacements and forces $\hat{\mathbf{{x}}}^{T} = \{ {\hat{\mathbf{{w}}}}^{T} \hat{\mathbf{{p}}}^{T} \}$, and matrices $\mathbf{{H}}$ and $\mathbf{{J}}$, both of size $2n \times 2n$, are defined as

$$ {\mathbf{{H}}}= \left[\textstyle\begin{array}{c@{\quad}c} - \mathbf{{M}}^{-1} {\mathbf{{C}}}^{T} & \mathbf{{M}}^{-1} \\ \mathbf{{E}}- \mathbf{{C}} \mathbf{{M}}^{-1} {\mathbf{{C}}}^{T} & \mathbf{{C}} \mathbf{{M}}^{-1} \end{array}\displaystyle \right] , \quad \mbox{and} \quad { \mathbf{{J}}}= \left[\textstyle\begin{array}{c@{\quad}c} {\mathbf{{O}}}& \mathbf{{I}} \\ -\mathbf{{I}}& \mathbf{{O}} \end{array}\displaystyle \right] . $$

(24)

The matrix $\mathbf{{H}}$ is Hamiltonian, that is, $(\mathbf{{J}} \mathbf{{H}}) = (\mathbf{{J}} \mathbf{{H}})^{T}$.

Hamilton’s principle provides two sets of equations for the problem. The first set ${\hat{\mathbf{{w}}}}' + \mathbf{{Z}} {\boldsymbol{\varepsilon }}_{R} = \partial H / \partial {\hat{\mathbf{{p}}}}$ is identical to Eqs. (23), that is, defines the nodal forces. The second set $\hat{\mathbf{{p}}}' = - \partial H / \partial {\hat{\mathbf{{w}}}}+ {{ \mathbb{M}}} {\boldsymbol{\varPi }} \mathbf{{a}}_{R}$ provides the governing equations of the problem. The combination of the two sets defines $2n$ first-order ordinary differential equations with constant coefficients

$$ {\hat{\mathbf{{x}}}}' = \mathbf{{J}} \frac{\partial H}{\partial {\hat{\mathbf{{x}}}}} = \mathbf{{H}} \hat{\mathbf{{x}}}- \left[\textstyle\begin{array}{c} {\mathbf{{Z}}} \\ \mathbf{{O}} \end{array}\displaystyle \right] {\boldsymbol{\varepsilon }}_{R} + \left[\textstyle\begin{array}{c} {\mathbf{{O}}} \\ {{ \mathbb{M}}} {\boldsymbol{\varPi }} \end{array}\displaystyle \right] {\mathbf{{a}}}_{R}, $$

(25)

where the identity $\mathbf{{J}}^{T} \mathbf{{J}}= \mathbf{{I}}$ was used. The corresponding homogenous problem $\hat{\mathbf{{x}}}^{\prime } = \mathbf{{H}} \hat{\mathbf{{x}}}$ provides the governing equations of the associated linear static beam problem.

Equations (25) are the governing equations for geometrically nonlinear dynamic three-dimensional beam problems. Although it can be solved directly, the computational cost is usually too high for practical beam problems. A proper utilization of the beam’s span-wise uniformity leads to a significant reduction of problem size. Clearly, the solution of Eq. (25) is determined by the nature of the eigenvalues of the Hamiltonian matrix $\mathbf{{H}}$, as discussed by Zhong [26] and Han and Bauchau [9, 11].

For linear static beam problem, that is, $\hat{\mathbf{{x}}}' = \mathbf{{H}} \hat{\mathbf{{x}}}$, the twelve null and purely imaginary eigenvalues of the Hamiltonian give rise to polynomial and trigonometric solutions [11], respectively, corresponding to the solution of Saint-Venant’s problem. Finally, the eigenvalues of the Hamiltonian matrix presenting nonvanishing real parts give rise to exponentially decaying solutions, which can be usually ignored because their effect is significant near the beam’s ends only.

Equations (25) show that nonlinear dynamics beam problems are represented by a nonhomogeneous Hamiltonian system. As expected from d’Alembert’s principle, inertial forces can be viewed as externally distributed loads: the matrix ${{ \mathbb{M}}} {\boldsymbol{\varPi }}$ and array $\mathbf{{a}}_{R}$ store the loading pattern over the cross-section and the corresponding load distribution along the reference line, respectively. Consequently, dynamic beam problems form a particular case of Almansi–Michell’s problem discussed by Han and Bauchau [27]. Clearly, the solutions not only depend on the eigenvalues of the matrix $\mathbf{{H}}$ but also on the nonhomogeneous terms related to inertial forces. To reduce problem size, the three-dimensional governing equations will be projected onto a subspace spanned by the twelve generalized eigenvectors of the Hamiltonian matrix associated with its null and purely imaginary eigenvalues and with a set of secondary warping modes related to the inertial forces.

4 Dimensional reduction

To solve Almansi–Michell’s problem, Han and Bauchau [27] expanded the applied load distribution function in Taylor series taking into account accordingly the secondary warping modes associated with the various orders of expansion. For simplicity, only the 0th-order expansion of the inertial force is considered here. The augmented projection is constructed as follows:

$$ {\hat{\mathbf{{x}}}}= \mathbf{{X}} \mathbf{{g}}+ \mathbf{{Q}} \mathbf{{a}}_{R}, $$

(26)

where the matrix $\mathbf{{X}}$, the matrix $\mathbf{{Q}}$, and the array $\mathbf{{g}}$ are defined as follows:

$$ {\mathbf{{X}}}= \left[\textstyle\begin{array}{c@{\quad}c} {\mathbf{{Z}}}& \mathbf{{W}} \\ \mathbf{{O}}& \mathbf{{Y}} \end{array}\displaystyle \right] ,\qquad \mathbf{{Q}}= \left[\textstyle\begin{array}{c} {\mathbf{{U}}} \\ \mathbf{{V}} \end{array}\displaystyle \right] ,\qquad \mathbf{{g}}= \begin{Bmatrix} {\mathbf{{u}}} \\ \mathbf{{f}} \end{Bmatrix} . $$

(27)

The matrix $\mathbf{{X}}$, of size $2n \times 12$, is symplectic because it stores the eigenvectors and generalized eigenvectors of the matrix $\mathbf{{H}}$ (see details in [9, 27]), implying the identities

$$ {\mathbf{{Z}}}^{T} {\mathbf{{Y}}}= \mathbf{{I}}\quad \mbox{and} \quad \mathbf{{W}} ^{T}{\mathbf{{Y}}}= \mathbf{{O}}. $$

(28)

The matrices $\mathbf{{W}}$ and $\mathbf{{Y}}$, each of size $n \times 6$, are interpreted as the nodal warping and forces, respectively, associated with unit sectional stress resultants. The matrices $\mathbf{{U}}$ and $\mathbf{{V}}$, each of size $n \times 11$, are yet undetermined, and their $i$th columns store the secondary warping and nodal forces, respectively, induced by the unit values of the $i$th entry of the acceleration array $\mathbf{{a}}_{R}$. Finally, the array $\mathbf{{g}}^{T} = \{\mathbf{{u}}^{T} \mathbf{{f}}^{T}\}$ stores the six components of the infinitesimal rigid-section motion $\mathbf{{u}}$ and stress resultants $\mathbf{{f}}$, both resolved in the material basis.

Using projection (26), the Hamiltonian matrix reduces to

$$\begin{aligned} {\mathbf{{H}}} \mathbf{{X}} & = \mathbf{{X}} \left[\textstyle\begin{array}{c@{\quad}c} - \tilde{\boldsymbol{\kappa }}_{R} & \mathbf{{S}}\\ \mathbf{{O}}& \tilde{\boldsymbol{\kappa }}_{R}^{T} \end{array}\displaystyle \right] , \end{aligned}$$

(29a)

$$\begin{aligned} \mathbf{{H}} \left[\textstyle\begin{array}{c} {\mathbf{{U}}}\\ \mathbf{{V}} \end{array}\displaystyle \right] & = \left[\textstyle\begin{array}{c} {\mathbf{{W}}}\\ \mathbf{{Y}} \end{array}\displaystyle \right] {\mathbf{{Z}}}^{T}{{{ \mathbb{M}}}} {\boldsymbol{\varPi }}- \left[\textstyle\begin{array}{c} {\mathbf{{O}}}\\ {{ \mathbb{M}}} {\boldsymbol{\varPi }} \end{array}\displaystyle \right] . \end{aligned}$$

(29b)

Equation (29a) is the governing equation for the nodal warping and forces stored in matrices $\mathbf{{W}}$ and $\mathbf{{Y}}$, respectively, and is obtained by considering the homogeneous part of the problem only; Eq. (29b) is the governing equation for the secondary warping $\mathbf{{U}}$ and is obtained from the nonhomogeneous part of the problem, assuming that the matrices $\mathbf{{W}}$ and $\mathbf{{Y}}$ are known. The matrix $\mathbf{{S}}$ will be interpreted later as the sectional compliance matrix.

As will be shown in Sects. 5 and 7, secondary warping affects the beam’s reduced governing equations and the stress recovery process. Numerical examples will show that the effects of secondary warping are typically small for beam undergoing low-frequency vibration.

5 The one-dimensional beam equations

Introducing coordinate transformation (26) in governing equations (27), pre-multiplying by $\mathbf{{X}}^{T} \mathbf{{J}}$, and using the symplectic orthogonal property (28) lead to the reduced equations

$$ \begin{Bmatrix} {\mathbf{{u}}} \\ \mathbf{{f}} \end{Bmatrix} ' = \left[\textstyle\begin{array}{c@{\quad}c} - \tilde{\boldsymbol{\kappa }}_{R} & \mathbf{{S}} \\ \mathbf{{O}}& \tilde{\boldsymbol{\kappa }}_{R}^{T} \end{array}\displaystyle \right] \begin{Bmatrix} { \mathbf{{u}}} \\ \mathbf{{f}} \end{Bmatrix} + \begin{Bmatrix} {\mathbf{{S}}} \mathbf{{G}} { \mathbf{{a}}}_{R} - {\boldsymbol{\varepsilon }}_{R} \\ \mathbf{{m}} \dot{{\boldsymbol{\upsilon }}}_{R} - \tilde{\boldsymbol{\upsilon }}_{R} ^{T} {\mathbf{{m}}} {\boldsymbol{\upsilon }}_{R} \end{Bmatrix} , $$

(30)

where sectional mass matrix $\mathbf{{m}}$ is defined by Eq. (17) and matrix $\mathbf{{G}}= - \mathbf{{Z}} ^{T} {\mathbf{{V}}}$ results from the secondary warping. Identity (19) is used to derive Eq. (30).

The last six equations of this set provide the equilibrium equations $\mathbf{{f}}^{\prime } + \tilde{\boldsymbol{\kappa }}_{R} {\mathbf{{f}}}= \mathbf{{m}} \dot{{\boldsymbol{\upsilon }}}_{R} - \tilde{\boldsymbol{\upsilon }}_{R}^{T} {\mathbf{{m}}} {\boldsymbol{\upsilon }}_{R}$, where the right-hand sides are the distributed inertial forces due to rigid-section motion. The first six equations define the sectional constitutive laws ${\boldsymbol{\varepsilon }}= {\boldsymbol{\varepsilon }}_{W} + {\boldsymbol{\varepsilon }}_{R} = \mathbf{{S}}(\mathbf{{f}}+ \mathbf{{G}} \mathbf{{a}}_{R})$, where the sectional strains due to warping are defined as

$$ {\boldsymbol{\varepsilon }}_{W} = \mathbf{{u}}^{\prime } + \tilde{\boldsymbol{\kappa }} _{R} {\mathbf{{u}}}, $$

(31)

and the symmetric matrix $\mathbf{{S}}$ stores the components of the sectional compliance matrix resolved in the material basis.

To complete the formulation, sets of strain- and velocity-displacement relationships must be developed. The motion of the cross-section combines the motion associated with the fictitious rigid-section (see Eq. (1b)) with the additional infinitesimal rigid-section motion $\mathbf{{u}}$ included in the warping field

$$ {\mathbf{{C}}}(\alpha_{1}) = \mathbf{{C}}_{R} ( \mathbf{{I}}+ \tilde{\mathbf{{u}}} ) . $$

(32)

For the infinitesimal motion $\mathbf{{u}}$, the corresponding motion tensor is found as the exponential map $\exp (\tilde{\mathbf{{u}}})$ and can be approximated by $\mathbf{{I}}+ \tilde{\mathbf{{u}}}$. The motion tensor $\mathbf{{C}}$ describes the average motion of the deformed cross-section including warping.

The components of beam’s curvature vector in its deformed configuration are

$$ \tilde{\boldsymbol{\kappa }}= \bigl[ {\mathbf{{C}}}_{R} ( \mathbf{{I}}+ \tilde{\mathbf{{u}}} ) \bigr] ^{-1} \bigl[ { \mathbf{{C}}}_{R} ( \mathbf{{I}}+ \tilde{\mathbf{{u}}} ) \bigr] ^{\prime } \approx \tilde{\boldsymbol{\kappa }}_{R} + \tilde{\boldsymbol{ \varepsilon }}_{W}, $$

(33)

where higher-order terms are neglected. Using Eq. (31) then results in ${\boldsymbol{\kappa }}- {\boldsymbol{\kappa }}_{0} = {\boldsymbol{\varepsilon }}_{R} + {\boldsymbol{\varepsilon }} _{W} = {\boldsymbol{\varepsilon }}$. The components of beam’s generalized velocity are

$$ \tilde{\boldsymbol{\upsilon }}= \bigl[ {\mathbf{{C}}}_{R} ( \mathbf{{I}}+ \tilde{\mathbf{{u}}} ) \bigr] ^{-1} \frac{\partial }{\partial t} \bigl[ {\mathbf{{C}}}_{R} ( \mathbf{{I}}+ \tilde{ \mathbf{{u}}} ) \bigr] \approx \tilde{\boldsymbol{\upsilon }}_{R} + \dot{ \mathbf{{u}}}. $$

(34)

Because $\mathbf{{u}}$ is infinitesimal, it is reasonable to assume that ${\boldsymbol{\kappa }}\approx {\boldsymbol{\kappa }}_{R}$, ${\boldsymbol{\upsilon }} \approx {\boldsymbol{\upsilon }}_{R}$, and $\mathbf{{a}}= \mathbf{{a}}_{R}$, where the array $\mathbf{{a}}$ stores the acceleration-related terms for the average rigid-section motion. The nonlinear equations for three-dimensional dynamic beam problems, Eqs. (25), have been reduced to a set of 24 equations:

$$\begin{aligned} {\boldsymbol{\upsilon }} & = \mathcal{A}\mathrm{xial} \bigl( \mathbf{{C}}^{-1} \dot{\mathbf{{C}}} \bigr) , \end{aligned}$$

(35a)

$$\begin{aligned} {\boldsymbol{\varepsilon }} & = \mathcal{A}\mathrm{xial} \bigl( \mathbf{{C}}^{-1} {\mathbf{{C}}}' \bigr) - \mathcal{A}\mathrm{xial} \bigl( \mathbf{{C}}_{0}^{-1} {\mathbf{{C}}}_{0}' \bigr) , \end{aligned}$$

(35b)

$$\begin{aligned} {\boldsymbol{\varepsilon }} & = \mathbf{{S}} ( \mathbf{{f}}+ \mathbf{{G}} \mathbf{{a}}_{R} ) , \end{aligned}$$

(35c)

$$\begin{aligned} \mathbf{{f}}^{\prime} - \tilde{\boldsymbol{\kappa }}^{T} {\mathbf{{f}}} & = \mathbf{{m}} \dot{{\boldsymbol{\upsilon }}} - \tilde{\boldsymbol{\upsilon }}^{T} { \mathbf{{m}}} {\boldsymbol{\upsilon }}. \end{aligned}$$

(35d)

Kinematic equations (35a) and (35b) define the sectional velocity and strain measures for the rigid-section motion. Equations (35c) and (35d) are constitutive and equilibrium equations, respectively, for nonlinear dynamic beam problems. The term $\mathbf{{G}} \mathbf{{a}}_{R}$ in Eq. (35c) represents the effects of secondary warping. Introducing constitutive equations (35c) into equilibrium equations (35d) leads to $(\mathbf{{S}} ^{-1} {\boldsymbol{\varepsilon }})' - \tilde{\boldsymbol{\kappa }}^{T} {\mathbf{{S}}}^{-1} {\boldsymbol{\varepsilon }}= \mathbf{{m}} \dot{{\boldsymbol{\upsilon }}} - \tilde{\boldsymbol{\upsilon }}^{T} {\mathbf{{m}}} {\boldsymbol{\upsilon }}- (\mathbf{{G}} \mathbf{{a}}_{R})' + \tilde{\boldsymbol{\kappa }}^{T} {\mathbf{{G}}} \mathbf{{a}}_{R}$. Clearly, the relative magnitudes of matrices $\mathbf{{G}}$ and $\mathbf{{m}}$ reveal the relative importance of contributions from rigid-section inertial forces and secondary warping induced inertial effects. Further, in the numerical examples, we will show that the matrix $\mathbf{{G}}$ is several orders magnitude smaller than the matrix $\mathbf{{m}}$ and, hence, can be ignored.

When the secondary warping due to the acceleration $\mathbf{{G}} \mathbf{{a}}_{R}$ is neglected, governing equations (35a)–(35d) becomes identical to those derived by Reissner [2] and Simo and coworkers [3, 4]. The present paper has underlined the assumptions required to obtain these equations. Furthermore, because it is based on a two-dimensional model of the cross-section, the present approach provides an accurate expression for the sectional compliance matrix and allows recovery of the three-dimensional stress state at any point in the beam; see Sect. 7.

6 The linear problem

The previous developments are valid for beams undergoing large motion but small strain. For linear problems, the beam undergoes small motion only, an important problem in its own right. The linear problem is obtained by setting $\mathbf{{C}}_{R} = \mathbf{{I}}$, which implies ${\boldsymbol{\varepsilon }}_{R} = \mathbf{{0}}$ and ${\boldsymbol{\upsilon }}_{R} = \mathbf{{0}}$. Moreover, the acceleration given by Eq. (7) reduces to $\mathbf{{a}}= \ddot{\mathbf{{w}}}$, and the beam’s governing equations become

$$ {\hat{\mathbf{{x}}}}' = \mathbf{{H}} \hat{\mathbf{{x}}}+ \begin{Bmatrix} {\mathbf{{O}}} \\ {{ \mathbb{M}}} \ddot{{\hat{\mathbf{{w}}}}} \end{Bmatrix} . $$

(36)

The strain- and velocity-displacement relationships, Eqs. (35a) and (35b), now become ${\boldsymbol{\upsilon }}= \dot{\mathbf{{u}}}$ and ${\boldsymbol{\varepsilon }}= \mathbf{{u}}^{\prime } + \tilde{\boldsymbol{\kappa }}{\mathbf{{u}}}$, respectively. The acceleration components simply reduce to $\ddot{\mathbf{{\mathcal{U}}}}$, and, finally, the reduced governing equations of the problem, Eq. (35a)–(35d), become

$$\begin{aligned} {\mathbf{{u}}}^{\prime} & = -\tilde{\boldsymbol{\kappa }} \mathbf{{u}}+ \mathbf{{S}} \mathbf{{f}}, \end{aligned}$$

(37a)

$$\begin{aligned} \mathbf{{f}}^{\prime} & = \mathbf{{m}} \ddot{\mathbf{{u}}} + \tilde{ \boldsymbol{\kappa }}^{T} {\mathbf{{f}}}. \end{aligned}$$

(37b)

The wave solutions of Eqs. (36) are expressed in terms of exponential functions: $\hat{\mathbf{{x}}}(\alpha _{1},t) = \bar{\mathbf{{x}}}\exp j(k \alpha_{1} - \omega t)$, where $\bar{\mathbf{{x}}}^{T} = \{ \bar{\mathbf{{w}}}^{T} \bar{\mathbf{{p}}}^{T} \}$ stores the amplitude of the variables, $j = \sqrt{-1}$ is the imaginary unit, the complex number $k = k_{r} + j k_{i}$ is the wavenumber, and $\omega$ is the circular frequency. Introducing this solution into Eq. (36) gives the following eigenvalue problem:

$$ j k \begin{Bmatrix} {\bar{\mathbf{{w}}}} \\ \bar{\mathbf{{p}}} \end{Bmatrix} = \left( \mathbf{{H}}- \left[\textstyle\begin{array}{c@{\quad}c} {\mathbf{{O}}}& \mathbf{{O}} \\ \omega^{2} {{{ \mathbb{M}}}}& \mathbf{{O}} \end{array}\displaystyle \right]\right ) \begin{Bmatrix} { \bar{\mathbf{{w}}}} \\ \bar{\mathbf{{p}}} \end{Bmatrix} . $$

(38)

The dispersion relationship, that is, the relationship between $\omega$ and $k$, is obtained easily by solving this eigenvalue problem: for a given frequency $\omega$, the wave numbers $k$ are the eigenvalues of Eq. (38). Because the system is Hamiltonian, the eigenvalues come in groups of four in the form $k = \pm k_{r} \pm j k_{i}$. Equivalently, eliminating $\bar{\mathbf{{p}}}$ from Eq. (38) yields the Hermitian eigenvalue problem

$$ \bigl[ k^{2} {\mathbf{{M}}}+ j k \bigl(\mathbf{{C}}- \mathbf{{C}}^{T}\bigr) + \mathbf{{E}}- \omega^{2} {{{ \mathbb{M}}}} \bigr] {\bar{\mathbf{{w}}}}= \mathbf{{0}}. $$

(39)

The same procedure is applied to obtain the dispersion curves of reduced problem (37a)–(37b): introducing the wave solutions $\mathbf{{u}}(\alpha_{1},t) = \bar{\mathbf{{u}}}\exp j(k \alpha _{1} - \omega t)$ and $\mathbf{{f}}(\alpha_{1}, t) = \bar{\mathbf{{f}}} \exp j(k \alpha_{1} - \omega t)$ leads to the following eigenvalue problem:

$$ j k \begin{Bmatrix} {\bar{\mathbf{{u}}}} \\ \bar{\mathbf{{f}}} \end{Bmatrix} = \left[\textstyle\begin{array}{c@{\quad}c} - \tilde{\boldsymbol{\kappa }}& \mathbf{{S}} \\ -\omega^{2} {\mathbf{{m}}}& \tilde{\boldsymbol{\kappa }}^{T} \end{array}\displaystyle \right] \begin{Bmatrix} {\bar{\mathbf{{u}}}} \\ \bar{\mathbf{{f}}} \end{Bmatrix} . $$

(40)

Eliminating the sectional stress resultant then yields the Hermitian eigenvalue problem

$$ \bigl[ k^{2} {\mathbf{{S}}}^{-1} + j k \bigl( \tilde{\boldsymbol{\kappa }}^{T}{\mathbf{{S}}} ^{-1} - \mathbf{{S}}^{-1}\tilde{\boldsymbol{\kappa }}\bigr) + \tilde{\boldsymbol{\kappa }} ^{T} {\mathbf{{S}}}^{-1} \tilde{\boldsymbol{\kappa }}- \omega^{2} {\mathbf{{m}}} \bigr] {\bar{\mathbf{{u}}}}= \mathbf{{0}}. $$

(41)

For a given frequency $\omega$, $2n$ and 12 eigenvalues result from the original (Eq. (39)) and reduced (Eq. (41)) eigenproblems, respectively. Note that $\exp j(k \alpha_{1} - \omega t) = \exp (- k_{i} \alpha_{1})\times \exp j (k_{r} \alpha_{1} - \omega t)$, and hence, the coefficient $k_{i}$ can be interpreted as the spatial decay rate of the corresponding mode: the modes with the smallest $| k_{i}|$ are the most important because they affect the largest portion of the beam. Accordingly, the dispersion relations provide a simple way of validating the dimensional reduction process: in the low-frequency range, the 12 dispersion curves of the reduced system should coincide with their 12 counterparts of the original system associated with the lowest magnitude of  $k_{i}$. Achenbach [30] has shown that the dispersion relationships predicted by the planar Timoshenko beam theory are in good agreement with those resulting from two-dimensional elasticity in the low-frequency range. Volovoi et al. [31] compared the dispersion relationships for composite beams based on the variational asymptotic method with those obtained from three-dimensional elasticity; they reported good correlation in the low-frequency range. This validation will be performed numerically in Sect. 9.1 for a set of more complex beam problems based on the proposed model.

7 Local stress recovery

Combining Eqs. (26) and (27) yields the nodal displacement and force fields as

$$\begin{aligned} {\hat{\mathbf{{w}}}} &= \mathbf{{Z}} \mathbf{{u}}+ \mathbf{{W}} \mathbf{{f}}+ \mathbf{{W}}_{f} \mathbf{{a}}_{R}, \end{aligned}$$

(42a)

$$\begin{aligned} \hat{\mathbf{{p}}} & = {\mathbf{{Y}}} \mathbf{{f}}+ \mathbf{{Y}}_{f} \mathbf{{a}}_{R}, \end{aligned}$$

(42b)

where $\mathbf{{W}}_{f} = \mathbf{{U}}- \mathbf{{W}} \mathbf{{Z}}^{T} \mathbf{{V}}$ and $\mathbf{{Y}}_{f} = \mathbf{{V}}- \mathbf{{Y}} \mathbf{{Z}}^{T} \mathbf{{V}}$. The first two terms on the right-hand side of Eq. (42a) describe the contributions of the rigid-section motion and stress resultants, respectively. The third term describes the effects of inertial forces and can be ignored for beams undergoing low-frequency motion.

Introducing the nodal displacements and their derivatives into Eq. (15b) yields the three-dimensional strain field ${\boldsymbol{\gamma }}= \mathbf{{A}} \mathbf{{N}}(\mathbf{{Z}} \mathbf{{u}} ^{\prime } + \mathbf{{W}} \mathbf{{f}}^{\prime }) + \mathbf{{B}} \mathbf{{N}}( \mathbf{{Z}} \mathbf{{u}}+ \mathbf{{W}} \mathbf{{f}})$. This expression can be simplified with the help of Eqs. (35a)–(35d) and the fact that rigid-body motion creates no strains, $\mathbf{{A}} \mathbf{{N}} \mathbf{{Z}}+ \mathbf{{B}} \mathbf{{N}} \mathbf{{Z}}= \mathbf{{O}}$, to find

$$ {\boldsymbol{\gamma }}= \bigl[ {\mathbf{{A}}} \mathbf{{N}} \bigl( \mathbf{{Z}} \mathbf{{S}}+ \mathbf{{W}} \tilde{\boldsymbol{\kappa }}^{T} \bigr) + \mathbf{{B}} \mathbf{{N}} \mathbf{{W}} \bigr] {\mathbf{{f}}}. $$

(43)

Finally, the three-dimensional stress field is obtained from the constitutive laws as ${\boldsymbol{\tau }}= \mathbf{{D}} {\boldsymbol{\gamma }}$. Introducing the orthogonality condition (28) into Eq. (42a) leads to $\mathbf{{u}}= \mathbf{{Y}}^{T} {\hat{\mathbf{{w}}}}$, which implies that the rigid-section motion is an average of the nodal displacements.

Another approach to validation of the dynamic model is to perform a modal analysis for the reduced one-dimensional model and compare the resulting mode shapes with those obtained from three-dimensional FEM analysis. Furthermore, the three-dimensional stress field recovered from the one-dimensional model can be compared with its counterpart obtained from the three-dimensional model. Such validation will be presented for specific beam problems in Sect. 9.2.

8 Overall analysis strategy

The overall analysis strategy is summarized in this section. In the first step, the sectional analysis uses standard finite element tools to evaluate the Hamiltonian of the system, Eq. (24), based on the stiffness matrices $\mathbf{{M}}$, $\mathbf{{C}}$, and $\mathbf{{E}}$ defined by Eqs. (22a)–(22c). The sectional analysis yields the recovery matrix $\mathbf{{W}}$ defined in Eq. (26), which represents the nodal warping associated with unit sectional stress resultants. The sectional compliance and mass matrices $\mathbf{{S}}$ and $\mathbf{{m}}$ are also provided by the sectional analysis. The second step of the process is a one-dimensional nonlinear analysis of the geometrically exact beam problem defined by Eqs. (35a)–(35d). In the final step, Eq. (43) is used to recover the three-dimensional stress field through a simple matrix multiplication. The inertial forces induced by warping are negligible compared to the inertial forces due to the rigid-section motion, as proved in Sect. 2.1. The secondary warping effects indicated by the matrix $\mathbf{{U}}$ in Eq. (26), $\mathbf{{G}} \mathbf{{a}}_{R}$ in Eq. (35c), and $\mathbf{{W}}_{f}$ in Eq. (42a) are also negligible. The numerical examples presented in Sect. 9 all use this solution procedure.

The proposed methodology presented here provides a unified analysis procedure for complex beam model in flexible multibody dynamics. The assumptions made in the derivations above and their implications are summarized as follows. (1) The beam undergoes large motion, but the strains and warping displacements remain small. (2) The beam undergoes low-frequency motion. For such problems, both of the warping induced inertial forces and the secondary warping resulting from inertial forces can be ignored. (3) Beam properties remain uniform along its span although sectional material properties and geometric configuration are arbitrary. (4) The beam’s span is much larger than a representative dimension of the cross-section. Consequently, the developments focus on the central solution because the contributions of the extremity solutions are negligible away from the beam ends.

9 Numerical examples

To validate the proposed approach, we present a set of numerical examples. The procedure described in the previous section will be used for the solution of the examples.

9.1 Dispersion curves of two typical cross-sections

Figure 3 depicts two cross-sections: (a) a solid section and (b) a box section. The square solid section is of dimension $b = 0.1\mbox{ m}$ and is made of steel with Young’s modulus $E = 207~\mbox{GPa}$, Poisson’s ratio $\nu = 0.3$, and the mass density $\rho_{1} = 7800~\mbox{kg}\,\mbox{m}^{- 3}$. The square box section is of dimension $b = 0.1\mbox{ m}$, and the wall consists of a single ply of graphite/epoxy material of thickness $t_{p} = 0.018\mbox{ m}$. The material mass density is $\rho_{2} = 1600~\mbox{kg}\,\mbox{m}^{- 3}$, and the material stiffness properties are: longitudinal modulus $E_{L} =181~\mbox{GPa}$, transverse modulus $E_{T} = 10.3~\mbox{GPa}$, shearing modulus $G_{\mathit{LT}} = 7.17~\mbox{GPa}$, and Poisson’s ratios $\nu_{\mathit{LT}} = 0.28$ and $\nu_{\mathit{TN}} = 0.33$. The lay-up angle is $30^{\circ }$; $0^{\circ }$ fibers are aligned with the axis of the beam, and a positive ply angle indicates a right-hand rotation about the local outer normal to the wall.

Fig. 3

Configuration of two cross-sections

The proposed approach used meshes of 36 and 20 eight-node two-dimensional elements for the analyses of solid and box cross-sections, respectively. The dispersion curves of the following four beam configurations were investigated: (1) $\mathbf{P} _{1}$: a straight beam with the isotropic solid section, (2) $\mathbf{P}_{2}$: a pretwisted beam ($\mathbf{{k}}^{T} = \{\pi , 0, 0 \}\mbox{ m}^{-1}$) with the isotropic solid section, (3) $\mathbf{P} _{3}$: a straight beam with the heterogeneous box section, and (4) $\mathbf{P}_{4}$: a pretwisted beam ($\mathbf{{k}}^{T} = \{ \pi , 0, 0 \}\mbox{ m}^{-1}$) with the heterogeneous box section.

To generate the dispersion curves, the following procedure was used. The wave numbers are evaluated at discrete frequencies $\omega _{k} = k \Delta \varOmega$, $k = 0, 1, 2, \ldots , N$. The Arnoldi algorithm is used to extract the eigenvalues of the system. For the reduced beam equations, all 12 eigenvalues are extracted; for the three-dimensional model, the 60 eigenvalues with the lowest absolute values are obtained. To draw the dispersion curves, the eigenvalues of the three-dimensional model must be tracked properly. For $k = 0$, the 20 eigenvalues with the lowest norm are retained. For the next frequency, $k = 1$, 20 eigenvalues are selected from the pool of the 60 eigenvalues with the lowest norm. The selection procedure identifies 20 eigenvalues that are in the close neighborhood of those selected at $k= 0$. The distances between the 20 eigenvalues at step $k = 0$ and all the eigenvalues obtained at $k= 1$ are evaluated; the distance is defined as the norm of the difference between the complex wave numbers. The sum of the distances of the 20 eigenvalues selected at $k= 1$ is the smallest for all choices of 20 eigenvalues within the pool of 60. A multiobject tracking algorithm is used for this task. The process then repeats for the successive values of $k$.

The dispersion curves for these four problems are shown in Figs. 4, 5, 6, and 7. The dispersion curves for the one- and three-dimensional beam models were obtained, as presented in Sect. 6. The wave numbers were normalized by the sectional dimension as $bk$, and the frequencies were normalized as $\omega / \varOmega$, where $\varOmega = \sqrt{E/( \rho_{1} b^{2})}$ and $\varOmega = \sqrt{E_{L} / (\rho_{2} b^{2})}$ for the solid and box sections, respectively. Because the eigenvalues appear in groups of four in the form $k = \pm k_{r} \pm j k_{i}$, the figures show the positive real and negative imaginary parts of the wave number only.

Fig. 4

Dispersion curves for beam $\mathbf{P}_{1}$. 1D model: dashed line, 3D model: solid line. Extension–torsion: (◁) and (▷); bending–shearing: (∘), ($\square$), and (×)

Fig. 5

Dispersion curves for beam $\mathbf{P}_{2}$. 1D model: dashed line, 3D model: solid line. Extension–torsion: (◁) and (▷); bending–shearing: (∘), ($\square$), and (×)

Fig. 6

Dispersion curves for beam $\mathbf{P}_{3}$. 1D model: dashed line, 3D model: solid line. Extension–torsion: (◁) and (▷); bending–shearing: (∘), ($\square$), and (×); extremity modes: (⋄)

Fig. 7

Dispersion curves for beam $\mathbf{P}_{4}$. 1D model: dashed line, 3D model: solid line. Extension-torsion: (◁) and (▷); bending-shearing: (∘), ($\square$), and (×); extremity modes: (⋄)

For each mode, the six stress resultants can be evaluated by integrating the out-of-plane stress components over the cross-section. Based on this information, the modes fall into two groups: the first group of modes, called the “extension–torsion” modes, present stress resultants involving extension forces and twisting moments only, the second group of modes, called the “bending–shearing” modes, present stress resultants involving bending moments and shear forces only. For static problems, the twelve modes with vanishing real parts form four Jordan chains [11]. Two chains, each of size two, are associated with deformation modes of the structure when subjected to the unit extension force and torque, respectively. The other two chains, each of size four, capture the deformation modes of the structure-subjected unit bending moments and shear forces in the two transverse directions.

Low-frequency dynamics problems can be viewed as small perturbations of static problems, but for dynamics problems, Luongo [32] pointed out that the Jordan chains break down. The two Jordan chains of length two degenerate into two pairs of real eigenvalues of opposite signs, and the corresponding modes exhibits both extension and torsion for problems $\mathbf{P}_{2}$, $\mathbf{P}_{3}$, and $\mathbf{P}_{4}$. For problem $\mathbf{P}_{1}$, the extension and torsion modes are decoupled. The two chains of length four degenerate into pairs of complex conjugate eigenvalues and two pairs of real eigenvalues of opposite signs, and the corresponding modes exhibit both shearing and bending. The multiplicities of each eigenvalue are listed in Table 1.

Table 1 Multiplicity of the eigenvalues $k$ and their low-frequency limit $b k_{r0} = \lim_{\omega \rightarrow 0} b k_{r} (\omega )$. Nature of the deformation: extension (E), torsion (T), bending (B), shearing (S)

For isotropic beams, problems $\mathbf{P}_{1}$ and $\mathbf{P}_{2}$, the dispersion curves of the one- and three-dimensional models are in close agreement with each other for $\omega / \varOmega \in [0, 2]$ or $\omega \in [0, 103]\mbox{ kHz}$. For composite beams, problems $\mathbf{P} _{3}$ and $\mathbf{P}_{4}$, good agreement is observed for $\omega / \varOmega \in [0, 0.06]$ or $\omega \in [0, 6.38]\mbox{ kHz}$. As frequency increases, one pair of extremity modes, that is, modes with vanishing resultants, becomes dominant because the associated $\operatorname{Im}(k)$ is very small. Clearly, both geometric configuration and material properties affect the range of validity of the one-dimensional beam model. As observed in these examples, the range of validity of the proposed dynamic analysis procedure is far smaller for beams made of anisotropic materials than for those made of isotropic materials. Clearly, the term “low-frequency vibration” must be quantified if it is to be used as a criterion for assessing the accuracy of beam models.

9.2 Modal analysis of a composite beam

To further assess the validity of the proposed beam model in the dynamic regime, a cantilevered composite beam of length $L = 2.0\mbox{ m}$ with the untwisted box section described in Sect. 9.1 was investigated. The proposed approach used 20 eight-node two-dimensional elements for the sectional analysis and 8 four-node one-dimensional elements for the beam analysis. A reference solution was obtained with ABAQUS using 20-node three-dimensional brick elements: 20 elements were used over the cross-section, and 80 along the beam’s span, as depicted in Fig. 8. Sectional analysis provides the beam’s mass properties as $m_{00} = 9.446~\mbox{kg}/\mbox{m}$ and $m_{22} = 0.01096~\mbox{kg}\,\mbox{m}$. The predicted sectional stiffness matrix is

$$ \frac{\mathbf{{S}}^{*-1}}{10^{5}} = \left[\textstyle\begin{array}{c@{\quad}c@{\quad}c@{\quad}c@{\quad}c@{\quad}c} 3840 & 0 & 0 & -66.71 & 0 & 0\\ 0 & 626.6 & 0 & 0 & 37.11 & 0\\ 0 & 0 & 626.6 & 0 & 0 & 37.11\\ - 66.71 & 0 & 0 & 2.246 & 0 & 0\\ 0 & 37.11 & 0 & 0 & 4.573 & 0\\ 0 & 0 & 37.11 & 0 & 0 & 4.573 \end{array}\displaystyle \right] , $$

(44)

where units of the entries are as follows: $\mbox{N}\,\mbox{m}^{-1}$ for $i, j = 1, 2, 3$, $\mbox{N}\,\mbox{m}$ for $i, j = 4, 5, 6$, and $N$ for the other entries. Material anisotropy causes extension–twisting and shearing–bending coupling to arise, resulting in the off-diagonal terms of the sectional stiffness matrix.

Fig. 8

Configuration of the composite box

As discussed in Sect. 5, the distributed inertial forces generate secondary warping characterized by the matrix $\mathbf{{G}}$ appearing in Eq. (30), and such effects are usually negligible. These arguments can be validated by evaluating the matrix $\mathbf{{G}}$ and noticing that the magnitude of this matrix is 3 to 4 orders smaller than the mass matrix $\mathbf{{m}}$ for this example.

Modal analysis was performed for both the proposed and ABAQUS models. Table 2 lists the first seven bending modes predicted by the two models; good correlation is observed between the two sets of predictions. Each natural frequency in bending listed in the table has two associated bending modes with eigenvectors in two orthogonal planes. In most cases, the natural frequencies predicted by the beam model were slightly lower than those predicted by the ABAQUS model. This stems from a difference in the boundary conditions: for the ABAQUS model, all displacement components at all nodes of the root section are constrained, whereas for the proposed model, average sectional displacement is constrained, but warping is allowed. Consequently, the beam model is more compliant than its three-dimensional counterpart, resulting in lower frequencies.

Table 2 Eigenvalues for the bending modes (Hz)

The bending mode shapes associated with the natural frequencies listed in Table 2 are depicted in Figs. 9 to 15. Each figure shows the two mode shapes predicted by the beam model (dashed lines) and the ABAQUS model (solid lines).

Fig. 9

First bending mode shapes: beam model, dashed line; ABAQUS model, solid line

Fig. 10

Second bending mode shapes: beam model, dashed line; ABAQUS model, solid line

Fig. 11

Third bending mode shapes: beam model, dashed line; ABAQUS model, solid line

Fig. 12

Fourth bending mode shapes: beam model, dashed line; ABAQUS model, solid line

Fig. 13

Fifth bending mode shapes: beam model, dashed line; ABAQUS model, solid line

Fig. 14

Sixth bending mode shapes: beam model, dashed line; ABAQUS model, solid line

Fig. 15

Seventh bending mode shapes: beam model, dashed line; ABAQUS model, solid line

Table 3 lists the first six torsion modes predicted by the two models; good correlation is observed between the two sets of predictions. The corresponding mode shapes are depicted in Figs. 16 to 21; for clarity of the figures, only the twist angle $\theta_{1}$ is shown, although other displacement and rotation components do not vanish due to elastic coupling terms; see Eq. (44).

Fig. 16

First torsion mode shapes: beam model, dashed line; ABAQUS model, solid line

Fig. 17

Second torsion mode shapes: beam model, dashed line; ABAQUS model, solid line

Fig. 18

Third torsion mode shapes: beam model, dashed line; ABAQUS model, solid line

Fig. 19

Fourth torsion mode shapes: beam model, dashed line; ABAQUS model, solid line

Fig. 20

Fifth torsion mode shapes: beam model, dashed line; ABAQUS model, solid line

Fig. 21

Sixth torsion mode shapes: beam model, dashed line; ABAQUS model, solid line

Table 3 Eigenvalues for the torsion modes (Hz)

As a final validation effort, the distributions of axial stress component over the cross-section at $\alpha_{1}= 1.6~\mbox{m}$ were evaluated. The distributions associated with the first bending mode are shown in Figs. 22 and 23 for the proposed and ABAQUS models, respectively. Figures 24 and 25 show the corresponding results for the seventh bending mode. Excellent correlation is observed for the first mode, whereas differences appear for the seventh mode. Indeed, as frequency increases, beam theory becomes less accurate. For this specific problem, the magnitudes of warping induced by distributed inertial forces $\mathbf{{W}}_{f} {\mathbf{{a}}}_{R}$ (see Eq. (42a)) are 2 to 3 orders smaller than those due to stress resultants $\mathbf{{W}} \mathbf{{f}}$. In many practical applications, the excitation amplitudes of the high-frequency modes are far smaller than those of the low-frequency modes, and hence, only the latter need to be known accurately. The proposed approach is ideally suited for such cases because it then provides an efficient and accurate solution of the problem.

Fig. 22

Axial stress component $\sigma_{11}$, the distribution for the 1st bending mode at $\alpha_{1} = 1.6\mbox{ m}$, beam model

Fig. 23

Axial stress component $\sigma_{11}$, the distribution for the 1$\mathrm{st}$ bending mode at $\alpha_{1} = 1.6\mbox{ m}$, ABAQUS model

Fig. 24

Axial stress component $\sigma_{11}$, the distribution for the 7th bending mode at $\alpha_{1} = 1.6\mbox{ m}$, beam model

Fig. 25

Axial stress component $\sigma_{11}$, the distribution for the 7$\mathrm{th}$ bending mode at $\alpha_{1} = 1.6\mbox{ m}$, ABAQUS model

9.3 The four-bar mechanism

The last example deals with a multibody dynamics application: the flexible four-bar mechanism shown in Fig. 26 is investigated. Bar 1 is of length 0.12 m and is connected to the ground at point A by means of a revolute joint. Bar 2 is of length 0.24 m and is connected to bar 1 at point B with a revolute joint. The cross-section of bar 2 is pretwisted uniformly by $2\pi$ along its axial line. Finally, bar 3 is of length 0.12 m and is connected to bar 2 and the ground at points C and D, respectively, by means of two revolute joints. Bars 1 and 2 are of square cross-section of size 16 by 16 mm; bar 3 has a square cross-section of size 8 by 8 mm. The three bars are made of steel: Young’s modulus $E =207~\mbox{GPa}$ and Poisson’s ratio $\nu = 0.3$. This benchmark problem has been treated by numerous researchers [33].

Fig. 26

Configuration of the four-bar mechanism

In the reference configuration, the bars of this mechanism intersect each other at 90 degree angles, and the axes of rotation of the revolute joints at points A, B, and D are normal to the plane of the mechanism. The axis of rotation of the revolute joint at point C is rotated by $+5$ degrees about the unit vector $\mathbf{{i}}_{2}$ indicated in Fig. 26 to simulate an initial defect in the mechanism. The angular velocity at point A of bar 1 is prescribed as

$$ \varOmega (t) = \textstyle\begin{cases} 0.3 [ 1 - \cos ( \pi t ) ] ~\mbox{rad}/\mbox{s}, & 0 \le t \le 1~\mbox{s}, \\ 0.6~\mbox{rad}/\mbox{s}, & t \ge 1~\mbox{s}. \end{cases} $$

(45)

For reference, a full three-dimensional FEM analysis was performed using ABAQUS. The two end-sections of each bar were enforced to remain rigid using multipoint constraints in ABAQUS. The four revolute joints are modeled using connector elements in ABAQUS. The meshes used in the proposed approach and ABAQUS are summarized in Table 4. The computational costs for both the proposed and ABAQUS analyses are also shown Table 4. In both cases, the main cost per iteration is the factorization of the stiffness matrix, which can be estimated [34] as $C \propto nm^{2}$, where $n$ is the size of the stiffness matrix, and $m$ its average half-bandwidth. The cost for sectional analysis is negligible because it is performed once only at the onset of the simulation, as discussed in Sect. 8. For this example, the proposed approach is four orders of magnitude more efficient than three-dimensional FEM analysis.

Table 4 Meshes in the proposed and ABAQUS analyses

The sectional analysis yielded the following sectional mass properties: $m_{00} = 1.9968$ and 0.4992 kg/m for bars 1 and 2 and for bar 3, respectively, and the corresponding mass moments of inertia per unit span are $m_{22} = 42.598$ and $2.6624~\mbox{mg}\,\mbox{m}^{2}/\mbox{m}$, respectively. The entries of the sectional stiffness matrix are denoted $C_{ij}$, and the nonvanishing entries are listed in Table 5. Due to the pre-twist of bar 2, extension–twisting and shearing–bending coupling terms appear, resulting in the off-diagonal entries $C_{14} = 8255.7~\mbox{N}\,\mbox{m}$ and $C_{25} = C_{36} = - 5204.0~\mbox{N}\,\mbox{m}$.

Table 5 Predicted sectional stiffness property

The simulation was run for 36 s, starting from initial conditions at rest. The time step sizes for the proposed and ABAQUS analyses were $\Delta t = 4$ and $2\mbox{ ms}$, respectively. For the beam analysis, larger time step sizes could be used without compromising accuracy significantly; ABAQUS did not converge for time step sizes $\Delta t > 2\mbox{ ms}$. Figures 27 and 28 show the axial force $F_{1}$ along the unit vector $\mathbf{{b}}_{1}$ and the bending moment $M_{2}$ about the unit vector $\mathbf{{b}}_{2}$, respectively, at point A of bar 1, for the proposed and ABAQUS models. Due to the small size of the brick elements, high-frequency numerical oscillations are observed in the ABAQUS simulation. For this problem, the largest entries of the matrix $\mathbf{{G}}$ are about 3 to 4 orders smaller than their counterparts in the matrix $\mathbf{{m}}$. Consequently, the associated inertial terms in Eq. (30) have negligible effect on the beam solutions.

Fig. 27

Reaction force $F_{1}$ at joint A. Proposed: dashed line; ABAQUS: thinner solid line

Fig. 28

Reaction force $M_{2}$ at joint A. Proposed: dashed line; ABAQUS: thinner solid line

The distributions of axial and shear stress components $\sigma_{11}$ and $\sigma_{13}$, respectively, over the cross-section of bar 2 at 0.08 m from point B were evaluated at time $t = 9.12~\mbox{s}$ using the beam and ABAQUS models and are shown in Fig. 29. The corresponding results for the cross-section of bar 2 at 0.16 m from point B were evaluated at time $t =30~\mbox{s}$ and are shown in Fig. 30. The beam model agrees well with the three-dimensional ABAQUS predictions. For this problem, the magnitudes of warping induced by distributed inertial forces (the term $\mathbf{{W}}_{f} {\mathbf{{a}}}_{R}$ in Eq. (42a)) are 2 orders smaller than those of warping due to stress resultants $\mathbf{{W}} \mathbf{{f}}$. Consequently, secondary warping has little effect on the three-dimensional stress distributions.

Fig. 29

Distribution of the stress component over cross-section at $\alpha_{1}= 0.08\mbox{ m}$ at time $t = 9.12\mbox{ s}$

Fig. 30

Distribution of the stress component over cross-section at $\alpha_{1} = 0.16\mbox{ m}$, at time $t = 30~\mbox{s}$

10 Conclusions

Most beam theories have been developed for application to dynamic problems, yet surprisingly little attention has been devoted to inertial effects. Warping deformation is known to affect sectional stiffness and stress distributions significantly and, hence, is included in the evaluation of the strain energy. On the other hand, cross-sections are assumed to remain rigid when evaluating the kinetic energy.

This paper has assessed the validity of beam theory proposed by the authors when applied to dynamic problems by answering two questions: (1) what is the warping field induced by inertial forces and (2) what is the effect of the secondary warping induced by the distributed inertial forces of the beam’s sectional stiffness and three-dimensional stress distributions?

Dispersion curves provide a powerful tool for describing the dynamic behavior of structures. To validate the proposed model, dispersion curves were computed for straight and pretwisted beams made of isotropic or anisotropic materials. In all cases, the dispersion curves computed by the proposed beam models were found to be in good agreement with those obtained from three-dimensional models in the low-frequency range. These examples show that the term “low-frequency warping” must be defined precisely: the beam’s geometric configuration and the nature of the materials it is made of alter the range of validity of the model.

The inertial forces induced by warping deformation were proved to be negligible compared to elastic forces. Numerical examples were used to assess the importance of secondary warping. For low-frequency warping, the effects of secondary warping were found to be negligible. To further assess the accuracy of the proposed model, the twenty lowest modes of a cantilevered beam-like structure were computed using both beam and three-dimensional models. The frequencies, mode shapes, and associated stress distributions predicted by the two models were found to be in good agreement.

With the proposed approach, the nonlinear dynamic three-dimensional equations of beams are decomposed into a linear sectional analysis and a nonlinear one-dimensional analysis along the beam’s span. The proposed approach can be integrated into the existing nonlinear beam models easily. It provides the beam’s sectional stiffness matrix that includes the effect of warping deformation. Furthermore, it enables the accurate evaluation of three-dimensional stress fields. The complete process is three to four orders of magnitude more computationally efficient than three-dimensional finite element analysis.