1 Introduction

Nonlinear evolution equations (NLEEs) have important applications in plasma physics, ocean dynamics, physiology, biology and other fields [1,2,3,4], and a lot of researchers have been engaged in exploring exact solutions of these equations. Among these solutions, the soliton solution is given by the exponential function which is exponentially localized in a certain direction, while the lump solution is expressed by the rational function which is localized in all directions in the space. Over the years, researchers have discovered many powerful methods for these solutions, such as the Hirota bilinear method [5], the inverse scattering method [6], the Bäcklund transform [7] and the Darboux transform [8, 9]. Recently, Ma has proposed a direct method to obtain the lump solution of the Kadomtsev–Petviashvili (KP) equation [10]. Soon later, many lump and interaction solutions of NLEEs were successfully obtained by symbolic computation [11,12,13,14,15,16,17,18,19,20,21,22]. Up to now, most of lump and interaction solutions are investigated only for NLEEs with constant coefficients. There are few studies concerning NLEEs with variable coefficients. However, when the media are inhomogeneous and/or the boundaries are nonuniform, the variable-coefficient NLEEs are able to model various situations more realistically than the constant-coefficient one [23,24,25,26]. In this work, we will focus on the generalized variable-coefficient KP (vcKP) equation

$$\begin{aligned} P_\mathrm{vcKP}(u):= & {} (u_t+f(t)uu_x+g(t)u_{xxx})_x+l(t)u_x\nonumber \\&+\,m(t)u_{yy}+n(t)u_{xy}+q(t)u_{xx}=0,\nonumber \\ \end{aligned}$$
(1)

where \(f(t)\ne 0,g(t)\ne 0,l(t),m(t),n(t),q(t)\) are all arbitrary functions of t and represent the nonlinearity, dispersion, perturbed effect, and disturbed wave velocity along the y direction, respectively. The vcKP equation (1) can describe many physical phenomena, such as long waves in turbulent flow over a sloping bottom [27], long waves on the surface of a three-dimensional fluid domain bounded below by slowly varying topography [28], and surface waves propagation in shallow seas and marine straits with varying depth and width [29, 30]. General line and parabola solitons of the vcKP equation (1) have recently been constructed for two-temperature ions in dusty plasma and the shallow water wave in fluids [31,32,33]. Indeed, the vcKP equation (1) contains several KP models with variable coefficients which appear in various branches of physics, including Korteweg-de Vries (KdV) equation, cylindrical KdV equation, KP equation and cylindrical KP equation. Some integrable properties of Eq. (1), namely the Bäcklund transformation, the bilinear form, the multi-soliton solution, the Grammian solution, and the Lax pair have been deduced [26, 34]. However, to our knowledge, the lump solution and the interaction solution of the vcKP equation (1) have not yet been given.

As mentioned above, the Hirota bilinear method [5] is direct and effective for constructing exact nonlinear wave solutions, in which the given nonlinear equation is converted to the bilinear form for the auxiliary variable through the appropriate transformation. With the different types of ansatz for the auxiliary function, a variety of such as soliton, rational, and periodic solutions can be derived. This kind of technique usually involves a lot of tedious algebraic computations, but the symbolic computation softwares such as Maple and Mathematica could quickly deal with this. More specifically, when the ansatz is taken as the quadratic function and the combination of quadratic and exponential functions, lump and lump–soliton interaction solutions were presented for various NLEEs such as the (\(2+1\))-dimensional KP equation [10, 11, 35], reduced p-gKP and p-gBKP equations [12], generalized KP-Boussinesq equation [14], BKP equation [16], generalized KdV equation [20, 22], generalized KP equation [36], Ito equation [19], and the (\(3+1\))-dimensional Jimbo–Miwa equation [18]. Until now, this treatment is only applied to the constant-coefficient equation, in which by vanishing the coefficients of variables x, y, z and t , one just need to solve a set of algebraic equations. However, when the original model is a variable-coefficient equation, we have to modify this kind of direct method. For example, there are several arbitrary functions of t in the (\(2+1\))-dimensional vcKP equation (1). Hence, the ansatz is changed as one including the functions of t, and only the coefficients of variables x and y are required to be zero, which yields a mixed system of algebraic equations and ordinary differential equations. With the aid of symbolic computation, solving this system leads to exact solutions with some constraint conditions. These solutions usually exhibit more abundant properties than ones in the constant-coefficient case.

The structure of this work is as follows. In Sect. 2, the bilinear form of Eq. (1) is given, and then the auxiliary function is taken as a positive quadratic function to construct the lump solution. In Sect. 3, the positive quadratic function is combined with the exponential function to derive the interaction solution of lump and line solitons. In Sect. 4, by combining the positive quadratic function with the hyperbolic cosine function, the interaction solution between the lump and the linear soliton pair is obtained. Conclusions are given in last section.

2 Lump solution

For the vcKP equation (1), it has a truncated Painlevé expansion [37],

$$\begin{aligned} u=\frac{u_0}{\phi ^2}+\frac{u_1}{\phi }+u_2, \end{aligned}$$
(2)

where \(\phi \), \(u_0\), \(u_1\), \(u_2\) are functions of x, y, t. Substituting (2) into the vcKP equation (1) and collecting the coefficients of \(\phi ^{-6}\) and \(\phi ^{-5}\) yields

$$\begin{aligned} \phi ^{-6}: u_0= -\frac{12g(t)\phi ^2_x}{f(t)},\ \ \phi ^{-5}: u_1=\frac{12g(t)\phi _{xx}}{f(t)}. \end{aligned}$$
(3)

If we take \(u_2=0\), solution (2) can be rewritten as

$$\begin{aligned} u=-\frac{12\phi ^2_xg(t)}{f(t)\phi ^2} +\frac{12g(t)\phi _{xx}}{f(t)\phi }=12\frac{g(t)}{f(t)}(\ln \phi )_{xx},\nonumber \\ \end{aligned}$$
(4)

which leads to the bilinear form of vcKP equation (1):

$$\begin{aligned} B_\mathrm{vcKP}(\phi ):= & {} (D_xD_t+g(t)D^4_x+q(t)D^2_x +n(t)D_xD_y\nonumber \\&+\,m(t)D^2_y)\phi \cdot \phi =0, \end{aligned}$$
(5)

with the conditions

$$\begin{aligned} g(t)=g_0f(t)\text {e}^{-\int l(t)\mathrm{d}t},m(t)=m_0f(t)\text {e}^{-\int l(t)\mathrm{d}t}.\nonumber \\ \end{aligned}$$
(6)

Here \(g_0\) and \(m_0\) are two arbitrary nonzero constants, and the Hirota bilinear operators \(D_x\), \(D_y\) and \(D_t\) in Eq. (5) are defined as [38]

$$\begin{aligned}&D^\alpha _x D^\beta _y D^\gamma _t(f\cdot g)\\&\quad =\bigg ( \frac{\partial }{\partial x} - \frac{\partial }{\partial x'} \bigg )^\alpha \bigg ( \frac{\partial }{\partial y} - \frac{\partial }{\partial y'} \bigg )^\beta \\&\qquad \bigg ( \frac{\partial }{\partial t} - \frac{\partial }{\partial t'} \bigg )^\gamma f(x,y,t)g(x',y',t')\bigg |_{x=x',y=y',t=t'}. \end{aligned}$$
Fig. 1
figure 1

Profiles of the lump solution (20): a three-dimensional graph at \(t=0\); b three-dimensional graph at \(x=0\); c three-dimensional graph at \(y=0\)

Full size image

The transformation (4) is also a characteristic transformation of the Bell polynomial theory of soliton equation [39, 40], and the vcKP equation (1) has a relationship with the bilinear equation (5),

$$\begin{aligned} P_\mathrm{vcKP}(u)=6\frac{g(t)}{f(t)} \bigg (\frac{B_\mathrm{vcKP}(\phi )}{\phi ^2} \bigg )_{xx}. \end{aligned}$$
(7)

Therefore, if \(\phi \) is solved from the bilinear vcKP equation (5), then the transformation (4) gives rise to a solution of the vcKP equation (1).

To search for the lump solution of the vcKP equation in Eq. (5), we start with

$$\begin{aligned} \phi= & {} h^2+k^2+a_7, \ \ h=a_1x+a_2y\nonumber \\&+\int s_1(t)\mathrm{d}t+a_3, \ \ k=a_4x+a_5y\nonumber \\&+\int s_2(t)\mathrm{d}t+a_6, \end{aligned}$$
(8)

where \(a_i (i=1,2\ldots 7)\) are real parameters, and \(s_i(t)(i=1,2)\) are two functions of t, they will be determined later. Substituting (8) into the bilinear vcKP equation (5), and taking all coefficients of the different polynomials of x and y be zero, then solving a set of algebraic equations for \(s_i(t)(i=1,2)\) and \(a_7\) gives the following parameters’ relations:

$$\begin{aligned} s_1(t)= & {} \frac{(a_1a^2_5-a_1a^2_2-2a_2a_4a_5)m(t)}{a^2_1+a^2_4}\nonumber \\&-\,a_2n(t)-a_1q(t), \nonumber \\ s_2(t)= & {} \frac{(a^2_2a_4-a_4a^2_5-2a_1a_2a_5)m(t)}{a^2_1+a^2_4} -a_5n(t)\nonumber \\&-\,a_4q(t), \nonumber \\ a_7= & {} -\frac{3g_0(a^2_1+a^2_4)^3}{m_0(a_1a_5-a_2a_4)^2}, \end{aligned}$$
(9)

which need to meet the following conditions

$$\begin{aligned}&(a)~a^2_1+a^2_4\ne 0, \ \ (b)~m_0g_0< 0, \nonumber \\&(c)~\varDelta :=(a_1a_5-a_2a_4)=\left| \begin{array}{cc} a_1 &{} a_2 \\ a_4 &{} a_5 \end{array}\right| \ne 0. \end{aligned}$$
(10)

Then a set of positive quadratic function solutions of the bilinear vcKP equation (5) can be obtained as follows:

$$\begin{aligned} \phi= & {} \bigg [a_1x+a_2y+\int \bigg (\frac{(a_1a^2_5-a_1a^2_2-2a_2a_4a_6)m(t)}{a^2_1+a^2_4}\nonumber \\&-a_2n(t)-a_1q(t) \bigg )\mathrm{d}t+a_3\bigg ]^2\nonumber \\&+\bigg [a_4x+a_5y+\int \bigg (\frac{(a^2_2a_4-a_4a^2_5-2a_1a_2a_5)m(t)}{a^2_1+a^2_4}\nonumber \\&-a_5n(t)-a_4q(t) \bigg )\mathrm{d}t+a_6 \bigg ]^2 -\frac{3g_0(a^2_1+a^2_4)^3}{m_0(a_1a_5-a_2a_4)^2}.\nonumber \\ \end{aligned}$$
(11)

Further, we get a class of lump solutions of the vcKP equation (1)

$$\begin{aligned} u=-\frac{48g(t)(a_1h+a_4k)^2}{f(t)\phi ^2} +\frac{24g(t)(a^2_1+a^2_4)}{f(t)\phi },\nonumber \\ \end{aligned}$$
(12)

where the functions h and k are defined by

$$\begin{aligned} h= & {} a_1x+a_2y+\int \bigg (\frac{(a_1a^2_5-a_1a^2_2-2a_2a_4a_6)m(t)}{a^2_1+a^2_4}\nonumber \\&-\,a_2n(t)-a_1q(t) \bigg )\mathrm{d}t+a_3, \end{aligned}$$
(13)
$$\begin{aligned} k= & {} a_4x+a_5y+\int \bigg (\frac{(a^2_2a_4-a_4a^2_5-2a_1a_2a_5)m(t)}{a^2_1+a^2_4}\nonumber \\&-\,a_5n(t)-a_4q(t) \bigg )\mathrm{d}t+a_6. \end{aligned}$$
(14)

In this class of lump solutions, the arbitrary parameters \(a_i (i=1\ldots 6)\) need to satisfy (10) to ensure that the solution (12) is well defined. The condition (c) leads to \(a_1a_4\ne 0\) or \(a^2_1+a^2_4\ne 0\). The lump solution u in (12) is analytic if and only if \(a_7>0\), that is to say, the conditions \(a_1a_5-a_2a_4\ne 0\) and \(m_0g_0<0\) guarantees both analyticity and localization of the solutions in the (x, y)- plane. For any given time t, the lump solution u approaches 0 if and only if \(h^2+k^2\rightarrow +\infty \), or equivalently, \(x^2+y^2\rightarrow +\infty \). In order to describe the moving path of the lump, let \(u_x=u_y=0\), all the critical points of u can be calculated as below

$$\begin{aligned} x= & {} \frac{a_2(a_6+\int s_2(t)\mathrm{d}t)-a_5(a_3+\int s_1(t)\mathrm{d}t)}{a_1a_5-a_2a_4}, \nonumber \\ y= & {} \frac{a_4(a_3+\int s_1(t)\mathrm{d}t)-a_1(a_6+\int s_2(t)\mathrm{d}t)}{a_1a_5-a_2a_4}, \end{aligned}$$
(15)

and

$$\begin{aligned} x= & {} \pm \sqrt{\frac{3a_7}{a^2_1+a^2_4}}\nonumber \\&-\frac{a_5(a_3+\int s_1(t)\mathrm{d}t)-a_2(a_6+\int s_2(t)\mathrm{d}t)}{a_1a_5-a_2a_4}, \end{aligned}$$
(16)
$$\begin{aligned} y= & {} \frac{a_4(a_3+\int s_1(t)\mathrm{d}t)-a_1(a_6+\int s_2(t)\mathrm{d}t)}{a_1a_5-a_2a_4}. \end{aligned}$$
(17)

Then one can find moving velocity of the lump

$$\begin{aligned} V=\sqrt{\frac{(a_2s_2(t)-s_1(t)a_5)^2+(a_1s_2(t)-s_1(t)a_4)^2}{(a_1a_5-a_2a_4)^2}},\nonumber \\ \end{aligned}$$
(18)

and the maximum and minimum amplitudes

$$\begin{aligned} A_\mathrm{max}= & {} -\frac{8m_0\text {e}^{-\int l(t)\mathrm{d}t}(a_1a_5-a_2a_4)^2}{(a^2_1+a^2_4)^2},\nonumber \\ A_\mathrm{min}= & {} \frac{m_0\text {e}^{-\int l(t)\mathrm{d}t}(a_1a_5-a_2a_4)^2}{(a^2_1+a^2_4)^2}. \end{aligned}$$
(19)

In order to analyze the propagation characteristics of the lump more specifically, four illustrated examples are listed to show more abundant structure due to the existence of variable coefficients in the vcKP equation (1).

For the first example, we choose the following functions and parameters,

$$\begin{aligned}&a_1=1,a_2=2,a_3=0,a_4=1,a_5=-1,a_6=0,\\&g(t)=1,m(t)=-1,f(t)=6,l(t)=0,\\&n(t)=0,q(t)=0. \end{aligned}$$

This trivial case corresponds to the classical KP equation [10] and the lump solution reads

$$\begin{aligned} u = -\frac{48(12x^2+12xy-48xt-24y^2-78yt+21t^2-16)}{(12x^2+12xy-48xt+30y^2 + 30yt+75t^2+16)^2}.\nonumber \\ \end{aligned}$$
(20)

Figure 1a–c displays the lump (20) at time \(t=0\), and \(x=0\), \(y=0\), respectively. This lump moves along the straight line \(y=-\frac{2}{5}x\) with the velocity \(v=\frac{\sqrt{29}}{2}\), and the maximum and minimum amplitudes are 3 and \(-\frac{3}{8}\), respectively.

For the second example, by selecting the functions and parameters as

$$\begin{aligned}&a_1=1,a_2=2,a_3=0,a_4=1,a_5=-1,a_6=0,\\&g(t)=6t,m(t)=-6t,f(t)=6t,l(t)=0,n(t)=t,q(t)=t, \end{aligned}$$

we can obtain the following lump solution

$$\begin{aligned} u = -\frac{2304(6x^2+6xy-81xt^2-12y^2-108yt^2+189t^4-8)}{(24x^2 + 24xy - 324xt^2 + 60y^2 + 108yt^2 + 1431t^4 + 32)^2}.\nonumber \\ \end{aligned}$$
(21)

Figure 2a–c exhibits the lump (21) at time \(t=0\), and \(x=2\), \(y=2\), respectively. This lump moves along the straight line \(y=-\frac{5}{16}x\) with the velocity \(v=\sqrt{281}t\), and the maximum and minimum amplitudes are 18 and \(-\frac{9}{4}\), respectively.

Fig. 2
figure 2

Profiles of the lump solution (21): a three-dimensional graph at \(t=0\); b three-dimensional graph at \(x=2\); c three-dimensional graph at \(y=2\)

Full size image

The functions and parameters in the third example are taken as

$$\begin{aligned}&a_1=1,\ \ a_2=2,\ \ a_3=0,\ \ a_4=1,\ \ a_5=-1,\\&a_6=0,\ \ g(t)=\cos (t),\\&m(t)=-\cos (t),\ \ f(t)=\cos (t),\ \ l(t)=0,\\&n(t)=\cos (t),\ \ q(t)=\cos (t). \end{aligned}$$

Then one can get the lump solution

$$\begin{aligned} u=-\frac{288(12x^2+12xy-84x\sin (t)-24y^2-42y\sin (t)+147\sin ^2(t)-16)}{(12x^2+12xy-84x\sin (t)+30y^2-42y\sin (t)+147\sin ^2(t)+16)^2}. \end{aligned}$$
(22)

Figure 3a–c illustrates the lump (22) at time \(t=0\), and \(x=0\), \(y=0\), respectively. This lump moves along the straight line \(y=0\) with the velocity \(v=\frac{7\cos (t)}{2}\), and the maximum and minimum amplitudes are 18 and \(-\frac{9}{4}\), respectively.

Fig. 3
figure 3

Profiles of the lump solution (22): a three-dimensional graph at \(t=0\) ; b three-dimensional graph at \(x=0\); c three-dimensional graph at \(y=0\)

Full size image

For the last example, the functions and parameters are selected as follows:

$$\begin{aligned}&a_1=1,a_2=-2,a_3=0,a_4=-2,a_5=1,\\&a_6=0,g(t)=6t,m(t)=-6t,f(t)=6t,\\&l(t)=0,n(t)=t^2,q(t)=t^2, \end{aligned}$$

which yields the lump solution

$$\begin{aligned} u=\frac{216[t^4(200t^2 + 7110t + 42687)-150xt^2(63-5t) -30yt^2(396 + 65t)-25(225x^2 + 63y^2-360xy-1875)]}{[t^4(10t^2 + 234t + 2025) + 3xt^2(126-10t)-30yt^2(36+t) + 225(x^2+y^2)-360xy+1875]^2}. \end{aligned}$$
(23)

Figure 4a–c shows the lump (23) at time \(t=0\), and \(x=0\), \(y=1\), respectively. This lump moves along the track \(l_0\): \(x=3t^2+\frac{t^3}{3},y=\frac{24t^2}{5}+\frac{t^3}{3}\) with the velocity \(v=\sqrt{2t^2+\frac{156}{5}t+\frac{3204}{25}}t\), and the maximum and minimum amplitudes are \(\frac{72}{25}\) and \(-\frac{9}{25}\), respectively.

Fig. 4
figure 4

Profiles of the lump solution (23): a three-dimensional graph at \(t=0\) ; b three-dimensional graph at \(x=0\); c three-dimensional graph at \(y=1\)

Full size image

In above four examples, the first one represents the classical constant-coefficient KP equation. Hence it gives a traditional lump which moves along the straight line with the fixed velocity. But the last three examples involve the KP equation with the variable-coefficient case, the lumps exhibit some novel characteristics. More specifically, one can see that the velocity, moving path and maximum height of the lump are completely characterized by the time functions. This suggests that the lump solution in the vcKP equation is able to model more various nonlinear phenomena.

3 Interaction solution between a lump and one line soliton

In soliton theory, soliton collision is an important phenomenon. It is known that the lump will keep its shape, velocity, and amplitude after the collision with the soliton solution, which means that the collision is completely elastic [41, 42]. However, for some integrable equations, the interactions are not completely elastic [43,44,45]. In this section, we consider the interaction solution between a lump and one line soliton of the vcKP equation (1). To this end, we redefine the function \(\phi \) as follows

$$\begin{aligned} \phi= & {} h^2+k^2+a_7+a_0e^\xi ,\ \ h=a_1x+a_2y\nonumber \\&+\int s_1(t)\mathrm{d}t+a_3,\ \ k=a_4x+a_5y+\int s_2(t)\mathrm{d}t\nonumber \\&+\,a_6,\ \ \xi =k_1x+k_2y+\int \omega _1(t)\mathrm{d}t, \end{aligned}$$
(24)

where \(a_i(i=0,1\ldots 7)\) and \(k_i(i=1,2)\) are real parameters, and \(s_1(t)\), \(s_2(t)\), and \(\omega _1(t)\) are three functions of t, they will be determined later. It is obvious that the rational function and the exponential function correspond to a lump and one line soliton, respectively. More specifically, the exponential term is dominant if \(\xi \gg 0\) and one line soliton exists, while the rational term is dominant if \(\xi \ll 0\) and the lump appears. Substituting (24) into the bilinear vcKP equation (5), one can derive the parameters’ relations:

Fig. 5
figure 5

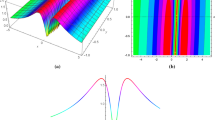
Profiles of the interaction solution (29): a–d are three-dimensional graphs at time \(t=-\,2, t=-\,1, t=0, t=3,\) respectively

Full size image
$$\begin{aligned}&k_1=\frac{\sqrt{-\frac{m_0}{3g_0}}(a_1a_5-a_2a_4)}{a^2_1+a^2_4},\nonumber \\&k_2=\frac{\sqrt{-\frac{m_0}{3g_0}} (a_1a_5-a_2a_4)(a_1a_2+a_4a_5)}{(a^2_1+a^2_4)^2},\nonumber \\&s_1(t)=\frac{(a_1a^2_5-a_1a^2_2-2a_2a_4a_5)m(t)}{a^2_1+a^2_4}\nonumber \\&\quad -a_2n(t)-a_1q(t), \nonumber \\&s_2(t)=\frac{(a^2_2a_4-a_4a^2_5-2a_1a_2a_5)m(t)}{a^2_1+a^2_4}\nonumber \\&\quad -a_5n(t)-a_4q(t), \nonumber \\&\omega _1(t)=-\frac{k_1^2[g(t)k_1^2 +q(t)]+k_2[k_2m(t)+ n(t)k_1]}{k_1}, \nonumber \\&a_7=-\frac{3g_0(a^2_1+a^2_4)^3}{m_0(a_1a_5-a_2a_4)^2}. \end{aligned}$$
(25)

These parameters need to satisfy the following conditions

$$\begin{aligned}&(a)~a_1a_4\ne 0, \ \ (b)~a_1a_5-a_2a_4\ne 0, \nonumber \\&(c)~m_0g_0<0, \ \ (d)~a_0>0. \end{aligned}$$
(26)

The interaction solution of u can be written as

$$\begin{aligned} u= & {} -\frac{12g(t)(2a_1h+2a_4k+a_0k_1e^\xi )^2}{f(t)\phi ^2}\nonumber \\&+\frac{12g(t)(2a^2_1+2a^2_4+a_0k^2_1e^\xi )}{f(t)\phi }; \end{aligned}$$
(27)

the condition (26) guarantees that the solution (27) is well defined. To study the interaction solution in detail, we choose the following set of parameters

$$\begin{aligned}&a_0=1,\ \ a_1=1,\ \ a_2=1,\ \ a_3=1,\ \ \nonumber \\&a_4=1,\ \ a_5=-1,\ \ a_6=1,\ \ a_7=3, \nonumber \\&g(t)=6t,\ \ m(t)=-12t,\ \ f(t)=6t,\nonumber \\&l(t)=0,\ \ n(t)=t,\ \ q(t)=t, \nonumber \\&s_1(t)=-14t,\ \ s_2(t)=-12t,\ \ \omega _1(t)=\frac{5\sqrt{6}t}{3},\nonumber \\&k_1=-\frac{\sqrt{6}}{3},\ \ k_2=0, \end{aligned}$$
(28)

which gives rise to the interaction solution

$$\begin{aligned} u= & {} \frac{8e^\xi [2x^2+2y^2+(85t^2-26x-2y-26\sqrt{6}-26)t^2 +4(1+\sqrt{6})x+11+4\sqrt{6}]}{(85t^4-26xt^2-2yt^2+2x^2 +2y^2-26t^2+4x+5+e^\xi )^2}\nonumber \\&-\frac{48[2x^2-2y^2+2t^2(42t^2-13x+y-13)+4x-1]}{(85t^4-26xt^2-2yt^2+2x^2+2y^2-26t^2+4x+5+e^\xi )^2}, \end{aligned}$$
(29)

with

$$\begin{aligned} \xi =-\frac{\sqrt{6}x}{3}+\frac{5\sqrt{6}t^2}{6}. \end{aligned}$$
(30)

As shown in Fig. 5, the interaction between a lump and one line soliton are still nonelastic but the track of the lump obeys the controllable function of time. It can be seen that the lump and the line soliton firstly are separated completely (Fig. 5a at \(t=-2\)). Then two local waves meet at a certain time and the amplitude of the lump decreases (Fig. 5b at \(t=-1\), c at \(t=0\)). The lump is absorbed by the line soliton gradually and their collision is show to be nonelastic. When the time increases, two waves separate from each other and move in their respective directions (Fig. 5d at \(t=3\)). Figure 5c, d exhibits the fusion and fission of this lump from the line soliton, respectively. Compared the vcKP equation (1) with the classical KP equation, the lump in fusion case in Ref. [46] moves along the straight line and finally is switched off when it leaves from the induced line soliton. However, the lump shown in Fig. 5 separate from the line soliton again eventually. Since in the expressions h and k corresponding to the lump, there are quadratic functions rather than line ones of time, and the track of the lump obeys the parabola.

Fig. 6
figure 6

Profiles of the interaction solution (36): a–g are three-dimensional graphs at time \(t=-\,4\), \(t=-\,1.8\), \(t=-\,0.5\), \(t=0\), \(t=1\), \(t=1.6\), \(t=3,\) respectively

Full size image

4 Interaction solution between a lump and line soliton pairs

Based on the collision between a lump and one line soliton, we start to discuss the interaction between a lump and line soliton pairs. To this end, the function \(\phi \) is supposed as

$$\begin{aligned} \phi= & {} h^2+k^2+a_7+a_0e^\xi +b_0e^{-\xi }, \nonumber \\ \xi= & {} k_1x+k_2y+\int \omega _1(t)\mathrm{d}t, \nonumber \\ h= & {} a_1x+a_2 y+\int s_1(t)\mathrm{d}t+a_3,\nonumber \\ k= & {} a_4x+a_5y+\int s_2(t)\mathrm{d}t+a_6, \end{aligned}$$
(31)

where \(a_i(i=0,1\ldots 7),k_i(i=1,2)\) and \(b_0\) are real parameters to be determined. Similarly, the rational function supports a lump and the exponential functions are responsible for the line soliton pairs respectively. For \(\xi \gg 0\) and \(\xi \ll 0\), the exponential terms are dominant and the line soliton pairs exists, while the lump only arises at the middle time. Substituting (31) into the bilinear vcKP equation (5) yields the following set of parameters’ relations:

$$\begin{aligned}&k_1=\frac{\sqrt{-\frac{m_0}{3g_0}}(a_1a_5-a_2a_4)}{a^2_1+a^2_4},\nonumber \\&k_2=\frac{\sqrt{-\frac{m_0}{3g_0}}(a_1a_5-a_2a_4)(a_1a_2+a_4a_5)}{(a^2_1+a^2_4)^2},\nonumber \\&s_1(t)=\frac{(a_1a^2_5-a_1a^2_2-2a_2a_4a_5)m(t)}{a^2_1+a^2_4}\nonumber \\&\quad -a_2n(t)-a_1q(t), \nonumber \\&s_2(t)=\frac{(a^2_2a_4-a_4a^2_5-2a_1a_2a_5)m(t)}{a^2_1+a^2_4}\nonumber \\&\quad -a_5n(t)-a_4q(t), \nonumber \\&\omega _1(t)=-\frac{k^2_1[g(t)k^2_1+q(t)]+k_2[k_2m(t)+n(t)k_1]}{k_1}, \nonumber \\&a_7=-\frac{3g_0(a^2_1+a^2_4)~[k^4_1a_0b_0+(a^2_1+a^2_4)^2]}{m_0(a_1a_5-a_2a_4)^2}.\nonumber \\ \end{aligned}$$
(32)

These parameters must meet the conditions

$$\begin{aligned}&(a)~a_1a_4\ne 0, \ \ (b)~a_1a_5-a_2a_4\ne 0, \nonumber \\&(c)~m_0g_0<0, \ \ (d)~a_0>0,b_0>0. \end{aligned}$$
(33)

They lead to a class of interaction solutions to the vcKP equation (1)

$$\begin{aligned} u= & {} -\frac{12g(t)(2a_1h+2a_4k+a_0k_1e^\xi -b_0k_1e^{-\xi })^2}{f(t)\phi ^2}\nonumber \\&+\frac{12g(t)(2a^2_1+2a^2_4+a_0k^2_1e^\xi +b_0k^2_1e^{-\xi })}{f(t)\phi };\nonumber \\ \end{aligned}$$
(34)

condition (33) ensures that the solution (34) is well defined. By selecting some appropriate parameters,

$$\begin{aligned}&a_0=1,\ \ b_0=1,\ \ a_1=1,\ \ a_2=1,\ \ a_3=1,\nonumber \\&a_4=1,\ \ a_5=-1,\ \ a_6=1,\ \ a_7=\frac{10}{3}, \nonumber \\&g(t)=6t,\ \ m(t)=-12t,\ \ f(t)=6t,\nonumber \\&l(t)=0,\ \ n(t)=t,\ \ q(t)=t, \nonumber \\&s_1(t)=-14t,\ \ s_2(t)=-12t,\ \ \omega _1(t)=\frac{5\sqrt{6}t}{3},\nonumber \\&k_1=-\frac{\sqrt{6}}{3},\ \ k_2=0, \end{aligned}$$
(35)

which yields

$$\begin{aligned} u= & {} \frac{48[3t^2\cosh \xi (85t^2-26x-2y-26)+6\cosh \xi (x^2+y^2+2x)+34\cosh \xi ]}{[6(x^2+y^2)-6t^2(13x+y)+3t^2(85t^2-26) +4(3x+4)+6\cosh \xi ]^2}\nonumber \\&+\frac{288\sqrt{6}\sinh \xi (2x-13t^2+2) +864[y^2-x^2+t^2(-42t^2+13x-y+13)-2x+1]}{[6(x^2+y^2) -6t^2(13x+y)+3t^2(85t^2-26)+4(3x+4)+6\cosh \xi ]^2}, \end{aligned}$$
(36)

with

$$\begin{aligned} \xi =-\frac{\sqrt{6}x}{3}+\frac{5\sqrt{6}t^2}{6}. \end{aligned}$$
(37)

Figure 6a–g shows the process of propagation for the rogue waves at different times. Figure 6a exhibits resonance soliton pairs, in which the lump is almost invisible. As the time t increases, Figure 6b presents this lump fission from the left line soliton. Figure 6c, d depicts the propagation process of the interaction solution, a rogue wave appears in the middle of resonance soliton pairs and connect them with each other, and the maximum amplitude of the lump solution is reached at time \(t=0\). Figure 6e–g shows that the lump was swallowed by soliton pairs and disappeared gradually. Compared the vcKP equation (1) with the KP equation in [46], this lump interacting with resonance soliton pairs exhibits a kind of special rogue wave in which the peak emerges and evolves with the varying route.

5 Conclusions

In this work, we have studied the vcKP equation which can model various nonlinear real situations in hydrodynamics, plasma physics and some other nonlinear science. Using the bilinear method and symbolic computation, lump, and lump–soliton interaction solutions are presented. These local solutions are derived by constructing the auxiliary function. Taking the positive quadratic function gives rise to the lump solution in which the parameters need to satisfy certain conditions to ensure the analyticity and localization of the lump. It is shown that the velocity, moving path, and maximum height of the lump are completely characterized by the time functions rather than the constant parameters. The interaction solution between the lump and the linear soliton is obtained by combining the positive quadratic function and the exponential function. The interaction between two kinds of waves are still nonelastic but the track of the lump obeys the controllable function of time. By adding the exponential function, the lump interacting with resonance soliton pairs displays a kind of special rogue wave in which the peak emerges and evolves with the varying route. Compared the vcKP equation with the constant-coefficient counterparts, lump and lump–soliton solutions for the vcKP equation possess more abundant properties. The dynamic behaviors of these solutions are discussed under the different parameters. These results may help us to understand the propagation of nonlinear waves in nonlinear science.