1 Introduction

Nonlinear evolution equations (NLEEs) are important in a variety of scientific and technological fields. Nonlinear wave structures have aroused the interest of many academics in recent decades due to their multiple properties seen in various disciplines of modern sciences. In the existence of solitary waves, nonlinear evolution models are employed to simulate the effect of surface for deep water and weakly nonlinear dispersive long waves. As a result, exact solutions of corresponding models are essential for studying dynamical structures and other features of physical phenomena in a variety of fields, including electromagnetism, physical chemistry, geophysics, ionised physics, elastic medium, fluid motion, fluid mechanics, elastic medium, nuclear physics, electrochemistry, optical fibres, energy physics, chemical mechanics, gravity, biostatistics, statistical and natural physics. Recently, bilinear approaches are more frequently used by renowned researcher to deal with many interesting models. Consequently, various forms of solitonic structures are elaborated in the form of lump solution [1], N-soliton solution [2], breather solution [3], bright soliton solution [4], soliton solution [5], dark soliton solution [6], Multiple-soliton solution [7, 8] and interaction solutions [9, 10]. A specific form of rational localized wave solution that decays algebraically to the background wave in space direction is known as the lump wave solution. The lump wave solution was first discovered in the study of Kadomtsev-Petviashvili equation. Consequently, finding lump-type wave solutions to nonlinear evolution equations and examining their dynamical behaviour have gained alot of attention in the field of nonlinear wave theory. The study of explicit solutions for various soliton equations has played a significant role in modern mathematics with implications in a variety of fields including mathematics, physics and other sciences. There are several well-established approaches for obtaining the exact solutions to various nonlinear models in the literature [11,12,13,14,15].

It is well acknowledged that the construction of exact solutions and the study of integrable properties for NLEEs play a significant role in various nonlinear physical and mathematical events. Such models play a key role to study a wide range of dynamical wave structures efficiently that occur in the real world and can be found in a variety of domains, including physics [16], applied mathematics [17] and engineering sciences [18]. There are numerous methods for obtaining their exact solutions, such as exp-function method [19, 20], Hirota bilinear method [21, 22], Lie group method [23, 24], B\(\ddot{a}\)cklund transformation [25, 26], variable separation method [27, 28], multiple exp-function method [29, 30], Darboux transformation [31, 32], extended tanh function method [33, 34], tanh method [35, 36], homogeneous balance method [37, 38], inverse scattering method [39, 40], multiple exp-function algorithm [41, 42], homoclinic approach [43], \(\phi ^6\)-model expansion method [44], Lie symmetry analysis [45, 46].

This paper is organized as follows: The (2+1)-dimensional pKP-BKP model is described in Sect. 2. In Sect. 3, the bilinear form for Eq. (4) is obtained. While Sect. 4 is devoted to the mathematical analysis of our considered model. The travelling wave solutions are retrieved in Sect. 5. Moreover, Sect. 6 contains discussion and results. Lastly, Sect. 7 contains conclusions.

2 The (2+1)-dimensional pKP-BKP model

The Kadomtsev-Petviashvili (KP) equation explains waves that are weakly dispersed [47, 48] with modest amplitudes propagating. The KP equation is an dispersive integrable equation with many soliton solutions that can be expressed in the Lax form. The KP hierarchy is a multi-dimensional structure with infinite dimensions with a variety of distinct formulations and symmetries. The B-type KP (B-KP) equation, as part of the KP-category equations, have garnered a significant amount of recent research in fluid dynamics and other areas [49, 50].

The (2 + 1)-dimensional integrable KP model may be expressed as [51]

$$\begin{aligned} \mu _{xt}+6(\mu \mu _{x})_{x}+\mu _{xxxx}-\mu _{yy}=0. \end{aligned}$$
(1)

Substituting \(\mu =\mu _{x}\) and using integration, the potential KP (pKP) equation

$$\begin{aligned} \mu _{xt}+6 \mu _{x} \mu _{xx}+\mu _{xxxx}-\mu _{yy}=0. \end{aligned}$$
(2)

is obtained using Eq. (1). Moreover, the (2 + 1)-dimensional integrable B-KP equation may be expressed as

$$\begin{aligned} (15 \mu _{x}^3+15 \mu _{x} \mu _{xxx}+\mu _{xxxxx})_{x}+5[\mu _{xxxy}+3(\mu _{x}\mu _{y})_{x}]+\mu _{xt}-5\mu _{yy}=0. \end{aligned}$$
(3)

The N-soliton solutions and infinite dimensional Lie algebra structures for Eqs. (1) and (3) are studied recently using various Hirota bilinear forms [52,53,54]. Consequently, a combined pKP-BKP equation is proposed, that can be expressed as [55]

$$\begin{aligned}&\alpha _1 \left( 45 \mu _{x}^2 \mu _{xx}+15 \mu _{xx} \mu _{xxx} +15 \mu _x \mu _{xxxx}+\mu _{xxxxxx}\right) \nonumber \\&\qquad\quad +\alpha _2 \left( 6 \mu _x \mu _{xx}+\mu _{xxxx}\right) \nonumber \\&\qquad\quad +\alpha _3 \left( 3 \mu _x \mu _{xy}+3 \mu _{xx} \mu _y-\mu _{xxxy}\right) +\alpha _4 \mu _{xx}+\alpha _5 \mu _{xt}+\alpha _6 \mu _{yy}=0, \end{aligned}$$
(4)

where \(\alpha _i\)(i= 1, 2,..., 6) are constants. If \(\alpha _1\) = \(\alpha _3\) = \(\alpha _4\) = 0, \(\alpha _2\) = \(\alpha _5\) =1, \(\alpha _6\) = -1, then Eq. (4) represents the pKP Eq. (2), that admits the weakly dispersive waves in a paraxial wave approximation and can alternatively be characterised as the evolution of lengthy ion-acoustic waves of modest amplitude propagating in plasma physics. However, if \(\alpha _1\) = \(\alpha _5\) =1, \(\alpha _2\) = \(\alpha _4\) = 0, \(\alpha _3\)= 5, \(\alpha _6\) = -5, Eq. (4) illustrates the BKP Eq. (3), that is a significant physical model that owns the isospectral soliton and may be characterised as waves in a particular form of nonuniform medium. Recently, a wide range of fresh analysis towards exact solutions to the given model (4) have been published. The N-soliton solution were constructed in [56]. The resonant multi-soliton, M-breather, M-lump and hybrid solutions were obtained in [57]. Lastly, the explicit solution and its soliton molecules were retrieved in [58].

3 Bilinear form of 4

The bilinear approach was first proposed by Hirota [59] in 1971 for constructing multiple solutions to integral nonlinear evolutionary equations. The main idea behind this technique is to employ some dependent variable transformation to change the NLEE in a form where the unknown function appears bilinearly. The bilinear approach is one of the most essential and extensively used methods for solving nonlinear partial differential equations. This strategy is based on using suitable transformations to convert nonlinear models into bilinear forms. Then, on the basis of the bilinear forms, N-soliton solutions, kink solutions, rational solutions, lump solutions, breather solutions, periodic soliton solutions and other exact solutions can be derived. To acquire the bilinear form of Eq. (4), we apply the transformation

$$\begin{aligned} \mu =2[ln F]_{x}. \end{aligned}$$
(5)

Consequently, we retrieve the bilinear form as

$$\begin{aligned} \left(\alpha _1 D_{x}^6+\alpha _2 D_{x}^4 +\alpha _3 D_{x}^3 D_{y} +\alpha _4 D_{x}^2+\alpha _5 D_{x}D_{t}+\alpha _6 D_{y}^2\right)F.F=0, \end{aligned}$$

so that the function D fulfills

$$\begin{aligned} D_{x}^{m}D_{t}^{n}(p.q)=\left( \frac{\partial }{\partial x}-\frac{\partial }{\partial x'}\right) ^m \left( \frac{\partial }{\partial t}-\frac{\partial }{\partial t'}\right) ^n \times p(x,t).q\left( x',t'\right) |x=x',t=t'. \end{aligned}$$

As a result, we get

$$\begin{aligned}&\alpha _1 \left( F F_{xxxxxx}-6F_x F_{xxxxx}+15 F_{xx} F_{xxxx}-10 F_{xxx}^2\right) \nonumber \\&\quad +\alpha _2 \left( F F_{xxxx}-4 F_x F_{xxx}+3 F_{xx}^2\right) \nonumber \\&\quad +\alpha _3 \left( F F_{xxxy}-3 F_x F_{xxy}+3 F_{xx} F_{xy}-F_{xxx}F_y\right) \nonumber \\&\quad +\alpha _4 \left( F F_{xx}-F_{x}^2\right) +\alpha _5 \left( F F_{xt}-F{x}F_{t}\right) +\alpha _6 \left( F F_{yy}-F_{y}^2\right) =0, \end{aligned}$$
(6)

obviously if F meets Eq. (4), then \(\mu =2[ln F]_{x}\) produces the solution of specified model (4) instantly.

4 Mathematical analysis

In this section, several significant forms are employed to extract the analytical solutions of Eq. (4).

4.1 Lump wave solutions

In this portion, we examine the operator F given by

$$\begin{aligned} F=\xi _1^2+\xi _2^2+g, \end{aligned}$$
(7)

where

$$\begin{aligned} \xi _1=l_1 x+l_2 y+l_3 t,~~~\xi _2=m_1 x+m_2 y+m_3 t, \end{aligned}$$

while \(l_i,~m_i\)’s, g are the constants to be determined. Using Eq. (7) into Eq. (6), we have a system of equations with several parameters. We get the following findings by resolving them utilizing a computational programme such as Mathematica.

Case 1:

$$\begin{aligned}&l_3=\frac{\alpha _6 l_1 m_2^2-\alpha _6 l_2^2 l_1-\alpha _4 l_1^3-m_1^2\alpha _4 l_1-2 \alpha _6 l_2 m_1 m_2}{\alpha _5 \left( l_1^2+m_1^2\right) },\\&\quad ~m_3=\frac{\alpha _6 l_2^2 m_1-\alpha _4 l_1^2 m_1-2 \alpha _6 l_1 l_2 m_2-\alpha _4 m_1^3-\alpha _6 m_2^2 m_1}{\alpha _5 \left( l_1^2+m_1^2\right) }, \end{aligned}$$

here \(l_1\), \(l_2\) \(m_1\), \(m_2\), g are free parameters. Hence utilizing all the above known values, Eq. (7) gives

$$\begin{aligned} F=g+\left( \frac{ \left( \alpha _6 l_1 m_2^2-\alpha _6 l_2^2 l_1-\alpha _4 l_1^3-m_1^2\alpha _4 l_1-2 \alpha _6 l_2 m_1 m_2\right) t}{\alpha _5 \left( l_1^2+m_1^2\right) }+l_1 x+l_2 y\right) ^2 \\ +\left( \frac{ \left( \alpha _6 l_2^2 m_1-\alpha _4 l_1^2 m_1-2 \alpha _6 l_1 l_2 m_2-\alpha _4 m_1^3-\alpha _6 m_2^2 m_1\right) t}{\alpha _5 \left( l_1^2+m_1^2\right) }+m_1 x+m_2 y\right) ^2. \end{aligned}$$

Utilizing the above result together with Eq. (5), we gain \(\mu _1(x,y,t)\).

Case 2:

$$\begin{aligned} l_1=0,~l_3=-\frac{2 \alpha _6 l_2 m_2}{\alpha _5 m_1},~m_3=\frac{\alpha _6 l_2^2-\alpha _4 m_1^2-\alpha _6 m_2^2}{\alpha _5 m_1}, \end{aligned}$$

where \(l_2\), \(m_1\), \(m_2\), g are free parameters. Hence utilizing all the above known values, Eq. (7) gives

$$\begin{aligned} F=g+\left( l_2 y-\frac{2 \alpha _6 l_2 m_2 t}{\alpha _5 m_1}\right) ^2+\left( \frac{t \left( \alpha _6 l_2^2-\alpha _4 m_1^2-\alpha _6 m_2^2\right) }{\alpha _5 m_1}+m_1 x+m_2 y\right) ^2. \end{aligned}$$
(8)

Utilizing Eq. (8) together with Eq. (5), we obtain the solution

$$\begin{aligned} \mu _2(x,y,t)=\frac{4 m_1 \left( \frac{t \left( \alpha _6 l_2^2-\alpha _4 m_1^2-\alpha _6 m_2^2\right) }{\alpha _5 m_1}+m_1 x+m_2 y\right) }{g+\left( \frac{t \left( \alpha _6 l_2^2-\alpha _4 m_1^2-\alpha _6 m_2^2\right) }{\alpha _5 m_1}+m_1 x+m_2 y\right) ^2+\left( l_2 y-\frac{2 \alpha _6 l_2 m_2 t}{\alpha _5 m_1}\right) ^2}. \end{aligned}$$
(9)

Case 3:

$$\begin{aligned} m_1=i l_1,~m_2=i l_2,~m_3=-\frac{i \left( 2 \alpha _4 l_1^2+\alpha _5 l_3 l_1+2 \alpha _6 l_2^2\right) }{\alpha _5 l_1}, \end{aligned}$$

where \(l_1\), \(l_2\), \(l_3\), g are free parameters. Hence utilizing all the above known values, Eq. (7) gives

$$\begin{aligned} F=g+\left( l_3 t+l_1 x+l_2 y\right) ^2+\left( -\frac{i t \left( 2 \alpha _4 l_1^2+\alpha _5 l_3 l_1+2 \alpha _6 l_2^2\right) }{\alpha _5 l_1}+i l_1 x+i l_2 y\right) ^2. \end{aligned}$$
(10)

Utilizing Eq. (10) together with Eq. (5), we retrieve the solution

$$\begin{aligned} \mu _3(x,y,t)=\frac{2 l_1 \left( l_3 t+l_1 x+l_2 y\right) +2 i l_1 \left( -\frac{i t \left( 2 \alpha _4 l_1^2+\alpha _5 l_3 l_1+2 \alpha _6 l_2^2\right) }{\alpha _5 l_1}+i l_1 x+i l_2 y\right) }{g+\left( -\frac{i t \left( 2 \alpha _4 l_1^2+\alpha _5 l_3 l_1+2 \alpha _6 l_2^2\right) }{\alpha _5 l_1}+i l_1 x+i l_2 y\right) ^2+\left( l_3 t+l_1 x+l_2 y\right) ^2}. \end{aligned}$$
(11)

4.2 Collision among lump wave and strip soliton

In this fragment, we use the operator

$$\begin{aligned} F=\omega _0+ \omega _1\xi _1^2+\omega _2\xi _2^2+\omega _3e^{\xi _3}, \end{aligned}$$
(12)

where

$$\begin{aligned}&\xi _1=l_0+l_1 x+l_2 y+l_3 t,~~\xi _2=m_0+m_1 x+m_2 y+m_3 t,\\&~~\xi _3=n_0+n_1 x+n_2 y+n_3 t, \end{aligned}$$

while \(l_i,~m_i,~n_i\)’s are the constants to be determined. These substitutions for  \(\xi _1\),  \(\xi _2\), and  \(\xi _3\) will be applicable throughout this paper. Using Eq. (12) into Eq. (6), we have a system of equations with several parameters. We get the following findings by resolving them utilizing a computational programme such as Mathematica. Case 1:

$$\begin{aligned} n_3=-\frac{\alpha _1 n_1^6+\alpha _2 n_1^4+\alpha _3 n_2 n_1^3+\alpha _4 n_1^2+\alpha _6 n_2^2}{\alpha _5 n_1},~\omega _1=0,~\omega _2=0, \end{aligned}$$

here \(n_0\), \(n_1\), \(n_2\), \(\omega _0\), \(\omega _3\) are free parameters. Hence utilizing all the above known values, Eq. (12) gives

$$\begin{aligned} F=\omega _0+\omega _3 \exp \left( n_0-\frac{t \left( \alpha _1 n_1^6+\alpha _2 n_1^4+\alpha _3 n_2 n_1^3+\alpha _4 n_1^2+\alpha _6 n_2^2\right) }{\alpha _5 n_1}+n_1 x+n_2 y\right) . \end{aligned}$$
(13)

Utilizing Eq. (13) together with Eq. (5), we acquire the solution

$$\begin{aligned} \mu _4(x,y,t)=\frac{2 \left( n_1 \omega _3 \exp \left( n_0-\frac{t \left( \alpha _1 n_1^6+\alpha _2 n_1^4+\alpha _3 n_2 n_1^3+\alpha _4 n_1^2+\alpha _6 n_2^2\right) }{\alpha _5 n_1}+n_1 x+n_2 y\right) \right) }{\omega _3 \exp \left( n_0-\frac{t \left( \alpha _1 n_1^6+\alpha _2 n_1^4+\alpha _3 n_2 n_1^3+\alpha _4 n_1^2+\alpha _6 n_2^2\right) }{\alpha _5 n_1}+n_1 x+n_2 y\right) +\omega _0}. \end{aligned}$$
(14)

Case 2:

$$\begin{aligned}&l_3=\frac{-\alpha _6 l_2^2 l_1 \omega _1-\alpha _4 l_1^3 \omega _1-\alpha _4 l_1 m_1^2 \omega _2+\alpha _6 l_1 m_2^2 \omega _2-2 \alpha _6 l_2 m_1 m_2 \omega _2}{\alpha _5 \left( l_1^2 \omega _1+m_1^2 \omega _2\right) },\\&\quad m_3=\frac{-\alpha _4 l_1^2 m_1 \omega _1+\alpha _6 l_2^2 m_1 \omega _1-2 \alpha _6 l_1 l_2 m_2 \omega _1-\alpha _4 m_1^3 \omega _2-\alpha _6 m_2^2 m_1 \omega _2}{\alpha _5 \left( l_1^2 \omega _1+m_1^2 \omega _2\right) },\\&\quad \omega _0=-\frac{3 \left( l_1^2 \omega _1+m_1^2 \omega _2\right) {}^2 \left( \alpha _2 l_1^2 \omega _1+\alpha _3 l_2 l_1 \omega _1+\alpha _2 m_1^2 \omega _2+\alpha _3 m_1 m_2 \omega _2\right) }{\alpha _6 \omega _1 \omega _2 \left( l_2 m_1-l_1 m_2\right) ^2},\\&\quad \omega _3=0, \end{aligned}$$

while \(l_0\), \(l_1\), \(l_2\), \(m_0\), \(m_1\), \(m_2\), \(\omega _1\), \(\omega _2\) are free parameters.

Utilizing all the above determined parameters in Eq. (12) and with the aid of Eq. (5), we have \(\mu _5(x,y,t)\).

Case 3:

$$\begin{aligned}&l_1=0,~l_2=\frac{\alpha _3 \alpha _5 l_3}{2 \alpha _2 \alpha _6},~m_2=-\frac{\alpha _2 m_1}{\alpha _3},~\omega _0=0,\\&\quad \omega _2=\frac{\alpha _3^4 \alpha _5^2 l_3^2 \omega _1}{4 \alpha _2^2 \alpha _6 m_1 \left( \alpha _6 \alpha _2^2 m_1+\alpha _3^2 \alpha _4 m_1+\alpha _3^2 \alpha _5 m_3\right) },~\omega _3=0, \end{aligned}$$

where \(l_0\), \(l_3\), \(m_0\), \(m_1\), \(m_3\), \(\omega _1\) are free parameters.

Hence utilizing all the above known values, Eq. (12) gives

$$\begin{aligned} F=\omega _1 \left( l_3 t+\frac{\alpha _3 \alpha _5 l_3 y}{2 \alpha _2 \alpha _6}+l_0\right) ^2+\frac{\alpha _5^2 \alpha _3^4 l_3^2 \omega _1 \left( m_3 t+m_1 x-\frac{\alpha _2 m_1 y}{\alpha _3}+m_0\right) ^2}{4 \alpha _2^2 \alpha _6 m_1 \left( \alpha _6 \alpha _2^2 m_1+\alpha _3^2 \alpha _4 m_1+\alpha _3^2 \alpha _5 m_3\right) }. \end{aligned}$$
(15)

Utilizing Eq. (15) together with Eq. (5), we gain \(\mu _6(x,y,t)\).

Case 4:

$$\begin{aligned}&l_2=\frac{i \sqrt{l_1} \left( -2 \alpha _4 l_1 m_1-\alpha _5 l_3 m_1-\alpha _5 l_1 m_3\right) }{\sqrt{2} \sqrt{\alpha _6} \sqrt{m_1} \sqrt{2 \alpha _4 l_1 m_1+\alpha _5 l_3 m_1+\alpha _5 l_1 m_3}},~\omega _0=0,\\&\quad \omega _2=-\frac{l_1^2 \omega _1}{m_1^2},~\omega _3=0,~m_2=-\frac{i \sqrt{m_1} \sqrt{2 \alpha _4 l_1 m_1+\alpha _5 l_3 m_1+\alpha _5 l_1 m_3}}{\sqrt{2} \sqrt{\alpha _6} \sqrt{l_1}}, \end{aligned}$$

where \(l_0\), \(l_1\), \(l_3\), \(m_0\), \(m_1\), \(m_3\), \(\omega _1\) are free parameters.

Hence utilizing all the above known values, Eq. (12) gives

$$\begin{aligned}&F=\omega _1 \left( \frac{i \sqrt{l_1} y \left( -2 \alpha _4 l_1 m_1-\alpha _5 l_3 m_1-\alpha _5 l_1 m_3\right) }{\sqrt{2} \sqrt{\alpha _6} \sqrt{m_1} \sqrt{2 \alpha _4 l_1 m_1+\alpha _5 l_3 m_1+\alpha _5 l_1 m_3}}+l_3 t+l_1 x+l_0\right) ^2\nonumber \\&-\frac{l_1^2 \omega _1 \left( -\frac{i \sqrt{m_1} y \sqrt{2 \alpha _4 l_1 m_1+\alpha _5 l_3 m_1+\alpha _5 l_1 m_3}}{\sqrt{2} \sqrt{\alpha _6} \sqrt{l_1}}+m_3 t+m_1 x+m_0\right) ^2}{m_1^2}. \end{aligned}$$
(16)

Utilizing Eq. (16) together with Eq. (5), we gain \(\mu _7(x,y,t)\).

4.3 Collision between lump wave and double stripes soliton

In this subsection, we review the operator F stated as

$$\begin{aligned} F=\omega _0+\omega _1 \xi _1^2 +\omega _2 \xi _2^2 +\omega _3 \cosh \left( \xi _3\right) . \end{aligned}$$
(17)

Using Eq. (17) into Eq. (6), we have a system of equations with several parameters. We get the following findings by resolving them utilizing a computational programme such as Mathematica.

Case 1:

$$\begin{aligned} n_3=-\frac{4 \alpha _2 n_1^4+4 \alpha _3 n_2 n_1^3+\alpha _4 n_1^2+\alpha _6 n_2^2}{\alpha _5 n_1},~\omega _0=0,~\omega _1=0,~\omega _2=0, \end{aligned}$$

where \(n_0\), \(n_1\), \(n_2\), \(\omega _3\) are free parameters.

Hence utilizing all the above known values, Eq. (17) gives

$$\begin{aligned} F=\omega _3 \cosh \left( -\frac{t \left( 4 \alpha _2 n_1^4+4 \alpha _3 n_2 n_1^3+\alpha _4 n_1^2+\alpha _6 n_2^2\right) }{\alpha _5 n_1}+n_1 x+n_2 y+n_0\right) . \end{aligned}$$
(18)

Utilizing Eq. (18) together with Eq. (5), we retrieve the solution

$$\begin{aligned} \mu _8(x,y,t)=2 n_1 \tanh \left( -\frac{t \left( 4 \alpha _2 n_1^4+4 \alpha _3 n_2 n_1^3+\alpha _4 n_1^2+\alpha _6 n_2^2\right) }{\alpha _5 n_1}+n_1 x+n_2 y+n_0\right) . \end{aligned}$$

Case 2:

$$\begin{aligned} l_1=\frac{l_2 m_1}{m_2},~l_3=-\frac{l_2 \left( 2 \alpha _4 m_1^2+\alpha _5 m_3 m_1+2 \alpha _6 m_2^2\right) }{\alpha _5 m_1 m_2},~\omega _2=-\frac{l_2^2 \omega _1}{m_2^2},~\omega _0=\omega _3=0, \end{aligned}$$

where \(l_0\), \(l_2\), \(m_0\), \(m_1\), \(m_2\), \(m_3\), \(\omega _1\) are free parameters.

Hence utilizing all the above known values, Eq. (17) gives

$$\begin{aligned}&F=\omega _1 \left( -\frac{l_2 t \left( 2 \alpha _4 m_1^2+\alpha _5 m_3 m_1+2 \alpha _6 m_2^2\right) }{\alpha _5 m_1 m_2}+\frac{l_2 m_1 x}{m_2}+l_2 y+l_0\right) ^2\nonumber \\&\qquad -\frac{l_2^2 \omega _1 \left( m_3 t+m_1 x+m_2 y+m_0\right) ^2}{m_2^2}. \end{aligned}$$
(19)

Utilizing Eq. (19) together with Eq. (5), we gain \(\mu _9(x,y,t)\).

Case 3:

$$\begin{aligned} l_3=\frac{-l_1^2 \alpha _4 \omega _1-\alpha _6 l_2^2 \omega _1+\alpha _6 m_2^2 \omega _2}{\alpha _5 l_1 \omega _1},~m_1=0,~m_3=-\frac{2 \alpha _6 l_2 m_2}{\alpha _5 l_1},~\omega _0=0,~\omega _3=0, \end{aligned}$$

where \(l_0\), \(l_1\), \(l_2\), \(m_0\), \(m_2\), \(\omega _1\), \(\omega _2\) are free parameters.

Hence utilizing all the above parameters, Eq. (17) gives

$$\begin{aligned}&F=\omega _1 \left( \frac{t \left( -l_1^2 \alpha _4 \omega _1-\alpha _6 l_2^2 \omega _1+\alpha _6 m_2^2 \omega _2\right) }{\alpha _5 l_1 \omega _1}+l_1 x+l_2 y+l_0\right) ^2\nonumber \\&\quad +\omega _2 \left( -\frac{2 \alpha _6 l_2 m_2 t}{\alpha _5 l_1}+m_2 y+m_0\right) ^2. \end{aligned}$$
(20)

Utilizing Eq. (20) together with Eq. (5), we have \(\mu _{10}(x,y,t)\).

Case 4:

$$\begin{aligned}&n_2=\frac{\sqrt{16 \alpha _3^2 n_1^6+4 \alpha _6 \left( -4 \alpha _2 n_1^4-\alpha _4 n_1^2-\alpha _5 n_3 n_1\right) }-4 \alpha _3 n_1^3}{2 \alpha _6},\nonumber \\&\quad ~\omega _0=0,~\omega _1=0,~\omega _2=0, \end{aligned}$$

where \(n_0\), \(n_1\), \(n_3\), \(\omega _3\) are free parameters.

Utilizing all the above determined parameters in Eq. (17) and with the aid of Eq. (5), we gain \(\mu _{11}(x,y,t)\).

4.4 Collision between lump and periodic waves

In this portion, we examine the operator F specified by

$$\begin{aligned} F=\omega _0+\omega _1 \xi _1^2 +\omega _2 \xi _2^2 +\omega _3 \cos \left( \xi _3\right) . \end{aligned}$$
(21)

Using Eq. (21) into Eq. (6), we have a system of equations with several parameters. We get the following findings by resolving them utilizing a computational programme such as Mathematica.

Case 1:

$$\begin{aligned} n_3=\frac{4 \alpha _2 n_1^4+4 \alpha _3 n_2 n_1^3-\alpha _4 n_1^2-\alpha _6 n_2^2}{\alpha _5 n_1},~\omega _0=0,~\omega _1=0,~\omega _2=0, \end{aligned}$$

where \(n_0\), \(n_1\), \(n_2\), \(\omega _3\) are free parameters.

Hence utilizing all the above known values, Eq. (21) gives

$$\begin{aligned} F=\omega _3 \cos \left( \frac{t \left( 4 \alpha _2 n_1^4+4 \alpha _3 n_2 n_1^3-\alpha _4 n_1^2-\alpha _6 n_2^2\right) }{\alpha _5 n_1}+n_1 x+n_2 y+n_0\right) . \end{aligned}$$
(22)

Utilizing Eq. (22) together with Eq. (5), we obtain the solution

$$\begin{aligned} \mu _{12}(x,y,t)=-2n_1 \tan \left( \frac{t \left( 4 \alpha _2 n_1^4+4 \alpha _3 n_2 n_1^3-\alpha _4 n_1^2-\alpha _6 n_2^2\right) }{\alpha _5 n_1}+n_1 x+n_2 y+n_0\right) . \end{aligned}$$

Case 2:

$$\begin{aligned} l_3=\frac{-2 \alpha _4 l_1^2 m_1-\alpha _5 l_1^2 m_3-2 \alpha _6 l_2^2 m_1}{\alpha _5 l_1 m_1},~m_2=\frac{l_2 m_1}{l_1},~\omega _2=-\frac{l_1^2 \omega _1}{m_1^2},~\omega _0=\omega _3=0, \end{aligned}$$

where \(l_0\), \(l_1\), \(l_2\), \(m_0\), \(m_1\), \(m_3\), \(\omega _1\) are free parameters.

Hence utilizing all the above parameters, Eq. (21) gives

$$\begin{aligned}&F=\omega _1 \left( \frac{t \left( -2 \alpha _4 l_1^2 m_1-\alpha _5 l_1^2 m_3-2 \alpha _6 l_2^2 m_1\right) }{\alpha _5 l_1 m_1}+l_1 x+l_2 y+l_0\right) ^2\nonumber \\&-\frac{l_1^2 \omega _1 \left( \frac{l_2 m_1 y}{l_1}+m_3 t+m_1 x+m_0\right) ^2}{m_1^2}. \end{aligned}$$
(23)

Utilizing Eq. (23) together with Eq. (5), we retrieve the solution \(\mu _{13}(x,y,t)\).

Case 3:

$$\begin{aligned}&l_3=\frac{-l_2^2 \alpha _6 l_1 \omega _1-\alpha _4 l_1^3 \omega _1-\alpha _4 l_1 m_1^2 \omega _2+\alpha _6 l_1 m_2^2 \omega _2-2 \alpha _6 l_2 m_1 m_2 \omega _2}{\alpha _5 \left( l_1^2 \omega _1+m_1^2 \omega _2\right) },\\&m_3=\frac{-\alpha _4 l_1^2 m_1 \omega _1+\alpha _6 l_2^2 m_1 \omega _1-2 \alpha _6 l_1 l_2 m_2 \omega _1-\alpha _4 m_1^3 \omega _2-\alpha _6 m_2^2 m_1 \omega _2}{\alpha _5 \left( l_1^2 \omega _1+m_1^2 \omega _2\right) },\\&\omega _0=0,~\omega _3=0, \end{aligned}$$

where \(l_0\), \(l_1\), \(l_2\), \(m_0\), \(m_1\), \(m_2\), \(\omega _1\), \(\omega _2\) are free parameters.

Utilizing all the above determined parameters in Eq. (21) and with the aid of Eq. (5), we gain \(\mu _{14}(x,y,t)\).

Case 4:

$$\begin{aligned}&n_2=\frac{4 \alpha _3 n_1^3-\sqrt{16 \alpha _3^2 n_1^6+4 \alpha _6 \left( 4 \alpha _2 n_1^4-\alpha _4 n_1^2-\alpha _5 n_3 n_1\right) }}{2 \alpha _6},\\&\quad \omega _0=0,~\omega _1=0,~\omega _2=0, \end{aligned}$$

where \(n_0\), \(n_1\), \(n_3\), \(\omega _3\) are free parameters.

Utilizing all the above determined parameters in Eq. (21) and with the aid of Eq. (5), we have \(\mu _{15}(x,y,t)\).

4.5 Collision among lump wave and double stripes soliton

Here, we get the operator F of the form

$$\begin{aligned} F=\omega _0+\omega _1 \xi _1^2+\omega _2 \cosh \left( \xi _2\right) +\omega _3 \cos \left( \xi _3\right) . \end{aligned}$$
(24)

Using Eq. (24) into Eq. (6), we have a system of equations with several parameters. We get the following findings by resolving them utilizing a computational programme such as Mathematica.

Case 1:

$$\begin{aligned}&n_3=\frac{-16 \alpha _1 n_1^6+4 \alpha _2 n_1^4+4 \alpha _3 n_2 n_1^3-\alpha _4 n_1^2-\alpha _6 n_2^2}{\alpha _5 n_1},~m_1=i n_1,~m_2=i n_2,\\&\quad m_3=-\frac{i \left( 16 \alpha _1 n_1^6-4 \alpha _2 n_1^4-4 \alpha _3 n_2 n_1^3+\alpha _4 n_1^2+\alpha _6 n_2^2\right) }{\alpha _5 n_1},~\omega _0=\omega _1=0, \end{aligned}$$

where \(n_0\), \(n_1\), \(n_2\), \(\omega _2\), \(\omega _3\) are free parameters.

Utilizing all the above determined parameters in Eq. (24) and with the aid of Eq. (5), we gain \(\mu _{16}(x,y,t)\).

Case 2:

$$\begin{aligned}&m_3=\frac{-16 \alpha _1 m_1^6-4 \alpha _2 m_1^4-4 \alpha _3 m_2 m_1^3-\alpha _4 m_1^2-\alpha _6 m_2^2}{\alpha _5 m_1},~n_1=i m_1,~n_2=i m_2,\\&\quad n_3=-\frac{i \left( 16 \alpha _1 m_1^6+4 \alpha _2 m_1^4+4 \alpha _3 m_2 m_1^3+\alpha _4 m_1^2+\alpha _6 m_2^2\right) }{\alpha _5 m_1},~\omega _0=\omega _1=0, \end{aligned}$$

where \(m_0\), \(m_1\), \(m_2\), \(n_0\), \(n_1\), \(n_2\), \(\omega _2\), \(\omega _3\) are free parameters.

Utilizing all the above determined parameters in Eq. (24) and with the aid of Eq. (5), we retrieve the solution \(\mu _{17}(x,y,t)\).

4.6 Periodic wave soliton

Lastly, we get the operator F as

$$\begin{aligned} F=\omega _0+\omega _1 e^{-\xi _1} +\omega _2 e^{\xi _1}+\omega _3 \cos \left( \xi _2\right) . \end{aligned}$$
(25)

Using Eq. (25) into Eq. (6), we have a system of equations with several parameters. We get the following findings by resolving them utilizing a computational programme such as Mathematica.

Case 1:

$$\begin{aligned} l_3=\frac{-16 \alpha _1 l_1^6-4 \alpha _2 l_1^4-4 \alpha _3 l_2 l_1^3-\alpha _4 l_1^2-\alpha _6 l_2^2}{\alpha _5 l_1},~\omega _3=\omega _0=0, \end{aligned}$$

where \(l_0\), \(l_1\), \(l_2\), \(\omega _1\), \(\omega _2\) are free parameters.

Hence utilizing all the above known values, Eq. (25) gives

$$\begin{aligned}&F=\omega _1 \exp (\frac{t \left( 16 \alpha _1 l_1^6+4 \alpha _2 l_1^4+4 \alpha _3 l_2 l_1^3+\alpha _4 l_1^2+\alpha _6 l_2^2\right) }{\alpha _5 l_1}-l_1 x-l_2 y-l_0)\\&\quad +\omega _2 \exp \left( \frac{t \left( -16 \alpha _1 l_1^6-4 \alpha _2 l_1^4-4 \alpha _3 l_2 l_1^3-\alpha _4 l_1^2-\alpha _6 l_2^2\right) }{\alpha _5 l_1}+l_1 x+l_2 y+l_0\right) . \end{aligned}$$

Utilizing the above result together with Eq. (5), we gain \(\mu _{18}(x,y,t)\).

Case 2:

$$\begin{aligned}&l_2=\frac{l_1 m_1 \left( \alpha _3 m_1 \left( l_1^2+m_1^2\right) +\alpha _6 m_2\right) -\chi }{\alpha _6 m_1^2},~\omega _2=0,~\omega _0=0,\\&\quad m_3=-\frac{m_1^2 \left( \alpha _4+16 \alpha _1 m_1^4-4 \alpha _2 m_1^2-4 \alpha _3 m_2 m_1\right) +\alpha _6 m_2^2}{\alpha _5 m_1},\\&\quad l_3=\frac{1}{\alpha _5 \alpha _6 m_1^3}(3 \alpha _3 l_1^2 m_1 \chi -3 \left( \alpha _3^2+2 \alpha _1 \alpha _6\right) l_1^5 m_1^3\\&\quad -2 l_1^3 m_1^2 \left( \left( \alpha _3^2-10 \alpha _1 \alpha _6\right) m_1^3+2 \alpha _2 \alpha _6 m_1+3 \alpha _3 \alpha _6 m_2\right) \\&\quad +l_1 m_1 \left( \alpha _3^2 m_1^6+\alpha _6 m_1^2 \left( -\alpha _4+10 \alpha _1 m_1^4-2 \alpha _3 m_2 m_1\right) -\alpha _6^2 m_2^2\right) \\&\quad +\chi \left( 2 \alpha _6 m_2-\alpha _3 m_1^3\right) ), \end{aligned}$$

where

$$\begin{aligned} \chi =\sqrt{m_1^3 \left( l_1^2+m_1^2\right) {}^2 \left( \left( \alpha _3^2+5 \alpha _1 \alpha _6\right) l_1^2 m_1+3 \alpha _6 \left( -5 \alpha _1 m_1^3+\alpha _2 m_1+\alpha _3 m_2\right) \right) }, \end{aligned}$$

where \(l_0\), \(l_1\), \(m_0\), \(m_1\), \(m_2\), \(\omega _1\), \(\omega _3\) are free parameters.

Utilizing all the above determined parameters in Eq. (25) and with the aid of Eq. (5), we get the solution \(\mu _{19}(x,y,t)\).

5 Travelling-wave solutions for Eq. (4)

In this section, we employ the polynomial-expansion method to find some new exact travelling wave solutions for Eq. (4). Consequently, we use the transformation stated as

$$\begin{aligned} \mu (x,y,t)= \Omega (\eta ),~~~~~~~\eta =a x+b y-c t, \end{aligned}$$
(26)

where a,  b are constants and  c is the velocity of the wave. Substituting Eq. (26) into Eq. (4), we have

$$\begin{aligned}&\alpha _1 a^6 \Omega ^{(6)}(\eta )+15 \alpha _1 a^5 \left( \Omega ^{(4)}(\eta ) \Omega '(\eta )+\Omega ^{(3)}(\eta ) \Omega ''(\eta )\right) \nonumber \\&\quad +45 \alpha _1 a^4 \Omega '(\eta )^2 \Omega ''(\eta )+\left( \alpha _4 a^2-\alpha _5 a c+\alpha _6 b^2\right) \Omega ''(\eta ) \nonumber \\&\quad + \left( a^4 \alpha _2-a^3 \alpha _3 b\right) \Omega ^{(4)}(\eta )+\left( 6 \alpha _2 a^3+6 \alpha _3 a^2 b\right) \Omega '(\eta ) \Omega ''(\eta )=0, \end{aligned}$$
(27)

through integration, we retrieve the result

$$\begin{aligned}&\alpha _1 a^6 \Omega ^{(5)}(\eta )+15 \alpha _1 a^5 \left( \Omega ^{(3)}(\eta ) \Omega '(\eta )\right) +15 \alpha _1 a^4 \Omega '(\eta )^3\nonumber \\&\quad +\left( \alpha _4 a^2-\alpha _5 a c+\alpha _6 b^2\right) \Omega '(\eta ) + \left( a^4 \alpha _2-a^3 \alpha _3 b\right) \Omega ^{(3)}(\eta )\nonumber \\&\quad +\left( 3 \alpha _2 a^3+3 \alpha _3 a^2 b\right) \Omega '(\eta )^2=0, \end{aligned}$$
(28)

Utilizing the specified method, we suppose the solution for Eq. (28) given by

$$\begin{aligned} \Omega (\eta )=\xi _0+\sum _{j=1}^m \xi _j \phi (\eta )^j+\sum _{j=1}^m \zeta _j \phi (\eta )^{-j}, \end{aligned}$$
(29)

while \(\phi (\eta )\) satisfies

$$\begin{aligned} \phi '(\eta )= \phi (\eta )^2+{\mathcal {R}}\phi (\eta )+{\mathcal {Q}}, \end{aligned}$$
(30)

here  \(\xi _0\), \(\xi _{j}\)’s, \(\zeta _{j}\)’s, \({\mathcal {R}}\), \({\mathcal {Q}}\) are constants and m is a positive integer. As a result, we retrieve the following exact solutions:

(1) when \({\mathcal {R}}=0\), \({\mathcal {Q}}=0\),

$$\begin{aligned} \phi (\eta )= -\frac{1}{\eta }; \end{aligned}$$
(31)

(2) when \({\mathcal {R}}\ne 0\), \({\mathcal {Q}}=0\),

$$\begin{aligned} \phi (\eta )= -\frac{{\mathcal {R}}}{{\mathcal {C}}_0 e^{-{\mathcal {R}} \eta }-1}, \end{aligned}$$
(32)

here \({\mathcal {C}}_0\) is the constant of integration;

(3) when \({\mathcal {R}}=0\), \({\mathcal {Q}}\ne 0\),

If \(Q>0\), then

$$\begin{aligned}&\quad \phi (\eta )=\sqrt{{\mathcal {Q}}} \tan \left( \sqrt{{\mathcal {Q}}} \eta \right) , \\&\quad \phi (\eta )=-\sqrt{-{\mathcal {Q}}} \cot \left( \sqrt{{\mathcal {Q}}} \eta \right) , \end{aligned}$$

If \(Q<0\), then

$$\begin{aligned}&\quad \phi (\eta )=-\sqrt{-{\mathcal {Q}}} \tanh \left( \sqrt{-{\mathcal {Q}}} \eta \right) ,\\&\quad \phi (\eta )=\sqrt{-{\mathcal {Q}}} \coth \left( \sqrt{-{\mathcal {Q}}} \eta \right) ; \end{aligned}$$

(4) when \({\mathcal {R}}\ne 0\), \({\mathcal {Q}}\ne 0\),

$$\begin{aligned} \phi (\eta )=\frac{\kappa _1-{\mathcal {C}}_1 \kappa _2 e^{\left( \kappa _1-\kappa _2\right) \eta }}{1-{\mathcal {C}}_1 e^{\left( \kappa _1-\kappa _2\right) \eta }}, \end{aligned}$$
(33)

where

$$\begin{aligned} \kappa _1=\frac{1}{4} \left( \sqrt{{\mathcal {R}}^2-4 {\mathcal {Q}}}-{\mathcal {R}}\right) ,~~\kappa _2=\frac{1}{4} \left( -\sqrt{{\mathcal {R}}^2-4 {\mathcal {Q}}}-{\mathcal {R}}\right) , \end{aligned}$$

here \({\mathcal {C}}_1\) is the constant of integration.

Comparing \(\Omega ^{(5)}(\eta )\) with \(\Omega '(\eta ) \Omega ^{(3)}(\eta )\) in Eq. (28) we have  \(m = 1\). As a result, Eq. (29) can be expressed as

$$\begin{aligned} \Omega (\eta )=\xi _0+\xi _1 \phi (\eta )+\frac{\zeta _1}{\phi (\eta )}. \end{aligned}$$
(34)

Utilizing Eq. (34) together with Eq. (30) into Eq. (28) and balancing the coefficients of  \(\phi ^i(\eta )\) to zero, we have a set of equations involving several parameters. We get the following findings by resolving them utilizing a computational programme such as Mathematica. Set 1:

$$\begin{aligned} {\mathcal {R}}={\mathcal {Q}}=\xi _1=0,~\zeta _1=\frac{3 \alpha _2 a^3+3 \alpha _3 a^2 b+Z}{30 a^4 \alpha _1}, \end{aligned}$$

where

$$\begin{aligned} Z=\sqrt{60 \alpha _1 a^4 \left( -a^2 \alpha _4+\alpha _5 a c-\alpha _6 b^2\right) +\left( 3 \alpha _2 a^3+3 \alpha _3 a^2 b\right) ^2}, \end{aligned}$$

Set 2:

$$\begin{aligned}&c=\frac{-4 \alpha _2^2 a^2+25 \alpha _1 \alpha _4 a^2-4 \alpha _2 \alpha _3 a b+24 \alpha _3^2 b^2+25 \alpha _1 \alpha _6 b^2}{25 a \alpha _1 \alpha _5},\\&\quad {\mathcal {R}}=\frac{\sqrt{-a \alpha _2-3 \alpha _3 b}}{\sqrt{5} a^{3/2} \sqrt{\alpha _1}},~\zeta _1={\mathcal {Q}}=0,~\xi _1=-4 a \end{aligned}$$

Set 3:

$$\begin{aligned}&{\mathcal {R}}=0,~{\mathcal {Q}}=\frac{a \alpha _2+3 \alpha _3 b}{80 a^3 \alpha _1},~\xi _1=-4 a,~\zeta _1=\frac{a \alpha _2+3 \alpha _3 b}{20 a^2 \alpha _1},\\&\quad c=\frac{-4 \alpha _2^2 a^2+25 \alpha _1 \alpha _4 a^2-4 \alpha _2 \alpha _3 a b+24 \alpha _3^2 b^2+25 \alpha _1 \alpha _6 b^2}{25 a \alpha _1 \alpha _5} \end{aligned}$$

Set 4:

$$\begin{aligned}&c=\frac{-4 \alpha _2^2 a^2+25 \alpha _1 \alpha _4 a^2-4 \alpha _2 \alpha _3 a b+24 \alpha _3^2 b^2+25 \alpha _1 \alpha _6 b^2}{25 a \alpha _1 \alpha _5},\\&\quad \zeta _1=0,~{\mathcal {R}}=\frac{i \sqrt{-20 \alpha _1 a^3 {\mathcal {Q}}+\alpha _2 a+3 \alpha _3 b}}{\sqrt{5} a^{3/2} \sqrt{\alpha _1}},~\xi _1=-4 a. \end{aligned}$$

Hence utilizing all the above determined results, we construct the travelling-wave solutions for Eq. (4) as

Type 1:     When \({\mathcal {R}}=0\) and \({\mathcal {Q}}=0\), we get the solution

$$\begin{aligned} \mu _{20}(x,y,t)=\xi _0+\frac{\left( 3 \alpha _2 a^3+3 \alpha _3 a^2 b+Z\right) (-a x-b y+c t)}{30 a^4 \alpha _1}, \end{aligned}$$
(35)

where

$$\begin{aligned} Z=\sqrt{60 \alpha _1 a^4 \left( -a^2 \alpha _4+\alpha _5 a c-\alpha _6 b^2\right) +\left( 3 \alpha _2 a^3+3 \alpha _3 a^2 b\right) ^2}. \end{aligned}$$

Type 2:     When \({\mathcal {R}}\ne 0\) and \({\mathcal {Q}}=0\), we obtain the solution

$$\begin{aligned} \mu _{21}(x,y,t)=\xi _0+\frac{4 \sqrt{-a \alpha _2-3 \alpha _3 b}}{\sqrt{5} \sqrt{a} \sqrt{\alpha _1} \left( {\mathcal {C}}_0 e^{-\frac{\eta \sqrt{-a \alpha _2-3 \alpha _3 b}}{\sqrt{5} a^{3/2} \sqrt{\alpha _1}}}-1\right) }, \end{aligned}$$
(36)

where

$$\begin{aligned} \eta =a x+b y-\frac{ \left( -4 \alpha _2^2 a^2+25 \alpha _1 \alpha _4 a^2-4 \alpha _2 \alpha _3 a b+24 \alpha _3^2 b^2+25 \alpha _1 \alpha _6 b^2\right) t}{25 a \alpha _1 \alpha _5}. \end{aligned}$$

Type 3:     When \({\mathcal {R}}=0\) and \({\mathcal {Q}}>0\), we attain the solution

$$\begin{aligned}&\mu _{22}(x,y,t)=\xi _0+\frac{\left( a \alpha _2+3 \alpha _3 b\right) \cot \left( \frac{\eta \sqrt{\frac{a \alpha _2+3 \alpha _3 b}{a^3 \alpha _1}}}{4 \sqrt{5}}\right) }{\sqrt{5} a^2 \alpha _1 \sqrt{\frac{a \alpha _2+3 \alpha _3 b}{a^3 \alpha _1}}}\nonumber \\&\quad -\frac{a \sqrt{\frac{a \alpha _2+3 \alpha _3 b}{a^3 \alpha _1}} \tan \left( \frac{\eta \sqrt{\frac{a \alpha _2+3 \alpha _3 b}{a^3 \alpha _1}}}{4 \sqrt{5}}\right) }{\sqrt{5}}, \end{aligned}$$
(37)

where

$$\begin{aligned} \eta =a x+b y-\frac{ \left( -4 \alpha _2^2 a^2+25 \alpha _1 \alpha _4 a^2-4 \alpha _2 \alpha _3 a b+24 \alpha _3^2 b^2+25 \alpha _1 \alpha _6 b^2\right) t}{25 a \alpha _1 \alpha _5}. \end{aligned}$$

Type 4:     When \({\mathcal {R}}=0\) and \({\mathcal {Q}}<0\), we retrieve the solution

$$\begin{aligned}&\mu _{23}(x,y,t)=\xi _0-\frac{\left( a \alpha _2+3 \alpha _3 b\right) \coth \left( \frac{\eta \sqrt{-\frac{a \alpha _2+3 \alpha _3 b}{a^3 \alpha _1}}}{4 \sqrt{5}}\right) }{\sqrt{5} a^2 \alpha _1 \sqrt{-\frac{a \alpha _2+3 \alpha _3 b}{a^3 \alpha _1}}}\nonumber \\&\quad +\frac{a \sqrt{-\frac{a \alpha _2+3 \alpha _3 b}{a^3 \alpha _1}} \tanh \left( \frac{\eta \sqrt{-\frac{a \alpha _2+3 \alpha _3 b}{a^3 \alpha _1}}}{4 \sqrt{5}}\right) }{\sqrt{5}}, \end{aligned}$$
(38)

where

$$\begin{aligned} \eta =a x+b y-\frac{ \left( -4 \alpha _2^2 a^2+25 \alpha _1 \alpha _4 a^2-4 \alpha _2 \alpha _3 a b+24 \alpha _3^2 b^2+25 \alpha _1 \alpha _6 b^2\right) t}{25 a \alpha _1 \alpha _5}. \end{aligned}$$

Type 5:     When \({\mathcal {R}}=0\) and \({\mathcal {Q}}<0\), we have

$$\begin{aligned} \mu _{24}(x,y,t)=\xi _0-4 a (\frac{\kappa _1-{\mathcal {C}}_1 \kappa _2 e^{\left( \kappa _1-\kappa _2\right) \eta }}{1-{\mathcal {C}}_1 e^{\left( \kappa _1-\kappa _2\right) \eta }}) \end{aligned}$$
(39)

where

$$\begin{aligned}&\quad \kappa _1=\frac{1}{4} \left( \sqrt{-\frac{-20 \alpha _1 a^3 {\mathcal {Q}}+\alpha _2 a+3 \alpha _3 b}{5 a^3 \alpha _1}-4 {\mathcal {Q}}}-\frac{i \sqrt{-20 \alpha _1 a^3 {\mathcal {Q}}+\alpha _2 a+3 \alpha _3 b}}{\sqrt{5} a^{3/2} \sqrt{\alpha _1}}\right) ,\\&\quad \kappa _2=\frac{1}{4} \left( -\sqrt{-\frac{-20 \alpha _1 a^3 {\mathcal {Q}}+\alpha _2 a+3 \alpha _3 b}{5 a^3 \alpha _1}-4 {\mathcal {Q}}}-\frac{i \sqrt{-20 \alpha _1 a^3 {\mathcal {Q}}+\alpha _2 a+3 \alpha _3 b}}{\sqrt{5} a^{3/2} \sqrt{\alpha _1}}\right) ,\\&\quad \eta =a x+b y-\frac{ \left( -4 \alpha _2^2 a^2+25 \alpha _1 \alpha _4 a^2-4 \alpha _2 \alpha _3 a b+24 \alpha _3^2 b^2+25 \alpha _1 \alpha _6 b^2\right) t}{25 a \alpha _1 \alpha _5}. \end{aligned}$$

6 Discussion and results

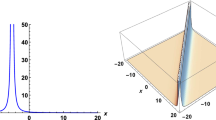
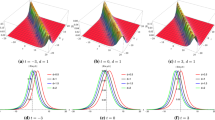
 The graphical description of the (2+1)-dimensional pKP-BKP equation are demonstrated in this section. Using a specified range of values, various forms of v-shaped, singular bell-shaped, periodic and bright solitons are displayed. Figure 1 depicts the profiles of \(|\mu _1(x,y,t)|\) which exhibits a v-shaped soliton solution using constants  \(\alpha _2=2,~\alpha _3=-1.5,~\alpha _4=0.4,~\alpha _5=0.5,~\alpha _6=0.75,~g=2.5,~l_1=0.4,~l_2=0.5,~m_1=-1.5,~m_2=0.45\). Moreover, Figs. 2,3,4,5,6 represent the v-shaped soliton solutions for various constant values. Figure 7 represents the behaviour of solution \(|\mu _3(x,y,t)|\) which illustrates the singular bell shaped solution using parameters  \(\alpha _4=0.45,~\alpha _5=0.55,~\alpha _6=0.75,~=2.5,~l_1=-0.4,~l_2=0.5,~l_3=0.6\). Consequently, Figs.  8,9,10,11 demonstrate the singular bell shaped solutions for specified parameters. Singularities may exist almost anywhere and they are surprisingly abundant in the mathematics used by physicists to understand the universe. Figure 12 depicts the behaviour of solution \(|\mu _{12}(x,y,t)|\) which describes the periodic solitary waves solution utilizing constants  \(\alpha _2=0.55,~\alpha _3=0.5,~\alpha _4=0.45,~\alpha _5=0.5,~\alpha _6=0.75,~n_0=0.15,~n_1=0.95,~n_2=-0.95\). Moreover, Figure 13 display the periodic solitary waves solutions for various constant values. Figure 14 represents the profiles of \(|\mu _{16}(x,y,t)|\) which illustrates the bright soliton solution utilizing parameters  \(\alpha _1=1.2,~\alpha _2=2,~\alpha _3=-1.5,~\alpha _4=0.4,~\alpha _5=0.5,~\alpha _6=0.75,~m_0=0.5,~n_0=-0.85,~n_1=0.225,~n_2=0.8,~\omega _2=0.75,~\omega _3=0.65\). Also, Figs.  15, 16 demonstrate the bright soliton solution for specified parameters. Lastly, we have illustrated 3D, contour and 2D graphs of various retrieved solutions to have a better understanding of the behaviour of solutions.

Fig. 1
figure 1

3D, contour and 2D plots for \(|\mu _1(x,y,t)|\) with  \(\alpha _2=2,~\alpha _3=-1.5,~\alpha _4=0.4,~\alpha _5=0.5,~\alpha _6=0.75,~g=2.5,~l_1=0.4,~l_2=0.5,~m_1=-1.5,~m_2=0.45\)

Full size image
Fig. 2
figure 2

3D, contour and 2D plots for \(|\mu _3(x,y,t)|\) with  \(\alpha _4=0.45,~\alpha _5=0.55,~\alpha _6=0.75,~=2.5,~l_1=-0.4,~l_2=0.5,~l_3=0.6\)

Full size image
Fig. 3
figure 3

3D, contour and 2D plots for \(|\mu _4(x,y,t)|\) with  \(\alpha _1=0.2,~\alpha _2=0.25,~\alpha _3=2.5,~\alpha _4=0.4,~\alpha _5=0.5,~\alpha _6=0.75,~n_0=0.7,~n_1=-1.5,~n_2=0.75,~n_3=0.25,~\omega _0=1.755,~\omega _3=-0.6\)

Full size image
Fig. 4
figure 4

3D, contour and 2D plots for \(|\mu _6(x,y,t)|\) with  \(\alpha _1=0.15,~\alpha _2=0.2,~\alpha _3=0.4,~\alpha _4=0.3,~\alpha _5=0.5,~\alpha _6=0.85,~l_0=0.1,~l_3=0.4,~m_0=0.5,~m_1=0.25,~m_3=0.35,~\omega _1=0.5\)

Full size image
Fig. 5
figure 5

3D, contour and 2D plots for \(|\mu _8(x,y,t)|\) with  \(\alpha _2=0.55,~\alpha _3=0.5,~\alpha _4=0.45,~\alpha _5=0.5,~\alpha _6=0.75,~n_0=0.15,~n_1=0.75,~n_2=-0.65\)

Full size image
Fig. 6
figure 6

3D, contour and 2D plots for \(|\mu _{10}(x,y,t)|\) with  \(\alpha _4=0.45,~\alpha _5=0.5,~\alpha _6=0.85,~l_0=0.15,~l_1=0.3,~l_2=0.35,~m_0=0.4,~m_2=0.25,~m_3=0.35,~\omega _1=0.5,~\omega _2=0.6\)

Full size image
Fig. 7
figure 7

3D, contour and 2D plots for \(|\mu _{12}(x,y,t)|\) with  \(\alpha _2=0.55,~\alpha _3=0.5,~\alpha _4=0.45,~\alpha _5=0.5,~\alpha _6=0.75,~n_0=0.15,~n_1=0.95,~n_2=-0.95\)

Full size image
Fig. 8
figure 8

3D, contour and 2D plots for \(|\mu _{13}(x,y,t)|\) with  \(\alpha _4=0.45,~\alpha _5=0.5,~\alpha _6=0.75,~l_0=0.5,~l_1=-2.75,~l_2=2.55,~m_0=0.5,~m_1=1.25,~m_3=1.55,~\omega _1=0.5\)

Full size image
Fig. 9
figure 9

3D, contour and 2D plots for \(|\mu _{15}(x,y,t)|\) with  \(\alpha _2=0.55,~\alpha _3=0.5,~\alpha _4=0.45,~\alpha _5=0.5,~\alpha _6=0.75,~n_0=0.15,~n_1=1.95,~n_3=0.95\)

Full size image
Fig. 10
figure 10

3D, contour and 2D plots for \(|\mu _{16}(x,y,t)|\) with  \(\alpha _1=1.2,~\alpha _2=2,~\alpha _3=-1.5,~\alpha _4=0.4,~\alpha _5=0.5,~\alpha _6=0.75,~m_0=0.5,~n_0=-0.85,~n_1=0.225,~n_2=0.8,~\omega _2=0.75,~\omega _3=0.65\)

Full size image
Fig. 11
figure 11

3D, contour and 2D plots for \(|\mu _{17}(x,y,t)|\) with  \(\alpha _1=0.45,~\alpha _2=0.25,~\alpha _3=0.25,~\alpha _4=0.3,~\alpha _5=0.4,~\alpha _6=0.35,~m_0=0.125,~m_1=0.35,~m_2=0.25,~n_0=0.125,~\omega _2=0.55,~\omega _3=0.75\)

Full size image
Fig. 12
figure 12

3D, contour and 2D plots for \(|\mu _{18}(x,y,t)|\) with  \(\alpha _1=0.15,~\alpha _2=0.25,~\alpha _3=0.5,~\alpha _4=0.4,~\alpha _5=0.5,~\alpha _6=0.55,~l_0=0.25,~l_1=-0.75,~l_2=0.35,~\omega _1=0.5,~\omega _2=0.85\)

Full size image
Fig. 13
figure 13

3D, contour and 2D plots for \(|\mu _{19}(x,y,t)|\) with  \(\alpha _1=0.2,~\alpha _2=0.25,~\alpha _3=0.5,~\alpha _4=0.4,~\alpha _5=0.5,~\alpha _6=0.55,~l_0=0.5,~l_1=0.65,~m_0=0.5,~m_1=0.75,~m_2=0.35,~\omega _1=1,~\omega _3=1\)

Full size image
Fig. 14
figure 14

3D, contour and 2D plots for \(|\mu _{21}(x,y,t)|\) with  \(a=0.7,~b=0.5,~c=0.5,~\alpha _1=0.6,~\alpha _2=1.2,~\alpha _3=0.5,~\alpha _4=0.45,~\alpha _5=0.55,~\alpha _6=0.75,~{\mathcal {C}}_0=0.5,~\xi _0=1.6\)

Full size image
Fig. 15
figure 15

3D, contour and 2D plots for \(|\mu _{23}(x,y,t)|\) with  \(a=0.75,~b=0.55,~c=0.65,~\alpha _1=0.5,~\alpha _2=1.12,~ _3=0.45,~\alpha _4=0.5,~\alpha _5=0.65,~\alpha _6=0.5,~\xi _0=1.56\)

Full size image
Fig. 16
figure 16

3D, contour and 2D plots for \(|\mu _{23}(x,y,t)|\) with  \(a=0.75,~b=0.55,~c=0.55,~\alpha _1=0.56,~\alpha _2=1.12,~\alpha _3=0.65,~M=0.45,~\alpha _4=0.455,~\alpha _5=0.55,~\alpha _6=0.75,~\xi _0=1.6,~{\mathcal {C}}_1=0.5\)

Full size image

7 Conclusion

In this manuscript, the (2+1)-dimensional pKP-BKP equation is investigated utilizing the Hirota bilinear method and the polynomial-expansion method. Consequently, we have generated a variety of fascinating exact solutions to the considered equation using various types of functions. Additionally, using Mathematica 11.0, we were able to generate numerous graphical representations of the specified solutions utilizing various parameters. Lastly, we assert that the methodologies under consideration are applicable to a wide range of NLEEs in mathematical physics.