Stability of Gaussian-type light bullets in the cubic-quintic-septimal nonlinear media with different diffractions under ${\mathcal {PT}}$-symmetric potentials

Abstract

From the governing equation $-(3+1)$-dimensional nonlinear Schrödinger equation with cubic-quintic-septimal nonlinearities, different diffractions and ${\mathcal {PT}}$-symmetric potentials, we obtain two kinds of analytical Gaussian-type light bullet solutions. The septimal nonlinear term has a strong impact on the formation of light bullets. The eigenvalue method and direct numerical simulation to analytical solutions imply that stable and unstable evolution of light bullets against white noise attributes to the coaction of cubic-quintic-septimal nonlinearities, dispersion, different diffractions and ${\mathcal {PT}}$-symmetric potential.

1 Introduction

As one of dispersive nonlinear evolutional equations [1,2,3], the nonlinear Schrödinger equation (NLSE) stands out as a prototypical and essential model to describe features of numerous fields in mathematical physics [4,5,6,7]. Based on NLSE, spatiotemporal optical similaritons in dual-core waveguide with an external source were studied [8]. In optics, high power of incident light makes the medium exhibit complicated nonlinearities. It is most common that Kerr nonlinearity compensates dispersion/diffraction to induce self-trapped soliton [9, 10]. The competition between focusing cubic and defocusing quintic nonlinearities supports stable soliton solution [11]. Higher-order nonlinearities lead to unstable soliton propagation in $(1 + 1)$-dimension [12]. In previous literatures [13, 14], higher-order dissipative terms are introduced to suppress the collapse.

When higher-order nonlinearity is considered, spatial solitons can also propagate stably. Recently, dissipative term is considered to induce $(2 + 1)$-dimensional bright spatial solitons in metal colloids with focusing quintic and defocusing septimal nonlinearities [15]. More recently, parity-time (${\mathcal {PT}}$) symmetric potentials, which are introduced from quantum mechanics [16], are used to produce stable localized spatial solitons to interplay with power-law nonlinearity [17]. Light bullet in ${\mathcal {PT}}$-potentials has also been discussed [18]. Light bullet in the media with same diffraction and ${\mathcal {PT}}$-potentials have also been studied [19]. Sech-type and Gaussian-type light bullet solutions to the generalized $(3 + 1)$-dimensional cubic-quintic NLSE in ${\mathcal {PT}}$-symmetric potentials were reported [20]. Therefore, ${\mathcal {PT}}$-symmetric potentials become a good tool to stabilize spatial and spatiotemporal solitons [17,18,19,20]. Moreover, controllable behaviors of rogue waves in ${\mathcal {PT}}$-potentials have also extensively discussed [21,22,23].

More recently, the stability of $(1 + 1)$-dimensional sech-type solitons is studied with the consequence of cubic-quintic-septimal nonlinearities and diffraction [24]. However, in this work [24], the ${\mathcal {PT}}$-symmetric potentials have not been studied. Considering that Gaussian shape is very fundamental shape of pulse in the optical experiment, in this paper, we study the stability of Gaussian-type light bullets (spatiotemporal solitons) under the interplay among cubic-quintic-septimal nonlinearity, dispersion, different diffractions and ${\mathcal {PT}}$-symmetric potentials based on the following NLSE

$$\begin{aligned} \text {i}u_z+ & {} \beta _1u_{xx}+\beta _2u_{yy}+\beta _3u_{tt}+\gamma _3|u|^{2}u\nonumber \\+ & {} \gamma _5|u|^{4}u+\gamma _7|u|^{6}u+[v(x,y,t)\nonumber \\+ & {} \text {i}w(x,y,t)]u=0, \end{aligned}$$

(1)

which describes the propagation of an optical pulse in a nonlinear medium of non-Kerr index which is perturbed by a complex profile $n=n_0[1+\delta n_R(x, y, t)+\text {i}\delta n_I(x, y, t)]$ with complex envelope of the electrical field u(z, x, y, t) and transverse spatial coordinates x, y and the retarded time t. The second to fourth terms describe different diffractions in (x, y)-directions and dispersion, the fifth to seventh terms denote the cubic, quintic and septimal nonlinearities. Last two terms represent the complex ${\mathcal {PT}}$-symmetric potential with odd function of the real component $v(x,y,t)\equiv k_0^2w_0^2\delta n_R(x,y,t)$ describing the index guiding and even function of imaginary component $w(x,y,t)\equiv k_0^2w_0^2\delta n_I(x,y,t)$ describing the gain/loss distribution. In semiconductor optical amplifiers, the gain/loss levels are approximate to $\pm 40\,\text {cm}^{-1}$ at wavelengths of $\approx 1\,\mu \text {m}$, which should be sufficient to observe ${\mathcal {PT}}$ behavior [25].

When $\beta _1=\beta _2=\beta _3$, Eq. (1) is the model in Ref. [19], where sech-type light bullet solutions were studied. If $\gamma _7=0$, higher-dimensional localized mode families were studied in ${\mathcal {PT}}$-symmetric potentials with competing nonlinearities and same values of dispersion and diffractions [26]. If the ${\mathcal {PT}}$-symmetric potentials disappear with $v(x,y,t)=w(x,y,t)=0$ and $\beta _2=\beta _3=0$, Eq. (1) is the model in Ref. [24].

2 Analytical light bullet solutions

Assuming analytical solutions of Eq. (1) in the form $u(z,x,y,t)=\varPhi (x,y,t)\exp [\text {i} \lambda z$ $+\text {i}\varTheta (x,y,t)]$, Eq. (1) is separated into real and imaginary parts as

$$\begin{aligned}&\beta _1\left[ \frac{\partial ^2\varPhi }{\partial x^2}-\varPhi \left( \frac{\partial \varTheta }{\partial x} \right) ^2\right] +\beta _2\left[ \frac{\partial ^2\varPhi }{\partial y^2}-\varPhi \left( \frac{\partial \varTheta }{\partial y} \right) ^2\right] \nonumber \\&\quad +\,\beta _3\left[ \frac{\partial ^2\varPhi }{\partial t^2}-\varPhi \left( \frac{\partial \varTheta }{\partial t} \right) ^2\right] \nonumber \\&\quad +\,[v(x,y,t)-\lambda ]\varPhi +\gamma _{3}\varPhi ^{3}{+}\gamma _{5}\varPhi ^{5}{+}\gamma _{7}\varPhi ^{7}=0, \end{aligned}$$

(2)

$$\begin{aligned}&\beta _1\left( \varPhi \frac{\partial ^2\varTheta }{\partial x^2}+2\frac{\partial \varPhi }{\partial x}\frac{\partial \varTheta }{\partial x}\right) +\beta _2\left( \varPhi \frac{\partial ^2\varTheta }{\partial y^2}+2\frac{\partial \varPhi }{\partial Y}\frac{\partial \varTheta }{\partial y}\right) \nonumber \\&\quad +\,\beta _3\left( \varPhi \frac{\partial ^2\varTheta }{\partial t^2}+2\frac{\partial \varPhi }{\partial t}\frac{\partial \varTheta }{\partial t}\right) \nonumber \\&\quad +\,w(x,y,t)\varPhi =0. \end{aligned}$$

(3)

Under two different ${\mathcal {PT}}$-symmetric potentials, we focus on two families of Gaussian-type light bullet solutions of Eq. (1) because Gaussian shape is very fundamental shape of pulse in the optical experiment.

2.1 Family 1

If the ${\mathcal {PT}}$-symmetric potential has the form

$$\begin{aligned} v(x,y,t)= & {} -4\left( \beta _1 b_1^4x^2+\beta _2 b_2^4y^2+\beta _3 b_3^4t^2\right) \nonumber \\&+\,\frac{w_{1}^2}{36\beta _1 b_1^4}\text {e}^{-2b_1^2x^2}+\frac{w_{2}^2}{36\beta _2 b_2^4}\text {e}^{-2b_2^2y^2}\nonumber \\&+\,\frac{w_{3}^2}{36\beta _3 b_3^4}\text {e}^{-2b_3^2t^2}\nonumber \\&-\,\gamma _3 \left( \frac{-v_1}{\gamma _7}\right) ^{1/3}\text {e}^{-2b_1^2x^2-2b_2^2y^2-2b_3^2t^2}\nonumber \\&-\,\gamma _5\left( \frac{-v_1}{\gamma _7}\right) ^{2/3}\text {e}^{-4b_1^2x^2 -4b_2^2y^2-4b_3^2t^2}\nonumber \\&+\,v_1\text {e}^{-6b_1^2x^2-6b_2^2y^2-6b_3^2t^2}, \end{aligned}$$

(4)

$$\begin{aligned} w(x,y,t)= & {} w_{1}x\text {e}^{-b_1^2x^2}+w_{2}y\text {e}^{-b_2^2y^2} +w_{3}t\text {e}^{-b_3^2t^2},\nonumber \\ \end{aligned}$$

(5)

with arbitrary constants $v_1,w_1,w_2,w_3,b_1,b_2$ and $b_3$, and considering the localization of solution as $\{x,y,t\}\rightarrow \pm \infty$, Eq. (1) has solution

$$\begin{aligned} u(z,x,y,t)= & {} \left( {-\frac{v_1}{\gamma _{7}}}\right) ^{\frac{1}{6}} \exp \left( -b_1^2x^2-b_2^2y^2-b_3^2t^2\right) \nonumber \\&\exp [\text {i}\varPsi (z,x,y,t)], \end{aligned}$$

(6)

where $\varPsi (z,x,y,t)=-2(\beta _1 b_1^2+\beta _2 b_2^2+\beta _3 b_3^2) z +\frac{w_1\sqrt{\pi }}{12\beta _1 b_1^3}\text {erf}(b_1x)+\frac{w_2\sqrt{\pi }}{12\beta _2 b_2^3}\text {erf}(b_2y)+\frac{w_3\sqrt{\pi }}{12\beta _3 b_3^3}\text {erf}(b_3t)$ with the error function $\text {erf}(X)=\frac{2}{\sqrt{\pi }}\int ^X_0e^{-\varsigma ^2}d\varsigma$ [27].

2.2 Family 2

If the ${\mathcal {PT}}$-symmetric potential reads

$$\begin{aligned} v(x,y,t)= & {} -\frac{4}{9}\left( \beta _1 b_1^4x^2+\beta _2 b_2^4y^2+\beta _3 b_3^4t^2\right) \nonumber \\&+\,\frac{9w_{1}^2}{100\beta _1 b_1^4}\text {e}^{-2b_1^2x^2}+\frac{9w_{2}^2}{100\beta _2 b_2^4}\text {e}^{-2b_2^2y^2}\nonumber \\&+\,\frac{9w_{3}^2}{100\beta _3 b_3^4}\text {e}^{-2b_3^2t^2}+v_2\text {e}^{-2b_1^2x^2-2b_2^2y^2-2b_3^2t^2}\nonumber \\&-\,\gamma _3\left( \frac{-v_2}{\gamma _7}\right) ^{1/3}\text {e}^{-\frac{2}{3} (b_1^2x^2+b_2^2y^2+b_3^2t^2)}\nonumber \\&-\,\gamma _5\left( \frac{-v_2}{\gamma _7}\right) ^{2/3}\text {e}^{-\frac{4}{3} (b_1^2x^2+b_2^2y^2+b_3^2t^2)}, \end{aligned}$$

(7)

$$\begin{aligned} w(x,y,t)= & {} w_{1}x\text {e}^{-b_1^2x^2}+w_{2}y\text {e}^{-b_2^2y^2}+w_{3}t\text {e}^{-b_3^2t^2},\nonumber \\ \end{aligned}$$

(8)

with arbitrary constants $v_2,w_1,w_2,w_3,b_1,b_2$ and $b_3$, and considering the localization of solution as $\{x,y,t\}\rightarrow \pm \infty$, solution of Eq. (1) reads

(9)

where $\varPsi (z,x,y,t)=-\frac{2}{3}(\beta _1 b_1^2+\beta _2 b_2^2+\beta _3 b_3^2) z +\frac{3w_1\sqrt{\pi }}{20\beta _1 b_1^3}\text {erf}(b_1x)+\frac{3w_2\sqrt{\pi }}{20\beta _2 b_2^3}\text {erf}(b_2y)+\frac{3w_3\sqrt{\pi }}{20\beta _3 b_3^3}\text {erf}(b_3t)$.

Fig. 1

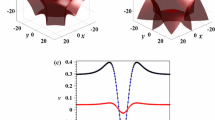
(Color online) Eigenvalues for solution (6) in the media with a focusing cubic, quintic and septimal nonlinearities, b focusing cubic and septimal nonlinearities with disappearing quintic nonlinearity, c focusing quintic and septimal nonlinearities with defocusing cubic nonlinearity, d focusing septimal and defocusing cubic nonlinearities with disappearing quintic nonlinearity, e defocusing cubic and septimal nonlinearities with focusing quintic nonlinearity and f defocusing cubic and septimal nonlinearities with disappearing quintic nonlinearity under the ${\mathcal {PT}}$-symmetric potential (4) and (5). Parameters are chosen as $\beta _1=0.5, \beta _2=0.46, \beta _3=0.45, b_1=0.5, b_2=0.48, b_3=0.47$ with a $w_{1}=0.056, w_{2}=0.057, w_3=0.057$, b $w_{1}=0.1, w_{2}=0.11,w_3=0.11$, c $w_{1}=0.3, w_{2}=0.21,w_3=0.21$, d $w_{1}=0.65, w_{2}=0.7,w_3=0.7$, and e, f $w_{1}=0.37, w_{2}=0.38,w_3=0.38$. Other parameters are shown in figures

3 Stability of light bullets from the eigenvalue method

We use the eigenvalue method to study the linear stability of analytical solutions (6) and (9) of Eq. (1). The perturbed solution reads $u(z,x,y,t)=\{u_0(x,y,t)+\varepsilon [R(x,y,t)+I(x,y,t)]\exp {(\text {i}\eta z)}\}\exp {(\text {i}\lambda z)}$, where $\varepsilon$ is an infinitesimal amplitude, $u_0(x,y,t)$ is an analytical solution (eigenmode) of Eq. (1), R(x, y, t) and I(x, y, t) are the real and imaginary parts of perturbation eigenfunctions, which may grow upon propagation with the perturbation growth rate $\eta$. If $\eta$ exists nonzero imaginary parts, the perturbed solution is linearly unstable, otherwise solution becomes stable.

Inserting the perturbed solution into Eq. (1) and linearizing it around the first-order term of $\varepsilon$ (the unperturbed one), the eigenvalue problem reads

$$\begin{aligned} \left( \begin{array}{cc} L_{+}&{}0\\ 0&{}L_{-} \end{array}\right) \left( \begin{array}{c} R\\ I \end{array}\right) =\eta \left( \begin{array}{c} I\\ R \end{array}\right) , \end{aligned}$$

(10)

where $\eta$ is an eigenvalue, R and I are eigenfunctions with Hermitian operators $L_{\pm }=-\beta _1\partial ^2_{x}-\beta _2\partial ^2_{y}-\beta _3\partial ^2_{t}-\sigma _{\pm }\gamma _3 u_0^2(x,y,t)-\mu _{\pm }\gamma _{5} u_0^{4}(x,y,t)-\nu _{\pm }\gamma _{7} u_0^{6}(x,y,t) -(v+\text {i}w)+\eta$ with $\sigma _{+}=3,\sigma _{-}=1$, $\mu _{+}=5,\mu _-=1$ and $\nu _{+}=7,\nu _-=1$.

From the eigenvalue spectra of the above problem (10), we know that the eigenvalue $\eta$ of solution (6) with (4) and (5) is real value only in the medium of focusing quintic and septimal nonlinearities with defocusing cubic nonlinearity [See Fig. 1(c)] when all parameters are chosen as those in figure; thus, solution (6) is stable in this medium, where values of $w_1, w_2$ and $w_3$ are smaller than the threshold values when parameters $\beta _1, \beta _2, \beta _3, \gamma _3, \gamma _5$ and $\gamma _7$ are chosen as some fixed values. For example, if parameters are chosen as $\beta _1=0.5, \beta _2=0.46, \beta _3=0.45, b_1=0.5, b_2=0.48, b_3=0.47$, the threshold values are close to $w_{1}\sim 0.3, w_{2}\sim 0.21, w_3\sim 0.21$. If values of $w_1, w_2$ and $w_3$ are chosen as those bigger than these threshold values, analytical solution (6) evolves unstably, however, smaller than these threshold values, analytical solution (6) becomes stable.

However, the eigenvalue $\eta$ exists imaginary parts in all other media, such as focusing cubic, quintic and septimal nonlinearities (See Fig. 1a), focusing cubic and septimal nonlinearities with disappearing quintic nonlinearity (See Fig. 1b), focusing septimal and defocusing cubic nonlinearities with disappearing quintic nonlinearity (See Fig. 1d), defocusing cubic and septimal nonlinearities with focusing quintic nonlinearity (See Fig. 1e) and defocusing cubic and septimal nonlinearities with disappearing quintic nonlinearity (See Fig. 1f); therefore, solution (6) is always unstable in these media. This result is different from that without considering ${\mathcal {PT}}$-symmetric potential in Ref. [24].

Fig. 2

(Color online) Eigenvalues for solution (9) in the media with a focusing cubic and septimal nonlinearities with disappearing quintic nonlinearity, b focusing quintic and septimal nonlinearities with defocusing cubic nonlinearity, c defocusing cubic and focusing septimal nonlinearities with disappearing quintic nonlinearity and d defocusing cubic and septimal nonlinearities with focusing quintic nonlinearity under the ${\mathcal {PT}}$-symmetric potential (7) and (8). Parameters are chosen as $\beta _1=0.5, \beta _2=0.46, \beta _3=0.45, b_1=0.5, b_2=0.48, b_3=0.47$ with a, c, d $w_{1}=0.1, w_{2}=0.11,w_3=0.11$ and b $w_{1}=0.3, w_{2}=0.21,w_3=0.21$. Other parameters are shown in figures

The similar eigenvalue method is used to solution (9) under the ${\mathcal {PT}}$-symmetric potential (7) and (8), and we find that the eigenvalue $\eta$ exists imaginary parts in all media regardless of focusing or defocusing cubic, quintic and septimal nonlinearities. As some examples, Figure 2 shows the imaginary eigenvalues for solution (9) in the media with focusing cubic and septimal nonlinearities with disappearing quintic nonlinearity (Fig. 2a), focusing quintic and septimal nonlinearities with defocusing cubic nonlinearity (Fig. 2b), defocusing cubic and focusing septimal nonlinearities with disappearing quintic nonlinearity (Fig. 2c) and defocusing cubic and septimal nonlinearities with focusing quintic nonlinearity (Fig. 2d). In these cases, solution (9) always evolves unstably.

4 Light bullets by interplay between cubic-quintic-septimal nonlinearities and ${\mathcal {PT}}$-symmetric potential

In the previous section, the stability of light bullets in different media is discussed by the eigenvalue method. In this section, based on these results from the eigenvalue method, we further study the role of cubic-quintic-septimal nonlinearities in the formation of light bullets by the split-step Fourier method. According to this method, we split Eq. (1) into a linear part including different diffraction and dispersion terms and a nonlinear part including the ${\mathcal {PT}}$-symmetric potential terms and cubic-quintic-septimal nonlinear terms. Actually, analytical solutions do not exactly describe the real situations; thus, it is valuable to study the stability of solutions against finite perturbations. We use the initial field coming from analytical solutions (6) and (9) with 5% initial white noise, and carry out the propagation of the optical pulse from z to $z+h$ in two steps with a small distance h, namely the nonlinear and linear parts play the role alone from z to $z+h/2$ (the first step) and then from $z+h/2$ to $z+h$ (the second step), respectively. This operation is worked again and again from initial distance to a long distance.

It is noted that the split-step Fourier method implies the periodic boundary conditions; thus, we need to analyze carefully the longitude and transverse step sizes, and choose the transverse window in order to ensure the numerical precision lest numerical instabilities from periodic boundary conditions. In Refs.[28, 29] computation precision in regard to the step size choice follows the criteria, namely step sizes in the longitude and transverse directions can be fixed from the spectrogram, and the transverse window can be chosen from the temporal figure.

From light bullet solutions (6) and (9), the septimal nonlinear coefficient $\gamma _7$ has strong impact on the formation of solution by influencing the amplitude of solutions. The real amplitude requires that $V_1\gamma _{7}<0$ or $V_2\gamma _{7}<0$, which indicates that light bullet solutions (6) and (9) can exist in focusing (positive) septimal nonlinearity with $\gamma _{7}>0$ as $V_1<0$ or $V_2<0$ and defocusing (negative) septimal nonlinearity with $\gamma _{7}<0$ as $V_1>0$ or $V_2>0$.

Fig. 3

(Color online) a Initial shape of intensity of light bullet (6); b, c, e, f Unstable light bullet (6) in the media corresponding to Figs. 1a, b, e, f at distance b $z=200$, c $z=400$, and e, f $z=100$; d Stable light bullet (6) in the medium corresponding to Fig. 1c at distance $z=400$. All parameters are chosen as those in Fig. 1

The stability of light bullet solutions (6) and (9) is related to the association of different cubic, quintic and septimal nonlinearities under the ${\mathcal {PT}}$-symmetric potential. Figure 3a exhibits the initial shape of light bullet (6) with a 5% white noise. In the medium of focusing septimal and defocusing cubic nonlinearities with disappearing quintic nonlinearity, the ${\mathcal {PT}}$ complex potential is strong enough to inhibit the collapse of light bullet solutions caused by diffraction, dispersion and nonlinearities. In Fig. 3d, the numerical simulation does not yield any visible instability, and the influence of initial 5% white noise is suppressed, and light bullet (6) stably evolves over hundreds of diffraction/dispersion lengths except for some small oscillations around its surface.

However, after the evolution of different distances, light bullet (6) displays unstable behaviors in the media of focusing cubic, quintic and septimal nonlinearities (Fig. 3b), focusing cubic and septimal nonlinearities with disappearing quintic nonlinearity (Fig. 3c), defocusing cubic and septimal nonlinearities with focusing quintic nonlinearity (Fig. 3e) and defocusing cubic and septimal nonlinearities with disappearing quintic nonlinearity (Fig. 3f). In these media, light bullet (6) cannot maintain its original shape, then is distorted and broken up, and ultimately collapses into noise.

Compared these plots in Figs. 3b, c, e and f, light bullet (6) is relatively stable in the medium of focusing cubic and septimal nonlinearities with disappearing quintic nonlinearity because there only exist some large oscillations around its surface and little collapse (Fig. 3c); however, the degree of collapse is strongest in the medium of defocusing cubic and septimal nonlinearities with focusing quintic nonlinearity (Fig. 3e).

Fig. 4

(Color online) Unstable light bullet (9) in the media corresponding to Fig. 2. All parameters are chosen as those in Fig. 2

When light bullet (9) evolves in various nonlinear media, it is unstable regardless of focusing or defocusing cubic, quintic and septimal nonlinearities under the ${\mathcal {PT}}$-symmetric potentials (7) and (8). Figure 4 demonstrates four examples of unstable evolution in the media corresponding to Fig. 2. In these cases, cubic-quintic-septimal nonlinearities, diffraction, dispersion and the ${\mathcal {PT}}$ complex potential cannot exactly balance, and the 5% white noise strongly influences the stable evolution of light bullet (9). Along the evolutional distance, light bullet (9) cannot maintain its original shape, alters from distortion to collapse and finally decays into noise.

5 Conclusions

In conclusion, a (3 + 1)-dimensional NLSE with cubic-quintic-septimal nonlinearities and ${\mathcal {PT}}$-symmetric potentials is studied, and two kinds of analytical Gaussian-type light bullet solutions are derived. In these solutions, the septimal nonlinear term has a strong impact on the formation of light bullets. Based on these analytical solutions, the eigenvalue method and direct numerical simulation are used to study the stability of light bullet solutions. Results indicate that light bullet solution (6) is stable only in the medium of focusing septimal and defocusing cubic nonlinearities with disappearing quintic nonlinearity under the ${\mathcal {PT}}$-symmetric potential; however, it is unstable in other media, such as focusing cubic, quintic and septimal nonlinearities, focusing cubic and septimal nonlinearities with disappearing quintic nonlinearity, defocusing cubic and septimal nonlinearities with focusing quintic nonlinearity and defocusing cubic and septimal nonlinearities with disappearing quintic nonlinearity. Moreover, light bullet (9) is unstable in various nonlinear media regardless of focusing or defocusing cubic, quintic and septimal nonlinearities under the ${\mathcal {PT}}$-symmetric potentials. These stable and unstable evolutions of light bullet against white noise attribute to the coaction of cubic-quintic-septimal nonlinearities, dispersion, diffraction and ${\mathcal {PT}}$-symmetric potential.