1 Introduction

Localized structures are intensely studied by engineers, physicists and mathematicians because of their potential application in different fields [1–5]. The current growth of interest in localized structures in \({\mathcal {PT}}\)-symmetric potentials is motivated by the pioneering theoretical contributions of Christodoulides et al. [6].

The parity-time (\({\mathcal {PT}}\)) symmetry has received considerable attention in quantum mechanics and optics since Bender and coworkers [6] in 1998 pointed out that non-Hermitian Hamiltonians can have an entirely real eigenvalue spectrum under the \({\mathcal {PT}}\)-symmetry constraint. The \({\mathcal {PT}}\) symmetry dictates that the potential has the following property \(V(x) =V^*(-x)\) with \(*\) denoting complex conjugation [6, 7]. Optics provide the most straightforward way to realize such systems by combining a spatially symmetric profile of the refractive index with symmetrically placed mutually balanced gain and loss [6].

Musslimani et al. [8] were the first research group to realize optical spatial solitons in \({\mathcal {PT}}\)-symmetric potentials. Stable bright spatial solitons [9], dark solitons and vortices [10] in nonlinear media with \({\mathcal {PT}}\)-symmetric potentials have been investigated. Spatiotemporal solitons [11–13] in nonlinear Kerr media with different \({\mathcal {PT}}\)-symmetric potentials have also been reported. Moreover, spatial [14] and spatiotemporal [15–17] solitons in power-law nonlinear media with \({\mathcal {PT}}\)-symmetric potentials have been discussed, too.

Rogue waves (RWs), as relatively large and spontaneous waves recorded and studied in oceanography [18], sometimes can be several times higher than the average wave crests. So far, the Peregrine solitons (PS) [19], the space-periodic Akhmediev breather (AB) [20] and the time-periodic Kuznetsov [21] or Ma [22] (KM) soliton have been suggested as theoretical prototypes to describe RWs [23]. Recently, based on the concept of nonautonomous solitons  [24], Dai et al. [25, 26] and Zhu et al. [27] also studied the controllable superposed AB and KM solitons, respectively. However, the controllable behaviors of the combined PS and AB have not been reported. Furthermore, although localized structures have been discussed in \({\mathcal {PT}}\)-symmetric couplers [28–31], the controllable behaviors of RWs in \({\mathcal {PT}}\)-symmetric coupled waveguides have hardly been investigated, too.

In this present paper, we obtain the combined PS and AB based on the coupled NLSE with variable coefficients in \({\mathcal {PT}}\)-symmetric coupled waveguides, and discuss the controllable behaviors including the complete excitation, recurrence, maintenance and restraint of the combined PS and AB. Two issues are firstly investigated in this present paper: (1) The combined PS and AB solution is firstly obtained in \({\mathcal {PT}}\)-symmetric coupled waveguides, and (2) the controllable behaviors of the combined PS and AB are also investigated firstly in \({\mathcal {PT}}\)-symmetric coupled waveguides. Our analysis and results are applicable for certain applications of synthetic \({\mathcal {PT}}\)-symmetric systems in nonlinear optics and condensed matter physics.

2 Model and exact solution

The dynamics of light beams and pulses in \({\mathcal {PT}}\)-symmetric coupled waveguides can be governed by the following coupled NLSE [32]

$$\begin{aligned}&{{\text {i}}}u_z+\frac{1}{2} u_{xx}+\left( \chi _1|u|^{2}+\chi |v|^2\right) u=-v+{{\text {i}}}\gamma u, \nonumber \\&{{\text {i}}}v_z+\frac{1}{2} v_{xx}+\left( \chi |u|^{2}+\chi _1|v|^2\right) v=-u-{{\text {i}}}\gamma v, \end{aligned}$$
(1)

where u(z, x) and v(z, x) are two normalized complex mode fields in two parallel planar waveguides and z and x are dimensionless propagation and transverse coordinates. In Eq. (1), the second term in the left-hand sides describes diffraction, the last two terms in the left-hand sides are the nonlinearly coupled terms of the self-phase-modulation (SPM) and cross-phase-modulation (XPM), and the first term in the right-hand sides denotes the coupling term between the modes propagating in the two waveguides. Here the positive and negative values of \(\chi \) and \(\chi _1\) represent the focusing and defocusing nonlinearities, respectively. The first terms in the right-hand sides of Eq. (1) account for the coupling between the modes propagating in the two waveguides. The opposite signs of the \(\gamma \) term in the second term of Eq. (1) describe the \({\mathcal {PT}}\)-balanced gain in the first equation of Eq. (1) and loss in the second equation of Eq. (1).

In a real waveguide, the core medium is inhomogeneous [33] because of the variation in the lattice parameters of the waveguide medium and the waveguide geometry (diameter fluctuations, etc). In these cases, the governing equations are various variable-coefficient NLSEs. In this paper, we consider the following equation

$$\begin{aligned}&{{\text {i}}}u_z+\frac{1}{2}\beta (z) u_{xx}+\left[ \chi _1(z)|u|^{2}+\chi (z)|v|^2\right] u\nonumber \\&\quad =\eta (z)(-v+{\text {i}}\gamma u), \nonumber \\&{{\text {i}}}v_z+\frac{1}{2}\beta (z) v_{xx}+\left[ \chi (z)|u|^{2}+\chi _1(z)|v|^2\right] v\nonumber \\&\quad =\eta (z)(-u-{\text {i}}\gamma v), \end{aligned}$$
(2)

where all terms have the same meaning as those in Eq. (1).

Fig. 1
figure 1

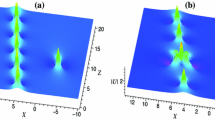
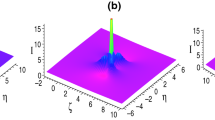
(Color online) The combined PS and AB for Eq. (4): a shifts are \(Z_0'=4,Z_0=-4\), b shifts are \(Z_0'=-4,Z_0=4\) and c shifts are \(Z_0'=Z_0=4\). Parameters are chosen as \(n=0.85{\text {i}},v=0.2,X_1=X_2=0\)

Full size image

In the following, we consider the gain/loss term is small enough, such as \(\gamma \le 1\), and thus, the energy through linear coupling is transferred from the core with gain to the lossy one, and modes can be excited in the system by input beams but do not arise spontaneously. Without loss of generality, we can make a change of variable with \(\gamma =\sin (\theta )\). In order to obtain \({\mathcal {PT}}\)-symmetric (+) and \({\mathcal {PT}}\)-antisymmetric (\(-\)) solutions of Eq. (2), we construct the following relation

$$\begin{aligned} v(x,z)= & {} \pm u(x,z)\exp {(\pm {\text {i}} \theta )}, \nonumber \\ u(x,z)= & {} A_0\alpha ^{\frac{1}{2}}(z)U\left[ Z\equiv \frac{D(z)\alpha (z)}{W_0^2},X\equiv \frac{x-x_c}{W(z)}\right] \nonumber \\&\times \exp \left\{ {{\text {i}}}[\cos (\theta ) \varLambda (z)+\phi (x,z)]\right\} , \end{aligned}$$
(3)

with the width \(W(z)=W_0/\alpha (z)\), the beam center \(x_c=x_0-(d_0+s_0x_0)D(z)\), the phase \(\phi (x,z)=-s_0\alpha (z)x^2/2-d_0\alpha (z)x-d_0D(z)\alpha (z)/2\), the chirp factor \(\alpha (z)=1-s_0D(z)\), the accumulated diffraction \(D(z)=\int _0^z\beta (s)\mathrm{d}s\) and \(\varLambda (z)=\int _0^z\eta (s)\mathrm{d}s\), then Eq. (2) can be transformed into the standard NLSE

$$\begin{aligned} {\text {i}} U_Z+\frac{1}{2} U_{XX}+|U|^{2}U=0. \end{aligned}$$
(4)

Moreover, the parameters of systems satisfy the following relation

$$\begin{aligned} \chi (z)+\chi _1(z)=\frac{\beta (z)\alpha (z)}{A_0^2W_0^2}. \end{aligned}$$
(5)

As we all know, the standard NLSE possesses abundant exact solutions, such as single and multiple bright and dark solitons, rational rogue wave solutions, KM solitons and ABs. Here we focus on the combined PS and AB. According to the modified DT technique in Ref. [23], based on the solution of NLSE (4), we can obtain the combined Peregrine soliton and AB solution of Eq. (2) as follows

(6)

where \(P=\kappa \{\kappa [\kappa ^2(4Z_{s2}^2+4X_{s2}'^2+1)-8]\cosh (\delta Z_{s1})+8 \delta \cos (\kappa X_{s1}')\}/8,Q=\kappa \{8Z_{s2}[\delta \cos (\kappa X_{s1}')-\kappa \cosh (\delta Z_{s1})]+\delta \kappa (4Z_{s2}^2+4X_{s2}'^2+1) \sinh (\delta Z_{s1})\}/4,R=-\{\delta [\kappa ^2(4Z_{s2}^2+4X_{s2}'^2+1)-16]\cos (\kappa X_{s1}')+\kappa ([\kappa ^2(4Z_{s2}^2+4X_{s2}'^2-3)+16] \cosh (\delta Z_{s1})-16\delta [Z_{s2}\sinh (\delta Z_{s1}) +X_{s2}'\sin (\kappa X_{s1}')])\}/(4\kappa )\) with \(Z_{s1}=Z-Z_{0}',Z_{s2}=Z-Z_{0},X_{s1}'=X_{s1}-v_0Z,X_{s2}'=X_{s2}-v_0Z,X_{sj}=X-X_{j},\delta =\kappa \sqrt{4-\kappa ^2}/2,\kappa =2\sqrt{1+n^2},j=1,2\). Here Z, X and \(\phi \) have the expressions in Eq. (3), \(v_0\) is an arbitrary constant, \(\kappa \) is the modulation frequency, and \(Z_0,Z_0'\) and \(X_{j}\) determine the center of solution in \(Z-X\) coordinates. If \(0<{\text {Im}}(n)<1\) and \({\text {Im}}(n)>1\) in solution (6), the PS is combined by AB and KM soliton, respectively.

3 Dynamical properties of the combined PS and AB

Here we give a nonlinear superposition structure of an AB with a PS in Fig. 1. In Fig. 1a, b, the PS is parallel with the AB, and they are separated. However, Fig. 1c displays that the PS is embedded in the AB.

In the following, we will analyze how to realize the control of these combined PS and AB structures by studying the relation between the effective propagation distance Z and the original propagation distance z. As the first example, we consider the following diffraction decreasing waveguide (DDW) with logarithmic profile [34, 35]

$$\begin{aligned} \beta (z)={\text {ln}}\left\{ e+\frac{z}{L}\left[ \exp \left( \frac{1}{C}\right) -e\right] \right\} , \end{aligned}$$
(7)

which is expressed in terms of the compression ratio parameter 1 / C (value of dispersion parameter \(\beta (z)\) at distance \(z=L\)) and length of the waveguide L with the natural logarithm e.

In the framework of NLSE (4), the AB in Fig. 1a and PS in Fig. 1b reach their maximal amplitudes at \(Z=Z_0\) and then disappear. In the DDW with logarithmic profile (7), the effective propagation distance Z has relation to the original propagation distance z with \(Z=\tfrac{\beta _0}{s_0W_0^2}\left( 1{+} \tfrac{e^{1/C}{-}e}{s_0\beta _0\{{{\text {ln}}} [(ze^{1/C}\!{+}(L-z)e)/L]-1\}[ze^{1/C}{+}(L-z)e]{+}e{-}e^{1/C}}\right) \). From this expression above, we can find that Z exists a maximal value \(Z_{\mathrm{m}}\), that is, when \(z=L(e-1)/(e-e^{1/C}), Z\rightarrow Z_{\mathrm{m}}=L\beta _0/[W_0(e-e^{1/C}-s_0\beta _0L)]\).

Fig. 2
figure 2

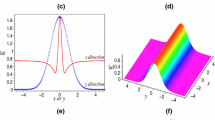
(Color online) Controllable behaviors of the combined PS and AB corresponding to Fig. 1a, b in the DDW with logarithmic profile: a, d complete excitation, b, e maintenance and c, f restraint. Parameters are chosen \(s_0=0.01,A_0=d_0=0.1,x_0=0.3,W_0=0.5,L=40,C=5\) with a, d \(\beta _0=0.2\), b, e \(\beta _0=0.037\) and c, f \(\beta _0=0.01\)

Full size image

From the analysis above, the real propagation distance z can choose from a certain value to infinity (\(+\infty \)); however, Z might be restricted in certain range and has a boundary or limit (such as \(Z_{\mathrm{m}}\)) from the relation between Z and z. The propagation behaviors of the combined PS and AB can be controlled by adjusting the relation between the maximal value \(Z_{\mathrm{m}}\) and the exciting location value \(Z_0\). When \(Z_{\mathrm{m}}\) is obviously bigger than \(Z_0\), the combined PS and ABs corresponding to Fig. 1a, b are excited very quickly in Fig. 2a, d. If \(Z_{\mathrm{max}}=Z_0\), the PS of the combined structure in Fig. 1a is completely excited, and the AB of the combined structure in Fig. 1a is excited to the maximum amplitude and maintain this amplitude a long distance with self-similar propagating behaviors (see Fig. 2b). On the contrary, the AB of the combined structure in Fig. 1b is completely excited, and the PS of the combined structure in Fig. 1b is excited to the maximum amplitude and maintain this amplitude a long distance with self-similar propagating behaviors (see Fig. 2e). When \(Z_{\mathrm{m}}<Z_0\), the thresholds of exciting the AB of the combined structure in Fig. 1a and the PS of the combined structure in Fig. 1b are never reached and the excitation of them is restrained (see Fig. 2c, f).

Fig. 3
figure 3

(Color online) Controllable behaviors of the combined PS and AB corresponding to Fig. 1c in the DDW with logarithmic profile: a complete excitation, b maintenance and c restraint. Parameters are chosen as the same as those in Fig. 2

Full size image
Fig. 4
figure 4

(Color online) Controllable behaviors of the combined PS and AB corresponding to Fig. 1a, b in the periodic amplification system: a, c recurrence and b, d restraint. Parameters are chosen as the same as those in Fig. 2 except for \(\sigma =0.01,\delta =0.3\) with a, c \(\beta _0=1\) and b, d \(\beta _0=0.1\)

Full size image

Figure 3 displays the controllable behaviors of the combined PS and AB in Fig. 1c. When \(Z_{\mathrm{m}}\) is remarkably bigger than \(Z_0\), the complete combined PS and AB corresponding to Fig. 1c is excited quickly (see Fig. 3a). If \(Z_{\mathrm{m}}=Z_0\), both the PS and AB in the combined PS and AB are excited to their maximal amplitudes and maintain a long distance (see Fig. 3b). At last, if \(Z_{\mathrm{m}}<Z_0\), wave in the framework of Eq. (4) is not sufficient to be excited, and restraint of the combined PS and AB will happen (see Fig. 3c). Only initial part of the combined PS and AB is produced, and these initial parts sustain a long distance.

Fig. 5
figure 5

(Color online) Controllable behaviors of the combined PS and AB corresponding to Fig. 1c in the periodic amplification system: a recurrence and b restraint. Parameters are chosen as the same as those in Fig. 4

Full size image

Besides these controllable behaviors in Figs. 2 and 3, we can find other behaviors, such as the recurrence of the combined PS and AB, in the second example, namely the periodic distributed amplification system (PDAS) [36, 37]

$$\begin{aligned} \beta (z)=\beta _{0}\exp (-\sigma z)\cos (\omega z), \end{aligned}$$
(8)

where \(\beta _{0}\) is the parameter related to the initial peak power in system. This system produces alternating regions of positive and negative values of \(\beta \), which are helpful for the eventual stability of solutions [38, 39]; especially, when \(\omega =0\) and \(\sigma >0\), Eq. (8) is an exponential DDW [27, 40]. Moreover, Eq. (8) with \(\sigma =0\) corresponds to the inhomogeneous fibers with a periodic modulation [38].

If we choose \(\beta \) as the PDAS expressed as (8), we can obtain the relation between Z and z as \(Z=\varLambda (z)/\{W_0^2[\sigma ^2+\omega ^2-s_0\varLambda (z)]\}\) with \(\varLambda (z)=\beta _0\{\sigma -\exp (-\sigma z)[\sigma \cos (\omega z)+\omega \sin (\omega z)]\}\). From this expression above, we can find that Z periodically oscillates with the increase in z and exists a maximal value \(Z_{\mathrm{m}}\); namely, when \(z=\pi /(2\omega ), Z\rightarrow Z_{\mathrm{m}}=\beta _0\{\sigma +\omega \exp [-\sigma \pi /(2\omega )]\}/W_0/\{\sigma ^2+\omega ^2-s_0 \beta _0(\sigma +\omega \exp [-\sigma \pi /(2\omega )])\}\). We can modulate the relation between \(Z_{\mathrm{m}}\) and \(Z_0\) to control the degree of excitation of the combined PS and AB.

In the PDAS, corresponding to the combined PS and AB in Fig. 1a, b, when \(Z_{\mathrm{m}}>Z_0\), the combined PS and AB will recur periodically (c.f. Figs. 4a or c, 1a). Figure 4a, c display two kinds of recurrence corresponding to Fig. 1a and b, respectively. The recurrence behavior in the form of a cluster for the combined PS and AB is shown in Fig. 4a, c. We call the combined PS and AB in Fig. 4a, c as clusters I and II, respectively, according to the occurrence sequence of PS and AB in the combined PS and AB. In cluster I, the PS appears prior to the AB along the propagation distance z, and in cluster II, the AB appears prior to the PS along the propagation distance z. Thus, this behavior in Fig. 4a is named the “I-II-I-II” mode after its occurrence sequence of the cluster, and this behavior in Fig. 4c is named the “II-I-II-I” mode after its occurrence sequence of the cluster. If \(Z_{\mathrm{m}}<Z_0\), the threshold of exciting the PS and AB is never reached and only the initial parts in the combined PS and AB are excited. The full excitation is restrained (see Fig. 4b, d).

In the PDAS, the combined PS and AB in Fig. 1c also exists the behaviors of recurrence and restraint. When \(Z_{\mathrm{m}}>Z_0\), the combined PS and AB also recurs periodically (c.f. Figs. 5a, 1c). When \(Z_{\mathrm{m}}<Z_0\), the threshold of exciting the combined PS and AB is never reached and their excitation is restrained or even eliminated (see Fig. 5b).

4 Conclusions

In conclusion, we investigate the coupled NLSE in \({\mathcal {PT}}\)-symmetric coupled waveguides with variable coefficients and obtain exact combined PS and AB solution. Based on this solution, by adjusting the relation between the maximal value \(Z_{\mathrm{m}}\) and the exciting location value \(Z_0\), we discuss the controllable behaviors including the complete excitation, recurrence, maintenance and restraint of the combined PS and AB. In the DDW with logarithmic profile, the combined PS and AB possesses the phenomena of the complete excitation, maintenance and restraint when \(Z_{\mathrm{m}}>Z_0, Z_{\mathrm{m}}=Z_0\) and \(Z_{\mathrm{m}}<Z_0\), respectively. In the PDAS, the combined PS and AB exists the behaviors of recurrence and restraint when \(Z_{\mathrm{m}}>Z_0\) and \(Z_{\mathrm{m}}<Z_0\), respectively. Our analysis and results are applicable for certain applications of synthetic \({\mathcal {PT}}\)-symmetric systems in nonlinear optics and condensed matter physics.