1 Introduction

In the last decades, considerable advances have been made in the investigation of solitons in various fields of physics and engineering [1–7]. In recent years, rogue waves (or freak waves)—single waves with amplitudes significantly larger than the surrounding waves—have also witnessed tremendous growth in various contexts of physics and engineering [8, 9].

More recently, controllable behaviors of rogue waves and the related breathers have been studied [10–18]. The control for rogue waves [14] and superposed breather [15] were discussed. Controllable breather and Kuznetsov-Ma (KM) soliton trains in parity-time (\(\mathcal {PT}\))-symmetric coupled waveguides have been reported [16]. Nonlinear tunneling effect of controllable combined KM soliton in \(\mathcal {PT}\)-symmetric nonlinear couplers has been discussed [17]. Controllable combined Peregrine soliton (PS) and KM soliton in \(\mathcal {PT}\)-symmetric nonlinear couplers have also been investigated [18].

In the periodic amplification system, the recurrence of PS with two peaks in a birefringent fiber with higher-order effects was reported [19]. Moreover, the recurrence of the combined PS and AB [20] and the recurrence of a KM soliton crossing Akhmediev breather (AB) [21] have also been studied in the periodic amplification system. These recurred behaviors in Refs. [19–21] originate from the periodic functions in the periodic amplification system.

In the diffraction/dispersion decreasing system (DDS), controllable behaviors of rogue waves [14, 22] and breathers [21, 23] were not reported to show the recurrence of excitation. However, we find that rogue wave and combined breather also possess the repeatedly excited behaviors in the DDS, which originates from different diffractions and dispersion of medium. The possibility of generation of the so-called nonlinear paired (or symbiotic) bright and dark solitons arising in the framework of the system of two coupled nonlinear Schrödinger equation (CNLSE) [24–26] was predicted. In this present paper, we study a (3+1)-dimensional CNLSE with different inhomogeneous diffractions and dispersion and discuss repeated behaviors of symbiotic rogue wave and combined breather, including complete excitation, rear excitation, peak excitation and initial excitation.

2 Symbiotic rogue wave and breather solutions

In a real situation, the variation of the fiber geometry brings the inhomogeneity of medium [27]. When two optical fields u and v propagating in the same fiber are considered, the interactions between them are governed by the variable-coefficient CNLSE as follows:

$$\begin{aligned}&\text {i}u_z+\frac{1}{2}\left[ \beta _1(z) u_{xx}+\beta _2(z)u_{yy}+\beta _3(z)u_{tt}\right] \nonumber \\&\quad +\,\chi (z)(\sigma _{11}|u|^{2}+\sigma _{12}|v|^2)u=\text {i}\gamma (z)u, \nonumber \\&\text {i}v_z+\frac{1}{2}\left[ \beta _1(z) v_{xx}+\,\beta _2(z)v_{yy}+\beta _3(z)v_{tt}\right] \nonumber \\&\quad +\chi (z)(\sigma _{21}|u|^{2}+\sigma _{22}|v|^2)v=\text {i}\gamma (z) v, \end{aligned}$$
(1)

with two normalized complex mode fields u(z, x, y, t) and v(z, x, y, t), dimensionless propagation distance z and dimensionless transverse coordinates x, y and time t. The second and third terms in the left-hand sides denote the diffractions with different transverse coordinates (x, y), the fourth term represents dispersion, and the last two terms in the left-hand sides stand for the self-focusing (\(\chi >0\)) or the self-defocusing (\(\chi <0\)) nonlinearity with the self-phase-modulation (SPM) and cross-phase modulation (XPM). The constants \(\sigma _{11}, \sigma _{12}, \sigma _{21}\) and \(\sigma _{22}\) determine the ratio of the coupling strengths of the XPM to the SPM. For linearly polarized eigenmodes \(\sigma _{11}=\sigma _{22}=1,\sigma _{12}=\sigma _{21}= 2/3\), whereas for circularly polarized modes \(\sigma _{11}=\sigma _{22}=1,\sigma _{12}=\sigma _{21}= 2\) with elliptically polarized eigenmodes \(\sigma _{11}=\sigma _{22}=1,2< \sigma _{12}=\sigma _{21}< 2/3\) [28]. These terms in the right-hand sides of Eq. (1) stand for the gain (\(\gamma >0\)) or the loss (\(\gamma <0\)).

Considering the relation between system parameters

$$\begin{aligned} \chi (z)= & {} \frac{G}{4BA_0^2}\left[ \frac{k^2\beta _1(z)\alpha _2(z)\alpha _3(z)}{\alpha _1(z)}\right. \nonumber \\&\left. +\frac{l^2\beta _2(z)\alpha _1(z)\alpha _3(z)}{\alpha _2(z)}+\frac{m^2\beta _3(z)\alpha _1(z)\alpha _2(z)}{\alpha _3(z)}\right] \nonumber \\&\times \exp {[-2\varGamma (z)]}, \end{aligned}$$
(2)

and using the following transformation

$$\begin{aligned}&\left\{ \begin{array}{cc}u(z,x,y,t)\\ v(z,x,y,t) \end{array}\right\} =\left\{ \begin{array}{cc}\sqrt{\left| \frac{\sigma _{22}-\sigma _{12}}{\sigma _{12}\sigma _{21}-\sigma _{11}\sigma _{22}}\right| }\\ \sqrt{\left| \frac{\sigma _{11}-\sigma _{21}}{\sigma _{12}\sigma _{21}-\sigma _{11}\sigma _{22}}\right| }\end{array}\right\} \nonumber \\&\quad \times A(z)U[Z(z),X(z,x,y,t)]\exp [\text {i}\phi (z,x,y,t)],\nonumber \\ \end{aligned}$$
(3)

with the amplitude \(A(z)=A_0[\alpha _1(z)\alpha _2(z)\alpha _3(z)]^{1/2}\exp {[\varGamma (z)]}\), the effective propagation distance \(Z(z)=\frac{1}{4B}[k^2\delta _1(z)\alpha _1(z)+l^2\delta _2(z)\alpha _2(z)+m^2\delta _3(z)\alpha _3(z)]\), the transformation variable \(X(z,x,y,t)=\frac{1}{2}[k\alpha _1(z)x+l\alpha _2(z)y+m\alpha _3(z)t]-\frac{1}{2}[kd\delta _1(z)\alpha _1(z)+le\delta _2(z)\alpha _2(z)+mf\delta _3(z)\alpha _3(z)]\), the phase \(\phi (z,x,y,t)=-\frac{1}{2}[a\alpha _1(z)x^2+b\alpha _2(z)y^2+c\alpha _3(z)t^2]+d\alpha _1(z)x+e\alpha _2(z)y+f\alpha _3(z)t -\frac{1}{2}[d^2\delta _1(z)\alpha _1(z)+e^2\delta _2(z)\alpha _2(z)+f^2\delta _3(z)\alpha _3(z)]\), the chirp factors \(\alpha _1(z)=1/[1-a\delta _1(z)],\alpha _2(z)=1/[1-b\delta _2(z)]\) and \(\alpha _3(z)=1/[1-c\delta _3(z)]\), the accumulated diffractions \(\delta _1(z)=\int _0^z\beta _1(s)\mathrm{d}s, \delta _2(z)=\int _0^z\beta _2(s)\mathrm{d}s\) and the accumulated dispersion \(\delta _3(z)=\int _0^z\beta _3(s)\mathrm{d}s\), the accumulated gain/loss \(\varGamma (z)=\int _0^z\gamma (s)\mathrm{d}s\) and constants a, b, c, d, e, f, k, l, m, Eq. (1) can be transformed into the famous NLSE with constant coefficients

$$\begin{aligned} \text {i}U_Z+\frac{B}{2} U_{XX}+G|U|^2U=0, \end{aligned}$$
(4)

with two constants B and G. Here we choose \(B=1\) and \(G=1\).

From the transformation (3) and the modified Darboux transformation technique in Ref. [8], symbiotic rogue wave solution of Eq. (1) reads

$$\begin{aligned}&\left\{ \begin{array}{cc}u(z,x,y,t)\\ v(z,x,y,t) \end{array}\right\} =\left\{ \begin{array}{cc}\sqrt{\left| \frac{\sigma _{22}-\sigma _{12}}{\sigma _{12}\sigma _{21}-\sigma _{11}\sigma _{22}}\right| }\\ \sqrt{\left| \frac{\sigma _{11}-\sigma _{21}}{\sigma _{12}\sigma _{21}-\sigma _{11}\sigma _{22}}\right| }\end{array}\right\} \nonumber \\&\quad \times A(z)\left[ (-1)^n+\frac{M_n+\text {i}(Z-Z_0)N_n}{L_n}\right] \nonumber \\&\quad \times \exp \left\{ \text {i}\left[ \left( 1-\frac{v^2}{2}\right) (Z-Z_0)+v_0X+\phi \right] \right\} ,\nonumber \\ \end{aligned}$$
(5)

where \(2M_1=L_1=8,N_1=1+4[X-v_0(Z-Z_0)]^2+4(Z-Z_0)^2\) for first-order rogue wave solution with \(n=1\) and \(M_2=[ \left( X-v_0 \left( Z-Z_0 \right) \right) ^{2}+ \left( Z- Z_0 \right) ^{2}+\) \(\frac{3}{4}][ \left( X-v_0 \left( Z-Z_0 \right) \right) ^{2} +5\left( Z-Z_0 \right) ^{2}+\frac{3}{4}] -\frac{3}{4}, N_2=\) \(\left( Z-Z_0 \right) \{ \left( Z-Z_0 \right) ^{2}\) \(-3[ X -v_0\left( Z-Z_0 \right) ] ^{2}+2[ ( X-v_0 \left( Z-Z_0 \right) ) ^{2}+ \left( Z-Z_0 \right) ^{2}] ^{2}-{\frac{15}{8}} \}, L_2=\frac{1}{3}[ ( X-v_0\) \(\left( Z-Z_0 \right) ) ^{2} + \left( Z-Z_0 \right) ^{2}]^{3}\) \(+\frac{1}{4} [( X-v_0 \left( Z-Z_0 \right) ) ^{2}-3 \left( Z-Z_0 \right) ^{2}] ^{2}+{\frac{9}{16}}\left( X-v_0 \left( Z-Z_0 \right) \right) ^{2}+{\frac{33}{16}}( Z-Z_0 ) ^{2}+{\frac{3}{64}}\) for second-order rogue wave with \(n=2\), X, Z and \(\phi \) are given below Eq. (3), and \(Z_0\) and \(v_0\) are two arbitrary constants.

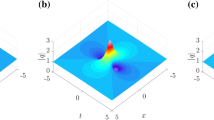
Moreover, from the transformation (3) and the modified Darboux transformation technique in Ref. [9], symbiotic combined rogue wave and breather solution of Eq. (1) reads

$$\begin{aligned}&\left\{ \begin{array}{cc}u(z,x,y,t)\\ v(z,x,y,t) \end{array}\right\} \nonumber \\&\quad =\left\{ \begin{array}{cc}\sqrt{\left| \frac{\sigma _{22}-\sigma _{12}}{\sigma _{12}\sigma _{21}-\sigma _{11}\sigma _{22}}\right| }\\ \sqrt{\left| \frac{\sigma _{11}-\sigma _{21}}{\sigma _{12}\sigma _{21}-\sigma _{11}\sigma _{22}}\right| }\end{array}\right\} A(z) \left[ 1+\frac{G+\text {i}F}{H}\right] \nonumber \\&\qquad \times \exp \left\{ \text {i}[(1-\frac{v^2}{2})(Z-Z_0)+v_0X+\phi ]\right\} , \end{aligned}$$
(6)

where \(G=\kappa \{\kappa [\kappa ^2(4Z_{s2}^2+4X_{s2}'^2+1)-8]\cosh (\delta Z_{s1})+\) \(8 \delta \cos (\kappa X_{s1}')\}/8,F=\kappa \{8Z_{s2}[\delta \cos (\kappa X_{s1}')-\kappa \cosh \) \((\delta Z_{s1})]\) \(+\delta \kappa (4Z_{s2}^2+4X_{s2}'^2+1) \sinh (\delta Z_{s1})\}/4,\) \(H=-\{\delta [\kappa ^2(4Z_{s2}^2+4X_{s2}'^2+1)-16]\cos (\kappa X_{s1}')+\kappa ([\kappa ^2(4Z_{s2}^2\) \(+4X_{s2}'^2-3)+16] \cosh (\delta Z_{s1})\) \(-16\delta [Z_{s2}\sinh (\delta Z_{s1}) +X_{s2}'\sin (\kappa X_{s1}')])\}/(4\kappa )\) with \(Z_{s1}=Z-Z_{0}',Z_{s2}=Z-Z_{0},X_{s1}'=X_{s1}-v_0Z,X_{s2}'=X_{s2}-v_0Z,X_{sj}=X-X_{j},\delta =\kappa \sqrt{4-\kappa ^2}/2,\kappa =2\sqrt{1+n^2},j=1,2\), with X, Z and \(\phi \) being given below Eq. (3), an arbitrary constant \(v_0\) and the modulation frequency \(\kappa \). \(Z_0,Z_0'\) and \(X_{j}\) decide the center of solution in \(Z-X\) coordinates. If \(0<\text {Im}(n)<1\) or \(\text {Im}(n)>1\) in solution (6), a rogue wave is combined by a breather or KM soliton, respectively. Here we choose \(Z_0=Z_0'\) and \(0<\text {Im}(n)<1\); thus, solution (6) describes a rogue wave embedded on a breather.

As said in Refs. [29, 30], nonautonomous solitons exist only under certain conditions and the parameter functions describing dispersion, nonlinearity and gain or absorption inhomogeneities cannot be chosen independently. Solutions (5) and (6) also exist under the relation between system parameters (2).

3 Repeatedly excited behaviors of rogue wave and combined breather

We consider repeatedly excited behaviors of rogue wave and combined breather in the following system with diffraction functions \(\beta _1(z),\beta _2(z)\) and dispersion function \(\beta _3(z)\) as [31–33]

$$\begin{aligned} \beta _j(z)=\beta _{j0}\exp (-g z), \end{aligned}$$
(7)

where positive parameters \(\beta _{j0}(j=1,2,3)\) and g are related to diffraction or dispersion. When \(g>0\), this system describes the exponential DDS.

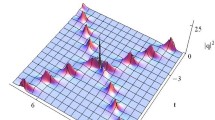
As we all know, second-order rogue wave (5) reaches its peak at location \(X=0,Z=Z_0\) and then gradually disappears in the \(Z-X\) coordinates. Based on the expression of Z below Eq. (3) and (7), we obtain \(Z=k^2\beta _{10}[1-\exp (-g z)]/[4g-4a\beta _{10}(1-\exp (-g z))]+l^2\beta _{20}[1-\exp (-g z)]/[4g-4b\beta _{20}(1-\exp (-g z))]+m^2\beta _{30}[1-\exp (-g z)]/[4g-4c\beta _{30}(1-\exp (-g z))]\), which hints that the value of Z approaches the maximum value \(Z_m=k^2\beta _{10}/[4(g-a\beta _{10})]+l^2\beta _{20}/[4(g-b\beta _{20})]+m^2\beta _{30}/[4(g-c\beta _{30})]\) as z approaches infinity. The degree of excitation of second-order rogue wave is decided by the relation between the maximum \(Z_{m}\) and peak location \(Z_0\).

Fig. 1
figure 1

a, d, g complete excitation, b, e, h peak excitation, and c, f, i initial excitation of the second-order rogue wave in the DDS, respectively. Parameters are chosen as \(A_0=0.5,k=0.9,l=1,m=1.1,a=d=0.45,b=e=0.5,c=f=0.55, \beta _{10}=0.25,\beta _{20}=0.3,\beta _{30}=0.35,Z_0=6,v_0=0.1,\sigma _{12}=\sigma _{21}=1.5,\sigma _{11}=\sigma _{22}=1\) with a \(g=0.115\), b \(g=0.1177\), c \(g=0.14\), d \(g=0.15\), e \(g=0.1593\), f \(g=0.17\), g \(g=0.2\), h \(g=0.2166\) and i \(g=0.23\), respectively. We take \(y=2,t=3\). Results are similar for other values of y and t

Full size image

When \(Z_{m}=Z_0\), the critical value of g can be obtained if other parameters are chosen as certain values. If parameters are chosen as \(k=0.9,l=1,m=1.1,a=0.45,b=0.5,c=0.55, \beta _{10}=0.25,\beta _{20}=0.3,\beta _{30}=0.35\), \(Z_{m}=Z_0=6\) produces triple roots of parameter g, namely \(g_1=0.1177, g_2=0.1593, g_3=0.2166\). We find that \(Z_{m}\) non-montonically changes, that is, \(Z_{m}\) increases and decreases again and again. Therefore, repeatedly excited behaviors of rogue wave will happen in the DDS.

Fig. 2
figure 2

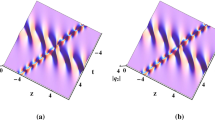
a, d, g complete excitation, b, e rear excitation, c, h peak excitation and f, i initial excitation of a rogue wave embedded on a breather in the DDS, respectively. Parameters are chosen as the same as those in Fig. 1 except for \(n=0.85\text {i},X_1=X_2=0\) with a \(g=0.115\), b \(g=0.117\), c \(g=0.1177\), d \(g=0.15\), e \(g=0.158\), f \(g=0.17\), g \(g=0.2\), h \(g=0.2166\) and i \(g=0.23\), respectively. We take \(y=2,t=3\). Results are similar for other values of y and t

Full size image

In the following, we discuss repeatedly excited behaviors for one of component u from the symbiotic solution. Actually, similar repeatedly excited behaviors will also happen for another component v of the symbiotic solution.

Figure 1 displays repeatedly excited behaviors of rogue wave with the add of values of g in the DDS. If \(g=0.115<g_1\) in Fig. 1a, then \(Z_{m}>Z_0\); thus, the complete second-order rogue wave is excited. If \(g=0.1177=g_1\) in Fig. 1b, then \(Z_{m}=Z_0\); thus, the second-order rogue wave is excited to the peak and self-similarly sustains its peak along the propagation distance. If \(g=0.14>g_1\), then \(Z_{m}<Z_0\) in Fig. 1c; thus, the threshold of exciting a complete rogue wave is never reached, and the rogue wave is only excited to the initial part. If \(g_1<g=0.15<g_2\) in Fig. 1d, then \(Z_{m}>Z_0\) again; thus, the full second-order rogue wave is excited again. If \(g_1<g=0.1593=g_2\) in Fig. 1e, the maintenance of peak excitation of rogue wave happens once again. If \(g=0.17>g_2\) in Fig. 1f, the complete excitation is restrained, and rogue wave is initially excited. If \(g_2<g=0.2<g_3\) in Fig. 1g, \(g=0.2166=g_3\) in Fig. 1h and \(g=0.23>g_3\) in Fig. 1i, the complete excitation, peak excitation and initial excitation of the second-order rogue wave will appear again. This phenomenon of repeated excitation has not been reported in the system with same diffractions and dispersion in Ref. [34].

Similar case of repeated excitation also happens for a rogue wave embedded on a breather. In the \(Z-X\) coordinates, the rogue wave and breather in solution (6) altogether reach their peaks at location \(X=0,Z=Z_0\) and then gradually disappear. Adjusting the relation between \(Z_m\) and \(Z_0\), we can also discuss controllable excitation of the rogue wave embedded on a breather.

Figure 2 exhibits repeatedly excited behaviors of the rogue wave embedded on a breather with the add of values of g in the DDS. If \(g=0.115<g_1\) in Fig. 2a, then \(Z_{m}>Z_0\); thus, the complete excitation of the rogue wave embedded on a breather appears. If \(g=0.117\) (a bit smaller than \(g_1\)) in Fig. 2b, rogue wave and breather are all excited rear part, and the rear part of rogue wave and breather do not disappear along z. If \(g=0.1177=g_1\) in Fig. 2c, then \(Z_{m}=Z_0\); thus, the rogue wave and breather are all excited to their peaks and self-similarly maintain their maximum amplitudes along the propagation distance. If \(g>g_1\), the complete excitation of the rogue wave embedded on a breather is restrained. If \(g_1<g=0.15<g_2\) in Fig. 2d, then \(Z_{m}>Z_0\) again; thus, the rogue wave embedded on a breather is excited again. If \(g=0.158\) (a bit smaller than \(g_2\)) in Fig. 2e, the rear excitation of rogue wave and breather happens again, and the rogue wave embedded on a breather propagates along z with a tail. If \(g=g_2\), the maintenance of peak excitation of rogue wave happens once again. If \(g=0.17>g_2\) in Fig. 2f, the complete excitation is restrained, and the rogue wave embedded on a breather is initially excited. If \(g_2<g=0.2<g_3\) in Fig. 2g, \(g=0.2166=g_3\) in Fig. 2h and \(g=0.23>g_3\) in Fig. 2i, the complete excitation, peak excitation and initial excitation of the rogue wave embedded on a breather will also happen. This phenomenon of repeated excitation has not been reported in the system with same diffractions and dispersion in Ref. [35]. Therefore, different diffractions and dispersion of medium lead to the repeatedly excited behaviors of rogue wave and combined breather in the DDS.

4 Summary

In summary, we investigate a (3+1)-dimensional CNLSE with different inhomogeneous diffractions and dispersion and construct rogue wave and combined breather solutions. From the relation between the transformation variable Z and real distance z, we obtain the maximum value of \(Z_m\) in DDS. Comparing values of \(Z_m\) and peak location \(Z_0\), we study complete excitation, rear excitation, peak excitation and initial excitation of rogue wave and combined breather. In DDS, a new phenomenon of repeatedly excited behaviors is discussed. The reason to appear these repeatedly excited behaviors is the existence of different diffractions and dispersion of medium. These repeated behaviors including complete excitation, rear excitation, peak excitation and initial excitation are discussed.