1 Introduction

The exact balance between dispersion/diffraction and nonlinearity can induce solitons characterized by fascinating shape-preserving wave phenomena in nonlinear media [1–10]. In optics, nonlinearities exhibit rich and complex phenomena. Kerr nonlinearity (one kind of common role) compensates dispersion/diffraction to form self-trapped soliton. Focusing Kerr-type media support the stable propagation of bright solitons [11]. However, in focusing quintic nonlinear media, the diffraction effect is not sufficient to balance the self-focusing, and consequently the beam undergoes critical collapse [12]. In this case, higher-order dissipative terms need to introduce to suppress the collapse [13].

Higher-order nonlinearities play an important role to stabilize the propagation of spatial solitons. The competition between focusing third-order and defocusing fifth-order nonlinearities supports stable soliton solution [14]. Besides the cubic and quintic terms, septimal nonlinearity may come into play to produce spatial solitons. Recently, (2 + 1)-dimensional bright spatial solitons were studied in metal colloids with focusing quintic and defocusing septimal nonlinearities and dissipative terms [15].

From above, dissipative terms are important to suppress the collapse [13, 15]. In recent investigation, the parity-time (\({\mathcal {PT}}\)) symmetric potential has a good effect to stabilize spatial and spatiotemporal solitons [18–20]. The \({\mathcal {PT}}\)-symmetry is firstly proposed in quantum mechanics [16] and then introduced into optics [17]. Stable two-dimensional localized modes were studied in anisotropic media with harmonic and \({\mathcal {PT}}\)-symmetric potentials [18]. Sech-type and Gaussian-type light bullet solutions of the generalized (3 +1)-dimensional cubic-quintic nonlinear Schrödinger equation (NLSE) in \({\mathcal {PT}}\)-symmetric potentials have also been discussed [19]. Stable localized spatial solitons in \({\mathcal {PT}}\)-symmetric potentials with power-law nonlinearity have also been discussed [20].

More recently, solitons in cubic-quintic-septimal nonlinear media without considering \({\mathcal {PT}}\)-symmetric potentials have been studied [22]. However, whether light bullets (spatiotemporal solitons) stably evolve is not reported under the coaction of cubic-quintic-septimal nonlinearity, dispersion, diffraction and \({\mathcal {PT}}\)-symmetric potentials although hidden features of three-dimensional nonautonomous soliton bullets have been studied [21]. In this paper, we investigate a (3+1)-dimensional NLSE with variable-coefficient dispersion/diffraction and cubic-quintic-septimal nonlinearities and obtain two families of analytical light bullet solutions with two types of \({\mathcal {PT}}\)-symmetric potentials. Based on these solutions, we use direct simulation to analyze the stability of light bullet solutions. Moreover, the compression and expansion of light bullets in the hyperbolic dispersion/diffraction system and periodic modulation system are investigated numerically.

2 Analytical light bullet solutions

The dynamics of light bullet in cubic-quintic-septimal nonlinear media with \({\mathcal {PT}}\)-symmetric potentials can be described by the following NLSE

$$\begin{aligned}&{\text {i}}u_z+ \beta (z)(u_{xx}+u_{yy}+u_{tt})+\gamma _3(z)|u|^{2}u\nonumber \\&\quad +\gamma _5(z)|u|^{4}u+\gamma _7(z)|u|^{6}u\nonumber \\&\quad +[v(z,\mathbf r )+\text {i}w(z,\mathbf r )]u=0, \end{aligned}$$
(1)

where complex envelope of the electrical field \(u(z,\mathbf r )\) with \(\mathbf r \equiv \{x,y,t\}\) and transverse spatial coordinates x, y and the retarded time t. Function \(\beta (z)\) is the coefficient of the diffraction/dispersion, \(\gamma _3(z), \gamma _5(z)\) and \(\gamma _7(z)\) are the cubic, quintic and septimal nonlinear coefficients. The real component \(v(z,\mathbf r )\) and imaginary component \(w(z,\mathbf r )\) of the complex \({\mathcal {PT}}\)-symmetric potential denote the index guiding and the gain/loss distribution, respectively, and are odd and even functions, respectively.

Under the condition

$$\begin{aligned} \gamma _{2m+1}(z)=\frac{\varGamma _{2m+1} }{B A_0^{2m}}\beta (z)\rho ^{3m-2}(z),\quad (m=1,2,3) \end{aligned}$$
(2)

and

$$\begin{aligned} v(z,x,y,t)= & {} \frac{\beta (z)}{B\rho ^{2}(z)}V(X,Y,T),\nonumber \\ w(z,x,y,t)= & {} \frac{\beta (z)}{B\rho ^{2}(z)}W(X,Y,T), \end{aligned}$$
(3)

we can use the one-to-one correspondence between u in Eq.(1) and U in Eq.(5)

$$\begin{aligned} u(z,x,y,t)= & {} \rho (z)U[Z(z),X(z,x),Y(z,y),T(z,t)]\nonumber \\&\exp [\text {i} \varphi (z,x,y,t)], \end{aligned}$$
(4)

where the amplitude \(\rho (z)=\rho _0\varrho ^{-\frac{3}{2}}(z)\), effective propagation distance \(Z(z)=\frac{1}{B\varrho (z)}\int ^z_0\beta (s)\text {d}s\), casted variables \(X(z,x)=\frac{x}{\varrho (z)},Y(z,y)=\frac{y}{\varrho (z)},T(z,t)=\frac{t}{\varrho (z)}\) and phase \(\varphi (z,x,y,t)=-\frac{s_0}{2\varrho (z)}(x^2+y^2+t^2)\) with width \(\varrho (z)=1-s_0\int ^z_0\beta (s)\text {d}s\), initial amplitude \(\rho _0\), and arbitrary chirp parameter \(s_0\), Eq.(1) is reduced into a (3+1)-dimensional NLSE

$$\begin{aligned}&\text {i} U_Z+\frac{1}{2}B( U_{XX}+U_{YY}+U_{TT})+\varGamma _3|U|^{2}U\nonumber \\&\quad +\,\varGamma _5|U|^{4}U+\varGamma _7|U|^{6}U\nonumber \\&\quad +\,[V(X,Y,T)+\text {i}W(X,Y,T)]U=0, \end{aligned}$$
(5)

with four constants \(B, \varGamma _3, \varGamma _5\) and \(\varGamma _7\).

Considering exact solutions of Eq. (5) can be written as \(U(Z,X,Y,T)=\varPhi (X,Y,T)\exp \left[ \text {i} \varOmega (Z,X,Y,T)\right] =\varPhi (X,Y,T)\exp \left[ \text {i} \mu Z+\text {i}\varTheta (X,Y,T)\right] \), we separate Eq. (5) into two equations about real and imaginary parts as

$$\begin{aligned}&B\left[ \frac{\partial ^2\varPhi }{\partial X^2}-\varPhi \left( \frac{\partial \varTheta }{\partial X} \right) ^2\right] +B\left[ \frac{\partial ^2\varPhi }{\partial Y^2}-\varPhi \left( \frac{\partial \varTheta }{\partial Y} \right) ^2\right] \nonumber \\&\quad +\,B\left[ \frac{\partial ^2\varPhi }{\partial T^2}-\varPhi \left( \frac{\partial \varTheta }{\partial T} \right) ^2\right] \nonumber \\&\quad +\,[V(X,Y,T)-\mu ]\varPhi +\varGamma _{3}\varPhi ^{3}\nonumber \\&\quad +\,\varGamma _{5}\varPhi ^{5}+\varGamma _{7}\varPhi ^{7}=0,\end{aligned}$$
(6)
$$\begin{aligned}&B\left( \varPhi \frac{\partial ^2\varTheta }{\partial X^2}+2\frac{\partial \varPhi }{\partial X}\frac{\partial \varTheta }{\partial X}\right) {+}B\left( \varPhi \frac{\partial ^2\varTheta }{\partial Y^2}{+}2\frac{\partial \varPhi }{\partial Y}\frac{\partial \varTheta }{\partial Y}\right) \nonumber \\&\quad +\,B\left( \varPhi \frac{\partial ^2\varTheta }{\partial T^2}+2\frac{\partial \varPhi }{\partial T}\frac{\partial \varTheta }{\partial T}\right) +W(X,Y,T)\varPhi =0.\nonumber \\ \end{aligned}$$
(7)

In this paper, we present two families of sech-type soliton solutions of Eq.(5) with two different \({\mathcal {PT}}\)-symmetric potentials.

2.1 Family 1

If the \({\mathcal {PT}}\)-symmetric potential has the form

$$\begin{aligned}&V(X,Y,T)=2B[{\text {sech}}^2(X)+{\text {sech}}^2(Y)\nonumber \\&\quad +\,{\text {sech}}^2(T)] +\frac{W_0^2}{(p+2)^2B}[{\text {sech}}^{2p}(X)\nonumber \\&\quad +\,{\text {sech}}^{2p}(Y)+{\text {sech}}^{2p}(T)]\nonumber \\&\quad -\,\varGamma _3\left( -\frac{V_1}{\varGamma _7}\right) ^{\frac{1}{3}} {\text {sech}}^{2}(X){\text {sech}}^{2}(Y){\text {sech}}^{2}(T)\nonumber \\&\quad -\,\varGamma _5\left( -\frac{V_1}{\varGamma _7}\right) ^{\frac{2}{3}} {\text {sech}}^{4}(X){\text {sech}}^{4}(Y){\text {sech}}^{4}(T) \nonumber \\&\quad +\, V_1{\text {sech}}^{6}(X){\text {sech}}^{6}(Y){\text {sech}}^{6}(T),\nonumber \\&W(X,Y,T)=W_{0}[{\text {sech}}^{p}(X){\text {tanh}}(X)\nonumber \\&\quad +\, {\text {sech}}^{p}(Y){\text {tanh}}(Y)+{\text {sech}}^{p}(T){\text {tanh}}(T)], \end{aligned}$$
(8)

with arbitrary constants \(V_1\) and \(W_0\), the localization condition \(\varPhi \rightarrow 0\) as \((X,Y,T)\rightarrow \pm \infty \) yields solution of Eq. (5) as

$$\begin{aligned}&U(Z,X,Y,T)=\left( -\frac{V_1}{\varGamma _{7}}\right) ^{\frac{1}{6}}{\text {sech}} (X){\text {sech}}(Y){\text {sech}}(T)\nonumber \\&\quad \exp \left\{ \text {i}\left[ 3BZ+\varTheta (X,Y,T)\right] \right\} , \end{aligned}$$
(9)

where

$$\begin{aligned}&\varTheta (X,Y,T)=\frac{W_0\sinh (X)}{(p+2)B}\ _2\nonumber \\&\quad F_1\left[ \frac{1}{2},\frac{p+1}{2},\frac{3}{2},-\sinh ^2(X)\right] \nonumber \\&\quad +\frac{W_0\sinh (Y)}{(p+2)B} \ _2F_1\left[ \frac{1}{2},\frac{p+1}{2},\frac{3}{2},-\sinh ^2(Y)\right] \nonumber \\&\quad +\frac{W_0\sinh (T)}{(p+2)B} \ _2F_1\left[ \frac{1}{2},\frac{p+1}{2},\frac{3}{2},-\sinh ^2(T)\right] , \end{aligned}$$
(10)

with the Hypergeometric function \(_2F_1(a,b,c,o)\) [23]. The \({\mathcal {PT}}\)-symmetric potential (8) is a higher dimensional generalization of the corresponding \({\mathcal {PT}}\)-symmetric potential in [20]. Parameter p strongly influences the nature of the gain and loss profile W(X, Y, T) and phase of soliton. The properties of asymptotical non-vanishing or vanishing (localization) of W(X, Y, T) are determined by the zero or nonzero value of p, respectively. If \(p=0\), \(\varTheta (X,Y,T)=\frac{W_{0}}{2B}(X+Y+T)\). If \(p=1\), \(\varTheta (X,Y,T){=}\frac{W_{0}}{3B}\{\arctan [\sinh (X)]+\arctan [\sinh (Y)]+\arctan [\sinh (T)]\}\). If \(p=2\), \(\varTheta (X,Y,T)=\frac{W_{0}}{4B}[\tanh (X)+\tanh (Y)+\tanh (T)]\). If \(p=3\), \(\varTheta (X,Y,T){=}\frac{W_{0}}{10B}\{\arctan [\sinh (X)]+{\text {tanh}}(X){\text {sech}}(X)+\arctan [\sinh (Y)]+{\text {tanh}}(Y){\text {sech}}(Y) +\arctan [\sinh (T)]+{\text {tanh}}(T){\text {sech}}(T)\}\).

2.2 Family 2

If the \({\mathcal {PT}}\)-symmetric potential has the form

$$\begin{aligned}&V(X,Y,T)=\frac{4B}{9}[{\text {sech}}^2(X)+{\text {sech}}^2(Y)+{\text {sech}}^2(T)]\nonumber \\&\quad +\,\frac{9W_0^2}{(3p+2)^2B}[{\text {sech}}^{2p}(X)+{\text {sech}}^{2p}(Y)\nonumber \\&\quad +\,{\text {sech}}^{2p}(T)]+V_2{\text {sech}}^{2} (X){\text {sech}}^{2}(Y){\text {sech}}^{2}(T)\nonumber \\&\quad -\,\varGamma _3\left( -\frac{V_2}{\varGamma _7}\right) ^{\frac{1}{3}}\nonumber \\&\quad \times {\text {sech}}^{\frac{2}{3}}(X){\text {sech}}^{\frac{2}{3}}(Y) {\text {sech}}^{\frac{2}{3}}(T)\nonumber \\&\quad -\,\varGamma _5\left( -\frac{V_2}{\varGamma _7}\right) ^{\frac{2}{3}} {\text {sech}}^{\frac{4}{3}}(X){\text {sech}}^{\frac{4}{3}}(Y) {\text {sech}}^{\frac{4}{3}}(T),\nonumber \\&W(X,Y,T)=W_{0}[{\text {sech}}^{p}(X){\text {tanh}}(X)\nonumber \\&\quad +\,{\text {sech}}^{p}(Y){\text {tanh}}(Y)+{\text {sech}}^{p}(T){\text {tanh}}(T)], \end{aligned}$$
(11)

with arbitrary constants \(V_2\) and \(W_0\), the localization condition \(\varPhi \rightarrow 0\) as \((x,y)\rightarrow \pm \infty \) yields solution of Eq. (5) as

$$\begin{aligned}&u(Z,X,Y,T)=\left[ \sqrt{-\frac{V_2}{\varGamma _{7}}}{\text {sech}}(X) {\text {sech}}(Y){\text {sech}}(T)\right] ^{\frac{1}{3}}\nonumber \\&\quad \exp \left\{ \text {i}\left[ \frac{B}{3}Z+\varTheta (X,Y,T)\right] \right\} , \end{aligned}$$
(12)

where

$$\begin{aligned}&\varTheta (X,Y,T)\nonumber \\&\quad =\frac{3W_0\sinh (X)}{(3p+2)B}\ _2F_1\left[ \frac{1}{2},\frac{p+1}{2},\frac{3}{2},-\sinh ^2(X)\right] \nonumber \\&\quad +\,\frac{3W_0\sinh (Y)}{(3p+2)B} \ _2F_1\left[ \frac{1}{2},\frac{p+1}{2},\frac{3}{2},-\sinh ^2(Y)\right] \nonumber \\&\quad +\,\frac{3W_0\sinh (T)}{(3p+2)B} \ _2F_1\left[ \frac{1}{2},\frac{p+1}{2},\frac{3}{2},-\sinh ^2(T)\right] .\nonumber \\ \end{aligned}$$
(13)
Fig. 1
figure 1

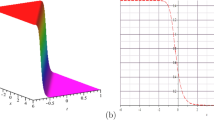
(Color online) a and b v and w of the \({\mathcal {PT}}\)-symmetric potential (3) with (8); c Comparison of v with different p at \(z=10,t=5,y=0\) in the diffraction/dispersion medium with hyperbolic profile. Parameters are chosen as \(p=1,\rho _0=0.6,W_0=0.08,V_1=-12,B=0.5,\varGamma _3=-1,\varGamma _5=0.5,\varGamma _7=1,C=2,L=50,s_0=0.02\)

Full size image

The \({\mathcal {PT}}\)-symmetric potential (11) is another high dimensional extension of the corresponding \({\mathcal {PT}}\)-symmetric potential in [20]. If \(p=0\), \(\varTheta (x,y)=\frac{3W_{0}}{2B}(X+Y+T)\). If \(p=1\), \(\varTheta (x,y)=\frac{3W_{0}}{5B}\{\arctan [\sinh (X)]+\arctan [\sinh (Y)]+\arctan [\sinh (T)]\}\). If \(p=2\), \(\varTheta (x,y)=\frac{3W_{0}}{8B}[\tanh (X)+\tanh (Y)+\tanh (T)]\). If \(p=3\), \(\varTheta (x,y)=\frac{3W_{0}}{22B}\{\arctan [\sinh (X)] +{\text {tanh}}(X){\text {sech}}(X)+\arctan [\sinh (Y)] +{\text {tanh}}(Y){\text {sech}}(Y) +\arctan [\sinh (T)]+{\text {tanh}}(T){\text {sech}}(T)\}\).

From the expression (4) and solutions (9), (12), exact solutions of Eq. (1) read

$$\begin{aligned}&u(z,x,y,t)= \rho _0\varrho ^{-\frac{3}{2}}(z)\left( -\frac{V_1}{\varGamma _{7}}\right) ^{\frac{1}{6}}\nonumber \\&\quad {\text {sech}}(X){\text {sech}}(Y){\text {sech}}(T)\nonumber \\&\quad \exp \left\{ \text {i}\left[ \varPsi (z,x,y,t)\right] \right\} , \end{aligned}$$
(14)

with \(\varPsi (z,x,y,t)=\varOmega (Z,X,Y,T)+\varphi (z,x,y,t)=3BZ+\varTheta (X,Y,T)+\varphi (z,x,y,t)\) and

$$\begin{aligned}&u(z,x,y,t)= \rho _0\varrho ^{-\frac{3}{2}}(z)\nonumber \\&\quad \left[ \sqrt{-\frac{V_2}{\varGamma _{7}}} {\text {sech}}(X){\text {sech}}(Y){\text {sech}}(T)\right] ^{\frac{1}{3}}\nonumber \\&\quad \exp \left\{ \text {i}\left[ \varPsi (z,x,y,t)\right] \right\} , \end{aligned}$$
(15)

where \(\varPsi (z,x,y,t)=\varOmega (Z,X,Y,T)+\varphi (z,x,y,t)=\frac{B}{3}Z+\varTheta (X,Y,T)+\varphi (z,x,y,t)\), Z, X, Y, T and \(\varphi (z,x,y,t)\) are expressed below (4), and \(\varTheta (X,Y,T)\) is given by (10) and (13).

3 Dynamics of light bullets

In soliton solutions (14) and (15), coefficient \(\gamma _7\) of the septimal term strongly influences the amplitude. The requirement of real property for amplitude of these solutions indicates that \(V_1\gamma _{7}<0\) or \(V_2\gamma _{7}<0\), namely these solutions can exist in defocusing septimal media with negative nonlinearity (\(\gamma _{7}<0\)) as \(V_1>0\) or \(V_2>0\) and in focusing septimal media with positive nonlinearity (\(\gamma _{7}>0\)) as \(V_1<0\) or \(V_2<0\). Moreover, form factor of solitons (14) and (15) including amplitude, width, phase and velocity are related to the diffraction/dispersion function \(\beta (z)\). Therefore, we study dynamics of light bullets in different diffraction/dispersion media:

(i) Hyperbolic profile [24–26], given by:

$$\begin{aligned} \beta (z)=\frac{L}{(C-1)z+L}, \end{aligned}$$
(16)

where L is length of the waveguide, and the inverse of C describes the compression ratio parameter (value of dispersion parameter \(\beta (z)\) at distance \(z=L\)) with the natural logarithm e. In these normalized profiles, diffraction coefficient \(\beta (z)\) monotonically decreases from 1 to a final value of \(1/\beta \) after a length L.

and

(ii) Periodic modulation profile [27], given by:

$$\begin{aligned} \beta (z)=\beta _0\cos (\kappa z), \end{aligned}$$
(17)

where \(\beta _0\) is initial diffraction/dispersion, and \(\kappa \) is related to the period of diffraction/dispersion.

The symmetric and anti-symmetric properties of v and w of the \({\mathcal {PT}}\)-symmetric potential (3) with (8 around the center \(x=0,y=0,t=0\) in the diffraction/dispersion medium with hyperbolic profile (16) are shown in Fig. 1a and b, respectively. Comparison of v with different p at \(z=10,t=5,y=0\) in the diffraction/dispersion medium with hyperbolic profile is shown in Fig. 1c. From it, we find that the dip adds obviously when the higher-order term alters from \(p=1\) to \(p=2\). However, the shape of v has a small change when the higher-order term alters from \(p=2\) to \(p=3\).

In real applications, usually analytical solutions are not exactly satisfied; thus, it is valuable to study the stability of solutions against finite perturbations with a 5 % white noise by the split-step Fourier method.

Fig. 2
figure 2

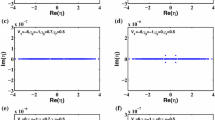
(Color online) a Initial shape of light bullet (14) in the diffraction/dispersion medium with hyperbolic profile; unstable light bullet (14) at distance \(z=100\) in the media of b focusing quintic and septimal nonlinearities with defocusing cubic nonlinearity, d focusing cubic, quintic and septimal nonlinearities and f focusing cubic and quintic nonlinearities with defocusing septimal nonlinearity; stable light bullet (14) at distance \(z=100\) in the media of c focusing septimal and defocusing cubic nonlinearities with disappearing quintic nonlinearity and e focusing cubic and septimal nonlinearities with disappearing quintic nonlinearity under the \({\mathcal {PT}}\)-symmetric potential (3), (8) with \(p=1\). Parameters are chosen as a, b \(V_1=-12,\varGamma _3=-1,\varGamma _5=0.5,\varGamma _7=1\), c \(V_1=-12,\varGamma _3=-1,\varGamma _5=0,\varGamma _7=1\), d \(V_1=-12,\varGamma _3=\varGamma _5=\varGamma _7=1\), e \(V_1=-12,\varGamma _3=1,\varGamma _5=0,\varGamma _7=1\) and f \(V_1=12,\varGamma _3=1,\varGamma _5=0.5,\varGamma _7=-1\). Other parameters are chosen as those in Fig. 1

Full size image
Fig. 3
figure 3

(Color online) a The part \(\varOmega (Z,X,Y,T)\) of phase in solution (14) with \(p=1\), b Comparison of \(\varOmega (Z,X,Y,T)\) with different p at \(z=10,t=5,y=0\), and c phase \(\varPsi (z,x,y,t)\) in solution (14) with \(p=1\) in the diffraction/dispersion medium with hyperbolic profile. Parameters are chosen as those in Fig. 1

Full size image

As reported in [28], when \(p=0\), the \({\mathcal {PT}}\)-symmetric potential is an extended Rosen–Morse potential. Soliton is unstable in this potential with asymptotical non-vanishing of W(x, y). Here we do not discuss this case. When \(p=1\), the \({\mathcal {PT}}\)-symmetric potential is an extended Scarf II potential. Under this \({\mathcal {PT}}\)-symmetric potential, the stable and unstable evolution of light bullet (14) in the media with different nonlinearities is displayed in Fig. 2.

After the evolution of \(z=100\) in the diffraction/dispersion medium with hyperbolic profile, light bullet (14) exhibits unstable behaviors in the media of focusing quintic and septimal nonlinearities with defocusing cubic nonlinearity (Fig. 2b), focusing cubic, quintic and septimal nonlinearities (Fig. 2d) and focusing cubic and quintic nonlinearities with defocusing septimal nonlinearity (Fig. 2f). In these media, light bullet (14) can not maintain their original shapes, then are collapse, and finally decay into noise. Comparing Fig. 2d with Fig. 2b, f, the degree of collapse is relatively weakest in the medium of focusing cubic, quintic and septimal nonlinearities (Fig. 2d); however, the degree of collapse is strongest in the medium of focusing cubic and quintic nonlinearities with defocusing septimal nonlinearity (Fig. 2f).

However, light bullet (14) stably evolves from \(z=0\) to \(z=100\) and sustains its original shape in the media of focusing septimal and defocusing cubic nonlinearities with disappearing quintic nonlinearity (Fig. 2c) and focusing cubic and septimal nonlinearities with disappearing quintic nonlinearity (Fig. 2e). Comparing Fig. 2c with Fig. 2e, more small oscillations around stable light bullet appear in Fig. 2c; thus, light bullet (14) evolves more stable in the medium of focusing septimal and defocusing cubic nonlinearities with disappearing quintic nonlinearity than in the medium of focusing septimal and defocusing cubic nonlinearities with disappearing quintic nonlinearity under the extended Scarf II potential.

For solution (9), the phase exhibits the phenomenon of transition at the center in Fig. 3a. From Fig. 3b, the range of transition decreases with the add of the value p describing higher-order terms of the \({\mathcal {PT}}\)-symmetric potential. For solution (14), the phase is made up of the harmonic term and the phase \(\varOmega (Z,X,Y,T)\) in solution (9). The shape of the phase \(\varPsi (z,x,y,t)\) in solution (14) under the extended Scarf II potential is shown in Fig. 3c.

Fig. 4
figure 4

(Color online) Stable light bullet (14) at distance \(z=100\) in the media of hyperbolic diffraction/dispersion and focusing quintic and septimal nonlinearities with defocusing cubic nonlinearity under the \({\mathcal {PT}}\)-symmetric potential (3), (8) with a \(p=2\) and c \(p=3\), and unstable light bullet (14) at distance \(z=100\) in the media of focusing quintic and septimal nonlinearities with disappearing cubic nonlinearity under the \({\mathcal {PT}}\)-symmetric potential (3), (8) with b \(p=2\) and d \(p=3\). Parameters are chosen as a, c \(V_1=-12,\varGamma _3=-1,\varGamma _5=0.5,\varGamma _7=1\), b, d \(V_1=-12,\varGamma _3=-1,\varGamma _5=0,\varGamma _7=1\). Other parameters are chosen as those in Fig. 1

Full size image

Under the \({\mathcal {PT}}\) complex potential (3), (8) with higher-order terms of \(p=2\) and \(p=3\), the stability of light bullet in nonlinear media appears different cases. Different from under the Scarf II potential, light bullet (14) appears the unstable behavior in the media of focusing quintic and septimal nonlinearities with disappearing cubic nonlinearity in Fig. 4b, d, it is distorted evolving after several diffraction lengths, and its original shape is not preserved, then spreads to the background, and next decays into noise. However, in the media of focusing quintic and septimal nonlinearities with defocusing cubic nonlinearity, light bullet (14) does not appear any visible instability except for some small oscillations originating from the white noise, which only influences the background of light bullet and produces some small oscillations around the light bullet in Fig. 4a, c. Compared with the shallow dip of the Scarf II potential (red circle in Fig. 1c), the dip of the \({\mathcal {PT}}\) complex potential (3), (8) with higher-order terms of \(p=2\) and \(p=3\) (black box and blue line in Fig. 1c) is uncommonly deep. Therefore, this stability of light bullet in Fig. 4a, c can be understood that the dip of the \({\mathcal {PT}}\) complex potential (3), (8) with higher-order terms of \(p=2\) and \(p=3\) counteracts with the effect of dispersion, diffraction and focusing quintic and septimal nonlinearities with defocusing cubic nonlinearity. This subtle interplay among dispersion, diffraction, nonlinearity and \({\mathcal {PT}}\)-symmetric potential leads to a stable evolution of light bullet in Fig. 4a, c.

Fig. 5
figure 5

(Color online) Unstable light bullet (15) at distance \(z=100\) in the media of hyperbolic diffraction/dispersion and focusing quintic and septimal nonlinearities with defocusing cubic nonlinearity under the \({\mathcal {PT}}\)-symmetric potential (3), (11) with a \(p=1\), b \(p=2\) and c \(p=3\). Other parameters are chosen as those in Fig. 1

Full size image
Fig. 6
figure 6

(Color online) Stable light bullet (14) in the media of periodic diffraction/dispersion and a–c focusing septimal and defocusing cubic nonlinearities with disappearing quintic nonlinearity and d–f focusing quintic and septimal nonlinearities with defocusing cubic nonlinearity at distances a, d \(z=7\), b, e \(z=55\) and c, f \(z=100\) under the \({\mathcal {PT}}\)-symmetric potential (3), (8) with a–c \(p=1\) and d–f \(p=2\). Parameters are chosen as \(\beta _0=0.6,\kappa =0.2\). Other parameters are chosen as those in Fig. 1

Full size image

When light bullet (15) evolves in various nonlinear media, it is unstable regardless of focusing or defocusing cubic, quintic and septimal nonlinearities under the \({\mathcal {PT}}\)-symmetric potentials (3) and (11) with \(p=1,2,3\). Figure 5 displays three examples of unstable evolution in the hyperbolic diffraction/dispersion medium.

When light bullet (14) evolves in periodic modulation system (17), compression and expansion of light bullets are shown in Fig. 6. Here we exhibit the compression and expansion of light bullets in stable case, i.e., focusing septimal and defocusing cubic nonlinearities with disappearing quintic nonlinearity under the Scarf II potential and focusing quintic and septimal nonlinearities with defocusing cubic nonlinearity under the \({\mathcal {PT}}\)-symmetric potentials (3) and (8) with \(p=2\). Comparing Fig. 6 with Figs. 2e, 4a, c, we find the evolution of light bullet in periodic modulation system is more stable than that in the hyperbolic dispersion/diffraction system because there are smaller oscillations around light bullet in periodic modulation system. It is a good agreement with results in Ref. [29], where it is reported that periodic sign-changing dispersion/diffraction and nonlinearity add the probability for an eventual stability of solutions.

4 Conclusions

In this paper, we study dynamics of light bullets in inhomogeneous cubic-quintic-septimal nonlinear media with \({\mathcal {PT}}\)-symmetric potentials, and the related results are concluded as follows.

(i) Analytical light bullets are obtained.

A (3+1)-dimensional NLSE with variable-coefficient dispersion/diffraction and cubic-quintic-septimal nonlinearities is studied, and two families of analytical light bullet solutions with two types of \({\mathcal {PT}}\)-symmetric potentials are obtained. In these solutions, the coefficient of the septimal nonlinear term strongly influences the form of light bullet.

(ii) Dynamics and stability of light bullets in the hyperbolic dispersion/diffraction medium are studied.

Light bullet solution (14) is stable in the media of focusing septimal and defocusing cubic nonlinearities with disappearing quintic nonlinearity and focusing cubic and septimal nonlinearities with disappearing quintic nonlinearity under the Scarf II potential; however, it is unstable in the media above under the \({\mathcal {PT}}\)-symmetric potential with higher-order terms (\(p=2\) and \(p=3\)), where light bullet solution (14) is stable in the media of focusing quintic and septimal nonlinearities with defocusing cubic nonlinearity. These stabilities originate from subtle interplay among dispersion, diffraction, nonlinearity and \({\mathcal {PT}}\)-symmetric potential. Moreover, light bullet (15) is unstable regardless of focusing or defocusing cubic, quintic and septimal nonlinearities under the \({\mathcal {PT}}\)-symmetric potentials with \(p=1,2,3\).

(iii) Compression and expansion of light bullets in periodic modulation system are investigated.

Compression and expansion of light bullets in the periodic modulation system are investigated numerically. The result indicates that evolution of light bullet in periodic modulation system is more stable than that in the hyperbolic dispersion/diffraction system because there are smaller oscillations around light bullet in periodic modulation system. Periodic sign-changing dispersion/diffraction and nonlinearity add the probability for an eventual stability of solutions.