A New Car Following Model Considering the Multi-headway Variation Forecast Effect

Abstract

An extended car following model is presented by considering the effect of Multi-Headway Variation Forecast (MHVF) effect in the real world. The model’s linear stability criterion was obtained by employing the linear stability theory. Theoretical analysis result shows that the new consideration leads to the stabilization of traffic systems. By means of nonlinear analysis method, the modified Korteweg-deVries (mKdV) equation near the critical point was derived, thus the propagation behavior of traffic jam can be characterized by the kink-antikink soliton solution for the mKdV equation. Numerical simulation is carried out and its results is in good agreement with the aforementioned theoretical analysis. Both of them show that the MHVF effect can suppress the emergence of traffic jamming and stabilize the vehicular system.

1 Introduction

In the past decades, the problem of traffic congestion has been widely concerned by scholars at home and abroad. A large number of traffic flow models [1,2,3,4,5] have been proposed to reveal the complex mechanism behind traffic congestion. These traffic flow models can be roughly divided into macroscopic models [6,7,8], microscopic models [9, 10], and mesoscopic models [11, 12] according to the modeling scale. The microscopic traffic flow model takes the individual vehicle as the research object. Generally, it can describe a single vehicle dynamics process in a very simple way, and can capture rich detailed characteristics of vehicle flow movement, so it plays an important basic role in many traffic flow models. Among a large number of microscopic traffic flow models, the most well known one is the optimal velocity (OV) model [10]. Hereafter, many researchers have attempted to improve the OV model. Since then, by introducing different factors, a series of extended ov models have been put forward to be closer to the reality of the transportation system. These expansion factors mainly include: negative speed difference information [13], positive speed difference information [14], multiple information of headway [15] and relative velocity [16], backward-looking effect [17], driver’s anticipation [18], curved road condition [19], interruption factors [20] and so on.

All of the above models can reproduce many complex phenomena in actual traffic. However, the variables of these models are generally dependent on current information and rarely involve the driver's prediction information about the future traffic situation. Recently, the study on the driver’s anticipation effect has attracted considerable attention of scholars since it is a universal psychological phenomenon in drivers’ behavior. Tang et al. [6, 18] explored how the Driver’s Forecast Effect (DFE) affects the stability of traffic flow. By introducing the factor of anticipation driving behavior into the car following model, Zheng et al. [21] examined the influence of anticipation effect upon the traffic flow via linear stability analysis and nonlinear analysis. In 2019, Wang et al. [22]developed a new car following model that takes into account the effect of headway variation tendency (HVT), the results show that HVT can improve the stability of traffic stream. By considering the effect of expected traffic variation tendencies on traffic flow, Zhang et al. [23] examined the predictive effect within a microscopic traffic model. The predictive effect on dynamics of traffic flow is also analyzed by employing the lattice hydrodynamic model [24]^. Further, Daljeet Kaur and Sapna Sharma [25] investigated the predictive effect in the two lane framework on the basis of lattice model in 2020. Although many forms of the anticipation effect are incorporated into the traffic flow model to stabilize the traffic flow system, the effect of multi-headway variation forecast (MHVF), i.e. the multiple headway variation tendencies of local traffic conditions at the future moment resulting from the driver’s forecast behaviour of the preceding vehicles group, has not been explored in the traffic flow model up to now.

In fact, with the help of intelligent transportation system platform, drivers can effectively perceive and estimate the information of headway variation tendency of preceding vehicles group in the next moment (multi-headway variation forecast, MHVF effect). Depending on this on-line traffic data, drivers take the appropriate measures (accelerate, maintain or slow down) to adjust their driving behavior in advance to adapt to downstream traffic conditions. And one can fully expect that the MHVF effect will have a noticeable impact on the dynamic characteristics of the vehicle following system. However, how does this effect affect the traffic dynamics under the ITS environment? This is an interesting but still open problem.

In view of the above reason, in this paper, we build a new model based on the car following theory, trying to reveal the effect of MHVF on the traffic flow. The stability and nonlinear characteristics of the new model are studied analytically, and the theoretical analysis results are verified by numerical simulation.

2 Models

For the single lane vehicle following system, Bando et al. proposed the famous OV model [10] as follows:

$$ \frac{dv_j (t)}{{dt}} = a[V(\Delta x_j (t)) - v_j (t)] $$

(1)

where the subscript $j$ is the vehicle label, $t$ represents the time variable. $a$ represents the driver's sensitivity coefficient, and its value is the reciprocal of the delay parameter $\tau$. $\Delta x_j (t) = x_{j + 1} - x_j$ is the headway between the leading car $j + 1$ and following car $j$ at time $t$_. variables $v_j (t)$ and $x_j (t)$ are the velocity and position of the $j$th car respectively. V($\cdot$) represents the optimal speed function. Through the comparative study with the traffic field data, it is found that the acceleration and deceleration parameters of the OV model are not within the normal range.

In order to improve the OV model's ability to simulate actual traffic, Helbing and Tilch [13] introduced the negative speed difference effect into the OV model and proposed the GF model. Further, Jiang et al. [14] investigated the positive speed difference effect and proposed the full velocity difference (FVD) model as follows:

$$ \frac{dv_j (t)}{{dt}} = a[V(\Delta x_j (t)) - v_j (t)] + \lambda \Delta v_j (t) $$

(2)

where $\Delta v_j (t) = v_{j + 1} (t) - v_j (t)$ is the relative speed of two consecutive car at time $t$.

$\lambda = k/\tau$ is the responding factor of the relative speed. The results show that FVD model can better describe the dynamic characteristics of the traffic system than OV and GF models. However, the defect of unrealistically high deceleration in the FVD model has not been eliminated [14].

In 2012, by considering the anticipation driving behavior, Zheng et al. [21] established a extended anticipation driving car-following (AD-CF) model. The model’s dynamics equation is as follows:

$$ \frac{dv_j (t)}{{dt}} = a\{ V[\Delta x_j (t) + T\Delta v_j (t)] - v_j (t)\} + \lambda \Delta v_j (t) $$

(3)

where $T$ represents the driver's forecast time, $T\Delta v_j (t)$ denotes the estimation of space headway in the next moment.

The AD-CF model can effectively stabilize traffic flow by introducing anticipation driving behavior. But the AD-CF model only considers the predictive information of nearest front car, and does not considers the effect of Multi-Headway Variation Forecast (MHVF effect), i.e. the prior variation tendency of space headway of multiple vehicles ahead in the next moment. In fact, the MHVF effect of preceding vehicles group reflects the overall traffic change trend of the downstream area, i.e., whether the traffic flow of preceding vehicles on a segment will cluster, dissipate, or simply maintain a constant headway. With the help of MHVF traffic data shared by preceding vehicles, the following car can sense the downstream traffic situation, then make a decision and adjust its velocity to the optimal state in advance. To capture the effect of MHVF on the stability of traffic flow, in this paper, we developed an extended car-following model (named MHVF model) under ITS environment, the dynamics equation reads:

$$ \frac{dv_j (t)}{{dt}} = a\{ V[\Delta x_j (t) + T\Delta \overline{v}_j (t)] - v_j (t)\} + \lambda \Delta v_j (t) $$

(4)

where $\Delta \overline{v}_j (t) = \sum_{l = 1}^n {\beta_l \Delta v_{j + l - 1} (t)}$ is the weighted sum of velocity difference of the preceding vehicles group, $\beta_l$ is the corresponding coefficient, $n$ denotes the number of the vehicles ahead considered. Term $T\Delta \overline{v}_j (t)$ denotes the predictive variation tendency of space headway of downstream traffic flow (consisting of car $j$ and its leading car $j + 1,j + 2, \ldots ,j + n$) in the future time, i.e. the key parameter $T\Delta \overline{v}_j (t)$ represents the MHVF effect. The modeling idea of the new model is that the acceleration output of the current jth vehicle at time t in the following system is not only affected by the velocity $v_j (t)$ and relative velocity $\Delta v_j (t)$, but also determined by the driver's estimation of multi-headway variation tendency $T\Delta \overline{v}_j (t)$. Therefore, the proposed model can be used to explore the dynamic property resulting from the MHVF effect under ITS environment.

It is well known that the effect of the vehicles ahead on vehicle motion decreases gradually as the distance between the considered vehicle and that ahead increases. So in this paper, we select the weighted function tentatively as $\beta_l = (1/3)^{l - 1}$.

For the convenience of subsequent analysis, the following formula can be obtained by first-order Taylor expansion of variable $V[\Delta x_j (t) + T\Delta \overline{v}_j (t)]$ in Eq. (4).

$$ \begin{gathered} V[\Delta x_j (t) + T\Delta \overline{v}_j (t)] = V[\Delta x_j (t) + T\sum_{l = 1}^n {\beta_l \Delta v_{j + l - 1} } ] \\ = V(\Delta x_j (t)) + TV^{\prime}(\Delta x_j (t))\sum_{l = 1}^n {\beta_l \Delta v_{j + l - 1} } (t) \\ \end{gathered} $$

(5)

Thus, Eq. (4) can be rewritten as follows:

$$ \frac{dv_j (t)}{{dt}} = a\{ V(\Delta x_j (t)) + TV^{\prime}(\Delta x_j (t))\sum_{l = 1}^n {\beta_l \Delta v_{j + l - 1} (t)} - v_j (t)\} + \lambda \Delta v_j (t) $$

(6)

When $T = 0$, the new model is reduced to the FVD model [14]. When $T > 0$, $n = 1$, the new model degenerates into the AD-CF model [21].

In this paper, we adopt the following optimal velocity function [10]:

$$ V(\Delta x_j (t)) = \frac{1}{2}v_{\max } [\tanh (\Delta x_j (t) - h_c ) + \tanh (h_c )] $$

(7)

where $v_{\max } = 2$ is the maximum velocity and $h_c = 4$ is the safe distance.

In order to facilitate the follow-up computer simulation and nonlinear analysis, Eq. (6) is rewritten into the form of headway variable:

$$ \begin{aligned} \Delta x_j (t + 2\tau ) & = \Delta x_j (t + \tau ) + \tau [V(\Delta x_{j + 1} (t)) - V(\Delta x_j (t))] \hfill \\ & \quad + T[V^{\prime}(\Delta x_{j + 1} (t)) - V^{\prime}(\Delta x_j (t))]\sum_{l = 1}^n {\beta_l [\Delta x_{j + l} (t + \tau )} - \Delta x_{j + l} (t)] \hfill \\ & \quad + TV^{\prime}(\Delta x_j (t)) \sum_{l = 1}^n \beta_l [\Delta x_{j + l} (t + \tau ) - \Delta x_{j + l} (t) - \Delta x_{j + l - 1} (t + \tau ) + \Delta x_{j + l - 1} (t)] \hfill \\ & \quad + k[\Delta x_{j + 1} (t + \tau ) - \Delta x_{j + 1} (t) - \Delta x_j (t + \tau ) + \Delta x_j (t)] \hfill \\ \end{aligned} $$

(8)

3 Linear Stability Analysis

In order to investigate the effect of MHVF on jamming transition in traffic flow, the linear stability analysis is carried out below. At the initial time, it is assumed that all vehicles move on the circular road at a uniform speed with headway $b$ and optimal speed $V(b)$. Obviously, at this time, the traffic flow is in an equilibrium state, and the coordinates of its steady-state solution can be expressed as:

$$ x_j^0 (t) = bj + V(b)t,\,b = L/N, $$

(9)

where, $N$ represents the total number of vehicles, and the parameter $L$ is the length of the ring road. In order to study the stability of the traffic flow under the small disturbance condition, the small disturbance signal $y_j (t)$ is applied to make the traffic flow produce motion deviation:

$$ x_j (t) = x_j^0 (t) + y_j (t) $$

(10)

Substituting Eq. (10) into Eq. (8) and linearizing them yield the following equation:

$$ \begin{aligned} \Delta y_j (t + 2\tau ) & = \Delta y_j (t + \tau ) + \tau V^{\prime}(b)[\Delta y_{j + 1} (t) - \Delta y_j (t)] \hfill \\ & + TV^{\prime}(b)\sum_{l = 1}^n \beta_l [\Delta y_{j + l} (t + \tau ) - \Delta y_{j + l} (t) - \Delta y_{j + l - 1} (t + \tau ) + \Delta y_{j + l - 1} (t)] \hfill \\ & + k[\Delta y_{j + 1} (t + \tau ) - \Delta y_{j + 1} (t) - \Delta y_j (t + \tau ) + \Delta y_j (t)] \hfill \\ \end{aligned} $$

(11)

where $V^{\prime} = dV(\Delta x_j )/d\Delta x_j \left|_{\Delta x_j = b} \right.$ and $\Delta y_j (t) = y_{j + 1} (t) - y_j (t)$.

By expanding $\Delta y_j (t) = Ae^{ikj + zt}$, we obtain the following equation for z:

$$ \begin{gathered} e^{2z\tau } - e^{z\tau } - \tau V^{\prime}(e^{ik} - 1) - TV^{\prime}(b)(e^{z\tau } - 1)\sum_{l = 1}^n {\beta_l [e^{ikl} - e^{ik(l - 1)} ]} \hfill \\ - k(e^{ik} - 1)(e^{z\tau } - 1) = 0 \hfill \\ \end{gathered} $$

(12)

Inserting $z = z_1 ik + z_2 (ik)^2 + \cdots$ into Eq. (13) and neglecting the higher order terms, one has the first order and second order terms of $ik$ respectively:

$$ z_1 = V^{\prime} $$

(13)

$$ z_2 = \frac{{V^{\prime}}}{2}(1 - 3V^{\prime}\tau + 2TV^{\prime}\sum_{l = 1}^n {\beta_l } + 2k) $$

(14)

If $z_2 < 0$, the uniformly steady-state flow becomes unstable for long-wavelength models, while the uniform flow is stable when $z_2 > 0$. Thus the neutral stable criteria for this steady state is given by

$$ \tau = \frac{{1 + 2k + 2TV^{\prime}\sum_{l = 1}^n {\beta_l } }}{{3V^{\prime}}} $$

(15)

For small disturbances with long wavelengths, the homogeneous traffic flow is stable in a condition where

$$ \tau < \frac{{1 + 2k + 2TV^{\prime}\sum_{l = 1}^n {\beta_l } }}{{3V^{\prime}}} $$

(16)

As $T = 0$, the result of stable condition is the same as that of the FVD model [14].

$$ \tau < \frac{1 + 2k}{{3V^{\prime}}} $$

(17)

As $T > 0$, $n = 1$, the stable condition is in accordance with the result of AD-CF model [21].

$$ \tau < \frac{{1 + 2k + 2TV^{\prime}}}{{3V^{\prime}}} $$

(18)

The result of stable condition for MHVF model is influenced by the parameter $T$ and $n$. This indicates that the stability of traffic is closely related to the prediction time step and the number of leading vehicles considered.

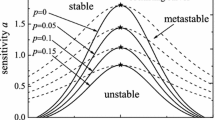
Figure  1 shows the neutral stable curves in the headway-sensitivity space ($\Delta x,a$) for the MHVF model with $T = 0.3$, $k = 0.1$ under different values of $n$. From Fig. 1, it can be seen that each neutral stability curve has a vertex $(h_c ,a_c )$, which is called the critical stability point. The neutral stability curve divides the phase space into two different regions. Above the neutral stability curve is the stable region, where the small interference signals in the traffic flow will evolve and disappear with the development of time t. Below the neutral stable is the unstable region, where the small disturbance signals will gradually diverge with the movement of traffic flow, Finally, it evolves into traffic jam spreading along the upstream of traffic flow. As $n = 1$, the corresponding neutral stability curve is consistent with AD-CF model [21]. In addition, Fig. 1 also clearly shows that with the increase of the number of vehicles $n$ considered ahead, the corresponding stability area gradually expands, which indicates that by considering the MHVF effect of preceding vehicles group, the new model has greatly improved the stability of vehicular system. Meanwhile, it is easy to find that in Fig. 1 the more vehicles we consider in the effect of MHVF, the more stable the traffic will be. However, it should be noted that when $n = 3,4$, the corresponding curves almost coincides, which shows that just considering the information of three vehicles in front ($n = 3$), the traffic jam can be suppressed effectively. That is to say $n = 3$ is the optimal state for MHVF model.

Fig. 1

Phase diagram in headway-sensitivity space ($\Delta x,a$) for MHVF model ($T = 0.3$, $k = 0.1$) under different values of $n$

Figure 2 is obtained by giving the different values of $T$ when $n = 3$, $k = 0.1$. It is easy to find that the neutral stability curves move down with the increase of forecast time T, which reveals that the estimated duration $T$ in MHVF effect has an important impact on traffic flow. What’s more, the stability is gradually improved with the increase of forecast time T. Especially, as $T = 0$, the neutral stability line is the same as that in the FVD model [14].

Fig. 2

Phase diagram in headway-sensitivity space ($\Delta x,a$ ) for MHVF model ($n = 3$, $k = 0.1$) under different values of $T$

4 Nonlinear Analysis and mKdV Equation

To investigate the effect of MHVF on traffic flow, nonlinear analysis is conducted to study the slowly varying behavior near the critical point $(h_c ,a_c )$. For extracting slow scales with the space variable j and the time variable t, the slow variable $X$ and $T$ are defined as follows:

$$ X = \varepsilon (j + bt)\,\,\,{\text{and}}\,\,\,T = \varepsilon^3 t,\,\,0 < \varepsilon \le 11 $$

(19)

where b is a constant to be determined. Given

$$ \Delta x_j (t) = h_c + \varepsilon R(X,T) $$

(20)

Bring formulas (19) and (20) into Eq. (8), then expand each item to the fifth order of $\varepsilon$ by using Taylor expansion method, and sort out the following formula:

$$ \begin{gathered} \varepsilon^2 [b - V^{\prime}]\partial_X R + \varepsilon^3 f_1 \partial_X^2 R + \varepsilon^4 [\partial_T R + f_2 \partial_X^3 R - f_3 \partial_X R^3 ] \hfill \\ + \varepsilon^5 f_4 \partial_T \partial_x R + f_5 \partial_X^4 R - f_6 \partial_X^2 R^3 ] = 0 \hfill \\ \end{gathered} $$

(21)

where

$$V^{\prime} = dV(\Delta x_j )/d\Delta x_j \left| { {\Delta x_j = h_c } {V^{\prime\prime\prime} = [d^3 V(\Delta x_j )/d\Delta x_j^3 ]}} \right| \Delta x_j = h_c ,$$

$$f_1 = \frac{{3b^2 \tau - V{\prime} - (2TV^{\prime}\sum_{l = 1}^n {\beta_l } + 2k)b}}{2},$$

$$\begin{aligned} f_2 & = \frac{{7b^3 \tau^2 - V{\prime} - 3bk(b\tau + 1) - 3b\tau TV^{\prime}\sum_{l = 1}^n {\beta_l } (b\tau + 2l - 1)}}{6},\\ f_3 & = \frac{{V{\prime\prime\prime}}}{6}, \\ f_4 &= 3b\tau - k - TV^{\prime}\sum_{l = 1}^n {\beta_l },\end{aligned}$$

$$\begin{aligned} f_5 & = \frac{5b^4 \tau^3 }{8} - \frac{{V^{\prime}}}{24} - \frac{k(4b + 4b^2 \tau + 4b^3 \tau^2 )}{{24}} \hfill \\ & - \frac{{TV^{\prime}\sum_{l = 1}^n {\beta_l [4b^3 \tau^2 + 6b^2 \tau (2l - 1) + 4b(3l^2 - 3l + 1)]} }}{24}, \hfill \\ f_6 & = \frac{{V^{\prime\prime\prime}}}{12}(1 + 2bT\sum_{l = 1}^n {\beta_l } ).\end{aligned}$$

Near the critical point $(h_c ,a_c )$, $\tau = (1 + \varepsilon^2 )\tau_c$, taking $b = V^{\prime}$ and eliminating the second order and third order terms of $\varepsilon$ from Eq. (21) result in the simplified equation:

$$ \varepsilon^4 [\partial_T R - g_1 \partial_X^3 R + g_2 \partial_X R^3 ] + \varepsilon^5 [g_3 \partial_X^2 R + g_4 \partial_X^4 R + g_5 \partial_X^2 R^3 ] = 00 $$

(22)

where

$$ g_1 = - \frac{{7b^3 \tau_c^2 - V^{\prime} - 3bk(b\tau_c + 1) - 3b\tau_c TV^{\prime}\sum_{l = 1}^n {\beta_l } (b\tau_c + 2l - 1)}}{6} $$

(23)

$$ g_2 = - \frac{{V^{\prime\prime\prime}}}{6}, \ldots g_3 = \frac{3}{2}b^2 \tau_c $$

(24)

$$ \begin{gathered} g_{41} = - \frac{1}{6}(3b\tau_c - k - TV^{\prime}\sum_{l = 1}^n {\beta_l )} [7b^3 \tau_c^2 - V^{\prime} - 3bk(b\tau_c + 1) \\ - 3b\tau_c TV^{\prime}\sum_{l = 1}^n {\beta_l } (b\tau_c + 2l - 1)] \\ \end{gathered} $$

(25)

$$ \begin{gathered} g_4 = g_{41} + \frac{5b^4 \tau_c^3 }{8} - \frac{{V^{\prime}}}{24} - \frac{k(4b + 4b^2 \tau_c + 4b^3 \tau_c^2 )}{{24}} \\ - \frac{{TV^{\prime}\sum_{l = 1}^n {\beta_l [4b^3 \tau_c^2 + 6b^2 \tau_c (2l - 1) + 4b(3l^2 - 3l + 1)]} }}{24} \\ \end{gathered} $$

(26)

$$ g_5 = \frac{1}{12}V^{\prime\prime\prime}[6b\tau_c - 2k - 2T(V^{\prime} + b)\sum\limits_{l = 1}^n {\beta_{l}} - 1] $$

(27)

To derive the regularized equation, the following transformations are performed on Eq. (22):

$$ T^{\prime} = g_1 T\,\,\,\,\,\,\,\,\,\,\,\,\,\,R = \sqrt {\frac{g_1 }{{g_2 }}} R^{\prime} $$

(28)

The standard mKdV equation with a $O(\varepsilon )$ correction term is given as follows:

$$ \partial_{T^{\prime}} R^{\prime} - \partial_X^3 R^{\prime} + \partial_X R^{\prime 3} + \varepsilon M[R^{\prime}] = 00 $$

(29)

where

$$ M[R^{\prime}] = \sqrt {\frac{1}{g_1 }} [g_3 \partial_X^{2} R^{\prime} + g_4 \partial_X^{4} R^{\prime} + \frac{g_1 g_5 }{{g_2 }}\partial_X^{2} R^{\prime 3} ] $$

(30)

Ignoring the term $O(\varepsilon )$ in Eq. (30), we obtain the standard mKdV equation with the kink–antikink wave solution.

$$ R^{\prime}_0 (X,T^{\prime}) = \sqrt c \tanh \sqrt{\frac{c}{2}} (X - cT^{\prime}) $$

(31)

With the method described in Ref. [26], we obtain the selected velocity $C$.

$$ C = \frac{5g_2 g_3 }{{2g_2 g_4 - 3g_1 g_5 }} $$

(32)

Hence, we obtain the kink-antikink soliton solution as follows:

$$ \Delta x_j (t) = h_c + \sqrt {\frac{g_1 C}{{g_2 }}(\frac{\tau }{\tau_c } - 1)} \tanh \sqrt {\frac{C}{2}(\frac{\tau }{\tau_c } - 1)} [j + (1 - Cg_1 (\frac{\tau }{\tau_c } - 1))t] $$

(33)

Then, amplitude $A$ of the kink-antikink soliton is given by

$$ A = \sqrt {\frac{g_1 c}{{g_2 }}(\frac{\tau }{\tau_c } - 1)} $$

(34)

The kink–antikink soliton solution shows that for the MHVF car following model, the traffic congestion is a kind of density wave near the critical point, which can be characterized by the free flow phase (low-density traffic flow) and the blocking phase (high-density traffic flow), and verifies that the occurrence of traffic jams(density wave) are related with both the forecast time duration $T$ and the number $n$ of the preceding vehicles considered in MHVF effect. Actually, in Figs. 3, 4, 5 and 6, the propagating backward kink–antikink density wave appears, which is in good agreement the analytical ones.

Fig. 3

Space–time evolution of the headways after t = 10,000 for the MHVF model ($a = {1}{\text{.48}}$, $k = 0.1$, $T = 0.3$) under the different value of n, where (a) n = 1, (b) n = 2, (c) n = 3 and (d) n = 4

Fig. 4

The headway profile at t = 10,300 for the MHVF model correspond to the panels in Fig. 3

Fig. 5

Space–time evolution of the headways after t = 10,000 for the MHVF model ($a = {1}{\text{.6}}$, $k = 0.1$, $n = 3$) under the different value of T, a T = 0, b T = 0.1, c T = 0.15 and d T = 0.3

Fig. 6

The headway profile at t = 10,300 for the MHVF model correspond to the panels in Fig. 5

Through the linear stability criterion Eq. (16), we get the value of the critical sensitivity $a_c$. According to the nonlinear analysis, we obtain the propagation velocity $C$ of the kink–antikink soliton solution by using Eq. (32). The computational values of $a_c$ and $C$ for MHVF car following model corresponding to the case of different parameters are listed in Tables 1 and 2, respectively. Table 1 is obtained by giving the different values of $n$ under $k = 0.1$ and $T = 0.3$. Table 2 shows the $a_c$ and $C$ for various values of $T$ when $k = 0.1$ and $n = 3$. It can be found clearly that with the increase of $n$ or $T$, the corresponding absolute values of both $a_c$ and $C$ decrease gradually, which means that the performance of stabilizing traffic flow has been improved.

Table 1 The critical sensitivity $a_c$ and the propagation velocity $C$ for various $n$ when with $k = 0.1$ and $T = 0.3$

Table 2 The critical sensitivity $a_c$ and the propagation velocity $C$ under different values of $T$ with $k = 0.1$ and $n = 3$

5 Numerical Simulation

In this section, the computer simulation is conducted to investigate the effect of MHVF on suppressing traffic jams, as well as, to check the validity of the above theoretical results. Under the periodic boundary condition, the following initial conditions are adopted:

$\Delta x_j (0) = \Delta x_j (1) = 4.0,$ for $j \ne 50,51$, $\Delta x_j (1) = 4.0 + 0.1,$ for $j = 50$, and $\Delta x_j (1) = 4.0 - 0.1,$ for $j = 51$. The total number of cars is $N = 100$.

Figure 3 displays the typical traffic patterns after a sufficiently long time $t = 10^4$ for the MHVF model under the condition $a = {1}{\text{.48}}$, $k = 0.1$, $T = 0.3$. The patterns (a), (b), (c) and (d) are the space–time evolution of the headway corresponding to the cases of $n = 1,2,3$ and 4 respectively. Pattern (a) with $n = 1$ shows the results obtained from AD-CF model [21]. In patterns (a) and (b), due to the linear stability condition is not satisfied according to Eq. (16), when the equilibrium traffic is disturbed by small disturbance, the traffic flow will fluctuate, and the propagating backward kink-antikink density wave appears as traffic jams. However, in comparing pattern (a) with (b) under the same sensitivity, traffic congestion is found to be much less serious in pattern (b), indicating that the number of preceding cars in the MHVF positively affects the stabilization of traffic flow. Besides that, from patterns (b)-(d) one can find that as the value of $n$ increases further, small disturbances are quickly absorbed. Especially, in patterns (c) and (d), where n = 3,4, the traffic jams disappear and the inhomogeneous traffic flow recovers to the uniform state under the same sensitivity, which means that just considering the signal of three vehicles ahead is enough for suppressing the traffic jams quickly and efficiently. Hence, for the MHVF model it means m = 3 is the optimal state.

Figure 4 indicates that the headway profiles obtained at t = 10,300 correspond to the panels in Fig. 3. Similar results can be concluded in Fig. 4. Therefore, the results of the simulation are in good agreement with those of the theoretical analysis for various value of n, and verifies that considering the effect of multi-headway variation forecast (MHVF) in traffic flow system is necessary.

When the model is in the optimal state (m = 3), the influence of prediction time T on the stability of traffic flow is further studied. The simulation inputs are shown in Figs. 5 and 6.

In Fig. 5, the headway of spatiotemporal evolution pattern at time $t = 10^4$ for different $T$($a = {1}{\text{.6}}$, $k = 0.1$, $n = 3$) is given. The headway profiles of density waves corresponding to Fig. 5 were shown in Fig. 6 at time t = 10,300 s. The patterns (a) of Figs. 5 and 6 with $T = 0$ corresponds to the solution of FVD model [14]. The patterns (b), (c), and (d) of Figs. 5 and 6 correspond to T = 0.1, 0.15 and 0.3, respectively. Comparing patterns (a) with patterns (b), (c), and (d) In Fig. 6 under the same sensitivity coefficient, it can be found that due to the forecast effect are considered, the amplitude of the stop-and-go wave in the patterns (a) is wider than that of patterns (b–d). The significant differences between pattern (a) and patterns (b–d) in Fig. 6 indicate that drivers’ forecast information of has an important effect on the traffic stability. In addition, one can find that with the increase of the forecast time coefficient T, the amplitudes variation trend of headway is decreased, which means the traffic flow system becomes more stable. Especially, setting $T = 0.3$, because the stability conditions are satisfied, the stop-and-go phenomenon disappears and traffic flow finally become stable in Fig. 6d as time progresses, further demonstrating that there is a positive correlation between the duration of forecast time in MHVF effect and the traffic flow stability. The similar results can also be concluded in Fig. 5.

Combined with the above theoretical analysis and numerical simulation, we can draw the following conclusions:

• (1) The results of numerical analysis are in good agreement with those of theoretical analysis, and show that the MHVF effect is conducive to enhance traffic stability and suppress traffic jams.

• (2) When MHVF effect is considered in the car following process, the stability of traffic flow relates with not only the number of leading vehicles $n$ whose information is involved, but also the forecast time duration $T$.

• (3) The stability of traffic system improves with the increase of the number $n$ of vehicles considered or the increase of the prediction time $T$ in MHVF effect.

• (4) $n = 3$ is the optimal state for the MHVF car following model, which means just collecting the information of three preceding vehicle is enough to smooth the traffic fluctuation and suppress traffic jams effectively, and illustrates there is no need to consider more preceding vehicles than three in the proposed model, so as to avoid collecting information more than needed and increasing the information burden of drivers.

6 Summary

In recent years, wireless communication and information technologies have been widely applied in ITS environment, and thus much more information is available for drivers than ever before. Many traffic flow models have been proposed to study the complex traffic phenomena by incorporating other vehicles’ traffic information provided by ITS, but few existing car-following models directly studied the multi-headway variation forecast (MHVF) effect. In this paper, we constructed a new car following model that considers the effect of MHVF to effectively curb the traffic congestion. Then, the stability judgment conditions of the new model are obtained by linear stability analysis. And the results show that the MHVF effect can effectively stabilize the car following system. In addition, through nonlinear analysis, the mKdV equation describing the propagation law of traffic density wave near the critical point of the system was derived, and its kink-antikink soliton solution was obtained. The analytical results were in good agreement with the simulation results.