1 Introduction

During the past decades, the dynamics of neural networks has become one important area of research due to their various potential utilizations in pattern recognition, optimization, parallel computation and image processing and so forth [1,2,3,4,5,6,7,8,9,10,11,12,13,14,15,16]. Because information processing and the inherent communication time of neurons need the finite switching speed [17], then time delay inevitably appears in neural networks. Thus numerous researchers consider the dynamical behavior of delayed neural networks and many interesting results on delayed neural networks have been reported [18,19,20,21,22,23,24,25,26,27,28,29,30,31,32,33].

For a long time, fractional calculus, which is a generalization of the traditional integer order differentiation and integral, has been payed little attention due to its complexity and the lack of the practical background [34]. Recently, many scholars find that fractional calculus is a valuable tool to describe memory and hereditary properties of dynamical processes [35, 36]. It has been applied in many areas such as applied mathematics, physics engineering and finance, etc. [37, 38]. For example, Lundstrom et al. [39] pointed out that fractional derivative provides neurons with a fundamental and general computation ability that can contribute to efficient information processing, stimulus anticipation and frequency-independent phase shifts of oscillatory neuronal firing. Anastasio [40] argued that the oculomotor integrator, which converts eye velocity into eye position commands, may be of fractional order. Anastassiou [41] mentioned that fractional-order recurrent neural networks play an important role in parameter estimation and neural network approximation taken at the fractional level resulted in higher rates of approximation. Thus it is significant to investigate the dynamical behaviors of fractional-order delayed neural networks. Recently there are some important results on delayed fractional-order neural networks. For instance, Wu and Zeng [42] studied the boundedness, Mittag–Leffler stability and asymptotical \(\alpha \)-periodicity of fractional-order fuzzy neural networks, Zhang et al. [43] analyzed the stability of fractional-order Hopfield neural networks with discontinuous activation functions, Chen et al. [44] established some sufficient conditions which ensure the stability and synchronization of memristor-based fractional-order delayed neural networks, Wang et al. [45] considered the asymptotic stability of delayed fractional-order neural networks with impulsive effects. For more knowledge on these topics, we refer the readers to [46,47,48,49,50,51,52,53,54].

Neural networks are said to be finite-time stable, if the states do not exceed some bounds within a prescribed fixed time-intervals when the initial states satisfy a specified bound [34]. We must point out that classical Lyapunov stability concepts require that the systems operate over an infinite time interval and is mainly concerned with the asymptotical behavior and seldom concerned with specified bounds on the states [34]. In many practical applications, it is important to remain the states within a certain bound during a specific time-interval. Thus the finite-time behavior of the networks is more important than the asymptotic behavior of the networks. The investigation on finite-time stability for fractional-order delayed neural networks has important theoretical value and practical significance [55,56,57,58,59].

In 2016, Chen et al. [60] considered the following fractional-order neural networks with delay

$$\begin{aligned} \left\{ \begin{array}{lc} \displaystyle D^\alpha {x}_i(t)=-c_ix_i(t)+\sum _{j=1}^na_{ij}f_j(x_j(t))+\sum _{j=1}^nb_{ij}g_j(x_j(t-\tau ))+I_i,\\ \displaystyle x_i(t)=\varphi _i(t), t\in [-\tau ,0], \end{array}\right. \end{aligned}$$
(1.1)

where \(0<\alpha <1,n\) corresponds to the number of units in a neural network. \(x_i(t)\) denotes the state of the ith neuron at time t, \(a_{ij}\) and \(b_{ij}\) denote the strengths of connectivity between j and i at time t and \(t-\tau \), respectively, \(\tau \) denotes the time delay required in transmitting a signal from the neuron j to the neuron i, \(I_i\) is the input to the neuron i, \(c_i\) is the charging rate for the neuron i,\(f_i(.)\) denotes activation functions. By means of inequality technique, authors established two delay-dependent sufficient criteria which ensure the stability of (1.1) over a finite-time interval.

Considering that the parameters of neural networks can not remain constants as time goes by, Wu et al. [61] considered the following delayed fractional delayed neural networks with time-varying coefficients

$$\begin{aligned} \left\{ \begin{array}{lc} \displaystyle D^\alpha {x}_i(t)=-c_ix_i(t)+\sum _{j=1}^na_{ij}(t)f_j(x_j(t))+\sum _{j=1}^nb_{ij}(t)g_j(x_j(t-\tau ))+I_i(t),\\ \displaystyle x_i(t)=\varphi _i(t), t\in [-\tau ,0]. \end{array}\right. \end{aligned}$$
(1.2)

By using Hölder inequality, Grönwall inequality and inequality scaling techniques, authors obtained some sufficient conditions which guarantee the finite-time stability of (1.2).

Here we would like to point out that the presence of an amount of parallel pathways of axon sizes and lengths often make the neural networks possess the spatial structure. Moreover, the amount of parallel pathways will be affected by various materials and topology. Thus time delay existing in neural networks often appears as proportional [62,63,64], i.e, the proportional delay function \(\tau (t)=t-qt\) is a monotonically increasing function with the increase of time \(t>0\), where \(0<q<1\) is a constant. In real world, proportional delay plays a key role in many fields such as web quality of serve routing decision, collection of current by the pantograph of an electric locomotive [65], nonlinear dynamics [66, 67], electrodynamics [68] and probability theory on algebraic structures [69].

Stimulated by the above viewpoint, in this paper, we considered the following fractional delayed neural networks with proportional delays

$$\begin{aligned} \left\{ \begin{array}{lc} \displaystyle D^\alpha {x}_i(t)=-c_ix_i(t)+\sum _{j=1}^na_{ij}(t)f_j(x_j(t))+\sum _{j=1}^nb_{ij}(t)g_j(x_j(q_jt))+I_i(t),\\ \displaystyle x_i(t)=\varphi _i(t), t\in [q_0,1], \end{array}\right. \end{aligned}$$
(1.3)

where \(i\in \Lambda =\{1,2,\cdots ,n\}, q_0=\min _{i\in \Lambda }\{q_i\}, t\ge 1, 0<\alpha <1,n\) corresponds to the number of units in a neural network. \(x_i(t)\) denotes the state of the ith neuron at time t, \(a_{ij}\) and \(b_{ij}\) denote the strengths of connectivity between j and i at time t and \(t-\tau _j(t)\), respectively, \(\tau _j(t)\) denotes the time delay required in transmitting a signal from the neuron j to the neuron i, \(I_i\) is the input to the neuron i, \(c_i\) is the charging rate for the neuron i,\(f_i(.)\) denotes activation functions, \(q_{j}, j\in \Lambda \) are proportional delay factors and satisfy \(0<q_{j}\le 1\), and \(q_{j}t=t-(1-q_{j})t\), in which \(\tau _{j}(t)=(1-q_{j})t\) is the transmission delay function, and \((1-q_{j})t\rightarrow \infty \) as \(q_{j}\ne 1, t\rightarrow \infty ,\) for all \(t\ge 1.\)

For convenience, we present some notations. \(R, R^{+}\) and \(Z^{+}\) denotes the sets of all real numbers, the sets of all positive real numbers and the sets of integer numbers, respectively. Let \(||x||=\sum _{i=1}^n|x_i|\) and \(||A||=\max _{1\le j\le n}\sum _{i=1}^n|a_{ij}|\) be the Euclidean vector norm and matrix norm, respectively, where \(x_i\) and \(a_{ij}\) are the elements of the vector x and the matrix A, respectively. Let \(\widetilde{C}=\widetilde{C}([q_0,1],R^n)\) be the space of all continuous function from \([q_0,1]\) to \(R^n\).

The key object of this article is to establish some sufficient conditions for the finite-time stability for fractional-order neural networks with proportional delays. The main highlights of this article consist of four points: (i) the analysis on the finite-time stability for fractional-order neural networks with proportional delays is firstly proposed; (ii) a set of new sufficient conditions which guarantee the finite-time stability of such fractional-order neural networks with proportional delays over a finite-time interval are established; (iii) the analysis methods can be applied to investigate many other similar fractional-order neural networks with proportional delays; (iv) to the best of our knowledge, it is the first time to focus on the finite-time stability for fractional-order neural networks with proportional delays.

The remainder of the paper is organized as follows. In Sect. 2, applying the differential inequality theory and fractional-order differential equation theory, we will establish a set of sufficient conditions which guarantee the finite-time stability of (1.1). In Sect. 3, simulation experiments are put into effect to verify the availability of theoretical findings. We ends this paper with a short conclusion in Sect. 4.

2 Preliminaries

In this section, we state some definitions and lemmas which will be used in next section.

Definition 2.1

[70] The fractional integral with noninteger order \(\alpha >0\) of function u(t) is defined as follows:

$$\begin{aligned} D_{t_0,t}^{-\alpha }u(t)=\frac{1}{\Gamma (\alpha )}\int _{t_0}^t(t-\theta )^{\alpha -1}u(\theta )d\theta , \end{aligned}$$

where \(\Gamma (.)\) denotes the Gamma function \(\Gamma (s)=\int _0^\infty t^{s-1}e^{-t}dt.\)

Definition 2.2

[70] The Riemann–Liouville derivative of fractional order \(\alpha \) of function u(t) is defined as follows:

$$\begin{aligned} _{RL}D_{t_0,t}^\alpha u(t)=\frac{d^k}{dt^k}D_{t_0,t}^{-(k-\alpha )}u(t)=\frac{d^k}{dt^k}\frac{1}{\Gamma (k-\alpha )}\int _{t_0}^t(t-\theta )^{k-\alpha -1}u(\theta )d\theta , \end{aligned}$$

where \(k-1<\alpha <k\in Z^{+}.\)

Definition 2.3

[67] The Caputo derivative of fractional order \(\alpha \) of function u(t) is defined as follows:

$$\begin{aligned} _{C}D_{t_0,t}^\alpha u(t)=D_{t_0,t}^{-(k-\alpha )}\frac{d^k}{dt^k}u(t)=\frac{1}{\Gamma (k-\alpha )}\int _{t_0}^t(t-\theta )^{k-\alpha -1}u^{(k)}(\theta )d\theta , \end{aligned}$$

where \(k-1<\alpha <k\in Z^{+}.\)

Lemma 2.1

[70] (Hölder inequality) Assume that \(a, b>1\) and \(\frac{1}{a}+\frac{1}{b}=1,\) if \(|f(.)|^a,|g(.)|^b\in L^1(E)\), then \(f(.)g(.)\in L^1(E)\) and

$$\begin{aligned} \int _E|f(u)g(u)|du\le \left( \int _E|f(u)|^adu\right) ^{\frac{1}{a}}\left( \int _E|g(u)|^bdu\right) ^{\frac{1}{b}} \end{aligned}$$
(2.1)

where \(L^1(E)\) is the Banach space of all Lebesgue measurable functions \(f:E\rightarrow R\) with \(\int _E|f(u)|du<\infty .\) In particular, if \(,a,b=2\) then (2.1) becomes the Cauchy–Schwarz inequality of the following form:

$$\begin{aligned} \left( \int _E|f(u)g(u)|du\right) ^2\le \left( \int _E|f(u)|^2du\right) \left( \int _E|g(u)|^2du\right) \end{aligned}$$
(2.2)

Lemma 2.2

[71] Let \(n\in N\) and \(u_1,u_2,\ldots ,u_n\) be nonnegative real numbers. Then for \(\rho >1\),

$$\begin{aligned} \left( \sum _{i=1}^nu_i\right) ^\rho \le n^{\rho -1}\sum _{i=1}^nu_i^\rho . \end{aligned}$$

Lemma 2.3

[72] (Grönwall inequality) If \(u(t)\le l(t)+\int _{t_0}^tk(\theta )u(\theta )d\theta , t\in [t_0, \varrho ),\) where all the functions involved are continuous on \([t_0,\varrho ),\varrho <\infty ,\) and \(k(t)\ge 0\), then u(t) satisfies

$$\begin{aligned} u(t)\le l(t)+\int _{t_0}^tk(\theta )u(\theta ) \exp \left[ \int _\theta ^t k(s)ds\right] d\theta , t\in [t_0, \varrho ). \end{aligned}$$
(2.3)

If, in addition, l(t) is nondecreasing, then

$$\begin{aligned} u(t)\le l(t)\exp \left( \int _\theta ^t k(s)ds\right) , t\in [t_0, \varrho ). \end{aligned}$$
(2.4)

Lemma 2.4

[73] If \(u(t)\in C^k[0,\infty )\) and \(k-1<\alpha <k\in Z^{+}\), then

  1. (i)

    \( D^{-\alpha }D^{-\beta }u(t)= D^{-(\alpha +\beta )}u(t),\alpha ,\beta \ge 0;\)

  2. (ii)

    \(D^{\alpha }D^{-\alpha }u(t)= u(t),\alpha \ge 0;\)

  3. (iii)

    \(D^{-\alpha }D^{\alpha }u(t)= u(t)-\sum _{j=1}^{k-1}\frac{t_j}{j!}u^{(j)}(0),\alpha \ge 0.\)

System (1.3) can be rewritten as following form:

$$\begin{aligned} \left\{ \begin{array}{lc} \displaystyle D^\alpha {x}(t)=-Cx(t)+A(t)F(x(t))+B(t)G(x(qt))+I(t),\\ \displaystyle x(t)=\varphi (t), t\in [q_0,1], \end{array}\right. \end{aligned}$$
(2.5)

where \(x(t)=(x_1(t),x_2(t),\ldots , x_n(t))^T\in R^n\) is the state vector of the cellular neural networks, \(0<\alpha <1\) is fractional order, \(F(x(t))=(f_1(x_1(t)), f_2(x_2(t)),\ldots ,f_n(x_n(t)))^T\), \(G(x(qt))=(g_1(x_1(q_1t)), g_2(x_2(q_2t)),\ldots ,\)\(g_n(x_n(q_nt)))^T\), \(f_j(x_j(t))\) and \(g_j(x_j(t))\) denote the activation function of the neurons, \(C=\text{ diag } (c_i), A(t)=(a_{ij}(t)),\)\( B(t)=(b_{ij}(t))\) are matrix functions respect to t, \(I_i(t)=(I_1(t),I_2(t),\ldots , I_n(t))^T\) is an external bias vector. Define the norm \(||\varphi ||=\sup _{s\in [q_0,1]}||\varphi (s)||,\) where \(\varphi \in \widetilde{C}\). Denote \(A=\sup _{t\ge 1}||A(t)||, B=\sup _{t\ge 1}||B(t)||.\)

If x(t) and y(t) are any solutions of (2.5) with different initial functions \(\varphi \in \widetilde{C}\) and \(\psi \in \widetilde{C}\), let \(y(t)-x(t)=u(t)=(u_1(t),u_2(t),\ldots , u_n(t))^T\), \(\vartheta =\phi -\varphi ,\) then we obtain one error system which takes the following form:

$$\begin{aligned} \left\{ \begin{array}{lc} \displaystyle D^\alpha {u}(t)=-Cu(t)+A(t)[F(y(t))-F(x(t))]+B(t)[G(y(qt))-G(x(qt))],\\ \displaystyle u(t)=\vartheta (t), t\in [q_0,1], \end{array}\right. \end{aligned}$$
(2.6)

Definition 2.4

For a given time \(T>0\) and positive number \(\iota <\delta \), a solution \(x^*(t)\) of (2.5) is said to be finite-time stable with respect to \((\iota ,\delta ,T)\) if for any solution x(t) of (2.5), \(||x(0)-x^*(0)||\le \iota \) implies that \(||x(t)-x^*(t)||<\delta \) for all \(t\in [q_0,T]\). System (2.5) is said to be finite-time stable with respect to \((\iota ,\delta ,T)\) if any solution \(x^*(t)\) of (2.5) is finite-time stable with respect to \((\iota ,\delta ,T)\).

Throughout this paper, we also make the following assumptions:

(H1) For each \(i,j\in \Lambda ,\)\(a_{ij}(t)\) and \(b_{ij}(t)\) are bounded functions defined on \(R^{+}\).

(H2) There exist constants \(L_f\ge 0\) and \(L_g\ge 0\) such that \(|F(u)-F(v)|\le L_f|u-v|,|G(u)-G(v)|\le L_g|u-v| \) for all \(u,v\in R.\)

(H3) The following condition holds.

$$\begin{aligned} \sqrt{ \frac{6+3\chi e^{(\chi +2) t}}{\chi +2}}<\frac{\iota }{\delta }, t\in J, \end{aligned}$$

where

$$\begin{aligned} \chi =\frac{6\Gamma (2\alpha -1)[(||C||+AL_f)^2+\frac{1}{q}(BL_g)^2] }{4^\alpha \Gamma ^2(\alpha )}. \end{aligned}$$

(H4) The following condition holds.

$$\begin{aligned} \root b \of {\frac{b3^{b-1}+3^{b-1}\chi ^*e^{(\chi ^*t+b)}}{b+\chi ^*}}<\frac{\iota }{\delta }, t\in J, \end{aligned}$$

where

$$\begin{aligned} \chi ^*=3^{b-1}\left( \frac{\Gamma [a(\alpha -1)+1]}{\Gamma ^a(\alpha ) a^{a(\alpha -1)}}\right) ^{\frac{b}{a}}\nonumber \\ \left[ (||C||+AL_f)^b+\frac{1}{q}(BL_g)^b\right] . \end{aligned}$$

and \(a,b>1\) and satisfy \(\frac{1}{a}+\frac{1}{b}=1.\)

Remark 2.1

In this paper, we will deal with the finite-time stability of (1.3) with Caputo derivative.

3 Main Results

In this section, we will establish two sufficient conditions which ensure the finite-time stability of system (1.3).

Theorem 3.1

In addition to (H1)–(H3), if \(\frac{1}{2}<\alpha <1\) is satisfied, then system (2.5) is finite time stable w.r.t. \((\iota ,\delta ,T)\).

Proof

Choose the initial time \(t_0=1, u(1)=\vartheta (1)\) as the initial condition of (2.6). In view of Lemma 2.4, we can conclude that the solution of system (2.6) takes the following form:

$$\begin{aligned} u(t)= & {} D^{-\alpha }\{-Cu(t)+A(t)[F(y(t))-F(x(t))]+B(t)[G(y(qt))-G(x(qt))]\}\nonumber \\= & {} \vartheta (1)+\frac{1}{\Gamma (\alpha )}\int _1^t(t-s)^{\alpha -1}\{-Cu(s)+A(s)[F(y(s))-F(x(s))]\nonumber \\&\quad +B(s)[G(y(qs))-G(x(qs))]\}ds. \end{aligned}$$
(3.1)

By (H1) and (H2), we have

$$\begin{aligned} ||u(t)||\le & {} ||\vartheta (1)||+\frac{1}{\Gamma (\alpha )}\int _1^t(t-s)^{\alpha -1}\{||C||||u(s)||\nonumber \\&\quad +AL_f||u(s)||+BL_g||u(qs)||\}ds \nonumber \\\le & {} ||\vartheta (1)||+\frac{1}{\Gamma (\alpha )}\int _1^t(t-s)^{\alpha -1}[(||C||+AL_f)||u(s)||]ds\nonumber \\&\quad +\frac{1}{\Gamma (\alpha )}\int _1^t(t-s)^{\alpha -1}BL_g||u(qs)||ds. \end{aligned}$$
(3.2)

Applying (2.2), we get

$$\begin{aligned} ||u(t)||\le & {} ||\vartheta (1)||+\frac{1}{\Gamma (\alpha )}\int _1^t(t-s)^{\alpha -1}e^s[(||C||+AL_f)e^{-s}||u(s)||]ds\nonumber \\&+\frac{1}{\Gamma (\alpha )}\int _1^t(t-s)^{\alpha -1}e^sBL_ge^{-s}||u(qs)||ds \nonumber \\\le & {} ||\vartheta (1)||+\frac{1}{\Gamma (\alpha )}\left( \int _1^t(t-s)^{2\alpha -2}e^{2s}ds\right) ^{\frac{1}{2}}\left( \int _1^t(||C||+AL_f)^2e^{-2s}||u(s)||^2ds\right) ^{\frac{1}{2}} \nonumber \\&+\frac{1}{\Gamma (\alpha )}\left( \int _1^t(t-s)^{2\alpha -2}e^{2s}ds\right) ^{\frac{1}{2}} \left( \int _1^t(BL_g)^2e^{-2s}||u(qs)||^2 ds\right) ^{\frac{1}{2}} \nonumber \\\le & {} ||\vartheta (1)||+\frac{1}{\Gamma (\alpha )}\left( \int _1^t(t-s)^{2\alpha -2}e^{2s}ds\right) ^{\frac{1}{2}}\Bigg [\left( \int _1^t(||C||+AL_f)^2e^{-2s}||u(s)||^2ds\right) ^{\frac{1}{2}} \nonumber \\&+\left( \int _1^t(BL_g)^2e^{-2s}||u(qs)||^2 ds\right) ^{\frac{1}{2}}\Bigg ]. \end{aligned}$$
(3.3)

Notice that

$$\begin{aligned} \int _1^t(t-s)^{2\alpha -2}e^{2s}ds= & {} \int _0^{t-1}\varrho ^{2\alpha -2}e^{2(t-\varrho )}d\varrho \nonumber \\= & {} e^{2t}\int _0^{t-1}\varrho ^{2\alpha -2}e^{-2\varrho }d\varrho \nonumber \\= & {} \frac{e^{2t}}{2^{2(\alpha -1)}} \int _0^{2(t-1)}\varsigma ^{2\alpha -2}e^{-\varsigma }d\varsigma \nonumber \\\le & {} \frac{2e^{2t}}{4^\alpha }\Gamma (2\alpha -1) \end{aligned}$$
(3.4)

It follows from (3.3) and (3.4) that

$$\begin{aligned} ||u(t)||\le & {} ||\vartheta (1)||+\frac{1}{\Gamma (\alpha )}\left( \frac{2e^{2t}}{4^\alpha }\Gamma (2\alpha -1)\right) ^{\frac{1}{2}}\Bigg [\left( \int _1^t(||C||+AL_f)^2e^{-2s}||u(s)||^2ds\right) ^{\frac{1}{2}} \nonumber \\&\quad +\left( \int _1^t(BL_g)^2e^{-2s}||u(qs)||^2 ds\right) ^{\frac{1}{2}}\Bigg ]. \end{aligned}$$
(3.5)

In view of Lemma 2.2, we let \(n=3\) and \(\omega =2\), then it follows from (3.5) that

$$\begin{aligned} ||u(t)||^2\le & {} 3||\vartheta (1)||^2+\frac{6e^{2t}\Gamma (2\alpha -1) }{4^\alpha \Gamma ^2(\alpha )}\Bigg [\int _1^t(||C||+AL_f)^2e^{-2s}||u(s)||^2ds \nonumber \\&\quad +\int _1^t(BL_g)^2e^{-2s}||u(qs)||^2 ds\Bigg ]\nonumber \\\le & {} 3||\vartheta (1)||^2+\frac{6e^{2t}\Gamma (2\alpha -1) }{4^\alpha \Gamma ^2(\alpha )}\Bigg [\int _1^t(||C||+AL_f)^2e^{-2s}||u(s)||^2ds \nonumber \\&\quad +\frac{1}{q}\int _q^{qt}(BL_g)^2e^{-2s}||u(s)||^2 e^{(1-\frac{1}{q})2s} ds\Bigg ]\nonumber \\\le & {} 3||\vartheta (1)||^2+\frac{6e^{2t}\Gamma (2\alpha -1)[(||C||+AL_f)^2+\frac{1}{q}(BL_g)^2] }{4^\alpha \Gamma ^2(\alpha )}\int _1^te^{-2s}||u(s)||^2ds \nonumber \\\le & {} 3||\vartheta ||^2+\frac{6e^{2t}\Gamma (2\alpha -1)[(||C||+AL_f)^2+\frac{1}{q}(BL_g)^2] }{4^\alpha \Gamma ^2(\alpha )}\int _1^te^{-2s}||u(s)||^2ds,\nonumber \\ \end{aligned}$$
(3.6)

which leads to

$$\begin{aligned} ||u(t)||^2e^{-2t}\le & {} 3e^{-2t}||\vartheta ||^2\nonumber \\&\quad +\frac{6\Gamma (2\alpha -1)[(||C||+AL_f)^2+\frac{1}{q}(BL_g)^2] }{4^\alpha \Gamma ^2(\alpha )}\int _1^te^{-2s}||u(s)||^2ds,\nonumber \\ \end{aligned}$$
(3.7)

Let \(\chi =\frac{6\Gamma (2\alpha -1)[(||C||+AL_f)^2+\frac{1}{q}(BL_g)^2] }{4^\alpha \Gamma ^2(\alpha )}.\) Then

$$\begin{aligned} ||u(t)||^2e^{-2t}\le & {} 3e^{-2t}||\vartheta ||^2+\chi \int _1^te^{-2s}||u(s)||^2ds. \end{aligned}$$
(3.8)

By the Grönwall inequality (2.3), we have

$$\begin{aligned} ||u(t)||^2e^{-2t}\le & {} 3e^{-2t}||\vartheta ||^2+\int _1^t\chi 3e^{-2s}||\vartheta ||^2\exp \left( \int _s^t\chi d\nu \right) ds \nonumber \\= & {} 3e^{-2t}||\vartheta ||^2+\int _1^t\chi 3e^{-2s}||\vartheta ||^2e^{\chi (t-s)}ds \nonumber \\= & {} \left( 3e^{-2t}+\frac{3\chi e^{\chi t}-3\chi e^{-2t}}{\chi +2}\right) ||\vartheta ||^2\nonumber \\= & {} \frac{6e^{-2t}+3\chi e^{\chi t}}{\chi +2} ||\vartheta ||^2. \end{aligned}$$
(3.9)

Then

$$\begin{aligned} ||u(t)||\le \sqrt{ \frac{6+3\chi e^{(\chi +2) t}}{\chi +2}}||\vartheta ||. \end{aligned}$$
(3.10)

Thus when \(||\vartheta ||< \delta ,\) if (H3) is fulfilled, then \(||u(t)||<\iota .\) According to the Definition 2.4, we can conclude that system (2.5) is finite-time stable. This completes the proof of Theorem 3.1. \(\square \)

Theorem 3.2

In addition to (H1),(H2) and (H4), if \(0<\alpha <\frac{1}{2}\) is satisfied, then system (2.5) is finite time stable w.r.t. \((\iota ,\delta ,T)\).

Proof

In view of proof of Theorem 3.1, we get

$$\begin{aligned} ||u(t)||\le & {} ||\vartheta (1)||+\frac{1}{\Gamma (\alpha )}\int _1^t(t-s)^{\alpha -1}[(||C||+AL_f)||u(s)||]ds\nonumber \\&\quad +\frac{1}{\Gamma (\alpha )}\int _1^t(t-s)^{\alpha -1}BL_g||u(qs)||ds \end{aligned}$$
(3.11)

Let \(a=1+\alpha ,b=1+\frac{1}{\alpha }.\) then \(a,b>1\) and \(\frac{1}{a}+\frac{1}{b}=1.\) In view of Hölder inequality (2.1), we get

$$\begin{aligned} ||u(t)||\le & {} ||\vartheta (1)||+\frac{1}{\Gamma (\alpha )}\int _1^t(t-s)^{\alpha -1}e^s[(||C||+AL_f)e^{-s}||u(s)||]ds\nonumber \\&+\frac{1}{\Gamma (\alpha )}\int _1^t(t-s)^{\alpha -1}e^sBL_ge^{-s}||u(qs)||ds\nonumber \\\le & {} ||\vartheta (1)||+\frac{1}{\Gamma (\alpha )}\left( \int _1^t(t-s)^{a(\alpha -1)}e^{as}ds\right) ^{\frac{1}{a}}\left( \int _1^t(||C||+AL_f)^be^{-bs}||u(s)||^bds\right) ^{\frac{1}{b}} \nonumber \\&+\frac{1}{\Gamma (\alpha )}\left( \int _1^t(t-s)^{a(\alpha -1)}e^{as}ds\right) ^{\frac{1}{a}} \left( \int _1^t(BL_g)^be^{-bs}||u(qs)||^b ds\right) ^{\frac{1}{b}} \nonumber \\\le & {} ||\vartheta (1)||+\frac{1}{\Gamma (\alpha )}\left( \int _1^t(t-s)^{a(\alpha -1)}e^{as}ds\right) ^{\frac{1}{a}}\Bigg [\left( \int _1^t(||C||+AL_f)^be^{-bs}||u(s)||^bds\right) ^{\frac{1}{b}} \nonumber \\&+\left( \int _1^t(BL_g)^be^{-bs}||u(qs)||^b ds\right) ^{\frac{1}{b}}\Bigg ]. \end{aligned}$$
(3.12)

Notice that

$$\begin{aligned} \int _1^t(t-s)^{a(\alpha -1)}e^{as}ds= & {} \int _0^{t-1}\varrho ^{a(\alpha -1)}e^{a(t-\varrho )}d\varrho \nonumber \\= & {} e^{at}\int _0^{t-1}\varrho ^{a(\alpha -1)}e^{-a\varrho }d\varrho \nonumber \\= & {} \frac{e^{at}}{a^{a(\alpha -1)}} \int _0^{a(t-1)}\varsigma ^{a(\alpha -1)}e^{-\varsigma }d\varsigma \nonumber \\\le & {} \frac{e^{at}\Gamma [a(\alpha -1)+1]}{a^{a(\alpha -1)}}. \end{aligned}$$
(3.13)

Based on (3.12) and (3.13), we have

$$\begin{aligned} ||u(t)||\le & {} ||\vartheta (1)||+\left( \frac{e^{at}\Gamma [a(\alpha -1)+1]}{\Gamma ^a(\alpha ) a^{a(\alpha -1)}}\right) ^{\frac{1}{a}}\Bigg [\left( \int _1^t(||C||+AL_f)^be^{-bs}||u(s)||^bds\right) ^{\frac{1}{b}} \nonumber \\&\quad +\left( \int _1^t(BL_g)^be^{-bs}||u(qs)||^b ds\right) ^{\frac{1}{b}}\Bigg ]. \end{aligned}$$
(3.14)

In view of Lemma 2.2, we let \(n=3\) and \(\omega =b\), then it follows from (3.14) that

$$\begin{aligned} ||u(t)||^b\le & {} 3^{b-1}||\vartheta (1)||^b+3^{b-1}\left( \frac{e^{at}\Gamma [a(\alpha -1)+1]}{\Gamma ^a(\alpha ) a^{a(\alpha -1)}}\right) ^{\frac{b}{a}}\Bigg [\int _1^t(||C||+AL_f)^be^{-bs}||u(s)||^bds \nonumber \\&\quad +\int _1^t(BL_g)^be^{-bs}||u(qs)||^b ds\Bigg ]\nonumber \\\le & {} 3^{b-1}||\vartheta (1)||^b+3^{b-1}\left( \frac{e^{at}\Gamma [a(\alpha -1)+1]}{\Gamma ^a(\alpha ) a^{a(\alpha -1)}}\right) ^{\frac{b}{a}}\Bigg [\int _1^t(||C||+AL_f)^be^{-bs}||u(s)||^bds \nonumber \\&\quad +\frac{1}{q}\int _q^{qt}(BL_g)^be^{-bs}||u(s)||^b e^{b(1-\frac{1}{q})s}ds\Bigg ]\nonumber \\\le & {} 3^{b-1}||\vartheta ||^b+3^{b-1}\left( \frac{e^{at}\Gamma [a(\alpha -1)+1]}{\Gamma ^a(\alpha ) a^{a(\alpha -1)}}\right) ^{\frac{b}{a}}\nonumber \\&\quad \times \left[ (||C||+AL_f)^b+\frac{1}{q}(BL_g)^b\right] \int _1^te^{-bs}||u(s)||^bds \end{aligned}$$
(3.15)

which leads to

$$\begin{aligned} ||u(t)||^be^{-bt}\le & {} 3^{b-1}e^{-bt}||\vartheta ||^b+3^{b-1}\left( \frac{\Gamma [a(\alpha -1)+1]}{\Gamma ^a(\alpha ) a^{a(\alpha -1)}}\right) ^{\frac{b}{a}}\nonumber \\&\times \left[ (||C||+AL_f)^b+\frac{1}{q}(BL_g)^b\right] \int _1^te^{-bs}||u(s)||^bds, \end{aligned}$$
(3.16)

Let

$$\begin{aligned} \chi ^*=3^{b-1}\left( \frac{\Gamma [a(\alpha -1)+1]}{\Gamma ^a(\alpha ) a^{a(\alpha -1)}}\right) ^{\frac{b}{a}}\nonumber \\ \left[ (||C||+AL_f)^b+\frac{1}{q}(BL_g)^b\right] . \end{aligned}$$

Then (3.16) can be written as

$$\begin{aligned} ||u(t)||^be^{-bt} \le 3^{b-1}e^{-bt}||\vartheta ||^b+\chi ^*\int _1^te^{-bs}||u(s)||^bds. \end{aligned}$$
(3.17)

By the Grönwall inequality (2.3), we have

$$\begin{aligned} ||u(t)||^be^{-bt}\le & {} 3^{b-1}e^{-bt}||\vartheta ||^b+\int _1^t \chi ^*3^{b-1}e^{-bt}e^{-bs}||u(s)||^b e^{\chi ^*(t-s)}ds \nonumber \\= & {} \frac{b3^{b-1}e^{-bt}+3^{b-1}\chi ^*e^{\chi ^*t}}{b+\chi ^*}||\vartheta ||^b. \end{aligned}$$
(3.18)

Then

$$\begin{aligned} ||u(t)||\le \root b \of {\frac{b3^{b-1}+3^{b-1}\chi ^*e^{(\chi ^*+b)t}}{b+\chi ^*}} ||\vartheta ||. \end{aligned}$$
(3.19)

Thus when \(||\vartheta ||< \delta ,\) if (H4) is fulfilled, then \(||u(t)||<\iota .\) According to the Definition 2.4, we can conclude that system (2.5) is finite-time stable. This completes the proof of Theorem 3.2. \(\square \)

Remark 3.1

Chen et al. [60] investigated the finite-time stability of a class of fractional order neural networks with constant delay and constant coefficients, Wu et al. [61] studied the finite-time stability of a class of fractional order neural networks with constant delay and time-varying coefficients. All the models considered in [60, 61] does not involves proportional delays. In this paper, we studies the the finite-time stability of cellular neural networks with proportional delays. All the obtained results in [60, 61] can not be applicable to the model (1.3) to obtain the finite-time stability of system (1.3). Up to now, there are no results on the finite-time stability of cellular neural networks with proportional delays. From the viewpoint, our results on finite-time stability for cellular neural networks with proportional delays are essentially new and complement earlier publications to some degree.

Remark 3.2

Proportional delay, which is unbounded, differs from the constant delay and bounded time-varying delay. Proportional delay and unbounded distributed delay are unbounded, but unbounded distributed delay usually requires the delay kernel function \(\kappa _{ij}: R\rightarrow R\) satisfies \(\int _0^\infty \kappa _{ij}(x)dx=1, \int _0^\infty x\kappa _{ij}(x)dx<\infty ,i,j=1,2,\ldots ,n,\) which make the distributed delay easier to deal with, proportional delay has no the restrict condition. Thus it is more difficult to handle the proportional delay than to handle the distributed delay in dynamical systems.

Remark 3.3

Li, Yang, Shi and Ho [74,75,76] considered the finite-time synchronization of delayed neural networks and chaotic systems. All the papers do not involve the fractional-order proportional delays. In this paper, we investigate the finite-time stability for fractional-order neural networks with proportional delays. All the derived results in [74,75,76] can not be applied to (1.3) to obtain the finite-time stability for (1.3). From the viewpoint, the main results of this article on finite-time stability for fractional-order neural networks with proportional delays are essentially innovative.

Remark 3.4

Theorems 3.1 and 3.2 are correct for all kinds of the fractional derivatives.

4 Examples

In this section, we will give two examples to verify the correctness of our main results obtained in previous section. The choice of all the parameters in the following examples is based on the practical implication of neural networks.

Example 4.1

Considering the following fractional-order neural networks with proportional delays

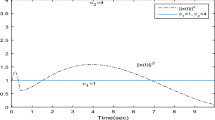
$$\begin{aligned} \left\{ \begin{array}{lc} \displaystyle D^\alpha {x}_1(t)=-c_1x_i(t)+\sum _{j=1}^2a_{1j}(t)f_j(x_j(t))+\sum _{j=1}^2b_{1j}(t)g_j(x_j(q_jt))+I_1(t), \\ \displaystyle D^\alpha {x}_2(t)=-c_2x_2(t)+\sum _{j=1}^na_{2j}(t)f_j(x_j(t))+\sum _{j=1}^2b_{2j}(t)g_j(x_j(q_jt))+I_2(t), \end{array}\right. \end{aligned}$$
(4.1)

where \(t>1, f_1(u)=f_2(u)=g_1(u)=g_2(u)=0.5(|u+1)-|u-1|),\alpha =0.6, c_1=0.2,c_2=0.3, a_{11}(t)=0.1\sin t, a_{12}(t)=0.3\sin t, a_{21}(t)=0.4\cos t, a_{22}(t)=0.5\cos t, b_{11}(t)=0.5\sin t, b_{12}(t)=0.5\cos t, b_{21}(t)=0.3\cos t, b_{22}(t)=0.2\cos t, I_1(t)=0.2\sin t, I_2(t)=0.4\sin t, q_1=0.2,q_2=0.1\) Then \(L_f=L_g=1, ||C||=0.3, A=0.5, B=0.5, \chi =5.5470\). Let \(\delta =0.1,\iota =1.\) We have \(\sqrt{ \frac{6+3\chi e^{(\chi +2) t}}{\chi +2}}<\frac{\iota }{\delta }\) and \(T=0.7024.\) Thus all the conditions in Theorem 3.1 are satisfied, then system (4.1) is finite time stable w.r.t. \(\{1,0.1,1\}\). This result can be shown in Figs. 1 and 2.

Fig. 1
figure 1

Numerical solutions of system (4.1): times series of \(x_1\)

Full size image
Fig. 2
figure 2

Numerical solutions of system (4.1): times series of \(x_2\)

Full size image

Example 4.2

Considering the following fractional-order neural networks with proportional delays

$$\begin{aligned} \left\{ \begin{array}{lc} \displaystyle D^\alpha {x}_1(t)=-c_1x_i(t)+\sum _{j=1}^2a_{1j}(t)f_j(x_j(t))+\sum _{j=1}^2b_{1j}(t)g_j(x_j(q_jt))+I_1(t), \\ \displaystyle D^\alpha {x}_2(t)=-c_2x_2(t)+\sum _{j=1}^na_{2j}(t)f_j(x_j(t))+\sum _{j=1}^2b_{2j}(t)g_j(x_j(q_jt))+I_2(t), \end{array}\right. \end{aligned}$$
(4.2)

where \(t>1, f_1(u)=f_2(u)=g_1(u)=g_2(u)=\tanh (u),\alpha =0.3, c_1=0.1,c_2=0.2, a_{11}(t)=0.2|\sin 2t|, a_{12}(t)=0.1|\sin 2t|, a_{21}(t)=0.4|\cos 2t|, a_{22}(t)=0.1|\cos 2t|, b_{11}(t)=0.3|\sin 2t|, b_{12}(t)=0.5|\cos 2t|, b_{21}(t)=0.3|\cos 2t|,\)\( b_{22}(t)=0.6|\cos 2t|, I_1(t)=0.2\sin ^2 t, I_2(t)=0.4\cos ^2 t, q_1=0.4,q_2=0.5\) Then \(L_f=L_g=1, ||C||=0.2, A=0.4, B=0.6, \chi ^*=4.7714\). Let \(\delta =0.2,\iota =1.5.\) We have \(\root b \of {\frac{b3^{b-1}+3^{b-1}\chi ^*e^{(\chi ^*+b)t}}{b+\chi ^*}}<\frac{\iota }{\delta } \) and \(T=0.5477.\) Thus all the conditions in Theorem 3.2 are satisfied, then system (4.2) is finite time stable w.r.t. \(\{1,0.2,1.5\}\). This result can be shown in Figs. 3 and 4.

Fig. 3
figure 3

Numerical solutions of system (4.2): times series of \(x_1\)

Full size image
Fig. 4
figure 4

Numerical solutions of system (4.2): times series of \(x_2\)

Full size image

5 Conclusions

The finite-time stability of fractional-order neural networks can effectively characterize the dynamical behavior of neural networks. Thus it has been widely investigated by numerous authors in recent years. In this article, we have discussed finite-time stability for fractional-order neural networks with proportional delays. By means of the differential inequality theory, fractional-order differential equation theory, some sufficient criteria which guarantee the stability of such fractional-order neural networks with proportional delays over a finite-time interval are established. It is shown that these sufficient conditions are easily tested only by very simple algebra operation. The derived results complement some earlier publications (for example [60, 61]). Furthermore, the research approach of this article can be transplanted to investigate some other similar fractional-order neural networks with proportional delays.