1 Introduction

In the real world, neural networks have been found everywhere such as in weather forecasting and business processes because neural networks can create simulations and predictions for complex systems and relationships [1,2,3,4,5,6]. It is well-known that fractional-order systems (FOSs) have attracted much attention due to their important applications in various areas of applied sciences over the past decades [7,8,9]. Fractional analysis has been considered and developed in the context of neural networks as artificial neural networks, Hopfield neural networks, etc. In fact, the fractional-order derivative provides neurons with a fundamental and general computational ability that contributes to efficient information processing and frequency-independent phase shifts in oscillatory neuronal firings [10,11,12,13,14,15,16]. So far, most of the existing literature have concerned with Lyapunov asymptotic stability, however, in many practical cases, one concerns the system behavior on finite-time interval, i.e., finite-time stability (FTS) [17]. The concept of FTS has been developed to control problems, which concern the design of admissible controllers ensuring the FTS of the closed-loop system. Many valuable results on finite-time control problems such as finite-time stabilization, finite-time optimal control, adaptive fuzzy finite-time optimal control, etc. have been obtained for this type of stability, see, [18,19,20,21] and the references therein. Therefore, problem of finite-time stability for neural networks described by fractional differential equations has attracted a lot of attention from scientists. It is notable that most of the results on the stability of FOS neural networks did not consider time delay. In many practical applications, time delay is well-known to be unavoidable and it can cause oscillation or instability of the system.

There are various approaches to studying FTS for FOSs with delays including Lyapunov function method, Gronwall and Holder inequality approach, etc. The authors of [22,23,24] studied FTS of linear FOSs by using a generalized fractional Gronwall inequality lemma. In [25], Yang et al. studied FTS of fractional-order neural networks (FONNs) with delay. Chen et al. in [26] used some Holder-type inequalities to propose new criteria for FTS. Combining the Holder inequality and Gronwall inequality, Wu et al. [27] obtained sufficient conditions for FTS of FONNs with constant delay. Based on this approach the authors of [28, 29] developed the similar results for the systems with proportional constant delays. On the other hand, noting that the Lyapunov–Krasovskii function (LKF) method is one of the powerful techniques to studying stability of dynamical systems with delays, however, the LKF method can not be helpfully applied for fractional-order time-delay systems. The difficulty lies in the finding LKF to apply the fractional Lyapunov stability theorem. In [30,31,32,33], the authors used fractional Lyapunov stability theorem to find appropriate LKF for FOSs with time-varying delay, however, the proof of the main theorem provides a gap due to a wrong application of fractional Lyapunov stability theorem. Hence, it is worth investigating the stability of FONNs with time-varying delay. In the paper [34], the authors provided some sufficient conditions for the FTS of singular fractional-order systems with with time-varying delay. Very recently, to avoid finding LKF the authors of [35] employed fractional-order Razumikhin stability theorem to derive criteria for \(H_\infty \) control of FONNs with time-varying delay. To our knowledge, problem of FTS for fractional-order neural networks with time-varying delays has not yet been fully studied in the literature.

Motivated the above discussion, in this paper, we investigate problem of FTS for a class of FONNs with time-varying delay. Especially, the time-varying delay considered in the FONNs is only required to be continuous and interval bounded. The contribution of this paper is twofold. First, considering FONNs with interval time-varying delay, we propose some auxiliary lemmas on the existence of solutions and on estimating the Caputo derivative of some specific quadratic functions. Second, using a proposed analytical approach based on the factional calculus combining with LMI technique, we provide sufficient conditions for FTS. The conditions are established in terms of a tractable LMI and Mittag–Leffler functions. It should be noted that the proposed approach of Laplace transforms and inf–sup method has not yet seen in the field of FONNs with time-varying delay, and the stability conditions obtained in this paper are delay-dependent and novel.

The article is structured as follows. Section 2 presents formulation of the problem and some auxiliary technical lemmas. In Sect. 3, the main result on FTS is presented with an illustrative example and its simulation.

Notations. \(\mathbb {R}^+\) denotes the set of all real positive numbers; \(\mathbb {R}^n\) denotes the Euclidean \(n-\) dimensional space with its scalar product \(x^{\top}y;\) \(\mathbb {R}^{n\times r}\) denotes the space of all \((n\times r)\)-matrices; \(A^{\top}\) denotes the transpose of A; matrix A is positive semi-definite \((A\ge 0)\) if \(x^{\top }Ax\ge 0,\) for all \(x\in \mathbb {R}^n;\) A is positive definite \((A>0)\) if \(x^{\top }Ax>0\) for all \(x\ne 0;\) \(A\ge B\) means \(A-B\ge 0\); \(C([-\tau ,0], \mathbb {R}^n)\) denotes the set of vector valued continuous functions from \([-\tau ,0]\) to \(\mathbb {R}^n\);

2 Preliminaries

We first recall from [7] basic concepts of fractional calculus and some auxiliary results for the use in next section.

Definition 1

[7] For \(\alpha \in (0,1)\) and \( f\in L^1[0,T],\) the fractional integral \(I^{\alpha }f(t),\) the Riemann derivative \(D_R^{\alpha }f(t)\) and the Caputo derivative \(D^\alpha _Cf(t)\) of order \(\alpha\), respectively are defined as

$$\begin{aligned} I^{\alpha }f(t) =&\frac{1}{\Gamma (\alpha )}\int _0^t(t-s)^{\alpha -1}f(s)ds,\\ D_R^{\alpha }f(t) =&\frac{d}{dt}(I^{1-\alpha }f(t)),\quad D^\alpha _Cf(t)= D_R^{\alpha }(f(t)-f(0)), \end{aligned}$$

where \(\Gamma (s) =\int \limits _{0}^{\infty }e^{-t}t^{s-1}dt, s > 0, \ t\in [0,T]\) is the Gamma function.

The function

$$\begin{aligned} E_{\alpha , \beta }(z)=\sum \limits _{n=0}^{\infty }\dfrac{z^n}{\Gamma (n\alpha +\beta )}, z\in \mathbb {C},\ \alpha>0,\ \beta >0 \end{aligned}$$

denotes Mittag–Leffler function. The Laplace transform of the integrable function g(.) is defined by \( \mathcal {L}[g(t)](s)=\int \limits _0^{\infty }e^{-s t}g(t)dt. \)

Lemma 1

[7] Assume that \(f_1(.), f_2(.)\) are exponentially bounded integrable functions on \(\mathbb {R}^+,\) and \(0<\alpha <1, \beta >0.\) Then

  1. (1)

    \(\mathcal {L}[D^{\alpha }_Cf_1(t)](s)=s^{\alpha }\mathcal {L}[f_1(t)](s)-s^{\alpha -1}f_1(0), \)

  2. (2)

    \( \mathcal {L}[t^{\alpha -1} E_{\alpha ,\alpha }(\beta t^{\alpha })](s)=\dfrac{1}{s^{\alpha }-\beta }, \quad \ \mathcal {L}[ E_{\alpha }(\beta t^{\alpha }) ](s)=\dfrac{s^{\alpha -1}}{s^{\alpha }-\beta }, \)

  3. (3)

    \( \mathcal {L}[f_1*f_2(t)](s)=\mathcal {L}[f_1(t)](s)\cdot \mathcal {L}[f_2(t)](s), \)

where \(f_1(t)*f_2(t):=\int \limits _{0}^t f_1(t-\tau )f_2(\tau )d\tau .\)

Consider the following FONNs with time-varying delay:

$$\begin{aligned} {\left\{ \begin{array}{ll} D^{\alpha }_C x_i(t)=-m_ix_i(t)+\sum \limits _{j=1}^n a_{ij}f_j (x_i(t)) +\sum \limits _{j=1}^n b_{ij}g_j (x_j(t-d(t))),\\ x_i(\theta )=\phi _i(\theta ),\, \theta \in [-d_2, 0],\, i=\overline{1, n}, \end{array}\right. } \end{aligned}$$
(1)

or in the matrix form:

$$\begin{aligned} D^{\alpha }_C x(t)=-Mx(t)+Ff(x(t))+Gg(x(t-d(t))), \end{aligned}$$
(2)

where \(x(t)= (x_i(t), ..., x_n(t))^{\top }\) is the state; the delay d(t) satisfies \( 0<d_1\le d(t)\le d_2,\ \forall t\ge 0; \) \(\phi (t)= (\phi _i(t), ..., \phi _n(t))^{\top }\) is the initial condition with the norm

$$\begin{aligned} \Vert \phi \Vert =\sup \limits _{\theta \in [-d_2,0]}\sqrt{ \sum \limits _{i=1}^n |\phi _i(\theta )|^2 }; \end{aligned}$$

the variation functions

$$\begin{aligned} f(x)=(f_1(x_1)),\dots ,f_n(x_n))^{\top },\quad g(x)=(g_1(x_1)),\dots ,g_n(x_n))^{\top }, \end{aligned}$$

satisfy \(f(0)=0,\ g(0)=0,\) and for all \(\xi ,\eta \in \mathbb {R},\ i=\overline{1,n}:\)

$$\begin{aligned} \begin{aligned} \exists l_i>0:&|f_i(\xi )-f_i(\eta )|\le l_i |\xi -\eta |,\\ \exists k_i>0:&|g_i(\xi )-g_i(\eta )|\le k_i |\xi -\eta |; \end{aligned} \end{aligned}$$
(3)

\(M=diag(m_1,m_2,\dots ,m_n);\) \(F=(a_{ij})_{n\times n},\ G=(b_{ij})_{n\times n}\) are the connections of the \(j^{th}\) neuron to the \(i^{th}\) neuron at time t.

Definition 2

Let \(c_1,c_2, T\) be given positive numbers. System (1) is FTS with respect to \((c_1,c_2, T)\) if

$$\begin{aligned} \Vert \phi \Vert ^2\le c_1\Rightarrow \Vert x(t)\Vert ^2\le c_2,\quad t\in [0,T]. \end{aligned}$$

Lemma 2

If \(\phi \in C([-d_2,0],\mathbb {R}^n)\) and the condition (3) holds, then system (1) has a unique solution \(x\in C([-d_2,T),\mathbb {R}^n).\)

Proof

From Volterra integral form of system (2) we have

$$\begin{aligned} x(t)=x(0)+I^{\alpha } [-Mx(t)+Ff(x(t))+Gg(x(t-d(t))) ], \end{aligned}$$

and consider the function

$$\begin{aligned} H(y)(t)= {\left\{ \begin{array}{ll} \phi (0)+I^{\alpha } [v_y(t) ]&{} \text{ if } t\ge 0,\\ \phi (t)&{} \text{ if } t\in [-d_2,0), \end{array}\right. } \end{aligned}$$

where

$$\begin{aligned} v_y(t)=-My(t)+Ff(y(t))+Gg(y(t-d(t))). \end{aligned}$$

Note that the function \(v_y(t)\) is continuous on [0, T] if \(y\in C([-d_2,T],\mathbb {R}^n).\) So we can see that function \(H(\cdot )\) maps \(C([-d_2,T],\mathbb {R}^n)\) into \(C([-d_2,T],\mathbb {R}^n).\) In fact from the uniform continuity of \(v_y(t)\) on [0, T],  there is a \(\delta >0\) such that for all \(t_1,t_2\in [0,T],\ t_2\le t_1,\) and

$$\begin{aligned} |t_1-t_2|\le \delta \Rightarrow |v_y(t_1)-v_y(t_2)|\le \varepsilon , \end{aligned}$$

hence

$$\begin{aligned} |H(y)(t_1)-H(y)(t_2)| \le&\dfrac{\varepsilon }{\Gamma (\alpha )}\Big |\int \limits _0^{t_2} s^{\alpha -1} ds\Big |+ \dfrac{1}{\Gamma (\alpha )}\sup \limits _{s\in [0,T]}|v_y(s)| \Big |\int \limits _{t_2}^{t_1} s^{\alpha -1} ds\Big |\\ \le&\dfrac{\varepsilon }{\Gamma (\alpha )} \dfrac{T^{\alpha }}{\alpha }+\dfrac{1}{\Gamma (\alpha )}\sup \limits _{s\in [0,T]}|v(s)| \Big | \dfrac{t_2^{\alpha }}{\alpha } -\dfrac{t_1^{\alpha }}{\alpha } \Big |, \end{aligned}$$

which also shows the continuity of H(y)(t) on \([-d_2,T].\) Next, for \(t\in [0,T],\ y,z\in C([-d_2,T],\mathbb {R}^n):\)

$$\begin{aligned} |v_y(t)-v_z(t)|\le&|M| |y(t)-z(t)|+ |F| |f(y(t))-f(z(t))|\\&\quad + |G| | g(y(t-d(t)))-g(z(t-d(t)))|\\ \le&( |M| + |F| \max \limits _i l_i+ |G| \max \limits _i k_i ) \sup \limits _{s\in [-d_2,T]} |y(s)-z(s)|, \end{aligned}$$

which leads to

$$\begin{aligned} |H(y)(t)-H(z)(t)|\le \dfrac{\gamma _1 t^{\alpha }}{\Gamma (\alpha )\alpha } \sup \limits _{s\in [-d_2,T]} |y(s)-z(s)|, \end{aligned}$$

where \(\gamma _1= |M| + |F| \max \limits _i l_i+ |G| \max \limits _i k_i .\) Similarly, by induction, we have for \( m=1,2...\)

$$\begin{aligned}&|H^m(y)(t)-H^m(z)(t)|\le \gamma _1\dfrac{t^{m\alpha }}{\Gamma (m\alpha +1)}\sup \limits _{s\in [-d_2,T]} |y(s)-z(s)|,\\&\quad \sup \limits _{s\in [-d_2,T]}|H^m(y)(s)-H^m(z)(s)| \le \dfrac{\gamma _1 T^{m\alpha }}{\Gamma (m\alpha +1)} \sup \limits _{s\in [-d_2,T]} |y(s)-z(s)|. \end{aligned}$$

Besides, the space \(C([-d_2,T],\mathbb {R}^n)\) with the norm \(\Vert y\Vert =\sup \limits _{s\in [-d_2,T]} |y(s)|\) is a Banach space. Hence,

$$\begin{aligned} H^m(\cdot ): C([-d_2,T],\mathbb {R}^n)\rightarrow C([-d_2,T],\mathbb {R}^n) \end{aligned}$$

is a contraction map with this sup norm as m enough large. Applying the fixed-point theorem, we derive the existence of a unique solution \(x\in C([-d_2,T],\mathbb {R}^n).\) \(\square \)

Lemma 3

[34] For \(d>0\) and \(N> 0,\) if function \(S: [-d,N]\rightarrow \mathbb {R}^+\) is non-decreasing and satisfies

$$\begin{aligned} S(t)\le a S(0)+bS(t-d ), a > 1, b\ge 0, t\ge 0, \end{aligned}$$

then

$$\begin{aligned} S(t)\le S(0)a\sum \limits _{j=0}^{[N/d]+1}b^j,\ \forall t\in [0,N]. \end{aligned}$$

3 Main result

This section provides new conditions for FTS of system (1) in term of a tractable LMI and Mittag–Leffler condition. Before proving the theorem, let us denote [d] by the integer part of d and

$$\begin{aligned} \gamma =&\dfrac{d_2}{2\max \limits _i k_i^2},\ \mathbb {I}_n=diag\{1,\dots ,1\}\in \mathbb {R}^{n\times n},\\ E_{11}=&-2PM-d_2P+\beta \max \limits _i l_i^2 \mathbb {I}_n, E_{12}= PF,\, E_{21}= [PF]^{\top },\ E_{13}=PG,\\ E_{31}=&[PG]^{\top },\, E_{22}= -\beta \mathbb {I}_n, \ E_{33}=-\gamma P,\ E_{44}=\mathbb {I}_n-P, \\ E_{55}=&P-2\mathbb {I}_n, \, \text{ all } \text{ the } \text{ others }\, E_{ij} = 0. \end{aligned}$$

Theorem 1

Let \(c_1, c_2, T\) be given positive numbers. System (1) is FTS with respect to \((c_1,c_2,T)\) if there exist a number \(\beta >0\) and a symmetric matrix \(P >0\) such that

$$\begin{aligned}&\begin{pmatrix} E_{11}&{} E_{12} &{} .&{}. &{}E_{15}\\ * &{}E_{22}&{}.&{}.&{}E_{25}\\ .&{} .&{} .&{}. &{}.&{}\\ * &{}*&{} .&{}. &{} E_{55}\\ \end{pmatrix}<0 \end{aligned}$$
(4)
$$\begin{aligned}&\dfrac{\lambda _{max}(P)}{\lambda _{min}(P)} E_{\alpha }(d_2 T^{\alpha })\sum \limits _{j=0}^{[T/d_1]+1}(E_{\alpha }(d_2 T^{\alpha }) -1)^j <\dfrac{c_2}{c_1}. \end{aligned}$$
(5)

Proof

Let us consider the following non-negative quadratic functional \( V(x(t))=x(t)^{\top }Px(t). \) Since the solution x(t) may not be non-differentiable, we propose the following result on estimating Caputo derivative of V(x(t)). \(\square \)

Lemma 4

For the solution \(x(t)\in C([-d_2,T],\mathbb {R}^n),\) the Caputo derivative \(D^{\alpha }_C(V(x(t)))\in C([0,T],\mathbb {R}^n)\) exists and \( D^{\alpha }_C[V(x(t))]\le 2x(t)^{\top }P D^{\alpha }_C x(t),\quad t\ge 0. \)

To prove the lemma, we note that \(x(t)\in C([-d_2,T],\mathbb {R}^n)\) (by Lemma 2), the function

$$\begin{aligned} u(t)=-Mx(t)+Ff(x(t))+Gg(x(t-d(t))), \end{aligned}$$

is continuous on [0, T]. Hence, we get

$$\begin{aligned} \Big |\dfrac{x(t)-x(0)}{t^{\alpha }}- \dfrac{u(0)}{\Gamma (\alpha +1)}\Big | =&\Big |\dfrac{\int \limits _0^t (t-s)^{\alpha -1}(u(s)-u(0))ds}{t^{\alpha }\Gamma (\alpha )}\Big |\\ \le&\sup \limits _{s\in [0,t]} \Big |u(s)-u(0)\Big | \Big |\dfrac{\int \limits _0^t (t-s)^{\alpha -1}ds}{t^{\alpha }\Gamma (\alpha )}\Big |\\ =&\dfrac{1}{\Gamma (\alpha +1)}\sup \limits _{s\in [0,t]} \Big |u(s)-u(0)\Big |\rightarrow 0, \end{aligned}$$

as \(t\rightarrow 0.\) In the other words,

$$\begin{aligned} \gamma _0:= \lim \limits _{t\rightarrow 0} \dfrac{x(t)-x(0)}{t^{\alpha }}=\dfrac{u(0)}{\Gamma (\alpha +1)}. \end{aligned}$$
(6)

Consequently,

$$\begin{aligned} \lim \limits _{t\rightarrow 0}\dfrac{ V(x(t))-V(x(0))}{t^{\alpha }} =2 \Big (x(0),\dfrac{Pu(0)}{\Gamma (\alpha +1)}\Big ). \end{aligned}$$
(7)

It is easy to calculate the following integral

$$\begin{aligned} \int _{\xi t}^t \frac{V(x(t))-V(x(s))}{(t-s)^{\alpha +1}}ds =&\int _{\xi t}^t \frac{(x(t)-x(s),2Px(t))}{(t-s)^{\alpha +1}}ds - \int _{\xi t}^t \frac{(x(t)-x(s),P[x(t)-x(s)])}{(t-s)^{\alpha +1}}ds\nonumber \\ =&I_1(t,\xi )-I_2(t,\xi ). \end{aligned}$$
(8)

From Theorem 2.2 of [36] it follows that \( D^{\alpha }_Cx=u\in C([0,T],\mathbb {R}^n),\) and when \(\xi \rightarrow 1^-,\) we have

$$\begin{aligned} \begin{aligned} |I_1(t,\xi )|=&\Big |\Big ( \int \limits _{\xi t}^t \dfrac{x(t)-x(\tau )}{(t-\tau )^{\alpha +1}}d\tau ,\ 2Px(t)\Big )\Big |\\ \le&\sup \limits _{0<t\le T}\Big | \int \limits _{\xi t}^t \dfrac{x(t)-x(\tau )}{(t-\tau )^{\alpha +1} }d\tau \Big |2\sup \limits _{t\in [0,T]}|Px(t)|\rightarrow 0, \end{aligned} \end{aligned}$$
(9)

when \(\xi \rightarrow 1^-,\) and

$$\begin{aligned} x=x(0)+\gamma _0 t^{\alpha }+x_0,\ x_0\in H_0^{\alpha }[0,T],\ t\in (0,T]. \end{aligned}$$

Hence, for \(0\le \xi t\le \tau < t\le T,\ \xi \in (0,1],\) we obtain that

$$\begin{aligned} \Big |\dfrac{x(t)-x(\tau )}{(t-\tau )^{\alpha }}\Big |\le&\Big |\gamma _0 \dfrac{t^{\alpha }- s^{\alpha }}{(t-\tau )^{\alpha }}\Big |+\Big |\dfrac{x_0(t)-x_0(\tau )}{(t-\tau )^{\alpha }}\Big |\\ =&\gamma _0 \dfrac{(t-\tau ) \alpha c^{\alpha -1}}{(t-\tau )^{\alpha }}+\Big |\dfrac{x_0(t)-x_0(\tau )}{(t-\tau )^{\alpha }}\Big |,\\ \le&k(\xi ):=\gamma _0 \alpha [1/\xi -1]^{1-\alpha }+\sup \limits _{0\le \tau <t\le T,|t-\tau |\le T(1-\xi ) } \Big |\dfrac{x_0(t)-x_0(\tau )}{(t-\tau )^{\alpha }}\Big |, \end{aligned}$$

where \(c\in (\tau ,t).\) Thus, as \(\xi \rightarrow 1^-,\) we get

$$\begin{aligned} \begin{aligned} |I_2(t,\xi )|&=\int \limits _{\xi t}^t \frac{(x(t)-x(\tau ),P[x(t)-x(\tau )])}{(t-\tau )^{\alpha +1}}d\tau \\&\le \dfrac{T^{\alpha }(1-\xi )^{\alpha }}{\alpha } \Vert P\Vert k(\xi )^2\rightarrow 0, \end{aligned} \end{aligned}$$
(10)

because \(k(\xi )\) is independent on \(\tau , t,\) and \(x_0\in H_0^{\alpha }[0,T].\) From (8), (9), (10), as \(\xi \rightarrow 1^-,\)

$$\begin{aligned} \sup \limits _{0<t\le T}\Big | \int \limits _{\xi t}^t (t-\tau )^{-\alpha -1}(V(x(t))-V(x(\tau )))d\tau \Big |\rightarrow 0. \end{aligned}$$
(11)

Using Theorem 2.2 of [36] and (7), (11) gives \(\exists D^{\alpha }_CV(x(t))\in C[0,T]\) and

$$\begin{aligned} \begin{aligned} D^{\alpha }_C(V(x(t)))(0)=&2 \Big (x(0),Pv(0)\Big ),\\ D^{\alpha }_C(V(x(t)))=&\dfrac{V(x(t))-V(x(0))}{t^{\alpha }\Gamma (1-\alpha )} +\dfrac{\alpha }{\Gamma (1-\alpha )} \int \limits _0^t \dfrac{V(x(t))-V(x(\tau ))}{(t-\tau )^{\alpha +1}}d\tau ,\ t\in (0,T]. \end{aligned} \end{aligned}$$
(12)

Besides we have \(D^{\alpha }_C x\in C[0,T]\) and

$$\begin{aligned} \begin{aligned} (D^{\alpha }_Cx)(0) =&\Gamma (\alpha +1)\dfrac{u(0)}{\Gamma (\alpha +1)}=u(0),\\ (D^{\alpha }_Cx)(t)=&\dfrac{1}{\Gamma (1-\alpha )}\Big (\frac{x(t)-x(0)}{t^{\alpha }}+ \dfrac{\alpha }{\Gamma (1-\alpha )}\int \limits _0^t \frac{x(t)-x(\tau )}{(t-\tau )^{1+\alpha }}d\tau \Big ). \end{aligned} \end{aligned}$$
(13)

The identities (12) and (13) lead to \(D^{\alpha }_C(V(x(t)))- 2(x(t),P D^{\alpha }_C x(t) )=0, t=0 \) and for \(t\in (0,T]\) to

$$\begin{aligned} \quad D^{\alpha }_C(V(x(t)))- 2(x(t),P D^{\alpha }_C x(t) )=&-\dfrac{V(x(t)-x(0))}{t^{\alpha }\Gamma (1-\alpha )}-\dfrac{\alpha }{\Gamma (1-\alpha )} \int \limits _0^t\dfrac{V(x(t)-x(\tau ))}{(t-\tau )^{\alpha +1}}d\tau \\ \le&0, \end{aligned}$$

which completes the proof of Lemma 4.

To finish the theorem’s proof, denoting

$$\begin{aligned} \xi (t)=[x(t),\ f(\cdot ),\ g(\cdot )]^{\top }, f(\cdot )=f(x(t)),\ g(\cdot )=g(x(t-d(t))), \end{aligned}$$

we obtain, by using Lemma 4, that

$$\begin{aligned} D^{\alpha }_CV(x(t)) \le&2 x(t)^{\top }P D^{\alpha }_C x(t)\nonumber \\ =&2 x(t)^{\top }P \Big (-Mx(t)+Ff(x(t))+Gg(\cdot ) \Big )\nonumber \\ \le&2 x(t)^{\top }P \Big (-Mx(t)+Ff(x(t))+Gg(\cdot ) \Big )\nonumber \\&-\beta f(\cdot )^{\top }f(\cdot )-\gamma g(\cdot )^{\top }Pg(\cdot ) +\beta \max \limits _i l_i^2\ x(t)^{\top }x(t)\nonumber \\&-d_2 x(t)^{\top }Px(t)+d_2V(x(t))+ \gamma g(\cdot )^{\top }Pg(\cdot )\nonumber \\ =&\xi (t)^{\top }[E_{ij}]_{3\times 3}\xi (t)+d_2V(x(t))+ \gamma g(\cdot )^{\top }Pg(\cdot )\nonumber \\ \le&d_2V(x(t))+\gamma g(\cdot )^{\top }Pg(\cdot ), \end{aligned}$$
(14)

because of \(\Vert f(\cdot )\Vert ^2\le \max \limits _i l_i^2\ \Vert x(t)\Vert ^2,\) and \([E_{ij}]_{3\times 3}<0\) (by the condition (4)). Let

$$\begin{aligned} U(t)=D^{\alpha }_CV(x(t))-d_2V(x(t)),\ t\ge 0. \end{aligned}$$
(15)

Using the Laplace transform (by Lemma 1-(i)) to the both sides of (15) gives

$$\begin{aligned} \mathcal {L}[U(t)](s)=s^{\alpha } \mathcal {L}[V(x(t))](s)-s^{\alpha -1}V(x(0)) -d_2\mathcal {L}[V(x(t))](s), \end{aligned}$$

equivalently

$$\begin{aligned} \mathcal {L}[V(x(t))](s)=(s^{\alpha }-d_2)^{-1}s^{\alpha -1}V(x(0)) +(s^{\alpha }-d_2)^{-1}\mathcal {L}[U(t)](s). \end{aligned}$$

Applying Lemma 1 -(ii), (iii), we obtain that

$$\begin{aligned} \mathcal {L}\Big [V(x(0)) E_{\alpha }(d_2 t^{\alpha })](s) =&(s^{\alpha }-d_2)^{-1}s^{\alpha -1}V(x(0))\\ \mathcal {L}\Big [t^{\alpha -1} E_{\alpha ,\alpha }(d_2t^{\alpha })* U(t)](s)=&(s^{\alpha }-d_2)^{-1}\mathcal {L}[U(t)](s), \end{aligned}$$

hence

$$\begin{aligned} \mathcal {L}[V(x(t))](s)= \mathcal {L}\Big [ V(x(0)) E_{\alpha }(d_2 t^{\alpha }) + t^{\alpha -1} E_{\alpha ,\alpha }(d_2t^{\alpha })* U(t) \Big ](s). \end{aligned}$$

Taking the inverse Laplace transform to the derived equation gives

$$\begin{aligned} V(x(t))=V(x(0)) E_{\alpha }(d_2 t^{\alpha }) +\int \limits _0^t \dfrac{U(s)}{(t-s)^{1-\alpha }}E_{\alpha ,\alpha }( d_2(t-s)^{\alpha } )ds. \end{aligned}$$
(16)

Using (14) and the inequality (3) we have

$$\begin{aligned} U(t)&\le \gamma g(\cdot )^{\top }Pg(\cdot )\le 2\gamma g(\cdot )^{\top }g(\cdot )\\&\le 2\gamma \max _i [k_i]^2 \sum \limits _{i=1}^n | x_i(t-d(t))|^2\\&\le d_2 x(t-d(t))^{\top }Px(t-d(t))=d_2 V(x(t-d(t))), \end{aligned}$$

then

$$\begin{aligned} \sup \limits _{s\in [0,t]} U(s)\le d_2\sup \limits _{\theta \in [-d_2,t-d_1]}V(x(\theta )). \end{aligned}$$
(17)

From (16) and (17) it gives

$$\begin{aligned} V(x(t))\le&V(x(0)) E_{\alpha }(d_2 t^{\alpha }) +\sup \limits _{s\in [0,t]} U(s) \int \limits _0^t \dfrac{E_{\alpha ,\alpha }( d_2(t-s)^{\alpha } )}{(t-s)^{1-\alpha }}ds\\ \le&V(x(0)) E_{\alpha }(d_2 t^{\alpha }) +(E_{\alpha }(d_2 t^{\alpha })-1) \sup \limits _{\theta \in [-d_2,t-d_1]}V(x(\theta )), \end{aligned}$$

Moreover, we have

$$\begin{aligned} \sup \limits _{\theta \in [-d_2,t]}V(x(\theta ))\le E_{\alpha }(d_2 T^{\alpha }) V(x(0)) +[E_{\alpha }(d_2 T^{\alpha }) -1] \sup \limits _{\theta \in [-d_2,t-d_1]}V(x(\theta )). \end{aligned}$$
(18)

Applying Lemma 3 with \( S(t)=\sup \limits _{\theta \in [-d_2,t]}V(x(\theta )), a=E_{\alpha }(d_2 T^{\alpha }), \) \(b=E_{\alpha }(d_2 T^{\alpha }) -1, \) and from (18) it follows that

$$\begin{aligned} \sup \limits _{\theta \in [-d_2,t]}V(x(\theta ))\le q\sup \limits _{\theta \in [-d_2,0]}V(x(\theta )) \le q \lambda _{max}(P) \Vert \phi \Vert ^2, \end{aligned}$$
(19)

, where \( q=E_{\alpha }(d_2 T^{\alpha })\sum \limits _{j=0}^{[T/d_1]+1}(E_{\alpha }(d_2 T^{\alpha }) -1)^j . \) For \(t\in [0,T],\) the conditions (5) and (19) show that

$$\begin{aligned} \Vert x(t)\Vert ^2&\le \dfrac{x(t)^{\top }Px(t)}{\lambda _{min}(P)}\le \dfrac{\sup \limits _{\theta \in [-d_2,t]}V(x(\theta ))}{\lambda _{min}(P)}\\&\le q\dfrac{\lambda _{max}(P)}{\lambda _{min}(P)} \Vert \phi \Vert ^2\le q\dfrac{\lambda _{max}(P)}{\lambda _{min}(P)} c_1\le c_2, \end{aligned}$$

which shows that system (1) is FTS with respect to \((c_1,c_2,T).\)

Remark 1

Note that the numbers \(c_1, c_2,\) do not involve in the LMI (4), we find the solutions \(P,\beta \) by solving LMI (4) and the condition (5) can be easily verified.

Remark 2

Theorem 1 proposed delay-dependent sufficient conditions for finite-time stability of FONNs with interval time-varying delay, which is a non-differentiable function, extends some existing results obtained in [23, 30,31,32,33], where the time delay is assumed to be differentiable. Moreover, for the case fractional derivative order \(\alpha =1,\) system (1) is reduced to normal fractional-order neural networks with time-varying delay and some existing results on FTS of such systems obtained in [4, 34, 37,38,39] can be derived from Theorem 1.

Remark 3

It should be pointed out that the advantage of our paper was proposing an approach based on the Laplace transform combining with the inf–sup method to study stability of FONNs with interval time-varying delay without using the fractional Lyapunov stability theorem.

Example 1

Consider FONNs (1) with the following system parameters

$$\begin{aligned} \alpha= & {} 0.5,\ d(t)= 0.1+0.05 |\sin (t)|,\\ M= & {} \begin{bmatrix} 1&{}0\\ 0&{}1\\ \end{bmatrix},\ A= \begin{bmatrix} 1&{}-1\\ 0&{}1\\ \end{bmatrix},\ B= \begin{bmatrix} 1&{}0\\ 1&{}1\\ \end{bmatrix},\ \end{aligned}$$

the neuron activation functions \(f,g: \mathbb {R}^2\rightarrow \mathbb {R}^2\) defined by

$$\begin{aligned} f(x)= & {} (f_1(x_1),f_2(x_2))^{\top },\ g(x)=(g_1(x_1),g_2(x_2))^{\top },\\ f_1(t)= & {} f_2(t)=g_1(t)=g_2(t)=0.08\dfrac{t}{1+t^2}, \end{aligned}$$

for all \(t\in \mathbb {R},\ (x_1,x_2)\in \mathbb {R}^2.\)

Fig. 1
figure 1

Time history of \(\Vert x(t)\Vert ^2\) of the system with \(\alpha =0.5\)

Full size image
Fig. 2
figure 2

Time history of \(\Vert x(t)\Vert ^2\) of the system with \(\alpha =0.6\)

Full size image

It can be shown that \( 0<d_1=0.1\le d(t)\le d_2=0.15, \) \(f(0)=g(0)=0,\) and the neuron activation functions satisfy the Lipschitz conditions (3) with \( l_1=l_2=k_1=k_2=0.1. \) Since the delay function d(t) is non-differentiable, the method used in [20, 30,31,32,33] cannot be applied. We use the LMI algorithm in MATLAB [40] to find solutions of (4) as

$$\begin{aligned} P= \begin{bmatrix} 1.7413&{} 0.1105\\ 0.1105&{} 1.7544 \end{bmatrix},\ \beta =5.8115. \end{aligned}$$

In this case, it can be computed that

$$\begin{aligned} \gamma =7.5,\ \lambda _{max}(P)=1.8586,\ \lambda _{min}(P)=1.6371. \end{aligned}$$

For \(c_1=1,\ c_2=4,\ T=10,\) we can check the condition (5) as

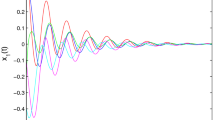
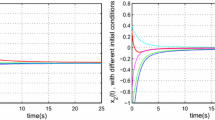
$$\begin{aligned} E_{\alpha }(d_2 T^{\alpha })\sum \limits _{j=0}^{[T/d_1]+1}(E_{\alpha }(d_2 T^{\alpha }) -1)^j \dfrac{\lambda _{max}(P)}{\lambda _{min}(P)} c_1 = 3.9939<4 \end{aligned}$$

Hence, by Theorem 1, the system (1) is FTS with respect to (1, 4, 10). Figure 1 and Figure 2 demonstrate the time history \(\Vert x(t)\Vert ^2\) of the system with initial condition \(\phi (t)=[0.65, 0.65],\ t\in [-0.15,\ 0]\) and \(\alpha = 0.5,\) and \(\alpha = 0.6,\), respectively.

4 Conclusions

In this paper, the finite-time stability problem for a class of FONNs with interval time-varying delay has been addressed. Based on a novel analytical approach, delay-dependent sufficient conditions for FTS are proposed. The conditions are presented in the form of a tractable LMI and Mittag–Leffler functions. Finite-time stability analysis of FONNs with unbounded time-varying delay may be interesting topics to study in the future, and an extension of this study to non-autonomous FONNs with delays is an open problem.