Finite-time stability criteria for a class of fractional-order neural networks with delay

Abstract

Finite-time stabilities of a class of fractional-order neural networks delayed systems with order $\alpha {:}$ $0<\alpha \le 0.5$ and $0.5<\alpha <1$ are addressed in this paper, respectively. By using inequality technique, two new delay-dependent sufficient conditions ensuring stability of such fractional-order neural networks over a finite-time interval are obtained. Obtained conditions are less conservative than that given in the earlier references. Two numerical examples are given to show the effectiveness of our proposed method.

1 Introduction

It is well known that neural networks have important potential utilization in optimization, signal processing, associative memory, parallel computation, pattern recognition, artificial intelligence, and so on, and such applications heavily depend on the dynamical behavior of neural networks, especially stability. So, the study of stability of neural networks has become one of the most active areas of research [1–6]. Note that these results mainly focus on integer-order neural networks model, in which dynamical behavior of the neurons is described by integer-order derivative. With the rapid development of fractional calculus and its advantages, some scholars claimed that it may be appropriate to depict the “memory” of neurons by using fractional-order derivative [7]. The reasons are that fractional calculus is nonlocal and has weakly singular kernels, and it provides an excellent instrument for the description of memory and hereditary properties of dynamical processes. Up to now, fractional-order neural networks have been attracted wide attention. Some positive and interesting results are obtained in biological neurons [7, 8], neural network approximation [9], parameter estimations [10], and so on. In particular, the dynamical behavior of fractional-order artificial neural networks has been a very recent and promising research topic. The chaotic behavior on fractional-order neural network models has been discussed by numerical simulations in Refs. [11–14], and stability analysis of fractional-order neural network has been discussed in Refs. [15–17]. Refs. [18, 19] considered chaotic synchronization in fractional-order neural networks. Mittag-Leffler stability and synchronization of memristor-based fractional-order neural networks were discussed in Ref. [20].

For the analysis of the stability of the neural network, asymptotic stability is an important concept, which implies convergence of the system trajectories to an equilibrium state over the infinite time, and much effort has been devoted to it. However, in some situations, one is not only interested in system stability (in the sense of Lyapunov), but also for the boundedness properties of system responses (for example, technical and practical stability). It should be paid attention to the fact that a system could be stable but still completely useless because it possesses undesirable transient performances. Thus, it is desirable that the dynamical system possesses the property that the trajectories must be within some bounds during a specific time interval. Hence, finite-time stability was proposed by non-Lyapunov point of view [21]. Neural networks are said to be finite-time stable; given a set of admissible initial conditions, the state trajectories of the system remain, over a prespecified finite-time interval, in a bounded region of the state space. Finite-time stability and asymptotic stability are independent concepts, which neither imply nor exclude each other. Some important results on finite-time stability are obtained, which were also carried out on fractional-order systems, for instance, sufficient conditions were derived for finite-time stability of linear fractional-order delayed systems in Refs.  [22–25].

In recent years, there have been some advances in stability theory and control of fractional differential systems [26–38]. However, due to the fact that fractional derivatives are nonlocal and have weakly singular kernels, the analysis on stability of fractional differential equations is more complex and difficult than that of classical differential equations, which causes the development of stability of fractional differential equations is a bit slow, and much attention has also been paid to explore robust stability conditions for fractional-order linear systems, see [39–42] and references therein. In fact, on fractional-order neural network as a typical fractional-order delayed nonlinear system, there is no effective way to analyze its stability. Although Ref. [43] proposed fractional-order Lyapunov direct method to analyze asymptotic stability for fractional-order nonlinear delayed systems in the sense of Lyapunov, to choose a suitable Lyapunov function and calculate the fractional-order derivative are very difficult. Here, our contribution is to adopt new methods and obtain some new sufficient conditions which guarantee that fractional-order delayed neural networks with order $\alpha {:}\,0<\alpha <1$ is stable over a finite-time interval.

The rest of the paper is organized as follows. Some necessary Definitions, Lemmas and model are given in Sect. 2. Main results are discussed in Sect. 3. Two simple examples are present in Sect. 4.

Notations: $\Vert x\Vert =\sum _{i=1}^n|x_i|$ and $\Vert A\Vert$ = max$_j\sum _{i=1}^n|a_{ij}|$ are the Euclidean vector norm and the matrix norm respectively, where $x_i$ and $a_{ij}$ are the element of the vector $x$ and the matrix $A$, respectively. $R^+$ and $Z^+$ are the sets of positive real and integer numbers, respectively.

2 Preliminaries and problem description

In this section, some notation, definitions and well-known results about fractional differential equations are presented firstly.

Definition 1

The fractional integral (Riemann–Liouville integral) $D_{t_0, t}^{-\alpha }$ with fractional order $\alpha \in R^+$ of function $x(t)$ is defined as

$$\begin{aligned} D_{t_0, t}^{-\alpha }x(t)=\frac{1}{\varGamma (\alpha )}\int _{t_0}^t(t-\tau )^{\alpha -1}x(\tau )\hbox {d}\tau , \end{aligned}$$

where $\varGamma (\cdot )$ is the gamma function, $\varGamma (\tau )=\int _0^\infty t^{\tau -1}e^{-t}\hbox {d}t$.

Definition 2

The Riemann–Liouville derivative of fractional order $\alpha$ of function $x(t)$ is given as

$$\begin{aligned} _{\hbox {RL}}D_{t_0,t}^\alpha x(t)= & {} \frac{\hbox {d}^n}{\hbox {d}t^n}D_{t_0,t}^{-(n-\alpha )} x(t) =\frac{\hbox {d}^n}{\hbox {d}t^n}\frac{1}{\varGamma (n-\alpha )} \int _{t_0}^t(t-\tau )^{(n-\alpha -1)}x(\tau )\hbox {d}\tau , \end{aligned}$$

where $n-1<\alpha <n\in Z^+$.

Definition 3

The Caputo derivative of fractional order $\alpha$ of function $x(t)$ is defined as follows:

$$\begin{aligned} _{C}D_{t_0,t}^\alpha x(t)=D_{t_0,t}^{-(n-\alpha )}\frac{\hbox {d}^n}{\hbox {d}t^n}x(t) =\frac{1}{\varGamma (n-\alpha )}\int _{t_0}^t(t-\tau )^{(n-\alpha -1)}x^{(n)}(\tau )\hbox {d}\tau , \end{aligned}$$

where $n-1<\alpha <n\in Z^+$.

Based on the definition of integral derivative and fractional derivative, it is recognized that the integral derivative of a function is only related to its nearby points, while the fractional derivative has a relationship with all of the function history information. That is, the next state of a system not only depends upon its current state but also upon its historical states starting from the initial time. As a result, a model described by fractional-order equations possesses memory. It is precisely to describe the state of neuron [16]. In the rest of this paper, we deal with fractional-order neural networks with delay involving Caputo derivative, and the notation $D^\alpha$ is chosen as the Caputo fractional derivative operator $D_{0,t}^\alpha$.

The dynamic behavior of a continuous fractional-order delayed neural networks can be described by the following differential equation:

$$\begin{aligned} \left\{ \begin{aligned}& D^{\alpha }x_i(t)=-c_ix_i(t)+\sum _{j=1}^na_{ij}f_j(x_j(t))+\sum _{j=1}^nb_{ij}g_j(x_j(t-\tau ))+I_i, \\ & x_i(t)=\phi _i(t),\quad \ t\in [-\tau , 0], \end{aligned} \right. \end{aligned}$$

(1)

or equivalently

$$\begin{aligned} D^{\alpha }x(t)=-Cx(t)+Af(x(t))+Bg(x(t-\tau ))+I, \end{aligned}$$

(2)

where $0<\alpha <1$, $n$ corresponds to the number of units in a neural network; $x(t)=(x_1(t),\ldots , x_n(t))^\mathrm{T}\in R^n$ corresponds to the state vector at time $t$; $f(x(t))=(f_1(x_1(t)),\,f_2(x_2(t)), \ldots , f_n(x_n(t)))^\mathrm{T}$ and $g(x(t))$ = $(g_1(x_1(t))$, $g_2(x_2(t))$,$\ldots$, $g_n(x_n(t)))^\mathrm{T}$ denote the neuron activation function, and $f(x)$, $g(x)$ are Lipschitz continuous, that is, there exist positive constants $F, G$ such that $\Vert f(u)-f(v)\Vert <F\Vert u-v\Vert ,\,\Vert g(u)-g(v)\Vert <G\Vert u-v\Vert , \forall u,v \in R^n$, where $F>0, G>0$; $C,A,B$ are constant matrices; $C=$ diag$(c_i>0)$ represents the rate with which the $i$th unit will reset its potential to the resting state in isolation when disconnected from the network and external inputs; $A=[a_{ij}]_{n\times n}$ and $B=[b_{ij}]_{n\times n}$ are the connection weight matrix and the delayed connection weight matrix, respectively; $\tau$ is the transmission delay and a nonnegative constant. $I=(I_1,I_2, \ldots , I_n)^\mathrm{T}$ is an external bias vector. The initial conditions associated with system (1) are of the form $x_i(t)=\phi _i(t),\ t\in [-\tau ,0],i\in N,$ define the norm $\Vert \phi \Vert =\sup _{\theta \in [-\tau ,0]}\Vert \phi (\theta )\Vert$. With a given initial function, system (1) is defined over time interval $J=[t_0, t_0+T]$, where quantity $T$ may be any a positive real number.

Definition 4

[23] The solution of system (1) is said to be finite-time stable w.r.t. $\{t_0, J, \delta , \varepsilon \}$, if and only if $\Vert \varphi (t_0)-\phi (t_0)\Vert <\delta$ imply $\Vert y(t, t_0, \varphi )-x(t, t_0, \phi )\Vert <\varepsilon$ for any two solutions $x(t, t_0, \phi )$ and $y(t, t_0, \varphi )$, $\forall t\in J=[t_0, t_0+T]$, where $\delta , \varepsilon$ are real positive numbers and index $\varepsilon$ stands for the set of all allowable states of the system and index $\delta$ for the set of all initial states of the system ($\delta <\varepsilon$).

In order to obtain main results, the following lemmas are presented for subsequent use.

Lemma 1

[44] If $x(t)\in C^m[0,\infty )$ and $m-1<\alpha <m\in z^+$, then

$$\begin{aligned}&(1)\quad D^{-\alpha }D^{-\beta } x(t)=D^{-(\alpha +\beta )}x(t), \quad \alpha , \beta \ge 0,\\&(2)\quad D^{\alpha }D^{-\beta } x(t)=x(t), \quad \alpha = \beta \ge 0,\\&(3)\quad D^{-\alpha }D^{\beta } x(t)=x(t)-\sum _{i=0}^{m-1}\frac{t^k}{k!}x^{(k)}(0), \quad \alpha = \beta \ge 0. \end{aligned}$$

Lemma 2

[45] (Hölder Inequality) Assume that $p,q>1$, and $\frac{1}{p}+\frac{1}{q}=1$, if $|f(\cdot )|^p$, $|g(\cdot )|^q \in L^1(E)$, then $f(\cdot )g(\cdot )\in L^1(E)$ and

$$\begin{aligned} \int _E |f(x)g(x)|\mathrm {d}x\le \left( \int _E|f(x)|^p \mathrm {d}x\right) ^{\frac{1}{p}} \left( \int _E|g(x)|^q\mathrm {d}x\right) ^{\frac{1}{q}}. \end{aligned}$$

where $L^1(E)$ be the Banach space of all Lebesgue measurable functions $f{:}\,E\rightarrow R$ with $\int _E|f(x)|\mathrm {d}x<\infty$.

Let $p=q=2$, it reduces to the Cauchy–Schwartz inequality as follows:

$$\begin{aligned} \left( \int _E |f(x)g(x)|\mathrm {d}x\right) ^2\le \left( \int _E|f(x)|^2\mathrm {d}x\right) \left( \int _E|g(x)|^2\mathrm {d}x\right) . \end{aligned}$$

Lemma 3

[46] Let $u(t), \omega (t), v(t)$ and $h(t)$ be nonnegative continuous functions on $R^+$, and let $r\ge 1$ be a real number. If

$$\begin{aligned} u(t)\le u_0(t)+\omega (t)\left( \int _0^tv(s)u^r(s)\mathrm {d}s\right) ^\frac{1}{r},\quad \ t\in R^+, \end{aligned}$$

then

$$\begin{aligned} \int _0^tv(s)u^r(s)\mathrm {d}s\le \left[ 1-(1-W(t))^\frac{1}{r}\right] ^{-r}\int _0^tv(s)u_0^r(s)W(s)\mathrm {d}s, \end{aligned}$$

where $W(t)=\exp \left( -\int _0^tv(s)\omega ^r(s)\mathrm {d}s\right)$.

Lemma 4

[45] (Generalized Bernoulli inequality) If $r\in R^+$, $x<1$ and $x\ne 0$, then, for $0<r<1$

$$\begin{aligned} (1-x)^r<1-r x . \end{aligned}$$

or

$$\begin{aligned} \left( 1-(1+x)^r\right) ^{-1}<(rx)^{-1}. \end{aligned}$$

3 Main results

In this section, two sufficient conditions are proposed for finite-time stability of a class of fractional-order neural networks delayed systems with order $\alpha {:}$ $0<\alpha \le 0.5$ and $0.5< \alpha <1$, respectively.

Theorem 1

When $\frac{1}{2}<\alpha <1$, if

$$\begin{aligned} (1+M_2)(1+2e^{(M_1+M_2e^{-\tau })^2t})e^t<\frac{\varepsilon }{\delta }, \end{aligned}$$

(3)

where $M_1=\frac{(\Vert C\Vert +\Vert A\Vert F)\sqrt{2\varGamma (2\alpha -1)}}{\varGamma (\alpha )2^\alpha }$, $M_2=\frac{\Vert B\Vert G\sqrt{2\varGamma (2\alpha -1)}}{\varGamma (\alpha )2^\alpha }$, then system (1) is finite-time stable w.r.t $\{0, J, \delta , \varepsilon \}$, $\delta <\varepsilon$.

Proof

Assume that $x(t)=(x_1(t),\ldots ,x_n(t))^\mathrm{T}$ and $y(t)=(y_1(t),\ldots ,y_n(t))^\mathrm{T}$ are any two solutions of (1) with different initial conditions $\phi (0)$ and $\varphi (0)$, and denote $e(t)=x(t)-y(t), \sigma (0)=\phi (0)-\varphi (0)$. It follows from the Lemma 1 that system (1) is equivalent to the following Volterra fractional integral equation with memory

$$\begin{aligned} e(t) &= {} \sigma (0)+\frac{1}{\varGamma (\alpha )}\int _{0}^t(t-s)^{\alpha -1}(-Ce(s)\\&+\,Af(x(s))-Af(y(s))+Bg(x(s-\tau ))-Bg(y(s-\tau )))\mathrm {d}s. \end{aligned}$$

It is easy to obtain that

$$\begin{aligned} \Vert e(t)\Vert\le & {} \Vert \sigma (0)\Vert \\&+\,\frac{1}{\varGamma (\alpha )}\int _{0}^t(t-s)^{\alpha -1}((\Vert C\Vert +\Vert A\Vert F)\Vert e(s)\Vert + \Vert B\Vert G\Vert e(s-\tau )\Vert )\mathrm {d}s. \end{aligned}$$

By using Lemma 2 (Cauchy–Schwarz inequality), one has

$$\begin{aligned} \Vert e(t)\Vert\le & {} \Vert \sigma (0)\Vert \nonumber \\&+\,\frac{(\Vert C\Vert +\Vert A\Vert F)}{\varGamma (\alpha )}\int _{0}^t(t-s)^{\alpha -1}e^{s}e^{-s}\Vert e(s)\Vert \mathrm {d}s\nonumber \\&+\,\frac{\Vert B\Vert G}{\varGamma (\alpha )}\int _{0}^t(t-s)^{\alpha -1} e^{s}e^{-s}\Vert e(s-\tau )\Vert \mathrm {d}s\nonumber \\\le & {} \Vert \sigma (0)\Vert +\frac{(\Vert C\Vert +\Vert A\Vert F)}{\varGamma (\alpha )}\left( \int _{0}^t(t-s)^{2\alpha -2}e^{2s}\mathrm {d}s\right) ^{\frac{1}{2}}\nonumber \\&\times \,\left( \int _{0}^te^{-2s}\Vert e(s)\Vert ^2\mathrm {d}s\right) ^{\frac{1}{2}}\nonumber \\&+\,\frac{\Vert B\Vert G}{\varGamma (\alpha )}\left( \int _{0}^t (t-s)^{2\alpha -2}e^{2s}\mathrm {d}s\right) ^{\frac{1}{2}} \left( \int _{0}^te^{-2s}\Vert e(s-\tau )\Vert ^2\mathrm {d}s\right) ^{\frac{1}{2}}. \end{aligned}$$

(4)

Note that

$$\begin{aligned} \int _0^t(t-s)^{(2\alpha -2)}e^{2s}\mathrm {d}s= & {} \int _0^tu^{(2\alpha -2)}e^{2(t-u)}\mathrm {d}u\nonumber \\= & {} e^{2t}\int _0^tu^{(2\alpha -2)}e^{-2u}\mathrm {d}u =\frac{2e^{2t}}{4^\alpha }\int _0^{2t}\theta ^{2\alpha -2}e^{-\theta }\mathrm {d}\theta <\frac{2e^{2t}}{4^\alpha }\varGamma (2\alpha -1). \end{aligned}$$

(5)

Substituting (5) into (4), one obtains that

$$\begin{aligned} \Vert e(t)\Vert\le & {} \Vert \sigma (0)\Vert \nonumber \\&+\,e^t\left(M_1\left(\int _{0}^te^{-2s}\Vert e(s)\Vert ^2\mathrm {d}s\right) ^{\frac{1}{2}} +M_2\left( \int _{0}^te^{-2s}\Vert e(s-\tau )\Vert ^2\mathrm {d}s\right) ^{\frac{1}{2}}\right), \end{aligned}$$

(6)

where $M_1=\frac{(\Vert C\Vert +\Vert A\Vert F)\sqrt{2\varGamma (2\alpha -1)}}{\varGamma (\alpha )2^\alpha }$, $M_2=\frac{\Vert B\Vert G\sqrt{2\varGamma (2\alpha -1)}}{\varGamma (\alpha )2^\alpha }$.

Note that $e(t)=\sigma (t)(t\in [-\tau ,0])$ and $\Vert \sigma (0)\Vert \le \Vert \sigma \Vert =\sup _{\theta \in [-\tau ,0]}\Vert \sigma (\theta )\Vert$, we see that

$$\begin{aligned} \int _{0}^te^{-2s}\Vert e(s-\tau )\Vert ^2\mathrm {d}s & \le {} e^{-2\tau } \int _{-\tau }^{t}e^{-2s}\Vert e(s)\Vert ^2\mathrm {d}s\nonumber \\ &= {} e^{-2\tau } \int _{-\tau }^{0}e^{-2s}\Vert e(s)\Vert ^2\mathrm {d}s+e^{-2\tau } \int _{0}^{t}e^{-2s}\Vert e(s)\Vert ^2\mathrm {d}s\nonumber \\\le & {} \Vert \sigma \Vert ^2+e^{-2\tau }\int _{0}^{t}e^{-2s}\Vert e(s)\Vert ^2\mathrm {d}s. \end{aligned}$$

(7)

Together (6) with (7), it follows

$$\begin{aligned} \Vert e(t)\Vert \le (\Vert \sigma \Vert +M_2\Vert \sigma \Vert e^t)+e^t(M_1+M_2e^{-\tau }) \left( \int _{0}^te^{-2s}\Vert e(s)\Vert ^2\mathrm {d}s\right) ^{\frac{1}{2}}, \end{aligned}$$

which implies

$$\begin{aligned} \Vert e(t)\Vert e^{-t}\le (\Vert \sigma \Vert +M_2\Vert \sigma \Vert )+(M_1+M_2e^{-\tau }) \left( \int _{0}^t(e^{-s}\Vert e(s)\Vert )^2\mathrm {d}s\right) ^{\frac{1}{2}}. \end{aligned}$$

Let $u_0(t)=\Vert \sigma \Vert +M_2\Vert \sigma \Vert$, $\omega (t)=(M_1+M_2e^{-\tau })$, $u(t)=e^{-t}\Vert e(t)\Vert$, $v(t)=1$ in Lemma 3, one have $W(t)=e^{-(M_1+M_2e^{-\tau })^2t}$ and

$$\begin{aligned} \Vert e(t)\Vert\le & {} (\Vert \sigma \Vert +M_2\Vert \sigma \Vert )\\&+\,(M_1+M_2e^{-\tau })([(1-(1-e^{-(M_1+M_2e^{-\tau })^2t})^\frac{1}{2})]^{-2}\\&\times \,\int _{0}^t(\Vert \sigma \Vert +M_2\Vert \sigma \Vert )^2e^{-(M_1+M_2e^{-\tau })^2s}\mathrm {d}s)^{\frac{1}{2}}. \end{aligned}$$

Let $r=\frac{1}{2}$, $x=e^{-(M_1+M_2e^{-\tau })^2t}$ in Lemma 4, we have

$$\begin{aligned} \left[ 1-\left( 1-(e^{-(M_1+M_2e^{-\tau })^2t})^\frac{1}{2}\right) \right] ^{-1}<2e^{(M_1+M_2e^{-\tau })^2t}, \end{aligned}$$

therefore,

$$\begin{aligned} \Vert e(t)\Vert e^{-t} &\le {} (\Vert \sigma \Vert +M_2\Vert \sigma \Vert ) +(M_1+M_2e^{-\tau })2e^{(M_1+M_2e^{-\tau })^2t}\\&\times \,\left( \int _{0}^t(\Vert \sigma \Vert +M_2\Vert \sigma \Vert )^2e^{-(M_1+M_2e^{-\tau })^2s}\mathrm {d}s\right) ^{\frac{1}{2}}\\ &\le {} (\Vert \sigma \Vert +M_2\Vert \sigma \Vert ) +(\Vert \sigma \Vert +M_2\Vert \sigma \Vert )2e^{(M_1+M_2e^{-\tau })^2t}\\ &= {} (1+M_2)(1+2e^{(M_1+M_2e^{-\tau })^2t})\Vert \sigma \Vert . \end{aligned}$$

So, if (3) is satisfied and $\Vert \sigma \Vert <\delta$, then $\Vert e(t)\Vert <\varepsilon$, $t\in J$, i.e., system (1) is finite-time stable.

Theorem 2

When $0<\alpha \le \frac{1}{2}$, if

$$\begin{aligned} (1+N_2)(1+qe^{(N_1+N_2e^{-\tau })^qt})e^t<\frac{\varepsilon }{\delta }, \end{aligned}$$

(8)

where $N_1=(\Vert C\Vert +\Vert A\Vert F)(\frac{\varGamma (p(\alpha -1)+1)}{{\varGamma ^p(\alpha )p^{p(\alpha -1)+1}}})^{\frac{1}{p}}$, $N_2=\Vert B\Vert G(\frac{\varGamma (p(\alpha -1)+1)}{{\varGamma ^p(\alpha )p^{p(\alpha -1)+1}}})^{\frac{1}{p}}$, $p=1+\alpha , q=1+\frac{1}{\alpha }$, then system (1) is finite time stable w.r.t $\{0, J, \delta , \varepsilon \}$, $\delta <\varepsilon$.

Proof

According to the process of Theorem 1, we can obtain the following estimation

$$\begin{aligned} \Vert e(t)\Vert\le & {} \Vert \sigma (0)\Vert \\&+\,\frac{1}{\varGamma (\alpha )}\int _{0}^t(t-s)^{\alpha -1}((\Vert C\Vert +\Vert A\Vert F)\Vert e(s)\Vert + \Vert B\Vert G\Vert e(s-\tau )\Vert )\mathrm {d}s. \end{aligned}$$

By setting $p=1+\alpha , q=1+\frac{1}{\alpha }$. Obviously, $\frac{1}{p}+\frac{1}{q}=1$. It follows from Lemma 2 that

$$\begin{aligned} \Vert e(t)\Vert\le & {} \Vert \sigma (0)\Vert +\frac{1}{\varGamma (\alpha )} \int _0^t(\Vert C\Vert +\Vert A\Vert F)(t-s)^{\alpha -1}e^se^{-s}\Vert e(s)\Vert \mathrm {d}s\nonumber \\&+\,\frac{1}{\varGamma (\alpha )}\int _0^t \Vert B\Vert G(t-s)^{\alpha -1}e^se^{-s}\Vert e(s-\tau )\Vert \mathrm {d}s\nonumber \\\le & {} \Vert \sigma (0)\Vert +\frac{\Vert C\Vert +\Vert A\Vert F}{\varGamma (\alpha )}\left( \int _0^t(t-s)^{p\alpha -p}e^{ps}\mathrm {d}s\right) ^\frac{1}{p}\nonumber \\&\times \,\left( \int _0^te^{-qs}\Vert e(s) \Vert ^q\mathrm {d}s\right) ^\frac{1}{q}\nonumber \\&+\,\frac{\Vert B\Vert G}{\varGamma (\alpha )} \left( \int _0^t(t-s)^{p\alpha -p}e^{ps}\mathrm {d}s\right) ^\frac{1}{p} \left( \int _0^te^{-qs}\Vert e(s-\tau )\Vert ^q\right) ^\frac{1}{q}\nonumber \\ &= {} \Vert \sigma (0)\Vert +\left( \int _0^t(t-s)^{p\alpha -p}e^{ps}\mathrm {d}s\right) ^\frac{1}{p} \nonumber \\&\times \,\left[ \frac{\Vert C\Vert +\Vert A\Vert F}{\varGamma (\alpha )} \left( \int _0^te^{-qs}\Vert e(s)\Vert ^q\right) ^\frac{1}{q}\right. \nonumber \\&\left. +\frac{\Vert B\Vert G}{\varGamma (\alpha )}\left( \int _0^te^{-qs}\Vert e(s-\tau ) \Vert ^q\right) ^\frac{1}{q}\right] . \end{aligned}$$

(9)

Note that

$$\begin{aligned} \int _{0}^t(t-s)^{p(\alpha -1)}e^{pt}\mathrm {d}s &= {} e^{pt} \int _{0}^t\theta ^{p(\alpha -1)}e^{-p\theta }\mathrm {d}\theta \nonumber \\ &= {} \frac{e^{pt}}{{p^{p(\alpha -1)+1}}} \int _{0}^{pt}\sigma ^{p(\alpha -1)}e^{-\sigma }\mathrm {d}\sigma \nonumber \\ &< {} \frac{e^{pt}}{{p^{p(\alpha -1)+1}}}\varGamma (p(\alpha -1)+1), \end{aligned}$$

(10)

where $p(\alpha -1)+1=\alpha ^2>0$.

Substituting (10) into (9), one gets

$$\begin{aligned} \Vert e(t)\Vert\le & {} \Vert \sigma (0)\Vert +\left( \frac{\varGamma (p(\alpha -1)+1)}{{p^{p(\alpha -1)+1}}}\right) ^{\frac{1}{p}}e^{t} \left[ \frac{\Vert C\Vert +\Vert A\Vert F}{\varGamma (\alpha )} \left( \int _0^te^{-qs}\Vert e(s)\Vert ^q\mathrm {d}s\right) ^\frac{1}{q}\right. \\&\left. +\frac{\Vert B\Vert G}{\varGamma (\alpha )}\left( \int _0^te^{-qs} \Vert e(s-\tau )\Vert ^q\mathrm {d}s\right) ^\frac{1}{q}\right] . \end{aligned}$$

From $\Vert \sigma (0)\Vert \le \Vert \sigma \Vert =\sup _{\theta \in [-\tau ,0]}\Vert \sigma (\theta )\Vert$, it yields

$$\begin{aligned} \Vert e(t)\Vert\le & {} \Vert \sigma (0)\Vert +\left( \frac{\varGamma (p(\alpha -1)+1)}{{p^{p(\alpha -1)+1}}}\right) ^{\frac{1}{p}}e^{t}\\&\times \,\left[ \frac{\Vert C\Vert +\Vert A\Vert F}{\varGamma (\alpha )} \left( \int _0^te^{-qs}\Vert e(s)\Vert ^q\mathrm {d}s\right) ^\frac{1}{q}\right. \\&\left. +\frac{\Vert B\Vert G}{\varGamma (\alpha )} \left( \int _{-\tau }^0e^{-qs}\Vert e(s)\Vert ^q\mathrm {d}s\right) ^\frac{1}{q} +\,\frac{\Vert B\Vert G}{\varGamma (\alpha )}\left( \int _0^te^{-qs} \Vert e(s)\Vert ^q\mathrm {d}s\right) ^\frac{1}{q}\right] \\\le & {} \Vert \sigma \Vert +N_2e^{t}\Vert \sigma \Vert +(N_1+N_2e^{-\tau })e^{t}\left( \int _0^te^{-qs}\Vert e(s)\Vert ^q\mathrm {d}s\right) ^\frac{1}{q}, \end{aligned}$$

where $N_1=(\Vert C\Vert +\Vert A\Vert F)(\frac{\varGamma (p(\alpha -1)+1)}{{\varGamma ^p(\alpha )p^{p(\alpha -1)+1}}})^{\frac{1}{p}}$, $N_2=\Vert B\Vert G(\frac{\varGamma (p(\alpha -1)+1)}{{\varGamma ^p(\alpha )p^{p(\alpha -1)+1}}})^{\frac{1}{p}}$, which means that

$$\begin{aligned} \Vert e(t)\Vert e^{-t}\le & {} \Vert \sigma \Vert +N_2\Vert \sigma \Vert +(N_1+N_2e^{-\tau })\left( \int _0^te^{-qs}\Vert e(s)\Vert ^q\mathrm {d}s\right) ^\frac{1}{q}. \end{aligned}$$

Denote $u_0(t)=\Vert \sigma \Vert +N_2\Vert \sigma \Vert$, $\omega (t)=(N_1+N_2e^{-\tau })$, $u(t)=e^{-t}\Vert e(t)\Vert$, $v(t)=1$ in Lemma 3, one gets $W(t)=e^{-(N_1+N_2e^{-\tau })^qt}$ and

$$\begin{aligned} \Vert e(t)\Vert e^{-t}\le & {} (\Vert \sigma \Vert +N_2\Vert \sigma \Vert )\nonumber \\&+\,(N_1+N_2e^{-\tau })([(1-(1-e^{-(N_1+N_2e^{-\tau })^{q}t})^\frac{1}{q})]^{-q}\nonumber \\&\times \, \int _{0}^t(\Vert \sigma \Vert +N_2\Vert \sigma \Vert )^2e^{-(N_1 +N_2e^{-\tau })^{q}s}\mathrm {d}s)^{\frac{1}{q}}. \end{aligned}$$

(11)

Let $r=\frac{1}{q}$ and $x=e^{-(N_1+N_2e^{-\tau })^qt}$ in Lemma 4, we have

$$\begin{aligned} \left[ 1-\left( 1-(e^{-(N_1+N_2e^{-\tau })^qt}\right) ^\frac{1}{q})\right] ^{-1}<\,qe^{(N_1+N_2e^{-\tau })^qt}. \end{aligned}$$

(12)

Combining (11) and (12), one obtains

$$\begin{aligned} \Vert e(t)\Vert e^{-t}\le & {} (\Vert \sigma \Vert +N_2\Vert \sigma \Vert ) +(N_1+N_2e^{-\tau })qe^{(N_1+N_2e^{-\tau })^qt}\\&\times \, \left( \int _{0}^t(\Vert \sigma \Vert +N_2 \Vert \sigma \Vert )^qe^{-(N_1+N_2e^{-\tau })^qs}\mathrm {d}s\right) ^{\frac{1}{q}}\\\le & {} (\Vert \sigma \Vert +N_2\Vert \sigma \Vert ) +(\Vert \sigma \Vert +N_2\Vert \sigma \Vert )qe^{(N_1+N_2e^{-\tau })^qt}\\= & {} (1+N_2)(1+qe^{(N_1+N_2e^{-\tau })^qt})\Vert \sigma \Vert . \end{aligned}$$

So, if (8) is satisfied and $\Vert \sigma \Vert <\delta$, then $\Vert e(t)\Vert <\varepsilon$, $t\in J$, i.e., system (1) is finite-time stable.

Remark 1

The fractional-order integral-differential operator is the extended concept of integer-order integral-differential operator. Under the definition of Caputo, one can easily arrives at a fact that Caputo derivative of a constant is equal to zero. Therefore, it follows from Ref. [47] that there is at least an equilibrium point for system (1). Further, according to Theorem 1 and 2, the following corollaries hold.

Corollary 1

When $\frac{1}{2}<\alpha <1$,if

$$\begin{aligned} (1+M_2)(1+2e^{(M_1+M_2e^{-\tau })^2t})e^t<\frac{\varepsilon }{\delta }, \end{aligned}$$

(13)

where $M_1=\frac{(\Vert C\Vert +\Vert A\Vert F)\sqrt{2\varGamma (2\alpha -1)}}{\varGamma (\alpha )2^\alpha }$, $M_2=\frac{\Vert B\Vert G\sqrt{2\varGamma (2\alpha -1)}}{\varGamma (\alpha )2^\alpha }$, then the equilibrium point of system (1) is finite -ime stable w.r.t $\{0, J, \delta , \varepsilon \}$, $\delta <\varepsilon$.

Corollary 2

When $0<\alpha \le \frac{1}{2}$, if

$$\begin{aligned} (1+N_2)(1+qe^{(N_1+N_2e^{-\tau })^qt})e^t<\frac{\varepsilon }{\delta }, \end{aligned}$$

(14)

where $N_1=(\Vert C\Vert +\Vert A\Vert F)(\frac{\varGamma (p(\alpha -1)+1)}{{\varGamma ^p(\alpha )p^{p(\alpha -1)+1}}})^{\frac{1}{p}}$, $N_2=\Vert B\Vert G(\frac{\varGamma (p(\alpha -1)+1)}{{\varGamma ^p(\alpha )p^{p(\alpha -1)+1}}})^{\frac{1}{p}}$, $p=1+\alpha , q=1+\frac{1}{\alpha }$, then the equilibrium point of system (1) is finite -ime stable w.r.t $\{0, J, \delta , \varepsilon \}$, $\delta <\varepsilon$.

Remark 2

Reference [16] discussed the uniform stability of system (1), but there exits some conservation that the initial conditions associated with system (1) equals zero. Reference [15] considered the finite-time stability of system (1), which only concerned the fractional-order $\alpha$ lying in $(1,2)$.

Remark 3

References [22–25] have considered the finite-time stability of fractional-order linear delayed systems, but without addressing nonlinear systems. Here, a typical fractional-order nonlinear delayed systems are discussed.

Remark 4

Quite a few delay-independent finite-time stability criteria were derived for fractional-order neural networks with delay in Refs.  [15, 48, 49]. Generally, delay-dependent results are less conservative than delay-independent ones when the delays are small. Here, two delay-dependent conditions are established.

Remark 5

From Definition 4, it is not hard to see that the bigger estimated time of finite-time stability will be better. For comparison, example proposed in Ref. [50] is given in next section. Numerical calculations show that the estimated time of finite-time stability obtained in this paper is bigger than that of Ref.  [50]. In addition, the obtained results in this paper are slightly simpler than that of Ref. [50] in form.

4 Numeric example

In this section, we consider two simple examples to illustrate the effectiveness of theoretical results.

Example 1

Consider the fractional-order delayed Hopfield neural model (1) with following parameters, which was presented in Ref. [50]

$$\begin{aligned}C=\left( \begin{array}{cc} 0.1\; &{}\; 0 \\ 0\; &{}\; 0.1\\ \end{array} \right) , \quad A=\left( \begin{array}{cc} 0.2\; &{}\; -0.1 \\ 0.1\; &{}\; 0.2\\ \end{array} \right) , \quad B=\left( \begin{array}{cc} -0.5\; &{}\; -0.1 \\ -0.2\; &{}\; -0.5\\ \end{array} \right) . \end{aligned}$$

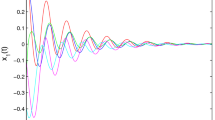
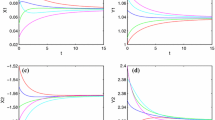
fractional order $\alpha =0.4$ or $\alpha =0.7$. The activation function is described by $f(x)=g(x)=\tanh x$, $\tau =0.1$. Clearly, $f(x)$ and $g(x)$ satisfy Lipschitz condition with $F=G=1$. $\Vert A\Vert =0.3, \Vert B\Vert =0.7, \Vert C\Vert =0.1$. Choosing the initial values $(0.08, 0.05)^\mathrm{T}$. There is a task of checking the finite-time stability w.r.t. $\{t_0=0; J=[0,4]; \delta =0.1; \varepsilon =1; \tau =0.1\}$. When $\alpha =0.7$, $M_1=0.3995$, $M_2=0.692$, according to Corollary 1, the estimated time of finite-time stability is $0.607$, which is bigger than $0.5542$ in Ref. [50]. The equilibrium point is finite-time stable, which is depicted in Fig. 1. When $\alpha =0.4$, $N_1=0.6099$, $N_2=1.0674$. It follows from inequality (14) that the estimated time of finite-time stability is $0.7522$, which is bigger than $0.6700$ in Ref. [50]. Conditions of Corollary 2 are satisfied. Therefore, the equilibrium point is finite-time stable. Numeric simulation is shown in Fig. 2.

Example 2

A fractional-order Hopfield neural network of three neurons with the following parameters is given

$$\begin{aligned}C=\left( \begin{array}{ccc} 0.4\; &{}\; 0 &{}\; 0\\ 0\; &{}\; 0.55 &{}\; 0\\ 0\; &{}\; 0 &{}\; 0.5\\ \end{array} \right) , \quad A=\left( \begin{array}{ccc} -0.04\; &{}\; 0.06 &{}\; 0.02\\ 0.03\; &{}\; -0.08 &{}\; 0.04\\ -0.05\; &{}\; -0.02 &{}\; 0.01\\ \end{array} \right) ,\quad B=\left( \begin{array}{ccc} 0.03\; &{}\; -0.04 &{}\; 0.05\\ -0.05\; &{}\; 0.02 &{}\; -0.03\\ 0.06\; &{}\; 0.04 &{}\; -0.04\\ \end{array} \right) . \end{aligned}$$

$\alpha =0.3$ or $\alpha =0.8$. The activation functions are given by $f(x)=\sin x, g(x)=\tanh x$, $\tau =0.2$. Obviously, $F=G=1$, $\Vert A\Vert =0.16, \Vert B\Vert =0.14, \Vert C\Vert =0.55$. The initial values are chosen as $(0.1, 0.2, 0.3)^\mathrm{T}$. One has to check the finite-time stability, w.r.t. $\{t_0=0; J=[0,4]; \delta =0.1; \varepsilon =1; \tau =0.2\}$. When $\alpha =0.8$, $M_1=0.5619$, $M_2=0.1192$, based on inequality (13), the estimated time of finite-time stability is $0.835$. The equilibrium point is finite-time stable, which is depicted in Fig. 3. When $\alpha =0.3$, $N_1=1.3827$, $N_2=0.2933$. It follows from inequality (14) that the estimated time of finite-time stability is $0.3183$. The time evolution of states is shown in Fig. 4.

Fig. 1

The time response curve of the system in example 1 (order $\alpha =0.7$)

Fig. 2

The time response curve of the system in example 1 (order $\alpha =0.4$)

Fig. 3

The time response curve of the system in example 2 (order $\alpha =0.8$)

Fig. 4

The time response curve of the system in example 2 (order $\alpha =0.3$)

5 Conclusion

In this paper, finite-time stability for a class fractional-order delayed neural networks with order $\alpha {:}\, 0<\alpha <0.5$ and $0.5<\alpha <1$ was considered. Two effective criteria to ensure the finite-time stability for this class of fractional order systems were derived. Illustrative examples are presented to demonstrate the effectiveness of the derived criteria.