1 Introductions

It is well known that the cellular neural networks (CNNs) are formed by many units called cells [1]. There are two basic CNNs. One is traditional CNNs which were first introduced by Chua and Yang [2, 3] and another is fuzzy CNNs (FCNNs) [4, 5] which integrate fuzzy logic into the structure of traditional CNNs and maintain local connectedness among cells. Different from previous CNNs, FCNNs have fuzzy logic between their template and input and/or output besides the “sum of product” operation. During the last decades, many researchers reveal that FCNNs have their potential in image processing and pattern recognition. In hardware implementation, time delays are inevitably occur due to the finite switching speed of the amplifiers and communication time. The qualitative research and analysis of FCNNs with delays have been investigated by numerous authors and much richer dynamics has been reported. For example, Wang and Ding [6] focused on the synchronization for delayed non-autonomous reaction–diffusion fuzzy cellular neural networks. Syed Ali and Balasubramaniam [7] considered the global asymptotic stability of stochastic fuzzy cellular neural networks with multiple discrete and distributed time-varying delays. Long and Xu [8] studied the global exponential p-stability of stochastic non-autonomous Takagi–Sugeno fuzzy cellular neural networks with time-varying delays and impulses. Rakkiyappan et al. [9] investigated the sampled-data state estimation for Markovian jumping fuzzy cellular neural networks with mode-dependent probabilistic time-varying delays. Yang et al. [10] gave a theoretical study on the exponential stability of impulsive stochastic fuzzy cellular neural networks with mixed delays and reaction–diffusion terms, Gan [11] made a discussion on the exponential synchronization of stochastic fuzzy cellular neural networks with reaction–diffusion terms via periodically intermittent control. Balasubramaniam et al. [12] presented the dynamical behaviors of interval fuzzy cellular neural networks with mixed delays under impulsive perturbations. Gan et al. [13] dealt with the exponential synchronization of stochastic fuzzy cellular neural networks with time delay in the leakage term and reaction–diffusion. Han [14] analyzed the global exponential stability of delayed fuzzy cellular neural networks with Markovian jumping parameters. Wang and Ding [15] established the conditions for synchronization for delayed non-autonomous reaction–diffusion fuzzy cellular neural networks. For more research on the dynamical behavior of fuzzy cellular neural networks, one can see [7, 16–37, 46–48].

It must be pointed out that neural networks usually have a spatial nature due to the presence of an amount of parallel pathways of variety of axon sizes and length. A distribution of conduction velocities along these pathways will lead to a distribution of propagation delays. Thus, the time-varying delays and continuous distributed delays are more appropriate to fuzzy cellular networks [38–42]. In this paper, we consider the fuzzy cellular neural networks with distributed delays as follows

$$\left\{ {\begin{array}{*{20}l} {\frac{{{\text{d}}x_{i} (t)}}{{{\text{d}}t}} = - a_{i} (t)x_{i} (t) + \sum\limits_{j = 1}^{m} {a_{ij} (t)f_{j} (y_{j} (t)) + \sum\limits_{j = 1}^{m} {b_{ij} (t)\mu_{j} (t) + I_{i} (t)} } } \\ {\quad \quad\quad + \mathop \wedge \nolimits_{j = 1}^{m} \alpha_{ij} (t)\int_{t - \tau }^{t} {k_{j} (t - s)f_{j} (y_{j} (s)){\text{d}}s + \wedge_{j = 1}^{m} T_{ij} (t)\mu_{j} (t)} } \\ {\quad \quad \quad + \vee_{j = 1}^{m} \beta_{ij} (t)\int_{t - \tau }^{t} {k_{j} (t - s)f_{j} (y_{j} (s)){\text{d}}s + \vee_{j = 1}^{m} H_{ij} (t)\mu_{j} (t),} } \\ {\frac{{{\text{d}}y_{j} (t)}}{{{\text{d}}t}} = - b_{j} (t)y_{j} (t) + \sum\limits_{i = 1}^{n} {c_{ji} (t)g_{i} (x_{i} (t)) + \sum\limits_{i = 1}^{n} {d_{ji} (t)\mu_{i} (t) + J_{j} (t)} } } \\ {\quad \quad \quad + \mathop \wedge \nolimits_{i = 1}^{n} \gamma_{ji} (t)\int_{t - \tau }^{t} {k_{i} (t - s)g_{i} (x_{i} (s))ds + \wedge_{i = 1}^{n} M_{ji} (t)\mu_{i} (t)} } \\ {\quad \quad \quad + \vee_{i = 1}^{n} \theta_{ji} (t)\int_{t - \tau }^{t} {k_{i} (t - s)g_{i} (g_{i} (s))ds + \vee_{i = 1}^{n} N_{ji} (t)\mu_{i} (t),} } \\ \end{array} } \right.$$
(1.1)

where \(a_{i} (t) \ge 0,\quad b_{j} (t) \ge 0,\quad a_{ij} (t) \ge 0,\quad b_{ij} (t) \ge 0,\) \(i = 1,2, \ldots ,n, \, j = 1,2, \ldots ,m,\quad x_{i} (t)\) and y j (t) stand for the activations of the i-th neuron in the X-layer and j-th neuron in the Y-layer, respectively, at time t; \(\wedge\) and \(\vee\) denote the fuzzy AND and fuzzy OR operations, respectively; f j , j = 1, 2, …, m, and g i , i = 1, 2, …, n, are the signal transmission functions; α ij (t) and β ij (t) are the elements of fuzzy feedback MIN and fuzzy feedback MAX in the X-layer at time t; T ij (t) and H ij (t) are the elements of fuzzy feed-forward MIN and fuzzy feed-forward MAX in the X-layer at time t; γ ij (t) and θ ji (t) are the elements of fuzzy feedback MIN and fuzzy feedback MAX in the Y-layer at time t, respectively; M ji (t) and N ji (t) are the elements of fuzzy feed-forward MIN and fuzzy feed-forward MAX in the Y-layer at time t, respectively; μ i(t) and μ j(t) stand for the external inputs at time t; I i (t) and J j (t) are the bias of the i-th neurons in the X-layer and the bias of the j-th neurons in the Y-layer at time t, respectively; k i (s) ≥ 0 is the feedback kernel, defined on the interval [0, τ] when τ is a positive finite number or [0, ∞] while τ is infinite. Kernels satisfy \(\int_{0}^{\tau } {k_{i} } (s){\text{d}}s = 1,\) \(\int_{0}^{\tau } {k_{j} } (s){\text{d}}s = 1,\) \(i = 1,2, \ldots ,n;\quad j = 1,2, \ldots ,m.\)

Throughout this paper, we always make the following assumptions:

(H1)

\(a_{i} (t),b_{j} (t),a_{ij} (t),b_{ij} (t),c_{ji} (t),d_{ji} (t),\alpha_{ij} (t),\beta_{ij} (t),\gamma_{ji} (t),\theta_{ji} (t),T_{ij} (t),\) \(H_{ij} (t),M_{ji} (t),N_{ji} (t),I_{i} (t),J_{j} (t)\) are continuous ω-periodic functions.

(H2)

\(f_{j} (.)\) and \(g_{i} (.)\) are Lipschitz continuous on R with Lipschitz constants \(L_{j}^{f} ,j = 1,2, \ldots ,m,\) and \(L_{i}^{g} ,i = 1,2, \ldots ,n\) and \(f_{j} (0) = g_{i} (0) = 0\), i.e., for all \(x,y \in R\), one has \(\left| {f_{j} (x) - f_{j} (y)} \right| \le L_{j}^{f} \left| {x - y} \right|,\left| {g_{i} (x) - g_{i} (y)} \right| \le L_{i}^{g} \left| {x - y} \right|.\)

(H3)

There exist constants Fj > 0 and Gi > 0 such that \(\left| {f_{j} (y)} \right| \le F_{j} ,\left| {g_{i} (y)} \right| \le G_{i}\) for \(i = 1,2, \ldots ,n,j = 1,2, \ldots ,m\) and \(x,y \in R\).

The principle object of this article is to explore the dynamics of system (1.1). That is, we will apply the Mawhin’s continuous theorem [43] and the method of Lyapunov function to study the existence and global asymptotic stability of periodic solutions of system (1.1).

The remainder of the paper is organized as follows: in Sect. 2, applying the coincidence degree and the related continuation theorem, some sufficient conditions for the existence of periodic solution of difference equations are established. Using the method of Lyapunov function, a series of sufficient conditions for the global asymptotic stability of the system are obtained in Sect. 3. In Sect. 4, we give an example and its numerical simulations which show the feasibility of the main results. The paper ends with a brief conclusion in Sect. 5.

2 Existence of Periodic Solutions

For convenience in the following discussing, we always use the notations:

$$f^{ - } = \mathop {\hbox{min} }\limits_{t \in [0,\omega ]} |f(t)|,\quad f^{ + } = \mathop {\hbox{max} }\limits_{t \in [0,\omega ]} |f(t)|,\quad \overline{f} : = \frac{1}{\omega }\int_{0}^{\omega } {f(t){\text{d}}t,\left\| f \right\|_{2} } = \left( {\int_{0}^{\omega } {\left| {f(t)} \right|^{2} {\text{d}}t} } \right)^{2} ,$$

where f(t) is an ω-periodic function defined on R. For any solutions

$$z(t) = \left( {x(t)^{T} ,y(t)^{T} } \right)^{T} = (x_{1} (t),x_{2} (t), \ldots ,x_{n} (t),y_{1} (t),y_{2} (t), \ldots ,y_{m} (t))^{T}$$

and

$$z^{*} (t) = \left( {x^{*} (t)^{T} ,y^{*} (t)^{T} } \right)^{T} = \left( {x_{1}^{*} (t),x_{2}^{*} (t), \ldots ,x_{n}^{*} (t),y_{1}^{*} (t),y_{2}^{*} (t), \ldots ,y_{m}^{*} (t)} \right)^{T}$$

of system (1.1), we define

$$\left\| {\left( {\phi^{T} ,\varphi^{T} } \right)^{T} - \left( {x^{*T} - y^{*T} } \right)^{T} } \right\| = \sum\limits_{i = 1}^{n} {\mathop {\hbox{max} }\limits_{t \in [0,\omega ]} \left| {\phi_{i} (t) - x_{i}^{*} (t)} \right|} + \sum\limits_{j = 1}^{m} {\mathop {\hbox{max} }\limits_{t \in [0,\omega ]} \left| {\varphi_{j} (t) - y_{j}^{*} (t)} \right|} .$$

In order to obtain the existence of periodic solutions of (1.1), we shall first make the following preparations.

Let X, Y be normed vector spaces, \(L:{\text{Dom}}L \subset X \to Y\) be a linear mapping, \(N:X \to Y\) be a continuous mapping. The mapping L will be called a Fredholm mapping of index zero if \(\dim {\text{Ker}}L = {\text{co}}\dim \text{Im} L < + \infty\) is closed in Y. If L is a Fredholm mapping of index zero and there exist continuous projectors \(P:X \to Y\) and \(Q:X \to Y\) such that \(\text{Im} P = {\text{Ker}}L\), \(\text{Im} L = {\text{Ker}}Q{\text{ = Im(}}I - Q )\). It follows that \(L|{\text{Dom}}L \cap {\text{Ker}}P{:} \, (I - P)X \to \text{Im} L\) is invertible. We denote the inverse of that map by K P . If Ω is an open bounded subset of X, the mapping N will be called L-compact on \(\overline{\Omega }\) if \(QN(\overline{\Omega } )\) is bounded and \(K_{P} (I - Q)N{:} \, \overline{\Omega } \to X\) is compact. Since \(\text{Im} Q\) is isomorphic to \({\text{Ker}}L\), there exists an isomorphism \(J{:} {\text{ ImQ}} \to {\text{Ker}}L.\)

Lemma 2.1

([43] Continuation Theorem) Let L be a Fredholm mapping of index zero and N be L-compact on \(\overline{\Omega }\). Suppose

  1. (a)

    For each \(\lambda \in (0,1)\) , every solution x of \(Lx = \lambda Nx\) is such that \(x \notin \partial \Omega\);

  2. (b)

    \(QNx \ne 0\) for each \(x \in {\text{Ker}}L \cap \partial \Omega\) and \({\rm deg}\{ JQN,\Omega \cap {\text{Ker}}L,0\} \ne 0\).

Then the equation \(Lx = Nx\) has at least one solution lying in \({\text{Dom}}L \cap \overline{\Omega }\).

Lemma 2.2

Aperiodic solution \(\left( {x^{*T} (t),y^{*T} (t)} \right)^{T}\) of system (1.1) is said to be globally exponentially stable if there exist constants \(\gamma > 0\) and \(M \ge 1\) such that \(\left| {x_{i} (t) - x_{i}^{*} (t)} \right| \le M\left\| {(\phi^{T} ,\varphi^{T} )^{T} - (x^{*T} - y^{*T} )^{T} } \right\|e^{ - \gamma t} ,\) for all \(t > 0,i = 1,2, \ldots ,n,\) \(\left| {y_{j} (t) - y_{j}^{*} (t)} \right| \le M\left\| {(\phi^{T} ,\varphi^{T} )^{T} - (x^{*T} - y^{*T} )^{T} } \right\|e^{ - \gamma t} ,\) for all \(t > 0,\quad i = 1,2, \ldots ,n,\) for any solution of system (1.1).

Lemma 2.3

Let x and y be two states of system (1.1). Then

$$\left| { \wedge_{j = 1}^{n} \alpha_{ij} (t)g_{j} (x) - \wedge_{j = 1}^{n} \alpha_{ij} (t)g_{j} (y)} \right| \le \sum\limits_{j = 1}^{n} {\left| {\alpha_{ij} (t)} \right|} \left| {g_{j} (x) - g_{j} (y)} \right|$$

and

$$\left| { \vee_{j = 1}^{n} \beta_{ij} (t)g_{j} (x) - \vee_{j = 1}^{n} \beta_{ij} (t)g_{j} (y)} \right| \le \sum\limits_{j = 1}^{n} {\left| {\beta_{ij} (t)} \right|\left| {g_{j} (x) - g_{j} (y)} \right|} .$$

In the following, we will ready to establish our result.

Theorem 2.1

Suppose that the conditions (H1)–(H3) hold, then system (1.1) has at least one ω periodic solution.

Proof

Let

$$X = Z = \{ z = (x_{1} ,x_{2} , \ldots ,x_{n} ,y_{1} ,y_{2} , \ldots ,y_{m} )^{T} \in C(R,R^{n + m} ):z(t + \omega ) = z(t)\}$$
(2.1)

and define

$$||z|| = \sum\limits_{i = 1}^{n} {\mathop {\hbox{max} }\limits_{t \in [0,\omega ]} |x_{i} (t)|} + \sum\limits_{j = 1}^{m} {\mathop {\hbox{max} }\limits_{t \in [0,\omega ]} |y_{j} (t)|} ,\quad z \in X\quad {\text{or}}\quad Z.$$
(2.2)

□

Equipped with the above norm \(||.||\), X and Z are Banach spaces. Let

$$(Lz)(t) = \dot{u} = \frac{{{\text{d}}u}}{{{\text{d}}t}},$$
(2.3)

and

$$\left\{ {\begin{array}{ll} {(Nz)_{i} (t) = - a_{i} (t)x_{i} (t) + \sum\limits_{j = 1}^{m} {a_{ij} (t)f_{j} (y_{j} (t)) + \sum\limits_{j = 1}^{m} {b_{ij} (t)\mu_{j} (t) + I_{i} (t)} } } \\ {\quad \quad \quad \quad \; + \mathop \wedge \nolimits_{j = 1}^{m} \alpha_{ij} (t)\int_{t - \tau }^{t} {k_{j} (t - s)f_{j} (y_{j} (s)){\text{d}}s + \wedge_{j = 1}^{m} T_{ij} (t)\mu_{j} (t)} } \\ {{\kern 1pt} \quad \quad \quad \quad + \vee_{j = 1}^{m} \beta_{ij} (t)\int_{t - \tau }^{t} {k_{j} (t - s)f_{j} (y_{j} (s)){\text{d}}s + \vee_{j = 1}^{m} H_{ij} (t)\mu_{j} (t),} } \\ {(Nz)_{n + j} (t) = - b_{j} (t)y_{j} (t) + \sum\limits_{i = 1}^{n} {c_{ji} (t)g_{i} (x_{i} (t)) + \sum\limits_{i = 1}^{n} {d_{ji} (t)\mu_{i} (t) + J_{j} (t)} } } \\ {\quad \quad \quad \quad \quad + \mathop \wedge \nolimits_{i = 1}^{n} \gamma_{ji} (t)\int_{t - \tau }^{t} {k_{i} (t - s)g_{i} (x_{i} (s)){\text{d}}s + \wedge_{i = 1}^{n} M_{ji} (t)\mu_{i} (t)} } \\ {\quad \quad \quad \quad \quad + \vee_{i = 1}^{n} \theta_{ji} (t)\int_{t - \tau }^{t} {k_{i} (t - s)g_{i} (g_{i} (s)){\text{d}}s + \vee_{i = 1}^{n} N_{ji} (t)\mu_{i} (t),} } \\ \end{array} } \right.$$
(2.4)

where \(z \in X\) and \(i = 1,2, \ldots ,n,\quad j = 1,2, \ldots ,m.\) Then it is trivial to see that L is a bounded linear operator and \({\text{Ker}}L = l_{c}^{\omega } ,\quad \text{Im} L = l_{c}^{\omega } ,\) and \(\dim {\text{Ker}}L = n + m = {\text{codim}} \; \text{Im} L\), then it follows that L is a Fredholm mapping of index zero. Define

$$Pz = \frac{1}{\omega }\int_{0}^{\omega } {z(t){\text{d}}t,z \in X,} \quad Qz = \frac{1}{\omega }\int_{0}^{\omega } {z(t){\text{d}}t,z \in Z.}$$

It is not difficult to show that P and Q are continuous projectors such that \(\text{Im} P = {\text{Ker}}L,\quad \text{Im} L = {\text{Ker}}Q = \text{Im} (I - Q)\). Furthermore, the generalized inverse (to L) K P : \(\text{Im} L \to {\text{Ker}}P \cap {\text{Dom}}L\) exists and is given by \(K_{P} (z) = \int_{0}^{\omega } {z(s){\text{d}}s - \frac{1}{\omega }} \int_{0}^{\omega } {\int_{0}^{s} {z(s){\text{d}}s.} }\) Obviously, QN and \(K_{P} (I - Q)N\) are continuous. Since X is a Banach space, using the Ascoli–Arzela theorem, it is not difficult to show that \(\overline{{K_{P} (I - Q)N(\overline{\Omega )} }}\) is compact for any open bounded set \(Q \subset X.\) Moreover, \(QN(\overline{\Omega )}\) is bounded. Thus, N is L-compact on \(\overline{\Omega }\) with any open bounded set \(Q \subset X.\)

Now we are at the point to search for an appropriate open, bounded subset Ω for the application of the continuation theorem. Corresponding to the operator equation \(Lx = \lambda Nx\), \(\lambda \in (0,1)\), we have

$$\left\{ {\begin{array}{ll} {\frac{{{\text{d}}x_{i} (t)}}{{{\text{d}}t}} = \lambda \left[ { - a_{i} (t)x_{i} (t) + \sum\limits_{j = 1}^{m} {a_{ij} (t)f_{j} (y_{j} (t)) + \sum\limits_{j = 1}^{m} {b_{ij} (t)\mu_{j} (t) + I_{i} (t)} } } \right.} \\ \quad{\quad \quad + \mathop \wedge \nolimits_{j = 1}^{m} \alpha_{ij} (t)\int_{t - \tau }^{t} {k_{j} (t - s)f_{j} (y_{j} (s)){\text{d}}s + \wedge_{j = 1}^{m} T_{ij} (t)\mu_{j} (t)} } \\ \quad {\left. {\quad \quad + \vee_{j = 1}^{m} \beta_{ij} (t)\int_{t - \tau }^{t} {k_{j} (t - s)f_{j} (y_{j} (s)){\text{d}}s + \vee_{j = 1}^{m} H_{ij} (t)\mu_{j} (t)} } \right]} \\ {\frac{{{\text{d}}y_{j} (t)}}{{{\text{d}}t}} = \lambda \left[ { - b_{j} (t)y_{j} (t) + \sum\limits_{i = 1}^{n} {c_{ji} (t)g_{i} (x_{i} (t)) + \sum\limits_{i = 1}^{n} {d_{ji} (t)\mu_{i} (t) + J_{j} (t)} } } \right.} \\\quad {\quad \quad + \mathop \wedge \nolimits_{i = 1}^{n} \gamma_{ji} (t)\int_{t - \tau }^{t} {k_{i} (t - s)g_{i} (x_{i} (s)){\text{d}}s + \wedge_{i = 1}^{n} M_{ji} (t)\mu_{i} (t)} } \\\quad {\left. {\quad \quad + \vee_{i = 1}^{n} \theta_{ji} (t)\int_{t - \tau }^{t} {k_{i} (t - s)g_{i} (g_{i} (s)){\text{d}}s + \vee_{i = 1}^{n} N_{ji} (t)\mu_{i} (t)} } \right].} \\ \end{array} } \right.$$
(2.5)

Suppose that \(z(t) = (x_{1} (t),x_{2} (t), \ldots ,x_{n} (t),\quad y_{1} (t),y_{2} (t), \ldots ,y_{m} (t))^{T} \in X\) is an arbitrary solution of system (2.5) for a certain \(\lambda \in (0,1)\), integrating (2.5) over \([0,\omega ]\), we obtain

$$\left\{{\begin{array}{ll} {\int_{0}^{\omega } {a_{i} (t)x_{i} (t){\text{d}}t} = \int_{0}^{\omega } {\left[ {\sum\limits_{j = 1}^{m} {a_{ij} (t)f_{j} (y_{j} (t)) + \sum\limits_{j = 1}^{m} {b_{ij} (t)\mu_{j} (t) + I_{i} (t)} } } \right.} } \\ {\quad \quad \quad \quad \quad \quad \quad + \mathop \wedge \nolimits_{j = 1}^{m} \alpha_{ij} (t)\int_{t - \tau }^{t} {k_{j} (t - s)f_{j} (y_{j} (s)){\text{d}}s + \wedge_{j = 1}^{m} T_{ij} (t)\mu_{j} (t)} } \\ { \left. { \quad \quad \quad \quad \quad \quad \quad + \vee_{j = 1}^{m} \beta_{ij} (t)\int_{t - \tau }^{t} {k_{j} (t - s)f_{j} (y_{j} (s)){\text{d}}s + \vee_{j = 1}^{m} H_{ij} (t)\mu_{j} (t)} } \right]{\text{d}}t,} \\ {\int_{0}^{\omega } {b_{j} (t)y_{j} (t){\text{d}}t} = \int_{0}^{\omega } {\left[ {\sum\limits_{i = 1}^{n} {c_{ji} (t)g_{i} (x_{i} (t)) + \sum\limits_{i = 1}^{n} {d_{ji} (t)\mu_{i} (t) + J_{j} (t)} } } \right.} } \\ {\quad \quad \quad \quad \quad \quad \quad + \mathop \wedge \nolimits_{i = 1}^{n} \gamma_{ji} (t)\int_{t - \tau }^{t} {k_{i} (t - s)g_{i} (x_{i} (s)){\text{d}}s + \wedge_{i = 1}^{n} M_{ji} (t)\mu_{i} (t)} } \\ { \quad \quad \quad \quad \quad \quad \quad \left. { + \vee_{i = 1}^{n} \theta_{ji} (t)\int_{t - \tau }^{t} {k_{i} (t - s)g_{i} (g_{i} (s)){\text{d}}s + \vee_{i = 1}^{n} N_{ji} (t)\mu_{i} (t)} } \right]{\text{d}}t.} \\ \end{array} } \right.$$
(2.6)

In view of the hypothesis that \(z = \{ z(t)\} \in X\), there exist \(\xi ,\eta \in [0,\omega ]\) such that

$$x_{i} (\xi ) = \mathop {\inf }\limits_{t \in [0,\omega ]} \{ x_{i} (t)\} ,\quad y_{j} (\eta ) = \mathop {\inf }\limits_{t \in [0,\omega ]} \{ y_{j} (t)\} \; (i = 1,2, \ldots ,n,j = 1,2, \ldots ,m).$$
(2.7)

From the first equation of (2.6), we have

$$\begin{aligned} \bar{a}_{i} \omega x_{i} (\xi ) & \le \int_{0}^{\omega } {\left[ {\left| {\sum\limits_{j = 1}^{m} {a_{ij} (t)f_{j} (y_{j} (t))} } \right|} \right.} + \left| {\sum\limits_{j = 1}^{m} {b_{ij} (t)\mu_{j} (t)} } \right| + \left| {I_{i} (t)} \right| \\ & \quad + \left| { \wedge_{j = 1}^{m} \alpha_{ij} (t)\int_{t - \tau }^{t} {k_{j} (t - s)f_{j} (y_{j} (s)){\text{d}}s} - \wedge_{j = 1}^{m} \alpha_{ij} (t)\int_{t - \tau }^{t} {k_{j} (t - s)f_{j} (0){\text{d}}s} } \right| \\ & \quad + \left| { \vee_{j = 1}^{m} \beta_{ij} (t)\int_{t - \tau }^{t} {k_{j} (t - s)f_{j} (y_{j} (s)){\text{d}}s} - \vee_{j = 1}^{m} \beta_{ij} (t)\int_{t - \tau }^{t} {k_{j} (t - s)f_{j} (0){\text{d}}s} } \right| \\ & \quad + \left. {\left| { \wedge_{j = 1}^{m} T_{ij} (t)\mu_{j} (t)} \right| + \left| { \vee_{j = 1}^{m} H_{ij} (t)\mu_{j} (t)} \right|} \right]{\text{d}}t, \\ \end{aligned}$$
(2.8)

which leads to

$$x_{i} (\xi ) \le \frac{1}{{\overline{{a_{i} }} }}\left[ {\sum\limits_{j = 1}^{m} {\left( {a_{ij}^{ + } + \alpha_{ij}^{ + } + \beta_{ij}^{ + } } \right)F_{j} + \sum\limits_{j = 1}^{m} {b_{ij}^{ + } \mu_{j}^{ + } + I_{i}^{ + } + \left( {T_{ij}^{ + } + H_{ij}^{ + } } \right)\mu_{j}^{ + } } } } \right]: = K_{i} ,$$
(2.9)

where \(i = 1,2, \ldots ,n.\) From the second equation of (2.6), we have

$$\begin{aligned} \overline{{b_{i} }} \omega y_{j} (\eta ) & \le \int_{0}^{\omega } {\left[ {\left| {\sum\limits_{i = 1}^{n} {c_{ji} (t)g_{i} (x_{i} (t))} } \right|} \right.} + \left| {\sum\limits_{i = 1}^{n} {d_{ji} (t)\mu_{i} (t)} } \right| + |J_{j} (t)| \\ & \quad + \left| { \wedge_{i = 1}^{n} \gamma_{ji} (t)\int_{t - \tau }^{t} {k_{i} (t - s)g_{i} (x_{i} (s)){\text{d}}s} - \wedge_{i = 1}^{n} \gamma_{ji} (t)\int_{t - \tau }^{t} {k_{i} (t - s)g_{i} (0){\text{d}}s} } \right| \\ & \quad + \left| { \vee_{i = 1}^{n} \theta_{ji} (t)\int_{t - \tau }^{t} {k_{i} (t - s)g_{i} (x_{i} (s)){\text{d}}s} - \vee_{i = 1}^{n} \theta_{ji} (t)\int_{t - \tau }^{t} {k_{i} (t - s)g_{i} (0){\text{d}}s} } \right| \\ & \quad + \left| { \wedge_{i = 1}^{n} M_{ji} (t)\mu_{i} (t)} \right| + \left. {\left| { \vee_{i = 1}^{n} N_{ji} (t)\mu_{i} (t)} \right|} \right]{\text{d}}t, \\ \end{aligned}$$
(2.10)

which leads to

$$y_{j} (\eta ) \le \frac{1}{{\overline{{b_{j} }} }}\left[ {\sum\limits_{i = 1}^{n} {\left( {c_{ji}^{ + } + \gamma_{ji}^{ + } + \theta_{ji}^{ + } } \right)G_{i} + \sum\limits_{i = 1}^{n} {d_{ji}^{ + } \mu_{i}^{ + } + J_{j}^{ + } + \left( {M_{ji}^{ + } + N_{ji}^{ + } } \right)\mu_{i}^{ + } } } } \right]: = P_{j} ,$$
(2.11)

where \(j = 1,2, \ldots ,m.\) Setting \(t_{0} = 0\) and \(t_{q + 1} = \omega\) and according to (2.5), (2.9) and (2.11), we have

$$\begin{aligned} & \int_{0}^{\omega } {|\dot{x}_{i} (t)|{\text{d}}t \le \sum\limits_{k = 1}^{q + 1} {\int_{k - 1}^{t} {|\dot{x}_{i} (t)|} } } {\text{d}}t \le \int_{0}^{\omega } {|a_{i} } (t)||x_{i} (t)|{\text{d}}t + \int_{0}^{\omega } {\sum\limits_{j = 1}^{m} {|b_{ij} (t)||\mu_{j} (t)|} } {\text{d}}t + \int_{0}^{\omega } {|I_{i} } (t)|{\text{d}}t \\ & \quad + \int_{0}^{\omega } {\left[ {\sum\limits_{j = 1}^{m} {(|a_{ij} (t)| + |\alpha_{ij} (t)| + |\beta_{ij} (t)|)} } \right]|f_{j} (y_{j} (t))|{\text{d}}t} \\ & \quad + \int_{0}^{\omega } {\left( {| \wedge_{j = 1}^{m} T_{ij} (t)\mu_{j} (t)| + | \vee_{j = 1}^{m} H_{ij} (t)\mu_{j} (t)|} \right){\text{d}}t} \\ & \quad \le \left( {\int_{0}^{\omega } {|a_{i} (t)|^{2} {\text{d}}t} } \right)^{ - } \left( {\int_{0}^{\omega } {|x_{i} (t)|^{2} {\text{d}}t} } \right)^{ - } + \sum\limits_{j = 1}^{m} {\left( {\int_{0}^{\omega } {|a_{ij} (t)|^{2} {\text{d}}t} } \right)^{ - } \left( {\int_{0}^{\omega } {|f_{i} (y_{j} (t))|^{2} {\text{d}}t} } \right)^{ - } } \\ & \quad + \sum\limits_{j = 1}^{m} {\left( {\int_{0}^{\omega } {|\alpha_{ij} (t)|^{2} {\text{d}}t} } \right)^{ - } \left( {\int_{0}^{\omega } {|f_{i} (y_{j} (t))|^{2} {\text{d}}t} } \right)^{ - } } + \sum\limits_{j = 1}^{m} {\left( {\int_{0}^{\omega } {|\beta_{ij} (t)|^{2} {\text{d}}t} } \right)^{ - } \left( {\int_{0}^{\omega } {|f_{i} (y_{j} (t))|^{2} {\text{d}}t} } \right)^{ - } } \\ & \quad + \sum\limits_{j = 1}^{m} {b_{ij}^{ + } } \mu_{j}^{ + } \omega + I_{i}^{ + } \omega + \left( {T_{ij}^{ + } + H_{ij}^{ + } } \right)\mu_{j}^{ + } \omega \\ & \quad \le a_{i}^{ + } ||x_{i} ||_{2} \sqrt \omega + \sum\limits_{j = 1}^{m} {\sqrt \omega \left( {a_{ij}^{ + } + \alpha_{ij}^{ + } + \beta_{ij}^{ + } } \right)} F_{j} + \sum\limits_{j = 1}^{m} {b_{ij}^{ + } } \mu_{j}^{ + } \omega + I_{i}^{ + } \omega + \left( {T_{ij}^{ + } + H_{ij}^{ + } } \right)\mu_{j}^{ + } \omega \\ \end{aligned}$$
(2.12)

Multiplying both sides of system (2.5) by x i (t) and integrating over [0,ω], we derive

$$\begin{aligned} 0 & = \int_{0}^{\omega } {x_{i} (t)\dot{x}_{i} (t){\text{d}}t = } - \lambda \int_{0}^{\omega } {a_{i} (t)x_{i}^{2} (t)} {\text{d}}t + \lambda \int_{0}^{\omega } {\sum\limits_{j = 1}^{m} {a_{ij} (t)f_{j} (y_{j} (t))x_{i} (t){\text{d}}t} } \\ & \quad + \lambda \int_{0}^{\omega } {\left[ { \wedge_{j = 1}^{m} \alpha_{ij} (t)\int_{t - \tau }^{t} {k_{j} (t - s)f_{j} (y_{j} (s)){\text{d}}s} } \right]} x_{i} (t){\text{d}}t \\ & \quad + \lambda \int_{0}^{\omega } {\left[ { \vee_{j = 1}^{m} \beta_{ij} (t)\int_{t - \tau }^{t} {k_{j} (t - s)f_{j} (y_{j} (s)){\text{d}}s} } \right]} x_{i} (t){\text{d}}t \\ & \quad + \lambda \int_{0}^{\omega } {\left[ {\sum\limits_{j = 1}^{m} {b_{ij} (t)\mu_{j} (t) + I_{i} (t) + \wedge_{j = 1}^{m} T_{ij} (t)\mu_{j} (t) + \vee_{j = 1}^{m} H_{ij} (t)\mu_{j} (t)} } \right]} x_{i} (t){\text{d}}t \\ \end{aligned}$$
(2.13)

It follows from (2.13) and Lemma 2.3 that

$$\begin{aligned} a_{i}^{ - } \int_{0}^{\omega } {|x_{i}^{2} (t)|{\text{d}}t} & \le \int_{0}^{\omega } {\sum\limits_{j = 1}^{m} {|a_{ij} (t)||f_{j} (y_{j} (t))||x_{i} (t)|{\text{d}}t} } \\ & \quad + \int_{0}^{\omega } {\left| { \wedge_{j = 1}^{m} \alpha_{ij} (t)\int_{t - \tau }^{t} {k_{j} (t - s)f_{j} (y_{j} (s)){\text{d}}s} } \right||} x_{i} (t)|{\text{d}}t \\ & \quad + \int_{0}^{\omega } {\left| { \vee_{j = 1}^{m} \beta_{ij} (t)\int_{t - \tau }^{t} {k_{j} (t - s)f_{j} (y_{j} (s)){\text{d}}s} } \right||} x_{i} (t)|{\text{d}}t \\ & \quad + \int_{0}^{\omega } {\left| {\sum\limits_{j = 1}^{m} {b_{ij} (t)\mu_{j} (t) + I_{i} (t)} } \right||} x_{i} (t)|{\text{d}}t \\ & \quad + \int_{0}^{\omega } {\left| { \wedge_{j = 1}^{m} T_{ij} (t)\mu_{j} (t) + \vee_{j = 1}^{m} H_{ij} (t)\mu_{j} (t)} \right||} x_{i} (t)|{\text{d}}t \\ & \quad \le \int_{0}^{\omega } {\sum\limits_{j = 1}^{m} {|a_{ij} (t)||f_{j} (y_{j} (t))||x_{i} (t)|{\text{d}}t} } \\ & \quad + \int_{0}^{\omega } {\sum\limits_{j = 1}^{m} {|\alpha_{ij} (t)|} |f_{j} (y_{j} (t))|} x_{i} (t)|{\text{d}}t \\ & \quad + \int_{0}^{\omega } {\sum\limits_{j}^{m} {|\beta_{ij} (t)|} |f_{j} (y_{j} (t))||} x_{i} (t)|{\text{d}}t \\ & \quad + \int_{0}^{\omega } {\left( {\sum\limits_{j = 1}^{m} {|b_{ij} (t)||\mu_{j} (t)| + |I_{i} (t)|} } \right)|} x_{i} (t)|{\text{d}}t \\ & \quad + \int_{0}^{\omega } {\left( { \wedge_{j = 1}^{m} |T_{ij} (t)||\mu_{j} (t)| + \vee_{j = 1}^{m} |H_{ij} (t)||\mu_{j} (t)|} \right)|} x_{i} (t)|{\text{d}}t \\ & \quad \le \left[ {\sum\limits_{j = 1}^{m} {\left( {a_{ij}^{ + } + \alpha_{ij}^{ + } + \beta_{ij}^{ + } } \right)M_{j} + \sum\limits_{j = 1}^{m} {b_{ij}^{ + } \mu_{j} + \left( {T_{ij}^{ + } + H_{ij}^{ + } } \right)\mu_{j}^{ + } + I_{i}^{ + } } } } \right]\sqrt \omega \left( {\int_{0}^{\omega } {|x_{i} (t)|^{2} } } \right)^{ - } . \\ \end{aligned}$$
(2.14)

Then we get

$$||x_{i} ||_{2} \le \frac{1}{{a_{i}^{ - } }}\left[ {\sum\limits_{j = 1}^{m} {\left( {a_{ij}^{ + } + \alpha_{ij}^{ + } + \beta_{ij}^{ + } } \right)M_{j} + \sum\limits_{j = 1}^{m} {b_{ij}^{ + } \mu_{j} + \left( {T_{ij}^{ + } + H_{ij}^{ + } } \right)\mu_{j}^{ + } + I_{i}^{ + } } } } \right]\sqrt \omega: = Q_{i} .$$
(2.15)

Thus it follows from (2.12) and (2.15) that

$$\begin{aligned} \int_{0}^{\omega } {|\dot{x}(t)|{\text{d}}t} & \le a_{i}^{ + } Q_{i} \sqrt \omega + \sum\limits_{j = 1}^{m} {\sqrt \omega \left( {a_{ij}^{ + } + \alpha_{ij}^{ + } + \beta_{ij}^{ + } } \right)F_{j} } \\ & \quad + \sum\limits_{j = 1}^{m} {b_{ij}^{ + } \mu_{j} \omega + I_{i}^{ + } \omega + \left( {T_{ij}^{ + } + H_{ij}^{ + } } \right)\mu_{j}^{ + } } \omega . \\ \end{aligned}$$
(2.16)

Setting t 0 = 0 and t q+1 = ω and according to (2.5), (2.11) and (2.16), we have

$$\begin{aligned} & \int_{0}^{\omega } {|\dot{y}_{j} (t)|{\text{d}}t \le \sum\limits_{k = 1}^{q + 1} {\int_{k - 1}^{t} {|\dot{y}_{j} (t)|} } } {\text{d}}t \le \int_{0}^{\omega } {|b_{j} } (t)||y_{j} (t)|{\text{d}}t + \int_{0}^{\omega } {\sum\limits_{i = 1}^{n} {|d_{ji} (t)||\mu_{i} (t)|} } {\text{d}}t + \int_{0}^{\omega } {|J_{j} } (t)|{\text{d}}t \\ & \quad + \int_{0}^{\omega } {\left[ {\sum\limits_{j = 1}^{n} {(|c_{ji} (t)| + |\gamma_{ji} (t)| + |\theta_{ji} (t)|)} } \right]|g_{i} (x_{i} (t))|{\text{d}}t} \\ & \quad + \int_{0}^{\omega } {\left( {| \wedge_{j = 1}^{n} M_{ji} (t)\mu_{i} (t)| + | \vee_{j = 1}^{n} N_{ji} (t)\mu_{i} (t)|} \right){\text{d}}t} \\ & \quad \le \left( {\int_{0}^{\omega } {|b_{j} (t)|^{2} {\text{d}}t} } \right)^{ - } \left( {\int_{0}^{\omega } {|y_{j} (t)|^{2} {\text{d}}t} } \right)^{ - } + \sum\limits_{i = 1}^{n} {\left( {\int_{0}^{\omega } {|c_{ji} (t)|^{2} {\text{d}}t} } \right)^{ - } \left( {\int_{0}^{\omega } {|g_{i} (x_{i} (t))|^{2} {\text{d}}t} } \right)^{ - } } \\ & \quad + \sum\limits_{i = 1}^{n} {\left( {\int_{0}^{\omega } {|\gamma_{ji} (t)|^{2} {\text{d}}t} } \right)^{ - } \left( {\int_{0}^{\omega } {|g_{i} (x_{i} (t))|^{2} {\text{d}}t} } \right)^{ - } } + \sum\limits_{i = 1}^{n} {\left( {\int_{0}^{\omega } {|\theta_{ji} (t)|^{2} {\text{d}}t} } \right)^{ - } \left( {\int_{0}^{\omega } {|g_{i} (x_{i} (t))|^{2} {\text{d}}t} } \right)^{ - } } \\ & \quad + \sum\limits_{i = 1}^{n} {b_{ji}^{ + } } \mu_{i}^{ + } \omega + J_{j}^{ + } \omega + \left( {M_{ji}^{ + } + N_{ji}^{ + } } \right)\mu_{i}^{ + } \omega \\ & \quad \le b_{j}^{ + } ||y_{j} ||_{2} \sqrt \omega + \sum\limits_{i = 1}^{n} {\sqrt \omega \left( {c_{ji}^{ + } + \gamma_{ji}^{ + } + \theta_{ji}^{ + } } \right)} G_{i} + \sum\limits_{i = 1}^{n} {d_{ji}^{ + } } \mu_{i}^{ + } \omega + J_{j}^{ + } \omega + \left( {M_{ji}^{ + } + N_{ji}^{ + } } \right)\mu_{i}^{ + } \omega . \\ \end{aligned}$$
(2.17)

Multiplying both sides of system (2.5) by y j (t) and integrating over [0,ω], we derive

$$\begin{aligned} 0 & = \int_{0}^{\omega } {y_{j} (t)\dot{y}_{j} (t){\text{d}}t = } - \lambda \int_{0}^{\omega } {b_{j} (t)y_{j}^{2} (t)} {\text{d}}t + \lambda \int_{0}^{\omega } {\sum\limits_{i = 1}^{n} {c_{ji} (t)g_{i} (x_{i} (t))y_{j} (t){\text{d}}t} } \\ & \quad + \lambda \int_{0}^{\omega } {\left[ { \wedge_{i = 1}^{n} \gamma_{ji} (t)\int_{t - \tau }^{t} {k_{i} (t - s)g_{i} (x_{i} (s)){\text{d}}s} } \right]} y_{j} (t){\text{d}}t \\ & \quad + \lambda \int_{0}^{\omega } {\left[ { \vee_{i = 1}^{n} \theta_{ji} (t)\int_{t - \tau }^{t} {k_{i} (t - s)g_{i} (x_{i} (s)){\text{d}}s} } \right]} y_{j} (t){\text{d}}t \\ & \quad + \lambda \int_{0}^{\omega } {\left[ {\sum\limits_{i = 1}^{n} {d_{ji} (t)\mu_{i} (t) + J_{j} (t) + \wedge_{i = 1}^{n} M_{ji} (t)\mu_{i} (t) + \vee_{i = 1}^{n} N_{ji} (t)\mu_{i} (t)} } \right]} y_{j} (t){\text{d}}t. \\ \end{aligned}$$
(2.18)

It follows from (2.18) and Lemma 2.3 that

$$\begin{aligned} b_{j}^{ - } \int_{0}^{\omega } {|y_{j}^{2} (t)|{\text{d}}t} & \le \int_{0}^{\omega } {\sum\limits_{i = 1}^{n} {|c_{ji} (t)||g_{i} (x_{i} (t))||y_{j} (t)|{\text{d}}t} } \\ & + \int_{0}^{\omega } {\left| { \wedge_{i = 1}^{n} \gamma_{ji} (t)\int_{t - \tau }^{t} {k_{i} (t - s)g_{i} (x_{i} (s)){\text{d}}s} } \right||} y_{j} (t)|{\text{d}}t \\ & + \int_{0}^{\omega } {\left| { \vee_{i = 1}^{n} \theta_{ji} (t)\int_{t - \tau }^{t} {k_{i} (t - s)g_{i} (x_{i} (s)){\text{d}}s} } \right||} y_{j} (t)|{\text{d}}t \\ & + \int_{0}^{\omega } {\left| {\sum\limits_{i = 1}^{n} {d_{ji} (t)\mu_{i} (t) + J_{j} (t)} } \right||} y_{j} (t)|{\text{d}}t \\ & + \int_{0}^{\omega } {\left| { \wedge_{i = 1}^{n} M_{ji} (t)\mu_{i} (t) + \vee_{i = 1}^{n} N_{ji} (t)\mu_{i} (t)} \right||} y_{j} (t)|{\text{d}}t \\ & \le \int_{0}^{\omega } {\sum\limits_{i = 1}^{n} {|c_{ji} (t)||g_{i} (x_{i} (t))||y_{j} (t)|{\text{d}}t} } \\ & + \int_{0}^{\omega } {\sum\limits_{i = 1}^{n} {|\gamma_{ji} (t)|} |g_{i} (x_{i} (t))|} y_{j} (t)|{\text{d}}t \\ & + \int_{0}^{\omega } {\sum\limits_{i = 1}^{n} {|\theta_{ji} (t)|} |g_{i} (x_{i} (t))||} y_{j} (t)|{\text{d}}t \\ & + \int_{0}^{\omega } {\left( {\sum\limits_{i = 1}^{n} {|d_{ji} (t)||\mu_{i} (t)| + |J_{j} (t)|} } \right)|} y_{j} (t)|{\text{d}}t \\ & + \int_{0}^{\omega } {\left( { \wedge_{i = 1}^{n} |M_{ji} (t)||\mu_{i} (t)| + \vee_{i = 1}^{n} |N_{ji} (t)||\mu_{i} (t)|} \right)|} y_{j} (t)|{\text{d}}t \\ & \le \left[ {\sum\limits_{i = 1}^{n} {\left( {c_{ji}^{ + } + \gamma_{ji}^{ + } + \theta_{ji}^{ + } } \right)G_{i} + \sum\limits_{i = 1}^{n} {d_{ji}^{ + } \mu_{i} + \left( {M_{ji}^{ + } + N_{ji}^{ + } } \right)\mu_{i}^{ + } + J_{j}^{ + } } } } \right]\sqrt \omega \left( {\int_{0}^{\omega } {|y_{j} (t)|^{2} } } \right)^{ - } . \\ \end{aligned}$$
(2.19)

Then we get

$$||y_{j} ||_{2} \le \frac{1}{{b_{j}^{ - } }}\left[ {\sum\limits_{i = 1}^{n} {\left( {c_{ji}^{ + } + \gamma_{ji}^{ + } + \theta_{ji}^{ + } } \right)G_{i} + \sum\limits_{i = 1}^{n} {d_{ji}^{ + } \mu_{i} + \left( {M_{ji}^{ + } + N_{ji}^{ + } } \right)\mu_{i}^{ + } + J_{j}^{ + } } } } \right]\sqrt \omega: = S_{j} .$$
(2.20)

Thus, it follows from (2.17) and (2.20) that

$$\begin{aligned} \int_{0}^{\omega } {|\dot{y}_{j} (t)|{\text{d}}t} & \le b_{j}^{ + } S_{j} \sqrt \omega + \sum\limits_{i = 1}^{n} {\sqrt \omega \left( {c_{ji}^{ + } + \gamma_{ji}^{ + } + \theta_{ji}^{ + } } \right)G_{i} } \\ & + \sum\limits_{i = 1}^{n} {d_{ji}^{ + } \mu_{i} \omega + J_{j}^{ + } \omega + \left( {M_{ji}^{ + } + N_{ji}^{ + } } \right)\mu_{i}^{ + } } \omega . \\ \end{aligned}$$
(2.21)

In view of (2.16) and (2.21), there exist positive constants \(\chi_{i} (i = 1,2, \ldots ,n)\) such that \(|x_{i} (t)| \le \chi_{i} ,\quad i = 1,2, \ldots ,n,\) for \(t \in [0,\omega ]\) and \(|yj(t)| \le \chi_{n + j} ,\quad j = 1,2, \ldots ,m,\) for \(t \in [0,\omega ].\) Obviously, \(\chi_{i} (i = 1,2, \ldots ,n + m)\) are independent of the choice of \(\lambda \in (0,1).\) Take

$$\Lambda = \sum\limits_{i = 1}^{n + m} {\chi_{i} } + \chi_{0} ,$$

where \(\chi_{0}\) is taken sufficiently large such that

$$\begin{aligned} \mathop {\hbox{min} }\limits_{1 \le i \le n} \bar{a}_{i} \Lambda & > \mathop {\hbox{max} }\limits_{1 \le i \le n} \left[ {\sum\limits_{j = 1}^{m} {|\bar{a}_{ij} |F_{j} + \sum\limits_{j = 1}^{m} {|\overline{{b_{ij} \mu_{j} }} | + \left| {\bar{I}_{i} } \right|} } } \right. \\ & \left. {\quad \sum\limits_{i = 1}^{n} {T_{ij}^{ + } } \mu_{j}^{ + } + \sum\limits_{i = 1}^{n} {H_{ij}^{ + } } \mu_{j}^{ + } + \sum\limits_{j = 1}^{m} {\left( {\left| {\bar{\alpha }_{ij} } \right| + \left| {\bar{\beta }_{ij} } \right|} \right)} F_{j} } \right], \\ \end{aligned}$$
$$\begin{aligned} \mathop {\hbox{min} }\limits_{1 \le j \le m} \bar{b}_{j} \Lambda & > \mathop {\hbox{max} }\limits_{1 \le j \le m} \left[ {\sum\limits_{i = 1}^{n} {|\bar{c}_{ji} |G_{i} + } \sum\limits_{i = 1}^{n} {|\overline{{d_{ji} \mu_{i} }} | + } |\bar{J}_{j} |} \right. \\ & \left. {\quad + \sum\limits_{i = 1}^{n} {M_{ji}^{ + } } \mu_{i}^{ + } + \sum\limits_{i = 1}^{n} {N_{ji}^{ + } } \mu_{i}^{ + } + \sum\limits_{i = 1}^{n} {\left( {\left| {\bar{\gamma }_{ji} } \right| + \left| {\bar{\theta }_{ji} } \right|} \right)} G_{i} } \right]. \\ \end{aligned}$$

Let

$$\Omega: = \{ z = (x_{1} (t),x_{2} (t), \ldots ,x_{n} (t),y_{1} (t),y_{2} (t), \ldots ,y_{m} (t))^{T} \in R^{n + m} |$$

\(||z|| = ||(x_{1} ,x_{2} , \ldots ,x_{n} ,y_{1} ,y_{2} , \ldots ,y_{m} )||^{T} < \Lambda \}\), then it is easy to see that Ω is an open, bounded set in X and verifies requirement (a) of Lemma 2.1. When \(z \in \partial \Omega \cap {\text{Ker}}L,\) \(z = (x_{1} ,x_{2} , \ldots ,x_{n} ,\quad y_{1} ,y_{2} , \ldots ,y_{m} )^{T}\) is a constant vector in \(R^{n + m}\) with

$$||z|| = |x_{1} | + |x_{2} | + \cdots + |x_{n} | + |y_{1} | + |y_{2} | + \cdots + |y_{m} | = \Lambda .$$

Then

$$QNz = QN(x_{1} ,x_{2} , \ldots ,x_{n} ,y_{1} ,y_{2} , \ldots ,y_{m} )^{T} = \left( {\bar{f}_{1} ,\bar{f}_{2} , \ldots ,\bar{f}_{n} ,\bar{f}_{n + 1} ,\bar{f}_{n + 2} , \ldots ,\bar{f}_{n + m} } \right)^{T} ,$$

where

$$\begin{aligned} \bar{f}_{i} & = - \bar{a}_{i} x_{i} + \sum\limits_{j = 1}^{m} {\bar{a}_{ij} f_{j} (y_{j} ) + \sum\limits_{j = 1}^{m} {\overline{{b_{ij} \mu_{j} }} + \bar{I}_{i} } } \\ & \quad + \mathop \wedge \nolimits_{j = 1}^{m} \bar{\alpha }_{ij} \int_{t - \tau }^{t} {k_{j} (t - s)f_{j} (y_{j} (s)){\text{d}}s + \frac{1}{\omega }\int_{0}^{\omega } { \wedge_{j = 1}^{m} T_{ij} (t)\mu_{j} (t){\text{d}}t} } \\ & \quad + \vee_{j = 1}^{m} \bar{\beta }_{ij} \int_{t - \tau }^{t} {k_{j} (t - s)f_{j} (y_{j} (s)){\text{d}}s + \frac{1}{\omega }\int_{0}^{\omega } { \vee_{j = 1}^{m} H_{ij} (t)\mu_{j} (t){\text{d}}t} ,} \\ \bar{f}_{n + j} & = - \bar{b}_{j} y_{j} + \sum\limits_{i = 1}^{n} {\bar{c}_{ji} g_{i} (x_{i} ) + \sum\limits_{i = 1}^{n} {\overline{{d_{ji} \mu_{i} }} + \bar{J}_{j} } } \\ & \quad + \mathop \wedge \nolimits_{i = 1}^{n} \bar{\gamma }_{ji} \int_{t - \tau }^{t} {k_{i} (t - s)g_{i} (x_{i} (s)){\text{d}}s + \frac{1}{\omega }\int_{0}^{\omega } { \wedge_{i = 1}^{n} M_{ji} (t)\mu_{i} (t){\text{d}}t} } \\ & \quad + \vee_{i = 1}^{n} \bar{\theta }_{ji} \int_{t - \tau }^{t} {k_{i} (t - s)g_{i} (g_{i} (s)){\text{d}}s + \frac{1}{\omega }\int_{0}^{\omega } { \vee_{i = 1}^{n} N_{ji} (t)\mu_{i} (t){\text{d}}t} .} \\ \end{aligned}$$

Thus,

$$\begin{aligned} \left\| {QNz} \right\| & = \sum\limits_{{i =1}}^{n} {\left| {\bar{a}_{i} x_{i} - \sum\limits_{{j = 1}}^{m}{\bar{a}_{{ij}} f_{j} (y_{j} ) - \sum\limits_{{j = 1}}^{m}{\overline{{b_{{ij}} \mu _{j} }} - \bar{I}_{i} } } } \right.}\hfill \\ &\quad - \wedge _{{j = 1}}^{m} \bar{\alpha }_{{ij}}\int_{{t - \tau }}^{t} {k_{j} (t - s)f_{j} (y_{j} (s)){\text{d}}s -\frac{1}{\omega }\int_{0}^{\omega } { \wedge _{{j = 1}}^{m} T_{{ij}}(t)\mu _{j} (t){\text{d}}t} } \hfill \\ & \left. {\quad - \vee_{{j = 1}}^{m} \bar{\beta }_{{ij}} \int_{{t - \tau }}^{t} {k_{j} (t- s)f_{j} (y_{j} (s)){\text{d}}s - \frac{1}{\omega }\int_{0}^{\omega} { \vee _{{j = 1}}^{m} H_{{ij}} (t)\mu _{j} (t){\text{d}}t} } }\right| \hfill \\ & \quad + \left| {\bar{b}_{j} y_{j} -\sum\limits_{{i = 1}}^{n} {\bar{c}_{{ji}} g_{i} (x_{i} ) -\sum\limits_{{i = 1}}^{n} {\overline{{d_{{ji}} \mu _{i} }} -\bar{J}_{j} } } } \right. \hfill \\ &\quad - \wedge _{{i = 1}}^{n} \bar{\gamma }_{{ji}} \int_{{t - \tau}}^{t} {k_{i} (t - s)g_{i} (x_{i} (s)){\text{d}}s - \frac{1}{\omega}\int_{0}^{\omega } { \wedge _{{i = 1}}^{n} M_{{ji}} (t)\mu _{i}(t){\text{d}}t} } \hfill \\ &\quad \left. { - \vee _{{i = 1}}^{n}\bar{\theta }_{{ji}} \int_{{t - \tau }}^{t} {k_{i} (t - s)g_{i}(g_{i} (s)){\text{d}}s - \frac{1}{\omega }\int_{0}^{\omega } { \vee_{{i = 1}}^{n} N_{{ji}} (t)\mu _{i} (t){\text{d}}t} } } \right|\hfill \\ &\quad \ge \sum\limits_{{i = 1}}^{n} {\bar{a}_{i} |x_{i}|} - \sum\limits_{{i = 1}}^{n} {\left[ {\sum\limits_{{j = 1}}^{m}{|\bar{a}_{{ij}} |F_{j} } + \sum\limits_{{j = 1}}^{m}{\overline{{|b_{{ij}} \mu _{j} |}} + \bar{I}_{i} + \sum\limits_{{i= 1}}^{n} {T_{{ij}}^{ + } \mu _{j}^{ + } + \sum\limits_{{i =1}}^{n} {H_{{ij}}^{ + } \mu _{j}^{ + } } } } } \right]} \hfill \\ &\quad - \sum\limits_{{i = 1}}^{n} {\left| { \wedge _{{j = 1}}^{m}\bar{\alpha }_{{ij}} \int_{{t - \tau }}^{t} {k_{j} (t - s)f_{j}(y_{j} (s)){\text{d}}s} - \wedge _{{j = 1}}^{m} \bar{\alpha}_{{ij}} \int_{{t - \tau }}^{t} {k_{j} (t - s)f_{j} (0){\text{d}}s}} \right|} \hfill \\ &\quad - \sum\limits_{{i = 1}}^{n} {\left| {\vee _{{j = 1}}^{m} \bar{\beta }_{{ij}} \int_{{t - \tau }}^{t}{k_{j} (t - s)f_{j} (y_{j} (s)){\text{d}}s} - \vee _{{j = 1}}^{m}\bar{\beta }_{{ij}} \int_{{t - \tau }}^{t} {k_{j} (t - s)f_{j}(0){\text{d}}s} } \right|} \hfill \\ &\quad + \sum\limits_{{i =1}}^{n} {\bar{b}_{{ij}} } |y_{{j|}} | - \sum\limits_{{j = 1}}^{m}{\left[ {\sum\limits_{{i = 1}}^{n} {|\bar{c}_{{ji}} |G_{i} +\sum\limits_{{i = 1}}^{n} {|\overline{{d_{{ji}} \mu }} _{i} | +|\bar{J}_{j} | + \sum\limits_{{i = 1}}^{n} {\bar{M}_{{ji}}^{ + } \mu_{i}^{ + } + \sum\limits_{{i = 1}}^{n} {\bar{N}_{{ji}}^{ + } \mu_{i}^{ + } + } } } } } \right]} \hfill \\ &\quad -\sum\limits_{{j = 1}}^{m} {\left| { \wedge _{{i = 1}}^{n}\bar{\gamma }_{{ji}} \int_{{t - \tau }}^{t} {k_{i} (t - s)g_{i}(x_{i} (s)){\text{d}}s} - \wedge _{{i = 1}}^{n} \bar{\gamma }_{{ji}}\int_{{t - \tau }}^{t} {k_{i} (t - s)g_{i} (0){\text{d}}s} }\right|} \hfill \\ &\quad - \sum\limits_{{j = 1}}^{m} {\left| {\vee _{{i = 1}}^{n} \bar{\theta }_{{ji}} \int_{{t - \tau }}^{t}{k_{i} (t - s)g_{i} (x_{i} (s)){\text{d}}s} - \vee _{{i = 1}}^{n}\bar{\theta }_{{ji}} \int_{{t - \tau }}^{t} {k_{i} (t - s)g_{i}(0){\text{d}}s} } \right|} \hfill \\ &\quad \ge \sum\limits_{{i =1}}^{n} {\bar{a}_{i} |x_{i} |} - \sum\limits_{{i = 1}}^{n} {\left[{\sum\limits_{{j = 1}}^{m} {|\bar{a}_{{ij}} |F_{j} } +\sum\limits_{{j = 1}}^{m} {\overline{{|b_{{ij}} \mu _{j} |}} +\left| {\bar{I}_{i} } \right|} } \right.} \hfill \\ &\quad +\left. {\sum\limits_{{i = 1}}^{n} {T_{{ij}}^{ + } \mu _{j}^{ + } +\sum\limits_{{i = 1}}^{n} {H_{{ij}}^{ + } \mu _{j}^{ + } } } +\sum\limits_{{j = 1}}^{m} {(|\bar{\alpha }_{{ij}} | + }|\bar{\beta}_{{ij}} |)F_{j} } \right] \hfill \\ &\quad + \sum\limits_{{j =1}}^{m} {\bar{b}_{j} |y_{j} |} - \sum\limits_{{j = 1}}^{m} {\left[{\sum\limits_{{i = 1}}^{n} {|\bar{c}_{{ji}} |G_{i} } +\sum\limits_{{i = 1}}^{n} {\overline{{|d_{{ji}} \mu _{i} |}} +\left| {\bar{J}_{j} } \right|} } \right.} \hfill \\ &\quad +\left. {\sum\limits_{{i = 1}}^{n} {M_{{ji}}^{ + } \mu _{i}^{ + } +\sum\limits_{{i = 1}}^{n} {N_{{ji}}^{ + } \mu _{i}^{ + } } } +\sum\limits_{{i = 1}}^{n} {(|\bar{\gamma }_{{ji}} | + } |\bar{\theta}_{{ji}} |)G_{i} } \right] \hfill \\ &\quad \ge \mathop {\min}\limits_{{1 \le i \le n}} \bar{a}_{i} |x_{i} | - \mathop {\max}\limits_{{1 \le i \le n}} \left[ {\sum\limits_{{j = 1}}^{m}{|\bar{a}_{{ij}} |F_{j} } + \sum\limits_{{j = 1}}^{m}{\overline{{|b_{{ij}} \mu _{j} |}} + \left| {\bar{I}_{i} } \right|}} \right. \hfill \\ & \quad \left. { + \sum\limits_{{i = 1}}^{n}{T_{{ij}}^{ + } \mu _{j}^{ + } + \sum\limits_{{i = 1}}^{n}{H_{{ij}}^{ + } \mu _{j}^{ + } } } + \sum\limits_{{j = 1}}^{m}{(|\bar{\alpha }_{{ij}} | + } |\bar{\beta }_{{ij}} |)F_{j} } \right]\hfill \\ & \quad + \mathop {\min }\limits_{{1 \le i \le n}}\bar{b}_{j} |y_{j} | - \mathop {\max }\limits_{{1 \le i \le n}}\left[ {\sum\limits_{{i = 1}}^{n} {|\bar{c}_{{ji}} |G_{i} } +\sum\limits_{{i = 1}}^{n} {\overline{{|d_{{ji}} \mu _{i} |}} +\left| {\bar{J}_{j} } \right|} } \right. \hfill \\ &\quad \left. { +\sum\limits_{{i = 1}}^{n} {M_{{ji}}^{ + } \mu _{i}^{ + } +\sum\limits_{{i = 1}}^{n} {N_{{ji}}^{ + } \mu _{i}^{ + } } } +\sum\limits_{{i = 1}}^{n} {(|\bar{\gamma }_{{ji}} | + |\bar{\theta}_{{ji}} |} )G_{i} } \right] > 0. \hfill \\ \end{aligned}$$

Therefore, \(QNz = QN(x_{1} ,x_{2} , \ldots ,x_{n} ,y_{1} ,y_{2} , \ldots ,y_{m} )^{T} \ne (0, \ldots ,0,0, \ldots ,0)^{T}\) for \((x_{1} ,x_{2} , \ldots ,x_{n} ,y_{1} ,y_{2} , \ldots ,y_{m} )^{T} \in \partial \Omega \cap {\text{Ker}}L\). So the condition (b) of Theorem 2.1 holds true.

Now let us consider homotopic \(\phi (x_{1} ,x_{2} , \ldots ,x_{n} ,y_{1} ,y_{2} , \ldots ,y_{m} ,\mu ) = \mu QNz + (1 - \mu )Gz,\mu \in [0,1],\) where \(Gz = ( - \bar{a}_{1} x_{1} , \ldots , - \bar{a}_{n} x_{n} , - \bar{b}_{1} y_{1} , \ldots , - \bar{b}_{m} y_{m} )^{T}\). Letting J = I be the identity mapping and by direct calculation, we get

$$\begin{aligned} & {\rm deg}\{ JQN(x_{1} ,x_{2} , \ldots ,x_{n} ,y_{1} ,y_{2} , \ldots ,y_{m} )^{T} ;\Omega \cap {\text{Ker}}L;0\} \\ & \quad = {\rm deg}\{ QN(x_{1} ,x_{2} , \ldots ,x_{n} ,y_{1} ,y_{2} , \ldots ,y_{m} )^{T} ;\Omega \cap {\text{Ker}}L;0\} \\ & \quad = {\rm deg}\{ \phi (x_{1} ,x_{2} , \ldots ,x_{n} ,y_{1} ,y_{2} , \ldots ,y_{m} ,1)^{T} ;\Omega \cap {\text{Ker}}L;0\} \\ & \quad = {\rm deg}\{ \phi (x_{1} ,x_{2} , \ldots ,x_{n} ,y_{1} ,y_{2} , \ldots ,y_{m} ,0)^{T} ;\Omega \cap {\text{Ker}}L;0\} \\ & \quad = {\text{sign}}\left\{ {{ \det }\left[ {\begin{array}{*{20}l} { - {\bar{\text{a}}}_{ 1} } & 0& 0& 0& 0& 0\\ 0 & \cdots & 0 & 0 & 0 & 0\\ 0 & 0 & { - {\bar{\text{a}}}_{n} } & 0 & 0 & 0\\ 0 & 0 & 0 & { - {\bar{\text{b}}}_{ 1} } & 0& 0\\ 0 & 0 & 0 & 0 & \cdots & 0 \\ 0 & 0 & 0 & 0 & 0 & { - {\bar{\text{b}}}_{m} } \\ \end{array} } \right] \, } \right\}. \\ \end{aligned}$$

Then

$$\begin{aligned} & {\rm deg}\{ JQN(x_{1} ,x_{2} , \ldots ,x_{n} ,y_{1} ,y_{2} , & ,y_{m} )^{T} ;\quad \Omega \cap {\text{Ker}}L;0\} \\ & \quad = {\text{sign\{ (}} - 1 )^{{n{ + }m}} \bar{a}_{1} \bar{a}_{2} \cdots \bar{a}_{n} \bar{b}_{1} \bar{b}_{2} \cdots \bar{b}_{n} \} \ne 0. \\ \end{aligned}$$

By now, we have proved that Ω verifies all requirements of Lemma 2.1, then it follows that \(Lz = Nz\) has at least one solution in \({\text{Dom}}L \cap \bar{\Omega }\), namely, system (1.1) has at least one ω-periodic solution. The proof is complete.

3 Global Exponential Stability of Periodic Solution

In this section, we shall present sufficient conditions for the global exponential stability of system (1.1).

Theorem 3.1

Suppose that (H1)–(H3) and the following assumption holds true:

(H3)

The following inequalities are satisfied:

$$a_{i}^{ - } - \left( {c_{ji}^{ + } + \gamma_{ji}^{ + } + \theta_{ji}^{ + } } \right)G_{i} > 0,\quad b_{j}^{ - } - \left( {a_{ij}^{ + } + \alpha_{ij}^{ + } + \beta_{ij}^{ + } } \right)F_{j} > 0.$$

then the periodic solution of system (1.1) is globally exponentially stable.

Proof

In view of Theorem 2.1, system (1.1) has an ω-periodic solution \(z^{*} (t) = \left( {x_{1}^{*} (t),x_{2}^{*} (t), \ldots ,x_{n}^{*} (t),y_{1}^{*} (t),y_{2}^{*} (t), \ldots ,y_{m}^{*} (t)} \right)^{T} .\)

Let \(z(t) = (x_{1} (t),x_{2} (t), \ldots ,x_{n} (t),y_{1} (t),y_{2} (t), \ldots ,y_{m} (t))^{T}\) be an arbitrary solution of system (1.1). Then it follows from (1.1) that

$$\begin{aligned} \frac{{{\rm d}(x_{i} (t) - \left( {x_{i}^{*} (t)} \right)}}{{{\text{d}}t}} & = - a_{i} (t)(x_{i} (t) - x_{i}^{*} (t)) + \sum\limits_{j = 1}^{m} {a_{ij} (t)\left(f_{j} (y_{j} (t)) - f_{j} \left( {y_{{_{j} }}^{*} (t)} \right)\right)} \\ & \quad + \mathop \wedge \nolimits_{j = 1}^{m} \alpha_{ij} (t)\int_{t - \tau }^{t} {k_{j} (t - s)f_{j} (y_{j} (s)){\text{d}}s - } \mathop \wedge \nolimits_{j = 1}^{m} \alpha_{ij} (t)\int_{t - \tau }^{t} {k_{j} (t - s)f_{j} \left( {y_{j}^{*} (s)} \right){\text{d}}s} \\ & \quad + \vee_{j = 1}^{m} \beta_{ij} (t)\int_{t - \tau }^{t} {k_{j} (t - s)f_{j} (y_{j} (s)){\text{d}}s - \vee_{j = 1}^{m} \beta_{ij} (t)\int_{t - \tau }^{t} {k_{j} (t - s)f_{j} \left( {y_{j}^{*} (s)} \right){\text{d}}s} } \\ \frac{{{\rm d}(y_{j} (t) - y_{j}^{*} (t))}}{{{\text{d}}t}} & = - b_{j} (t)(y_{j} (t) - y_{j}^{*} (t)) + \sum\limits_{i = 1}^{n} {c_{ji} (t)\left(g_{i} (x_{i} (t)) - g_{i} \left( {x_{i}^{*} (t)} \right)\right)} \\ & \quad + \mathop \wedge \nolimits_{i = 1}^{n} \gamma_{ji} (t)\int_{t - \tau }^{t} {k_{i} (t - s)g_{i} (x_{i} (s)){\text{d}}s - } \mathop \wedge \nolimits_{i = 1}^{n} \gamma_{ji} (t)\int_{t - \tau }^{t} {k_{i} (t - s)g_{i} \left( {x_{i}^{*} (s)} \right){\text{d}}s} \\ & \quad + \vee_{i = 1}^{n} \theta_{ji} (t)\int_{t - \tau }^{t} {k_{i} (t - s)g_{i} (x_{i} (s)){\text{d}}s - } \vee_{i = 1}^{n} \theta_{ji} (t)\int_{t - \tau }^{t} {k_{i} (t - s)g_{i} \left( {x_{i}^{*} (s)} \right){\text{d}}s} . \\ \end{aligned}$$

According to the assumptions (H2), (H3) and Lemma 2.3, we have

$$\begin{aligned} \frac{{{\rm d}\left| {x_{i} (t) - x_{i}^{*} (t)} \right|}}{{{\text{d}}t}} & = - a_{i} (t)\left| {x_{i} (t) - x_{i}^{*} (t)} \right| + \sum\limits_{j = 1}^{m} {|a_{ij} (t)|\left| {f_{j} (y_{j} (t)) - f_{j} \left( {y_{{_{j} }}^{*} (t)} \right)} \right|} \\ & \quad + \left| {\mathop \wedge \nolimits_{j = 1}^{m} \alpha_{ij} (t)\int_{t - \tau }^{t} {k_{j} (t - s)f_{j} (y_{j} (s)){\text{d}}s - } \mathop \wedge \nolimits_{j = 1}^{m} \alpha_{ij} (t)\int_{t - \tau }^{t} {k_{j} (t - s)f_{j} \left( {y_{j}^{*} (s)} \right){\text{d}}s} } \right| \\ & \quad + \left| { \vee_{j = 1}^{m} \beta_{ij} (t)\int_{t - \tau }^{t} {k_{j} (t - s)f_{j} (y_{j} (s)){\text{d}}s - \vee_{j = 1}^{m} \beta_{ij} (t)\int_{t - \tau }^{t} {k_{j} (t - s)f_{j} \left( {y_{j}^{*} (s)} \right){\text{d}}s} } } \right|, \\ & \quad \le - a_{i}^{ - } \left| {x_{i} (t) - x_{i}^{*} (t)} \right| + \sum\limits_{j = 1}^{m} {\left( {a_{ij}^{ + } + \alpha_{ij}^{ + } + \beta_{ij}^{ + } } \right)} F_{j} \left| {y_{j} (t) - y_{j}^{*} (t)} \right|, \\ \end{aligned}$$
(3.1)
$$\begin{aligned} \frac{{{\rm d}|y_{j} (t) - y_{j}^{*} (t)|}}{{{\text{d}}t}} & = - b_{j} (t)|y_{j} (t) - y_{j}^{*} (t)| + \sum\limits_{i = 1}^{n} {|c_{ji} (t)|\left| {g_{i} (x_{i} (t)) - g_{i} \left( {x_{i}^{*} (t)} \right)} \right|} \\ & \quad + \mathop {| \wedge }\nolimits_{i = 1}^{n} \gamma_{ji} (t)\int_{t - \tau }^{t} {k_{i} (t - s)g_{i} (x_{i} (s)){\text{d}}s - } \mathop \wedge \nolimits_{i = 1}^{n} \gamma_{ji} (t)\int_{t - \tau }^{t} {k_{i} (t - s)g_{i} (x_{i}^{*} (s)){\text{d}}s} | \\ & \quad + | \vee_{i = 1}^{n} \theta_{ji} (t)\int_{t - \tau }^{t} {k_{i} (t - s)g_{i} (x_{i} (s)){\text{d}}s - } \vee_{i = 1}^{n} \theta_{ji} (t)\int_{t - \tau }^{t} {k_{i} (t - s)g_{i} (x_{i}^{*} (s)){\text{d}}s} | \\ & \quad \le - b_{j}^{ - } |y_{j} (t) - y_{j}^{*} (t)| + \sum\limits_{i = 1}^{n} {\left( {c_{ji}^{ + } + \gamma_{ji}^{ + } + \theta_{ji}^{ + } } \right)} G_{i} \left| {x_{i} (t) - x_{i}^{*} (t)} \right|, \\ \end{aligned}$$
(3.2)

where \(\frac{\text{d}}{{\text{d}}t}\) stands for the upper right derivative. Define a function V by

$$V(t) = \sum\limits_{i = 1}^{n} {\left| {x_{i} (t) - x_{i}^{*} (t)} \right|} + \sum\limits_{j = 1}^{m} {\left| {y_{j} (t) - y_{j}^{*} (t)} \right|} .$$
(3.3)

By virtue of (3.1) and (3.2), we derive

$$\begin{aligned} \frac{{{\text{d}}^{ + } }}{{{\text{d}}t}} & = \sum\limits_{i = 1}^{n} {\frac{{{\text{d}}^{ + } }}{{{\text{d}}t}}\left| {x_{i} (t) - x_{i}^{*} (t)} \right|} + \sum\limits_{j = 1}^{m} {\frac{{{\text{d}}^{ + } }}{{{\text{d}}t}}\left| {y_{j} (t) - y_{j}^{*} (t)} \right|} \\ & \quad \le \sum\limits_{i = 1}^{n} {\left[ { - a_{i}^{ - } \left| {x_{i} (t) - x_{i}^{*} (t)} \right| + \sum\limits_{j = 1}^{m} {(a_{ij}^{ + } + \alpha_{ij}^{ + } + } \beta_{ij}^{ + } )F_{j} \left| {y_{j} (t) - y_{j}^{*} (t)} \right|} \right]} \\ & \quad + \sum\limits_{j = 1}^{m} {\left[ { - b_{j}^{ - } \left| {y_{j} (t) - y_{j}^{*} (t)} \right| + \sum\limits_{i = 1}^{n} {\left( {c_{ji}^{ + } + \gamma_{ji}^{ + } + \theta_{ji}^{ + } } \right)} G_{i} \left| {x_{i} (t) - x_{i}^{*} (t)} \right|} \right]} \\ & = - \sum\limits_{i = 1}^{n} {\left[ {a_{i}^{ - } - \left( {c_{ji}^{ + } + \gamma_{ji}^{ + } + \theta_{ji}^{ + } } \right)G_{i} } \right]} \left| {x_{i} (t) - x_{i}^{*} (t)} \right| \\ & \quad - \sum\limits_{j = 1}^{m} {\left[ {b_{j}^{ - } - \left( {a_{ij}^{ + } + \alpha_{ij}^{ + } + \beta_{ij}^{ + } } \right)F_{j} } \right]} \left| {y_{j} (t) - y_{j}^{*} (t)} \right|. \\ \end{aligned}$$
(3.4)

It follows from condition (H4) that there exists a positive constant ε such that

$$a_{i}^{ - } - \left( {c_{ji}^{ + } + \gamma_{ji}^{ + } + \theta_{ji}^{ + } } \right)G_{i} \ge \varepsilon ,$$

and

$$b_{j}^{ - } - \left( {a_{ij}^{ + } + \alpha_{ij}^{ + } + \beta_{ij}^{ + } } \right)F_{j} \ge \varepsilon$$

Then

$$\frac{{{\text{d}}^{ + } }}{{{\text{d}}t}} \le - \varepsilon V(t),\quad {\text{for}}\quad t \ge 0.$$
(3.5)

Then we have \(V(t) \le e^{ - \varepsilon t} V(0),\) for \(t \ge 0.\) Thus,

$$\sum\limits_{i = 1}^{n} {\left| {x_{i} (t) - x_{i}^{*} (t)} \right|} + \sum\limits_{j = 1}^{m} {\left| {y_{j} (t) - y_{j}^{*} (t)} \right|} \le e^{ - \varepsilon t} \left[ {\sum\limits_{i = 1}^{n} {|x_{i} (0) - x_{i}^{*} (0)} | + \sum\limits_{j = 1}^{m} {\left| {y_{j} (0) - y_{j}^{*} (0)} \right|} } \right].$$

Therefore, the periodic solution of system (1.1) is globally exponentially stable.

Remark 3.1

In [1, 44, 45], Cao established the sufficient conditions for the globally exponential stability of delayed cellular neural networks by constructing a suitable Lyapunov functional. All the coefficients of cellular neural networks are constants and there is no fuzzy logic. In this paper, we consider the existence and globally exponential stability of cellular neural networks with distributed delays with varying coefficients and fuzzy logic by the coincidence degree theory, Lyapunov function. (1.1) is more general than the systems in [1, 44, 45]. Moreover, the results in [1, 44, 45] cannot be applicable to system (1.1) to obtain the existence and exponential stability of periodic solutions. In addition, one also can observe that all the results in [8, 14] and references therein cannot be applicable to system (1.1) to obtain the existence and exponential stability of periodic solutions. This implies that the results of this paper are essentially new.

4 An Illustrate Example

In this section, we present numerical examples to illustrate the effectiveness of the obtained results. Consider the following fuzzy cellular neural network with distributed delays:

$$\left\{ {\begin{array}{*{20}l} {\frac{{{\text{d}}x_{i} (t)}}{{{\text{d}}t}} = - a_{i} (t)x_{i} (t) + \sum\limits_{j = 1}^{2} {a_{ij} (t)f_{j} (y_{j} (t)) + \sum\limits_{j = 1}^{2} {b_{ij} (t)\mu_{j} (t) + I_{i} (t)} } } \\ {\quad \quad \quad + \mathop \wedge \nolimits_{j = 1}^{2} \alpha_{ij} (t)\int_{t - \tau }^{t} {k_{j} (t - s)f_{j} (y_{j} (s)){\text{d}}s + \wedge_{j = 1}^{2} T_{ij} (t)\mu_{j} (t)} } \\ {\quad \quad \quad + \vee_{j = 1}^{2} \beta_{ij} (t)\int_{t - \tau }^{t} {k_{j} (t - s)f_{j} (y_{j} (s)){\text{d}}s + \vee_{j = 1}^{2} H_{ij} (t)\mu_{j} (t),} } \\ {\frac{{{\text{d}}y_{j} (t)}}{{{\text{d}}t}} = - b_{j} (t)y_{j} (t) + \sum\limits_{i = 1}^{2} {c_{ji} (t)g_{i} (x_{i} (t)) + \sum\limits_{i = 1}^{2} {d_{ji} (t)\mu_{i} (t) + J_{j} (t)} } } \\ {\quad \quad \quad + \mathop \wedge \nolimits_{i = 1}^{2} \gamma_{ji} (t)\int_{t - \tau }^{t} {k_{i} (t - s)g_{i} (x_{i} (s)){\text{d}}s + \wedge_{i = 1}^{2} M_{ji} (t)\mu_{i} (t)} } \\ {\quad \quad \quad + \vee_{i = 1}^{2} \theta_{ji} (t)\int_{t - \tau }^{t} {k_{i} (t - s)g_{i} (g_{i} (s)){\text{d}}s + \vee_{i = 1}^{2} N_{ji} (t)\mu_{i} (t),} } \\ \end{array} } \right.$$
(4.1)

where \(i, j = 1,2\), and \(a_{1} (t) = 15 - \sin 2t,\quad a_{2} (t) = 14 - \cos 2t,\quad b_{1} (t) = 14 + \cos 2t,\quad b_{2} (t) = 16 - \cos 2t,\)

$$a_{ij} (t) = 3 + \cos 2t,\quad b_{ij} (t) = 1 - \cos 2t,\quad \mu_{j} (t) = 2 + \cos 2t,\quad \alpha_{ij} (t) = 0.5 + \sin 2t,$$
$$\beta_{ij} (t) = 0.5 + \cos 2t,\quad T_{ij} (t) = 2 + \sin 2t,\quad H_{ij} (t) = 1 + \cos 2t,\quad c_{ij} (t) = 2 + \sin 2t,$$
$$\gamma_{ij} (t) = 1 + \cos 2t,\quad \theta_{ij} (t) = 2 + \sin 2t,\quad M_{ij} (t) = 2 + 2\cos 2t,\quad N_{ij} (t) = 2 + 2\sin 2t,$$
$$I_{i} (t) = 3 + 2\cos 2t,J_{j} (t) = 2 + 3\sin 2t,$$

Let

$$f_{i} (x) = g_{i} (x) = \frac{1}{2}(|x + 1| - |x - 1|)(i = 1,2).$$

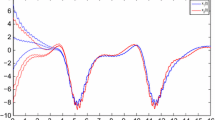
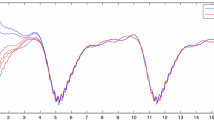
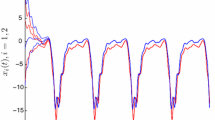
Then we have \(a_{1}^{ - } = 14,\quad a_{2}^{ - } = 3,\quad b_{1}^{ - } = 13,\quad b_{2}^{ - } = 15,\quad c_{ji}^{ + } = 3,\) \(\gamma_{ji}^{ + } = 2,\quad \theta_{ji}^{ + } = 3,\quad a_{ij}^{ + } = 4,\) \(\alpha_{ij}^{ + } = 1.5,\quad \beta_{ij}^{ + } = 1.5.\) It is easy to see that the following conditions \(a_{i}^{ - } - \left( {c_{ji}^{ + } + \gamma_{ji}^{ + } + \theta_{ji}^{ + } } \right)G_{i} > 0,\) \(b_{j}^{ - } - \left( {a_{ij}^{ + } + \alpha_{ij}^{ + } + \beta_{ij}^{ + } } \right)F_{j} > 0,\quad i,j = 1,2\) are satisfied. Thus, all the assumptions in Theorems 2.1 and 3.1 are fulfilled. Thus, we can conclude that system (4.1) has one π-periodic solution, which is globally exponentially stable. The results are illustrated in Fig. 1.

Fig. 1
figure 1

Transient response of state variables \(x_{1} (t),x_{2} (t),y_{1} (t)\) and y 2(t), where the blue line stands for x 1(t) the red line stands for x 2(t), th purple line stands for y 1(t) and the green line stands for y 2(t)

Full size image

5 Conclusions

In this paper, applying the continuation theorem of coincidence degree theory and the Lyapunov function methods, we investigate the existence and global exponential stability of a periodic solution for fuzzy cellular neural networks with distributed delays. Several simple sufficient conditions checking the global exponential stability and the existence of periodic solutions of the fuzzy cellular neural networks with distributed delays have been obtained. A numerical example is presented to illustrate the effectiveness of the derived results.