1 Introduction

Weight reduction is often the principal consideration for selecting fiber reinforced polymers over metals and for many applications, they provide a higher material index than metals and therefore suitable for minimum mass design. Depending on the application, there are other advantages of using fiber reinforced composites, such as higher damping, no corrosion, parts integration, control of thermal expansion and so on. Fiber-reinforced polymers have a great potential for replacing reinforced concrete and steel in bridges, buildings and other civil infrastructures. The principal reason for selecting these composites is their corrosion resistance, which leads to longer life and lower maintenance and repair costs. Another advantage of using fiber reinforced polymers for large bridge structures is their light weight, which means lower dead weight for the bridge, easier transportation from the production factory (where the composite structure can be prefabricated) to the bridge location, easier hauling and installation and less injuries to people in case of an earthquake . With lightweight construction, it is also possible to design bridges with longer span between the supports.

During the last few decades, fiber-reinforced theory has been successfully employed for modeling different processes and systems, specially in the area of engineering, mechanics and physics. Fiber-reinforced composites have many applications in commercial and industrial areas. Fiber-reinforced polymer composites are also used in building construction, furniture, power industry, oil industry, medical industry, aircraft, space, automotive, sporting goods etc. The elastic moduli for fiber-reinforced material were introduced by Hashin and Rosen (1964). Pipkin (1973) and Rogers (1975) did exciting works on the subject. Belfield et al. (1983) investigated the stress in elastic plates reinforced by fibers lying in concentric circles. Sengupta and Nath (2001) discussed the two-dimensional problem of surface waves in an anisotropic, fiber-reinforced solid elastic medium. Singh and Singh (2004) solved a two dimensional problem on reflection of plane waves at free surface of a fiber-reinforced elastic-half space.

Singh (2006) discussed the propagation of plane harmonic waves in a fiber-reinforced anisotropic thermoelastic medium. Othman and Atwa (2012) employed normal mode technique to study the propagation of plane waves in fiber-reinforced anisotropic thermoelastic half-space under the effect of magnetic field. Othman and Said (2012) studied the effect of rotation on two-dimensional problem of a fiber-reinforced thermoelastic medium with one relaxation time. Othman and Said (2015) in another article analyzed the effect of rotation on a fiber-reinforced medium under generalized magneto-thermoelasticity with internal heat source. Micromechanical finite element analysis of effective properties of a unidirectional short piezoelectric fiber reinforced composite is presented by Panda and Panda (2015). Reflection of thermoelastic waves from insulated boundary of a fiber-reinforced half-space under influence of rotation and magnetic field was investigated by Elsagheer and Abo-Dahab (2016).

The conventional theory of thermoelasticity can be used in several particular problems, although this turns out to predict an infinite speed of thermal signals, which is physically unrealistic. Generalized theories proposed by Lord and Shulman (1967) and Green and Lindsay (1972) are two well known theories of thermoelasticity to overcome this deficiency. After that, providing sufficient basic modifications in governing equations, Green and Naghdi (1991, 1992, 1993) produced an alternative theory which was further divided into three different parts, referred to as GN theory of type I, II, III. Under Green–Lindsay theory, Darabseh et al. (2012) studied the transient thermoelastic response of a thick hollow cylinder made of functionally graded material under thermal loading.

The elastic modulus is an important physical property of materials reflecting the elastic deformation capacity of the material when subjected to an applied external load. In most of the investigations, the material properties are assumed to be constant. However, it is well known that the physical properties of engineering materials vary with temperature. At high temperature, the material characteristics such as modulus of elasticity, Poisson’s ratio, coefficient of thermal expansion and the thermal conductivity are no longer constant, Lomakin (1976). Ezzat et al. (2001) solved a problem of generalized thermoelasticity with two relaxation times in an isotropic elastic medium with temperature-dependent mechanical properties. Aouadi (2006) examined the effect of temperature dependency of elastic modulus on the behavior of two-dimensional solutions in micropolar thermoelastic medium. Othman and Kumar (2009) constructed the model of generalized magneto-thermoelasticity in an isotropic perfectly conducting elastic medium under the effect of temperature dependent properties. Kalkal and Deswal (2014) adopted normal mode technique to investigate the effect of phase lags on three-dimensional wave propagation with temperature-dependent properties. Othman and Said (2014) investigated the influence of magnetic field and temperature dependent properties on the plane waves in a fiber-reinforced thermoelastic medium in the context of three-phase-lag theory and Green–Naghdi theory without energy dissipation.

Recent years have seen an ever growing interest in investigation of the problems related to initially stressed elastic medium, due to its numerous applications in various fields, such as earthquake engineering, seismology and geophysics. The earth is assumed to be under high initial stresses. The dynamic problem of an elastic medium under initial stress was solved by Biot (1965). The linear theory of thermoelasticity with hydrostatic initial stress for an isotropic medium was developed by Montanaro (1999). Abbas and Abd-Alla (2011) studied the two-dimensional problem of generalized thermoelasticity for a fiber-reinforced anisotropic thick plate under initial stress. Kumar et al. (2015) showed the effect of the initial stress on wave propagation in fiber-reinforced transversely isotropic thermoelastic medium. Deswal et al. (2016) studied the dynamical interactions of the thermal, elastic and diffusion fields under the fractional order generalized thermoelasticity theory with two-temperature and initial stress. Propagation of waves in an initially stressed generalized electro-microstretch thermoelastic medium with temperature dependent properties under the effect of rotation was investigated by Deswal et al. (2017). Yadav et al. (2017) analyzed the thermoelastic interactions in a homogeneous isotropic electro-microstretch semi-space caused by a mechanical source acting on an initially stressed surface.

In the present manuscript, we have studied the possibility of wave propagation in a fiber-reinforced initially stressed anisotropic thermoelastic medium with temperature dependent properties. The formulae for amplitude ratios and energy ratios corresponding to various reflected waves have been presented when a set of coupled waves strikes obliquely at boundary surface of the assumed model and their variations with angle of incidence are presented graphically. The phase speeds of various existing waves are computed and their variations are depicted graphically against frequency. It has been verified that during reflection phenomena, the sum of energy ratios is equal to unity at each angle of incidence. Some comparisons have been made in figures to estimate the effects of initial stress and temperature dependent properties.

The present information may be useful in some possible experiment based problems on wave propagation in fiber-reinforced initially stressed anisotropic thermoelastic medium with temperature dependent properties under Lord–Shulman and Green–Lindsay models. The efforts of this research are focused on systematically studying the difference of theories and effect of considered parameters in generalized thermoelastic medium. Currently there is no publication available that is related to reflection phenomenon in a fiber-reinforced initially stressed anisotropic thermoelastic medium with temperature dependent properties under Lord–Shulman and Green–Lindsay models. Hence, to address this issue, we have solved a two-dimensional problem in such type of medium.

2 Governing equations

In the context of Lord–Shulman (LS) and Green–Lindsay (GL) theories, the constitutive relations and field equations, after ignoring the body force for a fiber-reinforced thermoelastic anisotropic medium with initial stress are given as:

  1. (i)

    Constitutive relations [Belfield et al. (1983), Xiong and Tian (2016)]:

    $$\begin{aligned} \sigma _{ij}=& -P(\delta _{ij}+\omega _{ij})+\lambda e_{kk}\delta _{ij}+2\mu _Te_{ij}+\alpha (a_ka_me_{km}\delta _{ij}+a_ia_je_{kk})\nonumber \\&+2(\mu _L-\mu _T) (a_ia_k e_{kj}+a_ja_ke_{ki}) +\beta a_k a_m e_{km}a_ia_j-\beta _{ij}(\Theta +\tau _1{\dot{\Theta }})\delta _{ij}, \end{aligned}$$
    (1)

    where P is the initial pressure, \(\sigma _{ij}\) are the components of stress, \(e_{ij}\) are the components of strain, \(\lambda \), \(\mu _T\) are elastic constants, \(\alpha ,\beta ,\) and \((\mu _L-\mu _T)\) are reinforced parameters, \(\delta _{ij}\) is the Kronecker’s delta, \(\tau _1\) is the thermal relaxation time, T is the absolute temperature, \(T_0\) is the reference temperature chosen so that \(|(T-T_0)/{T_0}|\ll 1\), \(\Theta \) is temperature deviation from reference temperature i.e. \(\Theta =T-T_0\) and the components of vector \({\vec{a}}\) are \((a_1, a_2, a_3)\), where \(a^2_1+a^2_2+a^2_3=1\), \(\beta _{11}=(2\lambda +3\alpha +4\mu _{L}-2\mu _{T}+\beta )\alpha _{11}+ (\lambda +\alpha )\alpha _{22},\)\(\beta _{22}=(2\lambda +\alpha )\alpha _{11}+(\lambda +2\mu _T)\alpha _{22},\)\( \alpha _{11}\) and \(\alpha _{22} \) are coefficients of linear thermal expansion. The deformation tensor and \(\omega _{ij}\) can be expressed in terms of the displacement \(u_i\) as

    $$ e_{ij}= \frac{1}{2}(u_{i,j}+u_{j,i}),$$
    (2)
    $$ \omega _{ij}=\frac{1}{2}(u_{j,i}-u_{i,j}). $$
    (3)
  2. (ii)

    Equation of motion

    $$ \sigma_{ji,j}=\rho \ddot{u}_i, $$
    (4)

    where \(\rho \) is the mass density.

  3. (iii)

    The balance law of energy

    $$ q_{i,i}=\rho h-\dot{S} T_0, $$
    (5)

    where S is the entropy per unit volume and h is heat source per unit mass.

  4. (iv)

    The entropy linear equation

    $$ S=\frac{\rho C_E}{T_0}\Theta +\beta _{ij}e_{ij}, $$
    (6)

    where \(C_E\) is the specific heat.

  5. (v)

    Heat conduction law

    $$ q_i+\tau _0\dot{q}_i=-k_{ij}\Theta ,_i, $$
    (7)

    where \(q_i\) are the components of heat flux vector, \(\tau _0\) is the thermal relaxation time and \(k_{ij}\) is the thermal conductivity. Elimination of \(S,\; q_i\) and \(e_{ij}\) from Eqs. (2) and (5)–(7) in the absence of heat source yields the following coupled heat equation for the two models (LS and GL) as

    $$ k_{ij}\Theta ,_{ij}=\rho C_E\left( \frac{\partial }{\partial t}+\tau _0\frac{\partial ^2}{\partial t^2}\right) \Theta +T_0\left( \frac{\partial }{\partial t}+\eta _0\tau _0\frac{\partial ^2}{\partial t^2}\right) \beta _{ij} u_{i,j}, $$
    (8)

    where \(\eta _0\) is a unifying parameter, a comma followed by suffix denotes material derivative and a superposed dot denotes the derivative with respect to time t.

Moreover, the use of the relaxation times \(\tau _1\) in Eq.  (1), \(\tau _0\) and unifying parameter \(\eta _0\) in Eq.  (8) makes these fundamental equations valid for the two different theories of thermoelasticity:

  1. (i)

    Lord and Shulman’s theory (1967)

    $$ \tau _1=0, \tau _0> 0, \quad \eta _0=1.$$
  2. (ii)

    Green and Lindsay’s theory (1972)

    $$ \tau _1> 0, \tau _0> 0, \quad \eta _0=0. $$

Our aim is to examine the effect of the temperature dependent nature of the material. So we assume that [Othman and Said (2014)]

$$ (\lambda _1,\;\; \alpha _1,\;\;\beta _1,\;\;{\beta _1}_{ij},\;\;{\mu _L}_1,\;\;{\mu _T}_1) =\frac{1}{(1-\alpha ^*T_0)}(\lambda ,\;\; \alpha ,\;\; \beta ,\;\; \beta _{ij}, \;\;\mu _L, \;\;\mu _T), $$
(9)

where \(\alpha ^*\) is an empirical material constant.

3 Statement of the problem

We consider the problem of a fiber-reinforced anisotropic initially stressed half space with temperature dependent properties, initially at the uniform temperature \(T_0\). The rectangular cartesian co-ordinates are introduced having origin on the surface \((x=0)\) and x-axis pointing vertically downward into the half space, which is thus designated as \(x\ge 0\). We restrict our analysis to a two dimensional problem in \(xy-\)plane. Thus all the field quantities are independent of the variable z.

The components of displacement vector \(\vec{u}=(u_1, u_2, u_3)\) assume the form

$$ u=u_1=u(x, y, t),\;\;\;v=u_2=u(x,y,t), \;\; \text {and}\;\; w=u_3=0. $$
(10)

We choose the fiber direction as \(\vec{a}=(1,0,0)\), so that the preferred direction is \(x\)-axis. Eqs. (1), (4) and (8) with the help of (2), (3), (9) and (10), take the form

$$\begin{aligned} \sigma _{11}=A_1\frac{\partial u}{\partial x}+A_2\frac{\partial v}{\partial y}-{\alpha _0 \beta _1}_{11}\left( 1+\tau _1\frac{\partial }{\partial t}\right) \Theta -P, \end{aligned}$$
(11)
$$ \sigma _{22}= A_2\frac{\partial u}{\partial x}+A_3\frac{\partial v}{\partial y}-{\alpha _0 \beta _1}_{22}\left( 1+\tau _1\frac{\partial }{\partial t}\right) \Theta -P, $$
(12)
$$ \sigma _{12}= \left( \alpha _0{\mu _L}_1-\frac{P}{2}\right) \frac{\partial v}{\partial x}+\left( \alpha _0{\mu _L}_1+\frac{P}{2}\right) \frac{\partial u}{\partial y}, $$
(13)
$$ \sigma _{21}= \left( \alpha _0{\mu _L}_1-\frac{P}{2}\right) \frac{\partial u}{\partial y}+\left( \alpha _0{\mu _L}_1+\frac{P}{2}\right) \frac{\partial v}{\partial x,}$$
(14)
$$\begin{aligned} \rho \frac{\partial ^2u}{\partial t^2}= & {} A_1\frac{\partial ^2 u}{\partial x^2}+\left( A_2+\alpha _0{\mu _L}_1+\frac{P}{2}\right) \frac{\partial ^2v}{\partial y\partial x}+\left( \alpha _0{\mu _L}_1-\frac{P}{2}\right) \frac{\partial ^2 u}{\partial y^2} \nonumber \\&{ -\alpha _0{\beta _1}_{11}\left( \frac{\partial \Theta }{\partial x}+\tau _1\frac{\partial {\dot{\Theta }}}{\partial x}\right) ,}\end{aligned}$$
(15)
$$\begin{aligned} \rho \frac{\partial ^2v}{\partial t^2}=& A_3\frac{\partial ^2 v}{\partial y^2}+\left( A_2+\alpha _0{\mu _L}_1+\frac{P}{2}\right) \frac{\partial ^2u}{\partial y\partial x}+\left( \alpha _0{\mu _L}_1-\frac{P}{2}\right) \frac{\partial ^2 v}{\partial x^2} \\&{ -\alpha _0{\beta _1}_{22}\left( \frac{\partial \Theta }{\partial y}+\tau _1\frac{\partial {\dot{\Theta }}}{\partial y}\right) ,}\end{aligned}$$
(16)
$$\begin{aligned}&\left( k_{11}\frac{\partial ^2}{\partial x^2}+k_{22}\frac{\partial ^2}{\partial y^2}\right) \Theta -\rho \; C_E \left( \frac{\partial }{\partial t}+\tau _0\frac{\partial ^2}{\partial t^2}\right) \Theta \\&=T_0\left( \frac{\partial }{\partial t}+\tau _0\eta _0\frac{\partial ^2}{\partial t^2}\right) \left( {\beta _1}_{11}\frac{\partial u}{\partial x}+{\beta _1}_{22}\frac{\partial v}{\partial y}\right) \alpha _0, \end{aligned}$$
(17)

where \(A_1=(\lambda _1+2\alpha _1+\beta _1+4{\mu _L}_1-2{\mu _T}_1)\alpha _0\), \(A_2=(\alpha _1+\lambda _1)\alpha _0\), \(A_3=(\lambda _1+2{\mu _T}_1)\alpha _0,\)\(\alpha _0=(1-\alpha ^*T_0)\).

To facilitate the solution, we introduce non-dimensional variables as follows:

$$\begin{aligned} (x',y',u',v')&= {\chi }{c_1}(x,y,u,v), (t',\tau _0',\tau _1')=\chi {c_1^2}(t,\tau _0,\tau _1), \\ \Theta '&={\beta _1}_{11}\frac{\Theta }{\rho c_1^2},\;\;\; P'=\frac{P}{\rho c_1^2},\;\;\;\sigma '_{ij}=\frac{\sigma _{ij}}{\rho c_1^2}, \end{aligned}$$
(18)

where

$$ c_1^2=\frac{A_1}{\rho },\;\;\;\chi =\frac{\rho C_E}{k_{11}}. $$

Now, in terms of the non dimensional quantities defined in (18), Eqs. (15)–(17) along with some simplifications, provide the following relations (dropping the prime notation)

$$\begin{aligned} \frac{\partial ^2u}{\partial t^2}= & {} \frac{\partial ^2 u}{\partial x^2}+B_1\frac{\partial ^2 u}{\partial y^2}+B_2\frac{\partial ^2v}{\partial y\partial x}-\alpha _0\left( \frac{\partial \Theta }{\partial x}+\tau _1\frac{\partial {\dot{\Theta }}}{\partial x}\right) , \end{aligned}$$
(19)
$$\begin{aligned} \frac{\partial ^2v}{\partial t^2}= & {} B_2\frac{\partial ^2u}{\partial y\partial x}+B_1\frac{\partial ^2 v}{\partial x^2}++B_3\frac{\partial ^2 v}{\partial y^2} -\alpha _0 B_4\left( \frac{\partial \Theta }{\partial y}+\tau _1\frac{\partial {\dot{\Theta }}}{\partial y}\right) , \end{aligned}$$
(20)
$$\begin{aligned} \frac{\partial ^2\Theta }{\partial x^2}+B_5\frac{\partial ^2\Theta }{\partial y^2}= & {} \frac{\partial \Theta }{\partial t}+\tau _0\frac{\partial ^2\Theta }{\partial t^2}+B_6\frac{\partial ^2u}{\partial x\partial t}+B_7\frac{\partial ^2 v}{\partial t\partial y} +B_8\frac{\partial ^3 u}{\partial t^2\partial x}+B_9\frac{\partial ^3 v}{\partial t^2\partial y}, \end{aligned}$$
(21)

where

$$\begin{aligned} B_1&= \frac{2\alpha _0{\mu _L}_1-P\rho c^2_1}{2A_1},\;\;\;B_2=\frac{2\alpha _0{\mu _L}_1+2A_2+P\rho c^2_1}{2A_1},\;\;\;B_3=\frac{A_3}{A_1},\;\;\;B_4=\frac{{\beta _1}_{22}}{{\beta _1}_{11}},\\ B_{5}&= \frac{k_{22}}{k_{11}},\;\;\;B_{6}=\frac{T_0{\beta _1}_{11}^2\alpha _0}{A_1\rho C_E},\;\;\;B_{7}=B_6B_4,\;\;\;B_{8}=\frac{\eta _0T_0\alpha _0\tau _0{\beta _1}_{11}^2}{A_1\rho C_E},\;\;\;B_9=B_8B_4. \end{aligned}$$

4 Solution of the problem

Various types of waves generated in a homogeneous and anisotropic half space will be discussed in this section. To solve the Eqs. (19)–(21) analytically in the form of the harmonic travelling waves, we call the solution of the form:

$$(u, v,\theta )=(u^*, v^*,\theta ^*)\,\text {exp}{\{\iota k(-x\; \text {cos}\theta +y\; \text {sin}\theta )-\iota \omega t\}},$$
(22)

where k is the wave number, \(\omega \) is the angular frequency having the definition \(\omega =kV\), V being the phase velocity and the pair \( (\text {cos}\theta , \text {sin}\theta )\) denotes the projection of wave normal onto the xy-plane.

Making use of expression (22), Eqs. (19)–(21) take the form

$$ \left( k^2 D_1+\omega ^2\right) u^*+k^2 D_2 v^*+k D_3 \Theta ^*=0, $$
(23)
$$ k^2D_2u^*+\left( k^2D_4+\omega ^2\right) v^*+kD_5\Theta ^*= 0, $$
(24)
$$kD_6u^*+kD_7v^*+\left( k^2D_8+D_9\right) \Theta ^*=0,$$
(25)

where

$$\begin{aligned} D_1&= -\text {cos}^2\theta -B_1 \text {sin}^2\theta ,\;\; D_2=\text {cos}\theta \text {sin}\theta B_2,\;\;D_3=\iota \alpha _0\cos \theta +\tau _1\omega \cos \theta \alpha _0,\\ D_4&= -B_1\cos ^2\theta -B_3 \sin ^2\theta ,\;\;\; D_5=-\iota \alpha _0 B_4 \sin \theta -\alpha _0 B_4\tau _1\omega \sin \theta ,\\ D_6&= B_6\omega \cos \theta -\iota \cos \theta \omega ^2B_8,\;\;\;D_7=\iota B_9\omega ^2 \sin \theta -B_7\omega \sin \theta ,\\ D_8&= -\cos ^2\theta -B_5 \sin ^2\theta ,\;\;\;D_9=\iota \omega +\tau _0\omega ^2. \end{aligned}$$

The condition for the existence of non trivial solution of the homogeneous system of Eqs. (23)–(25) provides us the characteristic equation satisfied by V as

$$ V^6+A V^4+BV^2+C=0, $$
(26)

where

$$\begin{aligned} A&= \frac{\omega ^2(E_1E_9+E_2E_8-E_4E_6)}{E_2E_9},\;\;\;B=\frac{\omega ^4(E_1E_8+E_2E_7-E_4E_5-E_3E_6)}{E_2E_9},\\ C&=\frac{\omega ^6(E_1E_7-E_3E_5)}{E_2E_9},\;\;\;E_1=D_1D_5-D_2D_3,\;\;\;E_2=\omega ^2D_5,\;\;\;E_3=D_2D_5-D_3D_4,\\ E_4&= -\omega ^2D_3,\;\;\;E_5=-D_2D_8,\;\;\;E_6=D_5D_6-D_2D_9,\;\;\;E_7=-D_4D_8,\\ E_8&= D_5D_7-D_4D_9-\omega ^2D_8,\;\;\;E_9=-\omega ^2D_9. \end{aligned}$$

The roots of equation (26) give three values of \(V^2\) which correspond to three coupled waves, namely, quasi-longitudinal \((qP_1)\), quasi-transverse \((qP_2)\) and quasi-thermal \((qP_3)\) propagating with velocities \(V_1, V_2\) and \(V_3\) respectively.

5 Reflection phenomena

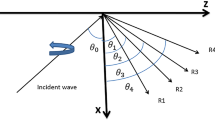
Here, we shall investigate the reflection phenomena of a coupled plane \(qP_1\) wave striking at the plane boundary of considered half-space, propagating with velocity \(V_1\) and making an angle \(\theta _0\) with the normal to the surface. In order to satisfy the boundary conditions, we postulate that incident \(qP_1\) wave generates three reflected coupled plane waves \( qP_{1,2,3}\) of amplitudes \(R_{1,2,3}\) propagating with phase speeds \(V_{1,2,3}\) and making angles \(\theta _{1,2,3}\) respectively with the normal as shown in Fig. 1. The full structure of the wave field consisting of the incident and reflected waves can be defined as

Fig. 1
figure 1

Geometry of the problem showing various reflected waves

Full size image
$$ (u,v,\theta )=(1,a_1,b_1)R_0P^-_0+\sum _{i=1}^3(1,a_i,b_i)R_iP^+_i $$
(27)

where \(P^-_0=\exp \{\iota k_1(y\sin \theta _0-x\cos \theta _0)-\iota \omega _1 t\}\), \(P^+_i=\exp \{\iota k_i(y\sin \theta _i+x\cos \theta _i)-\iota \omega _i t\}\), \(a_i\) and \(b_i(i=1,2,3)\) are the coupling parameters between u and v, u and \(\theta \) respectively. The expressions of the coupling parameters are given as

$$ a_i=\frac{k^2_i(D_1D_5-D_2D_3)+\omega ^2_iD_5}{\omega ^2_iD_3-k^2_i(D_2D_5-D_4D_3)}, b_i=-\frac{k^2_iD_1+\omega ^2+k^2_iD_2a_i}{k_iD_3}. $$

To determine the amplitudes \(R_0, \;\;R_1, \;\;R_2\) and \(R_3\), we postulate some boundary conditions at the surface \(x=0\). The appropriate boundary conditions of the problem can be written in mathematical form as

$$\sigma _{11}+P=0,\;\;\;\sigma _{12}=0\;\text { and}\; \Theta =0 \;\;\; \text {at}\;\; x=0. $$
(28)

In order to satisfy the boundary conditions (28), the wave numbers \(k_1,\;k_2,\;k_3\) and the incident and the reflected angles are connected by the relation \(k_1\sin \theta _0=k_1\sin \theta _1=k_2\sin \theta _2=k_3 \sin \theta _3\), which can also be expressed as (extended Snell’s law)

$$ \frac{\sin \theta _0}{V_1}=\frac{\sin \theta _1}{V_1}=\frac{\sin \theta _2}{V_2}=\frac{\sin \theta _3}{V_3}. $$
(29)

Using expressions (27) in boundary conditions (28) (after making non-dimensional), one can obtain a system of three non homogeneous equations in three unknowns, which can be written as

$$ \sum _{i=1}^3b_{ij}Z_j=Y_i,\;\;\; (i=1,2,3) $$
(30)

where

$$\begin{aligned} b_{1j}&= \{\iota k_j(\cos \theta _j+n_1a_j\sin \theta )-\alpha _0b_j+\iota \alpha _0\tau _1\omega _jb_j\},\\ b_{2j}&= (g_1a_j\cos \theta _j+g_2\sin \theta _j)\iota k_j,\;\;\; b_{3j}=b_j,\\ Z_j&= \frac{R_j}{R_0},\;\;\;\;\;(j=1,2,3) \end{aligned}$$

and

$$\begin{aligned} Y_1&= \{\iota k_1(\cos \theta _0-n_1 a_1\sin \theta _0)+\alpha _0 b_1-\iota \omega _1\tau _1 b_1\},\\ Y_2&= \iota k_1(g_1a_1\cos \theta _0-g_2\sin \theta _0), \;\;\;Y_3=-b_1,\\ n_1&= \frac{A_2}{A_1},\; g_1=\left( \frac{\alpha _0{\mu _L}_1}{A_1}-\frac{P}{2}\right) ,\;g_2=\left( \frac{\alpha _0{\mu _L}_1}{A_1}+\frac{P}{2}\right) . \end{aligned}$$

6 Energy partition

In order to check the physical rightness of this problem, we must certify the energy balance during reflection at the boundary surface. Following [Achenbach (1973)], the instantaneous rate of work of surface traction is the product of the surface traction and the particle velocity. This scalar product is called the power per unit area denoted by \(P^*\) and is given by

$$ P^*=(\sigma _{11}+P)\dot{u}+\sigma _{12} \dot{v}. $$
(31)

Let \(<P^*_0>\) denotes the average energy carried along incident wave, \(<P^*_i>\)\((i=1,2,3)\) denote the average energy carried along reflected coupled waves. The expressions for energy ratios \(E_i\)\((i=1,2,3)\) for reflected waves are given by

$$ E_i= \frac{<P^*_i>}{<P^*_0>}, $$
(32)
$$\begin{aligned} E_1=& P'\left\{\cos \theta _1+a_1\sin \theta _1\;n_1+\frac{(\iota \tau _1\omega _1-1)\alpha _0\;b_1}{\iota k_1} \right. \\& \left.+(g_1a_1\cos \theta _1+g_2\sin \theta _1)a_1\right\}| Z_1|^2, \end{aligned}$$
(33)
$$\begin{aligned} E_2=& P' \left\{\cos \theta _2+a_2\sin \theta _2\;n_1+\frac{(\iota \tau _1\omega _1-1)\alpha _0\;b_2}{\iota k_2} \right. \\ & \left. +(g_1a_2\cos \theta _2+g_2\sin \theta _2)a_2 \right\}\left( \frac{k_2}{k_1}\right) | Z_2|^2, \end{aligned}$$
(34)
$$\begin{aligned} E_3= &P' \left\{\cos \theta _3+a_3\sin \theta _3\;n_1+\frac{(\iota \tau _1\omega _1-1)\alpha _0\;b_3}{\iota k_3} \right.\\& \left.+(g_1a_3\cos \theta _3+g_2\sin \theta _3)a_3 \right\}\left( \frac{k_3}{k_1}\right) | Z_3|^2, \end{aligned}$$
(35)

where

$$\begin{aligned} P'=& \left\{-\cos \theta _0+a_1\sin \theta _0\;n_1+\frac{(\iota \tau _1\omega _1-1)\alpha _0\;b_1}{\iota k_1} \right.\\ &\left.+(g_2\sin \theta _0-g_1a_1\cos \theta _0)a_1\right\}^{-1}. \end{aligned}$$

We note that these energy ratios depend on the elastic properties of the medium, angle of incidence and amplitude ratios.

7 Special cases

7.1 Case I: without temperature dependent property

If we assume that the parameters \(\lambda ,\;\mu _L,\;\mu _T,\;\alpha ,\;\beta \) and \(\beta _{ij}\) are free from temperature dependent effect, i.e. \(\alpha ^*=0\), then we shall be dealing with a half space problem in an initially stressed fiber-reinforced thermoelastic medium. Taking into consideration the above mentioned modifications, Eq. (30) will provide us the reflection coefficients for the corresponding problem. If we further neglect the initial stress from the medium, then the results of the relevant problem coincide with those of Elsagheer and Abo-Dahab (2016) with appropriate changes in the boundary conditions after removing the rotation and magnetic effects.

7.2 Case II: without initial stress

If we neglect the presence of initial stress from the half space, then we shall be left with the problem of wave propagation and its reflection in fiber-reinforced thermoelastic medium with temperature dependent properties. For this purpose, we shall set P = 0. With this consideration, the corresponding reflection coefficients for incidence of a set of coupled waves can be obtained from the Eq. (30). If we further neglect the temperature dependence of parameters then the results of the relevant problem coincide with Singh (2006) with appropriate changes in the theory and boundary conditions.

8 Numerical results and discussions

With an aim to discuss the behavior of wave propagation through a fiber-reinforced, anisotropic initially stressed medium with temperature dependent mechanical properties in greater detail, a numerical analysis is carried out. For the purpose of numerical computation, the material constants of problem are taken [Singh (2006)] and [Othman (2014)] as:

$$\begin{aligned} \rho&= 2660\; \hbox{kg}\;\hbox{m}^{-3},\;\;{\mu _T}_1=1.89\times 10^{10}\; \hbox{N}\;\hbox{m}^{-2},\;\;\;\alpha _1=-1.28\times 10^{10}\; \hbox{N}\;\hbox{m}^{-2},\\ {\mu _L}_1&= 2.45\times 10^{10} \;\hbox{N}\;\hbox{m}^{-2},\;\;\lambda _1=7.59\times 10^{10}\;\hbox{N}\;\hbox{m}^{-2},\;\; \beta _1=0.32\times 10^{10}\;\hbox{N}\;\hbox{m}^{-2}, \\ k_{11}&= 0.0921\times \;10^{3} \;\hbox{J}\;\hbox{m}^{-1}\;\hbox{deg}^{-1}\;\hbox{s}^{-1},\;\;\;k_{22}=0.0963\times \;10^{3} \;\hbox{J}\;\hbox{m}^{-1}\;\hbox{deg}^{-1}\;s^{-1},\\ \alpha _{11}&= 0.017\times \;10^{4}\;\hbox{deg}^{-1},\;\;\;\alpha _{22}=0.015\times \;10^{4}\;\hbox{deg}^{-1},\;\;\;T_0=293\hbox{K},\\ C_E&= 0.787\times 10^{3} \hbox{J}\;\hbox{kg}^{-1}\;\;\hbox{deg}^{-1},\;\;\; \tau _0=0.02s,\;\; \tau _1=0.03 \hbox{s},\;\;\omega =2\;\;\hbox{s}^{-1}. \end{aligned}$$

With these numerical values of parameters, we have evaluated the amplitude ratios and energy ratios corresponding to incident \(qP_1\) wave at different angles of incidence varying from normal incidence to grazing incidence. We have examined the variations of amplitude ratios and energy ratios in the considered medium for three different cases. (i) Medium under initial stress and with temperature dependent properties (MISTD, \(\alpha ^*=0.005,\;\;P=1\), solid line) (ii) Medium under initial stress (MIS, \(P=1,\;\;\alpha ^*=0.0\), long dashed line) (iii) Medium with temperature dependent properties (MTD, \(\alpha ^*=0.005,\;\;P=0.0\), small dashed line). Figures 2, 3, 4 are plotted to observe the effects of temperature dependency of material constants and initial pressure on the profile of reflection coefficients. In Figs. 5, 6, 7, we have examined the variation of amplitude ratios in a fiber-reinforced initially stressed medium with temperature dependent properties under Lord–Shulman (LS, solid line) and Green–Lindsay (GL, long dashed line) models.The dependence of energy ratios of various reflected waves on angle of incidence is displayed in Fig. 8. Figures (9, 10, 11, 12) are plotted with the purpose to show the change in phase speeds with frequency. All the graphs except Figs. (5, 6, 7) are plotted for L–S theory only.

Fig. 2
figure 2

Effect of initial stress on the moduli of reflection coefficient \(Z_1\) for temperature dependent and independent properties

Full size image
Fig. 3
figure 3

Effect of initial stress on the moduli of reflection coefficient \(Z_2\) for temperature dependent and independent properties

Full size image
Fig. 4
figure 4

Effect of initial stress on the moduli of reflection coefficient \(Z_3\) for temperature dependent and independent properties

Full size image
Fig. 5
figure 5

Variations in reflection coefficient \(Z_1\) with angle of incidence

Full size image
Fig. 6
figure 6

Variations in reflection coefficient \(Z_2\) with angle of incidence

Full size image
Fig. 7
figure 7

Variations in reflection coefficient \(Z_3\) with angle of incidence

Full size image

Figure 2 is plotted to display the variations of moduli of amplitude ratio \(Z_1\) versus angle of incidence. From the figure, we observe that values of \(|Z_1|\) remain in the neighborhood of unity for all the cases in the entire range of angle of incidence. It can be noticed from the figure that the presence of initial stress has a slight increasing effect while temperature dependency of material constants has decreasing effect on the profile of amplitude ratio \(|Z_1|\). Figure 3 depicts the variations of absolute values of \(Z_2\) against angle of incidence. It can be noticed from the figure that the curve of \(|Z_2|\) for MISTD case is upper than that for both MIS and MTD cases. This has happened due to the temperature dependency of material constants and the presence of initial stress in the medium. Hence, temperature dependent material constants and initial stress parameter have increasing effect. The variations of reflection coefficient \(|Z_3|\) are illustrated in Fig. 4. The presence of temperature dependent material constants has an increasing impact on the profile of this reflection coefficient, while initial stress parameter has both increasing and decreasing impacts.

Figure 5 is drawn with the purpose to display a comparison of variation of reflection coefficient \(|Z_1|\) versus angle of incidence for LS and GL theories. It is clear from the figure that the values of \(|Z_1|\) for LS theory are found to be larger as compared to GL theory. It is also evident from the plot that the reflection coefficient \(|Z_1|\) has qualitatively similar behavior for LS and GL theories. However, dissimilarity lies on the ground of magnitude. The behavior of variation of reflection coefficient \(|Z_2|\) against angle of incidence has been expressed in Fig. 6 for LS and GL theories. This reflection coefficient experiences a similar pattern of variations in both the theories. We observe from the figure that the values of \(|Z_2|\) for GL theory are found to be large as compared to LS theory. In Fig. 7, we have plotted the curves to exhibit the variations of reflection coefficient \(|Z_3|\) for both the theories. The figure shows that the values of \(|Z_3|\) for LS theory are smaller than the values for GL theory in the entire range except at one point. The reflection coefficients \(|Z_3|\) enjoys a similar pattern of variations in both theories.

Figure 8 is plotted to analyze the variations of modulus of energy ratios of reflected waves with the angle of incidence \(\theta _0\) lying in the registered range of incident coupled wave moving with velocity \(V_1\). The curves of energy ratios \(|E_2|\) and \(|E_3|\) are plotted after mounting up their original values by \(10^{15}\) and \(10^{19}\) respectively. It is noticed from the figure that the values of \(|E_1|\) and sum are almost equal to 1.0 i.e. maximum energy is carried along reflected \(qP_1\) wave. Since the reflection coefficients \(|Z_2|\) and \(|Z_3|\) are found to be very small, therefore the corresponding energy ratios \(|E_2|\) and \(|E_3|\) are also very small in the entire range of angle of incidence except at grazing incidence, where their values are zero. It has been verified that at each angle of incidence \(\sum _{i=1}^3E_i\approx 1\) . Thus we conclude that energy balance law is verified for each angle of incidence.

Figure 9 is drawn to exhibit the variations of modulus of speed \(V_1\) with frequency. It is found from the figure that initial stress parameter has caused a very little impact, while the temperature dependency of material constants has strongly influenced the velocity \(V_1\). The presence of temperature dependency of material constants has a decreasing impact on the profile of \(V_1\), while initial stress parameter has both increasing and decreasing effects. For better presentation, the variations of phase speed \(V_1\) for MISTD, MIS and MTD cases have also been shown separately in Figs. 10a–c respectively. The frequency dependency of \(|V_2|\) is demonstrated graphically in Fig. 11. It can be noticed from the figure that the curve of \(|V_2|\) for MISTD case is lower than that for MTD case. This is due to the effect of initial stress parameter. From the numerical values, it can be observed that the presence of temperature dependency of material constants has both increasing and decreasing impacts on \(|V_2|\). In Fig. 12, a graphical representation is given for the variations of absolute values of velocity \(V_3\) with frequency. We have observed from the figure that the curve of \(|V_3|\) for MISTD case is higher than that for MIS case and lower than MTD case. The little differences between absolute values of phase speed in MISTD and MTD cases show the small effect of initial stress. The values of \(|V_3|\) show continuously increasing behavior with increasing frequency. The presence of temperature dependency of material constants has significantly increased the magnitude of \(|V_3|\).

Fig. 8
figure 8

Variations of modulus of energy ratios for various angles of incidence

Full size image
Fig. 9
figure 9

Variations of moduli of phase speed \(V_1\) with frequency

Full size image
Fig. 10
figure 10

(a, b, c) Variations of moduli of phase speed \(V_1\) with frequency

Full size image
Fig. 11
figure 11

Variations of moduli of phase speed \(V_2\) with frequency

Full size image
Fig. 12
figure 12

Variations of moduli of phase speed \(V_3\) with frequency

Full size image

9 Concluding remarks

In this paper, a mathematical treatment has been presented to discuss the phenomena of elastic wave propagation in a fiber-reinforced thermoelastic medium under initial stress and temperature dependent properties. The expressions giving the reflection coefficients and energy ratios have been presented graphically. From the analysis of the illustrations, we can arrive at the following conclusions:

  • Numerical results show that the reflection coefficients of various reflected waves are significantly affected by initial stress parameter and temperature dependence of material constants.

  • Temperature dependence of material constants has an increasing effect on reflection coefficient \(|Z_2|\) and \(|Z_3|,\) while decreasing effect is observed on reflection coefficient \(|Z_1|\).

  • While studying the numerical results, it is observed that the maximum amount of the incident energy goes along the reflected wave corresponding to the reflection coefficient \(|Z_1|\).

  • The modulus values of reflection coefficients \(|Z_2|\) and \(|Z_3|\)corresponding to an incident coupled wave are found to be small for LS theory as compared to GL theory, whereas, reverse happens for the reflection coefficient \(|Z_1|\).

  • The numerical results reveal that sum of the modulus values of energy ratios is approximately unity at each angle of incidence, thus proving the law of conservation of energy.

  • It is apparent from the Figs. 10, 11, 12 that the numerical values of phase speeds \(V_2\) and \(V_3\) have decreased due to the presence of initial stress, while increasing and decreasing effects are observed on phase speed \(V_1\). Presence of temperature dependent material constants decreases the numerical values of the phase speed \(V_1\), increases the numerical values of phase speed \(V_3\) and has both increasing and decreasing effects on the profile of phase speed \(V_2\).

Wave phenomenon in a thermoelastic medium is of great practical importance in various technological and geophysical circumstances. The propagation of waves along with other geophysical and geothermal data carries information about the structure and distribution of underground magnum. The wave propagation as part of exploration seismology helps in various economic activities like tracing of hydrocarbons and other mineral ores which are essential for various developmental activities like construction of dams, huge buildings, roads, bridges, the design of highways as well as foundation problems in soil mechanics. The introduction of initial stress and temperature dependent material constants to the generalized thermoelastic medium provides a more realistic model for these studies. The present theoretical results may provide interesting information for experimental scientists / researchers/ seismologists working on this subject.