2D problem of magneto-thermoelasticity fiber-reinforced medium under temperature dependent properties with three-phase-lag model

Abstract

The aim of the present work is to investigate the influence of magnetic field on wave propagation within a fiber-reinforced medium under the three-phase-lag theory and Green–Naghdi theory without energy dissipation. The modulus of the elasticity is given as a linear function of the reference temperature. The exact expression for the displacement components, temperature, and stress components are obtained by using normal mode analysis. Numerical results for the field quantities are given in the physical domain and illustrated graphically in the absence and presence of magnetic field. Comparisons are made between the results for the two different theories with and without temperature dependent properties as well as reinforcement. The results are a valuable contribution to the problem of practical design of such structures, for example to design stiffness, damping and so on into the right place of a structure by selecting the appropriate material properties.

1 Introduction

Generalized thermoelasticity theories have been developed with the objective of removing the paradox of infinite speed of thermal signals inherent in the conventional coupled dynamical theory of thermoelasticity in which parabolic type heat conduction equation is considered, contradict physical facts. During the last three decades, generalized theories involving finite speed of heat transportation (hyperbolic heat transport equation) in elastic solids have been developed to remove this paradox. The first generalization is proposed by Lord and Shulman [1] and is known as extended thermoelasticity theory (ETE), which involves one thermal relaxation time parameter (single-phase-lag model). The second generalization to the coupled thermoelasticity theory is developed by Green and Lindsay [2], which involving two relaxation times is known as temperature rate dependent thermoelasticity (TRDTE). Experimental studies indicate that the relaxation times can be of relevance in the cases involving a rapidly propagating crack tip, shock waves propagation, laser technique etc. Because of the experimental evidence in support of finiteness of heat propagation speed, the generalized thermoelasticity theories are considered to be more realistic than the conventional theory in dealing with practical problems involving very large heat fluxes at short intervals like those occurring in laser units and energy channels. The third generalization is known as low-temperature thermoelasticity introduced by Hetnarski and Ignaczak [3] called H–I theory. Most engineering materials such as metals possess a relatively high rate of thermal damping and thus are not suitable for use in experiments concerning second sound propagation. But, given the state of recent advances in material science, it may be possible in the foreseeable future to identify (or even manufacture for laboratory purposes) an idealized material for the purpose of studying the propagation of thermal waves at finite speed. The thermoelasticity without energy dissipation (TEWOED) and thermoelasticity with energy dissipation (TEWED) introduced by Green and Naghdi [4–6] and provides sufficient basic modifications in the constitutive equations that permit treatment of a much wider class of heat flow problems, labeled as types I, II, III. The natures of these three types of constitutive equations are such that when the respective theories are linearized, type-I is the same as the classical heat equation (based on Fourier’s law) whereas the linearized versions of type-II and type-III theories permit propagation of thermal waves at finite speed. The entropy flux vector in type II and III (i.e. TEWOED and TEWED) models are determined in terms of the potential that also determines stresses. When Fourier conductivity is dominant the temperature equation reduces to classical Fourier’s law of heat conduction and when the effect of conductivity is negligible the equation has undamped thermal wave solutions without energy dissipation. Applying the above theories of generalized thermoelasticity, several problems have been solved by Othman et al. [7, 8], Othman and Atwa [9–11], Roychoudhury and Bandyopadhyay [12], Chandrasekharaiah [13] etc. The fifth generalization to the thermoelasticity theory is known as the dual-phase-lag thermoelasticity developed by Tzou [14] and Chandrasekhariah [15]. Tzou considered micro-structural effects into the delayed response in time in the macroscopic formulation by taking into account that increase of the lattice temperature is delayed due to photon-electron interactions on the macroscopic level. Tzou [14] introduced two-phase-lag to both the heat flux vector and the temperature gradient. According to this model, classical Fourier’s law $\varvec{q} = - K{\mathbf{\nabla }}T$ has been replaced by $\varvec{q}\text{(P,t } + \tau_{\text{q}} \text ) = - K{\mathbf{\nabla }}{\rm T}\text{(P,t } + \tau_{\text{T}} \text{)}$, where the temperature gradient ${\mathbf{\nabla }}{\rm T}$ at a point P of the material at time $\text{t} + \tau_{\text{T}}$ corresponds to the heat flux vector $\varvec{q}$ at the same point at time $\text{t } + \tau_{\text{q}}$. Here K is the thermal conductivity of the material. The delay time $\tau_{\text{T}}$ is interpreted as that caused by the micro-structural interactions and is called the phase-lag of the temperature gradient. The other delay time $\tau_{\text{q}}$ is interpreted as the relaxation time due to the fast transient effects of thermal inertia and is called the phase-lag of the heat flux. For $\tau_{\text{q}} = \tau_{\text{T}} = 0,$ the Fourier’s law in two-phase-lag model is identical with classical Fourier’s law. If $\tau_{\text{q}} = \tau$ and $\tau_{\text{T}} = 0,$ Tzou [14] refers to the model as single-phase-lag model. The generalization is known as three-phase-lag thermoelasticity which is due to Roychoudhuri [16]. According to this model $\varvec{q}\left( {\text{P,t } + \tau_{\text{q}} } \right)\text{ } = - \left[ {K{\mathbf{\nabla }}{\rm T}\left( {\text{P,t } + \tau_{\text{T}} } \right)\text{ } + K^{*} {\mathbf{\nabla }}\nu \left( {\text{P,t } + \tau_{\nu } } \right)} \right]\text{,}$ where ${\mathbf{\nabla }}\nu \;(\dot{\nu } = T)$ is the thermal displacement gradient and $K^{*}$ is the additional material constant and $\tau_{\nu }$ is the phase-lag for thermal displacement gradient. To study some practical relevant problems and have found that in heat transfer problems involving very short time intervals and in the problems of very high heat fluxes, the hyperbolic equation gives significantly different results than the parabolic equation. According to this phenomenon the lagging behavior in the heat conduction in solid should not be ignored particularly when the elapsed times during a transient process are very small, say about $10^{ - 7}$ s or the heat flux is very much high. Three-phase-lag model is very useful in the problems of nuclear boiling, exothermic catalytic reactions, phonon-electron interactions, phonon-scattering etc., where the delay time $\tau_{q}$ captures the thermal wave behavior (a small scale response in time), the phase-lag $\tau_{T}$ captures the effect of phonon-electron interactions (a microscopic response in space), the other delay time $\tau_{\nu }$ is effective since, in the three-phase-lag model, the thermal displacement gradient is considered as a constitutive variable whereas in the conventional thermoelasticity theory temperature gradient is considered as a constitutive variable. There are materials which have natural anisotropy such as zinc, magnesium, sapphire, wood, some rocks and crystals, and also there are artificially manufactured materials such as fiber-reinforced composite materials, which exhibit anisotropic character. The advantage of composite materials over the traditional materials lies on their valuable strength, elastic and other properties [17]. A reinforced material may be regarded to some order of approximation, as homogeneous and anisotropic elastic medium having a certain kind of elastic symmetry depending on the symmetry of reinforcement. Some glass fiber reinforced plastics may be regarded as transversely isotropic. Thus problems of solid mechanics should not be restricted to the isotropic medium only. Increasing use of anisotropic media demands that the study of elastic problems should be extended to anisotropic medium also.

Fiber-reinforced composites are widely used in engineering structures, due to their superiority over the structural materials in applications requiring high strength and stiffness in lightweight components. A continuum model is used to explain the mechanical properties of such materials. A reinforced concrete member should be designed for all conditions of stresses that may occur and in accordance with principles of mechanics. The characteristic property of a reinforced concrete member is that its components, namely concrete and steel, act together as a single unit as long as they remain in the elastic condition i.e. the two components are bounded together so that there can be no relative displacement between them. In the case of an elastic solid reinforced by a series of parallel fibers, it is usual to assume transverse isotropy. In the linear case, the associated constitutive relations, relating infinitesimal stress and strain components have five material constants. In the last three decades, the analysis of stress and deformation of fiber-reinforced composite materials has been an important research area of solid mechanics. Belfield et al. [18] has introduced the idea of continuous self-reinforcement at every point of an elastic solid. One can find some work on transversely isotropic elasticity in the literature [19–22].

The normal mode analysis gives exact solutions without any assumed restrictions on temperature, displacement and stress distributions. It is applied to a wide range of problems in different branches (Othman and Singh [23]). It can be applied to boundary-layer problems, which are described by the linearized Navier–Stokes equations in electro hydrodynamics (Othman [24]; Othman and Sweilam [25]). The normal mode analysis is, in fact, to look for the solution in the Fourier transformed domain. Assume that all the field quantities are sufficiently smooth on the real line such that normal mode analysis of these functions exists.

The present paper is to investigate the influence of the magnetic field and the temperature properties dependent on the plane waves in a linearly fiber-reinforced thermoelastic isotropic medium in the context of the three-phase-lag theory. The problem has been solved numerically using the normal mode analysis. Numerical results for the temperature, displacement components and the stresses are represented graphically and the results are analyzed. The graphical results indicate that the effect of the magnetic field, the dependent and independent of temperature and the reinforcement on the plane waves in the fiber-reinforced thermoelastic medium are very pronounced. Comparisons are made with the results in the absence of the magnetic field and the reinforcement. Such problems are very important in many dynamical systems.

2 Formulation of the problem and basic equations

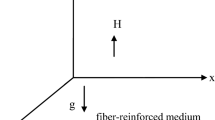
We consider the problem of a thermoelastic half-space $(x \ge 0)$. A magnetic field with a constant intensity $H = (0,0,H_{0} )$, acting parallel to the boundary plane (taken as the direction of the $z$-axis). The surface of a half-space is subjected to a thermal shock which is a function of $y$, and $t.$ Thus, all quantities considered will be functions of the time variable $t$, and the coordinates $x$ and $y$. The field equations and constitutive relations for a fiber-reinforced linearly thermoelastic isotropic medium with respect to the reinforcement direction $\varvec{a}$ in the three-phase-lag theory without body forces, body couples and heat sources are

(i) The stress–strain relation may be written as [18]

$$ \sigma_{ij} = \lambda e_{kk} \delta_{ij} + 2\mu_{T} e_{ij} + \alpha (a_{k} a_{m} e_{km} \delta_{ij} + a_{i} a_{j} e_{kk} ) + 2(\mu_{L} - \mu_{T} )(a_{i} a_{k} e_{kj} + a_{j} a_{k} e_{ki} ) + \beta \,a_{k} a_{m} e_{km} a_{i} a_{j} - \gamma \,\hat{T}\,\delta_{ij\,} , $$

(1)

where $\sigma_{ij}$’s are the components of stress, $e_{ij}$’s are the components of strain, $\lambda$, $\mu_{T}$’s are elastic constants, $\alpha ,\beta ,\left( {\mu_{L} - \mu_{T} } \right)$ and $\gamma$ are reinforcement parameters, $\delta_{ij}$ is the Kronecker delta, $\hat{T} = T - T_{ 0} ,$ where $T$ is the temperature above reference temperature $T_{0} ,$ and $\underline{a} \equiv (a_{1} ,\,a_{2} ,\,\,a_{3} ),$ $a_{1}^{2} + a_{2}^{2} + a_{3}^{2} = 1.$ We choose the fiber-direction as $\underline{a} \equiv (1,0,0).$ The strains can be expressed in terms of the displacement $u_{i}$ as

$$ e_{ij} = \frac{1}{2}(u_{i,\,j} + u_{j,\,i} ). $$

(2)

(ii) The dynamical equations of a fiber-reinforced magneto-thermoelastic medium

$$ \rho \ddot{\varvec{u}}_{i} = \sigma_{ij,j} + F_{i} ,\quad i,j = 1,2,3, \ldots $$

(3)

where $F_{\text{i}}$ is the Lorentz force and is given in the form,

$$ F_{\text{i}} = \mu_{0} \, (\varvec{J}\,{\text{x}}\,\varvec{H}\, )_{\text{i}} $$

(4)

The variation of the magnetic and electric fields are perfectly conducting slowly moving medium and are given by Maxwell’s equation [9]

$$ \varvec{J} = curl\,\varvec{h} - \varepsilon_{ 0} \dot{\varvec{E}}\text{,} $$

(5)

$$ curl\,\varvec{E} = - \mu_{0} {\dot{\mathbf{h}}}, $$

(6)

$$ \varvec{E} = - \mu_{0} (\dot{\varvec{u}} \times \varvec{H} ) , $$

(7)

$$ \nabla .\varvec{h} = 0, $$

(8)

where $\mu_{0}$ is the magnetic permeability, $\varepsilon_{0}$ is the electric permeability, $\varvec{J}$ is the current density vector, ${\dot{\mathbf{u}}}$ is the particle velocity of the medium and the small effect of temperature gradient on $\varvec{J}$ is also ignored. The dynamic displacement vector is actually measured from a steady state deformed position and the deformation is supposed to be small. Due to the application of the initial magnetic field $\varvec{H}$, there are an induced magnetic field $\,\varvec{h} = \, ( 0 ,\, 0 ,\,h )$ and an induced electric field $\varvec{E}$, as well as the simplified equations of electrodynamics of slowly moving medium for a homogeneous, thermal and electrically conducting elastic solid. Expressing the components of the vector $\varvec{J} = \, (J_{ 1} \, ,\,J_{ 2} \, ,\,J_{ 3} )$ in terms of displacement by eliminating the quantities $\varvec{h}$ and $\varvec{E}$ from Eq. (5), thus yields, where

$$ J_{1} = H_{o} \left( { - \frac{\partial e}{\partial y} + \mu_{0} \varepsilon_{0} \ddot{{v}}} \right),\;J_{2} = H_{o} \left( { - \frac{\partial e}{\partial x} + \mu_{0} \varepsilon_{0} \ddot{{u}}} \right),\;J_{3} = 0, $$

(9)

Substituting from Eq. (9) into Eq. (4), we get

$$ F_{ 1} = - \mu_{ 0} H_{ 0} \frac{\partial h}{\partial x} - \varepsilon_{ 0} \mu_{ 0}^{ 2} H_{ 0}^{ 2} \frac{{\partial^{ 2} u}}{{\partial t^{ 2} }},\;F_{2} = - \mu_{ 0} H_{ 0} \frac{\partial h}{\partial y} - \varepsilon_{ 0} \mu_{ 0}^{ 2} H_{ 0}^{ 2} \frac{{\partial^{ 2} v}}{{\partial t^{ 2} }},\;F_{ 3} = 0. $$

(10)

(iii) The generalized heat conduction equation in the three-phase-lag theory is given by [17]

$$ K^{*} \nabla^{2} T + \tau_{\nu }^{*} \nabla^{2} \dot{T} + K\tau_{T} \nabla^{2} \ddot{{T}} = \left( {1 + \tau_{q} \frac{\partial }{\partial t} + \frac{1}{2}\tau_{q}^{2} \frac{{\partial^{2} }}{{\partial t^{2} }}} \right)\left( {\rho C_{E} \ddot{{T}} + \gamma T_{0} \ddot{{e}}} \right), $$

(11)

where $K^{*}$ is the coefficient of thermal conductivity, $K$ is the additional material constant, $\rho \,$ is the mass density, $C_{E}$ is the specific heat at constant strain, $\tau_{T}$ and $\tau_{q}$ are the phase-lag of temperature gradient and the phase-lag of heat flux respectively. Also $\tau_{\nu }^{*} = K + \tau_{\nu } \,K^{*}$, where $\tau_{\nu }$ is the phase-lag of thermal displacement gradient. Equations (3) and (11), when $K = \tau_{T} = \tau_{q} = \tau_{\nu } = 0,$ reduce to the equations of TEWOED (GN-II) theory. In the above equations a dot denotes differentiation with respect to time, and a comma followed by a subscript denotes partial differentiation with respect to the corresponding coordinates.

We assume that [26]

$$ \lambda = \lambda_{1} (1 - \alpha^{ * } T_{0} ),\;\alpha = \alpha_{1} (1 - \alpha^{ * } T_{0} ),\;\mu = \mu_{1} (1 - \alpha^{ * } T_{0} ),\;\mu_{L} = \mu_{L1} (1 - \alpha^{ * } T_{0} ),\;\gamma = \gamma_{1} (1 - \alpha^{ * } T_{0} ),\mu_{T} = \mu_{T1} (1 - \alpha^{ * } T_{0} ),\;\beta = \beta_{1} (1 - \alpha^{ * } T_{0} ), $$

(12)

where $\lambda_{1} ,\alpha_{1} ,\mu_{1} ,\mu_{L1} ,\mu_{T1} ,\gamma_{1} ,\beta_{1}$ are constants of the material and $\alpha^{ * }$ is the linear temperature coefficient.

For plane strain deformation in the $x\, - y$ plane with displacement components $u = u (x ,y , {\text{t)}}$, $v = v (x ,y , {\text{t)}}$, $w = 0$. Using Eq. (12) in Eq. (1), we get

$$ \sigma_{xx} = \frac{1}{{\alpha_{0} }}\left[ {B_{11} u_{,x} + B_{12} v_{,y} - \gamma_{1} \hat{T}} \right] , $$

(13)

$$ \sigma_{yy} = \frac{1}{{\alpha_{0} }}\left[ {B_{12} u_{,x} + B_{22} v_{,y} - \gamma_{1} \hat{T}} \right] , $$

(14)

$$ \sigma_{zz} = \frac{1}{{\alpha_{0} }}\left[ {B_{12} u_{,x} + \lambda_{1} v_{,y} - \gamma_{1} \hat{T}} \right] , $$

(15)

$$ \sigma_{xy} = \frac{{\mu_{L1} }}{{\alpha_{0} }}\left( {u_{,y} + v_{,x} } \right),\quad \sigma_{xz} = \sigma_{yz} = 0, $$

(16)

where $B_{11} = \lambda_{1} + 2(\alpha_{1} + \mu_{T1} ) + 4(\mu_{L1} - \mu_{T1} ) + \beta_{1}$, $B_{12} = \lambda_{1} + \alpha_{1}$, $B_{22} = \lambda_{1} + 2\mu_{T1}$.

By substituting from Eqs. (13)–(16) and (10) in Eq. (3) and using the summation convection, we note that the third equation of motion in (3) is identically satisfied and first two equations become

$$ \rho \frac{{\partial^{ 2} u}}{{\partial t^{ 2} }} = \frac{1}{{\alpha_{0} }}\left( {B_{ 1 1} \frac{{\partial^{ 2} u}}{{\partial x^{ 2} }} + E_{2} \frac{{\partial^{ 2} v}}{\partial x\partial y} + E_{ 1} \frac{{\partial^{ 2} u}}{{\partial y^{ 2} }} - \gamma_{1} \frac{{\partial \hat{T}}}{\partial x}} \right) - \mu_{0} H_{0} \frac{\partial h}{\partial x} - \varepsilon_{0} \mu_{0}^{2} H_{0}^{2} \frac{{\partial^{ 2} u}}{{\partial t^{ 2} }}, $$

(17)

$$ \rho \,\frac{{\partial^{ 2} v}}{{\partial t^{ 2} }} = \frac{1}{{\alpha_{0} }}\left( {B_{ 2 2} \frac{{\partial^{ 2} v}}{{\partial y^{ 2} }} + E_{2} \frac{{\partial^{ 2} u}}{\partial x\partial y} + E_{ 1} \frac{{\partial^{ 2} v}}{{\partial x^{ 2} }} - \gamma_{1} \frac{{\partial \hat{T}}}{\partial y}} \right) - \mu_{0} H_{0} \frac{\partial h}{\partial y} - \varepsilon_{0} \mu_{0}^{2} H_{0}^{2} \frac{{\partial^{ 2} v}}{{\partial t^{ 2} }} , $$

(18)

where $E_{1} = \mu_{L1} ,$ $E_{2} = \alpha_{1} + \lambda_{1} + \mu_{L1} .$

Employing Eq. (12) and using Eq. (11), this yields

$$ K^{*} \nabla^{2} T + \tau_{\nu }^{*} \nabla^{2} \dot{T} + K\tau_{T} \nabla^{2} \ddot{{T}} = \left( {1 + \tau_{q} \frac{\partial }{\partial t} + \frac{1}{2}\tau_{q}^{2} \frac{{\partial^{2} }}{{\partial t^{2} }}} \right)\left( {\rho C_{E} \ddot{{T}} + \frac{{\gamma_{1} }}{{\alpha_{0} }}T_{0} \ddot{{e}}} \right), $$

(19)

Introducing the following dimensionless quantities:

$$ \begin{gathered} \left( {x^{{\prime }} ,y^{{\prime }} ,u^{{\prime }} ,v^{{\prime }} } \right) = c_{1} \eta (x,y,u,v), \hfill \\ \left( {t^{{\prime }} ,\tau_{q}^{{\prime }} ,\tau_{\nu }^{{\prime }} ,\tau_{T}^{{\prime }} } \right) = c_{1}^{2} \eta (t,\tau_{q} ,\tau_{\nu } ,\tau_{T} ),\hfill \\ h^{{\prime }} = \frac{h}{{H_{0} }},\theta = \frac{{\gamma_{1} \hat{T}}}{{(\lambda_{1} + 2\mu_{T1} )}},\sigma_{ij}^{{\prime }} = \frac{{\sigma_{ij} }}{{\mu_{T1} }},\quad i,j = 1,2 \hfill \\ \end{gathered}$$

(20)

where $\alpha_{0} = \frac{1}{{(1 - \alpha^{ * } T_{0} )}}$, $\eta = \frac{{\rho C_{E} }}{{K^{*} }}$, $c_{1}^{2} = \frac{{(\lambda_{1} + 2\mu_{T1} )}}{\rho }.$

Using the above non-dimensional variables then employing $h = - H_{0} \;e$, Eqs. (17)–(19) take the following form (dropping the primes for convenience)

$$ \alpha_{2} \frac{{\partial^{ 2} u}}{{\partial t^{ 2} }} = L_{ 1 1} \frac{{\partial^{ 2} u}}{{\partial x^{ 2} }} + L_{2} \frac{{\partial^{ 2} v}}{\partial x\partial y} + h_{ 1} \frac{{\partial^{ 2} u}}{{\partial y^{ 2} }} - \frac{\partial \theta }{\partial x} , $$

(21)

$$ \alpha_{2} \frac{{\partial^{ 2} v}}{{\partial t^{ 2} }} = L_{ 2 2} \frac{{\partial^{ 2} v}}{{\partial y^{ 2} }} + L_{ 2} \frac{{\partial^{ 2} u}}{\partial x\partial y} + h_{ 1} \frac{{\partial^{ 2} v}}{{\partial x^{ 2} }} - \frac{\partial \theta }{\partial y} , $$

(22)

$$ C_{K} \theta_{,ii} + C_{\nu } \dot{\theta }_{,ii} + C_{T} \ddot{\theta }_{,ii} = \left( {1 + \tau_{q} \frac{\partial }{\partial t} + \frac{1}{2}\tau_{q}^{2} \frac{{\partial^{2} }}{{\partial t^{2} }}} \right)\left( {\ddot{\theta } + \varepsilon \ddot{{e}}} \right), $$

(23)

where, $L_{11} = h_{11} + \alpha_{0} h_{0} H_{0} ,$ $L_{22} = h_{22} + \alpha_{0} h_{0} H_{0} ,$ $L_{2} = h_{2} + \alpha_{0} h_{0} H_{0} ,$ $\left( {h_{ 1} ,h_{2} ,h_{11} ,h_{ 2 2} } \right) \, = \frac{{\left( {E_{ 1} ,E_{ 2} ,B_{ 1 1} ,B_{22} } \right)}}{{\rho c_{1}^{2} }},$ $h_{ 0} \, = \frac{{\mu_{ 0} H_{0}^{2} }}{{\rho c_{1}^{2} }},$ $C_{K} = \frac{{K^{*} }}{{\rho C_{E} c_{1}^{2} }},$ $C_{\nu } = \frac{\eta K}{{\rho C_{E} }} + C_{K} \tau_{\nu } ,$ $C_{T} = \frac{{\eta K\tau_{T} }}{{\rho C_{E} }},$ $\varepsilon = \frac{{\gamma_{1}^{2}{T_{0}}}}{{\rho C_{E} \alpha_{0} (\lambda_{1} + 2\mu_{T1} )}}.$

3 Normal mode analysis

The solution of the considered physical variable can be decomposed in terms of normal modes as the following form:

$$ \left[ {u,v,\theta , \sigma_{ij} } \right](x,y,t) = \left[ { u^{*} ,v^{*} ,\theta^{*} , \sigma_{ij}^{*} } \right](x)\exp (\omega t + iby), $$

(24)

where $\omega$ is a complex constant, $i = \sqrt { - 1}$, $b$ is the wave number in the y-direction, and $u^{*} (x),$ $v^{*} (x),$ $\theta^{*} (x)$, and $\sigma_{ij}^{*} (x)$ are the amplitudes of the field quantities.

Subsisting from Eq. (24) in Eqs. (21)–(23), we get

$$ \left[ {L_{11} \text{D}^{2} - A_{1} } \right]u^{*} + ibL_{2} \text{D}v^{*} = \text{D}\theta^{*} , $$

(25)

$$ \text{i}bL_{2} \text{D}u^{*} + [h_{1} \text{D}^{2} - A_{2} ]v^{*} = \text{i}b\theta^{*} , $$

(26)

$$ A_{3} \text{D}u^{*} + \text{i}bA_{3} v^{*} = \left[ {A_{4} \text{D}^{2} - A_{5} } \right]\theta^{*} , $$

(27)

where $A_{1} = \alpha_{2} \omega^{2} + h_{1} b^{2} ,$ $A_{2} = \alpha_{2} \omega^{2} + L_{22} b^{2} ,$ $A_{3} = \varepsilon \omega^{2} \left( {1 + \tau_{q} \omega + \frac{1}{2}\tau_{q}^{2} \omega^{2} } \right),$ $A_{4} = C_{K} + C_{\nu } \omega + C_{T} \omega^{2} ,$ $A_{5} = C_{K} b^{2} \,+\,C_{\nu } \omega b^{2} + C_{T} \omega^{2} b^{2} + \omega^{2} \left( {1 + \tau_{q} \omega + \frac{1}{2}\tau_{q}^{2} \omega^{2} } \right),$ $\text{D} = \frac{\text{d}}{{\text{d}}x}.$

Eliminating $v^{ *} (x )$ and $\theta^{*} (x)$ between Eqs. (25)–(27), we obtain the sixth order ordinary differential equation satisfied with $u^{ *} (x ) ,$

$$ \left[ {\text{D}^{ 6} - A\text{D}^{ 4} + B\text{D}^{ 2} - C} \right]u^{ *} (x )= 0 , $$

(28)

where

$$ A = \frac{1}{{h_{1} L_{11} A_{4} }}\left\{ {h_{1} A_{3} - b^{2} L_{2}^{2} A_{4} + h_{1} A_{1} A_{4} + h_{1} L_{11} A_{5} + L_{11} A_{2} A_{4} } \right\}, $$

(29)

$$ B = \frac{1}{{h_{1} L_{11} A_{4} }}\{ {A_{3} A_{2} - 2b^{2} L_{2} A_{3} - b^{2} L_{2}^{2} A_{5} + h_{1} A_{1} A_{5} + A_{1} A_{2} A_{4} + L_{11} b^{2} A_{3} + L_{11} A_{2} A_{5} }\}, $$

(30)

$$ C = \frac{1}{{h_{1} L_{11} A_{4} }}\{ {b^{2} A_{1} A_{ 3} + A_{ 1} A_{ 2} A_{ 5} } \} $$

(31)

In a similar manner, we can show that $v^{ *} (x )$ and $\theta^{*} (x)$ satisfy the equation,

$$ \left[ {\text{D}^{ 6} - A\text{D}^{ 4} + B \, \text{D}^{ 2} - C \, } \right]\left\{ {v^{ *} (x ) ,\theta^{ *} (x )} \right\} = 0. $$

(32)

Equation (28) can be factorized as

$$ \left( {\text{D}^{ 2} - k_{ 1}^{ 2} } \right)\left( {\text{D}^{ 2} - k_{ 2}^{ 2} } \right)\left( {\text{D}^{ 2} - k_{ 3}^{ 2} } \right)u^{ *} (x )= 0 , $$

(33)

where $k_{n}^{ 2} (n = 1 , 2 , 3 )$ are the roots of the characteristic equation of Eq. (28):

The solution of Eq. (28), which is bounded as $x \to \infty ,$ is given by

$$ u^{ *} (x )= \sum\limits_{n = 1}^{ 3} {M_{n} } {\text{exp(}} - k_{n} x ). $$

(34)

Similarly,

$$ v^{ *} (x )= \sum\limits_{n = 1}^{ 3} {R_{1n} M_{n} } {\text{exp(}} - k_{n} x ), $$

(35)

$$ \theta^{ *} (x )= \sum\limits_{n = 1}^{ 3} {R_{2n} M_{n} } {\text{exp(}} - k_{n} x ), $$

(36)

where $R_{ 1n} = \frac{{ibA_{ 1} + (ibL_{2} - ibL_{11} )k_{n}^{ 2} }}{{h_{ 1} k_{n}^{ 3} - (A_{ 2} - b^{2} L_{2} )k_{n} }},$ $R_{ 2n} = \frac{{ - L_{11} k_{n}^{ 2} + A_{ 1} + ibL_{2} k_{n} R_{ 1n} }}{{k_{n} }}.$

Using Eqs. (20) and (24) in Eqs. (13)–(16), we obtain

$$ \sigma_{xx}^{*} = \frac{1}{{\alpha_{0} \mu_{T1} }}\left[ {B_{11} \text{D}u^{*} + \text{i}bB_{ 1 2} v^{*} - \left( {\lambda_{1} + 2\mu_{T1} } \right)\theta^{*} } \right], $$

(37)

$$ \sigma_{yy}^{*} = \frac{1}{{\alpha_{0} \mu_{T1} }}\left[ {B_{12} \text{D}u^{*} + \text{i}bB_{ 2 2} v^{*} - \left( {\lambda_{1} + 2\mu_{T1} } \right)\theta^{*} } \right], $$

(38)

$$ \sigma_{zz}^{*} = \frac{1}{{\alpha_{0} \mu_{T1} }}\left[ {B_{12} \text{D}u^{*} + \text{i}b\lambda_{1} v^{*} - \left( {\lambda_{1} + 2\mu_{T1} } \right)\theta^{*} } \right], $$

(39)

$$ \sigma_{xy}^{*} = \frac{{\mu_{L1} }}{{\alpha_{0} \mu_{T1} }}\left[ {\text{i}bu^{*} + \text{D}v^{*} } \right], $$

(40)

Introducing Eqs. (34)–(36) in Eqs. (37)–(40), this yields

$$ \sigma_{xx}^{*} = \sum\limits_{n = 1}^{ 3} {R_{3n} M_{n} } { \exp }\left( { - k_{n} x} \right) , $$

(41)

$$ \sigma_{yy}^{*} = \sum\limits_{n = 1}^{ 3} {R_{4n} M_{n} } { \exp }\left( { - k_{n} x} \right) , $$

(42)

$$ \sigma_{zz}^{*} = \sum\limits_{n = 1}^{3} {R_{5n} M_{n} } \exp \left( { - k_{n} x} \right), $$

(43)

$$ \sigma_{xy}^{*} = \sum\limits_{n = 1}^{3} {R_{6n} M_{n} } \exp \left( { - k_{n} x} \right), $$

(44)

where

$$ R_{3n} = \frac{1}{{\alpha_{0} \mu_{T1} }}\left[ { - B_{11} k_{n} + ibB_{12} R_{1n} - (\lambda_{1} + 2\mu_{T1} )R_{2n} } \right], $$

$$ R_{4n} = \frac{1}{{\alpha_{0} \mu_{T1} }}\left[ { - B_{12} k_{n} + ibB_{22} R_{1n} - (\lambda_{1} + 2\mu_{T1} )R_{2n} } \right], $$

$$ R_{5n} = \frac{1}{{\alpha_{0} \mu_{T1} }}\left[ { - B_{12} k_{n} + ib\lambda_{1} R_{1n} - (\lambda_{1} + 2\mu_{T1} )R_{2n} } \right], $$

$$ R_{6n} = \frac{{\mu_{L1} }}{{\alpha_{0} \mu_{T1} }}\left[ {ib - k_{n} R_{1n} } \right]. $$

4 Boundary condition

We consider the problem of a fiber-reinforced thermoelastic half-space under the effect of magnetic field which fills the region $\varOmega$ defined as follows:

$$ \varOmega = \left\{ {(x,y,z):0 \le x < \infty ,0 < y < \infty , - \infty < z < \infty } \right\}. $$

In order to determine the parameter $M_{n} (n = 1 , 2 , 3 )$, we need to consider the boundary conditions at $x = 0$ (after making dimensionless) as follows:

$$ \left. {\frac{\partial \theta }{\partial x} + h\theta } \right|_{x = 0} = 0 ,\;\sigma_{xx} = f ( 0.y ,t )= - f^{*} e^{\omega \,t + iby} ,\;\sigma_{xy} (0 , { }y ,t )= 0 , $$

(45)

$f{ (}y ,\,t )$ is an arbitrary function of y, t, and $f^{*}$ is a constant. In Eq. (45) when $h \to 0$ the problem corresponds to a thermal insulated boundary, and when $h \to \infty$ corresponds to an isothermal boundary (Singh et al. [27]). In the present article we consider the case $h \to 0$. Substituting the expressions of the variables considered into the above boundary conditions, we can obtain the following equations satisfied by the parameters:

$$ - \sum\limits_{n = 1}^{ 3} {k_{n} R_{ 2n} M_{n} } = 0,\;\sum\limits_{n = 1}^{ 3} {R_{ 3n} M_{n} } = - f^{*} ,\;\sum\limits_{n = 1}^{ 3} {R_{ 6n} M_{n} } = 0. $$

(46)

Solving the above system of equations in (46), we get the parameter $M_{n} \,\, (n = 1 , { 2,}\, 3 )$ defined as follows:

$$ M_{1} = \frac{{\varDelta_{1} }}{\varDelta },\;M_{2} = \frac{{\varDelta_{2} }}{\varDelta },\;M_{3} = \frac{{\varDelta_{3} }}{\varDelta }, $$

(47)

where $\varDelta = k_{1} R_{21} (R_{32} R_{63} - R_{33} R_{62} ) - k_{2} R_{22} (R_{31} R_{63} - R_{61} R_{33} ) + k_{3} R_{23} (R_{31} R_{62} - R_{32} R_{61} ),$ $\varDelta_{1} = f^{*} (k_{2} R_{22} R_{63} - k_{3} R_{23} R_{62} ),$ $\varDelta_{2} = - f^{*} (k_{1} R_{21} R_{63} - k_{3} R_{23} R_{61} ),$ $\varDelta_{2} = f^{*} (k_{1} R_{21} R_{62} - k_{2} R_{22} R_{61} ).$

5 Special cases of thermoelastic theory and particular cases

• (1) The corresponding equations for a fiber-reinforced linearly thermoelastic isotropic medium with temperature dependent and without magnetic field from the above mentioned cases by taking $H_{0} = 0.$

• (2) The corresponding equations for a fiber-reinforced linearly thermoelastic isotropic medium with magnetic field and without temperature dependent from the above mentioned cases by taking $\alpha^{*} = 0.$

• (3) The corresponding equations for an isotropic generalized thermoelastic medium with the magnetic field and with temperature dependent from the above mentioned cases by taking reinforcement parameters $\alpha ,\beta ,\left( {\mu_{L} - \mu_{T} } \right)$ vanish.

• (4) The corresponding equations for isotropic generalized thermoelastic medium with temperature dependent and without the magnetic field from the above mentioned cases by taking $\alpha ,\,$ $\beta ,$ $\left( {\mu_{L} - \mu_{T} } \right),$ $H_{0}$ vanish.

• (5) The corresponding equations for isotropic generalized thermoelastic medium with the magnetic field and without temperature dependent from the above mentioned cases by taking $\alpha ,\beta ,\left( {\mu_{L} - \mu_{T} } \right),\alpha^{*}$ vanish.

• (6) Equations of the three-phase-lag theory when, $K,\tau_{T} ,\tau_{q} ,\tau_{\nu } > 0.$

• (7) Equations of the TEWOED (GN-II) theory when, $K = \tau_{T} = \tau_{q} = \tau_{\nu } = 0.$

6 Numerical calculation and discussion

In order to illustrate the theoretical results obtained in preceding section and to compare these in the context of three-phase-lag theory and the TEWOED (GN-II) theory. We now present some numerical results for the physical constants as [28].

$$ \begin{gathered} \lambda_{1} = 7.59 \times 10^{8} \,{\text{N}} . {\text{m}}^{ - 2} ,\quad \mu_{T1} = 1.89 \times 10^{10} \,{\text{N}} . {\text{m}}^{ - 2} ,\quad \mu_{L1} = 2.45 \times 10^{10} \,{\text{N}} . {\text{m}}^{ - 2} ,\quad \rho = 8954\,{\text{kg}} . {\text{m}}^{ - 3} , \hfill \\ b = 0.8,\quad \alpha_{1} = - 1.28 \times 10^{10} \,{\text{N}} . {\text{m}}^{ - 2} ,\quad \beta_{1} = 0.32 \times 10^{10} \,{\text{N}} . {\text{m}}^{ - 2} ,\quad T_{0} = 300\,{\text{K}},\quad C_{E} = 383.1\,{\text{J}} . {\text{kg}}^{ - 1} .{\text{K}}^{ - 1} , \hfill \\ \tau_{T} = 0.9\,{\text{s}},\quad \alpha^{*} = 0.005\,{\text{K}}^{ - 1} ,\quad \tau_{q} = 0.9\,{\text{s}},\quad \tau_{\nu } = 0.9\,{\text{s}},\quad \alpha_{t} = 1.78 \times 10^{ - 4} \,{\text{K}}^{ - 1} ,\quad K^{*} = 386\,{\text{w}} . {\text{m}}^{ - 1} .{\text{K}}^{ - 1} ,\hfill \\ \mu_{1} = 3.86 \times 10^{10} {\text{kg}} . {\text{m}}^{ - 1} .{\text{s}}^{ - 2} ,\quad f^{*} = 0.5 ,\quad \mu_{0} = 1.9,\quad \varepsilon_{0}= 0.7, \quad K = 0,30\,{\text{w}} . {\text{m}}^{ - 1} .{\text{K}}^{ - 1} ,\quad \omega = \omega_{0} + i\xi ,\hfill \\ \omega_{0} = - 1,\quad \xi = 0.3. \hfill \\ \end{gathered} $$

The computations were carried out for a value of time $t = 0.9.$ The variation of the thermal temperature $\theta$, the displacement components $u,\,v$, and the stress components $\sigma_{xx} ,\,\,\sigma_{yy}$, and $\sigma_{xy}$ with distance$x$ in the plane $y = 0.9$ for the problem under consideration based on the three-phase-lag theory and the TEWOED (G-N II) theory. The results are shown in Figs. 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14, 15, 16, 17, and 18. The graphs show the four curves predicted by two different theories of thermoelasticity. In these figures, the solid lines represent the solution in the three-phase-lag theory and the dashed lines represent the solution derived using the TEWOED (G-N II) theory. Here all the variables are taken in non-dimensional forms.

Fig. 1

Horizontal displacement distribution u in the absence and presence of magnetic field

Fig. 2

Vertical displacement distribution v in the absence and presence of magnetic field

Fig. 3

Temperature distribution $\theta$ in the absence and presence of magnetic field

Fig. 4

Distribution of stress component $\sigma_{xx}$ in the absence and presence of magnetic field

Fig. 5

Distribution of stress component $\sigma_{xy}$ in the absence and presence of magnetic field

Fig. 6

Distribution of stress component $\sigma_{yy}$ in the absence and presence of magnetic field

Fig. 7

Horizontal displacement distribution u for dependent and independent temperature

Fig. 8

Vertical displacement distribution v for dependent and independent temperature

Fig. 9

Temperature distribution $\theta$ for dependent and independent temperature

Fig. 10

Distribution of stress component $\sigma_{xx}$ for dependent and independent temperature

Fig. 11

Distribution of stress component $\sigma_{xy}$ for dependent and independent temperature

Fig. 12

Distribution of stress component $\sigma_{yy}$ for dependent and independent temperature

Fig. 13

Horizontal displacement distribution u in the absence and presence of reinforcement

Fig. 14

Vertical displacement distribution v in the absence and presence of reinforcement

Fig. 15

Temperature distribution $\theta$ in the absence and presence of reinforcement

Fig. 16

Distribution of stress component $\sigma_{xx}$ in the absence and presence of reinforcement

Fig. 17

Distribution of stress component $\sigma_{xy}$ in the absence and presence of reinforcement

Fig. 18

Distribution of stress component $\sigma_{yy}$ in the absence and presence of reinforcement

Figures 1, 2, 3, 4, 5, and 6 show comparisons among the displacement components $u,v,$ the temperature $\theta ,$ and the stress components $\sigma_{xx} ,\sigma_{yy} ,$ and $\sigma_{xy}$ in the absence $(H_{0} = 0)$ and presence $(H_{0} = 85)$ of magnetic field with temperature dependent.

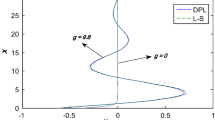
Figure 1 shows that the distribution of the horizontal displacement $u,$ in the context of the two theories, begins from negative values. In the context of the two theories, $u$ increases to a maximum value in the range $0\le x \le 0.9 ,$ then decreases, and also moves in a wave propagation for $H_{0} = 85.$ However, in the context of the two theories, $u$ increases to a maximum value in the range $0\le x \le 1.8,$ then decreases, and also moves in a wave propagation for $H_{0} = 0.$ Figure 2 depicts that the distribution of the vertical displacement $v,$ in the context of the two theories, begins from negative values. In the context of the two theories, $v$ increases to a maximum value in the range $0\le x \le 0.8 ,$ then decreases, and also moves in a wave propagation for $H_{0} = 85.$ However, in the context of the two theories, $v$ increases to a maximum value in the range $0\le x \le 1.8,$ then decreases, and also moves in a wave propagation for $H_{0} = 0.$ Figures 1 and 2 explain that $H_{0}$ has a decreasing effect on $u$ and $v.$ Figure 3 exhibits the distribution of the temperature $\theta$ and demonstrates that it begins from positive values. In the context of the two theories, $\theta$ increases to a maximum value in the range $0\le x \le 0.7 ,$ then decreases to a minimum value, and also moves in a wave propagation for $H_{0} = 85.$ However, in the context of the two theories, $\theta$ increases to a maximum value in the range $0\le x \le 0.5 ,$ then decreases to a minimum value, and also moves in a wave propagation for $H_{0} = 0.$ It is depicted that $H_{0}$ has an increasing effect on $\theta .$ Figure 4 explains that the distribution of the stress component $\sigma_{xx}$ begins from a negative value and satisfies the boundary condition at $x = 0.$ In the context of the two theories, $\sigma_{xx}$ decreases to a minimum value in the range $0\le x \le 0.4 ,$ then increases to maximum value, and also moves in a wave propagation for $H_{0} = 85.$ However, in the context of the two theories, $\sigma_{xx}$ decreases to a minimum value in the range $0\le x \le 0.6 ,$ then increases to maximum value, and also moves in a wave propagation for $H_{0} = 0.$ Figure 5 shows the distribution of the stress component $\sigma_{xy}$ and demonstrates that it reaches a zero value and satisfies the boundary condition at $x = 0.$ In the context of the two theories, $\sigma_{xy}$ decreases in the range $0\le x \le 0.3 ,$ then increases to a maximum value, and also moves in a wave propagation for $H_{0} = 0,\,\,85.$ Figure 6 depicts that the distribution of the stress component $\sigma_{yy}$, in the context of the two theories, begins from positive values. In the context of the two theories, $\sigma_{yy}$ increases to a maximum value in the range $0\le x \le 0.4 ,$ then decreases to a minimum value, and also moves in a wave propagation for $H_{0} = 85.$ However, in the context of the two theories, $\sigma_{yy}$ increases to a maximum value in the range $0\le x \le 0.6,$ then decreases to a minimum value, and also moves in a wave propagation for $H_{0} = 0.$

Figures 7, 8, 9, 10, 11, and 12 show comparisons among the displacement components $u,v,$ the temperature $\theta ,$ and the stress components $\sigma_{xx} ,\sigma_{yy} ,$ and $\sigma_{xy}$ for with (NTD) and without (WTD) temperature dependent in the presence of magnetic field.

Figure 7 shows that the distribution of the horizontal displacement $u,$ begins from negative values for NTD but it begins from positive values for WTD. In the context of the two theories, $u$ decreases in the range $0\le x \le 1.4 ,$ then become constant in the range $1.4 \le x \le 7$ for WTD. Figure 8 depicts that the distribution of the vertical displacement $v,$ in the context of the two theories, begins from negative values. In the context of the two theories, $v$ increases in the range $0\le x \le 0.8$ and then decrease in the range $0.8 \le x \le 7$ for WTD. Figure 9 exhibits the distribution of the temperature $\theta$ and demonstrates that it begins from positive values. In the context of the Green–Naghdi theory of type II, $\theta$ decreases in the range $0\le x \le 7$ for WTD. However, in the context of the three-phase-lag theory, $\theta$ constant in the range $0\le x \le 0. 2$ and then decreases in the range $0. 2\le x \le 7$ for WTD. Figure 10 explains that the distribution of the stress component $\sigma_{xx}$ begins from a negative value and satisfies the boundary condition at $x = 0.$ In the context of the two theories, $\sigma_{xx}$ increases in the range $0\le x \le 7$ for WTD. Figure 11 shows the distribution of the stress component $\sigma_{xy}$ and demonstrates that it reaches a zero value and satisfies the boundary condition at $x = 0.$ In the context of the two theories, $\sigma_{xy}$ decreases to a minimum value in the range $0\le x \le 0.6$ and then increases in the range $0. 6\le x \le 7$ for WTD. Figure 12 exhibits that the distribution of the stress component $\sigma_{yy} ,$ begins from positive values for all cases except in the context of the Green–Naghdi theory of type II for WTD it begins from a negative value. In the context of the three-phase-lag theory, $\sigma_{yy}$ decreases in the range $0\le x \le 0.5 ,$ then increases in the range $0. 5\le x \le 1 ,$ after then become constant in the range $1\le x \le 7$ for WTD. However, in the context of the Green–Naghdi theory of type II, $\sigma_{yy}$ increases in the range $0\le x \le 1$ and then become constant in the range $1\le x \le 7$ for WTD.

Figures 13, 14, 15, 16, 17, and 18 show comparisons among the displacement components $u,v,$ the temperature $\theta ,$ and the stress components $\sigma_{xx} ,\sigma_{yy} ,$ and $\sigma_{xy}$ in the absence (WRF) and presence (NRF) of the reinforcement with temperature dependent in the presence of magnetic field.

Figure 13 depicts that the distribution of the horizontal displacement $u,$ begins from negative values. In the context of the three-phase-lag theory, $u$ decreases in the range $0\le x \le 0.8 ,$ then increases to a maximum value, and also moves in wave propagation for WRF. However, in the context of the Green–Naghdi theory of type II, $u$ decreases to a minimum value in the range $0\le x \le 0.5 ,$ then increases to a maximum value, and also moves in wave propagation for WRF. Figure 14 shows that the distribution of the vertical displacement $v,$ in the context of the two theories, begins from negative values for NRF but from positive values for WRF. In the context of the three-phase-lag theory, $v$ increases to a maximum value in the range $0\le x \le 0.6 ,$ then decreases to a minimum value, and also moves in a wave propagation for WRF. However, in the context of the Green–Naghdi theory of type II, $v$ increases to a maximum value in the range $0\le x \le 0.4 ,$ then decreases to a minimum value, and also moves in wave propagation for WRF. Figure 15 exhibits the distribution of the temperature $\theta$ and demonstrates that it begins from positive values for NRF but from negative values for WRF. In the context of the three-phase-lag theory, $\theta$ decreases to a minimum value in the range $0\le x \le 0.4 ,$ then increases to a maximum value, and also moves in wave propagation for WRF. However, in the context of the Green–Naghdi theory of type II, $\theta$ decreases to a minimum value in the range $0\le x \le 0.2 ,$ then increases to a maximum value, and also moves in wave propagation for WRF. Figure 16 shows that the distribution of the stress component $\sigma_{xx}$ begins from a negative value and satisfies the boundary condition at $x = 0.$ In the context of the three-phase-lag theory, $\sigma_{xx}$ decreases to a minimum value in the range $0\le x \le 0.9 ,$ then increases to a maximum value, and also moves in a wave propagation for WRF. However, in the context of the Green–Naghdi theory of type II, $\sigma_{xx}$ decreases to a minimum value in the range $0\le x \le 0.7 ,$ then increases to a maximum value, and also moves in wave propagation for WRF. Figure 17 explains the distribution of the stress component $\sigma_{xy}$ and demonstrates that it reaches a zero value and satisfies the boundary condition at $x = 0.$ In the context of the three-phase-lag theory, $\sigma_{xy}$ decreases in the range $0\le x \le 0.3 ,$ then increases to a maximum value, and also moves in a wave propagation for WRF. However, in the context of the Green–Naghdi theory of type II, $\sigma_{xy}$ decreases in the range $0\le x \le 0.1 ,$ then increases to a maximum value, and also moves in wave propagation for WRF. Figure 18 depicts that the distribution of the stress component $\sigma_{yy} ,$ begins from positive values for NRF but it begins from negative value for WRF. In the context of the three-phase-lag theory, $\sigma_{yy}$ decreases to a minimum value in the range $0\le x \le 0.4 ,$ then increases to a maximum value, and also moves in wave propagation for WRF. However, in the context of the Green–Naghdi theory of type II, $\sigma_{yy}$ decreases to a minimum value in the range $0\le x \le 0.2 ,$ then increases to a maximum value, and also moves in wave propagation for WRF.

3D curves in Figs. 19, 20, 21, 22, 23, and 24 are giving 3D surface curves for the physical quantities i.e. the horizontal displacement, the vertical displacement, the temperature distribution, and the stress components $\sigma_{xx} ,\,\,\sigma_{yy}$, and $\sigma_{xy}$ for the thermal shock problem in the presence of magnetic field with temperature dependent in the context of the three-phase-lag theory. These figures are very important to study the dependence of these physical quantities on the vertical component of distance. The curves obtained are highly depending on the vertical distance from origin, all the physical quantities are moving in wave propagation.

Fig. 19

3D horizontal component of displacement against both components of distance based on three-phase-lag theory in the presence of magnetic field with temperature dependent

Fig. 20

3D vertical component of displacement against both components of distance based on three-phase-lag theory in the presence of magnetic field with temperature dependent

Fig. 21

3D temperature distribution against both components of distance based on three-phase-lag theory in the presence of magnetic field with temperature dependent

Fig. 22

3D distribution of stress component $\sigma_{xx}$ against both components of distance based on three-phase-lag theory in the presence of magnetic field with temperature dependent

Fig. 23

3D distribution of stress component $\sigma_{xy}$ against both components of distance based on three-phase-lag theory in the presence of magnetic field with temperature dependent

Fig. 24

3D distribution of stress component $\sigma_{yy}$ against both components of distance based on three-phase-lag theory in the presence of magnetic field with temperature dependent

7 Concluding remark

In the present study, the normal mode analysis is used to study the effect of temperature and magnetic field on the problem under consideration at the free surface of a fiber reinforcement thermoelastic half-space based on the three-phase-lag theory and the TEWOED (GN-II) theory. We obtain the following conclusions based on the above analysis: The values of all the physical quantities converge to zero with increasing of distance $x,$ and all functions are continuous.

• 1. It is clear that the magnetic field and temperature have important roles on the distribution of the field quantities.

• 2. All the physical quantities satisfy the boundary conditions.

• 3. Analytical solutions based upon normal mode analysis for the thermoelastic problem in solids have been developed and utilized.

• 4. The method that was used in the present article is applicable to a wide range of problems in hydrodynamics and thermoelasticity.

• 5. Deformation of the body depends on the nature of the applied forced as well as the type of boundary conditions.

• 6. There are significant differences in the field quantities under the Green–Naghdi theory of type II and three-phase-lag theory due to the phase-lag of temperature gradient and the phase-lag of heat flux.

• 7. The physical quantities are very depending on the vertical distance and horizontal distance.