Micromechanical finite element analysis of effective properties of a unidirectional short piezoelectric fiber reinforced composite

Abstract

A micromechanical finite element analysis of effective properties of a unidirectional short piezoelectric fiber reinforced composite is presented. The identical short piezoelectric fibers in the composite lamina are coaxial, equally spaced and aligned in the plane of lamina. A continuum micromechanics approach is utilized for predicting the effective electro-elastic material coefficients through the evaluation of Hill’s volume average electro-elastic coupled field concentration matrices. An electro-elastic finite element model of unit cell and the corresponding appropriate electro-elastic boundary conditions are presented for numerical evaluation of concentration matrices. The finite element based micromechanics model and the imposed boundary conditions are verified through the evaluation of effective coefficients of an existing unidirectional continuous piezoelectric fiber reinforced composite. The numerical illustrations reveal an improved effective piezoelectric coefficient over that of the fiber counterpart. It is found that the increase in the length ratio between a fiber and the corresponding unit cell not only causes improved piezoelectric coefficients but also makes the cross sectional area ratio (A _r ) between the same components as an important parameter for material coefficients. The optimal length and the optimal cross sectional A _r for improved effective piezoelectric coefficients at a specified fiber volume fraction are presented. The effect of fiber aspect ratio on the effective piezoelectric coefficients is also presented that reveals an upper limit of increasing fiber aspect ratio in order to achieve maximum possible improvement in the magnitude of an effective coefficient.

1 Introduction

Piezoelectricity is an electro-mechanical interaction between the mechanical and electrical states within a domain that usually happens in certain ceramics. Those ceramics are commonly known as the piezoelectric ceramics and are able to generate an electric field in response to an applied mechanical stress/strain and vice versa (James et al. 1998). These reversible effects in piezoelectric ceramics are exploited to develop piezoelectric distributed sensors and actuators in the design of advanced structures. The piezoelectric distributed sensors and actuators are generally attached or embedded to the host structure in order to achieve self-sensing and self-controlling capabilities of the overall structure that is known as smart structure (Miller and Hubbard 1987; Crawley and Luis 1987). The concept of smart structure is extensively employed for controlling the deformation/vibration of structures utilizing the monolithic piezoelectric ceramics (Crawley and Luis 1987; Baz and Poh 1988; Crawley and Lazarus 1991; Chang et al. 1992; Hwang et al. 1993; Chandrasekhara and Tenneti 1995; Batra et al. 1996; Inman et al. 1997; Ray 1998; Reddy 1999; Vel and Batra 2000; Shen 2001). But, the control authority of those monolithic piezoelectric actuators is very low because of small magnitudes of their piezoelectric stress/strain coefficients. Thus, further investigations have been carried out for improving the magnitudes of piezoelectric stress/strain coefficients of piezoelectric materials resulting in different types of piezoelectric composites (Smith and Auld 1991; Huang and Kuo 1996; Bent and Hagood 1997; Aboudi 1998; Mallik and Ray 2003; Ray 2006; Shu and Della 2008; Chakaraborty and Kumar 2009; Arockiarajan and Sakthivel 2012; Kalamkarov and Savi 2012; Venkatesh and Kar-Gupta 2013). Although any of the smart composites may be utilized for controlling different modes of deformation of structures, but the design of a particular smart composite is best suited for controlling a specific mode of deformation of structures. For instance, control of flexural mode of deformation of structures mainly requires in-plane normal actuating force and that can be achieved by the electrically induced in-plane normal stresses in the piezoelectric distributed actuators quantified by the piezoelectric coefficients, e ₃₁ and e ₃₂ when the applied electric field acts in the transverse or 3rd direction. Thus, for control of flexural vibration of structures, the piezoelectric actuator with higher magnitudes of e ₃₁ and e ₃₂ would be preferred. In this consequence, the longitudinally reinforced 1–3 piezoelectric composite (Mallik and Ray 2003) has an improved piezoelectric coefficient e ₃₁ and it is also reported as an effective distributed actuator material for flexural deformation control of structures (Ray and Mallik 2004, 2005; Ray and Sachade 2006). This smart composite is basically composed of unidirectional continuous monolithic piezoelectric fibers embedded in epoxy matrix material. The fibers are polled in the transverse direction and the applied electric field in the same direction causes the electrically induced in-plane actuating force mainly due to the coefficient, e ₃₁. Although the theoretical results (Ray and Sachade 2006) show it as an effective smart actuator material for flexural deformation control of structures, but drawbacks would arise in its practical use especially when the structure undergoes large/nonlinear flexural deformation or the host-structure surfaces are geometrically unconformable for integration of distributed actuators. Under such circumstances, the damage of long, thin and brittle unidirectional continuous piezoelectric fibers may happen that essentially hampers the control authority of the actuator. An alternative way is to utilize these actuators in form of patch, but still the aforementioned shortcoming remains inevitable depending on its (patch) size and location with respect to the boundary surfaces of the host structure. However, in order to mitigate such flaws, short-length piezoelectric fibers instead of the long fibers may be utilized. The use of the short-length fibers removes the susceptible breakage of the thin and brittle piezoelectric ceramic fibers and also, the actuator then can be used as a layer instead of its patch form. In this consideration, the improved magnitude of piezoelectric coefficient e ₃₁ for flexural deformation control of structures may be achieved by arranging the short piezoelectric fibers as unidirectional along a particular (1st) direction while they are poled along the corresponding transverse (3rd) direction. Although this arrangement of piezoelectric fibers in the composite may be useful in practice, but the corresponding magnitudes of effective piezoelectric coefficients are important for its (composite) effectual use as a material for distributed actuators in structural applications. Thus, in the present study, the effective electro-elastic coefficients of such a unidirectional short piezoelectric fiber reinforced composite are numerically determined utilizing a continuum micromechanics approach based on the assumption of homogenization. According to this approach, the effective electro-elastic coefficients can be determined through the evaluation of Hill’s volume average electro-elastic coupled field concentration factors (Hill 1963). Thus, in order to determine those factors, an electro-elastic finite element model of representative volume element (RVE) or unit cell is developed associated with the appropriate electro-mechanical boundary conditions. Although the consideration of appropriate electro-elastic boundary conditions for evaluation of the electro-elastic coupled field concentration factors is a difficult part of the analysis, those are presented in the present work. The developed finite element model and the applied electro-elastic boundary conditions are verified by evaluating the effective electro-elastic coefficients of an existing unidirectional continuous piezoelectric fiber reinforced composite. The numerical results present the variations of effective electro-elastic coefficients of the unidirectional short piezoelectric fiber reinforced composite with its fiber volume fraction and also show the improvement in the magnitude of piezoelectric coefficient e ₃₁ over that of the monolithic piezoelectric fiber counterpart. Because of the short-length fibers, the fiber volume fraction is not only the function of the cross sectional area ratio (A _r ) between the RVE and the corresponding fiber, but also the function of their length ratio (L _r ). Thus, the study is carried out to investigate the effects of these area and L _r on the effective material coefficients. Apart from these parameters, the effect of fiber aspect ratio on the effective material coefficients is also investigated.

2 Smart composite and representative volume element (RVE)

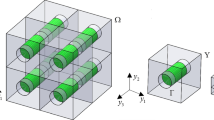
Figure 1 shows a lamina of unidirectional short-length piezoelectric fiber reinforced composite. The uniform short piezoelectric fibers are coaxial along the longitudinal x-direction and aligned in the plane of the lamina (xy-plane). The length, width and height of each fiber having rectangular cross-section are denoted by, l _f , a _f and b _f , respectively. The distances in between any two consecutive fibers along x, y and z directions are denoted by, p _c , q _c and r _c , respectively (Fig. 1). The fiber and matrix are assumed to be perfectly bonded with one another. The piezoelectric fibers are poled along the z-direction and the constituent materials are considered as linearly elastic. In order to determine the effective electro-mechanical properties, a continuum micromechanical approach based on the assumption of homogenization is utilized. Since the micromechanical analysis is confined to a RVE, two different fiber-matrix three-dimensional packs or RVEs are considered (Fig. 2) and separately used for predicting the effective electro-elastic material properties. In every type of RVEs, the fiber is coaxially located (Fig. 2). The length, width and height of a RVE are denoted as, l _c , a _c and b _c , respectively while the volume fractions of fiber and matrix phases are denoted by, η _f and η _m , respectively. The six boundary surfaces of RVE are defined by their normal directions as follows, −X _B for −X boundary plane, +X _B for +X boundary plane, −Y _B for −Y boundary plane, +Y _B for +Y boundary plane, −Z _B for −Z boundary plane, +Z _B for +Z boundary plane.

Fig. 1

Schematic diagram of unidirectional short piezoelectric fiber reinforced composite lamina

Fig. 2

Representative volume element (RVE), a RVE 1 and b RVE 2

3 Continuum micromechanics formulation

In the continuum micromechanics approach, the effective constitutive relation of a composite material is based on the composite volume averages of field quantities like stress, strain, electric field, electric displacement etc. For the present electro-elastic problem, the composite volume averages of field quantities like stress $\left( {\{ \bar{\sigma }\} } \right)$, strain $\left( {\{ \bar{\varepsilon }\} } \right)$, electric field $\{ \bar{E}\}$ and electric displacement $\{ \bar{D}\}$ vectors can be written according to the rule of mixture as follows,

$$ \begin{aligned} \left\{ {\bar{\sigma }} \right\} & = \eta_{f} \left\{ {\bar{\sigma }^{f} } \right\} + \eta_{m} \left\{ {\bar{\sigma }^{m} } \right\},\,\left\{ {\bar{\varepsilon }} \right\} = \eta_{f} \left\{ {\bar{\varepsilon }^{f} } \right\} + \eta_{m} \left\{ {\bar{\varepsilon }^{m} } \right\} \\ \left\{ {\bar{D}} \right\} & = \eta_{f} \left\{ {\bar{D}^{f} } \right\} + \eta_{m} \left\{ {\bar{D}^{m} } \right\},\,\left\{ {\bar{E}} \right\} = \eta_{f} \left\{ {\bar{E}^{f} } \right\} + \eta_{m} \left\{ {\bar{E}^{m} } \right\} \\ \end{aligned} $$

(1)

where, $\left\{ {\bar{\sigma }^{f} } \right\}\,/\,\left\{ {\bar{\varepsilon }^{f} } \right\}/\,\left\{ {\bar{D}^{f} } \right\}/\,\left\{ {\bar{E}^{f} } \right\}$ and $\left\{ {\bar{\sigma }^{m} } \right\}\,/\,\left\{ {\bar{\varepsilon }^{m} } \right\}/\,\left\{ {\bar{D}^{m} } \right\}/\,\left\{ {\bar{E}^{m} } \right\}$ are the volume average stress/strain/electric displacement/electric field vector for fiber and matrix phases, respectively. Those are also can be written as follows,

$$ \begin{aligned} \left\{ {\bar{\sigma }^{f} } \right\} & = \frac{1}{{V^{f} }}\int_{{\,V^{f} }} {\left\{ {\sigma^{f} } \right\}\,} dV^{f} ,\,\left\{ {\bar{\sigma }^{m} } \right\} = \frac{1}{{V^{m} }}\int_{{V^{m} }} {\left\{ {\sigma^{m} } \right\}} \,dV^{m} ,\,\left\{ {\bar{\varepsilon }^{f} } \right\} = \frac{1}{{V^{f} }}\int_{{V^{f} }} {\left\{ {\varepsilon^{f} } \right\}} dV^{f} \\ \left\{ {\bar{\varepsilon }^{m} } \right\} & = \frac{1}{{V^{m} }}\int_{{V^{m} }} {\left\{ {\varepsilon^{m} } \right\}} dV^{m} ,\,\left\{ {\bar{D}^{f} } \right\} = \frac{1}{{V^{f} }}\int_{{V^{f} }} {\left\{ {D^{f} } \right\}} dV^{f} ,\,\left\{ {\bar{D}^{m} } \right\} = \frac{1}{{V^{m} }}\int_{{V^{m} }} {\left\{ {D^{m} } \right\}} dV^{m} \\ \left\{ {\bar{E}^{f} } \right\} & = \frac{1}{{V^{f} }}\int_{{V^{f} }} {\left\{ {E^{f} } \right\}} dV^{f} ,\,\left\{ {\bar{E}^{m} } \right\} = \frac{1}{{V^{m} }}\int_{{V^{m} }} {\left\{ {E^{m} } \right\}} dV^{m} \\ \end{aligned} $$

(2)

In Eq. (2), V ^f and V ^m are the volumes of fiber and matrix phases, respectively; {σ ^f}/{ɛ ^f}/{D ^f}/{E ^f} and {σ ^m}/{ɛ ^m}/{D ^m}/{E ^m} are stress/strain/electric displacement/electric field vector at any point within the fiber and the matrix phase volumes, respectively. The linear constitutive relations for fiber and matrix phase materials in terms of the phase volume average field quantities can be written as,

$$ \begin{aligned} \left\{ {\bar{\sigma }^{f} } \right\} & = \left[ {C^{f} } \right]\left\{ {\bar{\varepsilon }^{f} } \right\} - \left[ {e^{f} } \right]\left\{ {\bar{E}^{f} } \right\},\,\left\{ {\bar{\sigma }^{m} } \right\} = \left[ {C^{m} } \right]\left\{ {\bar{\varepsilon }^{m} } \right\} \\ \left\{ {\bar{D}^{f} } \right\} & = \left[ {e^{f} } \right]^{\rm T} \left\{ {\bar{\varepsilon }^{f} } \right\} + \left[ { \in^{f} } \right]\left\{ {\bar{E}^{f} } \right\},\,\left\{ {\bar{D}^{m} } \right\} = \left[ { \in^{m} } \right]\left\{ {\bar{E}^{m} } \right\} \\ \end{aligned} $$

(3)

where, [C ^f] and [C ^m] are the elastic matrix of fiber and matrix phase materials; [e ^f] is the piezoelectric matrix of the piezoelectric fiber phase; [∊^f] and [∊^m] are the permittivity matrices for fiber and matrix phase materials, respectively. Note that the matrix phase material is piezoelectrically inactive. The explicit form of elastic, piezoelectric and permittivity matrices appearing in Eq. (3) are as follows,

$$ \begin{aligned} \left[ { \in^{f} } \right] & = \left[ {\begin{array}{*{20}c} { \in_{11}^{f} } & 0 & 0 \\ 0 & { \in_{22}^{f} } & 0 \\ 0 & 0 & { \in_{33}^{f} } \\ \end{array} } \right]\,,\,\left[ { \in^{m} } \right] = \left[ {\begin{array}{*{20}c} { \in_{11}^{m} } & 0 & 0 \\ 0 & { \in_{22}^{m} } & 0 \\ 0 & 0 & { \in_{33}^{m} } \\ \end{array} } \right]\,,\,\left[ {e^{f} } \right]^{\rm T} = \left[ {\begin{array}{*{20}c} 0 & 0 & 0 & 0 & {e_{15} } & 0 \\ 0 & 0 & 0 & {e_{24} } & 0 & 0 \\ {e_{31} } & {e_{32} } & {e_{33} } & 0 & 0 & 0 \\ \end{array} } \right] \\ \left[ {C^{f} } \right] & = \left[ {\begin{array}{*{20}c} {C_{11}^{f} } & {C_{12}^{f} } & {C_{13}^{f} } & 0 & 0 & 0 \\ {C_{21}^{f} } & {C_{22}^{f} } & {C_{23}^{f} } & 0 & 0 & 0 \\ {C_{31}^{f} } & {C_{32}^{f} } & {C_{33}^{f} } & 0 & 0 & 0 \\ 0 & 0 & 0 & {C_{44}^{f} } & 0 & 0 \\ 0 & 0 & 0 & 0 & {C_{55}^{f} } & 0 \\ 0 & 0 & 0 & 0 & 0 & {C_{66}^{f} } \\ \end{array} } \right]\,\,\,,\,\,\left[ {C^{m} } \right] = \left[ {\begin{array}{*{20}c} {C_{11}^{m} } & {C_{12}^{m} } & {C_{13}^{m} } & 0 & 0 & 0 \\ {C_{21}^{m} } & {C_{22}^{m} } & {C_{23}^{m} } & 0 & 0 & 0 \\ {C_{31}^{m} } & {C_{32}^{m} } & {C_{33}^{m} } & 0 & 0 & 0 \\ 0 & 0 & 0 & {C_{44}^{m} } & 0 & 0 \\ 0 & 0 & 0 & 0 & {C_{55}^{m} } & 0 \\ 0 & 0 & 0 & 0 & 0 & {C_{66}^{m} } \\ \end{array} } \right] \\ \end{aligned} $$

(4)

Introducing Eq. (3) in Eq. (1), the expressions of $\{ \bar{\sigma }\}$and $\{ \bar{D}\}$ can be obtained as,

$$ \begin{aligned} {\kern 1pt} \left\{ {\bar{\sigma }} \right\} & = \eta_{f} \left[ {C^{f} } \right]\left\{ {\bar{\varepsilon }^{f} } \right\} + \eta_{m} \left[ {C_{{}}^{m} } \right]\left\{ {\bar{\varepsilon }^{m} } \right\} - \eta_{f} \left[ {e^{f} } \right]\left\{ {\bar{E}^{f} } \right\} \\ \left\{ {\bar{D}} \right\} & = \eta_{f} \left[ { \in^{f} } \right]\left\{ {\bar{E}^{f} } \right\} + \eta_{m} \left[ { \in^{m} } \right]\left\{ {\bar{E}^{m} } \right\} + \eta_{f} \left[ {e^{f} } \right]^{\rm T} \left\{ {\bar{\varepsilon }^{f} } \right\} \\ \end{aligned} $$

(5)

Now, it is convenient to use the idea of phase volume average field concentration factors proposed by Hill (1963). Utilizing this idea, the phase volume average strain and electric field vectors for both fiber and matrix phases can be written as follows,

$$ \begin{aligned} \left\{ {\bar{\varepsilon }^{m} } \right\} & = \left[ {\bar{A}_{\varepsilon }^{m} } \right]\left\{ {\bar{\varepsilon }} \right\} + \left[ {\bar{A}_{\varepsilon E}^{m} } \right]\left\{ {\bar{E}} \right\},\,\,\,\left\{ {\bar{E}^{m} } \right\} = \left[ {\bar{A}_{E\varepsilon }^{m} } \right]\left\{ {\bar{\varepsilon }} \right\} + \left[ {\bar{A}_{E}^{m} } \right]\left\{ {\bar{E}} \right\}, \\ \left\{ {\bar{\varepsilon }^{f} } \right\} & = \left[ {\bar{A}_{\varepsilon }^{f} } \right]\left\{ {\bar{\varepsilon }} \right\} + \,\,\left[ {\bar{A}_{\varepsilon E}^{f} } \right]\left\{ {\bar{E}} \right\},\,\,\,\left\{ {\bar{E}^{f} } \right\} = \left[ {\bar{A}_{E\varepsilon }^{f} } \right]\left\{ {\bar{\varepsilon }} \right\} + \,\,\left[ {\bar{A}_{E}^{f} } \right]\left\{ {\bar{E}} \right\} \\ \end{aligned} $$

(6)

where, $\,{{\left[ {\bar{A}_{\varepsilon }^{m} } \right]\,} \mathord{\left/ {\vphantom {{\left[ {\bar{A}_{\varepsilon }^{m} } \right]\,} {\left[ {\bar{A}_{\varepsilon }^{f} } \right]\,}}} \right. \kern-0pt} {\left[ {\bar{A}_{\varepsilon }^{f} } \right]\,}},\,\,{{\left[ {\bar{A}_{\varepsilon E}^{m} } \right]\,} \mathord{\left/ {\vphantom {{\left[ {\bar{A}_{\varepsilon E}^{m} } \right]\,} {\left[ {\bar{A}_{\varepsilon E}^{f} } \right]\,}}} \right. \kern-0pt} {\left[ {\bar{A}_{\varepsilon E}^{f} } \right]\,}},\,\,{{\left[ {\bar{A}_{E\varepsilon }^{m} } \right]\,} \mathord{\left/ {\vphantom {{\left[ {\bar{A}_{E\varepsilon }^{m} } \right]\,} {\left[ {\bar{A}_{E\varepsilon }^{f} } \right]\,}}} \right. \kern-0pt} {\left[ {\bar{A}_{E\varepsilon }^{f} } \right]\,}}$ and $\,{{\left[ {\bar{A}_{E}^{m} } \right]\,} \mathord{\left/ {\vphantom {{\left[ {\bar{A}_{E}^{m} } \right]\,} {\left[ {\bar{A}_{E}^{f} } \right]\,}}} \right. \kern-0pt} {\left[ {\bar{A}_{E}^{f} } \right]\,}}$ are the matrix/fiber phase volume average strain, strain-electric field coupled, electric field-strain coupled and electric field concentration matrices, respectively. Introducing Eq. (6) in Eq. (5), the expressions of composite volume average stress ($\left\{ {\bar{\sigma }} \right\}$) and electric displacement ($\left\{ {\bar{D}} \right\}$) vectors can be obtained as,

$$ \begin{aligned} \left\{ {\bar{\sigma }} \right\} & = \left[ {\bar{C}} \right]\left\{ {\bar{\varepsilon }} \right\} - \left[ {\bar{e}} \right]\left\{ {\bar{E}} \right\} \\ \left\{ {\bar{D}} \right\} & = \left[ {\bar{e}} \right]^{\rm T} \left\{ {\bar{\varepsilon }} \right\} + \left[ {\bar{ \in }} \right]\left\{ {\bar{E}} \right\} \\ \left[ {\bar{C}} \right] & = \eta_{f} \left[ {C^{f} } \right]\left[ {\bar{A}_{\varepsilon }^{f} } \right] + \eta_{m} \left[ {C^{m} } \right]\left[ {\bar{A}_{\varepsilon }^{m} } \right] - \eta_{f} \left[ {e^{f} } \right]\left[ {\bar{A}_{E\varepsilon }^{f} } \right] \\ \left[ {\bar{e}} \right] & = \eta_{f} \left[ {e^{f} } \right]\left[ {\bar{A}_{E}^{f} } \right] - \eta_{m} \left[ {C^{m} } \right]\left[ {\bar{A}_{\varepsilon E}^{m} } \right] - \eta_{f} \left[ {C^{f} } \right]\left[ {\bar{A}_{\varepsilon E}^{f} } \right] \\ \left[ {\bar{e}} \right]^{\rm T} & = \eta_{f} \left[ { \in^{f} } \right]\left[ {\bar{A}_{E\varepsilon }^{f} } \right] + \eta_{m} \left[ { \in^{m} } \right]\left[ {\bar{A}_{E\varepsilon }^{m} } \right] + \eta_{f} \left[ {e^{f} } \right]^{\rm T} \left[ {\bar{A}_{\varepsilon }^{f} } \right] \\ \left[ {\bar{ \in }} \right] & = \eta_{f} \left[ {e^{f} } \right]^{\rm T} \left[ {\bar{A}_{\varepsilon E}^{f} } \right] + \eta_{m} \left[ { \in^{m} } \right]\left[ {\bar{A}_{E}^{m} } \right] + \eta_{f} \left[ { \in^{f} } \right]\left[ {\bar{A}_{E}^{f} } \right] \\ \end{aligned} $$

(7)

Note that, the $[\overline{e} ]$ matrix in Eq. (7) is obtained by two different expressions corresponding to two different electro-elastic coupled concentration matrices $\left(\left[ {\bar{A}_{E\varepsilon }^{f} } \right] \;{\text{and}}\; \left[ {\bar{A}_{\varepsilon E}^{f} } \right]\right)$. Using Eq. (6) in the expressions of $\{ \bar{\varepsilon }\}$ and $\{ \bar{E}\}$ (Eq. (1)), the following expressions can be obtained,

$$ \begin{aligned} & \left( {\left[ I \right] - \left\langle {\eta_{f} \left[ {\bar{A}_{\varepsilon }^{f} } \right] + \eta_{m} \left[ {\bar{A}_{\varepsilon }^{m} } \right]} \right\rangle } \right)\left\{ {\bar{\varepsilon }} \right\} = \left( {\eta_{f} \left[ {\bar{A}_{\varepsilon E}^{f} } \right] + \eta_{m} \left[ {\bar{A}_{\varepsilon E}^{m} } \right]} \right)\left\{ {\overline{E} } \right\} \\ & \left( {\left[ I \right] - \left\langle {\eta_{f} \left[ {\bar{A}_{E}^{f} } \right] + \eta_{m} \left[ {\bar{A}_{E}^{m} } \right]} \right\rangle } \right)\left\{ {\bar{E}} \right\} = \left( {\eta_{f} \left[ {\bar{A}_{E\varepsilon }^{f} } \right] + \eta_{m} \left[ {\bar{A}_{E\varepsilon }^{m} } \right]} \right)\left\{ {\bar{\varepsilon }} \right\} \\ \end{aligned} $$

(8)

where, [I] is the unity matrix. Equation (7) shows the expressions of effective electro-mechanical properties of the smart composite, in which, the different phase volume average concentration matrices are related by Eq. (8). However, the elastic matrix ($[\bar{C}]$) and the permittivity matrix ($[\bar{ \in }]$) of a linear piezoelectric material are defined at the constant values of electric field ($\{ \bar{E}\}$) and strain ($\{ \bar{\varepsilon }\}$), respectively, preferably at their zero values ($\{ \bar{E}\} = 0$ and $\{ \bar{\varepsilon }\} = 0$) (Dunn and Taya 1993). While the piezoelectric matrix ($[\bar{e}]$) of the same is defined either at constant electric field (preferably, $\{ \bar{E}\} = 0$) or at constant strain (preferably, $\{ \bar{\varepsilon }\} = 0$) (Dunn and Taya 1993). Thus, for these imposed conditions ($\{ \bar{E}\} = 0$ and $\{ \bar{\varepsilon }\} = 0$), the expressions of effective electro-mechanical properties (Eq. (7)) are modified in the subsequent derivation. For the condition imposed on electric field ($\{ \bar{E}\} = 0$), Eq. (8) reduces to the following expressions,

$$ \begin{gathered} \eta_{m} \left[ {\bar{A}_{\varepsilon }^{m} } \right] = \left[ I \right] - \eta_{f} \left[ {\bar{A}_{\varepsilon }^{f} } \right] \hfill \\ \;\,\eta_{m} \left[ {\bar{A}_{E\varepsilon }^{m} } \right] = - \eta_{f} \left[ {\bar{A}_{E\varepsilon }^{f} } \right] \hfill \\ \end{gathered} $$

(9)

Introducing Eq. (9) in Eq. (7), the following expressions of $\left[ {\bar{C}} \right]$and $\left[ {\bar{e}} \right]^{\rm T}$ can be obtained,

$$ \begin{aligned} \left[ {\bar{C}} \right] & = \eta_{f} \,\left( {\left[ {C^{f} } \right] - \left[ {C^{m} } \right]} \right)\,\,\left[ {\bar{A}_{\varepsilon }^{f} } \right] + \left[ {C_{{}}^{m} } \right] - \eta_{f} \left[ {e^{f} } \right]\left[ {\bar{A}_{E\varepsilon }^{f} } \right] \\ \left[ {\bar{e}} \right]^{\rm T} & = \,\eta_{f} \,\left( {\left[ { \in^{f} } \right] - \left[ { \in^{m} } \right]} \right)\,\left[ {\bar{A}_{E\varepsilon }^{f} } \right] + \eta_{f} \left[ {e^{f} } \right]^{\rm T} \left[ {\bar{A}_{\varepsilon }^{f} } \right] \\ \end{aligned} $$

(10)

For the condition imposed on strain $\left( {\{ \bar{\varepsilon }\} = 0} \right)$, Eq. (8) reduces to,

$$ \begin{aligned} \eta_{m} \left[ {\bar{A}_{\varepsilon E}^{m} } \right] & = - \eta_{f} \left[ {\bar{A}_{\varepsilon E}^{f} } \right] \\ \eta_{m} \left[ {\bar{A}_{E}^{m} } \right] & = \left[ I \right] - \eta_{f} \left[ {\bar{A}_{E}^{f} } \right] \\ \end{aligned} $$

(11)

Introducing Eq. (11) in Eq. (7), the following expressions for $[\bar{e}]$ and $[\bar{ \in }]$ can be obtained,

$$ \begin{aligned} \left[ {\bar{e}} \right] & = \eta_{f} \left[ {e^{f} } \right]\left[ {\bar{A}_{E}^{f} } \right] - \eta_{f} \left( {\left[ {C^{f} } \right] - \left[ {C^{m} } \right]} \right)\left[ {\bar{A}_{\varepsilon E}^{f} } \right] \\ \left[ {\bar{ \in }} \right] & = \eta_{f} \left[ {e^{f} } \right]^{\rm T} \left[ {\bar{A}_{\varepsilon E}^{f} } \right] + \eta_{f} \left( {\left[ { \in^{f} } \right] - \left[ { \in^{m} } \right]} \right)\left[ {\bar{A}_{E}^{f} } \right] + \left[ { \in_{m} } \right] \\ \end{aligned} $$

(12)

In the foregoing derivation, the expressions of effective elastic stiffness, $[\bar{C}]$, effective piezoelectric matrix $[\bar{e}]$, and effective permittivity matrix $[\bar{ \in }]$ of the smart composite are derived based on the specified conditions on the composite volume average electric field ($\{ \bar{E}\}$) and strain ($\{ \bar{\varepsilon }\}$) vectors. However, for the numerical evaluation of effective electro-mechanical properties of the present smart composite using Eqs. (10) and (12) under the specified electrical and elastic conditions, a three-dimensional electro-elastic finite element model of RVE is developed in the next section.

4 Finite element model of RVE

In this section, a three-dimensional linear electro-mechanical finite element model of the RVE is developed. The strain and electric field vectors at any point within the RVE can be expressed as,

$$ \begin{aligned} \left\{ {\begin{array}{*{20}c} {\{ \varepsilon \} } \\ {\{ E\} } \\ \end{array} } \right\} & = \left\{ {\begin{array}{*{20}c} {\varepsilon_{xx} } & {\varepsilon_{yy} } & {\varepsilon_{zz} } & {\gamma_{yz} } & {\gamma_{xz} } & {\gamma_{xy} } & {E_{x} } & {E_{y} } & {E_{z} } \\ \end{array} } \right\}^{\rm T} , \\ \varepsilon_{xx} & = \frac{\partial u}{\partial x}\,\,\,,\,\,\,\varepsilon_{yy} = \frac{\partial v}{\partial y}\,\,\,,\,\,\,\varepsilon_{zz} = \frac{\partial w}{\partial z},\,\,\gamma_{xy} = \frac{\partial u}{\partial y} + \frac{\partial v}{\partial x}\,\,\,,\,\,\,\gamma_{xz} = \frac{\partial u}{\partial z} + \frac{\partial w}{\partial x}\,\,\,,\,\,\,\gamma_{yz} = \frac{\partial v}{\partial z} + \frac{\partial w}{\partial y}, \\ E_{x} & = - \frac{\partial \phi }{\partial x}\,\,\,,\,\,\,E_{y} = - \frac{\partial \phi }{\partial y}\,\,\,,\,\,\,E_{z} = - \frac{\partial \phi }{\partial z} \\ \end{aligned} $$

(13)

where, ɛ _xx , ɛ _yy and ɛ _zz are the normal strains along x, y and z directions, respectively; γ _xz and γ _yz are the transverse shear strains in the xz and the yz-planes, respectively; γ _xy is the in-plane shear strain in the xy plane; Ex, E _y and E _z are the electric fields along x, y and z directions, respectively; u(x, y, z), v(x, y, z), w(x, y, z) are the displacements at any point in the RVE along x, y and z directions, respectively; ϕ(x, y, z) is the electric potential at any point within the RVE. Similar to the strain and electric field vectors (Eq. (13)), the stress and electric displacement vectors at any point within the RVE can be expressed as,

$$ \left\{ {\begin{array}{*{20}c} {\{ \sigma \} } \\ {\{ D\} } \\ \end{array} } \right\} = \left\{ {\begin{array}{*{20}c} {\sigma_{xx} } & {\sigma_{yy} } & {\sigma_{zz} } & {\tau_{yz} } & {\tau_{xz} } & {\tau_{xy} } & {D_{x} } & {D_{y} } & {D_{z} } \\ \end{array} } \right\}^{\text{T}} $$

(14)

where, σ _xx , σ _yy and σ _zz are the normal stresses along x, y and z directions, respectively; τ _xz and τ _yz are the transverse shear stresses in the xz and yz-planes, respectively; τ _xy is the in-plane shear stress in the xy-plane; D _x , D _y and D _z are the electric displacements along x, y and z directions, respectively. The displacements (u, v and w) and electric potential (ϕ) at any point within the RVE can be expressed in form of electro-elastic state vector ({d}) as follows,

$$ \left\{ d \right\} = \left\{ {\begin{array}{*{20}c} u & v & w & \phi \\ \end{array} } \right\}^{\rm T} $$

(15)

Using the electro-elastic state vector ({d}), the strain and electric field vectors (Eq. (13)), can be expressed in terms of an operator matrix ([L]) as follows,

$$ \left\{ {\begin{array}{*{20}c} { + \{ \varepsilon \} } \\ { - \{ E\} } \\ \end{array} } \right\} = \left[ L \right]\left\{ d \right\}\;\;\;[L] = \left[ {\begin{array}{*{20}c} {\frac{\partial }{\partial x}} & 0 & 0 & 0 & {\frac{\partial }{\partial z}} & {\frac{\partial }{\partial y}} & 0 & 0 & 0 \\ 0 & {\frac{\partial }{\partial y}} & 0 & {\frac{\partial }{\partial z}} & 0 & {\frac{\partial }{\partial x}} & 0 & 0 & 0 \\ 0 & 0 & {\frac{\partial }{\partial z}} & {\frac{\partial }{\partial y}} & {\frac{\partial }{\partial x}} & 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 & 0 & 0 & {\frac{\partial }{\partial x}} & {\frac{\partial }{\partial y}} & {\frac{\partial }{\partial z}} \\ \end{array} } \right]^{{\,\,{\rm T}}} $$

(16)

The constitutive relations for fiber and matrix phase materials within the RVE can be written as,

$$ \left\{ {\begin{array}{*{20}c} {\{ \sigma^{k} \} } \\ {\{ D^{k} \} } \\ \end{array} } \right\} = \left[ {Z^{k} } \right]\left\{ {\begin{array}{*{20}c} { + \{ \varepsilon \} } \\ { - \{ E\} } \\ \end{array} } \right\}\,\,\,,\,\,\,k = \,\,1,2 $$

(17)

where, the superscript k denotes the quantities within the fiber or the matrix phase volume according to its value as 1 or 2, respectively; the matrix [Z ^k] appearing in Eq. (17) is as follows,

$$ \left[ {Z^{1} } \right] = \left[ {\begin{array}{*{20}c} {\left[ {C^{f} } \right]} & {\;\;\left[ {e^{f} } \right]} \\ {\left[ {e^{f} } \right]^{\rm T} } & { - \left[ { \in^{f} } \right]} \\ \end{array} } \right]\,,\,\,\left[ {Z^{2} } \right] = \left[ {\begin{array}{*{20}c} {\left[ {C^{m} } \right]} & {\left[ 0 \right]} \\ {\left[ 0 \right]} & { - \left[ { \in^{m} } \right]} \\ \end{array} } \right], $$

(18)

The first variation of electro-elastic internal energy of the RVE can be expressed as (Tiersten 1969),

$$ \delta U = \sum\limits_{k = 1}^{2} {\int_{{\,V^{k} }} {\left( {\left\lfloor {\{ \begin{array}{*{20}c} {\delta \varepsilon \}^{T} } & { - \{ \delta E\}^{T} } \\ \end{array} } \right\rfloor \left\{ {\begin{array}{*{20}c} {\{ \sigma^{k} \} } \\ {\{ D^{k} \} } \\ \end{array} } \right\}} \right)} } \,\,dV^{k} $$

(19)

where, δ is an operator for first variation; V ^k is the volume of fiber (k = 1) or matrix (k = 2) phase material. Introducing Eqs. (17) and (16) in Eq. (19), the first variation of the electro-elastic internal energy (δU) can be written as,

$$ \delta U = \sum\limits_{k = 1}^{2} {\int_{{\,V^{k} }} {\left( {\left\{ {\delta d} \right\}^{\rm T} \,\,\left[ L \right]^{\rm T} \,\,\left[ {Z^{k} } \right]\,\,\left[ L \right]\,\,\left\{ {\delta d} \right\}} \right)} } \,\,dV^{k} $$

(20)

The volume of RVE is discreatized by 27 nodded isoparametric hexahedral elements. Accordingly, the electro-elastic state vector ({d}) for the i ^th node of an element can be expressed as,

$$ \left\{ {d_{i} } \right\} = \left\{ {\begin{array}{*{20}c} {u_{i} } & {v_{i} } & {w_{i} } & {\phi_{i} } \\ \end{array} } \right\}^{\rm T} \,,\,\,i = 1,2,3 \ldots ,27 $$

(21)

The electro-elastic state vector at any point within a typical element can be written as,

$$ \left\{ d \right\} = \left[ N \right]\left\{ {d^{e} } \right\} $$

(22)

where, [N] is the shape function matrix and {d ^e} is the elemental nodal electro-elastic state vector. Using Eq. (22) in Eq. (20), the simplified expression for the first variation of internal energy ($\delta U^{e}$) of a typical element can be expressed as,

$$ \begin{aligned} \delta U^{e} & = \left\{ {\delta d^{e} } \right\}^{\rm T} \left[ {K^{\,e} } \right]\,\left\{ {d^{e} } \right\} \\ \left[ {K^{\,e} } \right] & = \int_{{\,V_{e}^{k} }} {\left( {\left[ N \right]^{\rm T} \,\,\left[ L \right]^{\rm T} \,\,\left[ {Z^{k} } \right]\,\,\left[ L \right]\,\,\left[ N \right]} \right)\,\,dV_{\,e}^{\,k} } \\ \end{aligned} $$

(23)

where, V ^k _e is the elemental volume within fiber (k = 1) or matrix (k = 2) phase volume. Upon assembling the elemental governing equilibrium equations into the global space, the global equations of equilibrium can be obtained as follows,

$$ \delta U = \left\{ {\delta X} \right\}^{\rm T} \left[ K \right]\,\left\{ X \right\} $$

(24)

where, [K] is the global electro-elastic coefficient matrix; {X} is the global nodal electro-elastic state vector. The electro-elastic internal energy of RVE as illustrated in Eq. (24) is basically due to the applied nodal displacement and/or potential over the boundary surfaces of the RVE. In order to apply a nodal displacement or potential, the corresponding element, say X _i in the vector {X} is to be specified that yields $\delta X_{i} = 0$. For $\delta X_{i} = 0$, the t ^th row in [K] is to be deleted while a column of [K] with the same index, say {f _i } is also to be removed to constitute the displacement/potential load vector as follows,

$$ \delta U = \left\{ {\delta X_{r} } \right\}^{\rm T} \left( {\left[ {K_{r} } \right]\,\left\{ {X_{r} } \right\} + \{ f_{i} \} X_{i} } \right) $$

(25)

In Eq. (25), [K _r ] and {X _r } are the resulting electro-elastic coefficient matrix and nodal state vector, respectively, after imposition of the nodal displacement/potential boundary condition on t ^th element of, {X}. Equation (25) can also be written in generalized from as follows,

$$ \delta U = \left\{ {\delta X_{r} } \right\}^{T} \left( {\left[ {K_{r} } \right]\left\{ {X_{r} } \right\} - \{ P\} } \right),\;\;\{ P\} = - \sum\limits_{i = 1}^{{N_{d} }} {\{ f_{i} \} X_{i} } $$

(26)

where, N _d is the total number of specified elements in {X}. Applying the principle of minimum potential energy i.e. δU = 0, the following governing equations of equilibrium can be obtained,

$$ [K_{r} ]\{ X_{r} \} = \{ P\} $$

(27)

Equation (27) represents the linear electro-elastic finite element model of the RVE subjected to the displacement and/or potential boundary conditions. The displacement and electric potential fields within the RVE for a specified electro-elastic boundary condition can be obtained by the solution of Eq. (27). Corresponding to these solutions of displacement and electric potential fields, the volume average strain and electric field vectors for phase and composite volumes can be computed by the following expressions,

$$ \begin{aligned} \left\{ {\bar{\varepsilon }^{f} } \right\} & = \frac{1}{{V^{\,f} }}\left( {\sum\limits_{n = 1}^{{N^{{^{f} }} }} {\int_{{\,v_{n} }} {\left\{ {\varepsilon_{n} } \right\}dv_{n} } } } \right),\,\left\{ {\bar{E}^{f} } \right\} = \frac{1}{{V^{\,f} }}\left( {\sum\limits_{n = 1}^{{N^{{^{f} }} }} {\int_{{\,v_{n} }} {\left\{ {E_{n} } \right\}dv_{n} } } } \right), \\ \left\{ {\bar{\varepsilon }^{m} } \right\} & = \frac{1}{{V^{m} }}\left( {\sum\limits_{n = 1}^{{N^{m} }} {\int_{{\,v_{n} }} {\left\{ {\varepsilon_{n} } \right\}dv_{n} } } } \right)\,,\,\left\{ {\bar{E}^{m} } \right\} = \frac{1}{{V^{m} }}\left( {\sum\limits_{n = 1}^{{N^{{^{m} }} }} {\int_{{\,v_{n} }} {\left\{ {E_{n} } \right\}dv_{n} } } } \right), \\ \left\{ {\bar{\varepsilon }} \right\} & = \frac{1}{V}\left( {\sum\limits_{n = 1}^{N} {\int_{{v_{n} }} {\left\{ {\varepsilon_{n} } \right\}dv_{n} } } } \right),\,\left\{ {\bar{E}} \right\} = \frac{1}{V}\left( {\sum\limits_{n = 1}^{N} {\int_{{\,v_{n} }} {\left\{ {E_{n} } \right\}dv_{n} } } } \right) \\ \end{aligned} $$

(28)

where, N ^f, N ^m and N are the numbers of elements in fiber phase, matrix phase and composite volumes, respectively; {ɛ _n }and {E _n } are the strain and the electric field vectors, respectively for n ^th element; v _n is the volume of n ^th element. The strain ({ɛ _n }) and electric field ({E _n }) vectors for n ^th isoparametric element are computed using the standard method (Cook et al. 2001).

5 Numerical results and discussions

In this section, the effective electro-elastic properties of the unidirectional short piezoelectric fiber reinforced composite material are numerically evaluated considering the piezoelectric fiber and the matrix phase materials as PZT5H and Epoxy, respectively. The material properties of these constituent materials are given in Table 1. The cross sections of RVE and the corresponding piezoelectric fiber are considered as square sections (a _f  = b _f , a _c  = b _c ). Since the design of the present piezoelectric composite is for the development of distributed actuator material in structural applications, the numerical study is carried out mainly on its effective piezoelectric coefficients.

Table 1 Material properties of constituent materials (Ray 2006)

In order to determine the effective elastic and piezoelectric coefficients ($[\bar{C}]$ and $[\bar{e}]$), Eq. (10) can be used under the condition, $\{ \bar{E}\} = 0$. Although this condition $\left( {\{ \bar{E}\} = 0} \right)$ can be achieved by applying appropriate electric potential boundary conditions over the boundary surfaces of RVE, but the corresponding phase volume average fields, $\{ \bar{E}^{f} \}$ and $\{ \bar{E}^{m} \}$ may have non-zero values. Since there is no electro-elastic coupling in matrix phase material, $\{ \bar{E}^{m} \}$ has no effect on strain within the domain of RVE. But, $\{ \bar{E}^{f} \}$ causes the electrically induced strain within the domain of RVE and that is accounted by the electric field-strain coupled concentration matrix, $[\bar{A}_{E\varepsilon }^{f} ]$. However, for the numerical evaluation of, $[\bar{C}]$ and $[\bar{e}]$ using Eq. (10), the homogeneous electric potential boundary conditions over the boundary surfaces of RVE are applied (ϕ = 0 on −X _B , +X _B , −Y _B , +Y _B , −Z _B and +Z _B ) that yields, $\{ \bar{E}\} = 0$. Under this constraint of electric potential (ϕ), the elements of $[\bar{A}_{\varepsilon }^{f} ]$ and $[\bar{A}_{E\varepsilon }^{f} ]$ are determined by applying different homogeneous displacement boundary conditions over the boundary surfaces of RVE. For the constituent materials used in the present composite, the appropriate homogeneous displacement boundary conditions are listed in Table 2 together with the corresponding zero/non-zero elements of, $\{ \bar{\varepsilon }\}$. A particular type of boundary condition in Table 2 is chosen to obtain only one non-zero component of $\{ \bar{\varepsilon }\}$ that is used to compute a particular column of $[\bar{A}_{\varepsilon }^{f} ]$ or $[\bar{A}_{E\varepsilon }^{f} ]$ matrix using Eq. (6). Thus, a total of six columns in $[\bar{A}_{\varepsilon }^{f} ]$ or in $[\bar{A}_{E\varepsilon }^{f} ]$ can be computed by applying the six types of boundary conditions separately as described in Table 2. It may be noted here that for every type of boundary conditions, first the solutions for zero and non-zero components of, $\{ \bar{\varepsilon }\}$ and $\{ \bar{E}\}$ are verified according to the aforementioned strategy and then, the elements of, $[\bar{A}_{\varepsilon }^{f} ]$ and $[\bar{A}_{E\varepsilon }^{f} ]$ are computed using the relation defined by Eq. (6).

Table 2 Boundary conditions for determining elements of $\left\{ {\bar{\varepsilon }} \right\}$ under $\left\{ {\bar{E}} \right\} = 0$ (a, b and c are the dimensions of RVE along, x, y and z directions)

The elements of effective permittivity matrix ($[\bar{ \in }]$) can be evaluated using Eq. (12) under the condition, $\{ \bar{\varepsilon }\} = 0$. For this condition, $\{ \bar{\varepsilon }\} = 0$, $\{ \bar{\varepsilon }^{f} \}$ and $\{ \bar{\varepsilon }^{m} \}$ may have non-zero values due to the electro-elastic coupling in piezoelectric fiber phase. This coupling effect is accounted by the strain-electric field coupled concentration matrix, $[\bar{A}_{\varepsilon E}^{f} ]$. However, for numerical evaluation of, $[\bar{A}_{E}^{f} ]$ and $[\bar{A}_{\varepsilon E}^{f} ]$ Eq. (12) under the zero composite volume average stain ($\{ \bar{\varepsilon }\} = 0$), the electric field is applied along each of the three orthogonal (x, y and z) directions of RVE associated with the homogeneous displacement boundary conditions as listed in Table 3. It may be noted from this table that for every type of applied electric field, the homogeneous displacement boundary conditions are chosen to ensure, $\{ \bar{\varepsilon }\} = 0$ while the homogeneous electric potential boundary conditions yield only one non-zero component of, $\{ \bar{E}\}$. Thus, implementing these three types of boundary conditions separately, three columns in $[\bar{A}_{E}^{f} ]$ or in $[\bar{A}_{\varepsilon E}^{f} ]$ can be computed using Eq. (6). During computation of, $[\bar{A}_{E}^{f} ]$ and $[\bar{A}_{\varepsilon E}^{f} ]$, the required aforementioned strategy for every type of electro-mechanical boundary conditions (Table 3) is first verified and then, the elements of $[\bar{A}_{E}^{f} ]$ and $[\bar{A}_{\varepsilon E}^{f} ]$ are computed.

Table 3 Boundary conditions for determining elements of $\left\{ {\bar{E}} \right\}$ under $\left\{ {\bar{\varepsilon }} \right\} = 0$ (a, b and c are the dimensions of RVE along, x, y and z directions)

For evaluation of linear electro-elastic material properties, the magnitude of a homogeneous strain component ($\varepsilon_{xx}^{0} ,\;\varepsilon_{yy}^{0} ,\;\varepsilon_{zz}^{0} ,\;\gamma_{yz}^{0} ,\;\gamma_{xz}^{0} ,\;\gamma_{xy}^{0}$ (Table 2)) is considered as less than 0.5 %. A high electric field causes nonlinear material behavior of piezoelectric materials. Thus, for linear material coefficients, the magnitude of a homogeneous electric field component (E ⁰ _xx , E ⁰ _yy , E ⁰ _zz (Table 2)) is considered as less than 0.2 V/μm. The following dimensionless parameters are used for presenting the numerical results, where, $\bar{e}_{ij}^{{}}$ is the effective piezoelectric coefficient of composite and e ^p _ij is the piezoelectric coefficient of fiber phase,

$$ \begin{aligned} R_{31} = \bar{e}_{31} /e_{31}^{p} \,\,\;R_{32} = \bar{e}_{32} /e_{32}^{p} ,\;R_{33} = \bar{e}_{33} /e_{33}^{p} ,\;R_{24} = \bar{e}_{24} /e_{24}^{p} \,, \\ R_{15} = \bar{e}_{15}^{{}} /e_{15}^{p} \,L_{r} = l_{f} /l_{c}, \, A_{r} = \left( {a_{f}^{ 2} } \right)/\left( {a_{c}^{ 2} } \right)\end{aligned} $$

Since the properties of similar smart composite are not available in the literature, the present finite element formulation and the applied boundary conditions are verified considering the present composite as a unidirectional continuous piezoelectric fiber reinforced composite. The effective electro-elastic coefficients of this continuous piezoelectric fiber reinforced composite are evaluated and illustrated in Fig. 3 together with those for an identical smart composite obtained by analytical solutions (Mallik and Ray 2003). It may be observed from this figure that the present results are in good agreement with the published analytical results (Mallik and Ray 2003). This comparison verifies the present finite element formulation and also the implemented electro-elastic boundary conditions.

Fig. 3

Verification of computed effective electro-mechanical properties of a unidirectional continuous piezoelectric fiber reinforced smart composite with those of an identical smart composite obtained by analytical solutions (Ref. Mallik and Ray 2003)

Since the short fibers (L _r  < 1) are utilized in the present smart composite, its fiber volume fraction is the function of A _r and L _r ratios as, η _f  = A _r  × L _r . So, it is convenient to study the effect of fiber volume fraction on the effective coefficients of the composite in terms of the variations of A _r or L _r or both (A _r and L _r ). Figure 4 illustrates the variations of effective elastic and piezoelectric coefficients with the fiber volume fraction for two different RVEs (RVE 1 and RVE 2). The L _r is considered as constant (L _r  = 0.95) and the A _r is varied in order to achieve the variation of fiber volume fraction. Note that, since L _r  < 1, the maximum value of fiber volume fraction could not be reached to 100 %. Thus, the results in Fig. 4 are evaluated considering the fiber volume fraction up to 60 %. It may be observed from Fig. 4 that there is no significant difference between two different RVEs in prediction of effective elastic and piezoelectric coefficients. Thus, one of the RVEs (say, RVE 1) can be authentically used in evaluation of further results.

Fig. 4

Variations of, a effective piezoelectric coefficients (R ₃₁, R ₃₂, R ₃₃ and R ₁₅), b effective elastic coefficients (C ₁₁, C ₃₃ and C ₅₅), c effective elastic coefficients (C ₁₂, C ₂₃ and C₄₄) with the fiber volume fraction for two different RVEs (a _f  = b _f , a _c  = b _c and l _r  = 0.95)

It may also be observed from Fig. 4 that for a particular value of fiber volume faction, the value of R ₃₁ is significantly more than the value of R ₃₂ or R ₃₃. The value of R ₃₁ indicatively increases with the increasing fiber volume faction and exceeds the corresponding value of fiber phase material (R ₃₁ = 1) at a fiber volume faction of 50 % that is usually known as the critical piezoelectric fiber volume fraction. Thus, an improved piezoelectric coefficient can be achieved in the present smart composite that makes it an effective distributed actuator material in structural applications where the in-plane actuation with transverse applied voltage is the major requirement.

Figure 5 presents the variations of effective piezoelectric coefficients with the A _r for different values of L _r . This figure shows that for any value of L _r , the magnitudes of coefficients (R ₃₁, R ₃₂ and R ₃₃) significantly increase with the increasing A _r . Also, the corresponding rate of increase is more for the higher value of L _r . However, since the nature of the variation of a coefficient is almost the same for any value of L _r , the results suggest to consider maximum possible A _r for improved effective piezoelectric coefficients.

Fig. 5

Variations of effective piezoelectric coefficients, a R ₃₁, b R ₃₂ and c R ₃₃ with the area ratio (A _r ) for different values of length ratio (L _r )

Figure 6 demonstrates the variations of effective piezoelectric coefficients (R ₃₁, R ₃₂ and R ₃₃) with the L _r for different values of A _r . The figure demonstrates that for any value of A _r , all effective coefficients (R ₃₁, R ₃₂ and R ₃₃) nonlinearly increases with the increase of L _r and the coefficients reach to their maximum values when the fiber is continuous throughout the RVE (L _r  = 1). It may also be observed that the effect of A _r is almost insignificant unless the value of L _r is not high enough. Thus, the high L _r not only improves the magnitudes of effective piezoelectric coefficients but also makes the A _r as a more important parameter for the same coefficients.

Fig. 6

Variations of effective piezoelectric coefficients, a R ₃₁, b R ₃₂ and c R ₃₃ with the length ratio (L _r ) for different values of area ratio (A _r )

In the forgoing results (Figs. 5, 6), the variations of effective piezoelectric coefficients either with the A _r (at constant L _r ) or with the L _r (at constant A _r ) are demonstrated. For the variation of A _r or L _r, the fiber volume fraction of the smart composite also varies. Now, if the fiber volume fraction remains constant then it is important to find out the corresponding optimal values of A _r and L _r for maximum possible magnitudes of effective piezoelectric coefficients. Note that for a constant fiber volume fraction, the optimal value of A _r implies the optimal value of L _r since they are related by, η _f  = A _r  × L _r . However, in order to compute these optimal values, A _r is varied within its possible range following the relation, η _f  = A _r × L _r and the corresponding variations in the magnitudes of effective coefficients (R ₃₁, R ₃₂ and R ₃₃) are illustrated in Fig. 7. For η _f  = 0.4, the minimum value of A _r would be greater than 0.4 because of the constraint, L _r  < 1. Similarly, the maximum value of A _r would be less than 100 % according to the design aspects of composites. Thus, the variation of A _r for η _f  = 0.4 is considered within the possible range, 0.45 and 0.9. In a similar manner, the variation of A _r for η _f  = 0.5 is considered within the possible range, 0.55 and 0.9. Within the possible range of A _r for a given value of η _f , the variations of effective coefficients R ₃₁, R ₃₂ and R ₃₃ are illustrated in Fig. 7a, b and c, respectively. It may be observed from Fig. 7a or c that for the largest magnitude of R ₃₁ or R ₃₃, the optimal value of A _r may be chosen as, 0.45 or 0.55 for the fiber volume fraction of 0.4 or 0.5, respectively. Similarly, for the largest value of R ₃₂, Fig. 7b shows the optimal value of A _r as 0.7 for both specified values (0.4 and 0.5) of the fiber volume fraction. Thus, these results show different optimal values of A _r for different coefficients. Among those values, one would be selected based on the most important coefficient (R ₃₁) for the present smart composite.

Fig. 7

Variations of effective piezoelectric coefficients, a R ₃₁,b R ₃₂ and c R ₃₃ with the area ratio (A _r ) at constant fiber volume fraction (η _f )

The results in Figs. 5, 6 and 7 give an estimation about the magnitudes of L _r and A _r for improved coefficients (R ₃₁, R ₃₂ and R ₃₃). These results suggest a high value (near 1.0) of L _r for the improved coefficients at any fiber volume fraction. In accordance, if a high value of L _r is considered as fixed then the magnitudes of coefficients depend only on the A _r and its (A _r ) useful value can be estimated. Now, along with this estimation of A _r and L _r , a similar estimation in the value of the fiber aspect ratio (l _f /a _f ) is also required for improved piezoelectric coefficients. For this estimation, a high fixed value of length ratio (L _r  = 0.9) is considered and then the variations of coefficients with the fiber aspect ratio (l _f /a _f ) are evaluated for different values of A _r . The different A _r are achieved by different values of a _f . For each A _r or a _f , the length of the fiber (l _f ) is increased in order to vary the fiber aspect ratio (l _f /a _f ) from 1.0 to a higher value and the corresponding variations in the magnitudes of piezoelectric coefficients are illustrated in Fig. 8. Note that the increase of l _f causes the increase of l _c , but this increase in the value of l _c has no effect on the magnitudes of effective coefficients since the corresponding area and L _r remain constant. It may be observed from Fig. 8 that for a particular A _r , the magnitudes of R ₃₁ and R ₃₂ are equal at, l _f /a _f  = 1. In fact, the cubic shaped fiber for l _f /a _f  = 1 (a _f  = b _f  = l _f ) and the equality in the magnitudes of e ₃₁ and e₃₂ in fiber phase material cause, R ₃₁ = R ₃₂ at, l _f /a _f  = 1. However, Fig. 8 also demonstrates an important observation that for a particular A _r, all piezoelectric coefficients (R ₃₁, R ₃₂ and R ₃₃) significantly vary with the increasing fiber aspect ratio (l _f /a _f ). But, as this increasing ratio (l _f /a _f ) exceeds certain value, it has almost insignificant effect on the magnitudes of coefficients. Thus, the increasing fiber aspect ratio (l _f /a _f ) has an upper limit corresponding to an A _r even though this upper limit of fiber aspect ratio varies insignificantly with the A _r (Fig. 8). It may also be observed from Fig. 8 that the increase of fiber aspect ratio causes to increase the magnitude of, R ₃₁ while the magnitudes of other coefficients (R ₃₂, R ₃₃) decrease. Thus, this result suggests a higher fiber aspect ratio for improved magnitude of coefficient, R ₃₁, possibly up to its upper limit. It is to be noted here that, although the results in Fig. 8 are evaluated considering a particular value of L _r as 0.9, similar observations are also obtained for other values of the same parameter.

Fig. 8

Variations of effective piezoelectric coefficients, a R ₃₁, b R ₃₂ and c R ₃₃ with the fiber aspect ratio (l _f /a _f ) (L _r  = 0.9)

6 Conclusions

In the present work, a micromechanical finite element analysis of effective properties of a unidirectional short piezoelectric fiber reinforced composite is presented. The unidirectional identical short piezoelectric fibers in the composite lamina are coaxial along the longitudinal direction and aligned in the plane of lamina. The identical short fibers are equally spaced in the epoxy matrix material along any of the longitudinal, transverse and lateral directions of the lamina. A continuum micromechanics approach is utilized for predicting the effective material coefficients through the numerical evaluation of Hill’s volume average electro-elastic coupled field concentration matrices. An electro-elastic finite element model of RVE or unit cell associated with the appropriate electro-elastic boundary conditions are presented for evaluation of concentration matrices. The present finite element micromechanics model and boundary conditions are verified by computing the effective properties of an existing unidirectional continuous piezoelectric fiber reinforced composite. The numerical illustrations present the variations of effective electro-elastic coefficients of the unidirectional short piezoelectric composite with its fiber volume fraction and also show an improved piezoelectric coefficient e ₃₁ over that of the fiber counterpart as the fiber volume fraction exceeds a certain value. The analysis suggests maximum possible L _r between a short fiber and the corresponding RVE for improved effective piezoelectric coefficients. The consideration of maximum possible L _r is also inevitable in order to make the corresponding A _r as an important parameter for the magnitudes of effective coefficients. For the maximum magnitude of a piezoelectric coefficient at a specified fiber volume fraction, the optimal area and the optimal L _r in between the short fiber and the corresponding RVE are numerically assessed. It is observed that an increase in the length of the short fiber with respect to its cross sectional area improves the magnitude of, e ₃₁, but this increase is restricted to an upper limit of the increasing fiber length.