Comments on “Reflection of plane waves at the initially stressed surface of a fiber-reinforced thermoelastic half space with temperature dependent properties, Int J Mech Mater Des (2019) 15: 159–173”

Abstract

Snell’s law provides a mathematical basis for the continuation of wave-field at a boundary. In the paper under review, theoretical formulation fails in applying this law correctly. Consequently, the whole reflection procedure goes off-track and the study wanders in incorrect domain. Researchers in the field may note the mathematical discrepancies identifed in this incorrect procedure.

1 Introduction

Deswal et al. (2019) considered to study the reflection phenomenon for the incidence of plane harmonic waves at the plane boundary of initially stressed fiber-reinforced thermoelastic half space. Two different theories of generalized thermoelasticity are applied to compute the velocities, amplitude ratios and energy ratios for various reflected waves. Being thermoelastic, this medium behaves dissipative to the propagation of elastic waves. Then, with anisotropy induced by fiber-reinforcement and initial stress, this medium no longer remains isotropic. Mathematically, the complex coefficients $D_{j}$, through the relations (23)–(25) in Deswal et al. (2019), certify the dissipative character of the medium considered. The dependence of these coefficients on the propagation direction (i.e., angle $\theta$) defines the anisotropic propagation. Hence, the study in question deals with the reflection phenomenon at the plane boundary of a dissipative anisotropic semi-infinite medium. Throughout this text, the numbers in parentheses identify the equations or relations, as specified in Deswal et al. (2019).

2 Anisotropic attenuated propagation

The expressions (22) identify the time harmonic wave-field restricted to x–y plane of the considered medium. This medium being orthotropic, such a restriction demands three orthogonal symmetry planes to coincide with the coordinate planes in Euclidean space. Then, in the x–y plane, propagation is considered along a direction making angle $\theta$ with the x-direction. Roots of the equation (26), a cubic in $V^2$, defines the propagation of three bulk waves in considered medium. In this equation, the complex coefficients (A,  B,  C) involve the angle $\theta$, which implies the velocities ($V_1,V_2,V_3$) as functions of propagation direction. Hence, for any chosen $\theta$, a complex $V_j(\theta )$ is the velocity of the corresponding wave for propagation along the chosen direction. Then, with complex V, the frequency $\omega =kV$ cannot be real unless k is a complex number (real multiple of conjugate to V), which should imply the attenuated wave-field throughout the x–y plane. Consequently, with complex k, the phase $k(-x\cos \theta +y\sin \theta )-\omega t$ in expression (22) becomes complex. With real $\theta$, this phase defines same direction for propagation as well attenuation vector, i.e., homogeneous propagation of attenuated wave in considered medium. This represents only a special case of the inhomogeneous propagation, which is generally considered in any dissipative medium (Borcherdt 1982).

3 Reflection

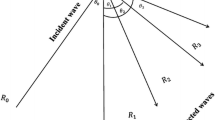
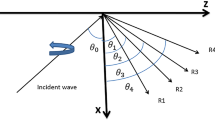
A harmonic plane wave ($qP_1$) is incident at the plane surface $x=0$, making an angle $\theta _0$ with the x-direction. For this $\theta _0$, the cubic equation (26) is solved into three complex velocities, $V_j,~(j=1,2,3)$. The direction dependence in anisotropy demands to consider the orientation of the angle $\theta _0$ as well. Then, $V_0=V_1(\theta _0)$ defines the velocity of $qP_1$ wave incident along the direction of $\theta _0$ (to be measured anti-clockwise from positive y-direction in figure 1). Similarly, for the incidence of $qP_2$ (or, $qP_3$) wave along the direction of $\theta _0$, $V_2(\theta _0)$ (or, $V_3(\theta _0))$ will denote the velocity of incident wave. It may be noticed that the coefficients $D_{j}$, and hence (A,  B,  C) in (26), change with the angle $\theta$. The presence of $'\sin \theta '$ in the expressions for $D_{j}$ implies different values for $V_1(\theta _1)$ and $V_1(\theta _0)=V_0(\theta _0)$, even when $\theta _1=-\theta _0$. That means, only $\theta _1=\theta _0$ (in magnitude as well as orientation) ensures that the velocity $V_1(\theta _1)$ of any reflected $qP_1$ wave is same as the velocity $V_0(\theta _0)$ of incident $qP_1$ wave. Unfortunately, with orientation, this equality can only be possible for normal incidence only. Even in magnitudes, this equality between angles of incidence and reflection cannot be assumed but needed to be derived from Snell’s law. In other words, the $'$angle of reflection = angle of incidence$'$ rule does not hold for any reflection at the boundary of anisotropic medium. Consequently, the velocity of reflected wave will be different from the velocity of incident wave, even when the type of reflected wave is same as that of the incident wave.

3.1 Snell’s Law

The identical horizontal slowness for all the waves at the plane surface $x=0$ defines the Snell’s law. That means, an identical $'k\sin \theta '$ for incident as well as all the reflected waves. Hence, the complex relations $k_0\sin \theta _0=k_1\sin \theta _1=k_2\sin \theta _2=k_3\sin \theta _3$ define a generalised Snell’s law. Else, the relations (29) make Snell’s law with complex (anisotropic) velocities $V_j=V_j(\theta _j),~(j=0,1,2,3)$. Hence, the relation ${\sin \theta _0\over V_0(\theta _0)}={\sin \theta _r\over V_r(\theta _r)}$ should provide the propagation characteristics (propagation direction, attenuation direction, complex velocity) of each reflected wave (identified with a value of $r=1,2,3)$. Note that $V_0(\theta _0)$ can be extracted from the cubic equation (26), for fixed (known) incidence angle $\theta _0$. Similarly, the velocity $V_r(\theta _r)$ of any reflected wave can come from (26), only when $\theta _r$ is known. Then, $V_r(\theta _0)$ cannot be considered as the velocities of reflected waves (except, for incidence along some particular symmetry directions).

3.2 Reflected wave: propagation characteristics

Consider the incidence of $qP_1$ wave with velocity $V_0=V_1(\theta _0)$ along the incident angle $\theta _0$. For the propagation characteristics of reflected $qP_1$ wave in x–y plane, it requires to solve ${\sin \theta _0\over V_1(\theta _0)}={\sin \theta _1\over V_1(\theta _1)}$ for $\theta _1$. But, through (26), this $\theta _1$ is implicit in the calculation of $V_1(\theta _1)$, as complex velocity of reflected $qP_1$ wave. Unfortunately, presence of anisotropy blocks the isotropy bye-pass of $\theta _1=\theta _0$. This requires solving the complex irrational equation $'{\sin \theta _0V_1(\theta _1) -V_1(\theta _0)}\sin \theta _1=0'$ for $\theta _1$, as a complex function of $\theta _0$. Similarly, for any other reflected wave along the direction of $\theta _r$ ($r=2$ or 3) in x–y plane, one needs to solve the relation ${\sin \theta _0\over V_1(\theta _0)}={\sin \theta _r\over V_r(\theta _r)}$ for angle $\theta _r$. Consequently, the direction (i.e., complex angle $\theta _r$) and the complex velocity $V_r$ of any reflected wave vary with the incident angle of $qP_1$ wave.

Finally, the reflection phenomenon demands to solve, in turn, ${\sin \theta _0\over V_0(\theta _0)}={\sin \theta _r\over V_r(\theta _r)},~(r=1,2,3),$ for $\theta _r$. Obviously, for incident $qP_1$ wave, we have $V_0(\theta _0)=V_1(\theta _0)$. On starting with a fixed real $\theta _0$ (assuming the incidence of homogeneous wave), the equation (26) gets three complex velocities $V_j(\theta _0),~(j=1,2,3)$. Incident wave is fixed through a value for j (e.g., $j=1$ for $qP_1$ wave). Now, with known $\theta _0$ (chosen) and complex velocity $V_1(\theta _0)$ of the incident $qP_1$ wave from (26), the relation ${\sin \theta _0\over V_0(\theta _0)}={\sin \theta _r\over V_r(\theta _r)}$ (from Snell’s law) defines a complex irrational equation, $\sin \theta _0 V_r(\theta _r)-\sin \theta _rV_0(\theta _0)=0$, in complex unknown $\theta _r$.

There may not be any standard method for solving a complex irrational equation for its one or all roots. Moreover, getting a real root ($\theta _r$) of the complex equation, $\sin \theta _0 V_r(\theta _r)-\sin \theta _rV_0(\theta _0)=0$, may not be less than a magic. Then, for complex values of $\theta _r$ and $V_r(\theta _r)$ from (26), the corresponding wave is represented by a complex slowness vector ($\mathbf{p}={\hat{N}}/V$; complex ${\hat{N}}$ such that ${\hat{N}}\cdot {\hat{N}}=1$). Consequently, each reflected wave should propagate as an inhomogeneous wave, having different directions for propagation and attenuation vectors. Then, the figure 1, in Deswal et al. (2019), cannot be a correct exhibition of the reflection phenomenon in the considered anisotropic dissipative medium.

4 Consequences

With incorrect directions as well as velocities of all the reflected waves, the whole reflection process in Deswal et al. (2019) goes off-track. The incorrect coefficients ($b_{ij}$ and $Y_i$) in (34) yield incorrect amplitude ratios ($Z_j$) as well as energy partition ($E_i$). Each of the complex $Z_j$ is resolved to define amplitude ratio ($|Z_j|$) and phase shift ($\arg Z_j$) for the corresponding reflected wave. Thus, the plots in figures 1 to 7 are exhibiting the incorrect and incomplete attributes of reflected waves. Further, these complex $Z_i$ yield the complex energy ratios (32)–(35) for different reflected waves. In fact, the energy partition at a boundary is represented through the real energy fluxes in the direction normal to the plane boundary (Achenbach 1973). That means, the plots of $|E_i|,~(i=1,2,3)$ in figure 8 show an incorrect partition of incident energy among the reflected waves at the boundary.

The phase velocities of all the reflected waves vary with the direction of incident wave as well. Hence, the various plots in figures 9 and 10 do not carry any meaning unless the incident direction is specified. Moreover, through the incorrect interpretation of Snell’s law, the complex velocities $V_j,~(j=1,2,3)$, cannot be accurate. Further, for any reflected wave in dissipative medium, magnitude of complex velocity keeps no physical significance. Rather, a complex V is used to define the phase velocity [$1/\mathfrak {R}(V^{-1}$)] and attenuation coefficient [$-\mathfrak {I}(V^2)/\mathfrak {R}(V^2)$].

5 Remarks

The way-out lies in solving the equations of motion in terms of vertical slowness for known horizontal slowness. This starts with writing the wave-field expression (22) in complex slowness vector, say $\mathbf{p}=(p_1,p_2,q)$, instead of wave velocity V. The resulting Christoffel system yields a homogeneous system of three equations in components of slowness vector. This system is solved into an algebraic equation of degree six in vertical slowness (q), while coeffcients being the functions of horizontal slowness $(p_1,p_2)$.

An incident (homogeneous) wave is considered with known (chosen) direction of propagation towards the boundary. This direction enables to calculate the velocity of incident wave from (26) and hence to define the horizontal slowness $(p_1,p_2)$. This horizontal slowness, identical for all the waves at a boundary (cf., Snell’s law), is used to calculate the coefficients of the sixth-degree algebraic equation in q. The six roots of this equation define six values for vertical slowness (q). Out of these six values, only three corresponds to the waves traveling away from the boundary, i.e., three reflected waves. Now, each vertical slowness value combines, in turn, with the common horizontal slowness to define the slowness vectors for three reflected waves. For a reflected wave, the corresponding slowness vector, $\mathbf{p}=(p_1,p_2,q)$, is resolved as $\mathbf{p}=\mathbf{P}+\imath \mathbf{A}$ to define the propagation vector $(\mathbf{P})$, attenuation vector ($\mathbf{A}$) and hence inhomogeneity (deviation of A from P). A relation $\mathbf{p}\cdot \mathbf{p}={1\over V^2}$ gets the complex velocity for this reflected wave, resulting from the considered homogeneous incident wave.

For inhomogeneous (general case) incident wave, there is different procedure to calculate the slowness vector of incident wave, which provides the common horizontal slowness to define Snell’s law. The relevant procedures may be found in Cerveny and Psencik (2005) or Sharma (2008). A more recent study (Sharma 2015) on solving Snell’s law at the boundaries of various elastic media can also be helpful.