1 Introduction

Conventional thermoelasticity is based on the principles of the classical theory of heat conductivity, specifically on the classical Fourier’s law, which relates the heat flux vector \(\vec {q}\) to the temperature gradient. In combination with the law of conservation of energy, this equation leads to the parabolic heat conduction equation. In non-classical theories, the Fourier’s law and heat conduction equation are replaced by more general equations. The subject of generalized thermoelasticity/non-classical thermoelasticity covers a wide range of extensions of thermoelasticity. In contrast to the conventional coupled thermoelasticity theory, which involves a parabolic-type heat transport equation, these generalized theories involving a hyperbolic-type heat transport equation are supported by experiments exhibiting the actual occurrence of wave-type heat transport in solids called the second-sound effect.

Generalized theories proposed by Lord and Shulman [1] and Green and Lindsay [2] are the first two well-known generalized theories of thermoelasticity. In the first model [1], the Fourier’s law of heat conduction is replaced by the Maxwell–Cattaneo’s law that introduces one thermal relaxation time parameter in the heat conduction law, whereas in the model of Green and Lindsay, two different relaxation times are introduced in the constitutive relations for the stress tensor and the entropy. An interesting review article by Chandrasekharaiah [3] contains many important results involving many modifications with a list of references. The next generalization to thermoelasticity is proposed by Green and Naghdi [4–6] who provided sufficient basic modifications in the constitutive equations that permit the treatment of a much wider class of heat flow problems labeled as GN-I, GN-II, and GN-III. GN models include a term called “thermal displacement gradient” among the independent constitutive variables.

The generalized thermoelasticity theory with the dual-phase-lag effect has been developed by Tzou [7] and Chandrasekharaiah [8]. Tzou [7] introduced two different phase lags, one for the heat flux vector and the other for the temperature gradient. According to this model, the classical Fourier’s law \(\vec {q}=-k\vec {\nabla }T\) has been replaced by \(\vec {q}\left( {P,t+\tau _q}\right) =-k\vec {\nabla }T\left( {P,t+\tau _T}\right) \), where the temperature gradient \(\vec {\nabla }T\) at a point \(P\) of the material at time \(t+\tau _T\) corresponds to the heat flux vector \(\vec {q}\) at the same point at time \(t+\tau _q \). The delay time \(\tau _T\) is supposed to be caused by the microstructural interactions (small scale effects of heat transport in space, such as phonon–electron interaction or phonon scattering) and is called the phase lag of the temperature gradient. The other delay time \(\tau _q\) is interpreted as the relaxation time due to the fast transient effects of the thermal inertia (or small scale effects of heat transport in time) and is called the phase lag of the heat flux. The stability of dual-phase-lag heat conduction was discussed by Quintanilla and Racke [9]. Hetnarski and Ignaczak [10] examined thoroughly these four models in a survey article by focussing on the theoretical significance of these models.

The most recent development in thermoelasticity theory is the thermoelasticity with three phase-lags (Roychoudhuri [11]). In this model, a phase-lag for the thermal displacement gradient is also introduced in addition to the phase-lags for the heat flux vector and the temperature gradient. According to this model, \(\vec {q}(P,t+\tau _q)=-\left[ k\vec {\nabla }T(P,t+\tau _T)+K^{*}\vec {\nabla }v(P,t+\tau _v)\right] \), where \(\vec {\nabla }\nu (\dot{v}=T)\) is the thermal displacement gradient, \(K^{*}\)(of physical dimension conductivity/time) is a material constant characteristic of the theory and \(\tau _v\) is the delay time in the thermal displacement gradient. The stability of the three phase-lag heat conduction equation and the relations among the three material parameters are discussed by Quintanilla and Racke [12]. Prasad et al. [13] reported the effects of phase lags on wave propagation in a homogeneous, isotropic, and unbounded solid due to a continuous line heat source. The problem of magneto-thermoelastic interactions in a unified formulation of different theories for a perfectly conducting medium has nicely been tackled by Das and Kanoria [14]. Very recently, Prasad et al. [15] have contributed their research efforts in formulating the boundary integral equation for the solution of equations in three-dimensional Euclidean space under coupled thermoelasticity with three phase-lags.

The elastic modulus is an important physical property of materials reflecting the elastic deformation capacity of the material when subjected to an applied external load. Most of the investigations were done under the assumption of the temperature-independent material properties, which limit the applicability of the solutions obtained to certain ranges of temperature. At high temperature the material characteristics such as the modulus of elasticity, Poisson’s ratio, the coefficient of thermal expansion, and the thermal conductivity are no longer constants [16]. In recent years, due to the progress in various fields in science and technology, it has become necessary to take into consideration the real behavior of the material characteristics. Keeping these facts in mind, several researchers [17–19] have examined the temperature dependence of the elastic modulus on the behavior of two-dimensional solutions in a generalized thermoelastic medium.

Many problems in engineering practice involve the determination of stresses and/or displacements in bodies that are three-dimensional. Exact analytical solutions are available only for a few three-dimensional problems with simple geometries and/or loading conditions. Hence, numerical or experimental analyses are generally required in solving such problems. Baksi et al. [20] have adopted an eigenvalue approach along with Laplace and Fourier transforms to investigate a three-dimensional magneto-thermoelasatic problem with rotation and a heat source. Ezzat and Youssef [21] have devoted themselves to the vibrational analysis of a three-dimensional thermal shock problem with one relaxation time. Employing normal mode analysis and an eigenvalue approach to the governing equations of Green and Naghdi model II, Sarkar and Lahiri [22] have solved a three-dimensional problem subject to a time-dependent heat source.

In spite of these recent studies of three-dimensional thermoelastic problems [20–22], hardly any attempt is made to investigate three-dimensional thermoelastic problems with a temperature-dependent modulus of elasticity in the two-phase-lag model. The main objective of this paper is to study the above mentioned three-dimensional problem based on the two-phase-lag model by employing normal mode analysis. The governing non-dimensional coupled equations in Cartesian coordinates are applied to a thermal shock problem in an elastic body which fills the half-space. This is followed by a numerical example of a copper-like material. Results of this analysis are also presented graphically.

2 Formulation of the Problem with Basic Equations

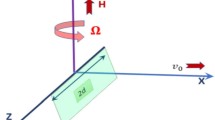
In the present paper, we consider an isotropic, homogeneous, and thermoelastic medium with temperature-dependent mechanical properties in three-dimensional space which fills the region \(\varOmega \), where \(\varOmega \) is defined by \(\varOmega =\{(x,y,z): 0\le x\le \infty , -\infty <y<\infty , -\infty <z<\infty \}\) subjected to a thermal shock on the bounding plane to the surface \(x =0\). The body is initially at rest and the surface \(x = 0\) is assumed to be traction-free. Following Tzou [7] and Chandrasekharaiah [8] generalized thermoelasticity theory with dual-phase-lag effect in the absence of body forces and internal heat sources, we state the basic field equations as follows:

  1. (a)

    The principle of balance of linear momentum leads to the equation of motion,

    $$\begin{aligned} \mu u_{i,jj} +(\lambda +\mu )u_{j,ij} -\beta _1 \theta ,_i =\rho \ddot{u}_i. \end{aligned}$$
    (1)
  2. (b)

    Equation of heat conduction According to the modified Fourier’s law of heat conduction \(\vec {q}(P,t+\tau _q)=-k\vec {\nabla }T(P,t+\tau _T)\) and equation of energy conservation \(q_{i,i} =-\rho T_\mathrm{0} \dot{S}\), we obtain equation of heat conduction as

    $$\begin{aligned} k\left( {1+\tau _T \frac{\partial }{\partial t}}\right) \nabla ^{2}\theta =\left( {1+\tau _q \frac{\partial }{\partial t}+\frac{1}{2}\tau _q^2 \frac{\partial ^{2}}{\partial t^{2}}}\right) \left( {\rho c_E \dot{\theta }+\beta _1 T_\mathrm{0} \dot{e}}\right) . \end{aligned}$$
    (2)
  3. (c)

    Constitutive equation

    $$\begin{aligned} \sigma _{ij} =2\mu e_{ij} +\lambda e\delta _{ij} -\beta _1 \theta \delta _{ij}. \end{aligned}$$
    (3)
  4. (d)

    Geometrical equation

    $$\begin{aligned} e_{ij} =\frac{1}{2}\left( {u_{i,j} +u_{j,i}}\right) . \end{aligned}$$
    (4)

In the preceding equations, \(i, j = 1, 2, 3\) refer to general coordinates, a comma followed by a suffix denotes material derivative, a superimposed dot denotes the derivative with respect to time and the tensor convention of summing over repeated indices is used, \(\lambda \) and \(\mu \) indicate Lame’s constants, \(\rho \) stands for the mass density, \(\sigma _{ij}\) stands for the components of the stress tensor, \(\theta =T-T_0, T\) is the absolute temperature of the medium, \(T_{0}\) is the reference temperature of the medium, \(k\) indicates thermal conductivity, \(c_E\) means the specific heat at constant strain, \(u_i\) denotes the components of the displacement vector, \(e_{ij}\) is the strain tensor, \(q_i\) indicates the component of heat flux vector, \(S\) means the entropy per unit mass, \(\beta _1\) is a material constant given by \(\beta _1 =(3\lambda +2\mu )\alpha _t , \alpha _t\) is the coefficient of linear thermal expansion, \(e\) is the cubical dilatation, \(\nabla ^{2}\) is the Laplacian operator, \(\delta _{ij}\) is the Kronecker delta function, and \(\tau _T\) and \(\tau _q\) are the phase lags of the temperature gradient and heat flux, respectively.

Our goal is to investigate the effect of the temperature dependence of the modulus of elasticity keeping the other elastic and thermal parameters constant; therefore, we assume

$$\begin{aligned} E=E_0 f(\theta ), \lambda =E_0 \lambda _0 f(\theta ), \mu =E_0 \mu _0 f(\theta ), \beta _1 =E_0 \beta _{10} f(\theta ), \end{aligned}$$
(5)

where \(f(\theta )\) is a given non-dimensional function of temperature, \(\lambda _0 =\frac{\nu }{(1+\nu )(1-2\nu )}, \mu _0 =\frac{1}{2(1+\nu )}, \beta _{10}=\frac{\alpha _t}{(1-2\nu )}\) and \(\nu \) is the Poisson’s ratio. In case of a temperature-independent modulus of elasticity, \(f(\theta )\equiv 1\hbox { and }E=E_0\).

Taking into consideration Eq. 5, Eqs. 1–3 are reduced to the forms,

$$\begin{aligned} \rho \ddot{u}_i&= E_0 f(\theta )\left[ {\left( {\lambda _0 +\mu _0}\right) e,_i +\mu _0 \nabla ^{2}u_i -\beta _{10} \theta ,_i}\right] \nonumber \\&+E_0 \left( {\lambda _0 e-\beta _{10} \theta }\right) f(\theta ),_i +2E_0 \mu _0 e_{ij} f(\theta ),_j,\end{aligned}$$
(6)
$$\begin{aligned} k\left( {1+\tau _T \frac{\partial }{\partial t}}\right) \nabla ^{2}\theta&= \left( {1+\tau _q \frac{\partial }{\partial t}+\frac{1}{2}\tau _q^2 \frac{\partial ^{2}}{\partial t^{2}}}\right) \left[ {\rho c_E \dot{\theta }+\beta _{10} E_0 f(\theta )T_0 \dot{e}}\right] ,\end{aligned}$$
(7)
$$\begin{aligned} \sigma _{ij}&= E_0 f(\theta )\left[ {2\mu _0 e_{ij} +\delta _{ij} \left( {\lambda _0 e-\beta _{10} \theta }\right) }\right] , \end{aligned}$$
(8)

respectively.

In generalized thermoelasticity as well as in the coupled theory, only the infinitesimal temperature deviations from the reference temperature are considered. Therefore, we consider a special case when \(|T-T_0 |\ll 1\) and \(f(\theta )=(1-\alpha ^{*}T_0)\), where \(\alpha ^{*}\) is an empirical material constant of dimension \((\frac{1}{K})\). Since \(f(\theta )\) is independent of spatial coordinates; hence, we have \(f(\theta ),_i =0\). In view of this, Eq. 6 becomes

$$\begin{aligned} \rho \ddot{u}_i =E_0 f(\theta )\left[ {\left( {\lambda _0 +\mu _0}\right) e,_i +\mu _0 \nabla ^{2}u_i -\beta _{10} \theta ,_i}\right] . \end{aligned}$$
(9)

Introducing the rectangular Cartesian coordinate system \((x,y,z)\) having an origin on the surface \(x=0\) with the \(x\)-axis vertical into the medium and the components of the displacement vector \(\vec {u}\) as \((u,v,w)\), the equation of motion, heat conduction equation, and constitutive relations can be expressed in component form as

$$\begin{aligned} \rho \ddot{u}&= E_0 f(\theta )\left[ \left( {\lambda _0 +2\mu _0}\right) \frac{\partial ^{2}u}{\partial x^{2}}\right. \nonumber \\&\left. +\,\mu _0 \left( {\frac{\partial ^{2}u}{\partial y^{2}}+\frac{\partial ^{2}u}{\partial z^{2}}}\right) +\left( {\lambda _0 +\mu _0}\right) \left( {\frac{\partial ^{2}v}{\partial x\partial y}+\frac{\partial ^{2}w}{\partial x\partial z}}\right) -\beta _{10} \frac{\partial \theta }{\partial x}\right] ,\end{aligned}$$
(10)
$$\begin{aligned} \rho \ddot{v}&= E_0 f(\theta )\left[ \left( {\lambda _0 +2\mu _0}\right) \frac{\partial ^{2}v}{\partial y^{2}}\right. \nonumber \\&\left. +\,\mu _0 \left( {\frac{\partial ^{2}v}{\partial x^{2}}+\frac{\partial ^{2}v}{\partial z^{2}}}\right) +\left( {\lambda _0 +\mu _0}\right) \left( {\frac{\partial ^{2}u}{\partial x\partial y}+\frac{\partial ^{2}w}{\partial y\partial z}}\right) -\beta _{10} \frac{\partial \theta }{\partial y}\right] ,\end{aligned}$$
(11)
$$\begin{aligned} \rho \ddot{w}&= E_0 f(\theta )\left[ \left( {\lambda _0 +2\mu _0}\right) \frac{\partial ^{2}w}{\partial z^{2}}\right. \nonumber \\&\left. +\,\mu _0 \left( {\frac{\partial ^{2}w}{\partial x^{2}}+\frac{\partial ^{2}w}{\partial y^{2}}}\right) +\left( {\lambda _0 +\mu _0}\right) \left( {\frac{\partial ^{2}u}{\partial x\partial z}+\frac{\partial ^{2}v}{\partial y\partial z}}\right) -\beta _{10} \frac{\partial \theta }{\partial z}\right] ,\end{aligned}$$
(12)
$$\begin{aligned}&k\left( {1+\tau _T \frac{\partial }{\partial t}}\right) \left( {\frac{\partial ^{2}\theta }{\partial x^{2}}+\frac{\partial ^{2}\theta }{\partial y^{2}}+\frac{\partial ^{2}\theta }{\partial z^{2}}}\right) \nonumber \\&= \left( {1\!+\!\tau _q \frac{\partial }{\partial t}\!+\!\frac{1}{2}\tau _q^2 \frac{\partial ^{2}}{\partial t^{2}}}\right) \left[ {\rho c_E \dot{\theta }\!+\!\beta _{10} E_0 T_0 f(\theta )\frac{\partial }{\partial t}\left( {\frac{\partial u}{\partial x}\!+\!\frac{\partial v}{\partial y}\!+\!\frac{\partial w}{\partial z}}\right) }\right] ,\qquad \quad \end{aligned}$$
(13)
$$\begin{aligned} \sigma _{xx}&= E_0 f(\theta )\left[ {2\mu _0 e_{xx} +\lambda _0 e-\beta _{10} \theta }\right] ,\end{aligned}$$
(14)
$$\begin{aligned} \sigma _{yy}&= E_0 f(\theta )\left[ {2\mu _0 e_{yy} +\lambda _0 e-\beta _{10} \theta }\right] ,\end{aligned}$$
(15)
$$\begin{aligned} \sigma _{zz}&= E_0 f(\theta )\left[ {2\mu _0 e_{zz} +\lambda _0 e-\beta _{10} \theta }\right] ,\end{aligned}$$
(16)
$$\begin{aligned} \sigma _{xy}&= 2\mu _0 E_0 f(\theta )e_{xy} =\mu _0 E_0 f(\theta )\left( {\frac{\partial u}{\partial y}+\frac{\partial v}{\partial x}}\right) ,\end{aligned}$$
(17)
$$\begin{aligned} \sigma _{xz}&= 2\mu _0 E_0 f(\theta )e_{xz} =\mu _0 E_0 f(\theta )\left( {\frac{\partial u}{\partial z}+\frac{\partial w}{\partial x}}\right) ,\end{aligned}$$
(18)
$$\begin{aligned} \sigma _{yz}&= 2\mu _0 E_0 f(\theta )e_{yz} =\mu _0 E_0 f(\theta )\left( {\frac{\partial v}{\partial z}+\frac{\partial w}{\partial y}}\right) , \end{aligned}$$
(19)

where

$$\begin{aligned} e_{xx} =\frac{\partial u}{\partial x}, e_{yy} =\frac{\partial v}{\partial y}, e_{zz} =\frac{\partial w}{\partial z}, \mathrm{{and}}\; e=e_{xx} +e_{yy} +e_{zz}. \end{aligned}$$

Equations of motion (Eqs. 10–12) can be recast to the following forms as

$$\begin{aligned} \rho \frac{\partial \ddot{u}}{\partial x}&= E_0 f(\theta )\left[ {\mu _0 \nabla ^{2}\frac{\partial u}{\partial x}+\left( {\lambda _0 +\mu _0}\right) \frac{\partial ^{2}e}{\partial x^{2}}-\beta _{10} \frac{\partial ^{2}\theta }{\partial x^{2}}}\right] ,\end{aligned}$$
(20)
$$\begin{aligned} \rho \frac{\partial \ddot{v}}{\partial y}&= E_0 f(\theta )\left[ {\mu _0 \nabla ^{2}\frac{\partial v}{\partial y}+\left( {\lambda _0 +\mu _0}\right) \frac{\partial ^{2}e}{\partial y^{2}}-\beta _{10} \frac{\partial ^{2}\theta }{\partial y^{2}}}\right] ,\end{aligned}$$
(21)
$$\begin{aligned} \rho \frac{\partial \ddot{w}}{\partial z}&= E_0 f(\theta )\left[ {\mu _0 \nabla ^{2}\frac{\partial w}{\partial z}+\left( {\lambda _0 +\mu _0}\right) \frac{\partial ^{2}e}{\partial z^{2}}-\beta _{10} \frac{\partial ^{2}\theta }{\partial z^{2}}}\right] . \end{aligned}$$
(22)

Proceeding with the analysis, we introduce the dimensionless terms as

$$\begin{aligned} ({x}',{y}',{z}',{u}',{v}',{w}')&= c_0 \eta _0 (x,y,z,u,v,w),\quad ({t}',{\tau }'_{q,T})=c_0^2 \eta _0 (t,\tau _{q,T}),\nonumber \\ \theta '&= \frac{\beta _{10} E_0 \theta }{\rho c_0^2}, {\sigma }'_{ij} =\frac{\sigma _{ij}}{\rho c_0^2} \end{aligned}$$
(23)

where

$$\begin{aligned} c_0^2 =\frac{\left( {\lambda _0 +2\mu _0}\right) E_0}{\rho } \ \hbox {and} \ \eta _0 =\frac{\rho c_E}{k}. \end{aligned}$$

Transferring the above equations to the non-dimensional forms, one can obtain

$$\begin{aligned} \alpha _0 \frac{\partial \ddot{u}}{\partial x}&= \delta \nabla ^{2}\frac{\partial u}{\partial x}+\left( {1-\delta }\right) \frac{\partial ^{2}e}{\partial x^{2}}-\frac{\partial ^{2}\theta }{\partial x^{2}},\end{aligned}$$
(24)
$$\begin{aligned} \alpha _0 \frac{\partial \ddot{v}}{\partial y}&= \delta \nabla ^{2}\frac{\partial v}{\partial y}+\left( {1-\delta }\right) \frac{\partial ^{2}e}{\partial y^{2}}-\frac{\partial ^{2}\theta }{\partial y^{2}},\end{aligned}$$
(25)
$$\begin{aligned} \alpha _0 \frac{\partial \ddot{w}}{\partial z}&= \delta \nabla ^{2}\frac{\partial w}{\partial z}+\left( {1-\delta }\right) \frac{\partial ^{2}e}{\partial z^{2}}-\frac{\partial ^{2}\theta }{\partial z^{2}},\end{aligned}$$
(26)
$$\begin{aligned} \left( {1+\tau _T \frac{\partial }{\partial t}}\right) \nabla ^{2}\theta&= \left( {1+\tau _q \frac{\partial }{\partial t}+\frac{1}{2}\tau _q^2 \frac{\partial ^{2}}{\partial t^{2}}}\right) \left( {\dot{\theta }+\delta _0 \dot{e}}\right) , \end{aligned}$$
(27)

where

$$\begin{aligned} \alpha _0 =\frac{1}{f(\theta )}=\frac{1}{1-\alpha ^{*}T_0}, \delta =\frac{\mu _0}{\lambda _0 +2\mu _0}, \delta _0 =\frac{\beta _{10}^2 E_0 T_0}{\rho c_E \alpha _0 (\lambda _0 +2\mu _0)} \end{aligned}$$

and we have dropped the primes for convenience.

In a similar manner, we can transform the constitutive relations in non-dimensional forms. The dimensionless expressions for the constitutive relations are defined in Appendix 1. By summing Eqs. 24–26, we arrive at

$$\begin{aligned} \alpha _0 \ddot{e}=\nabla ^{2}e-\nabla ^{2}\theta . \end{aligned}$$
(28)

We will consider the invariant stress \(\sigma \) to be the mean value of the principal stresses as follows:

$$\begin{aligned} \sigma =\frac{\sigma _{xx} +\sigma _{yy} +\sigma _{zz}}{3}. \end{aligned}$$
(29)

Substituting the values of \(\sigma _{xx}, \sigma _{yy}\), and \(\sigma _{zz}\) into the and above expression, one can obtain

$$\begin{aligned} \alpha _0 \sigma =\delta _1 e-\theta , \end{aligned}$$
(30)

where

$$\begin{aligned} \delta _1 =\frac{(3-4\delta )}{3}. \end{aligned}$$

3 Normal Mode Analysis

Generally, Laplace transformation and Fourier transformation are employed to solve a three-dimensional generalized thermoelastic problem. In the application of this method, the partial differential equations can be converted into ordinary differential equations. By solving differential equations in the transformation domain and adopting inverse Fourier transformation and inverse Laplace transformation in the time domain, the solutions of the problem can be obtained. But this method entails a tiresome process. The key problem is that it introduces a discrete error and truncation error in the process of numerical inverse integrated transformation, so the second sound of heat conduction cannot be fully demonstrated. To compensate for the defects of the above mentioned method, we solve the problem of generalized thermoelasticity by employing normal mode analysis to the considered equations.

In this method, the solutions of the physical variables can be decomposed in terms of normal modes in the following form:

$$\begin{aligned} (u,v,w,e,\theta , \sigma _{ij})(x,y,z,t)=\left( {u^{*},v^{*},w^{*},e^{*}, \theta ^{*},\sigma _{ij}^*}\right) (x)\hbox {e}^{[\omega t+ \iota (my+nz)]}, \end{aligned}$$
(31)

where \(u^{*}(x),v^{*}(x),w^{*}(x),e^{*}(x),\theta ^{*}(x)\), and \(\sigma _{ij}^*(x)\) are the amplitudes of the functions, \(\iota =\sqrt{-1}, \omega \) is the angular frequency, and \(m\) and \(n\) are the wave numbers in \(y\)- and \(z\)-directions, respectively.

By using the normal modes defined in Eq. 31 on Eqs. 27, 28, and 30 and then eliminating \(e^{*}(x)\) from the resulting expressions, we obtain the following system of ordinary differential equations:

$$\begin{aligned} (D^{2}-m^{2}-n^{2})\theta ^{*}(x)&= \gamma _1 \left[ (\delta _0 +\delta _1)\theta ^{*}(x)+\alpha _0 \delta _0 \sigma ^{*}(x)\right] ,\end{aligned}$$
(32)
$$\begin{aligned} (D^{2}-m^{2}-n^{2})\sigma ^{*}(x)&= a_1 \sigma ^{*}(x)+a_2 \theta ^{*}(x), \end{aligned}$$
(33)

where \(\gamma _{1}, a_{1}\), and \(a_{2}\) are given in Appendix 2.

Elimination of \(\theta ^{*}(x)\) from Eqs. 32 and 33 yields the following fourth-order differential equation:

$$\begin{aligned} (D^{4}-LD^{2}+M)\sigma ^{*}(x)=0, \end{aligned}$$
(34)

where

$$\begin{aligned} L\!=\!\alpha _1 \!+\!\alpha _2, M\!=\!\alpha _1 \alpha _2 \!-\!\alpha _0 \delta _0 \gamma _1 a_2, \alpha _1 \!=\!m^{2}+n^{2}+a_1, \alpha _2 =m^{2}+n^{2}+(\delta _0 +\delta _1)\gamma _1. \end{aligned}$$

Adopting the same procedure, we can establish the following equation satisfied by \(\theta ^{*}(x)\) as

$$\begin{aligned} (D^{4}-LD^{2}+M)\theta ^{*}(x)=0. \end{aligned}$$
(35)

Since the intent is that the solutions vanish at infinity so as to satisfy the regularity condition at infinity, we now consider the following solutions of Eqs. 34 and 35 as

$$\begin{aligned} \sigma ^{*}(x)&= \sum _{i=1}^2 {R_i \hbox {e}^{-\lambda _i x}},\end{aligned}$$
(36)
$$\begin{aligned} \theta ^{*}(x)&= \sum _{i=1}^2 {{R}'_i \hbox {e}^{-\lambda _i x}} , \end{aligned}$$
(37)

where \(\lambda _{i}, R_{i}\), and \(R_{i}^{{\prime }}\) are defined in Appendix 3.

By virtue of Eqs. 31, 36, and 37, Eq. 30 leads to

$$\begin{aligned} e^{*}(x)=\frac{1}{\delta _1}\sum _{i=1}^2 {(\alpha _0 +d_i)R_i \hbox {e}^{-\lambda _i x}}. \end{aligned}$$
(38)

4 Application

In order to determine the constants \(R_{1}\) and \(R_{2}\), we need to consider the following boundary conditions at the surface \(x = 0\):

  1. (a)

    Mechanical boundary conditions

We will consider that the bounding plane to the surface \(x = 0\) has no traction anywhere, so we have

$$\begin{aligned} \sigma (x,y,z,t)=\sigma _{xx} (x,y,z,t)=\sigma _{yy} (x,y,z,t)=\sigma _{zz} (x,y,z,t)=0, \end{aligned}$$

which provides

$$\begin{aligned} \sigma ^{*}(x)=\sigma _{xx}^*(x)=\sigma _{yy}^*(x)=\sigma _{zz}^*(x)=0. \end{aligned}$$
(39)
  1. (b)

    Thermal boundary condition

The bounding plane \(x = 0\) is subjected to a time-dependent thermal shock of the form,

$$\begin{aligned} \theta (x,y,z,t)=f(x,y,z,t), \end{aligned}$$

which, in view of Eqs. 23 and 31, gives

$$\begin{aligned} \theta ^{*}(x)=f^{*}(m,n,\omega ). \end{aligned}$$
(40)

Applying the boundary conditions (Eqs. 39 and 40) into Eqs. 36 and 37 and then solving the resulting system, one can find

$$\begin{aligned} R_1&= \frac{f^{*}(m,n,\omega )}{d_1 -d_2},\nonumber \\ R_2&= -\frac{f^{*}(m,n,\omega )}{d_1 -d_2}. \end{aligned}$$
(41)

Now, performing normal mode analysis over Eq. 24 and taking into account Eqs. 37 and 38, we arrive at

$$\begin{aligned} (D^{2}-\lambda _u^2)u^{*}(x)=l_1 \hbox {e}^{-\lambda _1 x}+l_2 \hbox {e}^{-\lambda _2 x}, \end{aligned}$$
(42)

where \(\lambda _u^2 =m^{2}+n^{2}+\frac{\alpha _0 \omega ^{2}}{\delta }\) and

$$\begin{aligned} l_i =\frac{1}{\delta }\left[ {\frac{(1-\delta )}{\delta _1}(\alpha _0 +d_i)-d_i}\right] \lambda _i R_i . \end{aligned}$$

The solution of the differential (Eq. 42) takes the form,

$$\begin{aligned} u^{*}(x)=R_3 \hbox {e}^{-\lambda _u x}+\frac{l_1 \hbox {e}^{-\lambda _1 x}}{\lambda _{1}^2 -\lambda _{{}u}^2}+\frac{l_2 \hbox {e}^{-\lambda _2 x}}{\lambda _{2}^2 -\lambda _{u}^2}, \end{aligned}$$
(43)

where \(\lambda _1^2 \ne \lambda _2^2 \ne \lambda _u^2\) and \(R_{3}\) is a constant to be determined.

From Eqs. 14 and 30 after using Eqs. 23 and 31, we have

$$\begin{aligned} \alpha _0 \sigma _{xx}^*(x)=2\delta Du^{*}(x)+\frac{(1-2\delta )}{\delta _1}\alpha _0 \sigma ^{*}(x)+\left( \frac{1-2\delta -\delta _1}{\delta _1}\right) \theta ^{*}(x). \end{aligned}$$
(44)

In view of the boundary conditions, the above equation transforms to

$$\begin{aligned} Du^{*}(x)=\frac{\left( {\delta _1 +2\delta -1}\right) }{2\delta \delta _1}f^{*}\left( {m,n,\omega }\right) \; \hbox {at}\, x = 0, \end{aligned}$$
(45)

which with the help of Eq. 43 supplies the following value of \(R_{3}\) as

$$\begin{aligned} R_3 =\frac{\left( {1-\delta _1 -2\delta }\right) }{2\delta \delta _1 \lambda _{u}}f^{*}\left( {m,n,\omega }\right) -\frac{\lambda _1 l_1}{\lambda _{u} \left( {\lambda _1^2 -\lambda _{u}^2}\right) }-\frac{\lambda _2 l_2}{\lambda _{u} \left( {\lambda _2^2 -\lambda _{u}^2}\right) }. \end{aligned}$$
(46)

Hence, the final solutions for the dimensionless stress \(\sigma \), temperature \(\theta \), strain \(e\), and displacement \(u\) can be deduced from Eqs. 36–38 and Eq. 43 by using Eq. 31 as follows (considering the real parts only):

$$\begin{aligned} \sigma (x,y,z,t)&= \hbox {e}^{\omega t}\cos (my+nz)\left[ {R_1 \hbox {e}^{-\lambda _1 x}+R_2 \hbox {e}^{-\lambda _2 x}}\right] ,\end{aligned}$$
(47)
$$\begin{aligned} \theta (x,y,z,t)&= \frac{\hbox {e}^{\omega t}\cos (my+nz)}{a_2}\left[ {\left( {\lambda _1^2 -\alpha _1}\right) R_1 \hbox {e}^{-\lambda _1 x}+\left( {\lambda _2^2 -\alpha _1}\right) R_2 \hbox {e}^{-\lambda _2 x}}\right] ,\end{aligned}$$
(48)
$$\begin{aligned} e(x,y,z,t)&= \frac{\hbox {e}^{\omega t}\cos (my+nz)}{\delta _1 a_2}\left[ \left( \lambda _1^2 -\alpha _1 +a_2 \alpha _0\right) R_1 \hbox {e}^{-\lambda _1 x}\right. \nonumber \\&\left. +\left( {\lambda _2^2 -\alpha _1 +a_2 \alpha _0}\right) R_2 \hbox {e}^{-\lambda _2 x}\right] ,\end{aligned}$$
(49)
$$\begin{aligned} u(x,y,z,t)&= \hbox {e}^{\omega t}\cos (my+nz)\left[ {R_3 \hbox {e}^{-\lambda _u x}+\frac{l_1}{\lambda _1^2 -\lambda _u^2}\hbox {e}^{-\lambda _1 x}+\frac{l_2}{\lambda _2^2 -\lambda _u^2}\hbox {e}^{-\lambda _2 x}}\right] .\nonumber \\ \end{aligned}$$
(50)

5 Numerical Example and Discussion

With an aim to illustrate the theoretical results obtained in the preceding sections, we now present some numerical results. The numerical work has been carried out with the help of computer programming using the software Matlab. In the calculation process, we consider the material medium as that of copper. Since \(\omega \) is the complex time constant, we have \(\omega =\omega _0 +\iota \zeta \) then \(\hbox {e}^{\omega t}=\hbox {e}^{\omega _0 t}\left( {\cos \zeta t+\iota \sin \zeta t}\right) \). So for small values of time, we can take \(\omega =\omega _0 (\hbox {real})\). The numerical constants (in SI units) of the problem are taken as [13]

$$\begin{aligned} E_{0}&= 10.4\times 10^{10}\,\hbox {kg } {\cdot } \hbox {m}^{-1}{\cdot } \hbox {s}^{-2}, v = 0.33, T_{0}= 293\,\hbox {K}, \rho = 8954\,\hbox {kg}{\cdot } \hbox {m}^{-3}\\ k&= 386\,\hbox {W}{\cdot } \hbox {m}^{-1}{\cdot } \hbox {K}^{-1}, \alpha _{t}= 1.78\times 10^{-5}\,\hbox {K}^{-1}, c_{E}= 383.1\, \hbox {J}{\cdot } \hbox {kg}^{-1}{\cdot } \hbox {K}^{-1}\\ \tau _{T}&= 0.15\,\hbox {s}, \tau _{q}= 0.2\,\hbox {s}, \alpha = 0.001\,\hbox {K}^{-1}. \end{aligned}$$

Values of other non-dimensional parameters arising in the present analysis are taken as

$$\begin{aligned} f^{*}=10,\quad \omega =1.0,\quad m=1.2,\quad n=1.3. \end{aligned}$$

Considering the above physical data, the non-dimensional field variables have been evaluated and results are presented in the form of graphs. Figures 1, 2, 3, and 4 display the distribution of values of the real part of displacement \(u\), temperature \(\theta \), stress \(\sigma \), and strain \(e\) for a wide range of \(x(0\le x\le 4)\) and for a wide range of dimensionless time \(t(0\le t\le 0.4)\) at the position \(y=z=1.0\), when the modulus of elasticity is taken as a linear function of the reference temperature \((\alpha ^{*}=0.001)\). Figures 5, 6, 7, and 8 represent the solutions of non-dimensional field quantities obtained in the case of a temperature-independent modulus of elasticity \((\alpha ^{*}=0.0)\). In Figs. 9, 10, 11, and 12, we have drawn the two-dimensional plots of the field variables in order to analyze the effects of the temperature modulus of elasticity and time simultaneously taking two values of the dimensionless time, namely, \(t = 0.1, 0.4\).

Fig. 1
figure 1

Profile of displacement distribution at \(\alpha ^{*}=0.001\)

Full size image
Fig. 2
figure 2

Profile of temperature distribution at \(\alpha ^{*}=0.001\)

Full size image
Fig. 3
figure 3

Profile of stress distribution at \(\alpha ^{*}=0.001\)

Full size image
Fig. 4
figure 4

Profile of strain distribution at \(\alpha ^{*}=0.001\)

Full size image
Fig. 5
figure 5

Profile of displacement distribution at \(\alpha ^{*}=0.0\)

Full size image
Fig. 6
figure 6

Profile of temperature distribution at \(\alpha ^{*}=0.0\)

Full size image
Fig. 7
figure 7

Profile of stress distribution at \(\alpha ^{*}=0.0\)

Full size image
Fig. 8
figure 8

Profile of strain distribution at \(\alpha ^{*}=0.0\)

Full size image
Fig. 9
figure 9

Displacement distribution versus \(x\)

Full size image
Fig. 10
figure 10

Temperature distribution versus \(x\)

Full size image
Fig. 11
figure 11

Stress distribution versus \(x\)

Full size image
Fig. 12
figure 12

Strain distribution versus \(x\)

Full size image

Figures 1, 5, and 9 depict the variations of the displacement distribution with distance \(x\). The displacement field starts with a maximum value in all the figures and then diminishes to zero with the passage of time. Effects of the temperature-dependent modulus of elasticity and time are quite pertinent on the displacement field and can be easily noticed from the figures. The values of the displacement distribution are less for \(\alpha ^{*}=0.001\) compared to those for \(\alpha ^{*}=0.0\); hence, the temperature-dependent modulus of elasticity has a decreasing effect on the profile of the displacement distribution. From Fig. 9, we notice that the displacement field increases as the time \(t\) increases and attains its maximum value at (x, y, z, t) = (0, 0, 0, 0.4). Also, it is clear that the speed of wave propagation of this field variable is finite and coincides with the physical behavior of the elastic materials.

Figures 2, 6, and 10 have been plotted to observe the variations of the temperature field \(\theta \). Very near to the point of application of the source, there is a significant difference in magnitudes of the temperature distribution and the values are maximum which complies with the real situation. It is also noticed that as \(t\) increases the rate of decay of the temperature field becomes fast. From the profile we find that considering the temperature-dependent modulus of elasticity or not leads to different results, which illustrates that the temperature-dependent modulus of elasticity has a salient effect on the temperature distribution. More specifically, it has increased the magnitude of the temperature distribution. Another important phenomenon observed is that the solution vanishes outside a bounded region of space which shows the existence of a wave front. This is the difference between the hyperbolic heat conduction model and the Fourier heat conduction model.

Variations of the stress distribution \(\sigma \) for the different cases considered have been shown in Figs. 3, 7, and 11. The stress field increases sharply in the initial range to attain its maximum value at \(x = 0.5\) and then decreases to zero following a smooth pattern. In these figures all the curves have a coincident starting point with the value zero (according to the boundary condition). The plots also display that different results can be obtained for the stress field while the temperature-dependent modulus of elasticity is considered or not. The stress field has large values when \(\alpha ^{*}=0.001\) as compared to the case when \(\alpha ^{*}=0.0,\) which clearly indicates that the temperature-dependent modulus of elasticity has an increasing effect on the stress distribution. The figures also reveal that the time factor acts to increase the magnitude of the stress distribution. The maximum impact zone of both the factors is around \(x = 0.4\), and this impact dies out with the passage of time. Also, the stress distribution has non-zero values only in a bounded region of space. Outside this region, the values vanish identically which is in agreement with the experimental results. However, the stress field has a qualitatively similar behavior for all the cases.

Dynamic effects of the temperature-dependent modulus of elasticity and time on the strain have been studied in Figs. 4, 8, and 12. The strain field follows a similar trend for all the cases considered having differences in magnitude. It is noted that values of the strain field are a maximum numerically in the vicinity of the source which is physically plausible and then diminish to zero as \(x\) diverges from the point of the source application. The strain field exhibits significant sensitivity towards the temperature-dependent modulus of elasticity and time. The temperature-dependent modulus of elasticity causes lessening of the magnitude of the strain field while the absolute values of the strain are larger as we increase the time. Hence, the time has an increasing effect on the profile of the strain distribution while the temperature-dependent modulus of elasticity has a decreasing effect. However, effects of these two factors become indistinct with the increase of distance from the boundary.

6 Concluding Remarks

In this paper, a mathematical treatment has been presented to explore the effects of the temperature-dependent modulus of elasticity and time on wave propagation in a three-dimensional model of thermoelasticity with two-phase-lags subjected to a time-dependent heat source. The problem has been solved theoretically and exemplified through a specific model. Though the figures are self explanatory in exhibiting the different peculiarities which occur in the propagation of waves, yet the following remarks may be added:

  1. 1.

    In all these figures, it is clear that the considered functions for the generalized theories are localized in a finite region of space surrounding the heat source and are identically zero outside this region. This is not the case for the coupled theory where an infinite speed of propagation is inherent and, hence, all the considered functions have a non-zero (although may be very small) value for any point in the medium.

  2. 2.

    From the distribution of temperature, we have found a wave-type heat propagation in the medium. With the passage of time, the heat wave front moves forward with a finite speed.

  3. 3.

    The temperature-dependent modulus of elasticity has a prominent effect on all the physical quantities. It has increased the magnitudes of the temperature and stress fields while it acts to decrease the magnitudes of the displacement and strain fields.

  4. 4.

    Numerical values of all the fields are noted to be smaller for the case when \(t = 0.1\) and the values increase with the increase in the value of time \(t\).

Analysis of the displacement, temperature, stress, and strain generated in a body due to the application of a thermal source is an interesting problem of thermoelasticity. The problem assumes great significance when we consider the real behavior of the material characteristics with appropriate geometry of the model. Hence, the inclusion of the temperature-dependent modulus of elasticity to the three-dimensional vibrational analysis of a thermoelastic medium makes it a more realistic model for these studies.