Introduction

Any porous medium is usually famed by its porosity defined as the fraction of the volume of void spaces over the total volume (between 0 and 1). Examples of porous media are very wide, ranging from natural substances (e.g. soil, rocks and biological tissues) to artificial ones (e.g. cements, ceramics), and porous medium concept is used in the different areas of engineering and applied sciences, for example, petroleum, construction or material science, filtration, geomechanics, soil mechanics, acoustics, etc. In particular, if the temperature and moisture distribution over agricultural fields are studied with this approach, then these ideas can be used in the control of environment pollution. Keeping all these in mind, development of many different fluid models has been discussed and few of them are analysed to explain fluid flow properties through non-Darcy porous media in the different books by Vafai [1], Pop and Ingham [2], and Nield and Bejan [3]. The power-law fluids, in particular pseudoplastic and dilatant fluids, are usually known as time independent non-Newtonian fluids (generalized Newtonian fluid). Shenoy [4], Mandal et al. [5], Cheng [6] and Kumar and Diwakar [7] have taken the power-law fluids to study the effects of physical parameters over different geometries because of its extensive applications in various technological fields, medical science and research. The study related to non-Darcy hydromagnetic free convection, combined heat and mass transfer, magnetohydrodynamics and mixed convective boundary layer flow over different geometries can be found in the papers [8,9,10,11,12,13]. RamReddy et al. [14] explained the Soret effect by considering stagnation point flow of a nanofluid in a non-Darcy porous medium. Some theoretical studies related to integral transform and applications in heat transfer problems can be found in the papers [15,16,17,18,19,20]. The effect of magnetic field on heat transfer in an L-shaped enclosure containing non-Newtonian fluid is presented by Jahanbakhshi et al. [21]. Kairi [22] has shown that the increment in the radius of a slender paraboloid in a porous medium reduces the heat transfer rate and the influence of radiation on the same is reduced for all the three types of power-law fluids.

The second law of thermodynamics gives an idea of optimization in the design of different devices involved in the thermal field by making the sum of thermal and frictional entropy generation rates minimum. To get an optimal set of operating and design conditions, one can minimize the system’s irreversibility. There is a basic difference between transfer of energy into a system in the form of heat and doing the same by work. Both can be of equal quantity but after being a part of system energy, these have much distinct character. This can be seen as the amount of energy involved in the process of energy transport (e.g. heat transfer), energy character and its change in the course of transport activity. So, in order to measure this character along with its possible decay in the process of energy transfer, entropy plays a very significant part. The entropy generation analysis has great importance in the manufacturing and upgrading of various thermofluid components, e.g. turbines, heat exchangers, pumps, energy storage systems, etc. Bejan [23, 24] studied the effectiveness of various factors involved in entropy generation in thermal systems. Khan and Gorla [25], and Gorla et al. [26] considered the non-Newtonian boundary layer flows over a horizontal plate and wedge immersed in a porous medium, respectively, and performed the second law analysis. Das et al. [27] explained the combined effects of Navier slip, convective heating and magnetic field on the analysis of entropy generation and an alternative irreversibility distribution parameter known as Bejan number. The entropy generation analysis for a nonlinear convective flow in a porous medium with stratification is done by Vasu et al. [28]. The numerical investigation of the entropy generation on MHD mixed convection flow of Cu-water nanofluid with partial slip influence is done by Chamkha et al. [29]. Similarly, Rashad et al. [30] performed a numerical investigation related to the impacts of a heat sink and the source size and location on the entropy generation and MHD free convection flow. Sheikholeslami et al. [31] demonstrated the heat transfer and entropy generation by considering nanofluid flow via heat exchanger. Recently, Noreen and Ain [32] investigated the entropy generation for electroosmotic flow across a non-Darcy porous medium by peristaltic pumping. The effects of partial slips, heated rotating inner cylinder and wavy heater block on entropy generation analysis are given in the papers [33,34,35].

The nonlinear density temperature relationship strongly influences the fluid flow and heat transfer characteristics (for more details, one can refer Pop and Ingham [2] and Partha [36] and citations therein). Due to the existence of inertial effects, thermal dispersion effect in a non-Darcy porous medium is very important and studied by Cheng [37] and Plumb [38] with their models. Also, Hong et al. [39] conducted the theoretical studies extensively on thermal dispersion. However, the dispersion effect together with nonlinear convection has been incorporated by Kameswaran et al. [40] in a non-Darcy (Forchheimer model) porous medium and revealed the fact that it enhances the heat transfer rate. The viscous dissipation plays an unavoidable role in highly viscous fluids with low thermal conductivity. Its importance in the free and forced convective flows at large Rayleigh numbers is also notable. The viscous dissipation effects in the natural convection are important because the induced kinetic energy is appreciable in comparison with the quantity of heat transferred. This occurs when either the equivalent body force is large or when the convection region is extensive. Though the flow is quite slow in this natural convection phenomenon, viscous dissipation effect plays an important role in natural convection in various devices that are subjected to large variations of gravitational force or that operate at high rotational speeds [41]. Many experimental and analytical studies on viscous dissipation in natural convection can be found in the literature [42,43,44,45]. The variations in viscous dissipation parameter are useful to analyse the fluid velocity and temperature in the convection process. In the case of uniform forced convective flow of a fluid saturated porous medium along a plane surface, its effect in the presence of wall temperature distribution is studied by Magyari et al. [46]. El-Amin et al. [47] considered a power-law type of non-Newtonian fluid flow over a vertical plate immersed in a porous medium to investigate its influence. On the other hand, Aydin and Kaya [48] studied its effect on Newtonian fluid forced convective flow over a flat plate immersed in a non-Darcian porous medium. Its effect on heat and mass transfers for natural convection in a nanofluid saturated non-Darcy porous medium along a vertical plate is discussed by Ramreddy et al. [49]. Chamkha et al. [50] examined the viscous dissipation effect in the presence of convective boundary condition by considering non-Darcy porous medium saturated with a nanofluid. The role of local production of thermal energy through the mechanism of viscous stresses in the free convective flow from a vertical plate for a power-law fluid saturated non-Darcy porous medium, is studied by Khidir et al. [51].

From literature survey, it is found that this type of flow study over a truncated cone is not attained proper attention. Due to great importance of the geometry in any fluid flow, it is a key factor in practical applications. For example, the fluid flow over a truncated cone is useful in medical science to design heartbeat controlling systems and in technical areas, e.g. industrial processing of melted plastics and manufacturing edible items or slurries. This flow model involving truncated cone has different engineering applications too, e.g. solar collectors, automobile industries, rotating heat exchangers, aeronautics and aerosols engines. Further, this model may be used extensively in oil recovery technology. This flow model over a truncated cone is very important because both the vertical plate (\(\xi =0\)) and full cone (\(\xi \rightarrow \infty \)) cases can be directly studied with this model by using two different values of streamwise coordinate. The main aim of this study is to show the impacts of different parameters on Nusselt number, entropy generation and Bejan number along with velocity and temperature profiles in pseudoplastic and dilatant fluids saturated Forchheimer type of non-Darcy porous medium. Further, this type of exploration is helpful to understand the characteristics related to heat transfer surrounding red hot radioactive subsurface storage location or cooling magmatic intrusion which involve heat transport theory.

Problem description and geometry

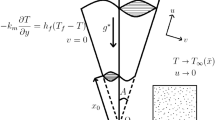
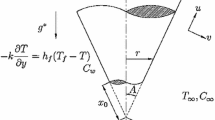
In this paper, the effect of viscous dissipation on a free convective flow over a truncated cone immersed in a Forchheimer type of non-Darcy porous medium saturated by dilatant and pseudoplastic fluids with nonlinear Boussinesq approximation and thermal dispersion, is considered. The physical model with coordinate system is displayed in Fig. 1. The leading edge of the truncated cone is kept at a distance \(x_{0}\) from the origin O, where x and y axes are taken along and normal to the surface of the truncated cone, respectively. The ambient medium and wall temperatures are taken as \(T_{\infty }\) and \(T_{\rm w}\), respectively, together with the modified streamwise coordinate \({\bar{x}}\), which is defined as \({\bar{x}}=x-x_{0}\) for the truncated cone. In addition, this fluid flow is taken for granted to be two-dimensional and steady along with the laminar behaviour and the porous medium is assumed to be homogeneous and isotropic. The flow intensity is taken to be moderate and the permeability of the medium is presumed to be less to certify the applicability of the Forchheimer flow model and negligence of boundary effect. Also, the nonlinear temperature density variations bring a significant influence on the flow field due to notably large changes in the temperature between the surface of truncated cone and the ambient fluid.

Fig. 1
figure 1

Geometry used in the problem

Full size image

One more assumption involved is that the boundary layer thickness is very small in comparison with the local radius of the truncated cone. So, the two radii, namely local radius at a point located in the boundary layer and the radius of the truncated cone, can be approximated by \( r=x \sin A \) (see Singh et al. [52]). Therefore, the equations and boundary conditions involved are valid only in the region \(x_0<x<\infty \). Hence, the above assumptions are physically realistic in nature with more relevance in practical situations.

Taking the boundary layer hypothesis into the consideration with above-mentioned assumptions and approximations, the flow governing equations over a truncated cone are given by [53,54,55,56]

$$\begin{aligned}&\frac{\partial (ru)}{\partial x} + \frac{\partial (rv)}{\partial y} = 0 \end{aligned}$$
(1)
$$\begin{aligned}&\frac{\partial {{u}^ {\rm n}}}{\partial y}+\frac{b{K^*}}{\nu }\frac{\partial {u^2}}{\partial y} \nonumber \\&\quad = \frac{{K^*} {g^{*}}{\beta _0}{\mathrm{cos}}A}{\nu }\left[ 1+ \frac{{2\beta _1}{\left( {T - T_{\infty } } \right) }}{\beta _0}\right] \frac{{\partial }T}{\partial y} \end{aligned}$$
(2)
$$\begin{aligned}&u\frac{\partial T}{\partial x} + v\frac{\partial T}{\partial y} \nonumber \\&\quad = \frac{\partial }{\partial y}\left( \alpha _* \frac{\partial T}{\partial y}\right) + \dfrac{\nu u}{K^*C_{\rm P}}\left( u^n+\dfrac{b K^*}{\nu }u^2\right) \end{aligned}$$
(3)

and the boundary conditions associated with these equations are

$$\begin{aligned}&v(x,\,y)=0,\quad T(x,\,y)=T_w,\quad \text{ at }\quad y=0\\&u(x,\,y) \rightarrow 0,\quad T(x,\,y) \rightarrow T_\infty\quad \text{ as }\quad y\rightarrow \infty \end{aligned}$$
(4)

where \(\nu \), \(\textit{b}\), A, \(g^*\), T, \(C_{\rm P}\) and (u, v) denote the kinematic viscosity, empirical constant, inclination of angle, acceleration due to gravity, temperature, specific heat capacity and Darcian velocities, respectively. A variable quantity \(\alpha _*=\alpha +\alpha _{\rm d}\) is used to denote the sum of the molecular diffusivity \(\alpha \) and the thermal diffusivity \(\alpha_{\rm d}=\chi u d\) followed by Plumb [38], where \(\chi \) denotes the coefficient of mechanical dispersion and its value is based on experiments and d represents the pore diameter. Next, we have considered the thermal expansion coefficients of first and second order, namely \(\beta _0\) and \(\beta _1\), respectively. Here, n is the power-law index (for \(n<1\), the fluid is pseudoplastic; for \(n>1\), the fluid is dilatant; and for \(n=1\), the fluid is Newtonian). \(K^*\) is the modified permeability of the porous medium which is a function of power-law index n, well explained by Christopher and Middleman [57] and Dharmadhikari and Kale [58].

The stream function \(\displaystyle {\psi }\) is introduced as \(\displaystyle {u =\frac{1}{r} \frac{{\partial \psi }}{{\partial y}}}\), \(\displaystyle {v = -\frac{1}{r} \frac{{\partial \psi }}{{\partial x}}}\) to satisfy the continuity equation (1) automatically. To get the non-dimensional form of Eqs. (2)–(3) and boundary conditions (4), the following dimensionless transformations are used

$$\begin{aligned}&\displaystyle {\xi = \frac{{\bar{x}}}{x_{0}}},{} \,\,\, \displaystyle {\eta = \frac{y}{{\bar{x}}}\,{{Ra}^{\frac{1}{2}}}},\,\,\, \displaystyle {\psi (\xi ,\eta ) ={\alpha \,r\,{Ra^{\frac{1}{2}}}\,f(\xi ,\eta )}}, \,\,\, \displaystyle {T(\xi ,\eta )= T_{\infty }+\left( {T_{\rm w}} - {T_{\infty } }\right) \,\theta (\xi ,\eta )} \end{aligned}$$
(5)

where \(Ra=\dfrac{\bar{x}}{\alpha }\left( \dfrac{\rho \,\beta _0\,g^*\,K^*\,cosA\,({T_{\rm w}}-{T_{\infty }})}{\mu }\right) ^{\frac{1}{\rm n}}\) is the local modified Darcy–Rayleigh number.

Using transformations (5) into Eqs. (2)–(3), the following resultant dimensionless equations are obtained

$$\begin{aligned}&n\,\left( {f'}\right) ^{{\rm n}-1}{{\, }}f''+2\,Gr^*\,f'{{\, }}f'' = (1 + 2\,{\alpha _1}\theta ){\theta '} \end{aligned}$$
(6)
$$\begin{aligned}&(1+Ds\,f')\theta ''+Ds\,f''\,\theta '+ \left( \frac{1}{2}+\frac{\xi }{\xi +1}\right) f\theta '\nonumber \\&\qquad -\xi \,S_T\,f' + \epsilon \xi f'\left[ \left( f'\right) ^{\rm n} + 2 Gr^* \left( f'\right) ^2\right] \nonumber \\&\quad = \xi \left( {{f'}\frac{\partial \theta }{\partial \xi } - \frac{\partial f}{\partial \xi }\theta '} \right) \end{aligned}$$
(7)

Previous boundary conditions (4) are converted into f and \(\theta \) form as

$$\begin{aligned}&2\,{\xi \,(\xi +1)}\left( {\frac{\partial f}{\partial \xi }} \right) +(3\,\xi +1)f(\xi ,\, \eta )= \,\,0,\,\,\,\,\,\,\,\theta (\xi , \, \eta ) = 1 \,\,\,\,at \,\,\,\,\eta = 0 \\&\,\,f'(\xi ,\eta ) \rightarrow 0, \,\,\,\,\,\,\,\theta (\xi ,\eta ) \rightarrow \,\, 0 \,\,\,\,as \,\,\,\,\eta \rightarrow \infty {} \end{aligned}$$
(8)

where the differentiation with respect to \(\eta \) is indicated by primes. In usual notations, \(Gr^*=\dfrac{b\,K^*}{\nu }\left( \dfrac{\alpha \,Ra}{{\bar{x}}}\right) ^{2-{\rm n}}\), \(\epsilon =\dfrac{\nu \, x_0}{K^*\, C_{\rm P} \,\,(T_{\rm w} - T_{\infty })}\left( \dfrac{\alpha \,Ra}{{\bar{x}}}\right) ^{\rm n}\),  \({\alpha _1}=\dfrac{{\beta _1}}{{\beta _0}}({T_{\rm w}}-{T_{\infty } })\), and    \(Ds=\dfrac{\chi d Ra}{{\bar{x}}}\). Here, \(Gr^*\) is the modified Grashof number, \(\epsilon \) is the viscous dissipation parameter, \(\alpha _1\) is the nonlinear density-temperature parameter and Ds is the thermal dispersion parameter. When \(x_0=0\), \(\xi \) becomes very large and this limiting case is used to get the fluid flow problem over a full cone. Likewise, when \(\xi = 0\,\) (i.e. \(x = x_0\)), the present problem reduces to fluid flow problem along a vertical plate.

Analysis of heat transfer and entropy generation

Non-dimensional form of heat transfer coefficient, commonly known as Nusselt number \(\displaystyle {Nu_{{\bar{\rm x}}}=-\frac{\bar{x}}{k}\dfrac{(k+k_{\rm d})}{({T_{\rm w}} - {T_{\infty }})}\left[ \frac{\partial T}{\partial y}\right] _{y=0}},\) is given by

$$\begin{aligned} \displaystyle {\dfrac{Nu_{{\bar{\rm x}}}}{{Ra^{\frac{1}{2}}}}= -\left[ 1+Ds\,f'(\xi ,0)\right] \theta '(\xi ,\,0)} \end{aligned}$$
(9)

where the addition of the dispersion thermal conductivity \(k_{\rm d}\) and the molecular thermal conductivity k is used as the effective thermal conductivity of the porous medium.

The available amount of energy in any system related to industrial or engineering processes, is destroyed by entropy generation and so this property plays significant role in these fields. It is therefore important to determine the entropy generation rate in any system so that the operation efficiency of the system can be optimized. The dimensional form of the expression for entropy generation related to the present flow problem is written as

$$\begin{aligned} S_{\rm g}'''=\dfrac{K^*}{T_{\infty }^{2}}\left( \frac{\partial T}{\partial y}\right) ^2 + \dfrac{\nu }{K^*\,C_{\rm P}\,T_{\infty }}\left( u^{{\rm n}+1}+\dfrac{b K^*}{\nu }u^3\right) . \end{aligned}$$
(10)

The characteristic entropy generation is defined as \(\displaystyle {\left( S_{\rm g}'''\right) _0=\dfrac{K^*}{T_{\infty }^{2}}\dfrac{(T_{\rm w}-T_{\infty })^2}{{\bar{x}}^2}}\) and so the non-dimensional form of entropy generation \(Ns=\dfrac{S_{\rm g}'''}{\left( S_{\rm g}'''\right) _0}\) can be written as

$$\begin{aligned} \frac{Ns}{Ra}=\theta '^2 + \dfrac{Br}{\Omega }\xi \left[ (f')^{{\rm n}+1} + Gr^* (f')^3\right] ,{} \end{aligned}$$
(11)

where \(Br=\dfrac{\alpha \,\nu \,x_0\,}{K^{*2}\,C_{\rm P}\,(T_{\rm w}-T_{\infty })}\left( \dfrac{\alpha \,Ra}{{\bar{x}}}\right) ^{2-{\text{n}}}\) is Brinkman number and \(\Omega =\dfrac{T_{\rm w} - T_{\infty }}{T_{\infty }}\) is the dimensionless temperature difference.

Equation (11) can be split into two parts as \(Ns = N_1 + N_2\) where \(N_1 = Ra \,\theta '^2\) and \(N_2 = \dfrac{Br\,Ra}{\Omega }\xi \left[ (f')^{{\rm n}+1} + Gr^* (f')^3\right] \). The first part denotes the entropy generation due to heat transfer and the second part is responsible for the entropy generation due to fluid friction. To check the domination of fluid friction irreversibility over heat transfer irreversibility, one more irreversibility distribution parameter is defined which is the ratio of entropy generation due to heat transfer over total entropy generation and known as Bejan number (Be). The expression for the Bejan number can be given as

$$\begin{aligned} Be = \dfrac{N_1}{Ns} = \dfrac{\theta '^2}{\theta '^2 + \dfrac{Br}{\Omega }\xi \left[ (f')^{{\rm n}+1} + Gr^* (f')^3\right] } \in [0, 1] \end{aligned}$$
(12)

In particular, \(Be=0\) shows that the irreversibility due to fluid friction dominates, but \(Be=1\) reveals that the irreversibility due to heat transfer dominates. Further, the irreversibility due to viscous dissipation and heat transfer are equal in the process of entropy generation if \(Be=0.5\).

Numerical solutions

The governing equations for this fluid flow along with the boundary conditions result in a complex nonlinear system of PDEs and its closed form of solutions cannot be obtained. So, Eqs. (6)–(8) are solved with the combination of local non-similarity approach and spectral local linearization method which gives accurate outcomes among other spectral methods for these kind of complex boundary layer equations. The details of this methodology are given in the following subsections:

Local non-similarity procedure

In this subsection, using the local similarity and non-similarity approach (see Sparrow and Yu [59]), the governing equations of present fluid flow problem are obtained in the form of a system of ordinary differential equations (ODEs) after the three level of truncations. Taking \(\xi \ll 1\) as a special case, the preliminary approximate solutions may be obtained from the local similarity equations by treating the terms carrying \(\displaystyle {\xi \frac{\partial }{\partial \xi }}\) as insignificant. So, the local similarity equations corresponding to the first level of truncation of Eqs. (6)–(8) can be written as

$$\begin{aligned}&n\,\left( {f'}\right) ^{{\rm n}-1}{{\, }}f''+2\,Gr^*\,f'{{\, }}f'' - (1 + 2\,{\alpha _1}\theta ){\theta '}=0 \end{aligned}$$
(13)
$$\begin{aligned}&(1+Ds\,f')\theta ''+Ds\,f''\,\theta '+ \left( \frac{1}{2}+\frac{\xi }{\xi +1}\right) f\theta '\nonumber \\&\quad + \epsilon \xi f'\left[ \left( f'\right) ^{\rm n} + 2 Gr^* \left( f'\right) ^2\right] = 0 \end{aligned}$$
(14)

along with the boundary conditions

$$\begin{aligned}&f(\xi ,0)= 0,\,\,\,\,\,\,\,\,\theta (\xi , 0) = 1,{} \\&\,\,f'(\xi ,\eta ) \rightarrow 0,\,\,\,\,\,\,\theta (\xi ,\eta ) \rightarrow 0 \,\,\,\,\text{ as } \,\,\,\,\eta \rightarrow \infty .{} \end{aligned}$$
(15)

In the second level of truncation, the local non-similarity nonlinear ODEs are obtained to get the ignored terms from the initial level of truncation by using freshly introduced variables \(\displaystyle {U = \frac{\partial f}{\partial \xi }\,\, \text{ and } \,\,V = \frac{\partial \theta }{\partial \xi }}\) . Thus, the truncation at second level gives

$$\begin{aligned}&n\,\left( {f'}\right) ^{{\text{n}}-1}{{\, }}f''+2\,Gr^*\,f'{{\, }}f'' -(1 + 2\,{\alpha _1}\theta ){\theta '}=0 \end{aligned}$$
(16)
$$\begin{aligned}&(1+Ds\,f')\theta ''+Ds\,f''\,\theta '+ \left( \frac{1}{2}+\frac{\xi }{\xi +1}\right) f\theta '\nonumber \\&\quad \quad + \epsilon \xi f'\left[ \left( f'\right) ^{\text{n}} + 2 Gr^* \left( f'\right) ^2\right] \nonumber \\&\qquad -\xi \left( {V\,f' - U\,\theta '} \right) =0 \end{aligned}$$
(17)

together with the updated BCs

$$\begin{aligned}&(3\,\xi +1)f(\xi ,0)+ 2\,{\xi \,(\xi +1)}{U(\xi ,0)}= 0,\,\,\,\ \,\theta (\xi , 0) = 1, \\&f'(\xi ,\eta ) \rightarrow 0,\,\,\,\,\,\,\theta (\xi ,\eta ) \rightarrow 0 \,\,\,\,\,\,\text{ as } \,\,\,\,\eta \rightarrow \infty . \end{aligned}$$
(18)

In the third and final level of truncation, Eqs. (16)–(18) are differentiated in respect of \(\xi \). Also, the involved partial derivatives of \(\displaystyle {U}\) and \(\displaystyle {V}\) are dropped. So, the final equations may be written as

$$\begin{aligned}&n\left( {f'}\right) ^{{\text{n}}-1}{{\, }}U'' + n(n-1)\left( {f'}\right) ^{{\text{n}}-2}{{\, }}f''U'\nonumber \\&\quad \quad +2\, Gr^*\,(f''{{\, }}U' +U''{{\, }}f')- \nonumber \\&\quad \quad -V'- 2\,{\alpha _1}(V{\theta '}+\theta {V'} )=0 \end{aligned}$$
(19)
$$\begin{aligned}&V'' + Ds(f'V'' + f''V') + \left( \frac{1}{2}+\dfrac{\xi }{\xi +1}\right) fV' \nonumber \\&\qquad + \xi UV'-f'V-\xi U'V + Ds(U'\theta '' + U''\theta ')\nonumber \\&\qquad +\left( \frac{1}{2}+\dfrac{\xi }{\xi +1}\right) U\theta ' + \theta 'U+\epsilon \,\xi \,(n+1)\,(f')^{\text{n}}U' \nonumber \\&\qquad + \epsilon \,(f')^{{\text{n}}+1} + 3\,\epsilon \,\xi \,Gr^*\,(f')^2\,U'\,\nonumber \\&\qquad +\,\epsilon \,Gr^*\,(f')^3+ \dfrac{1}{(\xi + 1)^2}f\theta '=0 \end{aligned}$$
(20)

in association with BCs

$$\begin{aligned}&3f(\xi ,0)+(7\xi +3)U(\xi ,0) = 0,\,\,\, V\left( {\xi ,0} \right) = 0\\&U'(\xi ,\eta ) \rightarrow 0,\,\,\,\,\,\,V(\xi ,\eta ) \rightarrow 0 \,\,\,\,\text{ as } \,\,\,\,\eta \rightarrow \infty . \end{aligned}$$
(21)

Local linearization method

In this subsection, the implementation of spectral local linearization method (SLLM) on this particular problem is discussed. One can get detailed explanation about linearization with examples in the work of Motsa and Sibanda [60]. SLLM is used by Motsa [61] to get the solution of a coupled system of nonlinear ODEs. The solution methodology of these equations involves three steps: (i) first, an innovative linearization procedure locally based on quasi-linearization is used to linearize Eqs. (16), (17), (19) and (20), (ii) next, the Chebyshev spectral collocation method is used to obtain the matrix form of the system of linear algebraic equations from the iterative sequence of linearized ODEs, and (iii) finally, using initial approximations (which are taken to satisfy the BCs), the final form of the following equations is solved iteratively:

$$\begin{aligned}&f_{{\text{r}}+1}''+a_{1,{\text{r}}}f_{{\text{r}}+1}'=K_{1,{\text{r}}} \end{aligned}$$
(22)
$$\begin{aligned}&\theta _{{\text{r}}+1}''+b_{1,r}\theta _{{\text{r}}+1}'=K_{2,{\text{r}}} \end{aligned}$$
(23)
$$\begin{aligned}&U_{{\text{r}}+1}''+x_{1,{\text{r}}}U_{{\text{r}}+1}'=K_{3,{\text{r}}} \end{aligned}$$
(24)
$$\begin{aligned}&V_{{\text{r}}+1}''+y_{1,{\text{r}}}V_{{\text{r}}+1}'+y_{2,{\text{r}}}V_{{\text{r}}+1}=K_{4,{\text{r}}} \end{aligned}$$
(25)

where \(a_{1,{\rm {r}}}=\dfrac{n(n-1)f_{\rm {r}}''\left( f_{\rm r}'\right) ^{{\text{n}}-2}+2Gr^*f_{\rm r}''}{n\left( f_{\rm r}'\right) ^{{\text{n}}-1}+2Gr^*f_{\rm r}'}\), \(K_{1,{\rm r}}=\dfrac{\left( \theta _{\rm r}'+2\alpha _{1}\theta _{\rm r}\theta _{\rm r}'\right) +n(n-1)f_{\rm r}''\left( f_{\rm r}'\right) ^{{\rm n}-1}+2Gr^{*}f_{\rm r}''f_{\rm r}'}{n\left( f_{\rm r}'\right) ^{{\rm {n}}-1}+2Gr^{*}f_{\rm r}'}\) \(b_{1,{\rm r}}=\dfrac{Dsf_{{\rm r}+1}''+\left( \frac{1}{2}+\frac{\xi }{\xi + 1}\right) f_{{\rm r}+1}+\xi U_{\rm r}}{1+Dsf_{{\rm r}+1}'}\), \(K_{2,{\rm r}}=\dfrac{\xi f_{{\rm r}+1}'V_{\rm r}-\xi \epsilon (f_{{\rm r}+1}')^{{\rm {n}}+1}-\xi \epsilon \, Gr^*(f_{{\rm r}+1}')^{3}}{1+Dsf_{{\rm r}+1}'}\), \(x_{1,{\rm r}}=\dfrac{n(n-1)f_{{\text{r}}+1}''\left( f_{{\text{r}}+1}'\right) ^{{\rm n}-2}+2Gr^*f_{{\rm r}+1}''}{n\left( f_{{\rm r}+1}'\right) ^{{\rm n}-1}+2Gr^*f_{{\rm r}+1}'}\), \(K_{3,{\rm r}}=\dfrac{\left( V_{\rm r}'+2\alpha _1\theta _{{\rm r}+1}'V_{{\rm r}}+2\alpha _1\theta _{{\rm r}+1}V_{{\rm r}}'\right) }{n\left( f_{{\rm r}+1}'\right) ^{{\rm n}-1}+2Gr^*f_{{\rm r}+1}'}\), \(y_{1,{\rm r}}=\dfrac{Dsf_{{\rm r}+1}''+\left( \frac{1}{2}+\frac{\xi }{\xi + 1}\right) f_{{\rm r}+1}+\xi U_{{\rm r}+1}}{1+Dsf_{{\rm r}+1}'}\), \(y_{2,{\rm r}}=\dfrac{-f_{{\rm r}+1}'-\xi U_{{\rm r}+1}'}{1+Dsf_{{\rm r}+1}'}\), \(K_{4,{\rm r}}=\dfrac{1}{1+Dsf_{{\rm r}+1}'}[-Ds\,\,(U_{{\rm r}+1}'\theta _{{\rm r}+1}''+U_{{\rm r}+1}''\theta _{{\rm r}+1}')-(\frac{3}{2}+\frac{\xi }{\xi + 1})\,\,U_{{\rm r}+1}\theta _{{\rm r}+1}'-\frac{1}{(\xi +1)^2}f_{{\rm r}+1}\theta _{{\rm r}+1}'- {}\epsilon (f'_{{\rm r}+1})^{{\rm n}+1} -(n+1)\epsilon \,\xi (f'_{{\rm r}+1})^{{\rm n}}\,U_{{\rm r}+1}' -3\,\epsilon \,\xi \,Gr^*\,(f_{{\rm r}+1})^2\,U_{{\rm r}+1}'- \epsilon \,Gr^*\,(f'_{{\rm r}+1})^{3}]\), with respect to the linearized BCs:

$$\begin{aligned}&{f_{{\rm r}+1}}(\xi ,0) = -\frac{2\xi (\xi +1)}{3\xi +1}U_{\rm r}(\xi ,0),\,\, \theta _{{\rm r}+1}(\xi ,0)=1,\,\, \\&U_{{\rm r}+1}(\xi ,0)=-\frac{3}{7\xi +3}{f_{{\rm r}+1}}(\xi ,0),\,\, V_{{\rm r}+1}(\xi ,0)=0,\\&f_{{\rm r}+1}'(\xi ,\eta ) \rightarrow 0,\,\theta _{{\rm r}+1}(\xi ,\eta ) \rightarrow 0,\\&\,U_{{\rm r}+1}'(\xi ,\eta ) \rightarrow 0,\,V_{{\rm r}+1}(\xi ,\eta ) \rightarrow 0,\, \text{ as } \,\,\,\,\eta \rightarrow \infty .{} \end{aligned}$$
(26)

The matrix representation of these equations can be given as

$$\begin{aligned} \mathbf{A }_{1}\,\mathbf{F }= & {} \mathbf{B }_{1}\\ \mathbf{A }_{2}\,\Theta= & {} \mathbf{B }_{2}\\ \mathbf{A }_{3}\,\mathbf{U }= & {} \mathbf{B }_{3}\\ \mathbf{A }_{4}\,\mathbf{V }= & {} \mathbf{B }_{4} \end{aligned}$$

where

$$\begin{aligned} \mathbf{A }_1= & {} \mathbf{D }^{2} +\hbox { diag}(a_{1,{\rm r}})\mathbf{D }, \,\,\,\,\,\mathbf{B }_1=K_{1,{\rm r}}\\ \mathbf{A }_2= & {} \mathbf{D }^{2} +\hbox { diag}(b_{1,{\rm r}})\mathbf{D }, \,\,\,\,\,\mathbf{B }_2=K_{2,{\rm r}}\\ \mathbf{A }_3= & {} \mathbf{D }^{2} +\hbox { diag}(x_{1,{\rm r}})\mathbf{D }, \,\,\,\,\,\mathbf{B }_3=K_{3,{\rm r}}\\ \mathbf{A }_4= & {} \mathbf{D }^{2} +\hbox { diag}(y_{1,{\rm r}})\mathbf{D } +\hbox { diag}(y_{2,{\rm r}})\mathbf{I }, \,\,\,\,\,\mathbf{B }_4=K_{4,{\rm r}} \end{aligned}$$

Here I is an identity matrix of the order \((N_{\rm x}+1)\) and F, \(\Theta \), U and V are the vectors containing approximate values of f, \(\theta \), U and V, which are estimated at the collocation points. Finally, these resultant equations along with the BCs are solved with the help of suitable initial approximations to study the fluid flow properties.

Results and discussion

The power-law fluids are mainly divided into two categories: pseudoplastic (shear thinning) and dilatant (shear thickening). There is decrement in the fluid viscosity with stress for the first and increment for the second one. The broad application range of these fluids in latest technical fields and modern science motivates us to study the flow of pseudoplastic and dilatant fluids in detail. The rheogram for obtained results in the fixed values of parameters is given in Fig. 2. In this part, the numerical findings related to the solutions of Eqs. (6)–(7) with the BCs (8) for various values of physical parameters, are discussed. All the computations in this solution procedure have been carried out with 50 collocation points (\({\rm i.e.} N_{\rm x}=50\)) in \(\eta \)-direction and \(L_{\rm x}=10\) is used for numerical approximations at infinity in \(\eta \)-direction. MATLAB software is used to implement the spectral local linearization method. The convergence test of the iteration scheme is also conducted by taking the norm of difference in the values of two consecutive iterations. We have presumed that the algorithm is convergent when these norms will be less to a fixed toleration level (say, \(\epsilon =10^{-10}\)). The two expressions used, for velocity and temperature at \((r+1)\)th iteration, for error norms are given as

$$\begin{aligned}&E_{\rm f}=\max ||f_{{\rm r}+1,{\rm i}}-f_{{\rm r},{\rm i}}||_{\infty },\,\,\,\,\,\,\,\, 0 \le i \le N_{\rm x},\\&E_{\uptheta }=\max ||\theta _{{\rm r}+1,{\rm i}}-\theta _{{\rm r},{\rm i}}||_{\infty },\,\,\,\,\,\,\,\, 0 \le i \le N_{\rm x}. \end{aligned}$$
Fig. 2
figure 2

The rheogram for obtained results when \(Gr^*=2.0\), \(Ds=1.5\), \(\alpha _1=0.1\), \(\epsilon =0.1\) and \(\xi = 1\)

Full size image

To plot these error trends, a logarithmic approach is adopted, i.e. the natural logarithmic value of the error is plotted with respect to iterations. In Figs. 3a–4b, the variation in the norm of residual errors over iteration level for both the governing Eqs. (16) and (17) with five values of \(\xi \) is shown. The first two figures show the trend for Newtonian fluid and other two show for non-Newtonian fluid. It is readily visible from all these plots that these residual errors are decreased with iterations in every case considered which indicates the convergence property. Moreover, the very less residual error, attained after few iterations, indicates the precision of the method involved to solve the governing equations of the present problem. In this way, validation of method used in this work is done.

Fig. 3
figure 3

Logarithmic value of residual errors over iterations for Newtonian fluid (\(n=1.0\)) when \(Ds=0.5\), \({\alpha _1}=0.1\), \({Gr^*}=0.1\), \(\epsilon =0.1\), \(\frac{Br}{\Omega }=1\)

Full size image
Fig. 4
figure 4

Logarithmic value of residual errors over iterations for non-Newtonian fluid (\(n=1.2\)) when \(Ds=2.5\), \({\alpha _1}=0.5\), \({Gr^*}=0.1\), \(\epsilon =0.1\), \(\frac{Br}{\Omega }=1\)

Full size image

To verify the correctness of the formulation and accuracy of calculations, the outcomes of this problem in the case of vertical plate (i.e. \({\xi }=0\)) when \(Ds=0\), \(\epsilon =0\) and \(\alpha _1=0\), are compared with the exact results (see Nakayama et al. [62]) and the results of Plumb and Huenefeld [63] for the Newtonian fluid case. The comparisons are matching at a good extent which is shown in Table 1. In the next subsections, the detailed analysis of power-law fluid flows over a truncated cone is done due to its emerging applications in diverse fields. Also, these results reveal few interesting facts involving boundary layer flow field, heat transfer and entropy generation rates for physically realistic values of pertinent parameters.

Table 1 Comparison of \(-\theta '(\xi ,\,0)\) for various values of \(Gr^*\) when \(\xi = 0\), \(Ds=0\), \(\epsilon =0\) and \(\alpha _1=0\): Newtonian fluid case (\(n=1\))
Full size table

Effect of viscous dissipation parameter (\(\epsilon \))

In this subsection, the graphs in Fig. 5a–e related to non-dimensional velocity and temperature profiles, heat transfer and entropy generation rates along with Bejan number, respectively, are displayed. The effect of viscous dissipation parameter on these profiles and quantities, is analysed properly for pseudoplastic, Newtonian and dilatant fluids. In the physical sense, \(\epsilon \) refers to the transformation of energy from the motion of fluid to the fluid’s internal energy. Viscous dissipation is high in the regions of large gradients, e.g. boundary layers, shear layers, etc. Velocity and temperature profiles are studied in respect of \(\eta \) and from Fig. 5a, it is observed that the velocities in dilatant fluid flow are higher when compared to the pseudoplastic fluid flow. The presence of \(\epsilon \) increases the velocity and temperature for each fluid, but the temperature is found to be higher in the case of pseudoplastic fluid. The presence of \(\epsilon \) makes the temperature of the system stable for all the fluids because viscous dissipation behaves like a source term in the fluid flow generating notable rise in the fluid temperature as the kinetic motion of fluid is converted to thermal energy. This observation has significance in the heat and fluid flow in microchannel having larger ratio of length to diameter. The non-dimensional heat transfer and entropy generation rates along with the Bejan number are analysed in respect of streamwise coordinate \(\xi \) and the variations in these quantities prove the non-similar nature of this problem. From Fig. 5c–e, it is seen that these quantities show decrements with increasing values of \(\epsilon \) for all the fluids. As the streamwise coordinate increases, there is continuous increment in the heat transfer and entropy generation rates, but opposite is observed with Bejan number. As expected, Bejan number approaches zero for higher values of \(\xi \). These smaller values of Bejan number indicate the domination of irreversibility due to fluid friction in the areas where streamwise coordinate is large. In all these three analyses, the dilatant fluid dominates. The entropy generation minimization is very useful in the thermal engineering and design variable selection in many efficient fluid systems.

Fig. 5
figure 5

Effect of \(\epsilon \) for the two values of n on a velocity profiles, b temperature profiles, c Nusselt number, d entropy generation and e Bejan number with the fixed values \(Ds=1.5\), \({\alpha _1}=0.1\), \({Gr^*}=1.0\), \(\xi =1.0\) (for a, b), \(\frac{Br}{\Omega }=1\)

Full size image

Effect of thermal dispersion parameter (Ds)

In this subsection, the thermal dispersion parameter effects on the non-dimensional velocity and temperature profiles, Nusselt number, entropy generation rate and Bejan number are shown in Fig. 6a–e. The first two graphs show the variations in respect of \(\eta \) and the later three show in respect of \(\xi \). The studies of pseudoplastic, Newtonian and dilatant fluids are combined in single figure. Basically, this effect brings up the effectiveness of non-uniform pore level velocity on the temperature field inside the particular porous medium. As there are sufficiently high velocities due to the fluid flow through a porous medium, hence the molecular diffusion is dominated by the thermal dispersion. Also, it shows the significance of combined changes from the velocity and temperature to the heat transportation. From Fig. 6a, b, it is observed that the presence of Ds enhances the velocity and temperature profiles for all the fluids and dilatant fluid dominates in the case of velocity profiles and pseudoplastic fluid dominates for the temperature profiles. It is found from Fig. 6c that the heat transfer rate is increased in the presence of dispersion parameter for all these fluids and there is domination of dilatant fluid in this case too. There is slight change in the heat transfer rate with \(\xi \) in the absence of dispersion but variation is comparatively larger in its presence. In Fig. 6d, e, the impact of Ds on entropy generation and Bejan number is shown and both are decreased for its higher values. The values of entropy generation rate and Bejan number are more for dilatant fluid in comparison with pseudoplastic and Newtonian fluids. With higher streamwise coordinate, as expected, entropy generation rate increases and Bejan number decreases. This entropy generation and Bejan number analysis give the idea of components and processes (mechanisms) of the system which provides real advantage in the improvement of the system efficiency by allocating proper engineering resources and efforts. Also, it can be said that the effect of thermal dispersion is significant when the inertial effect is frequent and its negligence can result in a decent amount of error.

Fig. 6
figure 6

Effect of Ds for the two values of n on a velocity profiles, b temperature profiles, c Nusselt number, d entropy generation and e Bejan number with the fixed values \({\alpha _1}=0.1\), \({Gr^*}=1.0\), \(\epsilon =0.1\), \(\xi =0.1\) (for a, b), \(\frac{Br}{\Omega }=1\)

Full size image

Effect of nonlinear convection parameter (\(\alpha _1\))

In this subsection, the graphs in Fig. 7a–e related to non-dimensional velocity and temperature profiles, heat transfer and entropy generation rates along with Bejan number, respectively, are shown. The nonlinear convection parameter effect on these profiles and quantities, is analysed properly for the pseudoplastic, Newtonian and dilatant fluids. This nonlinear convection parameter deals with the nonlinearity in the density temperature relationship. Due to this reason, it is also termed as nonlinear density temperature parameter. In the physical sense, \(\alpha _{1}>0\) refers to the relation \(T_{\rm w}>T_\infty \), so the surface of a truncated cone produces remarkable quantity of heat to the fluid flow region. Velocity and temperature profiles are studied in respect of \(\eta \) and from Fig. 7a, continuous increment is noticed in the velocity profiles with increase in \(\alpha _{1}\) value for all the fluids but overall there is domination of dilatant fluid. On the other hand, pseudoplastic fluid dominates in the case of temperature profile and it decreases with increase in \(\alpha _{1}\). The non-dimensional Nusselt number, entropy generation rate and Bejan number are analysed in respect of streamwise coordinate \(\xi \). From Fig. 7c–e, it is found that the heat transfer and entropy generation rates increase with increasing values of \(\alpha _{1}\) but Bejan number decreases for all the fluids. With increase in streamwise coordinate, continuous increments in heat transfer and entropy generation rates are seen but opposite is observed with Bejan number. The Bejan number lies between 0 and 1 and approaches zero for higher values of \(\xi \). The higher values of Bejan number show the domination of irreversibility due to heat transfer in the case of small \(\xi \). The Bejan number analysis is widely useful in various areas of heat transfer, e.g. electronic cooling, contact melting, lubrication, etc.

Fig. 7
figure 7

Effect of \(\alpha _{1}\) for the two values of n on a velocity profiles, b temperature profiles, c Nusselt number, d entropy generation and e Bejan number with the fixed values \(Ds=1.5\), \({Gr^*}=2.0\), \(\epsilon =0.1\), \(\xi =0.2\) (for a, b), \(\frac{Br}{\Omega }=1\)

Full size image

Conclusions

In this paper, the effects of viscous dissipation, thermal dispersion and nonlinear density-temperature parameters on the velocity and temperature profiles, heat transfer and entropy generation rates along with Bejan number for the dilatant, Newtonian and pseudoplastic fluid flows over a truncated cone in a non-Darcy porous medium, are discussed in detail. The consideration of power-law fluids over a truncated cone with viscous dissipation and thermal dispersion increased the number of non-dimensional parameters considerably, and hence, the nonlinear complexity of the present power-law fluid flow problem is increased significantly. Therefore, the flow governing equations are solved with the combination of local non-similarity approach and spectral local linearization method, and also noticed that this combination is working very well with minimum error when compared to spectral method alone. The conclusive remarks of this work for physically suitable values of the flow governing parameters, are:

  • The higher values of viscous dissipation, thermal dispersion and nonlinear convection parameters increase the velocity, and the dilatant fluid dominates over the Newtonian and pseudoplastic fluids.

  • The temperature profiles are increased in the presence of viscous dissipation and thermal dispersion parameters and decreased with higher values of nonlinear convection parameter for all the fluids.

  • The entropy generation and heat transfer rates increase with streamwise coordinate (\(\xi \)) for all the fluids irrespective of presence and absence of all these parameters which shows that the heat transfer and entropy generation rates for a truncated cone are less than that for full cone (higher values of \(\xi \)) and more than that for vertical plate (\(\xi =0\)).

  • The smaller values of Bejan number for higher values of \(\xi \) show the domination of irreversibility due to fluid friction in the case of full cone.

  • The analysis of entropy generation and Bejan number gives the idea about the stability of the system. Greater entropy generation results in unstable system.

  • This kind of study is useful in the field of high-temperature polymeric mixtures, aerosol technology, electronic cooling, contact melting, etc., which are related with temperature-dependent density.