Impacts of heated rotating inner cylinder and two-phase nanofluid model on entropy generation and mixed convection in a square cavity

Abstract

A numerical study is carried out on mixed convection and entropy generation of Al2O3/water nanofluid due to a rotating cylinder inside a square cavity. The numerical computations are performed taking the non-homogenous model of Buongiorno into consideration. The inner moving rotating circular cylinder is maintained at a constant hot temperature T_h and the other left and right vertical walls of the cavity are maintained at a constant cold temperature T_c. The bottom and top horizontal walls are maintained as adiabatic. The Galerkin weighted residual method is implemented to numerically solve the governing equations. The Rayleigh number (10⁴ ≤ Ra ≤ 10⁷), angular rotational velocity (0 ≤Ω≤ 600) nanoparticles loading (0 ≤ ϕ ≤ 0.04) and the dimensionless radius of rotating cylinder (0.1 ≤ R ≤ 0.4) are the governing parameters of this study. Numerical results for the streamlines, isotherms, isentropic lines, nanoparticle loading, local and average Nusselt number and Bejan number are obtained and presented graphically. A detailed discussion of the results is performed to highlight the physics of the problem.

1 Introduction

Nanofluids are suspensions consisting of nano-sized (< 100 nm) solid metal particles (Cu, Ag, Au, Ni) or its oxide (Al2O3, CuO, MgO, ZnO, SiO₂, Fe₂O₃, Fe₃O₄, TiO₂) in a carrier fluid (water, ethylene glycol, oil, etc.). These fluids are a great importance due to the its enormous heat transfer capability when compared traditional heat transfer fluids. Therefore, these fluids are used in many engineering systems where heat transfer applications from general to specific is important and nowadays, conventional fluids have been replaced by such these kinds of heat transfer fluids due to the their effective heat transfer ability. Nowadays, several studies are carried out to examine the flow and heat transfer characteristics of nanofluids in different geometries [1,2,3,4]. Cavities or enclosures are one of them which are using frequently in various applications such as, heat exchanger [5, 6], heat pipes [7,8,9], HVAC systems [10,11,12], renewable energy technologies [13, 14] etc.

In recent years, some numerical, analytical and experimental studies have been carried out on natural and mixed convective heat transfer problems in cavities filled with nanofluids [15,16,17,18,19,20]. Natural convection in a rectangular cavity is known to be one of the most basic and classical problems in heat transfer, but mixed convection is often considered for effective heat transfer which moving surfaces are considered commonly. It can be observed in a wide range of engineering applications such as heating and cooling systems, heat exchangers, solar power, microelectronics, drying technologies, nuclear reactors, chemical processing equipment’s etc. [21, 22]. Mixed convection problem of nanofluid flow was studied numerically by Malik and Nayak [23]. Four different cases were examined for flow behavior. The effect of Reynolds number, Richardson number, and volume fraction of nanoparticle on the flow and heat transfer characteristics were investigated. Also, mixed convection problem was studied by Abu-Nada and Chamkha [24] in a lid-driven inclined square cavity filled with nanofluid. They expressed that the increase in the nanoparticle volume fraction and inclination increased heat transfer for medium and large Richardson numbers. Another mixed convection study in an inclined enclosure was studied numerically using two-phase mixture model by Alinia et al. [25]. They used SiO₂/water nanofluid in their study and they concluded that the particle distribution is uniform for low Richardson number whereas non-uniformity situation observed for increasing Richardson number. Gibanov et al. [26] numerically studied the mixed convection of Al2O3/water nanofluid in a lid driven cavity considering entropy generation. Some governing parameters such as thermal conductivity ratio, thickness of solid wall, Ri number and volume fractions of nanoparticle effects were analyzed on the flow and heat transfer characteristics with the aid of streamlines, isotherms and isentropic lines. It was found that from their study heat transfer is enhanced and Be number is declined when nanoparticles volume fraction is increased.

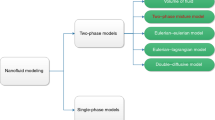
Generally, two main approaches have been used to numerically simulate the nanofluid flow. These are single phase (homogeneous model) and two-phase approaches. In single phase approach base fluid and nanoparticles are assumed to be in thermal equilibrium and have same velocity field. Although this method has ignored interactions between nanoparticles and base fluid molecules, it usually gives acceptable results in low volume fractions [27, 28]. But lately, the researchers turned to study with two-phase approach since it gives more precise results than single phase approach because of considering the Brownian effect and slip velocity between the base fluid and the nanoparticles [29, 30]. For example, two-phase mixture model was used in the study performed by Garoosi et al. [31] to search the mixed convection of nanofluids in an internal and external heated square cavity and Sheremet and Pop [32] considered the Brownian diffusion and thermophoresis effect to solve the similar problem for water based nanofluids. Buongiorno [29] has also proposed a two-phase model considering the Brownian motion and thermophoresis effect for nanofluids flow and he developed a two-component non-homogeneous equation that emphasized the superiority of these two effects. This model was used effectively by Sheremet et al. [33] for solving the natural convection of nanofluid inside the triangular cavities.

Since the problem of flow and heat transfer around the rotating substance can be seen in a wide range of engineering applications it must be the subject to be investigated for a better understanding of this phenomenon [34]. Therefore, the rotating surfaces play an important role in controlling the mixed convection heat transfer in cavities [35, 36]. There are numerous studies [37,38,39] in the open literature considering rotating cylinder effect on the flow and heat transfer characteristics in a cavity. One of them was considered in the study Hussain and Hussein [40]. Selimefendigil and Öztop [41] were developed a correlation for average Nu number in the study of mixed convection problem inside the cavity which has two adiabatic rotating circular cylinders for different nanofluids. They applied the finite element method to solve the problem. In other studies of Selimefendigil and Öztop [42], such a problem was investigated numerically under the magnetic field effect for Cu-water nanofluid. In those studies, different parameters effects (Ha number, Gr number, nanoparticle distribution and angular rotational velocity of the cylinder) on the heat and fluid flow were examined. It was concluded that from their studies increasing of Hatmann number has caused to decrease local and average heat transfer. A meaningful enhancement in the heat transfer were observed for angular rotational velocity of the cylinder in both studies. Natural and mixed convection heat transfer problem between differentially heated cylinders in an adiabatic enclosure filled with nanofluid was performed by Garoosi and Hoseininejad [43]. The results show that heat transfer increase and decrease depending on rotation direction of the hot and cold cylinders. Also, reducing of Nu number was observed by changing the position of the cold cylinder from vertical to horizontal mode. Natural convection [44] and mixed convection [45] of Al2O3/water nanofluid filled in a square cavity inside a wavy porous cavity with a solid circular cylinder in the presence of entropy generation were reported. They found that an increasing of Ra number has caused an enhancement in the heat transfer and, the rotation of the cylinder exhibits an adverse action on the convective heat transfer at Ra > 10⁵.

From the above-mentioned studies, it can be said that the mixed convection of different nanofluids inside cavities that shaped variously has been studied extensively due to the significance of heat transfer applications. However, to the best authors knowledge, the study of entropy generation and mixed convective heat transfer of Al2O3/water nanofluid filled in a square cavity with a rotating cylinder using two-phase nanofluid model has not been studied yet. This finding motivated and highlighted the originality of the present study. Therefore, the main purpose of the studied subject is to examine the effects of related parameters on the heat transfer and fluid flow. Parameters are as follows: Rayleigh number, angular rotational velocity, nanoparticle loading and rotating cylinder radius. It is believed that the aim of the current study plays a major role in many engineering applications, such as; heating and cooling systems, heat exchangers, solar power, microelectronics, drying technologies, nuclear reactors, chemical processing equipment’s, etc.

2 Mathematical formulation

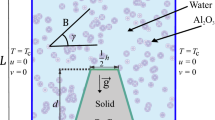
The present work considers steady mixed convective heat transfer conditions in a 2D square cavity with a length L in the presence of a central rotating circular cylinder with a radius r. The schemitic diagram of the problem is described in Fig. 1. The inner moving rotating circular cylinder is maintained at a constant hot temperature T_h and the other left and right vertical walls of the cavity are kept at a constant cold temperature T_c. The bottom and top horizontal walls are maintained as adiabatic. The impermeable condition is presumed for the boundaries of the taken domain and the liquid that fills the space between the external cavity (square) and the inner rotating cylinder is a nanofluid having Al₂O₃ nanoparticles with water as a base fluid. The Boussinesq approximation is assumed to be applicable. With the consideration of the above assumptions, the continuity, momentum and energy equations for a laminar flow of a Newtonian fluid are given by:

$$ \begin{array}{@{}rcl@{}} \nabla \cdot \textbf{v} &=& 0, \end{array} $$

(1)

$$ \begin{array}{@{}rcl@{}} \rho_{nf}\textbf{v} \cdot \nabla \textbf{v}&=&-\nabla p + \nabla \cdot \left( \mu_{nf}\nabla \textbf{v}\right)\\&&+(\rho \beta)_{nf}(T-T_{c})\mathbf{g}, \end{array} $$

(2)

$$ \begin{array}{@{}rcl@{}} (\rho C_{p})_{nf}\textbf{v} \cdot \nabla T&=&\nabla \cdot \left( k_{nf}\nabla T\right) - C_{p,p} J_{p}\cdot \nabla T, \end{array} $$

(3)

$$ \begin{array}{@{}rcl@{}} \textbf{v} \cdot \nabla \varphi&=&- \frac{1}{\rho_{p}}\nabla \cdot J_{p}, \end{array} $$

(4)

where v is the vector of velocity, g evaluates the vector of the gravitational acceleration, φ shows the nanoparticles local volume fraction and J_p describes the nanoparticles mass flux. The nanoparticles mass flux according to Buongiorno’s model can be explained as the following:

$$ \begin{array}{@{}rcl@{}} J_{p}&=&J_{p,B}+J_{p,T}, \end{array} $$

(5)

$$ \begin{array}{@{}rcl@{}} J_{p,B}&=&-\rho_{p} D_{B} \nabla \varphi,\quad D_{B}=\frac{k_{b} T}{3 \pi \mu_{f} d_{p}}, \end{array} $$

(6)

$$ \begin{array}{@{}rcl@{}} J_{p,T}&=&-\rho_{p} D_{T} \nabla T,\quad D_{T}=0.26\frac{k_{f}}{2k_{f}+k_{p}} \frac{\mu_{f}}{\rho_{f} T}\varphi. \end{array} $$

(7)

In the considered domain, the absolute velocity can be shown as [46]:

$$ |\textbf{V}|=|\Omega|R. $$

(8)

Based on the study of Costa and Raimundo [46], the modified form of the Richardson number that indicates the relative importance of the natural and forced convection is described as follows:

$$ Ri=\frac{Ra\cdot\text{Pr}}{4{\Omega}^{2}\cdot R^{4}} $$

(9)

for Ω≠ 0 and R≠ 0.

Fig. 1

Physical model of convection in a cavity together with the heated rotating cylinder and the coordinate system.

In the current study, we have used the following thermo-physical properties for the nanofluid [45, 47]:

$$ \begin{array}{@{}rcl@{}} (\rho C_{p})_{nf}\!&=&\!(1-\phi)(\rho C_{p})_{f}+\phi (\rho C_{p})_{p}, \end{array} $$

(10)

$$ \begin{array}{@{}rcl@{}} \alpha_{nf}\!&=&\!\frac{k_{nf}}{(\rho C_{p})_{nf}}, \end{array} $$

(11)

$$ \begin{array}{@{}rcl@{}} \rho_{nf}\!&=&\!(1-\phi)\rho_{f}+\phi \rho_{p}, \end{array} $$

(12)

$$ \begin{array}{@{}rcl@{}} {(\rho \beta )_{nf}} \!&=&\! (1 - \phi ){(\rho \beta )_{f}} + \phi {(\rho \beta )_{p}}, \end{array} $$

(13)

$$ \begin{array}{@{}rcl@{}} \frac{\mu_{nf}}{\mu_{f}} \!&=&\! 1/\left( 1-34.87\left( d_{p}/d_{f}\right)^{-0.3}\phi^{1.03}\right), \end{array} $$

(14)

$$ \begin{array}{@{}rcl@{}} \frac{k_{nf}}{k_{f}}\!&=&\! 1 \!+ 4.4 \text{Re}_{B}^{0.4} \text{Pr}^{0.66} \left( \!\frac{T}{T_{fr}}\!\right)^{\!10} \left( \!\frac{k_{p}}{k_{f}}\!\right)^{\!0.03} \phi^{0.66}, \end{array} $$

(15)

where d_f is the molecular diameter of water which is given as Corcione [47]:

$$ d_{f} = \frac{6 M}{N \pi \rho_{f}}, $$

(16)

by using water as the base fluid, the value of d_f can be obtained as the following:

$$ d_{f} = \left( \frac{6 \times 0.01801528}{6.022 \times 10^{23} \times \pi \times 998.26}\right)^{1/3}=3.85 \times 10^{-10} \mathrm{m}, $$

(17)

where (ρC_p)_nf shows the nanofluid heat capacitance, α_nf presents the effective thermal diffusivity of the nanofluid, ρ_nf is the effective density of nanofluid, β_nf explains the thermal expansion coefficient of nanofluids, water-Al₂O₃ and water-Al₂O₃ describe the dynamic viscosity ratio and thermal conductivity ratio of nanofluid, respectively.

Next, we are going to introduce the non-dimensional variables that are used in the current work as follows:

$$ \begin{array}{@{}rcl@{}} X&=&\frac{x}{L}, Y=\frac{y}{L}, \textbf{V} = \frac{\textbf{v} L}{\nu_{f}},\\ P &=& \frac{p L^{2}}{\rho_{nf} {\nu_{f}^{2}}}, \varphi^{\ast}=\frac{\varphi}{\phi}, D^{\ast}_{B}=\frac{D_{B}}{D_{B0}}, \\ D^{\ast}_{T}&=&\frac{D_{T}}{D_{T0}}, \delta = \frac{T_{c}}{{{T_{h}} - {T_{c}}}}, \theta=\frac{T-T_{c}}{T_{h}-T_{c}},\\ \Omega&=&\frac{\omega L^{2}}{\alpha_{f}}, R=\frac{r}{L}. \end{array} $$

(18)

Using those variables and the previous equations, we can obtain the following dimensionless governing equations:

$$ \begin{array}{@{}rcl@{}} \nabla\cdot \textbf{V} &=& 0, \end{array} $$

(19)

$$ \begin{array}{@{}rcl@{}} \textbf{V}\cdot \nabla \textbf{V} &=& - \nabla P + \frac{\rho_{f}}{\rho_{nf}} \frac{\mu_{nf}}{\mu_{f}} \nabla^{2} \textbf{V} + \frac{(\rho\beta)_{nf}}{\rho_{nf} \beta_{f}} \frac{1}{\text{Pr}} Ra \cdot \theta, \end{array} $$

(20)

$$ \begin{array}{@{}rcl@{}} \textbf{V}\cdot \nabla \theta &=& \frac{(\rho C_{p})_{f}}{(\rho C_{p})_{nf}} \frac{k_{nf}}{k_{f}} \frac{1}{\text{Pr}} \nabla^{2} \theta + \frac{(\rho C_{p})_{f}}{(\rho C_{p})_{nf}} \frac{D^{\ast}_{B}}{\text{Pr} \cdot Le} \nabla \varphi^{\ast} \cdot \nabla \theta \\ && + \frac{(\rho C_{p})_{f}}{(\rho C_{p})_{nf}} \frac{D^{\ast}_{T}}{\text{Pr} \cdot Le \cdot N_{BT}} \frac{\nabla \theta \cdot \nabla \theta}{1 + \delta \theta}, \end{array} $$

(21)

$$ \begin{array}{@{}rcl@{}} \textbf{V}\cdot \nabla \varphi^{\ast} &=& \frac{D^{\ast}_{B}}{Sc} \nabla^{2} \varphi^{\ast} + \frac{D^{\ast}_{T}}{Sc \cdot N_{BT}} \cdot \frac{\nabla^{2} \theta}{1 + \delta \theta}, \end{array} $$

(22)

where V is the dimensionless vector of velocity (U,V), $D_{B0}=\frac {k_{b} T_{c}}{3 \pi \mu _{f} d_{p}}$ and $D_{T0}=0.26\frac {k_{f}}{2k_{f}+k_{p}} \frac {\mu _{f}}{\rho _{f} \theta }\phi$ are references coefficient of Brownian diffusion and thermophoretic diffusion, $Sc=\frac {\nu _{f}}{D_{B0}}$ is Schmidt number, $N_{BT}=\frac {\phi D_{B0}T_{c}}{D_{T0}(T_{h}-T_{c})}$ is the diffusivity ratio parameter (Brownian diffusivity/thermophoretic diffusivity), $Le=\frac {k_{f}}{(\rho C_{p})_{f} \phi D_{B0}}$ is Lewis number, $Ra=\frac {g \rho _{f} \beta _{f}(T_{h} - T_{c})L^{3}}{\mu _{f} \alpha _{f}}$ is base fluid Rayleigh number and $\text {Pr}=\frac {\nu _{f}}{\alpha _{f}}$ is base fluid Prandtl number.

The dimensionless boundary conditions of Eqs. 19–22 are:

$$ \begin{array}{@{}rcl@{}} && \text{On the heated surface of the rotating solid cylinder:} \\ && U=-{\Omega}(Y-Y_{0}), V={\Omega}(X-X_{0}), \\ && \quad \frac{\partial \varphi^{\ast}}{\partial n}= - \frac{D^{\ast}_{T}}{D^{\ast}_{B}} \cdot \frac{1}{N_{BT}} \cdot \frac{1}{1 + \delta \theta} \frac{\partial \theta}{\partial n}, \theta=1, \end{array} $$

(23)

$$ \begin{array}{@{}rcl@{}} && \text{On the left cold wall of the cavity:} \\ && U = V = 0, \frac{\partial \varphi^{\ast}}{\partial n} = - \frac{D^{\ast}_{T}}{D^{\ast}_{B}} \cdot \frac{1}{N_{BT}} \cdot \frac{1}{1 + \delta \theta} \frac{\partial \theta}{\partial n}, \theta = 0, \end{array} $$

(24)

$$ \begin{array}{@{}rcl@{}} && \text{On the right cold wall of the cavity:} \\ && U = V = 0, \frac{\partial \varphi^{\ast}}{\partial n} = - \frac{D^{\ast}_{T}}{D^{\ast}_{B}} \cdot \frac{1}{N_{BT}} \cdot \frac{1}{1 + \delta \theta} \frac{\partial \theta}{\partial n}, \theta = 0, \end{array} $$

(25)

$$ \begin{array}{@{}rcl@{}} && \text{On the adiabatic horizontal walls:} \\ && U = V = 0, \frac{\partial \varphi^{\ast}}{\partial n}=0, \frac{\partial \theta}{\partial n}=0. \end{array} $$

(26)

The local Nusselt number along at the surface of the rotating solid cylinder is written as:

$$ \left.Nu=-k \frac{h_{y} L}{k}= -\frac{\partial \theta}{\partial n}\right\vert_{n={\Theta}}. $$

(27)

The average Nusselt number $\overline {Nu}$ is achieved by integrating the local Nusselt number

$$ \overline{Nu}=\frac{1}{2\pi}{\int}_{0}^{2\pi} Nu {\kern 1pt} {\mathrm{d}}{\Theta}. $$

(28)

The entropy generation relation is given by [44]:

$$ \begin{array}{@{}rcl@{}} && S=\frac{k_{nf}}{{T_{0}^{2}}} \left[ \left( \frac{\partial T}{\partial x}\right)^{2} + \left( \frac{\partial T}{\partial y}\right)^{2} \right] \\ && \quad \quad + \frac{\mu_{nf}}{T_{0}} \!\left[ 2\!\left( \frac{\partial u}{\partial x}\right)^{2} + 2\!\left( \frac{\partial v}{\partial y}\right)^{2} + \!\left( \frac{\partial u}{\partial x} + \frac{\partial v}{\partial x} \right)^{2} \right]. \end{array} $$

(29)

In dimensionless form, local entropy generation can be evaluated by the following:

$$ \begin{array}{@{}rcl@{}} S_{\textrm{GEN}}&=& \frac{k_{nf}}{k_{f}} \left[ \left( \frac{\partial \theta}{\partial X}\right)^{2} + \left( \frac{\partial \theta}{\partial Y}\right)^{2} \right] \\ && + \frac{\mu_{nf}}{\mu_{f}} N_{\mu} \left\{ 2 \left[ \left( \frac{\partial U}{\partial X}\right)^{2} + \left( \frac{\partial V}{\partial Y}\right)^{2} \right]\right.\\ &&+ \left. \left( \frac{\partial^{2} U}{\partial Y^{2}} + \frac{\partial^{2} V}{\partial X^{2}} \right)^{2} \right\}, \end{array} $$

(30)

where, $N_{\mu }=\frac {\mu _{f} T_{0}}{k_{f}} \left (\frac {\alpha _{f}}{L({\Delta } T)}\right )^{2}$ shows the ratio of irreversibility distribution and $S_{\textrm {GEN}}=S_{\text {gen}}\frac {{T_{0}^{2}} L^{2}}{k_{f} ({\Delta } T)^{2}}$.

The terms of Eq. 30 describe discretely in the following form:

$$ \begin{array}{@{}rcl@{}} S_{\textrm{GEN}}= S_{\theta} + S_{\Psi}, \end{array} $$

(31)

where S_𝜃 and S_Ψ identify the entropy generation due to the heat transfer irreversibility (HTI) and the nanofluid friction irreversibility (NFI), respectively.

$$ \begin{array}{@{}rcl@{}} S_{\theta} &=& \frac{k_{nf}}{k_{f}} \left[ \left( \frac{\partial \theta}{\partial X}\right)^{2} + \left( \frac{\partial \theta}{\partial Y}\right)^{2} \right] \end{array} $$

(32)

$$ \begin{array}{@{}rcl@{}} S_{\Psi} &=& \frac{\mu_{nf}}{\mu_{f}} N_{\mu} \left\{ 2 \left[ \left( \frac{\partial U}{\partial X}\right)^{2} + \left( \frac{\partial V}{\partial Y}\right)^{2} \right]\right.\\ &&+ \left. \left( \frac{\partial^{2} U}{\partial Y^{2}} + \frac{\partial^{2} V}{\partial X^{2}} \right)^{2} \right\}. \end{array} $$

(33)

By Integrating Eq. 31 over the domain, the global entropy generation (GEG) of the current two-dimensional study is described with the following:

$$ \begin{array}{@{}rcl@{}} \textrm{GEG} = \int S_{\textrm{GEN}} {\kern 1pt} {\mathrm{d}}X {\mathrm{d}}Y = \int S_{\theta} {\kern 1pt} {\mathrm{d}}X {\mathrm{d}}Y + \int S_{\Psi} {\kern 1pt} {\mathrm{d}}X {\mathrm{d}}Y. \end{array} $$

(34)

Next, Bejan number is evaluated in order to determine which is the dominant, heat transfer or nanofluid friction irreversibility as follows:

$$ \begin{array}{@{}rcl@{}} Be = \frac{\int S_{\theta} {\kern 1pt} {\mathrm{d}}X {\mathrm{d}}Y}{\int S_{\textrm{GEN}} {\kern 1pt} {\mathrm{d}}X {\mathrm{d}}Y}, \end{array} $$

(35)

when Be > 0.5, the HTI is the dominant, while when Be < 0.5, the NFI is the dominant.

3 Numerical method and validation

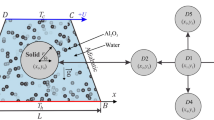
The Galerkin weighted residual finite element method is implemented to numerically solve the dimensionless governing equations Eqs. 19–22 object to the chosen boundary conditions of the cavity walls Eqs. 23–26. Such an analysis (FEM) considered mathematically very rigorous and it has a much stronger mathematical foundation than many other methods. It uses results from real and functional analysis. The computational domain of the current study is discretised into small triangular elements as described in Fig. 2. This procedure reduces the continuum problem, which has an infinite number of unknowns, to one with a finite number of unknowns at specified points referred to as nodes. For every variables of the flow and temperature field, various orders of Triangular Lagrange finite elements within the used computational domain are analysed. And for each conservation equation in the current work, acquiring of residuals is employed by replacing the new approximations within the governing equations. Formulation of the system of equations where the Galerkin methods can be used. Next, for simplifying the nonlinear expressions of the momentum equations, the algorithm of the Newton-Raphson iteration was utilized. The convergence of the current solution can be estimated once the relative error of the selected variables fulfills the below convergence criteria:

$$ \begin{array}{@{}rcl@{}} \left|\frac{{\Gamma}^{i+1}-{\Gamma}^{i}}{{\Gamma}^{i+1}}\right| \le \eta, \end{array} $$

where i describes the number of iteration and η explains the convergence criterion. In the existing numerical task, the setting of the convergence criterion was achieved at η = 10^− 6.

Fig. 2

FEM grid-points distribution for the grid size of 7634 elements

To ensure the independence of the present numerical solution on the grid size of the numerical domain, we have utilized various grid sizes to calculate the average Nusselt number ($\overline {Nu}$), Bejan number (Be) and global entropy generation (GEG) for the case of Ra = 10⁶, Ω = 250, ϕ = 0.02 and R = 0.2. The results are shown in Table 1 denote insignificant differences for the G6 grids and above. Therefore, for all computations in this paper for similar problems to this subsection, the G6 uniform grid is employed.

Table 1 Grid testing for $\overline {Nu}$, Be and GEG at different grid sizes for Ra = 10⁶, Ω = 250, ϕ = 0.02 and R = 0.2

For the purpose of validating the data, the current results are compared with published findings of Liao and Lin [48] for the case of natural convection heat transfer within a square enclosure containing an embedded heated cylinder at Ra = 2 × 10⁶, R = 0.2 and Pr = 7, as shown in Fig. 3. Another validation was made for the problem of natural convective heat transfer within a cavity that filled with nanofluid with the use of two-phase Buongiorno model of Sheikhzadeh et al. [49], Motlagh and Soltanipour [50] and the experimental findings of Ho et al. [51], as explained in Fig. 4. In addition, Figs. 5 and 6 show an excellent agreement for the fluid flow (streamlines), temperature distribution (isotherms), the distribution of nanoparticles of the numerical findings of Corcione et al. [52] using the same nanofluid model and the experimental results of Ho et al. [51]. Based on the presented validations, authors are quite confident about the numerical outcomes of the current numerical code.

Fig. 3

(top) streamlines and (bottom) isotherms; (left) Liao and Lin [48] and (right) present study for 2 × Ra = 10⁶, Pr = 7.0, Ω = 0, ϕ = 0 and R = 0.2

Fig. 4

Comparison of the mean Nusselt number obtained from present numerical simulation with the experimental results of Ho et al. [51], numerical results of Sheikhzadeh et al. [49] and numerical results of Motlagh and Soltanipour [50] for different values of Rayleigh numbers

Fig. 5

Streamlines (a), Corcione et al. [52] (left), present study (right), isotherms (b), Corcione et al. [52] (left), present study (right) for Ra = 10² (top) and Ra = 10⁶ (bottom) at ϕ = 0.02, R = 0 and D = 1

Fig. 6

Comparison of a thermal conductivity ratio with Chon et al. [54] and Corcione et al. [52] and b dynamic viscosity ratio with Ho et al. [51] and Corcione et al. [52]

4 Results and discussion

Numerical results of four parameters; Rayleigh number (10⁴ ≤ Ra ≤ 10⁷), angular rotational velocity (0 ≤Ω≤ 600), nanoparticles loading (0 ≤ ϕ ≤ 0.04) and the dimensionless radius of rotating cylinder (0.1 ≤ R ≤ 0.4) are described graphically as streamlines, isotherms, nanoparticle distribution, isentropic lines, local and average Nusselt numbers in Figs. 7, 8, 9, 10, 11, 12, 13, 14, 15, 16, 17, 18 and 19. In the numerical method values of some pertinent parameters are fixed as follows: Prandtl number (Pr = 4.623), Lewis number (Le = 3.5 × 10⁵), Schmidt number (Sc = 3.55 × 10⁴), ratio of Brownian to thermophoretic diffusivity (N_BT = 1.1), dimensionless length of the surface of the cylinder (Θ = 360) and normalized temperature parameter (δ = 155). Thermophysical properties of water and Al₂O₃ nanoparticles are given in Table 2.

Fig. 7

Variations of the streamlines, isotherms, nanoparticle distribution and isentropic lines evolution by Rayleigh number (Ra) for Ω = 250, ϕ = 0.02 and R = 0.2

Fig. 8

Variations of a the local Nusselt number interfaces with Θ and b global entropy generation (GEG) with Ω for different Ra at ϕ = 0.02 and R = 0.2

Fig. 9

Variations of a average Nusselt number and b Bejan number with Ω for different Ra at ϕ = 0.02 and R = 0.2.

Fig. 10

Variations of the streamlines, isotherms, nanoparticle distribution and isentropic lines evolution by rotational velocity (Ω) for Ra = 10⁶, ϕ = 0.02 and R = 0.2

Fig. 11

Variations of a the local Nusselt number interfaces with Θ and b global entropy generation (GEG) with Ra for different Ω at ϕ = 0.02 and R = 0.2

Fig. 12

Variations of a average Nusselt number and b Bejan number with Ra for different Ω at ϕ = 0.02 and R = 0.2

Fig. 13

Variations of the streamlines, isotherms, nanoparticle distribution and isentropic lines evolution by the solid volume fraction (ϕ) for Ω = 250, Ra = 10⁶ and R = 0.2

Fig. 14

Variations of a the local Nusselt number interfaces with Θ and b global entropy generation (GEG) with Ω for different ϕ at Ra = 10⁶ and R = 0.2

Fig. 15

Variations of a average Nusselt number and b Bejan number with Ra for different ϕ at Ω = 250 and R = 0.2

Fig. 16

Variations of a average Nusselt number and b Bejan number with Ω for different ϕ at Ra = 10⁶ and R = 0.2

Fig. 17

Variations of the streamlines, isotherms, nanoparticle distribution and isentropic lines evolution by the radius of the rotating cylinder (R) for Ω = 250, Ra = 10⁶ and ϕ = 0.02

Fig. 18

Variations of a the local Nusselt number interfaces with Θ and b global entropy generation (GEG) with Ω for different R at Ra = 10⁶ and ϕ = 0.02

Fig. 19

Variations of a average Nusselt number and b Bejan number with Ω for different R at Ra = 10⁶ and ϕ = 0.02

Table 2 Thermo-physical properties of water with Al₂O₃ nanoparticles at T = 310K [53]

4.1 Effect of rayleigh number

In Figs. 7–9 Rayleigh number (Ra) effects are depicted. The numerical results are graphically shown in these figures as streamlines, isotherms, nanoparticle distribution, isentropic lines, local and average number of Nu, global entropy generation and Bejan number. Figure 7 displays the effect of Ra number on the streamlines, isotherms, nanoparticle distribution and isentropic lines inside the square cavity for Ω = 250, ϕ = 0.02 and R = 0.2. Convective effects are meaningful caused by cylinder rotation at low Ra number and as can be seen from the figure, because of the predominance of heat conduction, the isotherms in the low Ra numbers are parallel to the vertical surface of the cavity. Then, as the Rayleigh number increases, it is parallel to the horizontal upper and lower surfaces. The particle distribution is nonuniform for low Rayleigh number while it remains almost uniform for high Ra numbers and it is also observed that from the figure isentropic lines densities are decreases with increase of Ra number.

Variations of the local Nu number with dimensionless length of the cylinder surface (Θ) for varying Ra numbers are given in Fig. 8a. As is evident from the graph, increasing the Ra number has caused an increment in the local Nu number. At low Ra number (Ra = 10⁴) there is no significant change in the local Nu number along Θ and it can be said it is almost the same. But for higher values of Ra number, the variations become a sinusoidal form. It was reached bigger values for the beginning of the Θ. After 0.35 value of the Θ, reductions were observed on the local Nu number values for high Ra numbers (Ra = 10⁶ and 10⁷). Then local Nu number reaches its smallest value at Θ = 1 for all cases and after it becomes increase. Global entropy generation change with dimensionless angular rotational velocity (Ω) for varying Ra numbers is also depicted in Fig. 8b. GEG is increasing with Ω for all Ra numbers, but there is a little change in GEG throughout Ω at low and moderate Ra numbers. The maximum GEG has occurred at the highest value of Ra number (Ra = 10⁷) as about 5000.

In Fig. 9a, the average Nu number variation versus dimensionless angular rotational velocity is represented for different Ra numbers. According to this figure, the average Nu number is a function of Ra number. Additionally, average Nu values are smaller for low Ra numbers due to the heat conduction-dominant regime, while it was increasing for higher values of Ra number (Ra = 10⁷). It can be noticed that after the value of 300 in Ω, average Nu number approaching together for low Ra number (Ra = 10³ and 10⁴). At Ra = 10⁷, the average Nu number is not change along the Ω. Bejan number is a significant parameter that indicates whether the heat transfer irreversibility (HTI) or the nanofluid flow irreversibility (NFI) is dominant. If Be > 0.5, the HTI is dominant, on the other hand, if Be < 0.5, the NFI is dominant. Changing of Be number with dimensionless angular rotational velocity for different Ra number is seen in Fig. 9b. It can be clearly seen from this figure Bejan number remains under 0.1 throughout the Ω for low Ra numbers where irreversibility due to the viscous effects dominate. Increasing Ra number has caused to increase Be number. Particularly, Be number is differ at the beginning points of the Ω and it starts to close each other after the point Ω = 300 for bigger values of Ra number. It can be noticed that the HTI is dominant for a fixed cylinder (Ω = 0) and it decreases with an enhancement in Ω. Also, entropy generation due to the viscous effects and the heat transfer effects are nearly equal at Ra = 10⁶ for a fixed cylinder.

4.2 Effect of the rotational velocity

Figures 10–12 illustrate the impacts of the cylinder’s rotational velocity. In Fig. 10, the streamlines, isotherms, nanoparticle distribution and the isentropic lines are presented for the Ra = 10⁶, ϕ = 0.02 and R = 0.2. An increment of the cylinder’s rotational velocity leads to the enhancement of the strength of the streamlines and the fluid heat flow motions along the clockwise direction which clearly enhance the extreme stream function values (see the Ψ_min values). However, this enhancement tends to decrease the size of the cell just near the cold left wall, along the counterclockwise direction. Due to the cylinder’s rotational velocity in positive direction, more of the isotherm lines move towards the left wall. The distribution of the nanoparticles shows significant growing with the rise of the velocity of solid cylinder, more nanoparticles move from the right segment of the cavity towards the left segment. The isentropic appears with great changes are affected by the increment of the rotational velocity, the entropy generation increases significantly (see the contour level legends). Greater amount of heat generated moves towards the top and vertical walls of the cavity.

Local Nusselt number variations interfaces with Θ and GEG versus Ra graphics are shown in Fig. 11 for various Ω at ϕ = 0.02 and R = 0.2. Local Nu number is a sinusoidal function of Θ. From the zero to Θ = 0.4 value, increasing of the rotational velocity has caused to decrease local Nu number, whereas reverse situation is observed until nearly Θ = 1. Then it starts to increase again. Global entropy generation is increasing after Ra > 10⁵ (Fig. 11b) whereas no remarkable change observed at Ra < 10⁵ for all rotational velocity except fixed one (Ω = 0). Maximum entropy generation was occurred at Ra = 10⁷ for all cases. Average Nu number is also increase with the increase in Ra number for all rotational velocity values of the cylinder and no remarkable change is observed except around Ra = 10⁵ (Fig. 12a). For Ra < 10⁵, Fig. 12b shows how irreversibility of heat transfer is dominated, whereas for cylinder rotation, the irreversibility is caused fundamentally from friction irreversibility of the nanofluid (Be < 0.5). However, due to the strong inertial forces after Ra = 10⁵ in Fig. 12b, NFI appears to be independent of the cylinder velocity.

4.3 Effect of nanoparticles loading

Nanoparticles loading or volume fraction effects are discussed in this subsection with the aid of Figs. 13–15 demonstrated. As seen from Fig. 13, increasing nanoparticle volume fractions shows less effects on isotherms and isentropic lines due to the viscous forces. However, streamlines’ strength increases, and greater amount of heat convection moves in clockwise direction which clearly enhance the extreme stream function values. In addition, the size of the streamlines’ cells along the counterclockwise direction just near the left cold wall decreases due to the fact that more nanoparticles move along this direction. More distribution of the nanoparticles appears just near the left vertical wall of the cavity which is clearly effected by the direction of the rotational velocity of the hot cylinder.

The variations of local Nusselt number and the variations of GEG with Ω for various ϕ are illustrated in Fig. 14. From the Fig. 14a, the local Nu number increases with the increase of ϕ. Global entropy generation (Fig. 14b) is linearly dependent on the nanoparticle volume fractions. It increases with Ω. The maximum entropy generation has occurred at ϕ = 0.04 value due to the friction increment. There exists a negligible change on the average Nu number for low Ra number at which the fluid friction is dominant; however, after Ra = 10⁵ the average Nu number is enhanced (Fig. 15a) with the increase on nanoparticle volume fractions due to the convective effects of cylinder and it shows a boost in total heat transfer with ϕ. When comparing Be number (Fig. 15b) to the nanoparticle loading, one can find out that, NFI is dominant. Increasing of the overall heat transfer with nanoparticle loading can also be seen in Fig. 16a. Average Nu number values become quite close to each other with increasing of Ω, except Ω = 500 at which, average Nu number tends to decrease depending on viscous and inertia forces. Figure 16b shows the dominance of the NFI. The rotation of the cylinder causes the increasing of NFI, particularly, its effect after Ω = 300 is more pronounced. Consequently, the Bejan number decreases with the nanoparticle loading which indicates HTI reduction.

4.4 Effect of rotating cylinder radius

The effects of the rotating cylinder radius are given in Figs. 17–19. Figure 17 displays the assessment of streamlines, isotherms, nanoparticle volume fractions and isentropic lines variations by the radius of solid cylinder. The flow streamlines and isotherms within the cavity are affected by cylinder rotation. Also, the size of cylinder impacts the fluid flow and heat transfer characteristics. When increase the cylinder size the gap between the cylinder surface and cavity wall is decreasing which lead to reduction of the streamlines. There are two main recirculating regions in the cavity left and right side of the cylinder for R = 0.1. It was observed weak recirculating zones for the higher values of R. Intensities of the isotherms increase with the increasing of R. When values of R increase, the local Nu number decreases (Fig. 18) and for a bigger heater (cylinder radius) the local heat exchange is less. Although entropy generation (Fig. 18b) increases with R, this increase is quite low before Ω = 300. There is no remarkable change in entropy generation along the Ω for small size of the cylinder (R = 1), whereas an effective increase was occurred for biggest value of R, around Ω = 300. From Fig. 19; it is seen that when R values increase, the average Nu number decreases, meaning that NFI is dominated and it is also an evidence of the decrease of Be number with Ω for all cylinder radius values. The averaged Nusselt number is not change significantly with the rotational velocity of the cylinder increases.

5 Conclusions

In this numerical study, the fluid flow and mixed convective heat transfer problem of Al2O3/water nanofluid inside a square cavity that has a solid circular cylinder is studied taking some governing parameters such as Rayleigh number, rotational velocity of cylinder, nanoparticle loading and rotating cylinder radius into consideration. The entropy generation is studied as well, and some concluding remarks are given as follows:

• 1. An increment of the cylinder’s rotational velocity leads to the increase of the strength of the streamlines and more of the fluid heat flow move in the clockwise direction.

• 2. When the Rayleigh number and the nanoparticle loading increase, the average Nusselt number and the convective heat transfer increase.

• 3. The global entropy generation caused by the heat transfer irreversibility increases with the nanoparticle loading and the angular rotational velocity for upper values of radius of the rotating cylinder.

• 4. It is found that the heat transfer irreversibility is dominant for a stationary cylinder (Ω = 0); whereas the generated entropy is caused fundamentally from the nanofluid friction irreversibility for a rotating cylinder.

• 5. It is found that using a cylinder with a smaller radius and a moderate rotational velocity obtains a better heat transfer rate.

• 6. For larger values of the radius of the rotating cylinder, the average Nusselt number is observed with low values.