Introduction

Natural convection heat transfer has been subject of many investigations due to its extensive application in engineering systems such as electronic cooling, ventilation, isolation of reactors, solar collectors and heat exchangers. Numerous numerical and experimental studies have been examined about the various aspects of the application of natural convection heat transfer in the enclosures. Many researchers have been studied natural or forced convection heat transfer in the presence of nanofluids [1,2,3,4,5,6,7,8,9,10,11]. Magnetohydrodynamics (MHD) shows the interaction between convection heat transfer and magnetic field is encountered in many areas in science and engineering such as astrophysics, nuclear and metallurgy applications [12]. The effect of magnetic field [13, 14] and constructal optimization [15] on natural convection heat transfer has been considered. Forced convection heat transfer for different stator blades of a heat exchanger was studied by Bayareh et al. [16].

On the other hand, Newtonian and non-Newtonian fluid flows in the enclosures have also been considered for a variety of applications, including food industries, polymer engineering and fluid transportation. In Newtonian fluids, the relation between shear stress and the rate of strain is linear. However, many industrial fluids exhibit non-Newtonian behavior. For example, molten solvents and polymers, atomic fluids and viscoelastic materials have non-Newtonian properties. Since these fluids are increasingly used in a wide range of industrial processes, understanding their transmission indicators is important.

Ozoe and Churchill [17] were the first researchers who examined the natural convection heat transfer of non-Newtonian fluids enclosed in a chamber. They examined the natural convection of both shear-thinning and shear-thickening fluids in a horizontal rectangular chamber. Their results showed that the critical Rayleigh number increases with the increase in power-law index. Kim et al. [18] studied the natural convection of a power-law non-Newtonian fluid in a vertical enclosure. They found that for a given Rayleigh number, the heat transfer rate increases for shear-thinning fluids in comparison with the Newtonian ones. Kefayati [19] studied natural convection of magnetohydrodynamics fluids and entropy generation in a square enclosure for a laminar flow of CuO–water nanofluid. They observed that as the Hartman number increases, entropy generation decreases. Also, the heat transfer increases with the volume fraction of nanoparticles, but it decreases with power-law index. Zhang and Che [20] presented two-dimensional numerical simulations to study the natural convection heat transfer of magnetohydrodynamics for CuO–water nanofluid in a square enclosure with four internal heat sources. The effect of Rayleigh and Hartman numbers and also the angle of positioning of the enclosure, as well as the volume fraction of nanoparticles, was studied. Their results showed that the application of the magnetic field in all Rayleigh numbers and the angles of the enclosure reduce convective heat transfer. Ghasemi et al. [21] studied the natural convection heat transfer in the presence of magnetic field for a square enclosure with cold vertical walls and horizontal insulating walls. They concluded that by increasing the Rayleigh number, heat transfer is improved. As the Hartman number increases, the heat transfer rate is reduced.

Lavasani et al. [22] studied the heat transfer of a square chamber filled with a nanofluid. They performed their research for Richardson numbers from 0.1 to 10 and the volume fraction of nanoparticles from 0 to 0.3, as well as the change in the height of the fin from 0.5 to 0.15. They concluded that for all the Richardson numbers, heat transfer increases using nanofluids. They found that as the Richardson number increases, the heat transfer rate increases for short fin heights. Jamesahar et al. [23] studied the natural convection heat transfer in a square chamber divided by a flexible membrane into two sub-enclosures, using the Lagrangian–Eulerian formula (ALE) method and concluded that the heat transfer with a flexible membrane is always higher than that with a rigid one. Ohta et al. [24] studied natural convection heat transfer of pseudoplastic fluids in a square box with floor heating and cooling from above. The results of their study indicated the importance of fluid concentration on the amount of heat transfer. Zablotsky et al. [25] examined the heat transfer of a ferro-fluid with variable-temperature properties in the presence of non-uniform magnetic fields. Their experiments were performed on a rectangular cell. The results showed that when the cell is heated from the bottom, the heat transfer rate increases in comparison with the case without magnetic field. Kefayati [26] examined the effect of the magnetic field on the heat transfer of a non-Newtonian fluid in a linearly heated container. The simulations were performed for a wide range of Rayleigh and Hartman numbers. The results showed that, irrespective of the flow index, as the Rayleigh and Hartman numbers increase, the heat transfer rate increases. Lamsaadi et al. [27] examined the natural convection of non-Newtonian power-law model in an enclosed chamber. They found that for a specific Rayleigh number, the rotation of enclosure between – 180 ≤ θ ≤ + 180 has a significant effect on the heat transfer rate. Raisi [28] investigated the effect of the existence of a pair of baffles on the natural convection heat transfer of a non-Newtonian fluid in a square chamber and showed that the reduction in the flow index reduces the apparent fluid viscosity and enhances the natural convection inside the chamber. Shahmardan and Norouzi [29] simulated a non-Newtonian fluid flow through a channel with a cavity. The non-Newtonian Carreau–Yasuda model is used to describe the stress dependence on the strain rate. Their numerical results showed that with decreasing the power-law index, the fully development length increases. Turan et al. [30] performed a complete study on the natural convection of non-Newtonian power-law fluids using the FLUENT commercial software and provided a correlation for Nusselt number in a wide range of Rayleigh and Prandtl numbers. Kasaeipour et al. [31] investigated the effect of the magnetic field on natural convection heat transfer of water–CuO nanofluid in a T-shaped enclosure. In this numerical study, the Hartman number was changed from 0 to 80 and the chamber was rotated at an angle of 0–90 degrees. Their results showed that the effect of the magnetic field on the average Nasselt number is higher for larger Rayleigh numbers.

More recent research on non-Newtonian fluids is found in investigations of Guha and Pradhan [32]. They found that shear-thickening non-Newtonian fluids have a better heat transfer in comparison with the Newtonian and shear-thinning fluids. Also, Kefayati [33] examined the heat transfer of a non-Newtonian molten polymer using lattice Boltzmann method in a square enclosure. Their results showed that the lattice Boltzmann method is a suitable method for solving this problem. Vinogradov et al. [34] investigated the heat transfer of shear-thickening fluids in square and rectangular chambers using power-law model. They showed that, despite the apparent difference in the heat transfer rate for Newtonian and non-Newtonian fluids, the same hydrodynamic behavior is observed for those fluids.

The objective of the present work is to investigate the magnetohydrodynamic natural convection in an inclined L-shaped enclosure saturated with a non-Newtonian fluid. The effect of magnetic field, shear thinning, shear thickening and orientation angle of the enclosure on thermal and flow fields is presented numerically.

Problem setup and governing equations

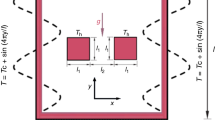
A schematic of the problem is shown in Fig. 1. The enclosure has the angle α with respect to the horizontal direction. The two walls of the enclosure are under constant heat flux q′′, the lower side is at temperature TC, and the other sides are at the temperature TH. No-slip boundary condition is imposed to all walls. The aspect ratio of the enclosure (AR = L/W) is assumed to be constant for all simulations.

Fig. 1
figure 1

A schematic of the present work

Full size image

The boundary layer flow is assumed to be laminar and steady. There is no heat loss of the viscosity. The Boussinesq approximation is employed for natural convection. In order to normalize the governing equations, the following parameters are defined:

$$X = \frac{x}{L}, Y = \frac{y}{L},\theta = \frac{{\left( {T - T_{\text{c}} } \right)k}}{{q^{{{\prime \prime }}} L}},U = \frac{uL}{\alpha }, V = \frac{vL}{\alpha }, P = \frac{p}{{\rho \left( {{\raise0.7ex\hbox{$\alpha $} \!\mathord{\left/ {\vphantom {\alpha L}}\right.\kern-0pt} \!\lower0.7ex\hbox{$L$}}} \right)^{2} }}$$
(1)

Therefore, the governing dimensionless equations for a laminar, two-dimensional and incompressible flow inside the enclosure are as follows:

Continuity:

$$\frac{\partial U}{\partial X} + \frac{\partial V}{\partial Y} = 0$$
(2)

Momentum in the x-direction:

$$U\frac{\partial U}{\partial X} + V\frac{\partial U}{\partial Y} = - \frac{\partial P}{\partial X} + \Pr^{*} .\left( {\frac{\partial }{\partial X}\left( {2\mu_{\text{a}}^{*} \frac{\partial U}{\partial X}} \right) + \frac{\partial }{\partial Y}\left( {\mu_{\text{a}}^{*} \left( {\frac{\partial U}{\partial Y} + \frac{\partial V}{\partial X}} \right)} \right)} \right) + {\text{Ra}} \,\Pr \sin \alpha .\theta + {\text{Ha}}^{2} \Pr^{*} \left( {V \sin \gamma \cos \gamma - U \sin^{2} \gamma } \right)$$
(3)

Momentum in the y-direction:

$$U\frac{\partial V}{\partial X} + V\frac{\partial V}{\partial Y} = - \frac{\partial P}{\partial Y} + \Pr^{*} .\left( {\frac{\partial }{\partial X}\left( {\mu_{\text{a}}^{*} \left( {\frac{\partial U}{\partial Y} + \frac{\partial V}{\partial X}} \right)} \right) + \frac{\partial }{\partial Y}\left( {2\mu_{\text{a}}^{*} \frac{\partial V}{\partial Y}} \right)} \right) + {\text{Ra}} \,\Pr \cos \alpha .\theta + {\text{Ha}}^{2} \Pr^{*} \left( {U \sin \gamma \cos \gamma - V \cos^{2} \gamma } \right)$$
(4)

Energy equation:

$$U\frac{\partial \theta }{\partial X} + V\frac{\partial \theta }{\partial Y} = \left( {\frac{{\partial^{2} \theta }}{{\partial X^{2} }} + \frac{{\partial^{2} \theta }}{{\partial Y^{2} }}} \right)$$
(5)

Power-law model is most commonly used in the description of pure non-Newtonian viscous fluids. The relation between shear stress and strain rate in this model is as follows.

$$\mu = \kappa \left\{ {2\left[ {\left( {\frac{\partial u}{\partial x}} \right)^{2} + \left( {\frac{\partial v}{\partial y}} \right)^{2} } \right] + \left( {\frac{\partial v}{\partial x} + \frac{\partial u}{\partial y}} \right)^{2} } \right\}^{{\frac{\text{n} - 1}{2}}}$$
(6)

where the variables n (flow index) and K (stability index) are empirical constants [35].

The governing non-dimensional parameters, Prandtl, Rayleigh and Hartman numbers, are defined as:

$$\Pr = \frac{k}{\rho }\alpha^{\text{n} - 2} L^{{2\left( {1 - \text{n}} \right)}}$$
(7)
$${\text{Ra}} = \frac{{g\beta \Delta TL^{2{\text{n}} + 1} }}{{\left( {\alpha^{\text{n}} \frac{k}{\rho }} \right)}}$$
(8)
$${\text{Ha}} = B_{0} L\sqrt {\frac{{\sigma_{\text{f}} }}{{\rho_{\text{f}} \vartheta_{\text{f}} }}}$$
(9)

Also, modified Prandtl and Rayleigh numbers are introduced for a uniform heat flux and defied as:

$${\text{Pr}}^{*} = \Pr^{\text{n} - 2}$$
(10)
$${\text{Ra}}^{*} = \frac{{g\beta \Delta TL^{3} }}{{\alpha \left( {\frac{k}{\rho }} \right)^{{{\raise0.7ex\hbox{$1$} \!\mathord{\left/ {\vphantom {1 {\left( {2 - {\text{n}}} \right)}}}\right.\kern-0pt} \!\lower0.7ex\hbox{${\left( {2 - {\text{n}}} \right)}$}}}} L^{{{\raise0.7ex\hbox{${2\left( {1 - {\text{n}}} \right)}$} \!\mathord{\left/ {\vphantom {{2\left( {1 - {\text{n}}} \right)} {\left( {2 - {\text{n}}} \right)}}}\right.\kern-0pt} \!\lower0.7ex\hbox{${\left( {2 - {\text{n}}} \right)}$}}}} }}$$
(11)

Dimensionless apparent viscosity \(\mu_{a}^{*}\) is:

$$\mu_{a}^{*} = k\dot{\gamma }^{*\text{n} - 1}$$
(12)

where the shear rate \(\dot{\gamma }^{*}\) is defined as:

$$\dot{\gamma }^{*} = \left[ {2\left( {\frac{\partial U}{\partial X}} \right)^{2} + 2\left( {\frac{\partial V}{\partial Y}} \right)^{2} + \left( {\frac{\partial U}{\partial Y} + \frac{\partial V }{\partial X}} \right)^{2} } \right]^{{\frac{1}{2}}}$$
(13)

Local Nusselt number is defined to evaluate the heat transfer rate:

$${\text{Nu}}_{\text{x}} = \left( {\frac{1}{\theta }} \right)_{{\text{Y}} = 0}$$
(14)

Average Nusselt number is obtained by the following relation:

$${\text{Nu}}_{\text{m}} = \mathop \int \limits_{0}^{1} {\text{Nu}}_{\text{x}} {\text{d}}X$$
(15)

In order to perform numerical simulations, the differential equations governing the problem must be converted to algebraic equations. Therefore, the equations are discretized by finite-difference method based on the control volume. The cold wall temperature is considered as reference temperature. Governing equations along with stated border conditions are algebralized by finite-volume method based on the volume control. The SIMPLE algorithm is used to solve algebraic equations simultaneously [21] using ANSYS FLUENT 6.3. The second-order upwind discretization and central difference schemes are used for the convection and diffusion terms, respectively. The convergence criterion for the governing equations is:

$$\varPhi = \mathop \sum \limits_{J} \mathop \sum \limits_{I} \left| {\frac{{\psi^{\epsilon + 1} - \psi^{\epsilon}}}{{\psi^{\epsilon + 1}}}} \right| \le 10^{- 5}$$
(16)

where ε is number of cells and is a variable such as U, V and Ө.

Results

Convergence study and validation

Table 1 shows the average Nusselt number for Ra* = 105, Pr* = 102, \(\alpha = 0^\circ\), \(\gamma = 45{^\circ }\) and n = 0.8 for different grid resolutions. The table shows that the average Nusselt number does not vary for the resolution above 70 × 70 grid points. In order to achieve a reasonable computational time, the 70 × 70 resolution is selected for further simulations.

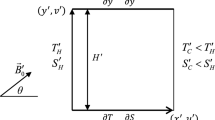
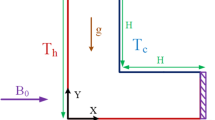
Table 1 Convergence study of average Nusselt number. Also, the percentage error according to the 80 × 80 grid resolution is presented
Full size table

Figure 2 illustrates a comparison between present simulations with the average Nusselt number reported by Turan et al. [30] and Vinogradov et al. [34]. Also, a schematic of the problems is shown in the figure. It is observed that present simulations are in excellent agreement with the numerical results.

Fig. 2
figure 2

Comparison of our simulations with numerical results of Turan et al. [30] and Vinogradov et al. [34]

Full size image

Magnetic effects on convective heat transfer

Numerous studies have been performed on natural convection flow of Newtonian fluid in an enclosure. In the present work, heat transfer of non-Newtonian fluids in an L-shaped enclosure with constant aspect ratio is studied for a range of 102 < Pr* < 104 and \(10^{3} < {\text{Ra}}^{ *} < 10^{5}\). It should be mentioned that the Prandtl number is high for most non-Newtonian fluids [36]. The flow index is in the range of 0.8 ≤ n ≤ 1.4. n < 1 and n > 1 correspond to shear-thinning and shear-thickening fluids, respectively. In Figs. 3 and 4, isotherms and streamlines are plotted for different angles of the enclosure at Ra* = 105, \(\gamma = 45{^\circ }\) and Pr* = 102. It can be seen that several vortices are formed horizontally and vertically in the enclosure. At a constant power-law index (n), the number of vortices decreases with the angle of the enclosure α. For example, for n = 0.8, four vortices are shown for α = 0. However, two vortices are observed for α = 60. The vortex created at the bottom of the enclosure extends to the whole channel with the angle α and gradually occupies the horizontal and vertical parts of the enclosure. At a constant angle, isotherms and streamlines are different for different power-law index. For shear-thickening fluids, the temperature distribution is more uniform in comparison with the shear-thinning ones. Also, the strength of vortices decreases with the power-law index. Therefore, smaller vortices are created for shear-thickening fluids. At the angle α = 60°, a vortex is generated in the lower corner of the enclosure due to larger effect of convection heat transfer. Generally, by increasing the angle of the enclosure with respect to the horizontal direction, the buoyancy force and natural convection become stronger and heat transfer increases. The distribution of buoyancy forces in the x- and y-directions due to the rotation of the enclosure leads to the variation of flow and thermal fields. It is also clear that flow index influences the heat transfer rate. The curvature of isotherms decreases due to the reduction in the heat transfer rate especially in the central part of the enclosure.

Fig. 3
figure 3

Isotherms for different values of \(\alpha\) at, \(\gamma = 45{^\circ }\) and \({\text{Ra}}^{ *} = 10^{5}\)

Full size image
Fig. 4
figure 4

Streamlines for different values of \(\alpha\) for \(\gamma = 45{^\circ }\) and \({\text{Ra}}^{ *} = 10^{5}\)

Full size image

The buoyancy force increases with the Rayleigh number. The streamlines and isotherms become more asymmetric results in the generation of more vortices in the flow field (not shown). This indicates that the dominant heat transfer mechanism changes from conduction heat transfer to natural convection one as the Rayleigh number increases.

In Fig. 5, the values of \(\frac{{ \overline{\text{Nu}} }}{{\overline{\text{Nu}}_{\text{n} = 1} }}\) are plotted for different Rayleigh numbers. It can be concluded that the heat transfer of pseudoplastic (shear-thinning) fluids is greater than that of Newtonian and non-Newtonian shear-thickening fluids. Even though the heat transfer of shear-thinning fluids is higher than that of shear-thickening ones, the enhancement rate (the slope of Nu curve) for shear-thickening fluids is larger than that for shear-thinning ones. For example, the rate of increase in average Nusselt number between α = 0° and α = 30° for n = 0.8 and n = 1.4 is 21.2 and 4.58%, respectively. This is due to that as the power-law index increases, the fluid viscosity increases and the conduction heat transfer becomes a dominant mechanism. Hence, it can be concluded that for shear-thinning fluids, the velocity increases leads to a decrease in the boundary layer thickness. In other words, the boundary layer thickens as the viscosity increases. As mentioned before, a vortex is generated at the bottom of the enclosure for n = 0.8 and α = 60°. Figure 5 demonstrates that average Nusselt number decreases for the enclosure angles greater than α = 60°.

Fig. 5
figure 5

Values of \(\frac{{ \overline{\text{Nu}} }}{{\overline{\text{Nu}}_{\text{n} = 1} }}\) for different values of \(\alpha\) at,\(\gamma = 45{^\circ }\)

Full size image

It is also found that average Nusselt number increases with modified Rayleigh number due to higher values of the ratio of buoyancy and viscous forces.

At the angle of inclination α = 0°, as the Rayleigh number decreases, the thermal behavior of Newtonian fluids is the same as that of non-Newtonian pseudoplastic fluids. The heat transfer for the case of Newtonian fluids does not depend on the inclination angle of the enclosure, but Nusselt number increases with power-law index for the case of shear-thickening fluids at constant Rayleigh numbers. According to this figure, the highest value of Nusselt number corresponds to the pseudoplastic fluids at \({ \Pr }^{ *} = 10^{2}\) and α = 60°. The lowest value of Nusselt number is obtained at α = 0° for all Rayleigh numbers. Also, it is found that the highest value of Nusselt number for the shear-thickening fluid occurs at \({ \Pr }^{ *} = 10^{2}\) and α = 90°. It can be seen that at \({ \Pr }^{ *} = 10^{2}\) and Ra* = 103, the heat transfer decreases with increasing the power-law index (n) at constant enclosure angle α. As a result, a shear-thickening fluid concludes higher convective heat transfer in comparison with Newtonian and non-Newtonian fluids. Therefore, shear-thinning and shear-thickening fluids have different thermal behavior at a constant modified Prandtl number (Fig. 6). While Nusselt number decreases with increasing Pr* for n < 1, it increases with Pr* for n > 1. This is valid for all angle of α. Shear-thinning fluids improve the rate of heat transfer at low Pr*, but shear-thickening fluids increase the Nusselt number at high Pr*. According to Fig. 6, it can be concluded that there is a competition between flow and thermal fields for different values of Pr* and n. Therefore, the optimal value of Pr* is different for shear-thinning and shear-thickening fluids at a constant modified Rayleigh number.

Fig. 6
figure 6

Values of \(\frac{{ \overline{\text{Nu}} }}{{\overline{\text{Nu}}_{{\text{n}} = 1} }}\) for different values of flow index n, Pr* and Ra* at \(\gamma = 45{^\circ }\)

Full size image

In Fig. 7, the average Nusselt number for the angle γ = 0° is plotted for different enclosure angles. The change in the magnetic field direction leads to the change in the flow symmetry. Compared to the results corresponding to γ = 45°, average Nusselt number increases with increasing the angle between the magnetic field and horizontal direction, γ. For example, the value of \(\frac{{ \overline{\text{Nu}} }}{{\overline{\text{Nu}}_{\text{n} = 1} }}\) for n = 0.8 at γ = 0° and γ = 45° is 1 and 1.12, respectively. A competition between the buoyancy and the Lorentz forces causes a different behavior in non-Newtonian fluids. It is worth noting that thermal behavior of shear-thinning fluids is approximately similar to that of Newtonian fluids for α < 60°. For α > 60°, Nusselt number of shear-thinning fluids increases as the enclosure angle increases. Shear-thickening fluids have a completely different behavior. For α > 60°, their Nusselt number increases with α. For α < 60°, they behave like Newtonian fluids.

Fig. 7
figure 7

Values of \(\frac{{ \overline{\text{Nu}}_{\text{n} = {\text{n}}} }}{{\overline{\text{Nu}}_{\text{n} = 1} }}\) for different values of flow index n, Pr* and Ra* at \(\gamma = 0^\circ\)

Full size image

Conclusions

The effect of magnetic field on convective heat transfer in an L-shaped enclosure filled with a non-Newtonian fluid was investigated numerically. The governing equations were solved by finite-volume method using the SIMPLE algorithm. The results demonstrated that the heat transfer increases with increasing the angle of the enclosure with respect to the horizontal direction. It was revealed that the heat transfer of shear-thinning fluids is greater than that of Newtonian and non-Newtonian shear-thickening fluids at constant values of Pr* and Ra*. Nusselt number decreases with increasing Pr* for shear-thinning fluids and it increases with Pr* for shear-thickening ones. The results showed that thermal behavior of shear-thinning and shear-thickening fluids is similar to that of Newtonian fluids for α < 60° and α > 60°, respectively.