Introduction

A medium (or material) which contains voids is termed as porous medium and its skeletal portion is usually called the frame or matrix. In general, a fluid (liquid or gas) is typically filled in these pores and any porous medium is normally distinguished by porosity described in terms of ratio of void space volume over total volume (between 0 and 1). Examples of porous media are very wide, ranging from natural substances (e.g., soil, rocks and biological tissues) to artificial substances (e.g., cements, ceramics) and different properties of these materials are only rationalized by treating them as porous media. Porous medium concept is used in different areas of engineering and applied science, for example, petroleum, construction or material science, filtration, geo-mechanics, soil mechanics, acoustics, etc. Flow of fluids (Newtonian or non-Newtonian) through porous matrix exerts a huge amount of interest among researchers and has emerged as a separate area of research. For example, it can be helpful in controlling environment pollution by finding moisture and temperature distribution in agricultural lands. Liu et al. [1] provided the finite element approach and its theoretical predictions for non-linear boundary value problem which is utilized to formulate the non-Fickian flow of fluid in porous media. Therefore, development and analysis of various fluid models are given to study the flow properties in non-Darcy porous media in different books (Ref. [2,3,4]).

The viscosity in two type of power-law fluids, shear thinning (pseudoplastic) and shear thickening (dilatant), decreases and increases with stress respectively. Due to wide application of power-law fluids in modern science and technology, Shenoy [5] and Cheng [6] studied influences of important parameters for applicable geometries. Mandal et al. [7] provided a numerical solution for the fluid models of pulsatile blood flow between an irregular stenosed arterial segment which is very useful in the areas related to medical science and research. The role of local production of thermal energy through viscous stress mechanism of power-law fluid flow due to buoyancy forces is studied by Khidir et al. [8]. Kairi [9] has shown that the increment in the radius of slender paraboloid in a porous medium reduces the Nusselt number for all shear thickening and thinning fluids.

Due to significance of the thermal stratification and its involvement in the major applications as heat exchangers used in domestic hot water tank, the study of thermal stratification in different porous media concepts has gained notable importance in modern times. The experimental and analytical results related to thermal stratification in lakes are given by Dake and Harleman [10]. From Knudsen and Furbo [11], one can get ideas about the use of heat exchangers in the storage tank and solar collector. In view of these applications, Narayana et al. [12] and Cheng [13] conducted independent studies on the free convective flow over vertical flat plate and vertical wavy surface, respectively, with dilatant and pseudoplastic fluids and concluded that the total Nusselt number value for wavy surface is more in comparison to the smooth surface. On the other hand, thermal dispersion effect plays a vital role due to inertial effect existence in a non-Darcy porous medium. In non-uniform geometries, particularly in the packed beds, flow of fluid through curvy paths led to the thermal dispersion at the pore level of the involved porous media. Several researchers, to point out few, Cheng [14] and Plumb [15], analysed different fluid flows and heat transfer with thermal dispersion. Hong et al. [16] treated \(\dfrac{\chi d u_\infty }{\alpha } = \chi Pe_{\chi }\) as Ds and then explained the flow analysis theoretically. By adopting the similar representations, Kairi and Murthy [17] conducted the study of free convective flows of dilatant or pseudoplastic fluids with thermal stratification and dispersion. Numerical study for the same fluid flow but without prescribing the temperature and concentration on the vertical surface, is presented by Srinivasacharya et al. [18] and concluded that the obtained similarity solutions are valid only for small values of X - location (i.e. \(0<X<1\)). Later, Vasu et al. [19] performed an entropy generation analysis for stratified flow along vertical surface (for elaborative discussions, see the citations therein).

In recent times, various real life flow applications are dealt in emerging scientific and technological areas and the nature of these flows are very complex, consequently the study related to heat transfer mechanism is also very tough. So convective boundary conditions are very important for this kind of flows, usually occurring in nuclear reactors, solar collectors etc. The similarity solutions of free convective power-law fluid flow past a convectively heated vertical surface are obtained by Ece and Buyuk [20]. Yao et al. [21] discussed the convective transport along shrinking and/or stretching wall problem. Many thermal systems operated at very high temperatures suffer the lose of its linear nature of density-temperature relation given by \(\,\,\rho -\rho _{\infty } + \rho _{\infty } \beta _0 (T - T_{\infty })=0\) (For more details, one can refer Pop and Ingham [3]). This gives the idea of non-linear Boussinesq approximation or non-linear convection where it has \(\,\rho -\rho _{\infty }+ \rho _{\infty } \beta _0 (T - T_{\infty }) \left[ 1 + \frac{\beta _1 (T - T_{\infty })}{\beta _0}\right] =0\,\,\) (Refer Partha [22] and its citations). A strong influence of this non-linearity is noticed on different fluid flow problems. The impact of dispersion on the non-linear convective flow of incompressible shear thickening and thinning fluids is investigated by RamReddy et al. [23] and it is concluded that the velocity and local Nusselt number are increased when the increment takes place in Ds parameter. But a detailed idea regarding the rates of flow as well as heat transfer of these dilatant and pseudoplastic fluids is yet to emerge.

Many engineering and industrial problems e.g., processing of melted plastics at a large level, edible items or slurries and polymers etc., require free convective power-law fluid flow from truncated cones subjected to the convective boundary condition in porous media. But from available literature, it is observed that this model is not studied so far although results of these kind of studies can serve as a useful productive tool to solve important engineering and industrial problems. There are some works available in the literature, namely, Na and Chiou [24], Gorla et al. [25], Cheng [26, 27] but these papers are only related to power-law fluid flow over truncated cone maintained at uniform wall temperature and/or subject to uniform heat flux conditions. This motivates us to analyze the above-said fluid flow problem in detail as it helps us to study various effects like: (i) ratio of internal thermal resistance of truncated cone surface to the thermal resistance of boundary layer in terms of Biot number, and (ii) effectiveness of non-uniform pore level velocity over temperature field within the specific porous medium in terms of thermal dispersion parameter. So, in this article, the natural convective flow over truncated cone in a power-law fluid saturated non-Darcy porous medium is mathematically modelled and then the associated governing equations are solved using non-similarity technique and spectral local linearization method. Later, the results are graphically analyzed in detail along with their proper physical significance and real life applications as seen in the cooling of magmatic intrusion or radioactive sub-surface storage location which involve convective transport theory.

Mathematical Formulation and Analysis

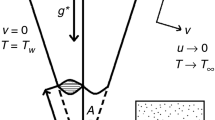
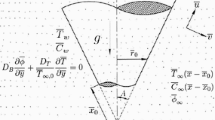
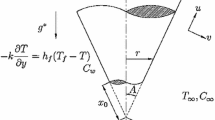
Figure 1 displays a mathematical configuration to study the natural convective flows related to thermally stratified dilatant and pseudoplastic fluids along a convectively heated truncated cone. The non-Darcian type of porous medium is taken in this analysis. The coordinate axes x and y are in the parallel and perpendicular directions to the truncated cone and \(x_{0}\) is the distance between its leading edge and origin O. Here, \(\bar{x}=x-x_{0}\) is considered as modified streamwise coordinate, \(T_{f}\) is the fluid temperature and \({T_\infty (\bar{x})=T_{\infty ,0}+A^*\bar{x}}\) is the temperature of the linearly stratified ambient medium which generates a stable thermal stratification. The stratification intensity is controlled by a parameter \(A^*\). This steady, two dimensional and laminar fluid flow is in thermodynamic equilibrium with porous medium. Also, to neglect boundary effect and apply the Forchheimer flow model, permeability of the medium is taken less with moderate flow intensity. In addition, there is notable significance of large changes in the temperatures of ambient medium and surface of the truncated cone.

Fig. 1
figure 1

Geometry used in the problem

Full size image

It is also presumed that the thickness of momentum and thermal boundary layer is very less compared to the local radius of truncated cone. The approximation \(\displaystyle {r=x\,sinA}\) [See Singh et al. [28]] shows the relation between truncated cone radius and local radius at a point situated in the boundary layer which implies \(x_0<x<\infty \) as the region in which governing equations and boundary conditions are valid. Hence, these assumptions are practical and more relevant.

So, the governing equations along with boundary conditions associated with this fluid flow model can be written as

$$\begin{aligned}&\frac{\partial (ru)}{\partial x} + \frac{\partial (rv)}{\partial y} = 0 \end{aligned}$$
(1)
$$\begin{aligned}&\frac{\partial {{u}^n}}{\partial y}+\frac{b{K^*}}{\nu }\frac{\partial {u^2}}{\partial y} = \frac{{K^*} {g^{*}}}{\nu }\left\{ \left[ {\beta _0}+ 2{\beta _1}{\left( {T - {T_{\infty }(\bar{x}) }} \right) }\right] \frac{{\partial }T}{\partial y} \right\} \mathrm{{cos}}A \end{aligned}$$
(2)
$$\begin{aligned}&u\frac{\partial T}{\partial x} + v\frac{\partial T}{\partial y} = \frac{\partial }{\partial y}\left( \alpha _* \frac{\partial T}{\partial y}\right) \end{aligned}$$
(3)
$$\begin{aligned}&v=0, - {k_{m}}\frac{\partial T}{\partial y} = {h_f}({T_f} - T), \text{ at } y=0 \nonumber \\&u \rightarrow 0, T \rightarrow {T_\infty (\bar{x})} \text{ as } y\rightarrow \infty \end{aligned}$$
(4)

where \(g^*\) is the acceleration due to gravity, \({h_f}\) is the convective heat transfer coefficient, \({k_m}\) is the thermal conductivity, \(\nu \) is the kinematic viscosity, A is the inclination of angle, T is the temperature, \(\textit{b}\) is the empirical constant and (u, v) are the Darcian velocities. A quantity \(\alpha _*\) is obtained by taking the sum of \(\alpha _d=\chi u d\) (thermal diffusivity) and \(\alpha \) (molecular diffusivity ) as per Plumb [15], where \(\chi \) is the mechanical dispersion coefficient and d is the pore diameter. Next, \(\beta _0\) and \(\beta _1\) are the \(1^{st}\) and \(2^{nd}\) order thermal expansion coefficients respectively. When \(n=1\) (the power-law index), the fluid becomes Newtonian and for \(n>1\) and \(n<1\), the fluid is dilatant and pseudoplastic respectively. \(K^*\) denotes the modified permeability of the porous medium which is a function of n (See [29] and [30] for more details).

The stream function \(\displaystyle {\psi }\) is introduced in such a way that it satisfies the equation of continuity (1) i.e., \(\displaystyle {u =\frac{1}{r} \frac{{\partial \psi }}{{\partial y}}}\), \(\displaystyle {v = - \frac{1}{r} \frac{{\partial \psi }}{{\partial x}}}\). The non-dimensional relations utilized to get the non-dimensional form of Eqs.(2)-(4) are

$$\begin{aligned} \begin{aligned} \displaystyle {\xi = \frac{\bar{x}}{x_{0}}},{} \,\,\, \displaystyle {\eta = \frac{y}{\bar{x}}\,{{Ra}^{\frac{1}{2}}}},\,\,\, \displaystyle {f(\xi ,\eta ) =\frac{{Ra^{-\frac{1}{2}}}}{{\alpha \,r}}\psi (\xi ,\eta )}, \,\,\, \displaystyle {\theta (\xi ,\eta )=\frac{T(\xi ,\eta )- {T_{\infty }(x-x_{0})}}{\left( {T_f} - {T_{\infty ,0} }\right) }} \end{aligned}\nonumber \\ \end{aligned}$$
(5)

where \(Ra=\dfrac{\bar{x}}{\alpha }\left( \dfrac{\rho \,\beta _0\,g^*\,K^*\,cosA\,({T_f}-{T_{\infty ,0}})}{\mu }\right) ^{\frac{1}{n}}\) is the local modified Darcy-Rayleigh number.

Using these transformations (5) in the Eqs. (1) to (3), the non-dimensional form of the above equations become

$$\begin{aligned}&\left[ n\left( {f'}\right) ^{n-1}+2\,{Gr^*}f'\right] \mathrm{{ }}f'' = (2\,{\alpha _1}\theta +1){\theta '} \end{aligned}$$
(6)
$$\begin{aligned}&\theta ''+\left( f'\,\theta ''+f''\,\theta '\right) Ds\,+ \left( \frac{\xi }{\xi +1}+0.5\right) f\theta '-S_T\,\xi \,f' = {\xi {f'}\frac{\partial \theta }{\partial \xi } - \xi \frac{\partial f}{\partial \xi }\theta '} \end{aligned}$$
(7)

The boundary conditions (4) in their transformed forms can be written as

$$\begin{aligned} \begin{aligned}&2\,{\xi \,(\xi +1)}{\left( {\frac{\partial f}{\partial \xi }} \right) _{\eta = 0}} + (3\,\xi +1)f(\xi ,0)=0,\\&\quad \theta '(\xi , 0) - Bi\,{\xi ^{\frac{1}{2}}}\left[ \theta (\xi ,0)\, -1 \,+ S_T \, \xi \right] =0, \\&\quad f'(\xi ,\eta ) \rightarrow 0,\,\,\,\,\,\,\theta (\xi ,\eta ) \rightarrow 0 \,\,\,\,as \,\,\,\,\eta \rightarrow \infty . \end{aligned} \end{aligned}$$
(8)

Here prime indicates the differentiation in respect of \(\eta \) and \(Gr^*=\dfrac{{b\,K^*}}{\nu }\left( \dfrac{\alpha Ra}{\bar{x}}\right) ^{2-n}\), \({\alpha _1} = \dfrac{{\beta _1}}{{\beta _0}}({T_f} - {T_{\infty ,0} })\), \(Ds=\dfrac{\chi d Ra}{\bar{x}}\), \(S_T = \dfrac{A^*x_{0}}{({T_f} - {T_{\infty ,0} })}\), \(Bi=\dfrac{h_f \sqrt{x_0}}{k_m}\left( \dfrac{{\bar{x}}}{Ra}\right) ^\frac{1}{2}\) represent the modified Grashof number, non-linear density-temperature parameter, thermal dispersion parameter, thermal stratification parameter and Biot number respectively. When \(\xi \rightarrow 0\,\) (i.e., \(x \rightarrow x_0\)), this problem is converted to flow problem past a vertical plate. Similarly, when \(x_0=0\), \(\xi \) becomes very large which is utilized to obtain the same problem with full cone as a geometry.

Non-dimensional representations of Nusselt number \(\displaystyle {Nu_x =-\frac{{\bar{x}}}{k}\dfrac{(k+k_d)}{({T_f} - {T_{\infty ,0}})}\left[ \frac{\partial T}{\partial y}\right] _{y=0}}\) and skin friction coefficient \(C_f=\dfrac{2}{\rho \,u_{*}^{2}}\left[ \mu \dfrac{\partial u}{\partial y}\right] _{y=0} \) are

$$\begin{aligned} \displaystyle {\dfrac{Nu_{\bar{x}}}{{Ra^{\frac{1}{2}}}}= -\left[ Ds\,f'(\xi ,0)+1\right] \theta '(\xi , \, 0)},\,\,\,\,\,\,\,\,\,\,\,\dfrac{1}{2}\dfrac{Ra^{\frac{1}{2}}}{Pr}C_f=f''(\xi ,0) \end{aligned}$$
(9)

Here \(u_{*}\) and \(\mu \) denote characteristic velocity and dynamic viscosity respectively, \(k_e\) (the effective thermal conductivity of the medium) is the sum of \(k_d\) (the dispersion thermal conductivity) and k (the molecular thermal conductivity), and Pr denotes the Prandtl number.

Numerical Solutions

The flow Eq. (6) accompanied with the energy Eq. (7) and BCs(8), constitute highly complex non-linear non-homogeneous system of PDEs and closed-form solutions for these kind of systems cannot be obtained. Therefore, the Eqs. (6)– (7) together with the BCs (8) are solved efficiently with local non-similarity technique and spectral local linearization method (SLLM). Combination of these methods has been proved to be appropriate and assures precise outcome for complex parabolic equations. The detailed explanations of these approaches and their implementations are given below:

Local Non-Similarity Procedure

The approach given by Sparrow and Yu [31], named as local similarity and non-similarity technique, is used to obtain the system of ODEs by employing the three levels of truncation. When \(\xi<<1\) , the preliminary approximation is found from the local similarity equations and insignificant terms involving \(\displaystyle {\xi \frac{\partial }{\partial \xi }}\) are removed. Consequently the local similarity equations for the first level truncation of Eqs.(6)-(8) are

$$\begin{aligned} \left[ n\,\left( {f'}\right) ^{n-1}+2\,{Gr^*}f'\right] \mathrm{{ }}f''- ( 2\,{\alpha _1}\theta +1){\theta '}=0 \end{aligned}$$
(10)
$$\begin{aligned} \theta ''+\left( f''\,\theta '+f'\,\theta ''\right) Ds\,+ \left( \frac{\xi }{\xi +1}+0.5\right) f\theta '-S_T\,\xi \,f' = 0 \end{aligned}$$
(11)

and the corresponding BCs are

$$\begin{aligned} \begin{aligned}&f(\xi ,0)=0,\,\,\theta '(\xi , 0) + Bi\,{\xi ^{\frac{1}{2}}}\left[ 1 - \theta (\xi ,0)\,-S_T \, \xi \right] =0,\\&f'(\xi ,\eta ) \rightarrow 0,\,\,\,\,\,\,\theta (\xi ,\eta ) \rightarrow 0 \,\,\,\,as \,\,\,\,\eta \rightarrow \infty . \end{aligned} \end{aligned}$$
(12)

The second level truncation involves the use of new variables \(\displaystyle {U = \frac{\partial f}{\partial \xi }, V = \frac{\partial \theta }{\partial \xi }}\), by which the local non-similarity non-linear ODEs are derived to get the previously omitted terms. Hence, updated governing equations are boundary conditions are

$$\begin{aligned}&\left[ n\,\left( {f'}\right) ^{n-1}+2\,{Gr^*}f'\right] \mathrm{{ }}f''- (2\,{\alpha _1}\theta +1){\theta '}=0 \end{aligned}$$
(13)
$$\begin{aligned}&\theta ''+\left( f''\,\theta '+f'\,\theta ''\right) Ds\,+ \left( \frac{\xi }{\xi +1}+0.5\right) f\theta '-S_T\,\xi \,f'-\xi \, V\,f' + \xi \, U\,\theta '=0 \nonumber \\ \end{aligned}$$
(14)
$$\begin{aligned}&(3\,\xi +1)f(\xi ,0)+ 2\,{(\xi +1)}\,\xi \,{U(\xi ,0)}=0,\nonumber \\&\theta '(\xi , 0) + Bi\,{\xi ^{\frac{1}{2}}}\left[ 1 - S_T \, \xi \, -\theta (\xi ,0)\right] , \nonumber \\&f'(\xi ,\eta ) \rightarrow 0,\,\,\,\,\,\,\theta (\xi ,\eta ) \rightarrow 0 \,\,\,\,as \,\,\,\,\eta \rightarrow \infty . \end{aligned}$$
(15)

Finally, in last truncation level, Eqs.(13)-(15) are differentiated in respect of \(\xi \) and all partial derivatives of U and V are removed. Therefore, the final equations are

$$\begin{aligned}&n\left( {f'}\right) ^{n-1}\mathrm{{ }}U'' + n(n-1)\left( {f'}\right) ^{n-2}\mathrm{{ }}f''U'+2Gr^*(U''\mathrm{{ }}f'+f''\mathrm{{ }}U') \nonumber \\&\quad -V'- 2\,{\alpha _1}(\theta {V'}+V{\theta '})=0 \end{aligned}$$
(16)
$$\begin{aligned}&V'' + Ds(f'V'' + f''V') + \left( \frac{1}{2}+\dfrac{\xi }{\xi +1}\right) fV' -f'V+ \xi UV'-\xi U'V \nonumber \\&\quad + Ds(U''\theta '+U'\theta '')+\left( \frac{1}{2}+\dfrac{\xi }{\xi +1}\right) U\theta ' - S_T f' - \xi S_T U' +\theta 'U + \dfrac{1}{(\xi + 1)^2}f\theta '\!=\!0 \nonumber \\ \end{aligned}$$
(17)

with boundary conditions

$$\begin{aligned} \begin{aligned}&3f(\xi ,0)+(7\xi +3)U(\xi ,0) = 0,\\&V'\left( {\xi ,0} \right) - Bi{\xi ^{\frac{1}{2}}}V\left( {\xi ,0} \right) + 0.5\, Bi{\xi ^{-\frac{1}{2}}}[1-\theta (\xi ,0)] - 1.5\, Bi{\xi ^{\frac{1}{2}}}S_T, \\&U'(\xi ,\eta ) \rightarrow 0,\,\,\,\,\,\,V(\xi ,\eta ) \rightarrow 0 \,\,\,\,as \,\,\,\,\eta \rightarrow \infty . \end{aligned} \end{aligned}$$
(18)

Spectral Local Linearization Method (SLLM)

SLLM is initially developed by Motsa [32] to find the solutions of non-linear coupled ODEs. The solution procedure of this problem with SLLM consists of the following three steps: (i) first, the Eqs.(13)-(14) and Eqs.(16)-(17) are decoupled using Gauss-Seidel method and then the well-known quasi-linearization technique is used to linearize the nonlinear components of the decoupled equations;

(ii) next, the Chebyshev spectral collocation method is adopted to transform the set of linearized ODEs into the set of algebraic equations in the matrix form;

(iii) finally, this matrix is solved iteratively using appropriate initial solutions.

$$\begin{aligned}&f_{r+1}''+a_{1,r}f_{r+1}'=K_{1,r} \end{aligned}$$
(19)
$$\begin{aligned}&\theta _{r+1}''+b_{1,r}\theta _{r+1}'=K_{2,r} \end{aligned}$$
(20)
$$\begin{aligned}&U_{r+1}''+x_{1,r}U_{r+1}'=K_{3,r} \end{aligned}$$
(21)
$$\begin{aligned}&V_{r+1}''+y_{1,r}V_{r+1}'+y_{2,r}V_{r+1}=K_{4,r} \end{aligned}$$
(22)

where

$$\begin{aligned}&a_{1,r}=\dfrac{n(n-1)f_{r}''\left( f_{r}'\right) ^{n-2}+2Gr^*f_{r}''}{n\left( f_{r}'\right) ^{n-1}+2Gr^*f_{r}'},\\&K_{1,r}=\dfrac{\theta _{r}'+2\alpha _1\theta _{r}\theta _{r}'+n(n-1)f_{r}''\left( f_{r}'\right) ^{n-1}+2Gr^*f_{r}''f_{r}'}{n\left( f_{r}'\right) ^{n-1}+2Gr^*f_{r}'},\\&b_{1,r}=\dfrac{Dsf_{r+1}''+\left( \frac{1}{2}+R\right) f_{r+1}+\xi U_{r}}{1+Dsf_{r+1}'},\\&K_{2,r}=\dfrac{\xi S_{T}f_{r+1}'+\xi f_{r+1}'V_{r}}{1+Dsf_{r+1}'},\\&x_{1,r}=\dfrac{n(n-1)\left( f_{r+1}'\right) ^{n-2}f_{r+1}''+2Gr^*f_{r+1}''}{2Gr^*f_{r+1}'+n\left( f_{r+1}'\right) ^{n-1}},\\&K_{3,r}=\dfrac{V_{r}'+2\alpha _1\theta _{r+1}'V_{r}+2\alpha _1\theta _{r+1}V_{r}'}{n\left( f_{r+1}'\right) ^{n-1}+2Gr^*f_{r+1}'},\\&y_{1,r}=\dfrac{Dsf_{r+1}''+\left( \frac{1}{2}+R\right) f_{r+1}+\xi U_{r+1}}{1+Dsf_{r+1}'}, y_{2,r}=\dfrac{-f_{r+1}'-\xi U_{r+1}'}{1+Dsf_{r+1}'},\\&K_{4,r}=\dfrac{-Ds\left( U_{r+1}'\theta _{r+1}''+U_{r+1}''\theta _{r+1}'\right) -\left( \frac{3}{2}+R\right) U_{r+1}\theta _{r+1}'+\xi S_{T}U_{r+1}'+S_{T}f_{r+1}' -\frac{1}{(\xi +1)^2}f_{r+1}\theta _{r+1}'}{1+Dsf_{r+1}'}, \end{aligned}$$

with linearized boundary conditions

$$\begin{aligned} \begin{aligned}&{f_{r+1}}(\xi ,0) = -\frac{2\xi (\xi +1)}{3\xi +1}U_{r}(\xi ,0),\\&\theta _{r+1}'(\xi ,0)-\xi ^{\frac{1}{2}} Bi \, \theta _{r+1}(\xi ,0)=-Bi\xi ^{\frac{1}{2}}+Bi\xi ^{\frac{3}{2}}S_{T},\\&U_{r+1}(\xi ,0)=-\frac{3}{7\xi +3}{f_{r+1}}(\xi ,0),\\&V_{r+1}'(\xi ,0)-Bi\xi ^{\frac{1}{2}}V_{r+1}(\xi ,0)=-\frac{1}{2}Bi\xi ^{\frac{-1}{2}}+\frac{1}{2}Bi\xi ^{\frac{-1}{2}}\theta _{r+1}(\xi ,0)+\frac{3}{2}Bi\xi ^{\frac{1}{2}}S_{T},\\&f_{r+1}'(\xi ,\eta ) \rightarrow 0,\,\theta _{r+1}(\xi ,\eta ) \rightarrow 0,\,U_{r+1}'(\xi ,\eta ) \rightarrow 0,\,V_{r+1}(\xi ,\eta ) \rightarrow 0,\, as \,\,\,\,\eta \rightarrow \infty . \end{aligned} \end{aligned}$$
(23)

The matrix representation of Eqs.(19)-(22) can be given as

$$\begin{aligned}&{\varvec{A}}_{1}\,{\varvec{F}}={\varvec{B}}_{1}\\&{\varvec{A}}_{2}\,{\varvec{\Theta }}={\varvec{B}}_{2}\\&{\varvec{A}}_{3}\,{\varvec{U}}={\varvec{B}}_{3}\\&{\varvec{A}}_{4}\,{\varvec{V}}={\varvec{B}}_{4} \end{aligned}$$

where

$$\begin{aligned}&{{\varvec{A}}_1}={{\varvec{D}}^{2}}+\hbox {diag}(a_{1,r}){{\varvec{D}}},{\,\,\,\,\,{\varvec{B}}_1}={{K}}_{1,r}\\&{{\varvec{A}}_2}={{\varvec{D}}^{2}}+\hbox {diag}(b_{1,r}){{\varvec{D}}},{\,\,\,\,\,{\varvec{B}}_2}=K_{2,r}\\&{{\varvec{A}}_3}={{\varvec{D}}^{2}}+\hbox {diag}(x_{1,r}){{\varvec{D}}},{\,\,\,\,{\varvec{B}}_3}=K_{3,r}\\&{{\varvec{A}}_4}={{\varvec{D}}^{2}}+\hbox {diag}(y_{1,r}){{\varvec{D}}}+\hbox {diag}(y_{2,r}){{\varvec{I}}},{\,\,\,\,\,{\varvec{B}}_4}=K_{4,r} \end{aligned}$$

where \({\varvec{I}}\) is \((N_x+1)^{th}\) order identity matrix and \({\varvec{F}}\), \({\varvec{\Theta }}\), \({\varvec{U}}\) and \({\varvec{V}}\) are the vectors containing f, \(\theta \), U and V values evaluated at the Gauss - Lobatto (collocation) points. The subsequent system of algebraic equations which are represented in the matrix form along with the BCs(23) are solved iteratively by making use of appropriate initial approximations to analyze the fluid flow behaviour.

Results and Discussion

This section includes the discussion of results attained by solving Eqs.(6)–(7) along with BCs(8) using the combined methods explained above for various physically reliable values of different parameters. All computations involved in this paper are done in MATLAB by taking 50 collocation points in \(\eta \)-direction (\(i.e.\, N_{x}=50\)) and \(L_x=10\) is fixed in the \(\eta \)-direction to get the asymptotic nature at infinity. The convergence property is shown by using the following expressions for the error in fluid velocity and fluid temperature at \((r+1)^{th}\) level

$$\begin{aligned}&E_{f}=max ||f_{r+1,i}-f_{r,i}||_{\infty },\,\,\,\,\,\,\,\, 0 \le i \le N_x,\\&E_{\theta }=max ||\theta _{r+1,i}-\theta _{r,i}||_{\infty },\,\,\,\,\,\,\,\, 0 \le i \le N_x. \end{aligned}$$

Figures 2a–3b display the variations in the norm of residual error with iterations for Eqs. (13) and (14) with different \(\xi \). The residual error is decreased with increase in iterations and its very less quantity in all the cases shows the convergence and accuracy of the method. Hence, the validation of this spectral local linearisation method is concluded.

Fig. 2
figure 2

Residual errors over iterations for Newtonian fluid when \(Ds=1.0\), \({\alpha _1}=0.1\), \(Gr^*=0.01\), \(Bi=1.0\), \(S_{T}=0.01\)

Full size image
Fig. 3
figure 3

Residual errors over iterations for non-Newtonian fluid when \(Ds=0.5\), \({\alpha _1}=0.1\), \(Gr^*=0.01\), \(Bi=1.0\), \(S_{T}=0.01\)

Full size image

Further, to check the accuracy of computations and the exactness of formulation, results of this problem in the case of wall temperature condition (\(\theta (\xi ,\, \eta )=1\) as \(Bi\rightarrow \infty \)) for vertical plate (i.e. \({\xi }\rightarrow 0\)) when \(Ds=0\), \(\alpha _1=0\) and \(S_T=0\), are also compared with the results of Plumb and Huenefeld [33] and the exact results (see Nakayama et al. [34] and citations therein) for the Newtonian fluid case. These comparisons are coinciding at a large extent as displayed in Table1. The results of this problem when \({\xi } \rightarrow 0\), \(n = 1\), \(\alpha _1 = 0\), \(S_T = 0\) and \(Bi \rightarrow \infty \), are tuned with the findings of Murthy and Singh [35], who investigated the impact of thermal dispersion parameter in natural convection. Further, the behavior of temperature and velocity profiles along with the skin friction coefficient and heat transfer rate for various values of streamwise coordinate \(\xi \) is given in tabular form for pseudoplastic fluid and dilatant fluid in Table2 and Table3 respectively. From these results, it is self evident that the solutions are not similar. This flow model reveals some interesting observations regarding heat transfer and boundary layer in the practically feasible range of important parameters and these are very useful in various emerging applications.

Table 1 Comparative analysis of \(-\theta '(\xi ,\,0)\) for different values of \(Gr^*\) when \(\xi \rightarrow 0\), \(Ds=0\), \(\alpha _1=0\), \(S_T=0\), \(Bi\rightarrow \infty \) and \(n=1\) (Newtonian fluid)
Full size table
Table 2 The non-dimensional velocities, temperatures, Nusselt number and skin friction coefficients for various values of \(\xi \) when \(Gr^*=1.0\), \(Ds=0.5\), \(\alpha _1=1.0\), \(Bi=1.0\), \(S_T=0.01\) and n=0.8 (psudoplastic fluids)
Full size table
Table 3 The non-dimensional velocities, temperatures, Nusselt number and skin friction coefficients for various values of \(\xi \) when \(Gr^*=1.0\), \(Ds=0.5\), \(\alpha _1=1.0\), \(Bi=1.0\), \(S_T=0.01\) and n=1.2 (dilatant fluids)
Full size table

Impact of Biot Number (Bi)

The variations in the non-dimensional velocities, temperatures, heat transfer rates and skin friction coefficients for different Bi are portrayed graphically in Figs. 4a–4d where all other parameters are given fixed values. Bi is defined as the proportion of internally heated resistance in the truncated cone surface to the boundary layer heated resistance. Figure 4a depicts the fluid velocity increments with higher values of Bi and dilatant fluid is more influenced in comparison of pseudoplastic fluid. In Fig. 4b, the influence of Bi on temperature profiles is displayed which shows that the higher values of temperature are obtained with the increment in Biot number. It is clear from this figure that the temperature is more for both the fluids when the surface is subjected to wall temperature condition (i.e., \(\theta (\xi , 0) = 1-\xi \, S_T\) which is obtained when \(Bi \rightarrow \infty \)) in comparison to the convectively heated surface (as shown in Boundary condition (8)). The variations in Nusselt number with non-linear convection parameter \(\alpha _{1}\) for various values of Biot number are shown in Fig. 4c. There is domination of dilatant fluid over pseudoplastic fluid and higher rate of heat transfer is noticed with increment in Bi. Similarly, in Fig. 4d, the changes in skin friction coefficient with \(\alpha _{1}\) for different values of Bi are displayed. Less negative values are obtained for dilatant fluid with an increment of Bi and this negativity increases with Biot number increment. This type of analysis where the temperature of surface is fixed in later stage, may be very useful in many applications because if the surface temperature is fixed initially, it may further result into damage of materials involved in the experiment or even in industry.

Fig. 4
figure 4

The a non-dimensional velocity, b non-dimensional temperature, c non-dimensional Nusselt number and d non-dimensional skin friction coefficient profiles for different values of n and Bi

Full size image

Impact of Thermal Stratification Parameter (\(S_{T}\))

In the Figs. 5a–5d, the significance of \(S_T\) on non-dimensional velocities of the fluid flow, temperatures, heat transfer rates and skin friction coefficients are depicted. There are decrements in the velocity and temperature profiles in the case of increasing values of stable stratification (i.e., for \(S_T>0\)) for both dilatant and pseudoplastic fluids. Due to \(S_{T}\) increment, density of the fluid is increased which results the decrement in the convective flow and so the velocity profiles are decreased and the effect is less for pseudoplastic fluid. Also, in the presence of \(S_T\), the temperature variation between the surface of the truncated cone and the marginal fluid decreases, which thickens the thermal boundary layer resulting into temperature profile decrement. In Fig. 5c, the impact of stratification on Nusselt number with \(\alpha _{1}\) is shown for dilatant and pseudoplastic fluids. Increase in \(S_{T}\) values results into the decrement of Nusselt number for both the fluids. Nusselt number is noticed to be less in the case of pseudoplastic fluids. Fig. 5d shows the impact of stratification on the skin friction coefficient with \(\alpha _{1}\) and increment in \(S_{T}\) makes skin friction values less negative for dilatant and pseudoplastic fluids and there is rapid variation with \(\alpha _{1}\) values.

Fig. 5
figure 5

The a non-dimensional velocity, b non-dimensional temperature, c non-dimensional Nusselt number and d non-dimensional skin friction coefficient profiles for different values of n and \(S_{T}\)

Full size image

Impact of Thermal Dispersion Parameter (Ds)

The variations in the non-dimensional velocities, temperatures, Nusselt number and skin friction coefficients are depicted in Figs. 6a–6d. Thermal dispersion raises the potency of non-uniform pore level velocities on the temperature field in a certain porous medium. In addition, the importance of integrated variations in temperature and velocity profiles to the heat transportation can also be seen with the help of thermal dispersion. It is found from the Fig. 6a that there is increment in velocities when thermal dispersion parameter is present in the case of dilatant and pseudoplastic fluids. Likewise, Fig. 6b portrays that there is again increment in the temperature profiles for non-zero values of Ds. Due to higher flow velocities in the porous medium, thermal dispersion dominates molecular diffusion. Hence, a detailed analysis must be given about its impact on heat transfer properties in this study. In view of this, the impact of Ds with \(\alpha _{1}\) on Nusselt number is shown in Fig. 6c. With enhanced values of Ds, the heat transfer is also enhanced for both dilatant and pseudoplastic fluids. The values for dilatant fluid are found to be more. The influence of Ds on the skin friction coefficient with \(\alpha _{1}\) is displayed in Fig. 6d. When Ds is increased, less negative skin friction is observed for the two fluids. The magnitude of Ds is higher for pseudoplastic fluids than dilatant fluids.

Fig. 6
figure 6

The a non-dimensional velocity, b non-dimensional temperature, c non-dimensional Nusselt number and d non-dimensional skin friction coefficient profiles for different values of n and Ds

Full size image

Impact of Non-Linear Convection Parameter (\(\alpha _{1}\))

The effect of \(\alpha _{1}\) on the dimensionless velocities and temperatures are displayed in Figs. 7a–7b. The non-linear convection parameter shows a non-linear relationship between temperature and density. Physically, \(\alpha _{1}>0\) refers the expression \(T_f>T_\infty \), so the truncated cone surface gives significant amount of heat to the fluid flow region. The presence and absence of \(\alpha _{1}\) is taken to analyse its influence when other parameters are assigned specific values. Fig. 7a displays that the presence of \(\alpha _{1}\) makes velocity to increase and this effect is less for pseudoplastic fluid. Fig. 7b displays the temperature decrements in the presence of \(\alpha _{1}\) for both the fluids and these decrements are found to be more in the case of pseudoplastic fluid. As \(\alpha _{1}\) increases, from Figs. 4c–4d and Figs. 6c–6d, it is evident that the Nusselt number and skin friction are less affected for pseudoplastic fluids than dilatant fluids in the presence/absence of either convective boundary condition or thermal dispersion. With the increment in \(\alpha _{1}\), the Nusselt number is identified to be more for pseudoplastic fluids when compared to dilatant fluids with/without \(S_T\) as displayed in Fig. 5c. The behaviour of skin friction coefficient is noticed to be opposite to that of the Nusselt number as shown in Fig. 5d with the enhancement in the parameter \(\alpha _{1}\).

Fig. 7
figure 7

The a non-dimensional velocity and b non-dimensional temperature distributions for different values of n and \(\alpha _1\)

Full size image

Conclusion

The impacts of Biot number, thermal dispersion and non-linear convection on the thermally stratified power-law fluid over the truncated cone situated in a non-Darcy porous medium, are discussed in this work. The consideration of these effects increased the number of non-dimensional parameters and hence increased the non-linear complexity of this problem. So, the governing equations are handled by local non-similarity and spectral local linearization approaches. These kinds of analyses play very important part in the area of polymeric mixtures maintained at very high temperatures, aerosol technology etc., and these all are related to temperature-dependent density. In future work, one can try to solve boundary layer equations related to this model for fractional order cases by following the papers [36, 37] which involve a method free from restrictive cases or linearization and it may provide the exact solution in terms of a uniformly convergent series. The decisive observations for this work can be itemized as:

  • The velocities, temperatures and Nusselt number are increased for larger Bi but the skin friction coefficient is reduced for pseudoplastic and dilatant fluids.

  • Thermal stratification parameter influences temperature, velocity and rate of heat transfer in a similar way and all these face decrement with higher values of \(S_T\). But, the different trend is seen in the skin friction coefficient case.

  • The effect of Ds on the temperature, velocity, heat transfer rate and skin friction coefficient is all positive as all these profiles are increased with its presence.

  • The impact of non-linear convection parameter \(\alpha _1\) on velocity and temperature profiles is opposite in nature as its presence gives increment in the velocity profiles, and decrement in the temperature profiles.