Abstract
We study the semi-discrete directed random polymer model introduced by O’Connell and Yor. We obtain a representation for the moment generating function of the polymer partition function in terms of a determinantal measure. This measure is an extension of the probability measure of the eigenvalues for the Gaussian unitary ensemble in random matrix theory. To establish the relation, we introduce another determinantal measure on larger degrees of freedom and consider its few properties, from which the representation above follows immediately.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction
In this paper we consider a directed random polymer model in random media in two (one discrete and one continuous) dimension introduced by O’Connell and Yor [59]. For N independent one-dimensional standard Brownian motions \(B_j(t),~j=1,\ldots ,N\) and the parameter \(\beta (>0)\) representing the inverse temperature, the polymer partition function is defined by
Here \(B_j(s,t)=B_j(t)-B_j(s),~j=2,\ldots ,N\) for \(s<t\) and \(-B_1(s_1)-B_2(s_1,s_2)-\cdots -B_N(s_{N-1},t)\) represents the energy of the polymer. In the last fifteen years much progress has been made on this O’Connell-Yor polymer model, by which we can access some explicit information about \(Z_N(t)\) and the polymer free energy \(F_N(t)=-\log (Z_N(t))/\beta \) [7, 10, 11, 36, 41, 45–47, 54, 57, 72]. The first breakthrough was made in the zero temperature \((\beta \rightarrow \infty )\) case. In this limit, \(-F_N(t)\) becomes
where \(-f_N(t)\) is the ground state energy. For \(f_N(t)\), the following relation was established [7, 36]:
where \(P_{\text {GUE}}(x_1,\ldots ,x_N;t)\) is the probability density function of the eigenvalues in the Gaussian unitary ensemble (GUE) in random matrix theory [3, 35, 52]. This type of connection of the ground state energy of a directed polymer in random media with random matrix theory was first obtained for a directed random polymer model on a discrete space \(\mathbb {Z}_+^2\) [42] by using the Robinson–Schensted–Knuth (RSK) correspondence. Equation (1.3) can be regarded as its continuous analogue. Note that (1.4) is written in the form of a product of the Vandermonde determinant \(\prod _{1\le j<k\le N}(x_k-x_j)\). This feature implies that the m-point correlation function is described by an \(m\times m\) determinant, i.e. the eigenvalues of the GUE are a typical example of the determinantal point processes [73]. In addition based on this fact and explicit expression of the correlation kernel, we can study the asymptotic behavior of \(f_N(t)\) in the limit \(N\rightarrow \infty \). In [7, 36], it has been shown that under a proper scaling, the limiting distribution of \(f_N(t)\) becomes the GUE Tracy–Widom distribution [75].
In this paper, we provide a representation for a moment generating function of the polymer partition function (1.1) which holds for arbitrary \(\beta (>0)\):
where \(f_F(x)=1/(e^{\beta x}+1)\) is the Fermi distribution function and
For more details see Definition 1 and Theorem 2 below. This is a simple generalization of (1.3) to the case of finite temperature. We easily find that it recovers (1.3) in the zero-temperature limit (\(\beta \rightarrow \infty \)). Note that the function \(W(x_1,\ldots ,x_N;t)\) is also written as a product of two determinants and thus retains the determinantal structure in (1.4).
In most cases, to find a finite temperature generalization of results for zero-temperature case is highly nontrivial and in fact often impossible. But for the O’Connell-Yor polymer model and a few related models, rich mathematical structures have been discovered for finite temperature and the studies on this topic entered a new stage [2, 10, 25, 37, 57, 61, 66–69]. O’Connell [57] found a connection to the quantum Toda lattice, and based on the developments in its studies and the geometric RSK correspondence, it was revealed that the law of the free energy \(F_N(t)\) is expressed as
Here the probability measure \(m(x_1,\ldots ,x_N;t)\prod _{j=1}^Ndx_j\), which is called the Whittaker measure, is defined by the density function \(m(x_1,\ldots ,x_N;t)\) in terms of the Whittaker function \(\Psi _{\lambda }(x_1,\ldots ,x_N)\) (for the definition, see [57]) and the Sklyanin measure \(s_N(\lambda )d\lambda \) (see (2.10) below) as follows,
where \(\lambda \) represents \((\lambda _1,\ldots ,\lambda _N)\). In contrast to (1.4), the density function (1.9) is not known to be expressed as a product of determinants and the process associated with (1.9) does not seem to be determinantal. Nevertheless some determinantal formulas for the O’Connell-Yor polymer have been found: First in [57], O’Connell showed a determinantal representation for the moment generating function (LHS of (1.5)) in terms of the Sklyanin measure. (See (2.9) below.) Next in [10], Borodin and Corwin obtained a Fredholm determinant representation for the same moment generating function (see (4.23) below). A direct proof of the equivalence between the two determinantal expressions was given in [13]. In [10], by considering its continuous limit, the authors also obtained an explicit representation of the free energy distribution for the directed random polymer in two continuous dimension described by stochastic heat equation (SHE) [10, 11]. The distribution in this limit, which describes the universal crossover between the Kardar–Parisi–Zhang (KPZ) and the Edwards–Wilkinson universality class, was first obtained in [2, 66–69] and can be interpreted also as the height distribution for the KPZ equation [44]. Furthermore in [10], they consider not only the O’Connell-Yor model but a class of stochastic processes having the similar Fredholm determinant expressions, the Macdonald processes, the probability measures on a sequence of partitions which are written in terms of the Macdonald symmetric functions and include the Whittaker measure defined by (1.8) as a limiting case.
The purpose of this paper is to investigate further the mechanism of appearance of such determinantal structures and (1.5) is the central formula in our study. Although \(W(x_1,\ldots ,x_N;t)\prod _{j=1}^Ndx_j\) defined by (1.6) is not a probability measure but a signed measure except when \(\beta \rightarrow \infty \), a remarkable feature of this measure is that it is determinantal for arbitrary \(\beta \) contrary to the Whittaker measure (1.9). This determinantal structure allows us to use the conventional techniques developed in the random matrix theory and thus from the relation we readily get a Fredholm determinant representation with a kernel using biorthogonal functions which is regarded as a generalization of the kernel with the Hermite polynomials for the GUE. In (1.6), the parameter \(\beta \), which originally represents the inverse temperature in the polymer model appears in the Fermi distribution function \(f_F(x-u)\) with the chemical potential u as well as \(\psi _k(x;t)\) (1.7) in RHS. This fact with the determinantal structure suggests that the RHS might have something to do with the free Fermions at a finite temperature. Related to this, a curious relation of the height of the KPZ equation with Fermions has been discussed in [28].
For establishing (1.5), we introduce a measure on a larger space \(\mathbb {R}^{N(N+1)/2}\). By integrating the measure in two different ways, we get its two marginal weights. In one formula appears a determinant which solves the N dimensional diffusion equation with some condition (see (2.11), (3.6), and (3.7)) and the other one with a symmetrization is exactly the RHS of (1.5). The relation (1.5) follows immediately from the equivalence of these two expressions. Our approach is similar to the one by Warren [78] for getting the relation (1.3). Actually in the zero-temperature limit \(\beta \rightarrow \infty \), we see that the integration of the measure is written in terms of the probability measure introduced in [78], which describes the positions of the reflected Brownian particles on the Gelfand–Tsetlin cone. Note that the Macdonald processes (especially the Whittaker process in our case) [10] are also other generalizations of [78]. Although the Whittaker process has rich integrable properties, they do not inherit the determinantal structure of [78]. On the other hand, our measure is described without using the Whittaker functions and keeps the determinantal structure. Furthermore combining (1.5) with the fact that the quantity can be rewritten as the Fredholm determinant found in [10] (Corollary 13 and Proposition 15 below), our approach can be considered as another proof of the equivalence between (4.23) and (2.9) in [13]. One feature of our proof is to bring to light the larger determinantal structure behind the two relations.
This paper is organized as follows. In the next section, after stating the definition of a determinantal measure, we give our main result, Theorem 2 and its proof. The proof consists of two major steps: we first introduce in Lemma 3 a determinantal representation for the moment generating function which is a deformed version of the representation (2.9) in [57]. Next we introduce another determinantal measure on larger space \(\mathbb {R}^{N(N+1)/2}\) and then we find two relations about its integrations which play a key role in deriving our main result. In Sect. 3 we show that this approach can be considered as an extension of the one in [78]. In Sect. 4., we consider the Fredholm determinant formula with biorthogonal kernel obtained by applying conventional random matrix techniques to our main result. The scaling limit to the KPZ equation is discussed in Sect. 5. We check that our kernel goes to the one obtained in the studies of the KPZ equation. A concluding remark is given in the last section.
2 Main Result
In this section, we introduce a measure \(W(x_1,\ldots ,x_N;t)\prod _{j=1}^Ndx_j\) (1.6), state our main result and give its proof.
2.1 Definition and Result
Definition 1
Let \(\psi _k(x;t),~k=1,2,\ldots \) be
For \((x_1,\ldots ,x_N)\in \mathbb {R}^N\), a function \(W(x_1,\ldots ,x_N;t)\) is defined by
Remark
We find that \(W(x_1,\ldots ,x_N;t)\) is a real function on \(\mathbb {R}^N,\) since by definition \(\psi _k(x;t)\) is real for any \(k=0,1,2,\ldots , N-1, \beta >0\) and \(t>0\). But in general, the positivity of this measure is not guaranteed. For example \(\psi _0(x;t)\) shows a damped oscillation and can take a negative value for some x. Thus at least for the case \(N=1\), \(W(x,t)=\psi _0(x;t)\) can be negative.
We discuss the zero-temperature limit \(\beta \rightarrow \infty \) of \(W(x_1,\ldots ,x_N;t)\). Noting \(\Gamma (1)=1\), we see
where we used the integral representations of the nth order Hermite polynomial \(H_n(x)\) (see e.g. Sect. 6.1 in [5]),
Note that \((t/2)^{k/2}H_k(x/\sqrt{2t})\) is a monic polynomial (i.e. the coefficient of the highest degree is 1) and
Thus we find
where \(P_{\text {GUE}}(x_1,\ldots ,x_N;t)\) is defined by (1.4). The function \(W(x_1,\ldots ,x_N;t)\) can be regarded as a deformation of (1.4) which keeps its determinantal structure.
In this paper, we provide a determinantal representation for the moment generating function of the polymer partition function (1.1) in terms of the function (2.2).
Theorem 2
where \(f_F(x)=1/(e^{\beta x}+1)\) is the Fermi distribution function.
By (1.2), (2.6) and the simple facts
we find that the zero temperature limit of (2.7) becomes (1.3).
Because of the determinantal structure of \(W(x_1,\ldots ,x_N;t)\), we can get the Fredholm determinant representation for the moment generating function by using the techniques in random matrix theory. Recently another Fredholm determinant representation has been given based on properties of Macdonald difference operators [10]. The equivalence between them will be shown in Sect. 4.
2.2 Proof
Here we provide a proof of Theorem 2. Our starting point is the representation for the moment generating function given in [57]:
where \(0<\epsilon <\beta \) and \(s_N(\lambda )d\lambda \) is the Sklyanin measure defined by
This relation was obtained by using the properties of the Whittaker functions [22, 74] and the Whittaker measure (1.9).
Lemma 3
where \(f_F(x)\) is defined below (2.7) and
with \(0<\epsilon <\beta \).
We will discuss an interpretation of (2.12) in the next section. In this definition, we have arranged \(x_i\)’s in the reversed order so as to relate (3.17), the zero-temperature limit of (2.12), to the stochastic processes defined later in (3.20).
Proof
Noting the relation
we rewrite RHS of (2.9) as
where in the last equality, we used the Andréief identity (also known as the Cauchy-Binet identity) [4]: For the functions \(g_j(x),~h_j(x)\), \(j=1,2,\dots ,N,\) such that all integrations below are well-defined, we have
We notice that the factor \(e^{-u\lambda }\Gamma (-\lambda /\beta )^ N({\sin (\pi \lambda /\beta )}/{\pi })^{N-1}\)in (2.15) can be written as
where we used the reflection formula for the Gamma function and the relation (4.31). From (2.15) and (2.17), we arrive at the desired expression (2.11). \(\square \)
From (2.11), we see that for the derivation of our main result (2.7), it is sufficient to prove the relation
where \(f_F(x)\) is defined below (2.7) and \(W(x_1,\ldots , x_N;t)\) is given in Definition 1. Note that this is a relation for the integrated values on \(\mathbb {R}^N\). To establish this we introduce a measure on the larger space \(\mathbb {R}^{N(N+1)/2}\).
Definition 4
Let \(\underline{x}_k\) be an array \((x^{(1)},\ldots , x^{(k)})\) where \(x^{(j)}=(x^{(j)}_1,\ldots ,x^{(j)}_j)\in \mathbb {R}^{j}\) and \(d\underline{x}_k=\prod _{j=1}^k\prod _{i=1}^jdx^{(j)}_i\). We define a measure \(R_u(\underline{x}_N;t)d\underline{x}_N\) by
Here \(x^{(j-1)}_0=u\), \(F_{1j}(x;t)\) is given by \(F_{ij}(x;t)\) (2.13) with \(i=1\) and \(f_i(x), i=1,2,\ldots \) is defined by using the Fermi and Bose distribution functions, \(f_F(x):=1/(e^{\beta x}+1)\) and \(f_B(x):=1/(e^{\beta x}-1)\) respectively as follows.
Remark
The reason why both the Bose and Fermi distributions appear in our approach is not clear. The interrelations between them (see (2.28)–(2.30) below) will play an important role in the following discussions.
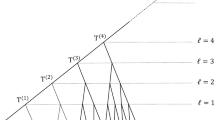
As in Fig 1. we usually represent the array \(\underline{x}_N\) graphically in the triangular shape. Although no ordering is imposed on \(\underline{x}_N\), in the zero-temperature limit, \(R_u(\underline{x}_N;t)\) has the support on the ordered arrays as in Fig. 1a (see (3.34)). Figure 1b represents the other ordered array called the Gelfand–Tsetlin pattern (see (3.23)).
As discussed later we will find that the moment generating function of the O’Connell-Yor polymer model is expressed as the integration of this measure \(R_u(\underline{x}_N;t)\) over \(\mathbb {R}^{N(N+1)/2}\). We have other choices for the definition of \(R_u(\underline{x}_N;t)\) which give the same integration value. One example is
This comes form the following consideration. Let \(f_{\text {sym}}(\underline{x}_N)\) be a function which is symmetric under permutations of \(x^{(j)}_1,\ldots ,x^{(j)}_j\) for each \(j\in \{1,2,\ldots ,N\}\). Then we see that \(R_u(\underline{x}_N;t)\) (2.19) and \(\bar{R}_u(\underline{x}_N;t)\) have the same integration value:
It can be shown as follows. From the symmetry of \(f_{\text {sym}}(\underline{x}_N)\), LHS of the equation above becomes
Here \(\tilde{R}_u(\underline{x}_N;t)\) is defined by
where \(S_j\) is the permutation of \(1,2,\ldots ,j\) and \(\underline{x}_N^\sigma \) denotes \((x^{\sigma ^{(1)}},\ldots , x^{\sigma ^{(N)}})\) with \(x^{\sigma ^{(j)}}=(x^{(j)}_{\sigma ^{(j)}(1)},\ldots , x^{(j)}_{\sigma ^{(j)}(j)})\). We easily find the equivalence \(\tilde{R}_u(\underline{x}_N;t)=\bar{R}_u(\underline{x}_N;t)\). Note that
Here in the last equality, \(\tau ^{(j)}\in S_j,~j=1,2,\ldots ,N\) is defined by using \(\sigma ^{(j-1)}\) and \(\sigma ^{(j)}\) as \(\sigma ^{(j-1)}\tau ^{(j)}(k)=\sigma ^{(j)}(k),~k=1,\ldots ,j\), where we regard \(\sigma ^{(j-1)}\) as an element of \(S_j\) with \(\sigma ^{(j-1)}(j)=j\). Further in the last equality we used \(\sigma ^{(N)}=\prod _{j=1}^N\tau ^{(j)}\). Substituting (2.25) into (2.24) and using the definition of the determinant, we have \(\tilde{R}_u(\underline{x}_N;t)=\bar{R}_u(\underline{x}_N;t)\).
The function \(\bar{R}_u(\underline{x}_N;t)\) (2.21) has a similar determinantal structure to the Schur process [60]. The Schur process is a probability measure on the sequence of partitions \(\{\lambda ^{(j)}\}_{j=1,\ldots ,N},\) where \(\lambda ^{(j)}:=\{(\lambda ^{(j)}_1,\ldots ,\lambda ^{(j)}_j)|\lambda ^{(j)}_i\in \mathbb {Z},~\lambda ^{(j)}_1 \ge \cdots \ge \lambda ^{(j)}_j\ge 0\}\), described as products of the skew Schur functions \(s_{\lambda /\mu }(x_1,\ldots ,x_n)\). For the ascending case (see Definition 2.7 in [10]), the probability measure is expressed as
where \(a_j,~b_j,~j=1,\ldots ,N\) are positive variables. We note that \(s_{\lambda ^{(k)}/\lambda ^{(k-1)}} (a_k)\) is expressed as a kth order determinant and \(s_{\lambda ^{(N)}}(b_1,\ldots , b_N)\) as a Nth order determinant by the Jacobi-Trudi identity [50],
where \(h_{k}(x_1,\ldots ,x_n)\) is a complete symmetric polynomial with degree k and \(\ell (\lambda )\) is the length of the partition \(\lambda \). Thus (2.21) and (2.26) have a common structure of N products of determinants with increasing size times an Nth order determinant.
In the following we provide the relations about two marginals of \(R_u(\underline{x}_N;t)\) (2.19), from which (2.18) immediately follows. For this purpose, we give two formulas for \(f_F(x)\) and \(f_B(x)\) (2.20). First we define a multiple convolution \(g^{*(m)}f(x)~m=0,1,2,\ldots \) for a functions f(x) on \(\mathbb {R}\) and an integral operator g with the kernel \(g(x-y)\) as
Using this definition, the formulas are written as follows:
Lemma 5
We regard all integrations below as the Cauchy principal values. For \(\beta >0\), \(a\in \mathbb {C}\) with \(-\beta <\text {Re~}a<0\) and \(m=0,1,2,\ldots \), we have
where \(q_m(x)\) is an mth order polynomial with the coefficient of the highest degree being 1 / m!.
A proof of this lemma will be given in Appendix 1. The polynomial \(q_m(x)\) in (2.30) is defined inductively by (7.11)-(7.13). But in our later discussion we will not use its explicit form.
From (2.13) and (2.29), we readily obtain for \(m=0,1,2,\ldots \),
where we define \(\tilde{f}_B(x):=f_B(-x)\).
Using (2.30) and (2.31), we obtain the following relations.
Theorem 6
Let the measures \(dA_1\) and \(dA_2\) be
Then we have
Here \(G(x^{(1)}_1,\ldots ,x^{(N)}_1;t)\) is defined by (2.12) and
where \(q_j(x)\) is defined below (2.30).
We easily see that (2.18) can be obtained from these relations (2.33) and (2.34): Integrating the both hand sides of them over the remaining degrees of freedom (\((x^{(1)}_1,\ldots , x^{(N)}_1)\) for (2.33) and \((x^{(N)}_1,\ldots ,x^{(N)}_N)\) for (2.34)), we get two different expression about the integrated value of \(R_u(\underline{x}_N;t)\)
where \(d\underline{x}_N=\prod _{1\le i\le j\le N}x^{(j)}_i\). RHS of the second relation is further rewritten as
and the symmetrized \(\bar{W}(x_1,\ldots ,x_N;t)\) in this equation is nothing but \(W(x^{(N)}_1,\ldots ,x^{(N)}_1;t)\) (2.2) since
Here in the second equality we used the fact that \(q_{j}(x)\) is a jth order polynomial with the coefficient of the highest degree being 1 / j! and \(F_{1j}(x;t)=\psi _{j}(x;t)\).
Proof of Theorem 6
First we derive (2.33). By the definition of (2.19), LHS of (2.33) becomes
Here \(\tilde{f}_B(x)\) is defined below (2.31). Applying (2.31) to this equation we obtain (2.33).
Next we derive (2.34). We see that the factor \(dA_2\prod _{1\le i\le j\le N}f_i(x^{(j)}_i-x^{(j-1)}_{i-1})\) in \(R_u(\underline{x_N};t)\) (2.19) can be decomposed to
and from (2.30) the integration of the factor for each k is represented as
where \(q_m(x)\) is given in (2.30). Eq. (2.34) follows immediately from this relation. \(\square \)
3 Dynamics of the Two Marginals
The purpose of this section is to have a better understanding of the two quantities, \(W(x_1,\ldots ,x_N;t)\) (2.2) and \(G(x_1,\ldots ,x_N;t)\) (2.12), which arose as partially integrated quantities of \(R_u(\underline{x}_N;t)\) (2.19) in Theorem 6 (for W a symmetrization is also necessary, see (2.39)). We will first consider the evolution equations of these two quantities. Next we will see that the zero-temperature limit of the equation for \(W(x_1,\ldots ,x_N;t)\) is nothing but the evolution equation for the Brownian particles with reflection interaction while \(W(x_1,\ldots ,x_N;t)\) satisfies the one for the GUE Dyson’s Brownian motion [31] regardless of the value of \(\beta \). Furthermore we will find that our idea using \(R_u(\underline{x}_N;t)\) in an enlarged space \(\mathbb {R}^{N(N+1)/2}\) (Theorem 6) is similar to the argument in [78] although we need a modification of [78] about the ordering in an enlarged space.
3.1 Evolution Equations of \(G(x_1,\ldots ,x_N;t)\) and \(W(x_1,\ldots ,x_N;t)\)
Let us first summarize the properties of \(F_{jk}(x;t)\) \(j,k\in \{1,2,\ldots \}\) (2.13) all of which are easily confirmed by simple observations:
where \(\psi _k(x;t)\) in (3.1) and \(\tilde{f}_B(x)\) in (3.3) are defined by (2.1) and below (2.31). Eq. (3.3) is equivalent to (2.31) while (3.4) is obtained from the relation
for \(|\text {Re}~b|<\beta /2\). This relation is easily given by (2.29) with \(a=b-\beta /2\).
We see that due to (3.2) and the multilinearity of a determinant, \(G(x_1,\ldots ,x_N;t)\) (2.12) satisfies the diffusion equation.
In addition, by (3.4), it satisfies the condition
for \(j=1,2,\ldots , N-1\). Though this condition is unusual, we will see that it is regarded as a finite temperature generalization of the Neumann boundary conditions at \(x_j=x_{j+1},~j=1,\ldots , N-1\) in the zero temperature limit (see (3.19)).
On the other hand, from (3.2) with the harmonicity of the Vandermonde determinant in (2.2), we see that \(W(x_1,\ldots ,x_N;t)\) satisfies the Kolmogorov forward equation of the GUE Dyson’s Brownian motion [31], which is a dynamical generalization of the GUE,
The time evolution equation for the GUE Dyson’s Brownian motion can be transformed to the imaginary-time Schrödinger equation with free-Fermionic Hamiltonian (e.g. see Chapter 11 in [35]). On the other hand note that the density function of the Whittaker measure (1.9) does not solve such a simple free-Fermionic time evolution equation (3.8).
3.2 The Zero-Temperature Limit and a Brownian Particle System with Reflection Interactions
Let us consider the zero temperature limit of the Eqs. (3.6) with (3.7) and (3.8). Note that for \(x\ne 0\),
where \(\tilde{f}_B(x)\) is defined below (2.31) and \(1_{>0}(x)\) and \(1_{<0}(x)\) are the step functions defined by
In addition we have
where \(\mathcal {F}_n(x;t)\) is defined for \(n\in \mathbb {Z}\) and \(\epsilon >0\) as
Here we summarize a few properties of the function which are the zero temperature limit of (3.1)–(3.4) for \(F_{jk}(x;t)\).
where in (3.13), \(\psi _k(x;t)\) is defined by (2.1) and \(H_k(x)\) is the kth order Hermite polynomial [5]. The second equality in (3.13) has appeared as (2.3). Note that (3.16) corresponds to the zero-temperature limit of (3.4), since RHS of (3.5) goes to \(-be^{-bx}\) in the zero-temperature limit and thus the integral operator with the kernel \(\pi ^2e^{\beta (y-x)/2}/\beta ^2(e^{\beta (y-x)}-1)\) is equivalent to differentiation in the zero temperature limit when its action is restricted to \(e^{-b x}\).
Let \(\mathcal {G}(x_1,\ldots ,x_N;t)\) be the zero-temperature limit of \(G(x_1,\ldots ,x_N;t)\) (2.12) defined on \(\mathbb {R}^N\). From (3.11), we find
The function \(\mathcal {G}(x_1,\ldots ,x_N;t)\) appeared as a solution to the Schrödinger equation for the derivative nonlinear Schrödinger type model [70]. As discussed in [70], using (3.14) and (3.16) with basic properties of a determinant, we find that for \(x_1\ne \cdots \ne x_N\), \(\mathcal {G}(x_1,\ldots ,x_N;t)\) satisfies the diffusion equation,
with the boundary condition
The probabilistic interpretation of \(\mathcal {G}(x_1,\ldots ,x_N;t)\) has been given in [78]. Let \(X_i(t),~i=1,\ldots ,N\) be the stochastic processes with N-components described by
where \(y_i\in \mathbb {R}\) satisfying \(y_1<y_2<\cdots <y_N\) represent initial positions, \(B_i(t)\) denotes the standard Brownian motion and \(L^-_i(t)\) is twice the semimartingale local time at zero of \(X_i-X_{i-1}\) for \(i=2,\ldots ,N\) while \(L^-_1(t)=0\). The system (3.20) describes the N-Brownian particles system with one-sided reflection interaction, i.e. the ith particle is reflected from the \(i-1\)th particle for \(i=2,3,\ldots ,N\). Warren [78] found that the transition density of this system from \(y_i\) to \(x_i\), \(i=1,\ldots ,N\) is written as \(\mathcal {G}(x_1-y_1,\ldots ,x_N-y_N;t)\). Such kind of determinantal transition density was first obtained for the totally asymmetric simple exclusion process (TASEP) in [71]. Furthermore, based on the determinantal structures, various techniques for discussing the space-time joint distributions for the particle positions or current have been developed for TASEP [15, 17–21, 56, 64, 65] and the reflected Brownian particle system (3.20) [32, 33].
On the other hand, we have seen in (2.6) that the zero temperature limit of \(W(x_1,\ldots ,x_N;t)\) (2.2) is the GUE density \(P_{\text {GUE}}(x_1,\ldots ,x_N;t)\) (1.4). Note that \(P_{\text {GUE}}(x_1,\ldots ,x_N;t)\) also satisfies (3.8) since it holds for arbitrary \(\beta \) i.e:
From (2.6), (3.9), and (3.11), we find that the zero-temperature limit of (2.18) is
Warren [78] showed that this relation, which connects the two different processes, is obtained in the following way. First one introduces a process on the \(N(N+1)/2\)-dimensional Gelfand–Tsetlin cone whose two marginals describe the above two processes. The Gelfand–Tsetlin cone \(\text {GT}_k,~k=1,2,\ldots \) is defined as
For the graphical representation of an element of \(\text {GT}_k\), see Fig. 1b. Next we introduce a following stochastic process on \(\text {GT}_N\). Let \((X^{(1)}(t),\ldots ,X^{(N)}(t))\) with \(X^{(j)}(t)=(X^{(j)}_1(t),\ldots ,X^{(j)}_j(t))\) be a process defined by
where \(B^{(j)}_i(t)\) are the \(N(N+1)/2\) independent Brownian motions starting at the origin, \(y^{(j)}_i\) represent the initial positions and the process \(L^{(j)-}_i(t)\) and \(L^{(j)+}_i(t)\) are twice the semimartingale local time at zero of \(X^{(j)}_i-X^{(j-1)}_{i}\) and \(X^{(j)}_i-X^{(j-1)}_{i-1}\) respectively. Equation (3.24) describes the interacting particle systems where each \(X^{(j)}_i(t)\) is a Brownian motion reflected from \(X^{(j-1)}_{i-1}(t)\) to a negative direction and from \(X^{(j-1)}_i(t)\) to a positive direction. In [16], Borodin and Ferrari also introduced similar processes on the discrete Gelfand–Tsetlin cone where the probability measure at a particular time is described by the Schur process [60].
The pdf of the system (3.24) at time t can be given explicitly : For the case of \(y^{(j)}_i=0\), it is expressed as
where \(\underline{x}_N\) is defined above (2.19) and \(1_{\text {GT}}(\underline{x}_k)\) represents the indicator function on GT\(_k\). The pdfs of the two marginals, \((x^{(1)}_1,\ldots ,x^{(N)}_1)\) and \((x^{(N)}_1,\ldots ,x^{(N)}_N)\) for \(\mathcal {Q}_{\text {GT}}(\underline{x}_N;t)\) was obtained as follows:
Proposition 7
(Proposition 6 and 8 in [78])
where \(\mathcal {G}(x_1,\ldots ,x_N;t)\), \(P_\mathrm{{GUE}}(x^{(N)}_1,\ldots ,x^{(N)}_N;t)\), \(1_{>0}(x)\) and \(dA_1,~dA_2\) are defined by (3.17), (1.4), (3.10) and (2.32) respectively.
Remark
Note that \(\mathcal {G}(x^{(1)}_1,\ldots ,x^{(N)}_1;t)\) in (3.26) can be replaced by an arbitrary function on \(\mathbb {R}^N\)such that it corresponds to \(\mathcal {G}(x^{(1)}_1,\ldots ,x^{(N)}_1;t)\) in the region \(x^{(1)}_1<x^{(2)}_1<\cdots <x^{(N)}_1\). For later discussion on a generalization of finite temperature, we chose it as \(\mathcal {G}(x^{(1)}_1,\ldots ,x^{(N)}_1;t)\) on the whole \(\mathbb {R}^N\).
We see that the relation (3.22) is obtained from this theorem. By decomposing the integral on \(\underline{x}_N\) in two different ways, we clearly have
Applying (3.26) and (3.27) to this equation, we get
Due to the symmetry of \(P_{\text {GUE}}(x_1,\ldots ,x_N;t)\) under the permutations of \(x_1,\ldots ,x_N\), we readily see that RHS of this equation is equal to RHS of (3.22). Also we find that LHS of (3.29) becomes
where in the first equality we used for \(k=2,\ldots , N\) and \((x^{(1)}_1,\ldots ,x^{(N)}_1)\in (-\infty ,u]^N\)
Note that \(\mathcal {G}(x^{(1)}_1,\ldots ,x^{(N)}_1;t)\) is defined on \(\mathbb {R}^N\) and is finite even outside the region \(x^{(1)}_1<x^{(2)}_1<\cdots <x^{(N)}_1\). (See Remark. of Proposition 7.) Eq. (3.31) is obtained from the following observation: putting the last factor \(1_{>0}(x^{(k-1)}_1-x^{(k)}_1)\) in the \(N-k-1\)th row of the determinant \(\mathcal {G}(x^{(1)}_1,\ldots ,x^{(N)}_1;t)\) in (3.31) then applying (3.15), we get the determinant which has the same two rows.
Thus (3.22) is obtained from Proposition 7. This is similar to the situation of (2.18) and Theorem 6. This naive observation gives us the impression that the pdf \(\mathcal {Q}_{\text {GT}}(\underline{x}_N;t)\) (3.25) is the zero-temperature limit of the weight \(R_u(\underline{x}_N;t)\) (2.19). However in fact this is not the case. Let \(\mathcal {R}_u(\underline{x}_N;t):=\lim _{\beta \rightarrow \infty }R_u(\underline{x}_N;t)\). From (3.9) and (3.11) one has
From (2.5) and (3.13), it is further rewritten as
where \(1_{V_k}(\underline{x}_k)\) is the indicator function on an ordered set \(V_k\) defined by
For the graphical representation of an element of (3.34), see Fig. 1a. Comparing (3.25) with (3.33), we see that they have the same form but their supports (\(\text {GT}_N\) and \(V_N\)) are different. We further notice that \(V_N\) with an additional order \(x^{(m)}_{\ell }\le x^{(m+1)}_{\ell },~1\le \ell \le m\le N-1\) corresponds to GT\(_N\).
Hence our approach using \(\mathcal {R}_u(\underline{x}_N;t)\) can be regarded as a modification of Warren’s arguments on \(\text {GT}_N\) to the ones on the partially ordered spece \(V_N\). Let us focus on two marginals \((x^{(1)}_1,x^{(2)}_1,\ldots , x^{(N)}_1)\) and \((x^{(N)}_1,x^{(N)}_2, \cdots , x^{(N)}_N)\) for \(\mathcal {R}_u(\underline{x}_N;t)\) (3.33). By taking the zero-temperature limit of Theorem 6, we have the following analogue of Proposition 7:
Proposition 8
where for the definition of \(dA_1\) and \(dA_2\), see (2.32), \(\mathcal {G}(x^{(1)}_1,\ldots ,x^{(N)}_1;t)\) is given by (3.17) and
Proof
It is obtained by taking the zero-temperature limit \((\beta \rightarrow \infty )\) in Theorem 6. \(\square \)
As discussed in (2.39), \(P_{\text {GUE}}(x_1,\ldots ,x_N;t)\) (1.4) can be interpreted as the symmetric version of \(P_u(x_1,\ldots ,x_N;t)\):
Therefore by the similar discussion in (3.28), we see that the relation (3.22) is obtained also from Proposition 8.
The fact that both Proposition 7 and 8 lead to (3.22) implies the relation
This equivalence of their integration values is generalized in the following way.
Proposition 9
Let \(f_\mathrm{sym}(\underline{x}_N) \) be the function defined above (2.22). Then we have
An essential step of the proof of this proposition is represented as the following.
Lemma 10
The proof of this lemma will be given in Appendix 2. Using this lemma we readily derive Proposition 9.
Proof of Proposition 9
Substituting the definition of \(\mathcal {R}_u(\underline{x}_N;t)\) (3.33) into (3.40), we see that the LHS of (3.40) is rewritten as
where in the second equality we use Lemma 10. \(\square \)
4 Fredholm Determinant Formulas
4.1 A Fredholm Determinant with a Biorthogonal Kernel
The function \(W(x_1,\ldots ,x_N;t)\) (1.6) has a notable determinantal structure that it is described by a product of two determinants. This allows us to apply the results of random matrix theory and determinantal point processes developed in [43, 76] and to get the Fredholm determinant representation.
To see this we provide a lemma. Let \(\phi _j(x;t),~j=0,1,2,\ldots \) be
where the contour encloses the origin anticlockwise with radius smaller than \(\beta \). We find \(\phi _j(x;t)\) and \(\psi _k(x;t)\) (2.1) satisfy the biorthonormal relation:
Lemma 11
For \(j,k\in \{0,1,2,\ldots \}\), we have
Proof
Substituting the definitions (2.1) and (4.1) into LHS of (4.2), one has
As the integrand in this equation is analytic on \(\mathbb {C}\) with respect to w, we can shift the integration path as \(w=w'-i v,~w'\in \mathbb {R}\). Then using
we find
\(\square \)
The residue calculus shows that the function \(\phi _j(x;t)\) is a jth order polynomial in x and the coefficient of the highest order is 1 / j!. As the Vandermonde determinant in (2.2) is expressed as
\(W(x_1,\ldots ,x_N;t)\) is rewritten as a product of two determinants
From Lemma 11 and (4.7), we obtain a Fredholm determinant representation for the moment generating function. Throughout this paper, we follow [10] for the notation on Fredholm determinants.
Proposition 12
where g(x) is an arbitrary function such that the left hand side is well-defined and in the right hand side \(\det \left( 1-\bar{g}K\right) _{L^2(\mathbb {R})}\) represents a Fredholm determinant defined by
Here \(\bar{g}(x)=1-g(x)\) and K(x, y; t) is written in terms of the biorthogonal functions \(\psi _j(x,t)\) (2.1) and \(\phi _k(x,t)\) (4.1) as
Proof
We readily obtain this representation by applying the techniques in [76] with Lemma 11 to LHS of (4.8). For reference, here is an outline of the proof. First, using the Andréief (Cauchy-Binet) identity (2.16), we have
where \(A_{j,k},~j,k=1,\ldots ,N\) is defined as
In the first equality of (4.11), we used (4.7) with (2.16) and in the last one we used Lemma 11. We further rewrite \(A_{jk}\) as
by using
Applying the identity for Fredholm determinants,
and noting
we arrive at our desired expression. \(\square \)
Combining this proposition with Theorem 2, we readily obtain
Corollary 13
where the right hand side is the Fredholm determinant (4.9) with the kernel \(\bar{f}_u(x_i)K(x_i,x_j;t)\), \(\bar{f}_u(x_j)=1-f_F(x_j-u)\), and \(K(x_i,x_j;t)\) is defined in (4.10).
As in (2.3), we see
which is due to another representation of the nth order Hermite polynomial \(H_n(x)\) (see e.g. Sect. 6.1 in [5]),
where the contour encloses the origin anticlockwise. From (2.3) and (4.18), we find
Here RHS appears as a correlation kernel of the eigenvalues in the GUE random matrices [52].
Thus \(K(x_i,x_j;t)\) is a simple biorthogonal deformation of the kernel with Hermite polynomials which appears in the eigenvalue correlations of \(N\times N\) GUE random matrices. Using this Fredholm determinant expression (4.17), we can understand a few asymptotic properties of the partition function by applying saddle point analyses to the kernel as will be discussed in Sect. 5.
4.2 A Representation from the Macdonald Processes
In [57], O’Connell first introduced the probability measure on \(\mathbb {R}^N\) which is called the Whittaker measure \(m(x_1,\ldots ,x_N;t)\prod _{j=1}^Ndx_j\) whose density function \(m(x_1,\ldots ,x_N;t)\) is defined in terms of the Whittaker function \(\Psi _{\lambda }(x_1,\ldots ,x_N)\) (see [57]),
where throughout this paper we denote \(\lambda =(\lambda _1,\ldots ,\lambda _N)\) and \(s_N(\lambda )\) is defined by (2.10). Then he showed the following relation about the distribution of the free energy \(F_N(t)=-\log (Z_N(t))/\beta \) (see Theorem 3.1 and Corollary 4.1 in [57]),
The density function \(m(x_1, \cdots , x_N;t)\) (4.21) is also a finite temperature extension of \(P_{\text {GUE}}(x_1, \cdots , x_N;t)\) (1.4). Actually it has been known that \(m(x_1,\ldots ,x_N;t)\) converges to \(P_{\text {GUE}}(x_1,\ldots ,x_N;t)\) in the zero-temperature limit. (See Sect. 6 in [57]). In contrast to \(W(x_1,\ldots , x_N;t)\) (2.2), however, this extension does not inherit the determinantal structure which \(P_{\text {GUE}}(x_1,\ldots ,x_N;t)\) has and thus we cannot apply the techniques in random matrix theory which is useful especially for asymptotic analyses of the GUE. This fact necessitated the developments of new methods [2, 10, 11, 13, 14, 24, 29, 30, 66–69]. By using the techniques of the Macdonald difference operators [10] and the duality [14], one can get a Fredholm determinant expression for the moment generating function of the partition function, which allows us to access the asymptotic properties.
Proposition 14
([10])
where \(C_0\) denotes the contour enclosing only the origin positively with radius \(r<\beta /2\) and the kernel \(L(v,v';t)\) is written as
Here \(\delta \) satisfies the condition \(r<\delta <\beta -r\).
We can show the equivalence between the two expressions (4.17) and (4.23).
Proposition 15
where \(\bar{f}_u(x)=1-f_F(x-u)\) and \(K(x,x';t)\) and \(L(v,v';t)\) are defined (4.10) and (4.24) respectively.
Proof
Substituting the definitions (2.1) and (4.1) into (4.10), we have
For the definition of \(C_0\), see below (4.23). Here we changed \(w\rightarrow -iw\) in (2.1) and shift the path of w by \(\delta \) which is larger than the radius of v. We notice that although the last expression in (4.26) consists of two terms proportional to \(1/(v-w)\) and \((w/v)^N/(v-w)\), the integration of the term proportional to \(1/(v-w)\) with respect to v vanishes. Thus we see
where we set
Here we use the relation for Fredholm determinants, \(\det (1-AB)_{L^2(\mathbb {R})}=\det (1-BA)_{L^2(C_0)}\), where the kernel \(-(BA)(v,v')\) on RHS reads
Using the relation
we perform the integration over x in (4.30) as
Note that because of the conditions \(0<r<\beta /2\) and \(r<\delta <\beta -r\) (see below (4.23) and (4.24) respectively), (4.31) is applicable to the above equation. Thus from (4.30) and (4.32), we have
\(\square \)
5 The Scaling Limit to the KPZ Equation
In this section, we discuss a scaling limit of the O’Connell-Yor polymer model. When both N and t are large with its ratio N / t fixed, it has been known that the polymer free energy \(F_N(t)\) defined below (1.1) is proportional to N on average and the fluctuation around the average is of order \(N^{1/3}\) [54, 72]. Furthermore recently it has been shown in [10] that the limiting distribution of the free energy fluctuation under the \(N^{1/3}\) scaling is the GUE Tracy–Widom distribution [75]. This type of the limit theorem has been obtained also for other models related to the O’Connell-Yor model [6, 13, 26, 34, 58, 77]. These results reflect the strong universality known as the KPZ universality class.
Although we expect that the same result on the Tracy–Widom asymptotics can be obtained from our representation (4.17), we consider another scaling limit where the partition function goes to the solution to the stochastic heat equation (SHE) (or equivalently, the free energy goes to the solution to the Kardar–Parisi–Zhang (KPZ) equation). This scaling limit to the KPZ equation has also been known to be universal although in a weaker sense compared with the KPZ universality stated above [1, 9, 27]. The height distribution of the KPZ equation has been obtained for a droplet initial data in [2, 66–69]. Since then, explicit forms of the height distribution have been given for the KPZ equation and related models for a few initial data [10–12, 23, 38, 39, 49, 62, 63]. In particular for the O’Connell-Yor model (1.1), the limiting distribution of the polymer free energy has been obtained by applying the saddle point method to the kernel (4.24) [10, 11].
In this section, we confirm that a similar saddle point analysis can be applicable to our biorthogonal kernel (4.10). Since our kernel has a simple form, we find that the nontrivial part of this problem reduces only to the asymptotic analyses of the functions \(\psi _k(x;t)\) (2.1) and \(\phi _k(x;t)\) (4.1).
5.1 The O’Connell-Yor Polymer Model and the KPZ Equation
Before discussing the saddle point analysis, let us briefly review the scaling limit to the KPZ equation. Hereafter we will write out explicitly the dependence on \(\beta \) of the polymer partition function (1.1) as \(Z_{N,\beta }(t)\).
Let \(\tilde{Z}_{j,\beta }(t):=e^{-t-\beta ^2t/2}{Z}_{j,\beta }(t),~j=1,\ldots ,N\). By Itô’s formula, we easily find that it satisfies the stochastic differential equations
where we set \(\tilde{Z}_{0,\beta }(t)=0\) and interpret the second term of this equation as Itô type. Now let us take the diffusion scaling for (5.1): we set
and at the same time we scale \(\beta \) as
then take the large M limit. the scaling exponent \(-1/4\) in (5.3) is known to be universal: it characterizes the disorder regime referred to as the intermediate disorder regime [1], which lies between weak and strong disorder regimes in directed polymer models in random media in \(1+1\) dimension.
This \(M^{-1/4}\) scaling can be explained in the following heuristic way. Let \(B_{j}(t),~j=1,\ldots ,N\) be N independent one dimensional standard Brownian motions. For \(N_1,N_2\in \{1,2,\ldots ,N\}\), we have
where \(\langle \cdot \rangle \) represents the expectation value with respect to the Brownian motions. Now we consider its large M limit under the same scaling as (5.2) i.e. \(t=MT\) and
Noting that \(\lim _{M\rightarrow \infty }\sqrt{M}\delta _{N_1,N_2}=\delta (X_1-X_2)\) under (5.5), we see
This suggests in a heuristic sense,
Here \(\eta (T,X)\) with \(T>0\) and \(X\in \mathbb {R}\) is the space-time white noise with mean 0 and \(\delta \)-function covariance,
Thus considering (5.7), we choose the scaling of \(\beta \) (5.3).
Under the scaling (5.2) and (5.3), the following limiting property is established.
Here \(\mathcal {Z}(T,X)\) is the solution to the SHE with the \(\delta \)-function initial condition,
where \(\eta (T,X)\) is the space-time white noise with mean 0 and \(\delta \)-function covariance (5.8). The SHE (5.10) is known to be well-defined if we interpret the multiplicative noise term as Itô-type [8, 55]. Using this equation, the solution to the KPZ equation can be defined via
which is called the Cole-Hopf solution to the KPZ equation. Recently a new regularization for the KPZ equation was developed in [37] (see also [48]).
According to [10], a rigorous estimate about the convergence to the SHE (5.9) has been obtained for the O’Connell-Yor model [53] based on the results in [1]. This type of convergence has been discussed also in interacting particle processes [9, 27]. For reference we offer a sketch of the derivation of (5.9). For this purpose, we provide the following lemma,
Lemma 16
For \(\tilde{Z}_{N,\beta }(t)\) defined above (5.1), one has
where \(Po(t,n):=e^{-t}t^n/n!\) denotes the Poissonian density and \(N_0=1, N_{k+1}=N, s_0=t_0=0, s_N=t_{k+1}=t\). \(\Delta _n(s,t)\) denotes the region of the integration \(s<t_1<\dots <t_n<t\) and the Itô integrals on RHS, referred to as the multiple Itô integrals [40, 51], are performed in time order (i.e. the order of \(t_1,\ldots ,t_N\)).
Proof
By the definition of \(Z_N(t)\) (1.1), we have
with \(s_0\)=0 and the integrand of RHS is expressed as
Here we use the relation on a one-dimensional standard Brownian motion B(t): one has for \(t>s>0\) and \(\beta >0\),
where the Itô integrals on RHS, referred to us the multiple Itô integrals, are performed in time order (i.e. the order of \(t_1,\ldots ,t_N\)) [40, 51]. Using this, we get
Substituting this into (5.14), and performing the integration on \(s_1,\ldots ,s_{N-1}\), we have
where we set \(M_0=1,~M_{m+1}=N\). Now we introduce the new variables \(N_j,~t_j,~j=1,\ldots ,k\) by the relation
Then one has \( dB_{M_j}(t_{M_j,\ell })=dB_{N_{n_1+\cdots +n_{j-1}+\ell }}(t_{n_1+\cdots +n_{j-1}+\ell })\) leading to
Further from (5.19), we have
where we set \(N_0=1,~N_{k+1}=N\). Substituting these (5.20) and (5.21) into (5.18) and noting the summations \(\sum _{m=0}^{\infty }\sum _{1\le M_1<\cdots <M_m\le N} \sum _{\begin{array}{c} n_1,\ldots ,n_m=1 \\ n_1+\cdots +n_m=k \end{array}}^{\infty }\) can be summarized as the simple form \(\sum _{1\le N_1\le \cdots \le N_k\le N}\), we obtain (5.13). \(\square \)
Note that under the scaling (5.2), the Poissonian density Po(t, N) goes to the Gaussian density \(g(T,X)=\exp ({-{X^2}/{2T}})/{\sqrt{2\pi T}}\), i.e.
Furthermore by Theorems 4.3 and 4.5 in [1], for a function \(f(t_1,\ldots ,t_k, N_1,\ldots ,N_k)\) that converges to \({\mathfrak {f}}(u_1,\ldots ,u_k;y_1,\ldots ,y_k)\) under the scaling \(t_i=u_i M\) and \(N_i=u_iM-y_i\sqrt{M},~i=1,\ldots ,k\), we have
where \(\eta (t,y)\) is the space-time white noise with the \(\delta \)-covariances (5.8). Thus from (5.13), (5.22) and (5.23), we have under the scaling (5.2),
where \(t_0=0,t_{k+1}=T,y_0=0,y_{k+1}=X\). Since we easily find that RHS of this equation is the solution of the SHE with \(\delta \)-function initial data (5.10), we obtain (5.9).
5.2 The Asymptotics of the Kernel
In [10], Borodin and Corwin discussed the asymptotics of the Fredholm determinant (4.23) under the scaling limit to the KPZ equation, especially the limiting property of the kernel (4.24) based on the saddle point method. Here we check that a similar saddle point method is applicable to our biorthogonal kernel (4.10). The scaling limit we consider is (5.9) discussed above, but here we adopt its rephrased version stated in [10],
where C(N, T, X) is
which is more suitable for our purpose. To see the equivalence between (5.9) and (5.25), we rewrite the relation (5.9) as
where we scale \(t,~\beta \) as
Furthermore focusing on the scaling property of the partition function \(Z_{N,\beta }(t)=Z_{N,1}(\beta ^2 t) /\beta ^{2(N-1)}\), we find
in distribution. Noticing under the scaling (5.28)
where C(N, T, X) is defined in (5.26), we find that (5.27) is equivalent to (5.25).
For the moment generating function, (5.25) implies
where on LHS, u is set to be
with C(T, N, X) (5.26), and in the last equality in (5.31) we used (5.12). The notions of the KPZ universality class tell us that the fluctuation of the height h(T, X) and the position X are scaled as \(T^{1/3}\) and \(T^{2/3}\) respectively for large T. Considering them, we set
where \(\gamma _T=(T/2)^{1/3}\). The first term \(-\gamma _T^3/12=-T/24\) represents the macroscopic growth with a constant velocity. The height fluctuation is expressed as \(\tilde{h}(T,Y)\) and the term \(Y^2\) reflects the fact that the SHE with delta-function initial data in (5.11) corresponds to the parabolic growth in the KPZ equation [2, 66, 69]. Thus substituting \(u'=\gamma _ts-\gamma _T^3/12-\gamma _TY^2\), \(X=2\gamma _T^2Y\) into (5.32), we arrive at the modified scaling
Hence (5.31) is rewritten as
with the scaling (5.34). This is the scaling limit of the moment generating function from the O’Connell-Yor polymer to the KPZ equation.
It has been known that RHS of this equation can be represented as the Fredholm determinant [24, 29, 30],
where the kernel \(\mathcal {K}_{\text {KPZ}}(\xi _1,\xi _2)\) is expressed as
Note that Y does not appear in RHS of this equation. This kernel first appeared in the studies of the KPZ equation for the narrow wedge initial condition [2, 66–69]. From the relation (5.36) we readily get the distribution of the scaled height \(\tilde{h}(T,Y)\) given in (5.33).
By combining the formula (4.17) for the O’Connell-Yor polymer and the limiting relation (5.35) from the O’Connell-Yor polymer to the KPZ equation, we can obtain (5.36) by showing
under (5.34). This was indeed already discussed in [10] by using the kernel (4.24) . Here we show that the kernel (5.37) appears rather easily from the scaling limit of our biorthogonal kernel (4.17). Using the saddle point method, we get the following:
Proposition 17
Here the kernel is expressed in terms of \(\phi _k(x_1;t)\) and \(\psi _k(x_2;t)\) defined by (4.1) and (2.1) respectively as
and we set u to be (5.34) and
Since the factor \(e^{\frac{\gamma _T}{2}(\xi _1-\xi _2)}\) in (5.39) does not contribute to the Fredholm determinant, we get (5.38) (though for a complete proof one has to prove the convergence of the Fredholm determinant itself, not only the kernel). Note that (5.40) has a similar structure to the kernel (4.20) in the GUE random matrices. When we discuss certain large N limits in the GUE such as the bulk and the edge scaling limit, the nontrivial step reduces to the scaling limit of the Hermite polynomial in (4.20). The same thing happens in our case: the only nontrivial step for getting (5.39) is the asymptotics of the functions \(\psi _k(x;t)\) (2.1) and \(\phi _k(x;t)\) (4.1). Based on the saddle point method, we obtain the following results of which the proof is given in Appendix 3.
Lemma 18
where we set \(x_i\) as (5.41) and k and t as
The constant C(N) is represented as \( C(N)=e^{\sum _{j=1}^5C_j} \) in terms of \(C_1,\ldots ,C_5\) defined by (9.10), (9.14) and (9.16) in Appendix 3.
On the other hand, when we take the same limit for the other representation (4.23), we can apply the saddle point analysis also to the kernel (4.24) and can get the limiting kernel. But since it does not correspond to the kernel (5.37) directly, we need an additional step to show the equivalence between the Fredholm determinant with the limiting kernel and that with (5.37) (see Sect. 5.4.3 in [10]).
Proof of Proposition 17
Combining the estimate (5.42) with the simple fact
under (5.34) and (5.41), we immediately obtain the result (5.39). \(\square \)
6 Conclusion
For the O’Connell-Yor directed random polymer model, we have established the representation (2.7) of the moment generating function for the partition function in terms of a determinantal function which is regarded as a one-parameter deformation of the eigenvalue density function of the GUE random matrices.
There are some special mathematical structures behind the O’Connell-Yor model which play a crucial role in deriving the relation. The first one has been the determinantal representation (2.11) which is essentially the one with the Sklyanin measure in [57]. Next we have introduced another determinantal measure in enlarged degrees of freedom (2.19). Our main theorem has been readily obtained from a simple fact about two marginals of this measure (Theorem 6).
We can regard our approach as a generalization of the one in [78] which retains its determinantal structures. To see this we needed to reinterpret the dynamics in the Gelfand–Tsetlin cone introduced in [78] using the weight (3.33) supported on the partially ordered space \(V_N\) (3.34). Our approach is a natural generalization of [78] from this viewpoint. It would be an interesting future problem to find a clear relation with the Macdonald process [10], which is another generalization of [78].
Applying familiar techniques in random matrix theory to the main result, we have readily obtained the Fredholm determinant representation of the moment generating function whose kernel is expressed as the biorthogonal functions both of which are simple deformations of the Hermite polynomials. The asymptotics of the kernel under the scaling limit to the KPZ equation can be estimated easily by the saddle point analysis.
References
Alberts, T., Khanin, K., Quastel, J.: The intermediate disorder regime for directed polymers in dimension 1+1. Ann. Probab. 42, 1212–1256 (2014)
Amir, G., Corwin, I., Quastel, J.: Probability distribution of the free energy of the continuum directed random polymer in 1 + 1 dimensions. Commun. Pure Appl. Math. 64, 466–537 (2011)
Anderson, G.W., Guionnet, A., Zeitouni, O.: An Introduction to Random Matrices. Cambridge University Press, Cambridge (2010)
Andréief, C.: Note sur une relation les integrales de nies des produits des fonctions. Mém. de la Soc. Sci. Bordx. 2, 1–14 (1883)
Andrews, G.E., Askey, R.: Special Functions. Cambridge University Press, Cambridge (2014)
Barraquand, G., Corwin, I.: Random-walk in Beta-distributed random environment (2015). arXiv:1503.04117
Baryshnikov, Y.: GUEs and queues. Probab. Theory Relat. Fields 119, 256–274 (2001)
Bertini, L., Cancrini, N.: The stochastic heat equation: Feynman-Kac formula and intermittence. J. Stat. Phys. 78, 1377–1401 (1995)
Bertini, L., Giacomin, G.: Stochastic Burgers and KPZ equations from particle systems. Commun. Math. Phys. 183, 571–607 (1997)
Borodin, A., Corwin, I.: Macdonald processes. Probab. Theory Relat. Fields 158, 225–400 (2014)
Borodin, A., Corwin, I., Ferrari, P.L.: Free energy fluctuations for directed polymers in random media in 1\(+\)1dimension. Commun. Pure Appl. Math. 67, 1129–1214 (2014)
Borodin, A., Corwin, I., Ferrari, P.L., Vető, B.: Height fluctuations for the stationary KPZ equation. Math. Phys. Anal. Geom. 18(2015), 20 (2015)
Borodin, A., Corwin, I., Remenik, D.: Log-gamma polymer free energy fluctuations via a fredholm determinant identity. Commun. Math. Phys. 324, 215–232 (2013)
Borodin, A., Corwin, I., Sasamoto, T.: From duality to determinants for q-TASEP and ASEP. Ann. Probab. 42, 2314–2382 (2014)
Borodin, A., Ferrari, P.L.: Large time asymptotics of growth models on space-like paths I: PushASEP. Electron. J. Probab. 13, 1380–1418 (2008)
Borodin, A., Ferrari, P.L.: Anisotropic growth of random surfaces in \(2+1\) dimensions. Commun. Math. Phys. 325, 603–684 (2014)
Borodin, A., Ferrari, P.L., Prähofer, M.: Fluctuations in the discrete TASEP with periodic initial configurations and the airy \(_1\) process. Int. Math. Res. Pap. 2007, rpm002 (2007)
Borodin, A., Ferrari, P.L., Prähofer, M., Sasamoto, T.: Fluctuation properties of the TASEP with periodic initial configuration. J. Stat. Phys. 129, 1055–1080 (2007)
Borodin, A., Ferrari, P.L., Sasamoto, T.: Large time asymptotics of growth models on space-like paths II: PNG and parallel TASEP. Commun. Math. Phys. 283, 417–449 (2008)
Borodin, A., Ferrari, P.L., Sasamoto, T.: Transition between Airy\(_1\) and Airy\(_2\) processes and TASEP fluctuations. Commun. Pure Appl. Math. 61, 1603–1629 (2008)
Borodin, A., Ferrari, P.L., Sasamoto, T.: Two speed TASEP. J. Stat. Phys. 137, 936–977 (2009)
Bump, D.: The Rankin Selberg Method: A Survey, Number Theory, Trace Formulas and Discrete Groups. Academic Press, New York (1989)
Calabrese, P., Le Doussal, P.: Exact solution for the KPZ equation with flat initial conditions. Phys. Rev. Lett. 106, 250603 (2011)
Calabrese, P., Le Doussal, P., Rosso, A.: Free-energy distribution of the directed polymer at high temperature. EPL 90, 20002 (2010)
Corwin, I., O’Connell, N., Seppäläinen, T., Zygouras, N.: Tropical combinatorics and Whittaker functions. Duke Math. J. 163, 513–563 (2014)
Corwin, I., Seppäläinen, T., Shen, H.: The strict-weak lattice polymer. J. Stat. Phys. 160, 1027–1053 (2015)
Corwin, I., Tsai, L-C.: KPZ equation limit of higher-spin exclusion processes (2015). arXiv:1505.04158
Dean, D.S., Le Doussal, P., Majumdar, S.N., Schehr, G.: Finite temperature free fermions and the Kardar-Parisi-Zhang equation at finite time. Phys. Rev. Lett. 114, 110402 (2015)
Dotsenko, V.: Bethe ansatz derivation of the Tracy-Widom distribution for one-dimensional directed polymers. EPL 90, 20003 (2010)
Dotsenko, V.: Replica Bethe ansatz derivation of the Tracy-Widom distribution of the free energy fluctuations in one-dimensional directed polymers. J. Stat. Mech. 2010, P07010 (2010)
Dyson, F.J.: A Brownian-motion model for the eigenvalues of a random matrix. J. Math. Phys. 3, 1191–1198 (1962)
Ferrari, P.L., Spohn, H., Weiss, T.: Brownian motions with one-sided collisions: the stationary case (2015). arXiv:1502.01468
Ferrari, P.L., Spohn, H., Weiss, T.: Scaling limit for Brownian motions with one-sided collisions. Ann. Appl. Probab. 25, 1349–1382 (2015)
Ferrari, P.L., Vető, B.: Tracy-Widom asymptotics for q-TASEP. Ann. Inst. H. Poincaré Probab. Stat. 51, 1465–1485 (2015)
Forrester, P.J.: Log-gases and random matrices. Princeton University Press, Princeton (2010)
Gravner, J., Tracy, C.A., Widom, H.: Limit theorems for height fluctuations in a class of discrete space and time growth models. J. Stat. Phys. 102, 1085–1132 (2001)
Hairer, M.: Solving the KPZ equation. Ann. Math. 178, 559–664 (2013)
Imamura, T., Sasamoto, T.: Exact solution for the stationary Kardar-Parisi-Zhang equation. Phys. Rev. Lett. 108, 190603 (2012)
Imamura, T., Sasamoto, T.: Stationary correlations for the 1D KPZ equation. J. Stat. Phys. 150, 908–939 (2013)
Itô, K.: Multiple Wiener integral. J. Math. Soc. Jpn. 3, 157–169 (1951)
Janjigian, C.: Large deviations of the free energy in the O’Connell-Yor polymer. J. Stat. Phys. 160, 1054–1080 (2015)
Johansson, K.: Shape fluctuations and random matrices. Commun. Math. Phys. 209, 437–476 (2000)
Johansson, K.: Discrete polynuclear growth and determinantal processes. Commun. Math. Phys. 242, 277–329 (2004)
Kardar, M., Parisi, G., Zhang, Y.C.: Dynamic scaling of growing interfaces. Phys. Rev. Lett. 56, 889–892 (1986)
Katori, M.: O’Connell’s process as a vicious Brownian motion. Phys. Rev. E 84, 061144 (2011)
Katori, M.: Survival probability of mutually killing Brownian motions and the O’Connell process. J. Stat. Phys. 147, 206–223 (2012)
Katori, M.: System of complex Brownian motions associated with the O’Connell process. J. Stat. Phys. 149, 411–431 (2012)
Kupiainen, A.: Renormalization group and stochastic PDEs. Ann. H. Poincaré 17, 497–535 (2016)
Le Doussal, P., Calabrese, P.: The KPZ equation with flat initial condition and the directed polymer with one free end. J. Stat. Mech. 2012, P06001 (2012)
Macdonald, I.G.: Symmetric Functions and Hall Polynomials. Clarendon Press, Oxford (1995)
Major, P.: Multiple Wiener-Itô Integrals with Applications to Limit Theorems. Lecture Notes in Mathematics, 2nd edn, p. 849. Springer, New York (2013)
Mehta, M.L.: Random Matrices. Elsevier, Amsterdam (2004)
Moreno Flores, G., Quastel, J.: unpublished
Moriarty, J., O’Connell, N.: On the free energy of a directed polymer in a Brownian environment. Markov Process. Relat. Fields 13, 251–266 (2007)
Mueller, C.: On the support of solutions to the heat equation with noise. Stoch. Stoch. Rep. 37, 225–245 (1991)
Nagao, T., Sasamoto, T.: Asymmetric simple exclusion process and modified random matrix ensembles. Nucl. Phys. B 699, 487–502 (2004)
O’Connell, N.: Directed polymers and the quantum Toda lattice. Ann. Probab. 40, 437–458 (2012)
O’Connell, N., Ortmann, J.: Tracy-Widom asymptotics for a random polymer model with gamma-distributed weights. Electron. J. Probab. 20, 1–18 (2015)
O’Connell, N., Yor, M.: Brownian analogues of Burke’s theorem. Stoch. Process. Appl. 96, 285–304 (2001)
Okounkov, A., Reshetikhin, N.: Correlation function of Schur process with application to local geometry of a random 3-dimensional Young diagram. J. Am. Math. Soc. 16, 581–603 (2003)
O’Connell, N., Seppäläinen, T., Zygouras, N.: Geometric RSK correspondence, Whittaker functions and symmetrized random polymers. Inven. Math. 197, 361–416 (2014)
Ortmann, J., Quastel, J., Remenik, D.: A Pfaffian representation for flat ASEP (2015). arXiv:1501.05626
Ortmann, J., Quastel, J., Remenik, D.: Exact formulas for random growth with half-flat initial data. Ann. Appl. Probab. 26, 507–548 (2016)
Rakos, A., Schütz, G.M.: Current distribution and random matrix ensembles for an integrable asymmetric fragmentation process. J. Stat. Phys. 118, 511–530 (2005)
Sasamoto, T.: Spatial correlations of the 1D KPZ surface on a flat substrate. J. Phys. A 38, L549–L556 (2005)
Sasamoto, T., Spohn, H.: Exact height distributions for the KPZ equation with narrow wedge initial condition. Nucl. Phys. B 834, 523–542 (2010)
Sasamoto, T., Spohn, H.: One-dimensional Kardar-Parisi-Zhang equation: an exact solution and its universality. Phys. Rev. Lett. 104, 230602 (2010)
Sasamoto, T., Spohn, H.: The \(1+1\)-dimensional Kardar-Parisi-Zhang equation and its universality class. J. Stat. Mech. 2010, P11013 (2010)
Sasamoto, T., Spohn, H.: The crossover regime for the weakly asymmetric simple exclusion process. J. Stat. Phys. 140, 209–231 (2010)
Sasamoto, T., Wadati, M.: Determinant form solution for the derivative nonlinear Schrödinger type model. J. Phys. Soc. Jpn. 67, 784–790 (1998)
Schütz, G.M.: Exact solution of the master equation for the asymmetric exclusion process. J. Stat. Phys. 88, 427–445 (1997)
Seppäläinen, T., Valkó, B.: Bounds for scaling exponents for a 1+1 dimensional directed polymer in a Brownian environment. ALEA 7, 451–476 (2010)
Soshnikov, A.: Determinantal random point fields. Russ. Math. Surv. 55, 923–975 (2000)
Stade, E.: Archimedean \(L\)-factors on GL\((n)\times \)GL(n) and generalized Barnes integrals. Israel J. Math. 127, 201–219 (2002)
Tracy, C.A., Widom, H.: Level-spacing distributions and the Airy kernel. Commun. Math. Phys. 159, 151–174 (1994)
Tracy, C.A., Widom, H.: Correlation functions, cluster functions, and spacing distributions for random matrices. J. Stat. Phys. 92, 809–835 (1998)
Vető, B.: Tracy-Widom limit of q-Hahn TASEP. Electron. J. Probab. 20, 1–22 (2015)
Warren, J.: Dyson’s Brownian motions, intertwining and interlacing. Electron. J. Probab. 12, 573–590 (2007)
Acknowledgments
The work of T. I. and T. S. is supported by KAKENHI (25800215) and KAKENHI (25103004, 15K05203, 14510499) respectively.
Author information
Authors and Affiliations
Corresponding author
Additional information
This is one of several papers published in JSP comprising the “Special Issue: KPZ” (Volume (169), Issue (4), year (2015)).
Appendices
Appendix 1: Proof of Lemma 5
First we give a proof of (2.29). For this purpose, it is sufficient to show the case of \(m=1,~x=0\),
Furthermore setting \(e^{\beta x}=y\), \(a/\beta =b\), one sees that (7.1) is rewritten as
where \(h_b(y)=y^{-b-1}/(y-1)\) and we take the branch cut of \(h_b(y)\) to be the positive real axis. Hence here we prove (7.2). We set the contour C as depicted in Fig. 2 with \(\alpha =1\). From the Cauchy integral theorem, we find
Dividing the contour C into \(C_i,~i=1,\ldots ,6\) as in Fig. 2, we find that by simple calculations,
where note that the factors \(e^{2\pi i b}\)s come from the cut locus of \(y^{-b}\).
which leads to (7.2).
Next we give a proof of (2.30). For this purpose we first show the following relation. Let \(I_j(x),~j=1,2,\ldots \), \(x\in (0,\infty )\), be
Then we have
where \(r_k(x)~(k=0,1,2,\ldots )\) is a kth order polynomial of x where the coefficient of the highest degree is 1 / k. This relation (7.7) can be derived by considering the integration of \(m_j(w;x):=(\log w)^j/((x-w)(w+1)),~x>0\) with respect to w along the contour C in Fig. 2 with \(\alpha =x\) and \(R>1\).
Note that
where RHS corresponds to the residue of \(m_j(w;x)\) at \(w=-1\). As in the previous case (7.4), one easily gets
Substituting (7.9) into (7.8), we find
Thus we obtain
which leads to (7.7).
Here we show (2.30). We find that (2.30) is rewritten as
where \(q_m(x)\) is defined below (2.30) and the functions \(J_F(x)\) and \(J_B(x)\) on \(\mathbb {R}_+\) are defined by \(J_F(x)=1/(x+1)\) and \(J_B(x)=1/\beta x\).
We prove (7.12) by using (7.7) and by mathematical induction: suppose that (7.12) holds for \(m=N-1\). Then we get
where \(c_k (k=0,1,\ldots ,N-2)\) is the coefficient of \(x^k\) in \(q_{N-1}(x)\) and in the last equality we used the assumption for the mathematical induction and (7.6). Considering (7.7), we arrive at (7.12). \(\square \)
Appendix 2: Proof of Lemma 10
To show Lemma 10, we will use the following identity. For \((x_1,\ldots , x_{N-1})\in \mathbb {R}^{N-1}\) satisfying \(x_1>\cdots >x_{N-1}\) and \((y_1,\ldots ,y_N)\in \mathbb {R}^N\), we have
where \(S_N\) is the permutation of \((1,2,\ldots ,N)\). For the proof of (8.1), it is sufficient to show for \(m=1,2, \cdots , N\),
where, as in (8.1), we assume the condition \(x_1>x_2>\cdots >x_{N-1}\). This can easily be obtained by noting that
where in the first equality we used the fact that the factor \(1_{>0}(x_{m-1}-y_{\sigma (m)})\) can be omitted in this equation thanks to the factor \(1_{>0}(x_m-y_{\sigma (m)})\) with the condition \(x_{m-1}>x_{m}\) and the last equality follows from the fact that the term with \(\sigma \) cancels the term with \(\sigma '\) where \(\sigma '\) is defined in terms of \(\sigma \) as \(\sigma '(m)=\sigma (m+1)\) and \(\sigma '(m+1)=\sigma (m)\) with \(\sigma '(k)=\sigma (k)\) for \(k\ne m,~m+1\).
Using (8.2), we have for \(x_1>x_2>\cdots >x_{N-1}\)
where for the first and the third equality, we used (8.2) with \(m=1\) and \(m=2\) respectively. Performing the procedure in (8.4) repeatedly, we arrive at (8.1).
Now we give a proof of the lemma by the mathematical induction. The case \(N=1\) in is trivial. Suppose that it holds for \(N-1\). Then noticing
we see that LHS of (3.41) is written as
where in the second equality we used the assumption for \(N-1\). Note that in the rightmost side of (8.6), the condition \(x^{(N-1)}_{\sigma ^{(N-1)}(1)}>x^{(N-1)}_{\sigma ^{(N-1)}(2)}>\cdots > x^{(N-1)}_{\sigma ^{(N-1)}(N-1)}\) holds for the support of \(1_{\text {GT}}(\underline{x}_{N-1}^{\sigma })\). Thus we can apply (8.1) to the rightmost side. We see that it becomes
which completes the proof of Lemma 10. \(\square \)
Appendix 3: The Saddle Point Analysis of \(\psi _k(x;t)\)
In this Appendix, we give a proof of (5.42) based on the saddle point method in a similar way to Sect. 5.4.3 in [10]. Here we deal with the case of general Y while the case of \(Y=0\) was considered in [10]. We focus mainly on the limit about \(\psi _k(x;t)\) (2.1) in (5.42) since the case \(\phi _k(x;t)\) (4.1) can also be estimated in a parallel way. Changing the variable as \(w=-i\sqrt{N}z\), (2.1) becomes
where
Substituting (5.41) and (5.43) into (9.2), we arrange the first three terms in ascending order of powers of N as
Using the Stirling formula
for the last term in (9.2), we have
Thus from (9.3) and (9.5), \(f_N(z)\) (9.2) can be expressed as
Here \(C_1\), which does not depend on z is written as
We note that f(z) above has a double saddle point \(z_c=T^{-1/2}\) such that \(f'(z_c)=f''(z_c)=0\). We expand f(z), g(z), h(z) around \(z_c\). Noting \(f'''(z_c)=2\gamma _T^3\), \(g'(z_c)=0,~g''(z_c)=2\gamma _T^2Y-\gamma _T^3\), \(h'(z_c)=\gamma _T^3/4-\gamma _T^2Y+\gamma _T(\lambda -\xi _i+Y^2)\), we get
where \(C_2,~C_3\) and \(C_4\) are
Thus from (9.6)–(9.13) and under the scaling \(\frac{z'}{\sqrt{N}}=(z-z_c)\), we have
where \(C_1,\ldots ,C_4\) are defined in (9.10) and (9.14) and \(C_5\) is
Further changing the variable \(z'+Y/\gamma _T-1/2=-iv/\gamma _T\), we obtain
Hence from (9.1) and (9.17), we get the limiting form of \(\psi _k(x_i;t)\)
which is nothing but (5.42).
As with (9.1), we rewrite \(\phi _k(x;t)\) (4.1) by the change of variable \(v=\sqrt{N}z\),
where \(f_N(z;t,x)\) is given in (9.2). Applying the same techniques as above to this equation, we get the result for \(\phi _k(x;t)\).
Rights and permissions
About this article
Cite this article
Imamura, T., Sasamoto, T. Determinantal Structures in the O’Connell-Yor Directed Random Polymer Model. J Stat Phys 163, 675–713 (2016). https://doi.org/10.1007/s10955-016-1492-1
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s10955-016-1492-1