Random Copolymers

Abstract

A (directed) random polymer in d + 1 dimensions is a random walk in d dimensions whose law is transformed by a random potential. The time axis is considered as an additional dimension. The best known and most famous case is the directed polymer in random environment which has a potential given by independent random variables in space and time. Some of the basic questions are open even in 1 + 1 dimensions which is believed to be connected with the KPZ universality class. The main focus of the notes is on the so-called copolymer, first discussed in the physics literature by Garel, Huse, Leibler and Orland in 1989 which models the behavior of a polymer at an interface. Important rigorous results have first been obtained by Sinai and Bolthausen-den Hollander, and have later been developed by many authors. A basic object of interest is a critical line in the parameter space which separates a localized phase from a delocalized one. Particularly interesting is the behavior at the weak disorder limit where the phase transition is characterized by a universal critical tangent whose existence had first been proved in the Bolthausen-den Hollander paper, and whose exact value is still open. This critical tangent is discussed in detail, and new bounds are derived, partly based on large deviation techniques developed by Birkner, Greven, and den Hollander.

1 Introduction: Random Polymers, Different Models

A very challenging model in probability theory is the “directed polymer” in random environment. We formulate it in d + 1 dimensions: The “polymer” is the sequence $\left \{\left (n,S_{n}\right )\right \}_{n\in \mathbb{N}_{0}}$ with S ₀ = 0, and $\left \{S_{n}\right \}$ is a random walk on $\mathbb{Z}^{d}$, e.g. nearest neighbor, symmetric. We write P _N for the law of $\left \{S_{n}\right \}_{0\leq n\leq N}.$ It is the uniform distribution on all nearest-neighbor paths in $\mathbb{Z}^{d}$, starting in 0, and of length N. This law is transformed by a random Hamiltonian through a “time-space” random field $\omega = \left \{\omega \left (n,x\right )\right \}_{n\in \mathbb{N}_{0},\ x\in \mathbb{Z}^{d}}$. The law, governing this random field is always denoted by $\mathbb{P}$. The random Hamiltonian

$$\displaystyle{-H_{N,\omega }\left (S\right )\mathop{ =}\limits^{\mathrm{ def}}\sum _{j=1}^{N}\omega \left (j,S_{ j}\right ),}$$

transforms the path measure P _N to a random path measure

$$\displaystyle{\hat{P}_{\beta,N,\omega }\left (S\right )\mathop{ =}\limits^{\mathrm{ def}} \frac{1} {Z_{\beta,N,\omega }}\exp \left [-\beta H_{N,\omega }\left (S\right )\right ]P_{N}\left (S\right ).}$$

with inverse temperature β > 0, where

$$\displaystyle{Z_{\beta,N,\omega } = E_{N}\exp \left [-\beta H_{N,\omega }\left (S\right )\right ] = \left (2d\right )^{-N}\sum _{ S}\exp \left [-\beta H_{N,\omega }\left (S\right )\right ].}$$

Occasionally, we will use some slight modifications, for instance attaching the randomness ω to bonds and not to sites, and often, we will pin down the endpoint S _N to 0 (which simplifies slightly the proof of the existence of the free energy). Sometimes, we also use β as a parameter inside H, not necessarily as a prefactor.

Some of the standard examples are:

• The usual directed polymer in random environment which has $\omega \left (i,x\right )$ i.i.d. in space-time.

• The pinning model: This has $\omega \left (i,x\right ) = 0$ for x ≠ 0. So there is a random effect only on the one-dimensional “defect line” $\left \{\left (n,0\right ): n \in \mathbb{N}_{0}\right \}.$ It is traditional to write the Hamiltonian with two parameters

  $$\displaystyle{H_{N}\left (S\right ) =\sum _{ j=1}^{N}\left (\beta \omega _{ j} + h\right )1_{S_{j}=0},}$$

  β ≥ 0, $h \in \mathbb{R}$, and one assumes that $\mathbb{E}\omega _{i} = 0$ and $\mathop{\mathrm{{\ast}}}\nolimits var\omega _{i} = 1$.

• The copolymer: This is defined only for d = 1 and it has

  $$\displaystyle{\omega \left (i,x\right ) = \left \{\begin{array}{cc} \omega _{i} &\mathrm{if\ }x > 0 \\ -\omega _{i}&\mathrm{if\ }x < 0\end{array} \right.,}$$

  with ω _i i.i.d. It means that at a “time” point i for which ω _i  > 0, the walk prefers to be on the positive side, and of ω _i  < 0 the opposite. As the ω _i fluctuate wildly, it is not clear what the behavior of the path under $\hat{P}$ is for typical ω. It is convenient to replace ω _i by ω _i + h and assume that $\mathbb{E}\omega _{i} = 0$. $h \in \mathbb{R}$ is then an additional parameter which is responsible for an asymmetry: If h > 0, then positive S _i are stronger preferred if ω _i  > 0 than negative S _i when ω _i  < 0. This gives the Hamiltonian

  $$\displaystyle{H_{\omega,\,\,N}\left (S\right ) =\sum _{ j=1}^{N}\left (\omega _{ j} + h\right )\mathop{\mathrm{{\ast}}}\nolimits sign\left (S_{j}\right ).}$$

  It is however convenient to take $\mathop{\mathrm{{\ast}}}\nolimits sign\left (S_{j-1} + S_{j}\right )$ instead of $\mathop{\mathrm{{\ast}}}\nolimits sign\left (S_{j}\right )$ in order to avoid ties when the random walk hits 0. In this modification, the Hamiltonian is

  $$\displaystyle{ H_{\omega,\,\,N}\left (S\right ) =\sum _{ j=0}^{N-1}\left (\omega _{ j} + h\right )\mathop{\mathrm{{\ast}}}\nolimits sign\left (S_{j} + S_{j+1}\right ). }$$

  (1)

  In the case of copolymer, one typically takes β in the standard way as a multiplicative parameter.

• A case which has attracted a lot of attention is when $\omega \left (i,x\right )$ does not depend on i but only on x. This is closely related to the parabolic Anderson model, and there are hundreds of research papers on this and related models. Work in this framework has be done by Carmona, Molchanov, Sznitman, Sinai, Gärtner, den Hollander, and many others with many difficult and striking results. For this Hamiltonian, also the so-called annealed model is great interest. This refers to transforming the path measure by $\mathbb{E}\exp \left [-\beta H\right ]$. Early quite spectacular results with ω _j given by coin-tossing had been obtained by Donsker and Varadhan, Sznitman, myself, Povel and others. We can’t discuss this case at all in these notes at all, as a half way exhausting presentation would require hundreds of pages. For some of the very deep results, see the monograph by Sznitman [28].

There are many other models, which have been investigated in the literature. The directed polymer is the most difficult one, and despite of a lot of recent progress, many of the key problems are still open.

The basic problems are quite the same for all the models, namely to investigate the localization-delocalization behavior. It turns out that if the disorder ω is strong enough (or β large enough) then it is able to force the path measure into narrow favorable tunnels. For the directed polymer, these tunnels itself are random (determined by ω), but for the pinning and the copolymer, a localization can only happen by the path hanging around the defect line 0. Often, there is a phase transition from localized to delocalized behavior. This is also present for the directed polymer for d ≥ 3, as will shortly be discussed in the next section.

In these notes, we concentrate on the copolymer and present some older and some recent results and techniques. In particular, we discuss the an application of the large deviation method of [3, 4] worked out in [10]. I however also present in Sect. 6 an “elementary” version of the crucial lower bound which is bypassing the use of complicated large deviation techniques. I start with two short chapters on the directed polymer and the pinning model, essentially citing some results from the literature.

2 The Directed Polymer

The first rigorous result on the directed polymer was proved by Imbrie and Spencer in 1988 [22], namely that in d ≥ 3 there is a high-temperature region where the random potential has essentially no influence on the path behavior. Shortly later, I found in [8] a very simple argument for this result. As it is very short, I present the argument here.

Theorem 1

Assume that the $\omega \left (i,x\right ),\ i \in \mathbb{N},\ x \in \mathbb{Z}^{d}$ are i.i.d. and satisfy $M\left (\beta \right )\mathop{ =}\limits^{\mathrm{ def}}\mathbb{E}\exp \left [\beta \omega \left (i,x\right )\right ] < \infty$ for all β, and consider the directed polymer as described above. If d ≥ 3 and β > 0 is small enough, then

$$\displaystyle{ \lim _{N\rightarrow \infty }Z_{N,\beta,\omega }/\mathbb{E}Z_{N,\beta } > 0 }$$

(2)

$\mathbb{P}$ -almost surely, and

$$\displaystyle{ \lim _{N\rightarrow \infty } \frac{1} {N}\hat{E}_{\beta,N,\omega }\left (\left \vert S_{N}\right \vert ^{2}\right ) = 1. }$$

(3)

Furthermore, for $\mathbb{P}$ -almost all ω, $S_{N}/\sqrt{N}$ under $\hat{P}_{\beta,N,\omega }$ is asymptotically centered Gaussian with covariance matrix d ⁻¹ I _d , I _d being the identity matrix.

Remark 2

Imbrie and Spencer proved (2) and (3). The CLT was first proved in [8].

Proof

We restrict to (2) and (3). Evidently,

$$\displaystyle{\mathbb{E}Z_{N,\beta } = M\left (\beta \right )^{N},}$$

and

$$\displaystyle{M_{N}\mathop{ =}\limits^{\mathrm{ def}}Z_{N,\beta,\omega }/\mathbb{E}Z_{N,\beta } = Z_{N,\beta,\omega }M\left (\beta \right )^{-N}}$$

is a martingale with respect to the filtration $\mathcal{F}_{N}\mathop{ =}\limits^{\mathrm{ def}}\sigma \left (\omega \left (i,x\right ): x \in \mathbb{Z}^{d},i \leq N\right ).$ As it is positive, and has expectation 1, it converges almost surely to a nonnegative random variable ζ. The crucial property is that for β small and d ≥ 3, the second moment stays bounded:

$$\displaystyle\begin{array}{rcl} \mathbb{E}M_{N}^{2}& =& M\left (\beta \right )^{-2N}2^{-2Nd}\sum _{ S,S^{{\prime}}}\mathbb{E}\exp \left [\sum \nolimits _{i=1}^{N}\beta \left [\omega \left (i,S_{ i}\right ) +\omega \left (i,S_{i}^{{\prime}}\right )\right ]\right ] {}\\ & =& M\left (\beta \right )^{-2N}2^{-2Nd}\sum _{ S,S^{{\prime}}}\prod _{i=1}^{N}\mathbb{E}\exp \left [\beta \omega \left (i,S_{ i}\right ) +\beta \omega \left (i,S_{i}^{{\prime}}\right )\right ]. {}\\ \end{array}$$

If S _i ≠ S _i ^′, we have

$$\displaystyle{\mathbb{E}\exp \left [\beta \omega \left (i,S_{i}\right ) +\beta \omega \left (i,S_{i}^{{\prime}}\right )\right ] = M\left (\beta \right )^{2},}$$

and if S _i  = S _i ^′

$$\displaystyle{\mathbb{E}\exp \left [\beta \omega \left (i,S_{i}\right ) +\beta \omega \left (i,S_{i}^{{\prime}}\right )\right ] = M\left (2\beta \right ).}$$

Therefore, if we put

$$\displaystyle{\theta _{N}\mathop{ =}\limits^{\mathrm{ def}}\#\left \{i \leq N: S_{i} = S_{i}^{{\prime}}\right \},}$$

we get

$$\displaystyle{\mathbb{E}M_{N}^{2} = E_{ N}^{\otimes 2}\left (\exp \left [\theta _{ N}\left [\log M\left (2\beta \right ) - 2\log M\left (\beta \right )\right ]\right ]\right ).}$$

As we assume d ≥ 3, θ _N  ≤ θ _∞ has an exponential moment, i.e. for some $\delta \left (d\right ) > 0$ one has

$$\displaystyle{\sup _{N}E_{N}^{\otimes 2}\exp \left [\delta \theta _{ N}\right ] < \infty.}$$

Therefore, if β > 0 is small enough, the martingale $\left \{M_{N}\right \}$ is L ₂-bounded, and therefore converges in L ₁ (and also in L ₂). So $\mathbb{E}\zeta = 1$ implying $\mathbb{P}\left (\zeta > 0\right ) > 0$.

On the other hand, it is evident that the event $\left \{\zeta > 0\right \}$ is a tail event for the sequence $\left \{\hat{\mathcal{F}}_{N}\right \},\ \hat{\mathcal{F}}_{N}\mathop{ =}\limits^{\mathrm{ def}}\sigma \left (\omega \left (i,x\right ): x \in \mathbb{Z}^{d},\ i \geq N\right ),$ and so the Kolmogorov 0-1-law implies $\mathbb{P}\left (\zeta > 0\right ) = 1$. This proves (2).

For (3), write $S_{n} = \left (S_{n,1},\ldots,S_{n,d}\right ).$ Define for $i,j \leq d,\ n \in \mathbb{N}$

$$\displaystyle{Y _{n}^{i,\,\,j}\mathop{ =}\limits^{\mathrm{ def}}\left \{\begin{array}{cc} S_{n,\,i}^{2} - n/d&\mathrm{for\ }i = j \\ S_{n,\,i}S_{n,\,j} & \mathrm{for\ }i\neq j \end{array} \right..}$$

As is well known, and easily checked, the sequences $\left \{Y _{n}^{i,j}\right \}_{n\in \mathbb{N}}$ are martingales under the law of the random walk. From that, it follows that

$$\displaystyle{\gamma _{N}^{i,\,j}\mathop{ =}\limits^{\mathrm{ def}}E_{ N}\left (Y _{n}^{i,\,j}M\left (\beta \right )^{-N}\exp \left [\beta \sum \nolimits _{ i=1}^{N}\omega \left (i,S_{ i}\right )\right ]\right )}$$

are $\left \{\mathcal{F}_{N}\right \}$-martingales under $\mathbb{P}$. A computation as done above in the proof of (2) reveals that if β is small enough, the martingales

$$\displaystyle{\sum _{k=1}^{N}k^{-1}\left (\gamma _{ k}^{i,\,j} -\gamma _{ k-1}^{i,\,j}\right )}$$

(with $Y _{0}^{i,j}\mathop{ =}\limits^{\mathrm{ def}}0$) are L ₂-bounded and therefore converge almost surely. From the Kronecker lemma, one concludes that

$$\displaystyle{\lim _{N\rightarrow \infty } \frac{1} {N}\gamma _{N}^{i,j} = 0}$$

almost surely. Together with (2), this proves (3). ■ 

There are many more recent and deeper results on the topic. Here is an (incomplete) list of results which have been obtained.

• The directed polymer is said to be in the strong disorder regime if ζ = 0 a.s., and in the weak disorder regime if ζ > 0 a.s. The application of the Kolmogorov 0-1-law above does not depend on the dimension, and therefore ζ = 0 almost surely, or ζ > 0 almost surely. Comets and Yoshida proved in [15] that there exists a critical value β _cr, depending on the law of the disorder and the dimension such that the system is in the weak disorder regime for β < β _cr and in the strong disorder regime for β > β _cr. Furthermore, they proved that β _cr = 0 for d = 1, 2, and that a CLT holds always in the weak disorder regime (see [16]).

• It is not difficult to see that the free energy exists and is self-averaging:

  $$\displaystyle{f\left (\beta \right )\mathop{ =}\limits^{\mathrm{ def}}\lim _{N\rightarrow \infty } \frac{1} {N}\log Z_{N,\beta } =\lim _{N\rightarrow \infty } \frac{1} {N}\mathbb{E}\log Z_{N,\beta }}$$

  Jensen’s inequality shows that

  $$\displaystyle{f\left (\beta \right ) \leq f^{\mathrm{ann}}\left (\beta \right )\mathop{ =}\limits^{\mathrm{ def}}\lim _{ N\rightarrow \infty } \frac{1} {N}\log \mathbb{E}Z_{N,\beta } =\log M\left (\beta \right ).}$$

  The system is called to be in the very strong disorder regime if $f\left (\beta \right )\neq f^{\mathrm{ann}}\left (\beta \right ).$

  It was proved that for d = 1 in [14], and for d = 2 in [24], that the system is in the very strong disorder regime for any positive β. 

• In the strong disorder regime, one always has a localization property: There exists $c = c\left (\beta \right ) > 0$ such that for $\mathbb{P}$-almost all ω, one has

  $$\displaystyle{\liminf _{N\rightarrow \infty } \frac{1} {N}\sum _{n=1}^{N}\hat{P}_{\beta,n-1,\omega }^{\otimes 2}\left (S_{ n}^{\left (1\right )} = S_{ n}^{\left (2\right )}\right ) \geq c.}$$

  Here $S_{n}^{\left (1\right )},S_{n}^{\left (2\right )}$ are two independent realizations (“replicas”) of the walk under the measure $\hat{P}_{\beta,n-1,\omega }$. In other words, two independent replicas share a positive proportion of the time at the same place, in sharp contrast to the behavior of independent standard random walks. The result had first been proved by Carmona and Hu [13] and Comets et al. [17].

• Whereas the properties in the weak disorder regime in d ≥ 3 are now fully understood, in the strong disorder regime, many of the properties are still completely open even for d = 1. The one-dimensional directed polymer is believed to belong to the so-called KPZ universality class. KPZ stands for Kardar-Parisi-Zhang who investigated (non-rigorously) an ill-posed stochastic PDE which is supposed to describe the directed polymer and many other interface models in an appropriate scaling limit.

  Under $\mathbb{P} \otimes \hat{ P}_{\beta,N,\omega }$, the deviation of S _N from the origin is believed to be of order N ^2∕3. The random environment is supposed to create random channels which deviate from the origin at this order, and then, for fixed ω, the paths are forced to localize in these channels. There are a number of very special models for which such a behavior has been proved (see [23]). The investigation of the KPZ class has been one of the main research topics in probability theory over the past years, with many deep results. But for the very “simplest” directed polymer with d = 1, given by the ordinary random walk and coin tossing ± 1 random environment, it is not even proved that the deviation of the end point under $\mathbb{P} \otimes \hat{ P}_{\beta,N,\omega }$ is larger than of order $\sqrt{n}.$

3 On the Pinning Model

The pinning polymer model is considerably simpler than the directed polymer. The localization, if present, has to be around 0. This is also true for the copolymer discussed in more details later.

There is a natural generalization of the pinning and the copolymer: One remarks that the Hamiltonian does not at all depend on the exact path at excursions away from 0. Essentially only the lengths of the return times to 0 count. For the copolymer it also matters whether the path is positive or negative on excursions, but the exact path along these excursions is also totally irrelevant. If we write 0 = τ ₀ < τ ₁ < τ ₂ < ⋯ for the sequence of return times and τ for the collection, then τ _i −τ _i−1 are i.i.d. with

$$\displaystyle{\rho \left (n\right )\mathop{ =}\limits^{\mathrm{ def}}P\left (\tau _{i} -\tau _{i-1} = n\right ) \approx \mathop{\mathrm{{\ast}}}\nolimits const \times n^{-3/2}}$$

for n even. We generalize this by allowing

$$\displaystyle{\rho \left (n\right ) = n^{-\alpha }L\left (n\right )}$$

with α > 1, and L a slowly varying function. Some of the results don’t depend on such a form but need only that

$$\displaystyle{ \lim _{n\rightarrow \infty }\frac{\log \rho \left (n\right )} {\log n} = -\alpha }$$

(4)

exists and is > 1. In the case where α > 2, the return times have a finite moment which simplifies things. The more interesting case is with 1 < α < 2. We write τ for the set of return times: $\tau \mathop{=}\limits^{\mathrm{ def}}\left \{\tau _{0}\mathop{ =}\limits^{\mathrm{ def}}0,\tau _{1},\ldots \right \}.$ It is also interesting to consider transient cases where $\sum _{n}\rho \left (n\right ) < 1$, but we will always stick to the recurrent case with $\sum _{n}\rho \left (n\right ) = 1$, and where the τ _i  < ∞ for all i.

In order to avoid boring periodicity discussions, we assume $\rho \left (n\right ) > 0$ for all large enough n, although it excludes the application to the standard random walk case presented in the introduction. Evidently, this is a very minor point.

The partition function Z of the pinning model can then be expressed by

$$\displaystyle{Z_{N,\omega } = E\left (\exp \left [\sum \nolimits _{n=1}^{N}\left (\beta \omega _{ n} + h\right )1_{n\in \tau }\right ]1_{N\in \tau }\right ).}$$

We include 1 _N ∈ τ for convenience (it is of no real importance). E refers to the distribution of τ. 

Consider the so-called quenched free energy

$$\displaystyle{f\left (\beta,h\right )\mathop{ =}\limits^{\mathrm{ def}}\lim _{N\rightarrow \infty } \frac{1} {N}\mathbb{E}\log Z_{N,\omega }.}$$

The existence of this limit follows by a simple subadditivity argument which works nicely because we included 1 _N ∈ τ :

$$\displaystyle\begin{array}{rcl} Z_{N+M,\omega }& =& E\left (\exp \left [\sum \nolimits _{n=1}^{N+M}\left (\beta \omega _{ n} + h\right )1_{n\in \tau }\right ]1_{N+M\in \tau }\right ) {}\\ & \geq & E\left (\exp \left [\sum \nolimits _{n=1}^{N+M}\left (\beta \omega _{ n} + h\right )1_{n\in \tau }\right ]1_{N\in \tau }1_{N+M\in \tau }\right ) {}\\ & =& E\left (\exp \left [\sum \nolimits _{n=1}^{N}\left (\beta \omega _{ n} + h\right )1_{n\in \tau }\right ]1_{N\in \tau }\right ) {}\\ & & \times E\left (\exp \left [\sum \nolimits _{n=1}^{M}\left (\beta \omega _{ N+n} + h\right )1_{n\in \tau }\right ]1_{M\in \tau }\right ), {}\\ \end{array}$$

and so

$$\displaystyle{Z_{N+M,\omega } \geq Z_{N,\omega }Z_{M,\theta _{N}\left (\omega \right )}}$$

where $\theta _{N}\left (\omega \right ) = \left (\omega _{N+1},\omega _{N+2},\ldots \right )$ which has the same distribution as ω. Therefore

$$\displaystyle{\mathbb{E}\log Z_{N+M} \geq \mathbb{E}\log Z_{N} + \mathbb{E}\log Z_{M}.}$$

From that the existence of the $f\left (\beta,h\right )$ follows, and one can easily derive lower and upper bounds:

$$\displaystyle\begin{array}{rcl} Z_{N}& \geq & E\left (\exp \left [\sum \nolimits _{n=1}^{N}\left (\beta \omega _{ n} + h\right )1_{n\in \tau }\right ]1_{\tau _{1}=N}\right ) {}\\ & =& E\left (\exp \left [\beta \omega _{N} + h\right ]1_{\tau _{1}=N}\right ) =\rho \left (N\right )\exp \left [\beta \omega _{N} + h\right ], {}\\ \end{array}$$

so $f\left (\beta,h\right ) \geq 0.$

An upper bound follows from the important annealed bound: By Jensen and Fubini, one has

$$\displaystyle\begin{array}{rcl} \mathbb{E}\log Z_{N}& \leq & \log \mathbb{E}Z_{N} =\log E\left (1_{\tau _{1}=N}\prod \nolimits _{n\in \tau,\ n\leq N}\mathrm{e}^{h}\mathbb{E}\mathrm{e}^{\beta \omega _{n} }\right ) {}\\ & =& \log E\left (1_{\tau _{1}=N}\prod \nolimits _{n\in \tau,\ n\leq N}\mathrm{e}^{h+\log M\left (\beta \right )}\right ), {}\\ \end{array}$$

where $M\left (\beta \right )\mathop{ =}\limits^{\mathrm{ def}}\mathbb{E}\mathrm{e}^{\beta \omega _{1}}$, which we always assume to be finite for all β. Therefore, $f\left (\beta,h\right ) \leq h +\log M\left (\beta \right ) < \infty.$

$$\displaystyle{f^{\mathrm{\mathrm{ann}}}\left (\beta,h\right )\mathop{ =}\limits^{\mathrm{ def}}\lim _{ N\rightarrow \infty } \frac{1} {N}\log \mathbb{E}Z_{N}}$$

is called the annealed free energy. The above computation shows

$$\displaystyle{f\left (\beta,h\right ) \leq f^{\mathrm{\mathrm{ann}}}\left (\beta,h\right ) = f\left (0,h +\log M\left (\beta \right )\right ).}$$

One therefore sees that the annealed partition function and path measure is nothing but the path measure in the absence of disorder and shifted parameter. The model without disorder (and therefore also the annealed model) has a very trivial localization-delocalization transition: If h > 0, then $f\left (0,h\right ) > 0$ and the paths in the transformed measure spend a positive fraction of the time at 0 as n → ∞, $h_{c}\left (0\right ) =\inf \left \{\beta: f\left (0,h\right ) > 0\right \} = 0$. In the transient case where $\sum _{n}\rho \left (n\right ) < 1$, one of course has $h_{c}\left (0\right ) > 0$ (a fact which has been used in the proof of Theorem 1). If we define

$$\displaystyle{h_{\mathrm{cr}}\left (\beta \right )\mathop{ =}\limits^{\mathrm{ def}}\inf \left \{h: f\left (\beta,h\right ) > 0\right \},}$$

then the above considerations imply $h_{\mathrm{cr}}\left (\beta \right ) \geq -\log M\left (\beta \right )$ (or $\geq h_{\mathrm{cr}}\left (0\right ) -\log M\left (\beta \right )$ in case $h_{\mathrm{cr}}\left (0\right )\neq 0$).

A question which has attracted considerable attention is about the sharpness of the above inequality. If $h_{\mathrm{cr}}\left (\beta \right ) > h_{\mathrm{cr}}\left (0\right ) -\log M\left (\beta \right )$ then one says that disorder is relevant, and if one has equality, that disorder is irrelevant.

This question has attracted considerable attention. Here a summary of results which have been obtained for the pinning model.

• Ken Alexander in [1], and with a different proof Fabio Toninelli in [30], showed that in the case of Gaussian disorder, for α < 3∕2 and β small enough, one has $h_{\mathrm{cr}}\left (\beta \right ) = h_{\mathrm{cr}}\left (0\right ) -\log M\left (\beta \right )$. Actually, considerably more information is obtained in these papers. For a more general result, not assuming Gaussian disorder, and with an elegant short proof, see [25].

• For α > 3∕2, disorder is always relevant, and the critical values are always different for β > 0. This was proved in [19].

• Finally, also the critical case with α = 3∕2 was investigated in [21] with a very sophisticated refinements of the methods in [19].

For the state of art before 2007, see also the excellent monograph by Giacomin [20].

We will see in the next chapters that for the copolymer, the situation is rather different, and disorder is always relevant in the above sense.

4 The Random Copolymer

4.1 The Localization-Delocalization Critical Line

The copolymer is quite a bit more complicated than the pinning model, and a number of important questions are still open. The partition function is

$$\displaystyle{Z_{N,\omega } = E\exp \left [\beta \sum \nolimits _{j=0}^{N-1}\left (\omega _{ j} + h\right )\mathop{\mathrm{{\ast}}}\nolimits sign\left (S_{j} + S_{j+1}\right )\right ]1_{S_{N}=0}.}$$

We again assume

$$\displaystyle{\mathbb{E}\omega _{i} = 0,\ \mathbb{E}\omega _{i}^{2} = 1.}$$

In addition, we assume that the distribution of the ω _i is symmetric, which simplifies some points. We again also assume

$$\displaystyle{M\left (\beta \right ) = \mathbb{E}\mathrm{e}^{\beta \omega _{i}} < \infty }$$

for all β. 

We write this in terms of the return times τ _i to the origin. As in the case of the pinning model, we allow for essentially arbitrary i.i.d. distributions ρ of τ _i −τ _i−1. We assume that the renewal sequence is recurrent and that (4) is satisfied. In some situations, we assume more, but generally we make no efforts to achieve the best possible conditions for the results. We can then write the partition function in terms of τ and the signs of the excursions, call them $\varepsilon _{i}:$

$$\displaystyle{ Z_{N,\omega } = E\exp \left [\sum \nolimits _{n:\tau _{n}\leq N}\varepsilon _{n}\sum \nolimits _{j=\tau _{n-1}+1}^{\tau _{n} }\beta \left (\omega _{j} + h\right )\right ]1_{N\in \tau }, }$$

(5)

here E referring to taking the expectation for the $\tau _{i},\varepsilon _{i}.$ The $\varepsilon _{n}$ can however trivially be integrated out, and we get

$$\displaystyle{Z_{N,\omega } = E\prod _{n:\tau _{n}\leq N}\cosh \left [\sum \nolimits _{j=\tau _{n-1}+1}^{\tau _{n} }\beta \left (\omega _{j} + h\right )\right ]1_{N\in \tau },}$$

and the existence of the free energy

$$\displaystyle{f\left (\beta,h\right ) =\lim _{N\rightarrow \infty } \frac{1} {N}\log Z_{N,\omega } =\lim _{N\rightarrow \infty } \frac{1} {N}\mathbb{E}\log Z_{N,\omega }}$$

follows in the same way as in the pinning model. For the model here, we can assume h ≥ 0 as the case with negative h is just symmetric.

One gets a trivial lower bound by restricting to τ ₁ = N:

$$\displaystyle\begin{array}{rcl} Z_{N,\omega }& =& E\prod _{n:\tau _{n}\leq N}\cosh \left [\sum \nolimits _{j=\tau _{n-1}+1}^{\tau _{n} }\beta \left (\omega _{j} + h\right )\right ]1_{N\in \tau } {}\\ &\geq & E\cosh \left [\sum \nolimits _{j=1}^{n}\beta \left (\omega _{ j} + h\right )\right ]1_{\tau _{1}=N} {}\\ & =& \frac{1} {2}\rho \left (N\right )\exp \left [\beta \sum \nolimits _{j=1}^{N}\omega _{ j} + N\beta h\right ]. {}\\ \end{array}$$

Therefore, by the law of large number for the ω _i , and $\lim _{N\rightarrow \infty } \frac{1} {N}\log \frac{1} {2}\rho \left (N\right ) = 0$, we have

$$\displaystyle{f\left (\beta,h\right ) \geq \beta h,}$$

and we call

$$\displaystyle{ \bar{f}\left (\beta,h\right )\mathop{ =}\limits^{\mathrm{ def}}f\left (\beta,h\right ) -\beta h }$$

(6)

the excess free energy. There is however a small but important trick by a modification of the Hamiltonian, which has a slightly different finite N free energy: We simply subtract 1 from the $\varepsilon _{n}$ in (5) which evidently, in the quenched free energy leads to $\bar{f}\left (\beta,h\right )$. After integrating out the $\varepsilon _{n}$, we have for this modified partition function

$$\displaystyle\begin{array}{rcl} \bar{Z}_{N,\omega }& =& E\exp \left [\sum \nolimits _{n:\tau _{n}\leq N}\left (\varepsilon _{n} - 1\right )\sum \nolimits _{j=\tau _{n-1}+1}^{\tau _{n} }\beta \left (\omega _{j} + h\right )\right ]1_{N\in \tau }, \\ & =& E\prod _{n:\tau _{n}\leq N}\left [\frac{1} {2} +\exp \left [-2\sum \nolimits _{j=\tau _{n-1}+1}^{\tau _{n} }\beta \left (\omega _{j} + h\right )\right ]\right ]1_{N\in \tau } \\ & =& E\prod _{n:\tau _{n}\leq N}\left [\frac{1} {2} + \frac{1} {2}\exp \left [-2\beta \sigma _{n}\left (\boldsymbol{\omega }\right ) - 2\beta hl_{n}\right ]\right ]1_{N\in \tau } \\ & =& E1_{N\in \tau }\exp \left [\sum \nolimits _{n:\tau _{n}\leq N}\log \left [\frac{1} {2} + \frac{1} {2}\exp \left [-2\beta \sigma _{n} - 2\beta hl_{n}\right ]\right ]\right ]. {}\end{array}$$

(7)

where

$$\displaystyle{\sigma _{n}\left (\boldsymbol{\omega }\right )\mathop{ =}\limits^{\mathrm{ def}}\sum _{j=\tau _{n-1}+1}^{\tau _{n} }\omega _{j},\ l_{n}\mathop{ =}\limits^{\mathrm{ def}}\tau _{n} -\tau _{n-1}}$$

By the law of large numbers, we get

$$\displaystyle{\lim _{N\rightarrow \infty } \frac{1} {N}\log \bar{Z}_{N,\omega } = f\left (\beta,h\right ) - h\beta =\bar{ f}\left (\beta,h\right ).}$$

The advantage of this modification (called Morita-correction) is that the corresponding annealed free energy (which is different from the annealed free energy for the original Hamiltonian) behaves better.

It is plausible that the path measure of the copolymer is localized if $f\left (\beta,h\right ) >\beta h$ i.e. $\bar{f}\left (\beta,h\right ) > 0$ and delocalized if $\bar{f}\left (\beta,h\right ) = 0.$ We will not really go into a detailed discussion of the path properties under the Gibbs measure. That $\bar{f}\left (\beta,h\right ) > 0$ implies that the paths, under the Gibbs measure, are strongly localized around the origin has been proved by Biskup and den Hollander [5]. Such a pathwise localization had already been proved by Sinai [27] for the h = 0 case. The path behavior in the case when $\bar{f}\left (\beta,h\right ) = 0$ is still less clear. Pathwise delocalization has only be proved for large enough h, strictly above the critical value which we introduce shortly.

For the moment, we take the behavior of $\bar{f}\left (\beta,h\right )$ as the definition of localization and delocalization:

$$\displaystyle\begin{array}{rcl} \mathcal{L}\mathop{ =}\limits^{\mathrm{ def}}\left \{\left (\beta,h\right ):\beta > 0,\ h \geq 0,\ \bar{f}\left (\beta,h\right ) > 0\right \}& &{}\end{array}$$

(8)

$$\displaystyle\begin{array}{rcl} \mathcal{D}\mathop{ =}\limits^{\mathrm{ def}}\left \{\left (\beta,h\right ):\beta > 0,\ h \geq 0,\ \bar{f}\left (\beta,h\right ) = 0\right \},& &{}\end{array}$$

(9)

and we call $\mathcal{L}$ the localized region, and $\mathcal{D}$ the delocalized one.

Proposition 3

• a) For any β > 0, there exists $h_{\mathrm{cr}}\left (\beta \right ) > 0$ such that $\left (\beta,h\right ) \in \mathcal{L}$ when $h < h_{\mathrm{cr}}\left (\beta \right )$ and $\left (\beta,h\right ) \in \mathcal{D}$ when $h \geq h_{\mathrm{cr}}\left (\beta \right )$ .

• b) $\lim _{\beta \rightarrow 0}h_{\mathrm{cr}}\left (\beta \right ) = 0$ .

• c) The function $\beta \rightarrow h_{\mathrm{cr}}\left (\beta \right )$ is continuous and increasing in β.

That $\left (\beta,h\right ) \in \mathcal{D}$ for large enough h follows from the annealed bound, as we will see in a moment. That for a fixed β, $\left (\beta,h\right ) \in \mathcal{D}$ for small enough h will be a consequence of the bound given in Sect. 4.2. (b) will then also follow. I don’t prove (c) here which is technical but not difficult result. For the standard random walk case with α = 3∕2, a proof is in [9], and the general case is proved in [20].

By Jensen’s inequality, we have

$$\displaystyle{ \mathbb{E}\log \bar{Z}_{N,\omega } \leq \log \mathbb{E}\bar{Z}_{N,\omega }. }$$

(10)

The right hand side is much easier to evaluate than the left hand side:

$$\displaystyle{ \mathbb{E}\bar{Z}_{N,\omega } = E\prod _{n:\tau _{n}\leq N}\left (\frac{1} {2} + \frac{1} {2}\exp \left [-2\beta l_{n} + l_{n}\log M\left (2\beta \right )\right ]\right )1_{S_{N}=0}. }$$

(It would be $M\left (-2\beta \right )$, but as we assume symmetry, this is $M\left (2\beta \right )$). If we define

$$\displaystyle{f^{\mathrm{\mathrm{ann}}}\left (\beta,h\right )\mathop{ =}\limits^{\mathrm{ def}}\lim _{ N\rightarrow \infty } \frac{1} {N}\log \mathbb{E}\bar{Z}_{N,\omega },}$$

then we see that $f^{\mathrm{\mathrm{ann}}}\left (\beta,h\right ) = 0$ if and only if

$$\displaystyle{-2\beta h +\log M\left (2\beta \right ) \leq 0,}$$

and $f^{\mathrm{\mathrm{ann}}}\left (\beta,h\right ) > 0$ otherwise. Therefore, the corresponding annealed critical value is

$$\displaystyle{h_{\mathrm{cr}}^{\mathrm{\mathrm{ann}}}\left (\beta \right ) = \frac{M\left (2\beta \right )} {2\beta } }$$

above which the annealed free energy is 0. From (10), we get

$$\displaystyle{\bar{f}\left (\beta,h\right ) \leq f^{\mathrm{\mathrm{ann}}}\left (\beta,h\right ),}$$

and so we have proved

Proposition 4

$$\displaystyle{h_{\mathrm{cr}}\left (\beta \right ) \leq h_{\mathrm{cr}}^{\mathrm{\mathrm{ann}}}\left (\beta \right ) = \frac{M\left (2\beta \right )} {2\beta }.}$$

We will later see that in sharp contrast to the situation in the last chapter, the inequality is strict for all β > 0.

For notational convenience we will use f instead of $\bar{f}$, and one should keep in mind that it is the Morita-corrected free energy.

4.2 The Monthus-Bodineau-Giacomin Lower Bound

Theorem 5

For the copolymer model

$$\displaystyle{h_{\mathrm{cr}}\left (\beta \right ) \geq \frac{\alpha } {2\beta }\log M\left (\frac{2\beta } {\alpha } \right ).}$$

(Remark that the bound is given by $h_{\mathrm{cr}}^{\mathrm{\mathrm{ann}}}\left (\beta /\alpha \right )$ ).

Proof

Let $k \in \mathbb{N}$ and divide $\mathbb{N}$ into blocks I _j of length k: $I_{j}\mathop{ =}\limits^{\mathrm{ def}}\left \{\left (j - 1\right )k + 1,jk\right \}.$ We fix some negative x, and we call the interval I _j to be good, provided $\sum _{n\in I_{j}}\omega _{n} \leq kx$. This notion depends on k and x < 0.

By the Cramer theorem, denoting $\pi \left (k\right )$ to be the $\mathbb{P}$-probability that I ₁ is good

$$\displaystyle{ \lim _{k\rightarrow \infty }\frac{1} {k}\log \pi \left (k\right ) = -I\left (x\right ) }$$

(11)

where

$$\displaystyle{I\left (x\right ) =\sup _{\lambda }\left [\lambda x - M\left (\lambda \right )\right ].}$$

Given N ≥ k, denote by $\mathcal{J}_{k,x,N}\left (\omega \right )$ the set of the good intervals which are contained in $\left \{1,\ldots,N - 1\right \}.$ Remark that this set is defined in terms of the environment ω (and k, x, N of course). Depending on $\mathcal{J}_{k,x,N}$,we fix one specific sequence τ and sequence $\varepsilon$ of signs (for the “excursions”): τ contains exactly the endpoints of the intervals in $\mathcal{J}_{k,x,N}$ and N. Remark that because we have taken the intervals to be in $\left \{1,\ldots,N - 1\right \},$ we have now an odd number of points in τ. The signs $\varepsilon _{i}$ of the excursions are chosen to be negative for the good intervals and positive otherwise.

If $M_{N}\mathop{ =}\limits^{\mathrm{ def}}\left \vert \mathcal{J}_{k,x,N}\right \vert$ and l ₁, …, l _M  ≥ 1 are the distances between the good intervals (l ₁ left endpoint of the first good interval), and L is the right endpoint of the last good interval, then we get for the above specific chosen τ and $\varepsilon$, the Hamiltonian as

$$\displaystyle{2M_{N}k\left (x + h\right )}$$

and the P-probability for this special “path” as

$$\displaystyle{2^{-2M-1}\rho \left (N - L\right )\rho \left (k\right )^{M_{N} }\prod _{i=1}^{M_{N} }\rho \left (l_{i}\right ),}$$

and therefore

$$\displaystyle{\bar{Z}_{N} \geq 2^{-2M_{N}-1}\rho \left (N - L\right )\rho \left (k\right )^{M_{N} }\exp \left [-2\beta M_{N}k\left (x + h\right )\right ]\prod _{i=1}^{M_{N} }\rho \left (l_{i}\right ).}$$

By the law of large numbers, we have $\lim _{N\rightarrow \infty }M_{N}/N =\pi \left (k\right )/k$ almost surely, and therefore

$$\displaystyle\begin{array}{rcl} f\left (\beta,h\right )& \geq & -\frac{\pi \left (k\right )} {k} 2\log 2 + \frac{\pi \left (k\right )} {k} \log \rho \left (k\right ) \\ & & -2\beta \pi \left (k\right )\left (x + h\right ) + \frac{\pi \left (k\right )} {k} \mathbb{E}\log \rho \left (l_{1}\right ).{}\end{array}$$

(12)

This bound holds for any $k \in \mathbb{N},\ x \leq 0.$ For k → ∞, the right hand side evidently goes to 0, but we claim that for $h < \frac{\alpha } {2\beta }\log M\left (\frac{2\beta } {\alpha } \right )$, we can make it positive, by choosing k appropriately.

To prove this, we first observe that by our assumption (4) and (11), we have

$$\displaystyle{\lim _{k\rightarrow \infty }\frac{1} {k}\mathbb{E}\log \rho \left (l_{1}\right ) \geq -\alpha I\left (x\right ).}$$

and furthermore, inverting the Legendre transform for the rate function I:

$$\displaystyle{\sup _{x\leq 0}\left [-2\beta x -\alpha I\left (x\right )\right ] =\alpha M\left (\frac{2\beta } {\alpha } \right ).}$$

Therefore, the rhs of (12) is for k → ∞, by optimizing over x ≤ 0: 

$$\displaystyle\begin{array}{rcl} & & \pi \left (k\right )\left [-\frac{2\log 2} {k} + \frac{\log \rho \left (k\right )} {k} - 2\beta h +\alpha M\left (\frac{2\beta } {\alpha } \right ) + o\left (1\right )\right ] {}\\ & & \quad =\pi \left (k\right )\left [-2\beta h +\alpha M\left (\frac{2\beta } {\alpha } \right ) + o\left (1\right )\right ]. {}\\ \end{array}$$

As soon as $h < \frac{\alpha } {2\beta }M\left (\frac{2\beta } {\alpha } \right ),$ the bracket is positive for large k, and therefore, we have proved

$$\displaystyle{h_{\mathrm{cr}}\left (\beta \right ) \geq \frac{\alpha } {2\beta }\log M\left (\frac{2\beta } {\alpha } \right ).}$$

 ■ 

The proof above is due to Bodineau and Giacomin [6]. The basic idea of the above proof was originally presented in non-rigorous terms in [26], where it was argued that $h_{\mathrm{cr}}^{\mathrm{\mathrm{ann}}}\left (\beta /\alpha \right )$ is the correct critical line. This conjecture was open for a considerable time. Later, it however became clear that it cannot be correct. It first came out from a fully controlled numerical study [12]. It was first rigorously proved in [7] for large enough α (still α < 2, but not including α = 3∕2), and then $h_{\mathrm{cr}}\left (\beta \right ) > \frac{\alpha } {2\beta }\log M\left (\frac{2\beta } {\alpha } \right )$ was proved in [10] for all α > 1. I present an elementary self-contained proof in Sect. 6.

4.3 The Proof of the Existence of the Tangent at the Critical Line at the Origin

By the annealed bound in Proposition 4 and the lower bound in Theorem 5 we have squeezed the critical line between two simple curves

$$\displaystyle{ \frac{\alpha } {2\beta }\log M\left (\frac{2\beta } {\alpha } \right ) \leq h_{\mathrm{cr}}\left (\beta \right ) \leq \frac{1} {2\beta }\log M\left (2\beta \right ).}$$

The upper bound has tangent 1 at the origin and the lower bound tangent 1∕α. This because we have assumed that the variance of the ω _i is 1. It is therefore natural to suspect that the critical line has a tangent at the origin which is between 1∕α and 1.

The proof of the existence of such a tangent turned out to be highly non-trivial. It had first been done in [9] for the standard random walk case (with α = 3∕2) and for more general situations later by Caravenna and Giacomin [11]. More important than just the existence of the tangent is the fact that it is universal in the sense that it depends only on α and not on the exact distribution of the ω _i . This had not been proved explicitly in [9], where just the coin tossing distribution for the ω _i was used, but as the proof is done via a Brownian approximation, it strongly suggests this universality property. For recent results about this universality property, see [2]. I sketch here the key steps in the original argument in [9].

We first define a continuous model which starts with two Brownian motions, $\left (\omega _{t}\right )_{t\geq 0}$ for the environment, and $\left (B_{t}\right )_{t\geq 0}$ for the random walk. We then define the quenched path measure

$$\displaystyle{ Q_{t}^{\beta,h,\omega }\left (\left (B_{ s}\right )_{0\leq s\leq t}\right ) = \frac{1} {Z_{t}^{\beta,h,\omega }}\exp \left [-2\beta \int _{0}^{t}\Delta _{ s}\left (B\right )\left [d\omega _{s} + hds\right ]\right ] }$$

(13)

where $\Delta _{s}\left (B\right )$ is 1 if B _s  < 0, and 0 otherwise. It is not difficult to prove that

$$\displaystyle{\phi \left (\beta,h\right )\mathop{ =}\limits^{\mathrm{ def}}\lim _{t\rightarrow \infty }\frac{1} {t}\log Z_{t}^{\beta,h,\omega }}$$

exists, and is non-random and ≥ 0. The problem is to decide if it is 0 or not. From a scaling $\left \{\left (B_{s},\omega _{s}\right )\right \}_{s\leq t}\mathop{ =}\limits^{ \mathcal{L}}\left (aB_{s/a^{2}},a\omega _{s/a^{2}}\right )_{s\leq t},$ we get that

$$\displaystyle{Z_{t}^{\beta,h}\mathop{ =}\limits^{ \mathcal{L}}Z_{ t/a^{2}}^{a\beta,ah},}$$

and therefore

$$\displaystyle{\phi \left (\beta,h\right ) = \frac{1} {a^{2}}\phi \left (a\beta,ah\right )}$$

for all a > 0. Therefore, there is only one parameter left:

$$\displaystyle{\phi \left (\beta,h\right ) =\beta ^{2}\phi \left (1,h/\beta \right ).}$$

In a similar way as in the discrete model (although there are some technical difficulties, see also [20]), one proves that there is a critical value κ such that $\phi \left (1,h\right ) = 0$ for h > κ, and $\phi \left (1,h\right ) > 0$ for h ≤ κ. Furthermore, the same type of arguments as in the discrete case (here with α = 3∕2) give the bounds

$$\displaystyle{\frac{2} {3} \leq \kappa \leq 1.}$$

Theorem 6

For the random walk case (i.e. α = 3∕2) with free energy f, one has

• a)
  $$\displaystyle{\lim _{a\rightarrow 0} \frac{1} {a^{2}}f\left (a\beta,ah\right ) =\phi \left (\beta,h\right ).}$$

• b) The critical curve $h_{\mathrm{cr}}\left (\beta \right )$ satisfies

  $$\displaystyle{\lim _{\beta \rightarrow 0}\frac{h_{\mathrm{cr}}\left (\beta \right )} {\beta } =\kappa }$$

As explained above, κ is really the object of interest in the model.

(b) is unfortunately not quite a consequence of (a), unfortunately because the proof of (b) is much more difficult than the proof of (a). (a) gives only a one-sided bound: If r < κ then from (a) we get

$$\displaystyle{\lim _{\beta \rightarrow 0}\frac{1} {\beta ^{2}} f\left (\beta,r\beta \right ) =\phi \left (1,r\right ) > 0,}$$

and therefore $f\left (\beta,r\beta \right ) > 0$ for small enough β, implying $h_{\mathrm{cr}}\left (\beta \right ) \geq r\beta$ for small enough β, i.e.

$$\displaystyle{\liminf _{\beta \rightarrow 0}\frac{h_{\mathrm{cr}}\left (\beta \right )} {\beta } \geq \kappa.}$$

The other bound in (b) however does not follow from (a). If r > κ, then (a) implies only

$$\displaystyle{\lim _{\beta \rightarrow 0}\frac{1} {\beta ^{2}} f\left (\beta,r\beta \right ) = 0,}$$

but this does not exclude $f\left (\beta,r\beta \right ) > 0$ for small β. We would like to prove that for r > κ one has $f\left (\beta,r\beta \right ) = 0$ for small enough β. 

In order to get the result about the tangent, we need a better control of $\beta ^{-2}f\left (\beta,\beta h\right )$ in terms of ϕ than that provided by (a). In fact, in [9] we prove

Theorem 7

Let h > 0, H ≥ 0 and ρ > 0 satisfy $\left (1+\rho \right )H \leq h.$ Then for small enough β, one has

$$\displaystyle{ \frac{1} {\beta ^{2}\left (1+\rho \right )}f\left (\beta,\beta h\right ) \leq \phi \left (1,H\right ) \leq \frac{1+\rho } {\beta ^{2}} f\left (\beta,\beta h\right ).}$$

These estimates are sufficient to prove Theorem 6.

The proof of Theorem 7 is rather tricky and uses a complicated double truncation on the excursion lengths, and cannot be given here in all details.

The arguments are however quite interesting, I think, and are based on a kind of partial quenched versus annealed computations which I just shortly sketch. Readers interested in the details of the argument should also study the paper of Caravenna and Giacomin [11] where essentially the same is proved in a more general setup. They use the same arguments, but in a somewhat streamlined version.

Assume that there is a random Hamiltonian H _N which can be split into two parts $H = H^{\left (I\right )} + H^{\left (II\right )}.$ Then

$$\displaystyle\begin{array}{rcl} E\exp \left [-H_{N}\right ]& =& E\exp \left [-H_{N}^{\left (I\right )}\right ]\exp \left [-H_{ N}^{\left (II\right )}\right ] {}\\ & \leq & \left (E\exp \left [-\left (1+\rho \right )H_{N}^{\left (I\right )}\right ]\right )^{1/\left (1+\rho \right )} {}\\ & & \times \left (E\exp \left [-\left (1 +\rho ^{-1}\right )H_{ N}^{\left (I\right )}\right ]\right )^{1/\left (1+\rho ^{-1}\right ) }, {}\\ \end{array}$$

and therefore

$$\displaystyle\begin{array}{rcl} \frac{1} {N}\mathbb{E}\log E\mathrm{e}^{-H_{N} }& \leq & \frac{1} {N\left (1+\rho \right )}\mathbb{E}\log E\exp \left [-\left (1+\rho \right )H_{N}^{\left (I\right )}\right ] \\ & & + \frac{1} {N\left (1 +\rho ^{-1}\right )}\mathbb{E}\log E\exp \left [-\left (1 +\rho ^{-1}\right )H_{ N}^{\left (II\right )}\right ] \\ & \leq & \frac{1} {N\left (1+\rho \right )}\mathbb{E}\log E\exp \left [-\left (1+\rho \right )H_{N}^{\left (I\right )}\right ] \\ & & + \frac{1} {N\left (1 +\rho ^{-1}\right )}\log \mathbb{E}E\exp \left [-\left (1 +\rho ^{-1}\right )H_{ N}^{\left (II\right )}\right ].{}\end{array}$$

(14)

The crucial point will be to choose $H^{\left (II\right )}$ in such a way that

$$\displaystyle{\lim _{N\rightarrow \infty } \frac{1} {N}\log \mathbb{E}E\exp \left [-\left (1 +\rho ^{-1}\right )H_{ N}^{\left (II\right )}\right ] \leq 0,}$$

so that we obtain

$$\displaystyle{ \lim _{N\rightarrow \infty } \frac{1} {N}\mathbb{E}\log E\mathrm{e}^{-H_{N} } \leq \lim _{N\rightarrow \infty } \frac{1} {N\left (1+\rho \right )}\mathbb{E}\log E\exp \left [-\left (1+\rho \right )H_{N}^{\left (I\right )}\right ]. }$$

(15)

For the proof, we stay with the form (7) of the partition function, and the corresponding finite N free energy

$$\displaystyle{F_{N}\mathop{ =}\limits^{\mathrm{ def}} \frac{1} {N}\mathbb{E}\log E\exp \left [-2\beta \sum \nolimits _{n:\tau _{n}\leq N}\Delta _{n}\left (\varepsilon \right )\sum \nolimits _{j=\tau _{n-1}}^{\tau _{n} }\left (\omega _{j} + h\right )\right ].}$$

In order to make use of the i.i.d. properties of the time lengths between successive returns of the random walk to 0, we drop the final 1 _N ∈ τ in the original partition function.

The key idea of the proof is that as β → 0, excursions of length much smaller than 1∕β ² don’t contribute. Also for the continuous model (13) for fixed β = 1, it turns out that short excursion of the Brownian motion don’t contribute substantially. For the longer excursions, one can apply the convergence of the random walk to Brownian motion. A proof of part (a) of Theorem 6 is relatively straightforward, but as remarked above, not sufficient to proof the existence and identification of the tangent.

The strategy of the proof is first to prove that a quite complicated truncation mechanism with which is cutting out irrelevant excursions does not change the free energy. Then we replace ω _i by standard Gaussian ones, and finally go to the Brownian motion, still with the cuts of the excursions, and in the last step finally prove that one can put back the short excursions for the Brownian which had been kept out. So, in the end, we perform four transformation steps, each one with a version of the above explained semi-annealed estimates.

To give an impression of the technical complications, I describe the splitting in the first step. We will need two additional (small) parameters $0 <\varepsilon <\delta.$ We divide $\left \{1,\ldots,T\beta ^{-2}\right \}$ into subintervals $I_{1},I_{2},,\ldots,I_{T/\varepsilon }$ of length $\varepsilon \beta ^{-2}.$ (We will always assume that T β ⁻² is integer, and divisible by $\varepsilon \beta ^{-2}$ to avoid trivial adjustments, and similarly in other situations). We call I _j occupied if there is a τ _n in I _j . We then define a random sequence of natural numbers $\sigma _{0}\mathop{ =}\limits^{\mathrm{ def}}0 <\sigma _{1} <\sigma _{2} < \cdots$ with the property that the $I_{\sigma _{i}}$ are occupied. However, we always want to have a gap condition between the σ’s depending on the larger parameter δ:

$$\displaystyle{\sigma _{k} =\inf \left \{j \geq \sigma _{k-1} +\delta /\varepsilon: I_{j}\ \mathrm{occupied}\right \}.}$$

We also define

$$\displaystyle\begin{array}{rcl} \bar{I}_{k}& \mathop{=}\limits^{\mathrm{ def}}& \bigcup \nolimits _{j\in (\sigma _{k-1},\sigma _{k}]}I_{j} \cap (0,N\beta ^{-2}], {}\\ m\left (T,\varepsilon,\beta \right )& \mathop{=}\limits^{\mathrm{ def}}& \min \left \{k:\sigma _{k} \geq T\varepsilon ^{-1}\right \}. {}\\ \end{array}$$

For 1 ≤ k ≤ m we put s _k  = 1 if the excursion ending at the first zero in $I_{\sigma _{k}}$ is negative, and s _k  = 0 otherwise. (There is a slight correction needed for s _m which we neglect.) We then define

$$\displaystyle{F_{T,\varepsilon,\delta }^{{\prime}}\left (\beta,h\right )\mathop{ =}\limits^{\mathrm{ def}} \frac{1} {T}\mathbb{E}\log E\exp \left [-2\beta H^{{\prime}}\right ]}$$

with

$$\displaystyle{H_{T,\varepsilon,\delta }^{{\prime}}\left (\beta,h\right )\mathop{ =}\limits^{\mathrm{ def}}\sum _{ k=1}^{m}s_{ k}\left (Z_{k}\left (\omega \right ) +\beta h\left \vert \bar{I}_{k}\right \vert \right ),\ Z_{k}\mathop{ =}\limits^{\mathrm{ def}}\sum _{j\in \bar{I}_{k}}\omega _{j},}$$

and we recall that

$$\displaystyle{\beta ^{-2}F_{ T\beta ^{-2}}\left (\beta,\beta h\right ) = \frac{1} {T}\mathbb{E}\log E\exp \left [-2\beta H_{T}\left (\beta,h\right )\right ]}$$

with

$$\displaystyle{H_{T}\left (\beta,h\right )\mathop{ =}\limits^{\mathrm{ def}}\sum \nolimits _{j=0}^{T\beta ^{-2} }\Delta _{j}\left (\omega _{j} +\beta h\right ).}$$

So, we have the same form. Remark first that there is a trivial rescaling property: If κ > 0 then

$$\displaystyle\begin{array}{rcl} H_{T,\varepsilon,\delta }^{{\prime}}\left (\beta,\kappa h\right )& =& H_{\kappa ^{ 2}T,\kappa ^{2}\varepsilon,\kappa ^{2}\delta }^{{\prime}}\left (\kappa \beta,h\right ) {}\\ H_{T}\left (\beta,\kappa h\right )& =& H_{\kappa ^{2}T}\left (\kappa \beta,h\right ). {}\\ \end{array}$$

We also have

$$\displaystyle\begin{array}{rcl} H_{T}\left (\beta,h_{1}\right ) - H_{T,\varepsilon,\delta }^{{\prime}}\left (\beta,h_{ 2}\right )& =& \beta \left (h_{1} - h_{2}\right )\sum _{k=1}^{m}\sum _{ j\in \bar{I}_{k}}\Delta _{j} {}\\ & & +\sum _{k=1}^{m}\sum _{ j\in \bar{I}_{k}}\left (\beta h_{2} +\omega _{j}\right )\left (\Delta _{j} - s_{k}\right ). {}\\ \end{array}$$

We now use (14) with H _T and

$$\displaystyle\begin{array}{rcl} H_{T}^{\left (I\right )}\left (\beta,h\right )& =& H_{ T,\varepsilon,\delta }^{{\prime}}\left (\beta,\left (1+\rho \right )H\right ) {}\\ & =& H_{T\left (1+\rho \right )^{2},\varepsilon \left (1+\rho \right )^{2},\delta \left (1+\rho \right )^{2}}^{{\prime}}\left (\beta,H\right ), {}\\ H_{T}^{\left (II\right )}\left (\beta,h\right )& =& H_{ T}\left (\beta,h\right ) - H_{T}^{\left (I\right )}\left (\beta,h\right ) {}\\ \end{array}$$

Then one finally proves

Lemma 8

For any h,H,ρ there exists δ ₀ such that for δ ≤δ ₀ there exists $\varepsilon _{0}\left (\delta \right )$ such that for $\varepsilon \leq \varepsilon _{0}\left (\delta \right )$ there exists $\beta _{0}\left (\delta,\varepsilon \right )$ such that for $\beta \leq \beta _{0}\left (\delta,\varepsilon \right )$

$$\displaystyle{\limsup _{T\rightarrow \infty }\frac{1} {T}\log E\mathbb{E}\exp \left [-2\beta \left (1 +\rho ^{-1}\right )H_{ T}^{\left (II\right )}\right ] \leq 0}$$

The proof is too complicated, and probably too boring, to be presented here. This is just the first step, but fortunately, the most complicated one. After finding the suitable $\varepsilon -\delta$-truncations, it is possible to replace the coin tossing ω _i by Gaussian ones, but again we have to achieve an estimate (15), and afterwards one can switch to the Brownian model with truncations, and in the end, one removes the truncations.

It should also be clear that a proof of part (a) of Theorem 6 is considerably simpler, as one does not really need an estimate as sharp as that in Theorem 7.

Although, we didn’t do it in [9], it is clear that the argument works with general distributions for the ω _i , subject to an exponential moment condition $M\left (\beta \right ) < \infty$ for all β.

5 The Large Deviation Principles by Birkner and Birkner-Greven-den Hollander, and Their Applications to the Copolymer

Considerable progress in the understanding of the copolymer was achieved with ideas originally developed by Birkner in [3]. The setup he had developed there could not be used directly for the polymer problems with the renewal process having only polynomially decaying tails. A bit later, his approach was extended in [4], and in this form, the LDP did in principle apply to the copolymer, but there were still a number of tricky issues to be handled. This has finally be done in [10]. Probably, the most striking application was the proof that the tangent κ of the critical line at the origin is strictly larger than 1∕α, disproving an old conjecture of Cécile Monthus.

I will present later in Sect. 6 an elementary proof of this lower bound, bypassing the somewhat heavy large deviation machinery, but the argument is in its core still the one given in [10], and the elementary proof would probably have been difficult to find without the general setup.¹

I give here on outline of the general large deviation principles. We first need a couple of definitions

• $\mathcal{W}$ is the set of finite length sequences of real numbers. These sequences we call “words”. For $w \in \mathcal{W},$ $\ell\left (w\right )$ denotes the length of the word, so that

  $$\displaystyle{w = \left (x_{1},\ldots,x_{\ell\left (w\right )}\right ),\ x_{i} \in \mathbb{R},}$$

  and we set

  $$\displaystyle{\sigma \left (w\right )\mathop{ =}\limits^{\mathrm{ def}}\sum _{i=1}^{\ell\left (w\right )}x_{ i}.}$$

  $\mathcal{W}$ comes with a naturally defined Borel σ-field $\mathcal{B}_{\mathcal{W}}$.

• We define $\varphi: \mathcal{W}\rightarrow \mathbb{R}^{+}$ by

  $$\displaystyle{ \varphi \left (w\right ) = \frac{1} {2}\left (1 +\exp \left [-2\beta h\ell\left (w\right ) - 2\beta \sigma \left (w\right )\right ]\right ),\ \phi \mathop{=}\limits^{\mathrm{ def}}\log \varphi }$$

  (16)

  Occasionally, we emphasize the dependence on β, h by writing $\varphi _{\beta,h}$, ϕ _β, h .

• The concatenation map attaches to a finite or infinite sequence $\mathbf{w} = \left (w_{1},w_{2},\ldots \right )$ of words the corresponding sequence of real numbers: $\mathop{\mathrm{{\ast}}}\nolimits co: \mathcal{W}^{\mathbb{N}} \rightarrow \mathbb{R}^{\mathbb{N}}:$ If $w_{i} = \left (x_{i,1},x_{i,2},\ldots,x_{i,n_{i}}\right )$ then $\mathop{\mathrm{{\ast}}}\nolimits co\left (w_{1},w_{2},\ldots \right ) = \left (x_{1,1},\ldots,x_{1,n_{1}},x_{2,1},\ldots,x_{2,n_{2}},x_{3,1},\ldots \right ).$ In case of a finite sequence of words, $\mathop{\mathrm{{\ast}}}\nolimits co$ maps $\mathcal{W}^{n}$ to $\mathcal{W}$.

• $\mathcal{P}^{\mathrm{inv}}$ denotes the set of stationary probability measures on $\left (\mathcal{W}^{\mathbb{N}},\mathcal{B}_{\mathcal{W}}^{\otimes \mathbb{N}}\right ).$

• For $Q \in \mathcal{P}^{\mathrm{inv}},$ m _Q is the average length of the words under Q. m _Q may be infinite. $\mathcal{P}^{\mathrm{inv,\ fin}}$ is the set of measures in $\mathcal{P}^{\mathrm{inv}}$ for which m _Q is finite.

• For $Q \in \mathcal{P}^{\mathrm{inv}}$ $Q\mathop{\mathrm{{\ast}}}\nolimits co^{-1}$ is a probability measure on $\mathbb{R}^{\mathbb{N}}$. It is fairly evident that, in general, it will not be stationary. In order to get a stationary measure, one has to do an averaging procedure which requires that m _Q  < ∞. In this case we define can define a mapping $\Psi _{Q}: \mathcal{P}^{\mathrm{inv}} \cap \left \{Q: m_{Q} < \infty \right \}\rightarrow \mathcal{P}^{\mathrm{inv}}\left (\mathbb{R}^{\mathbb{N}}\right )$ by

  $$\displaystyle{\Psi _{Q} = \frac{1} {m_{Q}}E_{Q}\left (\sum \nolimits _{k=0}^{\tau _{1}-1}\delta _{ \theta ^{\kappa }\mathop{ \mathrm{{\ast}}}\nolimits co\left (Y \right )}\right ).}$$

  τ ₁: the length of the first word of $Y \in \mathcal{W}^{\mathbb{N}}.\ \theta$ is the shift operation on $\mathbb{R}^{\mathbb{N}}.$

Consider now a probability distribution ν on $\mathbb{R}$, and a sequence $\boldsymbol{\omega }= \left \{\omega _{n}\right \}$ of i.i.d. random variables distributed according to ν. We write $\mathbb{P}$ for $\nu ^{\otimes \mathbb{N}}$. Then consider also a probability measure ρ on $\mathbb{N}$ and a sequence $\left \{\zeta _{n}\right \}$ of i.i.d. random variables distributed according to ρ, and write $\tau _{0}\mathop{ =}\limits^{\mathrm{ def}}0,\ \tau _{n}\mathop{ =}\limits^{\mathrm{ def}}\sum _{i=1}^{n}\tau _{i}.$ As before we write τ for the collection $\left \{\tau _{i}\right \}$ of the renewal points. We write P for the law governing this renewal sequence. Together with $\boldsymbol{\omega }$ this defines a sequence of words $W\left (\left (\boldsymbol{\omega },\tau \right )\right )\mathop{ =}\limits^{\mathrm{ def}}\left \{w_{n}\left (\boldsymbol{\omega },\tau \right )\right \}_{n\geq 1}$ by

$$\displaystyle{w_{n}\left (\boldsymbol{\omega },\tau \right )\mathop{ =}\limits^{\mathrm{ def}}\left (\omega _{\tau _{n-1}+1},\ldots,\omega _{\tau _{n}}\right ).}$$

Fixing N we consider the periodized sequence of words

$$\displaystyle{W_{N}\mathop{ =}\limits^{\mathrm{ def}}\left (w_{1},w_{2},\ldots,w_{N},w_{1},w_{2},\ldots \right ),}$$

and for 0 ≤ n ≤ N − 1 the shifts θ _n W _N of this sequence. The empirical distribution is then defined by

$$\displaystyle{L_{N}\left (\boldsymbol{\omega },\tau \right )\mathop{ =}\limits^{\mathrm{ def}} \frac{1} {N}\sum _{n=0}^{N-1}\delta _{ \theta _{n}W_{N}\left (\boldsymbol{\omega },\tau \right )}.}$$

Evidently, $L_{N}\left (\boldsymbol{\omega },\tau \right )$ is a random element in $\mathcal{P}^{\mathrm{inv}}$.

As usual in disordered systems, one has two natural situations to consider. First, the so-called quenched law is the law of $L_{N}\left (\boldsymbol{\omega },\tau \right )$ for fixed $\boldsymbol{\omega }$ under the probability measure P for the renewal sequence τ. One then tries to obtain properties of L _N in the N → ∞ limit which hold for $\mathbb{P}$-almost all $\boldsymbol{\omega }$. The averaged or annealed law of L _N is obtained under the product measure $\mathbb{P} \otimes P$.

For given ν, ρ we consider the probability q _ρ, ν on $\mathcal{W}$: The distribution of the length of the word is given by ρ, and conditionally on the length $\left \{\ell= k\right \}$ the distribution of the “letters” is the k-fold product of ν, i.e.

$$\displaystyle{q_{\rho,\nu }\left (d\left (x_{1},\ldots,x_{n}\right )\right ) =\rho \left (n\right )\prod _{i=1}^{n}\nu \left (dx_{ i}\right ).}$$

We also need the specific relative entropy $H\left (Q\vert q_{\rho,\nu }^{\otimes \mathbb{N}}\right )$ for $Q \in \mathcal{P}^{\mathrm{inv}}$ defined by

$$\displaystyle{H\left (Q\vert q_{\rho,\nu }^{\otimes \mathbb{N}}\right )\mathop{ =}\limits^{\mathrm{ def}}\lim _{ N\rightarrow \infty } \frac{1} {N}I\left (Q_{N}\vert q_{\rho,\nu }^{\otimes N}\right ),}$$

where Q _N is the marginal of Q on the first N components, and $I\left (\cdot \vert \cdot \right )$ is the usual relative entropy (or Kullback-Leibler information). The sequence $N^{-1}I\left (Q_{N}\vert q_{\rho,\nu }^{\otimes N}\right )$ is increasing in N. In particular, it follows that

$$\displaystyle{ H\left (Q\vert q_{\rho,\nu }^{\otimes \mathbb{N}}\right ) \geq I\left (Q_{ 1}\vert q_{\rho,\nu }\right ) }$$

(17)

The quenched LDP by Birkner [3] goes as follows:

Theorem 9 (Birkner)

Assume that ρ has an exponential moment, i.e. that for some α > 0

$$\displaystyle{\sum _{n}\mathrm{e}^{\alpha n}\rho \left (n\right ) < \infty.}$$

For $\mathbb{P}$ -almost all ω, L _N satisfies a good LDP with rate function

$$\displaystyle{I_{\mathrm{Birkner}}^{\mathrm{qu}}\left (Q\right )\mathop{ =}\limits^{\mathrm{ def}}\left \{\begin{array}{cc} H\left (Q\vert q_{\rho,\nu }^{\otimes \mathbb{N}}\right )&\mathrm{if\ }\Psi _{ Q} =\nu ^{\otimes \mathbb{N}} \\ \infty & \mathrm{if\ }\Psi _{Q}\neq \nu ^{\otimes \mathbb{N}} \end{array} \right..}$$

This LDP is crucial for the application in [10], but it’s direct use is limited, first by the assumption that ρ has an exponential moment, and secondly, by the somewhat complicated definition of the rate function. The condition on $\Psi _{Q} =\nu ^{\otimes \mathbb{N}}$ makes the application quite difficult.

The LDP was extended in [4] to the case where ρ has polynomial tails. The formulation needs quite some care, mainly as the rate function may be finite for measures Q with m _Q  = ∞. 

Theorem 10 (Birkner, Greven, den Hollander)

Assume that ρ satisfies (4) with 1 < α < ∞. Then, for $\mathbb{P}$ -almost all ω, L _N satisfies a good LDP with a rate function I ^qu given in the following way. If m _Q < ∞, then

$$\displaystyle{I^{\mathrm{qu}}\left (Q\right ) = H\left (Q\vert q_{\rho,\nu }^{\otimes \mathbb{N}}\right ) + \left (\alpha -1\right )m_{ Q}H\left (\Psi _{Q}\vert \nu ^{\otimes \mathbb{N}}\right ).}$$

If m _Q = ∞ then

$$\displaystyle{I^{\mathrm{qu}}\left (Q\right ) =\lim _{ n\rightarrow \infty }I^{\mathrm{qu}}\left (\left [Q\right ]_{ n}\right ).}$$

Here $\left [Q\right ]_{n}$ is the induced measure under the truncation map $\mathbf{w} = \left (w_{1},w_{2},\ldots \right ) \in \mathcal{W}^{\mathbb{N}} \rightarrow \left [\mathbf{w}\right ]_{n} = \left (\left [w_{1}\right ]_{n},\left [w_{2}\right ]_{n},\ldots \right ),$ $\left [w\right ]_{n}$ obtained by truncating the word w at length n.

Remark 11

The averaged version of the above LDP is a standard result in large deviation theory: Under the joint law $\mathbb{P} \otimes P$, $\left \{L_{n}\right \}$ satisfies a good LDP with rate function $H\left (Q\vert \nu _{\rho }^{\otimes \mathbb{N}}\right ).$ This is the standard Donsker-Varadhan “level 3” LDP. See for instance [18]. The nice feature of the Birkner-Greven-den Hollander LDP is that it gives a fairly concrete expression $\left (\alpha -1\right )m_{Q}H\left (\Psi _{Q}\vert \nu ^{\otimes \mathbb{N}}\right )$ for the difference between the annealed and the quenched situation.

We will not prove these results here. A good outline is given in the introduction of [4]. Roughly, the explanation for the term $\left (\alpha -1\right )m_{Q}H\left (\Psi _{Q}\vert \nu ^{\otimes \mathbb{N}}\right )$ is like follows. In order to achieve L _N  ≈ Q in the quenched situation, i.e. with $\boldsymbol{\omega }$ fixed, one has either $\Psi _{Q} =\nu ^{\otimes \mathbb{N}},$ in which case $H\left (\Psi _{Q}\vert \nu ^{\otimes \mathbb{N}}\right ),$ and the probability is just $\approx \exp \left [-NH\left (Q\vert q_{\rho,\nu }^{\otimes \mathbb{N}}\right )\right ]$, as in the Birkner case, or the renewal process has to first make a big first step to in one (or very few) jumps, in order to reach a portion of the sequence $\boldsymbol{\omega }$ which looks typically under $\Psi _{Q}$. Such a jump has to be exponentially long in N, and if the renewal sequence is coming from i.i.d. variables ζ _i having an exponential tail, this would cost double exponential, and would not be possible. Therefore, in the Birkner LDP, one just has a rate function which is ∞ in case $\Psi _{Q}\neq \nu ^{\otimes \mathbb{N}}$. However, in the case of polynomial tails, such an exponential excursion costs only an exponential price, and therefore, it is of the appropriate order for a LDP. At first sight, one may think that for $\rho \left (n\right ) \approx n^{-\alpha }$ the price should come with a factor α and not α − 1. The reason that the correction is given as $\left (\alpha -1\right )m_{Q}H\left (\Psi _{Q}\vert \nu ^{\otimes \mathbb{N}}\right )$ is coming from an entropic gain in the relation $Q \leftrightarrow \Psi _{Q}$. This is somewhat difficult to see in the general picture, but it also appears in the more elementary computation done here in Sect. 6.

Proposition 12

Assume that $Q \in \mathcal{P}^{\mathrm{inv}}$ satisfies $I^{\mathrm{qu}}\left (Q\right ) < 0.$ Then there exists a sequence $\left \{Q_{n}\right \} \subset \mathcal{P}^{\mathrm{inv}}$ which satisfies $\Psi _{Q_{n}} =\nu ^{\otimes \mathbb{N}}$ which weakly converges to Q and which satisfies

$$\displaystyle{\lim _{n\rightarrow \infty }H\left (Q_{n}\vert \nu _{\rho }^{\otimes \mathbb{N}}\right ) = I^{\mathrm{qu}}\left (Q\right ).}$$

The statement looks at first sight strange, as it claims that the crucial second summand in $I^{\mathrm{qu}}\left (Q\right )$ is produced by an approximation where it is 0. The proposition is however at the very heart of the application to the copolymer, and we give the details of the proof. The result is not stated exactly in this form in [4], but it comes out from considerations done there.

We come now to the application to the copolymer.

The starting point is to not look first at a fixed end point but investigate what happens with a fixed number N of excursions. We also need an artificial “killing” parameter g ≥ 0. Let

$$\displaystyle{F_{N,g,\beta,h}\left (\omega \right ) =\sum _{0<k_{1}<\cdots <k_{N}}\prod _{i=1}^{N}\rho \left (k_{ i} - k_{i-1}\right )\mathrm{e}^{-g\left (k_{i}-k_{i-1}\right )}\prod _{ i=1}^{N}\varphi _{ \beta,h}\left (w_{i}\left (\omega \right )\right ),}$$

where

$$\displaystyle{w_{i}\left (\omega \right )\mathop{ =}\limits^{\mathrm{ def}}\left (\omega _{k_{i}+1},\ldots,\omega _{k_{i+1}}\right ),\ k_{0}\mathop{ =}\limits^{\mathrm{ def}}0}$$

Evidently, we have

$$\displaystyle{\sum _{n}\mathrm{e}^{-gn}\overline{Z}_{ n} =\sum _{N}F_{N,g},}$$

where $\overline{Z}_{n}$ is the partition function (7).

Lemma 13

• a)
  $$\displaystyle{s^{\mathrm{qu}}\left (\beta,h,g\right )\mathop{ =}\limits^{\mathrm{ def}}\lim _{ n\rightarrow \infty } \frac{1} {N}\log F_{N} =\lim _{n\rightarrow \infty } \frac{1} {N}\mathbb{E}\log F_{N}}$$

  exists, and is a convex function of g which is finite for g > 0. Particularly $g \rightarrow S^{\mathrm{qu}}\left (\beta,h,g\right )$ is continuous as a function of g on the positive axis, except possibly at g = 0.

• b) The free energy of the copolymer given by (6) is given by

  $$\displaystyle{f\left (\beta,h\right ) =\inf \left \{g \geq 0: s^{\mathrm{qu}}\left (\beta,h,g\right ) < 0\right \}.}$$

• c) $\left (\beta,h\right ) \in \mathcal{D}$ (see (9) ) if and only if

  $$\displaystyle{s^{\mathrm{qu}}\left (\beta,h,0+\right )\mathop{ =}\limits^{\mathrm{ def}}\lim _{ g\downarrow 0}s^{\mathrm{qu}}\left (\beta,h,g\right ) \leq 0.}$$

The proof of the finiteness of $s^{\mathrm{qu}}\left (\beta,h,g\right )$ for all g > 0 is quite tricky and involves some detailed estimates. From that, the rest of the lemma is quite straightforward. I difficult unsolved problem is the continuity at g = 0 which we expect to be correct but which we had been unable to prove. However, for the discussion of localization and delocalization in terms of the free energy, this is not important.

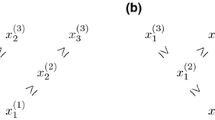
The critical point $h_{\mathrm{c}}^{\mathrm{qu}}\left (\beta \right )$ is therefore characterized by the following pictures:

The main result in [10] is the following variation formula:

Theorem 14

• a) If g > 0 then $s^{\mathrm{qu}}\left (\beta,h,g\right ) = s_{\mathrm{\mathop{\mathrm{{\ast}}}\nolimits var}}^{\mathrm{qu}}\left (\beta,h,g\right )$ where

  $$\displaystyle{s_{\mathrm{\mathop{\mathrm{{\ast}}}\nolimits var}}^{\mathrm{qu}}\left (\beta,h,g\right ) =\sup _{ Q\in \mathcal{P}^{\mathrm{inv},\mathrm{fin}}\cap \mathcal{R}}\left [\int \phi _{\beta,h}\left (w\right )Q\pi _{1}^{-1}\left (dw\right ) - gm_{ Q} - H\left (Q\vert q_{\rho,\nu }^{\mathbb{N}}\right )\right ],}$$

  where $\mathcal{R}\mathop{ =}\limits^{\mathrm{ def}}\left \{Q \in \mathcal{P}^{\mathrm{inv}}: \Psi _{Q} =\nu ^{\otimes \mathbb{N}}\right \},$ and where $\pi _{1}: \mathcal{W}^{\mathbb{N}} \rightarrow \mathcal{W}$ is the projection on the first factor. (Remember that $\ell\left (w\right )$ is the length of a word w, and $\sigma \left (w\right ) =\sum _{ i=1}^{\ell\left (w\right )}x_{i}$ when $w = \left (x_{1},\ldots,x_{\ell\left (w\right )}\right ).$ )

• b) $g \rightarrow s_{\mathrm{\mathop{\mathrm{{\ast}}}\nolimits var}}^{\mathrm{qu}}\left (\beta,h,g\right )$ is convex and continuous on [0,∞) (possibly ∞ at g = 0).

• c) At g = 0, we have the alternative variational characterization

  $$\displaystyle\begin{array}{rcl} s_{\mathrm{\mathop{\mathrm{{\ast}}}\nolimits var}}^{\mathrm{qu}}\left (\beta,h,0\right )& =& \sup _{ Q\in \mathcal{P}^{\mathrm{inv},\mathrm{fin}}}\Big[\int \phi _{\beta,h}\left (w\right )Q\pi _{1}^{-1}\left (dw\right ) {}\\ & & -H\left (Q\vert q_{\rho,\nu }^{\mathbb{N}}\right ) -\left (\alpha -1\right )m_{ Q}H\left (\Psi _{Q}\vert \nu ^{\otimes \mathbb{N}}\right )\Big]. {}\\ \end{array}$$

Part (a) follows from an application of Theorem 9, given the estimates one has to prove $s^{\mathrm{qu}}\left (\beta,h,g\right ) < \infty$. As it is, it is not very useful because the set $\mathcal{R}$ is not very easy to handle. The continuity of $s_{\mathrm{\mathop{\mathrm{{\ast}}}\nolimits var}}^{\mathrm{qu}}\left (\beta,h,g\right )$ at g = 0 and the alternative description of $s_{\mathrm{\mathop{\mathrm{{\ast}}}\nolimits var}}^{\mathrm{qu}}\left (\beta,h,0\right )$ in terms of the variational formula from Theorem 10 was the main and most complicated task in [10].

Corollary 15

$$\displaystyle{\left (\beta,h\right ) \in \mathcal{D}\Longleftrightarrow s_{\mathrm{\mathop{\mathrm{{\ast}}}\nolimits var}}^{\mathrm{qu}}\left (\beta,h,0\right ) \leq 0.}$$

A consequence of the above corollary is the following result on the behavior of $h_{\mathrm{c}}^{\mathrm{qu}}\left (\beta \right )$.

Theorem 16

• a) $h_{\mathrm{c}}^{\mathrm{qu}}\left (\beta \right ) > h_{\mathrm{c}}^{\mathrm{ann}}\left (\frac{\beta }{\alpha }\right )$ for all β > 0,α > 1 and $\kappa \left (\alpha \right ) > 1/\alpha.$ For 1 < α < 2, the lower bound for the slope is

  $$\displaystyle{\kappa \left (\alpha \right ) \geq B\left (\alpha \right )/\alpha,}$$

  where $B\left (\alpha \right ) > 1.$ (The exact bound is given in Sect.  6 .)

• b) $h_{\mathrm{c}}^{\mathrm{qu}}\left (\beta \right ) < h_{\mathrm{c}}^{\mathrm{ann}}\left (\beta \right )$ for all β,α > 1.

The result in (b) has been proved also by Toninelli [31] using a fractional moment bound. Toninelli’s method also proves $\kappa \left (\alpha \right ) < 1$ which is unfortunately not (yet) coming out from our bound. Although, at the moment, the LDP method does not prove $\kappa \left (\alpha \right ) < 1$, I believe that it gives considerable insights, and probably will be improved in the course of time.²

We prove part (a) in a completely self-contained way in the next chapter. The argument there is essentially the one given in [10], but bypassing the somewhat heavy large deviation machinery.

Proof of Theorem 16(b)

From (17) it follows that

$$\displaystyle{ H\left (Q\vert q_{\rho,\nu }^{\mathbb{N}}\right ) \geq I\left (Q_{ 1}\vert q_{\rho,\nu }\right ),\ H\left (\Psi _{Q}\vert \nu ^{\mathbb{N}}\right ) \geq I\left (\left (\Psi _{ Q}\right )_{1}\vert \nu \right ), }$$

(18)

where Q ₁ is the first marginal of Q and $\left (\Psi _{Q}\right )_{1}$ the marginal of the first component of $\Psi _{Q}.$ So, we get

$$\displaystyle{s_{\mathrm{\mathop{\mathrm{{\ast}}}\nolimits var}}^{\mathrm{qu}}\left (\beta,h,0\right ) \leq \sup _{ q:m_{q}<\infty }\Big[\int q\left (dw\right )\phi _{\beta,h}\left (w\right ) - I\left (q\vert q_{\rho,\nu }\right ) -\left (\alpha -1\right )m_{q}h\left (\pi \left (q\right )\vert \nu \right )\Big].}$$

The supremum is over probability measures on the set of words. $\pi \left (q\right )$ is the first marginal of $\Psi _{q^{\otimes \mathbb{N}}}.$ It is obtained by averaging properly over the marginals measures of q. Actually, as q _ρ, ν , conditioned on the length of the words being n, is invariant under the (cyclic) permutation mappings $\mathbb{R}^{n} \rightarrow \mathbb{R}^{n}$, one can restrict the above supremum to q which have the same invariance property. Then $\pi \left (q\right ) =\sum _{n}\left (q^{\left (n\right )}\right )_{1}$, where $q^{\left (n\right )}$ is the restriction of q to words of length n. 

We define the measure q ^∗ on $\mathcal{W}$ by

$$\displaystyle{q_{\beta,h}^{{\ast}} = \frac{1} {z\left (\beta,h\right )}\varphi _{\beta,h}dq_{\rho,\nu },}$$

with

$$\displaystyle{z\left (\beta,h\right ) =\int \varphi _{\beta,h}dq_{\rho,\nu } = \frac{1} {2} + \frac{1} {2}\sum _{m}\rho \left (m\right )\mathrm{e}^{-2\beta hm}\left (\int \mathrm{e}^{-2\beta x}q\left (dx\right )\right )^{m}}$$

which is finite for $h \geq h_{\mathrm{cr}}^{\mathrm{\mathrm{ann}}}\left (\beta \right ).$ So q ^∗ is well defined for these values. Remark that $z\left (\beta,h_{\mathrm{cr}}^{\mathrm{\mathrm{ann}}}\left (\beta \right )\right ) = 1.$ We use

$$\displaystyle\begin{array}{rcl} I\left (q\vert q_{\rho,\nu }\right )& =& I\left (q\vert q_{\beta,h}^{{\ast}}\right ) -\log z\left (\beta,h\right ) +\int \log \varphi _{\beta,h}\left (w\right )q\left (dw\right ) {}\\ & =& I\left (q\vert q_{\beta,h}^{{\ast}}\right ) -\log z\left (\beta,h\right ) +\int \phi _{\beta,h}\left (w\right )q\left (dw\right ). {}\\ \end{array}$$

(Remember that $\phi =\log \varphi$, (16).) Therefore

$$\displaystyle{s_{\mathrm{\mathop{\mathrm{{\ast}}}\nolimits var}}^{\mathrm{qu}}\left (\beta,h,0\right ) \leq \log z\left (\beta,h\right ) -\inf _{ q:m_{q}<\infty }\left [I\left (q\vert q_{\beta,h}^{{\ast}}\right ) + \left (\alpha -1\right )m_{ q}h\left (\pi \left (q\right )\vert \nu \right )\right ].}$$

At $h = h_{\mathrm{cr}}^{\mathrm{\mathrm{ann}}}\left (\beta \right ),$ $\log z\left (\beta,h\right ) = 0$, and one easily sees that the infimum is positive. The first part $I\left (q\vert q_{\beta,h}^{{\ast}}\right )$ has its infimum at q = q _β, h ^∗, but it’s evident that the marginal $\pi \left (q_{\beta,h}^{{\ast}}\right )\neq \nu.$ Therefore

$$\displaystyle{s_{\mathrm{\mathop{\mathrm{{\ast}}}\nolimits var}}^{\mathrm{qu}}\left (\beta,h_{\mathrm{ cr}}^{\mathrm{\mathrm{ann}}}\left (\beta \right ),0\right ),}$$

and so it follows that $h_{\mathrm{cr}}\left (\beta \right ) < h_{\mathrm{cr}}^{\mathrm{\mathrm{ann}}}\left (\beta \right ).$ ■ 

Remark 17

One of course hopes that this would lead to κ < 1, but unfortunately, it is not true. One can prove that with the bound for $h_{\mathrm{cr}}\left (\beta \right )$ one obtains from this estimate, say $h^{{\ast}}\left (\beta \right )$, it holds that

$$\displaystyle{\lim _{\beta \rightarrow 0}\frac{h^{{\ast}}\left (\beta \right )} {\beta } = 1.}$$

So, although the rather crude estimates (18) are good enough to prove $h_{\mathrm{cr}}\left (\beta \right ) < h_{\mathrm{cr}}^{\mathrm{\mathrm{ann}}}\left (\beta \right ),$ they are not good enough for $\kappa \left (\alpha \right ) < 1$.

6 A Proof of a Lower Bound

I give here a self-contained proof of the lower bound of Theorem 16(a). It does not use the variational formula from Theorem 14, but it is very much inspired by it.

For convenience, we take ν coin tossing, i.e. $E = \left \{-1,1\right \} \subset \mathbb{R},$ and $\nu \left (1\right ) =\nu \left (-1\right ) = 1/2$. Given $K \in \mathbb{N}$, we write $\mathcal{W}_{K}$ for the set of words of length ≤ K.

We make the following assumptions

• The $\rho \left (n\right ) > 0$ for all $n \in \mathbb{N}$ and

  $$\displaystyle{\lim _{n\rightarrow \infty }\frac{-\log \rho \left (n\right )} {\log n} =\alpha \in \left (1,\infty \right )}$$

• μ is a probability measure on $\mathcal{W}_{K}$ for some $K \in \mathbb{N}$, and that all words in $\mathcal{W}_{K}$ have positive weight.

We write m _μ for the mean word length under μ: 

$$\displaystyle{m_{\mu } =\sum _{w\in \mathcal{W}_{K}}\ell\left (w\right )\mu \left (w\right ).}$$

Proposition 18

If there exists μ such that

$$\displaystyle{\int \phi _{\beta,h}\left (w\right )\mu \left (dw\right ) >\alpha I\left (\mu \vert q_{\rho,\nu }\right ),}$$

then $f\left (\beta,h\right ) > 0.$

Remark that $q_{\rho,\nu }\left (w\right ) > 0$ for all words, as we have assumed that $\rho \left (n\right ) > 0$ for all n. Therefore, $I\left (\mu \vert q_{\rho,\nu }\right ) < \infty$.

$$\displaystyle\begin{array}{rcl} I\left (\mu \vert q_{\rho,\nu }\right )& =& \sum _{w\in \mathcal{W}_{K}}\mu \left (w\right )\log \frac{\mu \left (w\right )} {q_{\rho,\nu }\left (w\right )} \\ & =& -h\left (\mu \right ) -\sum _{k=1}^{K}\sum _{ w:\ell\left (w\right )=k}\mu \left (w\right )\log \left (\rho \left (k\right )2^{-k}\right ) \\ & =& -h\left (\mu \right ) -\sum _{w\in \mathcal{W}_{K}}\mu \left (w\right )\log \rho \left (\ell\left (w\right )\right ) + m_{\mu }\log 2, {}\end{array}$$

(19)

where

$$\displaystyle{h\left (\mu \right ) = -\sum _{w\in \mathcal{W}_{K}}\mu \left (w\right )\log \mu \left (w\right ).}$$

Let $\mathcal{S}_{K}$ be the set of all finite sentences with words in $\mathcal{W}_{K}$, i.e. the set of finite length sequences of words in $\mathcal{W}_{K}$.

We define probability measures Q _n on $\mathcal{S}_{K}$ which have the additional parameter $n \in \mathbb{N}$. For that, we define probability measures χ _n on $\mathbb{N}$ by

$$\displaystyle{\chi _{n}\left (k\right ) = 2^{-\left \vert k-n\right \vert }\left [3 - 2^{-n+1}\right ]^{-1},\ 1 \leq k < \infty.}$$

It is readily checked that

$$\displaystyle{\sum _{k}k\chi _{n}\left (k\right ) = n + O\left (2^{-n}\right ).}$$

(The law χ _n is essentially symmetric around n except for the truncation on the negative integers.)

We then define Q _n by

$$\displaystyle{Q_{n}\left (w_{1},\ldots,w_{k}\right )\mathop{ =}\limits^{\mathrm{ def}}\chi _{n}\left (k\right )\prod _{j=1}^{k}\mu \left (w_{ j}\right ).}$$

We denote the length of a sentence in $\mathcal{S}_{K}$, in terms of the number of words in it, by σ. This random variable has of course distribution χ _n under Q _n . 

For a word $\mathbf{x} = \left (x_{1},\ldots,x_{N}\right ),\ x_{i} \in E$, define $\mathcal{S}_{K}\left (\mathbf{x}\right )$ to be the set of sentences $\mathbf{w} \in \mathcal{S}_{K}$ with $\mathop{\mathrm{{\ast}}}\nolimits co\left (\mathbf{w}\right ) = \mathbf{x}$.

Below, we use C for a constant ≥ 1 which may depend on μ, but on nothing else, particularly not on n.

Lemma 19

Given N and two words $\mathbf{x} = \left (x_{1},\ldots,x_{N}\right ),$ and x ^′ which is obtained from x by adding one letter from E at an arbitrary place, one has

$$\displaystyle{ \frac{1} {C}Q_{n}\left (\mathcal{S}_{K}\left (\mathbf{x}^{{\prime}}\right )\right ) \leq Q_{ n}\left (\mathcal{S}_{K}\left (\mathbf{x}\right )\right ) \leq CQ_{n}\left (\mathcal{S}_{K}\left (\mathbf{x}^{{\prime}}\right )\right ).}$$

Proof

Let

$$\displaystyle{\mathbf{x}^{{\prime}} = \left (x_{ 1},\ldots,x_{i},y,x_{i+1},\ldots,x_{N}\right ).}$$

We define a mapping $f: \mathcal{S}_{K}\left (\mathbf{x}\right ) \rightarrow \mathcal{S}_{K}\left (\mathbf{x}^{{\prime}}\right )$. Let $\mathbf{w} = \left (w_{1},\ldots,w_{n}\right ) \in \mathcal{S}_{K}\left (\mathbf{x}\right )$ and w _j be the word which contains x _i . If w _j does not contain x _i+1, we simply add the word $\left (y\right )$ to w at the right place, and obtain $\mathbf{w}^{{\prime}}\in \mathcal{S}_{K}\left (\mathbf{x}^{{\prime}}\right )$. In case w _j contains x _i and x _i+1, and its length is less than K, we replace w _j by the word w _j ^′ which is obtained by adding the letter y at the right place. Again this leads to a $\mathbf{w}^{{\prime}}\in \mathcal{S}_{K}\left (\mathbf{x}^{{\prime}}\right )$. Finally, if w _j contains x _i and x _i+1 and has maximal length K, we split the word into $\left (\cdots \,,x_{i}\right )$ and $\left (x_{i+1},\cdots \,\right )$ and add y to the first one on the right side, and obtain a sentence $\mathbf{w}^{{\prime}}\in \mathcal{S}_{K}\left (x^{{\prime}}\right ).$ Then we put $f\left (\mathbf{w}\right ) = \mathbf{w}^{{\prime}}$. f is evidently injective and we have $Q_{n}\left (\mathbf{w}\right ) \leq CQ_{n}\left (f\left (\mathbf{w}\right )\right )$. Therefore

$$\displaystyle{\sum _{\mathbf{w}\in \mathcal{S}_{K}\left (\mathbf{x}\right )}Q_{n}\left (\mathbf{w}\right ) \leq C\sum _{\mathbf{w}\in \mathcal{S}_{K}\left (\mathbf{x}\right )}Q_{n}\left (f\left (\mathbf{w}\right )\right ) \leq C\sum _{\mathbf{w}^{{\prime}}\in \mathcal{S}_{K}\left (\mathbf{x}^{{\prime}}\right )}Q_{n}\left (\mathbf{w}^{{\prime}}\right ).}$$

We can also define a mapping $f^{{\prime}}: \mathcal{S}_{K}\left (\mathbf{x}^{{\prime}}\right ) \rightarrow \mathcal{S}_{K}\left (\mathbf{x}\right )$ by either shortening one word or deleting on (in case $\left (y\right )$ is a word in the sentence). This is not injective, but evidently, at maximum two sentences in $\mathcal{S}_{K}\left (\mathbf{x}^{{\prime}}\right )$ can be mapped to a single sentence in $\mathcal{S}_{K}\left (\mathbf{x}\right )$. Also, again $Q_{n}\left (\mathbf{w}^{{\prime}}\right ) \leq CQ_{n}\left (f\left (\mathbf{w}^{{\prime}}\right )\right )$ for some constant C. Therefore,

$$\displaystyle\begin{array}{rcl} \sum _{\mathbf{w}^{{\prime}}\in \mathcal{S}_{K}\left (\mathbf{x}^{{\prime}}\right )}Q_{n}\left (\mathbf{w}^{{\prime}}\right )& =& \sum _{\mathbf{ w\in }\mathcal{S}_{K}\left (\mathbf{x}\right )}\sum _{\mathbf{w}^{{\prime}}:f^{{\prime}}\left (\mathbf{w}^{{\prime}}\right )=\mathbf{w}}Q_{n}\left (\mathbf{w}^{{\prime}}\right ) {}\\ & \leq & C\sum _{\mathbf{w\in }\mathcal{S}_{K}\left (\mathbf{x}\right )}\sum _{\mathbf{w}^{{\prime}}:f^{{\prime}}\left (\mathbf{w}^{{\prime}}\right )=\mathbf{w}}Q_{n}\left (\mathbf{w}\right ) {}\\ & \leq & 2C\sum _{\mathbf{w\in }\mathcal{S}_{K}\left (\mathbf{x}\right )}Q_{n}\left (\mathbf{w}\right ). {}\\ \end{array}$$

By adjusting C, the claim follows. ■ 

We define $F: \mathcal{S}_{K} \rightarrow \mathbb{R}^{+}$ by

$$\displaystyle{F\left (\mathbf{w}\right )\mathop{ =}\limits^{\mathrm{ def}}Q_{n}\left (\mathcal{S}_{K}\left (\mathop{\mathrm{{\ast}}}\nolimits co\left (\mathbf{w}\right )\right )\right ).}$$

For $k \in \mathbb{N}$, we also write F _k for the restriction of F to $\mathcal{S}_{K}^{\left (k\right )}$, the sentences in $\mathcal{S}_{K}$ having exactly k words. Let d _H be the Hamming distance on $\mathcal{S}_{K}^{\left (k\right )}$, i.e.

$$\displaystyle{d_{H}\left (\mathbf{w},\mathbf{w}^{{\prime}}\right )\mathop{ =}\limits^{\mathrm{ def}}\#\left \{i: w_{ i}\neq w_{i}^{{\prime}}\right \}.}$$

An immediate corollary of Lemma 19 is

Lemma 20

• a) If $\mathbf{w},\mathbf{w}^{{\prime}}\in \mathcal{S}_{K}^{\left (k\right )}$ then

  $$\displaystyle{F_{k}\left (\mathbf{w}\right ) \leq C^{d_{H}\left (\mathbf{w},\mathbf{w}^{{\prime}}\right ) }F_{k}\left (\mathbf{w}^{{\prime}}\right ).}$$

• b) If $\mathbf{w} = \left (w_{1},\ldots,w_{k}\right ),\ \mathbf{w}^{{\prime}} = \left (w_{1},\ldots,w_{k},w_{k+1}\right ),$ then

  $$\displaystyle{ \frac{1} {C} \leq \frac{F_{k}\left (\mathbf{w}\right )} {F_{k+1}\left (\mathbf{w}^{{\prime}}\right )} \leq C.}$$

Corollary 21

There exists C > 0, depending only on K,μ, such that

$$\displaystyle{Q_{n}\left (\left \vert \log F - E_{Q_{n}}\log F\right \vert \geq t\right ) \leq C\left [\exp \left [- \frac{t^{2}} {Cn}\right ] +\exp \left [-\frac{\sqrt{n}} {C} \right ]\right ].}$$

Proof

$$\displaystyle\begin{array}{rcl} Q_{n}\left (\left \vert \log F - E_{Q_{n}}\log F\right \vert \geq t\right )& =& \sum _{k:\left \vert k-n\right \vert \leq \sqrt{n}}\chi _{n}\left (k\right )\mu ^{\otimes k}\left (\left \vert \log F_{ k} - E_{Q_{n}}\log F\right \vert \geq t\right ) {}\\ & & +C2^{-\sqrt{n}}, {}\\ \end{array}$$

and so we only have the estimate the first summands.

By one of the basic (end easily proved) concentration inequalities of Talagrand, see [29, Proposition 2.1.1], one has from Lemma 20(a)

$$\displaystyle{\mu ^{\otimes k}\left (\left \vert \log F_{ k} -\mathop{\mathrm{{\ast}}}\nolimits med\left (\log F_{k}\right )\right \vert \geq t\right ) \leq C\exp \left [- \frac{t^{2}} {Ck}\right ],}$$

where $\mathop{\mathrm{{\ast}}}\nolimits med\left (\log F_{k}\right )$ is any median of the distribution of logF _k under μ ^⊗k, and as this inequality also implies $\left \vert \mathop{\mathrm{{\ast}}}\nolimits med\left (\log F_{k}\right ) -\int \log F_{k}\ d\mu ^{\otimes k}\right \vert \leq C\sqrt{k}$, we can replace the median by the expectation under μ ^⊗k which we denote by E _k logF _k . However, from Lemma 20(b), we get

$$\displaystyle{\left \vert E_{k}\log F_{k} - E_{Q_{n}}\log F\right \vert \leq C\left \vert n - k\right \vert.}$$

As we have restricted k to an $\sqrt{n}$-neighborhood of n, we can estimate

$$\displaystyle\begin{array}{rcl} & & \mu ^{\otimes k}\left (\left \vert \log F_{ k} - E_{Q_{n}}\log F\right \vert \geq t\right ) {}\\ & & \quad \leq \mu ^{\otimes k}\left (\left \vert \log F_{ k} - E_{k}\log F_{k}\right \vert \geq \max \left (t - C\sqrt{n},0\right )\right ) {}\\ & & \quad \leq C\exp \left [-\frac{\max \nolimits ^{2}\left (t - C\sqrt{n},0\right )} {Cn} \right ], {}\\ \end{array}$$

and the right hand side is again estimated by $C\exp \left [-t^{2}/Cn\right ],$ by adjusting C. So the claim follows. ■ 

We fix n (large) and put $N\mathop{ =}\limits^{\mathrm{ def}}\left [nm_{\mu }\right ]$. For the rest of the proof, N will always be tied to n in this way. Then, consider the event

$$\displaystyle{A_{n}^{0}\mathop{ =}\limits^{\mathrm{ def}}\left \{\mathbf{w} \in \mathcal{S}_{ K}: \left \vert \log F\left (\mathbf{w}\right ) - E_{Q_{n}}\log F\right \vert \leq n^{3/4}\right \},}$$

and

$$\displaystyle\begin{array}{rcl} A_{n}& =& A_{n}^{0} \cap \left \{\mathbf{w}:\ell \left (\mathbf{w}\right ) = N\right \} \cap \left \{\left \vert \lambda \left (\mathbf{w}\right ) - n\right \vert \leq n^{3/4}\right \} {}\\ & & \quad \cap \left \{\left \Vert \frac{1} {n}\sum \nolimits _{i=1}^{\lambda }\delta _{ w_{i}}-\mu \right \Vert _{\mathrm{\mathop{\mathrm{{\ast}}}\nolimits var}} \leq n^{-1/4}\right \} {}\\ \end{array}$$

where for a finite sentence w we write $\ell\left (\mathbf{w}\right )$ for the sum of lengths of the words, $\lambda \left (\mathbf{w}\right )$ for the number of words in the sentence, and $\left \Vert \cdot \right \Vert _{\mathrm{\mathop{\mathrm{{\ast}}}\nolimits var}}$ denotes the total variation distance.

Below, we need

$$\displaystyle{ \gamma \left (\mu \right )\mathop{ =}\limits^{\mathrm{ def}} -\lim _{n\rightarrow \infty }\frac{1} {n}\log E_{Q_{n}}\log F. }$$

(20)

The proof of its existence is not difficult, but we don’t really need it. The right hand side stays trivially bounded as F ≤ 1 and $F\left (\mathbf{w}\right ) \geq Q_{n}\left (\mathbf{w}\right )$. All we need is the limit along an arbitrary subsequence, and we define $\gamma \left (\mu \right )$ to be the limit along such a subsequence. In all the arguments which follow, we always assume n to belong to this subsequence (if necessary). For notational convenience, we still use n instead. From $F\left (\mathbf{w}\right ) \geq Q_{n}\left (\mathbf{w}\right )$ we immediately get

$$\displaystyle{\gamma \left (\mu \right ) \leq h\left (\mu \right )\mathop{ =}\limits^{\mathrm{ def}}\sum _{w} -\mu \left (w\right )\log \mu \left (w\right )}$$

but we need a better bound later.

By a local CLT, one immediately sees that

$$\displaystyle{Q_{n}\left (\ell\left (\mathbf{w}\right ) = N\right ) \geq cn^{-1/2},}$$

and using the concentration inequality of the corollary, and large deviation estimates for $n^{-1}\sum \nolimits _{i=1}^{\lambda }\delta _{w_{i}}$, we also have

$$\displaystyle{ Q_{n}\left (A_{n}\right ) \geq cn^{-1/2}. }$$

(21)

It is straightforward to give an estimate of the number of elements in A _n :

Lemma 22

For fixed μ and n →∞

$$\displaystyle{\left \vert A_{n}\right \vert =\exp \left [nh\left (\mu \right ) + o\left (n\right )\right ].}$$

Proof

This is immediate from $Q_{n}\left (A_{n}\right ) =\exp \left [o\left (n\right )\right ]$, and from $Q_{n}\left (\mathbf{w}\right ) =\exp \left [-nh\left (\mu \right ) + o\left (n\right )\right ]$ which follows from $\left \vert \lambda \left (\mathbf{w}\right ) - n\right \vert \leq n^{3/4}$ and

$$\displaystyle{\left \Vert n^{-1}\sum \nolimits _{ i=1}^{\lambda }\delta _{ w_{i}}-\mu \right \Vert _{\mathrm{\mathop{\mathrm{{\ast}}}\nolimits var}} \leq n^{-1/4}.}$$

 ■ 

$X_{n}\mathop{ =}\limits^{\mathrm{ def}}\left \{\mathop{\mathrm{{\ast}}}\nolimits co\left (\mathbf{w}\right ): \mathbf{w} \in A_{n}\right \}$ is a subset of E ^N. For every x ∈ X _n , we write

$$\displaystyle{A_{n}\left (\mathbf{x}\right )\mathop{ =}\limits^{\mathrm{ def}}\left \{\mathbf{w} \in A_{n}:\mathop{ \mathrm{{\ast}}}\nolimits co\left (\mathbf{w}\right ) = \mathbf{x}\right \}.}$$

Lemma 23

There exists a subset $\hat{X}_{n} \subset X_{n}$ such that

$$\displaystyle{\left \vert \hat{X}_{n}\right \vert =\exp \left [\gamma \left (\mu \right )n + o\left (n\right )\right ],}$$

and

$$\displaystyle{\left \vert A_{n}\left (\mathbf{x}\right )\right \vert =\exp \left [\left [h\left (\mu \right ) -\gamma \left (\mu \right )\right ]n + o\left (n\right )\right ],}$$

uniformly in $\mathbf{x} \in \hat{ X}_{n}.$

Proof

If $\mathbf{x} =\mathop{ \mathrm{{\ast}}}\nolimits co\left (\mathbf{w}\right )$ for some w ∈ A _n ⁰, we have for

$$\displaystyle{\bar{A}_{n}\left (\mathbf{x}\right )\mathop{ =}\limits^{\mathrm{ def}}\left \{\mathbf{w} \in A_{n}^{0}:\mathop{ \mathrm{{\ast}}}\nolimits co\left (\mathbf{w}\right ) = \mathbf{x}\right \}}$$

that $Q_{n}\left (\bar{A}_{n}\left (\mathbf{x}\right )\right ) =\exp \left [-\gamma \left (\mu \right )n + o\left (n\right )\right ]$. Therefore

$$\displaystyle{ \left \vert X_{n}\right \vert \leq \exp \left [\gamma \left (\mu \right )n + o\left (n\right )\right ], }$$

(22)

and as $A_{n}\left (\mathbf{x}\right ) \subset \bar{ A}_{n}\left (\mathbf{x}\right )$, we get

$$\displaystyle{Q_{n}\left (A_{n}\left (\mathbf{x}\right )\right ) \leq \exp \left [-\gamma \left (\mu \right )n + o\left (n\right )\right ].}$$

Let $\varepsilon _{n} \rightarrow 0$ be a sequence of positive numbers such that $\varepsilon _{n}n \gg o\left (n\right )$ for the various $o\left (n\right )$-terms above. Then define

$$\displaystyle{\Gamma \mathop{ =}\limits^{\mathrm{ def}}\left \{\mathbf{x} \in X_{n}: Q_{n}\left (A_{n}\left (\mathbf{x}\right )\right ) \leq \exp \left [-\gamma \left (\mu \right )n -\varepsilon _{n}n\right ]\right \}.}$$

Then

$$\displaystyle\begin{array}{rcl} cn^{-1}& \leq & Q_{ n}\left (\bigcup \nolimits _{\mathbf{x}\in X_{n}}A_{n}\left (\mathbf{x}\right )\right ) \leq \left \vert \Gamma \right \vert \exp \left [-\gamma \left (\mu \right )n -\varepsilon _{n}n\right ] {}\\ & & +\left \vert X_{n}\setminus \Gamma \right \vert \exp \left [-\gamma \left (\mu \right )n + o\left (n\right )\right ] {}\\ & \leq & \exp \left [o\left (n\right ) -\varepsilon _{n}n\right ] + \left \vert X_{n}\setminus \Gamma \right \vert \exp \left [-\gamma \left (\mu \right )n + o\left (n\right )\right ], {}\\ \end{array}$$

the second inequality by (22), and therefore $\hat{X}_{n}\mathop{ =}\limits^{\mathrm{ def}}X_{n}\setminus \Gamma$ satisfies

$$\displaystyle{\left \vert \hat{X}_{n}\right \vert \geq cn^{-1}\exp \left [\gamma \left (\mu \right )n + o\left (n\right )\right ] =\exp \left [\gamma \left (\mu \right )n + o\left (n\right )\right ],}$$

and by construction, we have for any $\mathbf{x} \in \hat{ X}_{n}$

$$\exp \left [-\gamma \left (\mu \right )n -\varepsilon _{n}n\right ] \leq Q_{n}\left (A_{n}\left (\mathbf{x}\right )\right ) \leq \exp \left[-\gamma \left (\mu \right )n + o\left (n\right )\right].$$

On the other hand, for all elements $\mathbf{w} \in A_{n}\left (\mathbf{x}\right )$, we have

$$\displaystyle{Q_{n}\left (\mathbf{w}\right ) =\exp \left [-nh\left (\mu \right ) + o\left (n\right )\right ],}$$

and so the claim follows. ■ 

The above considerations lead to an estimate of $\gamma \left (\mu \right )$ which will be important below. To derive this, remark that for $\mathbf{x} \in \hat{ X}_{n}$, the set of words in $A_{n}\left (\mathbf{x}\right )$ is in one to one correspondence with a set of sequences $\mathbf{l} = \left (l_{1},\ldots,l_{\sigma }\right )$ of integers ≤ K,  n − n ^3∕4 ≤ k ≤ n + n ^3∕4, and $\sum _{i}l_{i} = N$ which defines the sequence of in $A_{n}\left (\mathbf{x}\right )$ through cutting $\mathbf{x} = \left (x_{1},\ldots,x_{N}\right )$ into the words $w_{1} = \left (x_{1},\ldots,x_{l_{1}}\right ),\ w_{2} = \left (x_{l_{1}+1},\ldots,x_{l_{1}+l_{2}}\right ),\ldots$. By an abuse of notation, we use $A_{n}\left (\mathbf{x}\right )$ also for this sequence of integer. Let ρ _μ be the distribution of $\ell\left (w\right )$ under μ. If $\mathbf{l} \in A_{n}\left (x\right )$, one has

$$\displaystyle{\#\left \{i: l_{i}\left (k\right ) = n\rho _{\mu }\left (k\right ) + o\left (n\right )\right \}.}$$

Therefore,

$$\displaystyle{\left \vert A_{n}\left (\mathbf{x}\right )\right \vert \leq \exp \left [nh\left (\rho _{\mu }\right ) + o\left (n\right )\right ],}$$

where

$$\displaystyle{h\left (\rho _{\mu }\right ) = -\sum _{k=1}^{K}\rho _{ \mu }\left (k\right )\log \rho _{\mu }\left (k\right )}$$

leading to

$$\displaystyle\begin{array}{rcl} h\left (\mu \right ) -\gamma \left (\mu \right )& \leq & h\left (\rho _{\mu }\right ), \\ \gamma \left (\mu \right )& \geq & h\left (\mu \right ) - h\left (\rho _{\mu }\right ).{}\end{array}$$

(23)

For $\mathbf{x} \in \hat{ X}_{n}$, we define $\xi _{n}\left (\mathbf{x}\right )$ as the partition function obtained through summation over $\mathbf{l} \in A_{n}\left (\mathbf{x}\right )$, i.e.

$$\displaystyle\begin{array}{rcl} \xi _{n}\left (\mathbf{x}\right )& =& \sum _{\mathbf{w}\in A_{n}\left (\mathbf{x}\right )}\prod _{j=1}^{\sigma \left (\mathbf{w}\right )}\rho \left (l_{ j}\right )\prod _{j=1}^{\sigma \left (\mathbf{w}\right )}\varphi \left (w_{ j}\right ) {}\\ & =& \sum _{\mathbf{w}\in A_{n}\left (\mathbf{x}\right )}\exp \left [\sum \nolimits _{j=1}^{\sigma \left (\mathbf{w}\right )}\log \rho \left (l_{ j}\right ) +\sum \nolimits _{ j=1}^{\sigma \left (\mathbf{w}\right )}\phi \left (w_{ j}\right )\right ]. {}\\ \end{array}$$

By the construction of $A_{n}\left (\mathbf{x}\right )$, we have for all $\mathbf{w} \in A_{n}\left (\mathbf{x}\right )$ and $\mathbf{x} \in \hat{ X}_{n}$

$$\displaystyle\begin{array}{rcl} \sum \nolimits _{j=1}^{\sigma \left (\mathbf{w}\right )}\log \rho \left (l_{ j}\right )& = n\sum _{w\in \mathcal{W}_{K}}\mu \left (w\right )\log \rho \left (\ell\left (w\right )\right ) + o\left (n\right )& {}\\ \sum \nolimits _{j=1}^{\sigma \left (\mathbf{w}\right )}\phi \left (w_{ j}\right )& = n\sum _{w\in \mathcal{W}_{K}}\mu \left (w\right )\phi \left (w\right ) + o\left (n\right ), & {}\\ \end{array}$$

and therefore

$$\displaystyle\begin{array}{rcl} \xi _{n}\left (\mathbf{x}\right )& =& \left \vert A_{n}\left (\mathbf{x}\right )\right \vert {}\\ & & \times \exp \left [n\left (\sum \nolimits _{w\in \mathcal{W}_{K}}\mu \left (w\right )\left (\log \rho \left (\ell\left (w\right )\right ) +\phi \left (w\right )\right )\right ) + o\left (n\right )\right ] {}\\ & =& \exp \Big[n\Big\{h\left (\mu \right ) -\gamma \left (\mu \right ) {}\\ & & +\sum \nolimits _{w\in \mathcal{W}_{K}}\mu \left (w\right )\left (\log \rho \left (\ell\left (w\right )\right ) +\phi \left (w\right )\right )\Big\} + o\left (n\right )\Big] {}\\ \end{array}$$

For a fixed sequence $\mathbf{x} \in E^{\mathbb{N}}$ we construct a lower bound for the partition function. This lower bound will depend on n besides of course on x. We first divide $\mathbb{N}$ into the intervals

$$\displaystyle{I_{j}\mathop{ =}\limits^{\mathrm{ def}}\left \{\left (j - 1\right )N + 1,\ldots,jN\right \},}$$

and write x _j for the restriction of x to I _j viewed as an element in E ^N. Then we write τ ₁ < τ ₂ < ⋯ for the successive occurrences of $\mathbf{x}_{\tau } \in \hat{ X}_{n}$. $\nu ^{\otimes \mathbb{N}}$-almost surely, all the τ _j are finite and the τ _j −τ _j−1 are i.i.d. geometrically distributed with success probabilities

$$\displaystyle{\delta _{n}\mathop{ =}\limits^{\mathrm{ def}}\frac{\left \vert \hat{X}_{n}\right \vert } {2^{N}} =\exp \left [\gamma \left (\mu \right )n - N\log 2 + o\left (n\right )\right ].}$$

For $T \in \mathbb{N}$, we define

$$\displaystyle{R_{T} =\max \left \{k:\tau _{k} < T\right \}.}$$

Then we get the lower bound for $Z_{NT}\left (\mathbf{x}\right ):$

$$\displaystyle{Z_{NT}\left (\mathbf{x}\right ) \geq \left (\frac{1} {2}\right )^{R_{T}+1}\prod _{ j=1}^{R_{T} }\rho \left (\left (\tau _{j} -\tau _{j-1}\right )N\right )\prod _{j=1}^{R_{T} }\xi _{n}\left (\mathbf{x}_{\tau _{j}}\right ).}$$

Therefore

$$\displaystyle\begin{array}{rcl} \frac{1} {NT}\log Z_{NT}\left (\mathbf{x}\right )& \geq & \frac{R_{T} + 1} {NT} \log \frac{1} {2} + \frac{1} {NT}\sum _{j=1}^{R_{T} }\log \rho \left (\left (\tau _{j} -\tau _{j-1}\right )N\right ) {}\\ & & + \frac{1} {NT}\sum _{j=1}^{R_{T} }\log \xi _{n}\left (\mathbf{x}_{\tau _{j}}\right ). {}\\ \end{array}$$

We let first T → ∞ with fixed (large) n. By the law of large numbers, one has for $\mu ^{\otimes \mathbb{N}}$-almost all $\mathbf{x} \in E^{\mathbb{N}}$

$$\displaystyle{\lim _{T\rightarrow \infty }\frac{R_{T}} {T} =\delta _{n}.}$$

So, the first summand on the right hand side above goes to

$$\displaystyle{ \frac{\delta _{n}} {N}\log \frac{1} {2} =\delta _{n}o\left (1\right ).}$$

and the third summand to

$$\displaystyle{ \frac{\delta _{n}} {m_{\mu }}\left [\left \{h\left (\mu \right ) -\gamma \left (\mu \right ) +\sum \nolimits _{w\in \mathcal{W}_{K}}\rho _{\mu }\left (k\right )\log \rho \left (k\right ) +\mu \left (\phi \right )\right \} + o\left (1\right )\right ].}$$

$o\left (1\right )$ here refers to n → ∞. Hence the first summand can be incorporated into the $o\left (1\right )$ summand above.

The second summand converges, as T → ∞, to

$$\displaystyle\begin{array}{rcl} \frac{\delta _{n}} {N}E\log \rho \left (\eta _{n}N\right )& =& -\alpha \frac{\delta _{n}} {N}\left (\log N + E\log \eta _{n}\right ) +\delta _{n}o\left (1\right ) {}\\ & =& -\alpha \frac{\delta _{n}} {N}E\log \eta _{n} +\delta _{n}o\left (1\right ) {}\\ & =& \alpha \frac{\delta _{n}} {N}\left [\gamma \left (\mu \right )n - N\log 2\right ] +\delta _{n}o\left (1\right ) {}\\ & =& \frac{\delta _{n}} {m_{\mu }}\left [\alpha \gamma \left (\mu \right ) -\alpha m_{\mu }\log 2\right ] +\delta _{n}o\left (1\right ) {}\\ \end{array}$$

where η _n is geometrically distributed with parameter δ _n . 

Therefore,

$$\displaystyle\begin{array}{rcl} \liminf _{T\rightarrow \infty } \frac{1} {NT}\log Z_{NT}\left (\mathbf{x}\right )& \geq & \frac{\delta _{n}} {m_{\mu }}\Big[\left (\alpha -1\right )\gamma \left (\mu \right ) -\alpha m_{\mu }\log 2 {}\\ & & +h\left (\mu \right ) +\sum \nolimits _{w\in \mathcal{W}_{K}}\rho _{\mu }\left (k\right )\log \rho \left (k\right ) +\mu \left (\phi \right ) + o\left (1\right )\Big] {}\\ & =& \frac{\delta _{n}} {m_{\mu }}\Big[\left (\alpha -1\right )\left [\gamma \left (\mu \right ) - m_{\mu }\log 2\right ] - I\left (\mu \vert q_{\rho,\nu }\right ) {}\\ & & +\mu \left (\phi \right ) + o\left (1\right )\Big]. {}\\ \end{array}$$

Using (23) $\gamma \left (\mu \right ) \geq h\left (\mu \right ) - h\left (\rho _{\mu }\right )$ and

$$\displaystyle{-h\left (\rho _{\mu }\right ) =\sum _{k}\rho _{\mu }\left (k\right )\log \rho _{\mu }\left (k\right ) \geq \sum _{k}\rho _{\mu }\left (k\right )\log \rho \left (k\right ),}$$

we get that the right hand side above is

$$\displaystyle\begin{array}{rcl} & & \geq \frac{\delta _{n}} {m_{\mu }}\left [\left (\alpha -1\right )\left [h\left (\mu \right ) - h\left (\rho _{\mu }\right ) - m_{\mu }\log 2\right ] - I\left (\mu \vert q_{\rho,\nu }\right ) +\mu \left (\phi \right ) + o\left (1\right )\right ] {}\\ & & \geq \frac{\delta _{n}} {m_{\mu }}\Bigg[\left (\alpha -1\right )\left [h\left (\mu \right ) +\sum _{k}\rho _{\mu }\left (k\right )\log \rho \left (k\right ) - m_{\mu }\log 2\right ] {}\\ & & \quad - I\left (\mu \vert q_{\rho,\nu }\right ) +\mu \left (\phi \right ) + o\left (1\right )\Bigg] {}\\ & & = \frac{\delta _{n}} {m_{\mu }}\left [\left (\alpha -1\right )\left [-I\left (\mu \vert q_{\rho,\nu }\right )\right ] - I\left (\mu \vert q_{\rho,\nu }\right ) +\mu \left (\phi \right )\right ] +\delta _{n}o\left (1\right ) {}\\ & & = \frac{\delta _{n}} {m_{\mu }}\left [\mu \left (\phi \right ) -\alpha I\left (\mu \vert q_{\rho,\nu }\right ) + o\left (1\right )\right ]. {}\\ \end{array}$$

Therefore, if $\mu \left (\phi \right ) -\alpha I\left (\mu \vert q_{\rho,\nu }\right ) > 0$ for large enough n. Therefore, we have proved Proposition 18.

Remark 24

• a) I would like to emphasize a tricky point in the above argument. At first sight, it appears that the rather trivial estimate (23) makes $\gamma \left (\mu \right )$ essentially useless. This is however not true as $\gamma \left (\mu \right )$ appears twice in the estimates above, leading in the end to the crucial fact that γ appears with a factor $\left (\alpha -1\right )$, in fact for the very same reason, of course, as α − 1 appears in the LDP in Theorem 10. Only after this partial cancellation, we use (23). The fact that $\gamma \left (\mu \right )$ enters twice, once with the factor − 1 and once with the factor α is due to the equipartition property of Lemma 23 which here is proved through the concentration of measure property in Corollary 21. In the general setup of [3, 4], this was proved via rather complicated arguments from a Shannon-McMillan-Breiman theorem, but here, as we just consider a product measure on the words, a simpler argument works.

• b) Without replacing $\gamma \left (\mu \right )$ by $h\left (\mu \right ) - h\left (\rho _{\mu }\right )$, the estimate would of course be better as, generally, $\gamma \left (\mu \right )\neq h\left (\mu \right ) - h\left (\rho _{\mu }\right )$. However, it seems to be difficult to evaluate $\gamma \left (\mu \right )$ precisely. Even if this could be done, the estimate above would most probably not give a sharp bound for $h_{\mathrm{cr}}\left (\beta \right )$. The sharp bound is of course encoded in the full large deviation principle given in Corollary 15 above, but there, an exact evaluation seems to be completely hopeless.

The above bound is sufficient to prove a lower bound for $h_{\mathrm{cr}}\left (\beta \right )$ of Theorem 16(a), which is strictly better than the Bodineau-Giacomin lower bound and also proves that the tangent at the origin is strictly bigger than 1∕α.

It is actually easy to determine what the optimal choice of μ is:

$$\displaystyle\begin{array}{rcl} \mu \left (w\right )& =& \frac{1} {z}\exp \left [\frac{1} {\alpha } \phi \left (w\right )\right ]q_{\rho,\nu }\left (w\right ) {}\\ & =& \frac{1} {z}\left [\frac{1} {2} + \frac{1} {2}\exp \left [-2\beta h\ell\left (w\right ) - 2\beta \sigma \left (w\right )\right ]\right ]^{1/\alpha }q_{\rho,\nu }\left (w\right ), {}\\ \end{array}$$

where z is the appropriate norming:

$$\displaystyle{z = z\left (\beta,h,\alpha \right ) =\sum _{\mathbf{w}}\left [\frac{1} {2} + \frac{1} {2}\exp \left [-2\beta h\ell\left (w\right ) - 2\beta \sigma \left (w\right )\right ]\right ]^{1/\alpha }q_{\rho,\nu }\left (w\right ).}$$

This choice does of course not satisfy the condition that it charges only words in $\mathcal{W}_{K}$ for some K, but a simple approximation which we leave to the reader shows that if

$$\displaystyle{\mu \left (\phi \right ) -\alpha I\left (\mu \vert q_{\rho,\nu }\right ) > 0}$$

for this μ, then it is also true for a suitably truncated distribution charging only words in $\mathcal{W}_{K}$ for some large enough K. 

For the above choice of μ, one has

$$\displaystyle{\mu \left (\phi \right ) -\alpha I\left (\mu \vert q_{\rho,\nu }\right ) =\alpha \log z,}$$

and therefore, we see that if

$$\displaystyle{\sum _{\mathbf{w}}\left [\frac{1} {2} + \frac{1} {2}\exp \left [-2\beta h\ell\left (w\right ) - 2\beta \sigma \left (w\right )\right ]\right ]^{1/\alpha }q_{\rho,\nu }\left (w\right ) > 1,}$$

one has $h_{\mathrm{cr}}\left (\beta \right ) > h$

Corollary 25

For all β > 0, one has

$$\displaystyle{h_{\mathrm{cr}}\left (\beta \right ) > h_{\mathrm{BG}}\left (\beta \right ) = \frac{\alpha } {2\beta }M\left (\frac{2\beta } {\alpha } \right ).}$$

Proof

$$\displaystyle{z\left (\beta,h_{\mathrm{BG}}\left (\beta \right ),\alpha \right ) =\sum _{x}q_{\rho,\nu }\left (x\right )\left \{\frac{1} {2}\left (1 + U\left (x\right )^{\alpha }\right )\right \}^{1/\alpha },}$$

where

$$\displaystyle{U\left (x\right ) =\exp \left [-\left (M\left (\frac{2\beta } {\alpha } \right )\ell\left (x\right ) + \frac{2\beta } {\alpha } \sigma \left (x\right )\right )\right ].}$$

Remark that

$$\displaystyle{\sum _{\mathbf{x}}q_{\rho,\nu }\left (x\right )U\left (x\right ) = 1}$$

by the definition of M. An elementary computation shows that

$$\displaystyle{f_{\alpha }\left (t\right )\mathop{ =}\limits^{\mathrm{ def}}\left \{\left (1 + t\right )^{\alpha }/2\right \}^{1/\alpha }}$$

is strictly convex on $\mathbb{R}^{+}$ for α > 1. Therefore

$$\displaystyle\begin{array}{rcl} z\left (\beta,h_{\mathrm{BG}}\left (\beta \right ),\alpha \right )& =& \sum _{\mathbf{x}}q_{\rho,\nu }\left (x\right )f_{\alpha }\left (U\left (x\right )\right ) > f_{\alpha }\left (\sum _{\mathbf{x}}q_{\rho,\nu }\left (x\right )U\left (x\right )\right ) {}\\ & =& f_{\alpha }\left (1\right ) = 1. {}\\ \end{array}$$

This proves the claim. ■ 

We next derive a lower bound for the tangent of $h_{\mathrm{cr}}\left (\beta \right )$ at the origin. To formulate the result, consider first the integral

$$\displaystyle{I_{\alpha }\left (b\right )\mathop{ =}\limits^{\mathrm{ def}}\int _{0}^{\infty }dy\ y^{-\alpha }\left [E\left (f_{\alpha }\left (\mathrm{e}^{-2by-2\sqrt{y}Z}\right )\right ) - 1\right ]}$$

where Z is a standard normal random variable. The integral is convergent for 1 < α < 2, and b ≥ 1. For y ∼ 0, the term in the square bracket is of order y, and so the integral converges near 0. At y ∼ ∞, we have

$$\displaystyle{Ef_{\alpha }\left (\mathrm{e}^{-2by-2\sqrt{y}Z}\right ) \leq \frac{1} {2^{1/\alpha }}\left (1 + E\mathrm{e}^{-2by-2\sqrt{y}Z}\right )}$$

which is bounded in y for b ≥ 1, and as α > 1, the integral converges at y ∼ ∞. For b = 1, one has

$$\displaystyle{E\left (f_{\alpha }\left (\mathrm{e}^{-2by-2\sqrt{y}Z}\right )\right ) > f_{\alpha }\left (E\mathrm{e}^{-2y-2\sqrt{y}Z}\right ) = f_{\alpha }\left (1\right ) = 1,}$$

and therefore

$$\displaystyle{I_{\alpha }\left (1\right ) > 0.}$$

On the other hand, it is easy to see that

$$\displaystyle{\lim _{b\rightarrow \infty }I_{\alpha }\left (b\right ) = -\infty,}$$

and that $I_{\alpha }\left (b\right )$ is continuous and strictly decreasing on $\left (1,\infty \right ).$ Therefore, there exists a unique $B = B\left (\alpha \right ) > 1$ with $I_{\alpha }\left (B\left (\alpha \right )\right ) = 0$.

Corollary 26

$$\displaystyle{\liminf _{\beta \rightarrow 0}\frac{h_{\mathrm{cr}}\left (\beta \right )} {\beta } \left \{\begin{array}{cc} \geq B\left (\alpha \right )&\mathrm{for\ }1 <\alpha < 2 \\ \geq \frac{1+\alpha } {2\alpha } & \mathrm{for\ }\alpha \geq 2 \end{array} \right..}$$

Proof

We prove only the first case as this disproves a long-standing conjecture by Cécile Monthus for the standard random walk case, i.e. α = 2∕3. We choose $1 < B < B\left (\alpha \right )$ and show that

$$\displaystyle{z\left (\beta, \frac{B\beta } {\alpha },\alpha \right ) > 1}$$

for all β > 0 small enough which implies the claim.

By an elementary substitution, we have

$$\displaystyle{z\left (\beta, \frac{B\beta } {\alpha },\alpha \right ) =\sum _{y\in \left (\frac{\beta }{\alpha }\right )^{2}\mathbb{N}}\rho \left (y\left (\frac{\alpha } {\beta }\right )^{2}\right )Ef_{\alpha }\left (Z_{ y,B}\right ),}$$

where

$$\displaystyle{Z_{y,B}\mathop{ =}\limits^{\mathrm{ def}}\exp \left [-2By - 2\sqrt{y}X_{y}\right ],}$$

and for i.i.d. symmetric coin tossing variables ξ _i

$$\displaystyle{X_{y} = \frac{\xi _{1} + \cdots \xi _{m}} {\sqrt{m}},\ m = \frac{y\alpha ^{2}} {\beta ^{2}}.}$$

If $\rho \left (k\right ) \sim Ak^{-\alpha }$, then a Riemann approximation, together with the CLT for X _y , yields

$$\displaystyle\begin{array}{rcl} & & \lim _{\beta \rightarrow 0} \frac{1} {\beta ^{2\left (\alpha -1\right )}}\left [z\left (\beta, \frac{B\beta } {\alpha },\alpha \right ) - 1\right ] {}\\ & & \quad = \frac{A} {\alpha ^{2\left (\alpha -1\right )}}\int _{0}^{\infty }dy\ y^{-\alpha }\left [E\left (f_{\alpha }\left (\mathrm{e}^{-2by-2\sqrt{y}Z}\right )\right ) - 1\right ] {}\\ & & \quad = I_{\alpha }\left (B\right ) > 0 {}\\ \end{array}$$

as $B < B\left (\alpha \right ).$ We therefore conclude that

$$\displaystyle{z\left (\beta, \frac{B\beta } {\alpha },\alpha \right ) > 1}$$

for small enough β > 0. ■ 

Remark 27

It should be remarked that the estimate on the tangent at the origin, which is in a way the main relevant object being “universal”, comes out from the improved estimate for the critical line. My feeling is that one is still quite far away from a thorough understanding of this tangent. It could well be that for β ∼ 0, there is some structural behavior which would allow to get the tangent explicitly.