1 Introduction

The analog circuit diagnosis methods are classified into two main categories [1, 2, 4, 10]: the simulation before test (SBT) and the simulation after test (SAT) approach. Since each circuit under test (CUT) consists of more than two test points, especially for the medium and large scale circuits, it’s impractical and too expensive to test the responses of all the test points to diagnose the faulty circuit. At the same time, not every test point is measurable and some measurements are redundant. Therefore, the optimum selection of test points is especially important. But in the integer-coded technique, the global minimum set of test points can only be guaranteed by the exhaustive search method (search every candidate test points and the combinations of them until all the listed faults are isolated), which has been proven to be NP-hard [15, 17]. If the optimal test points can be selected by other non-exhaustive way, the testing time will be reduced greatly.

The fault dictionary is a very important and practical method of SBT approach, especially in the diagnosing of catastrophic faults. A fault dictionary is a set of measurements of the CUT simulated under potentially faulty conditions (including fault-free case) and organized before the test. The measurements could be at different test points, test frequencies, and sampling times [17, 23]. There are three important phases in the fault dictionary approach [14]. First of all, a network is simulated for each of the anticipated faults (including fault-free case) excited by the chosen stimuli (dc or ac), and the signatures of the responses are stored and organized in the dictionary for use. In order to obtain obvious differences between the faulty conditions, choosing proper stimulus is still important. The genetic algorithm is used for choosing the optimum test stimulus in reference [3]. The second phase is the selection of test points. An optimum selection of test points is the main work of this stage. By doing this, we can achieve the desired degree of fault diagnosis with less test points and save the fault test and diagnosis time greatly. The last phase is fault isolation. At the time of testing, the CUT is excited by the same stimuli that are used in constructing the dictionary, and measurements are made at the preselected test points. They are compared with the responses stored in the fault dictionary to identify the fault according to the preset criteria. This is in essence a pattern recognition approach [8, 9]. This paper mainly focuses on the second phase.

The test-point selection problem for the analog circuit fault dictionary has been studied extensively in many papers. Varghese [21] proposed a heuristic method based on given performance indexes to find the sets of test points. Hochwald and Bastian [7] proposed the concept of ambiguity sets and developed logical rules to select the test points. Lin and Elcherif [10] proposed two heuristic methods based on the two criteria proposed by Hochwald and Bastian. Stenbakken and Souders [18] proposed QR factorization for the circuit sensitivity matrix. Spaandonk and Kevenaar [16] proposed to select the test-point set by combining the decomposition method of the system’s sensitivity matrix and an iterative algorithm. Prasad and Babu [14] proposed four algorithms based on three strategies of inclusive approach and three strategies of exclusive approach. Pinjala and Kim [13] proposed a method to find the test point set by computing the information content of all the candidate test points. An entropy-based approach was proposed by Starzyk [17] to select the near minimum test-point set. Golonek and Rutkowsk [5] used a genetic algorithm based method to determine the optimal set of test points. Yang and Tian [23] used the graph node search method to find the near minimum test-point set, and in paper [22], they proposed a more accurate fault-pair Boolean table technique, which overcame the shortcoming of not all the faults can be isolated by the traditional integer-coded table technique. Luo and Wang [11] discussed the voltage gap of ambiguity set, and proposed to determine the ambiguity gaps by the normal distribution characteristics. They used the extended fault dictionary and the overlapped area values together to select the test points. L. Milor and V. Visvanathan [6] proposed to select the test points in conjunction with the test generation algorithm and increase the accuracy of the test by using an iterative search technique. Stratigopoulos, H.-G.D.and Makris, Y [19] proposed to select the test points based on actual classification rates. Zhang and He [25] proposed a method based on fuzzy theory and ant colony algorithm to select the optimum test points of analog circuits.

The integer-coded fault dictionary technique was first proposed by Lin and Elcherif [10]. This technique has been proven to be an effective tool for the optimum test-point selection problem. The test-point selection algorithms in reference [5, 13, 14, 17, 23, 24] are all based on this technique. Therefore, the accuracy of these algorithms is closely related to the integer-coded fault dictionary. According to the existing methods, the different test points may be selected to construct the optimal test point set based on different criteria for the same CUT. A selected test-point set without redundant test points does not mean that this set is a minimum set. Seldom references are related to how to judge the effectiveness of the criterion until now. So the criterion is especially important for the test-point selection problem.

As discussed above, the ambiguity gap calculation method and the fault dictionary construction technique are the key to the problem. In reference [22], the authors chose the constant 0.2 V as the ambiguity gap, and demonstrated that the fault-pair Boolean table technique is more accurate than the integer-coded table technique. There are two different kinds of values in the fault-pair Boolean table (1 or 0). The value in the table equals to 1 represents that the corresponding test node can isolate this pair of faults, and 0 represents that the corresponding test node cannot isolate this pair of faults. However, the accuracy of their method is limited by the 0.2 V ambiguity gap criterion. In reference [11], the authors proposed to calculate the ambiguity gaps and the overlapped area values (represent the failure probability for ambiguity faults) based on the normal distribution principle, which overcame the disadvantage of keeping the ambiguity gap a constant value (such as 0.7 V or 0.2 V). This method can be considered as an extension of the integer-coded technique, and the accuracy of the method is also limited by the way of constructing the integer-coded fault table. In order to improve their methods and overcome the disadvantages of them, we combined the fault-pair concept in reference [22] and the ambiguity gaps calculation method in reference [11] together, defined a new way to calculate the fault-pair isolation capability of the test points, and developed a new test point selection method by the proposed fault-pair isolation table. Different values in the table have different meanings, and represent different fault pair isolation probability of the corresponding test point. It can be concluded that the bigger of the fault isolation probability value in the table, the more possibility to isolate this pair of faults. The results of the analog circuits’ examples and the statistical experiments in the paper show that the proposed method is effective, feasible and can improve the fault diagnosis performance.

For analog circuits, faults can be classified into two categories: catastrophic faults and parametric faults [12]. Since about 90 % of all the analog faults found in practice are single catastrophic faults [7, 23] and the components are always with parameter tolerance, single catastrophic faults with parameter tolerance in analog circuits are considered in this paper. Section 2 introduces the more accurate ambiguity gap calculation method based on the normal distribution, and the new proposed fault-pair isolation table that represents the fault isolation capability of the candidate test points is illustrated. The new proposed test point selection algorithm based on the fault-pair isolation table is given in this section as well. Section 3 gives two analog circuit examples to demonstrate the excellent performance of the proposed algorithm by comparing it with other reported algorithms. Statistical experiments are utilized for the evaluation of the final solution quality of the proposed algorithm in Section 4. Finally, brief conclusions are given in Section 5.

The nomenclatures of this paper are as follows:

nj :

The test point j

fi :

The fault i

NT :

Number of candidate test points

Nf :

Number of all the faults (including fault-free case)

Sopt :

Desired test point set

Sc :

Candidate test point set

NIi :

Number of test points that can isolate the ith fault pair

I1(nj):

Count the number of 1’s associated with test point nj

Is(nj):

Sum of the fault-pair isolation probability values of test point nj

2 New Algorithm for Test Point Selection

The ambiguity gap is a very important parameter during the construction of the fault dictionary. Using different ambiguity gaps can obtain different fault dictionaries. Therefore, choosing the accurate and reasonable ambiguity gaps can improve the accuracy of the method. Since the circuit output approximately satisfies the normal distribution [11], the mean and standard deviation values of each fault case can be calculated according to the statistical theory. On the basis of normal distribution theory, the normal curve of every fault can be drawn by fitting its mean and standard deviation values. Using the normal distribution character to choose the optimum ambiguity gaps is really a good choice. As there are three different relative positions of two normal curves which indicate different fault isolation possibilities, we defined a new method to calculate the fault isolation probability of these two faults and constructed the fault-pair isolation table in this section. The new proposed test point selection algorithm based on the fault-pair isolation table is also introduced below.

2.1 Ambiguity Gap Based on Normal Distribution

Ambiguity group is defined as that any two faulty cases fall into the same ambiguity set if the gap between the voltage values of their responses is less than a specific value. Hochwald and Bastian [7] first proposed the concept of ambiguity sets and defined a diode drop (0.7 V) as the ambiguity gap. In paper [20, 22], authors pointed out that set the voltage gap as 0.2 V was more suitable for low-voltage analog circuit. But the actual testing results prove that the voltage gap of 0.7 V and 0.2 V is not always effective and accurate. The ambiguity gap may be larger or smaller for various faults under different faulty conditions. Luo and Wang [11] discussed the shortage of 0.7 V ambiguity gap and proposed to construct the ambiguity gap based on normal distribution.

In practice, the component parameters change in a tolerance range approximately follows the normal distribution, and the output responses also follow the normal distribution according to the law of great numbers [11]. The statistical method can help to obtain the mean and standard deviation values of each fault case, instead of using finite sample data to represent all the possible status of the CUT. Due to the normal distribution theory, the normal curve which can be drawn by fitting the mean and standard deviation values is able to describe the distribution of probability density of the response voltages. The area size between the normal curve and the horizontal axis reflects the probability of the response voltages falling into this region. The voltage intervals are overlapped and meanwhile the corresponding normal curves also have overlapped area for the ambiguity group. The overlapped area represents the failure probability of diagnosing the ambiguity faults [11].

If we obtain the response voltage samples {v i1, v i2, ⋯, v in } of f i , the ambiguity gap can be calculated as follows [11]:

$$ \begin{array}{c} Gap\left({f}_i\right)=\left[\mu \left({f}_i\right)-w\cdot \sigma \left({f}_i\right),\mu \left({f}_i\right)+w\cdot \sigma \left({f}_i\right)\right]\\ {}=\mu \left({v}_{i1},\cdots, {v}_{in}\right)-w\cdot \sigma \left({v}_{i1},\cdots, {v}_{in}\right),\mu \left({v}_{i1},\cdots, {v}_{in}\right)+w\cdot \sigma \left({v}_{i1},\cdots, {v}_{in}\right)\end{array} $$
(1)

where μ(f i ) is the mean voltage response value in the existence of fault f i , and σ(f i ) is the standard deviation voltage response value in the existence of fault f i , w is the interval parameter that used to control the area proportion of the normal distribution interval. Since the tails of a normal curves outspread infinitely, a finite horizontal axis interval should be used in practice. When w is 1.96, the area proportion is 95.45 %, and if w is 2.58, the area proportion is 99.73 %. Therefore, we can control the intervals by setting different w values.

Generally, two normal curves have three different relative positions which show different fault isolation possibilities. Suppose f1 and f2 are two kinds of faults, the normal distribution curves of f1 and f2 have three different relative positions, which are shown in Fig. 1 respectively. The horizontal axis in Fig. 1 represents the voltage value of the test node. We define [Vf1min, Vf1max] (Vf1min ≤ Vf1max) as the ambiguity gap of f1, and [Vf2min, Vf2max] (Vf2min ≤ Vf2max) as the ambiguity gap of f2. If the curves f1 and f2 have no overlapping area as shown in (a) of Fig. 1, faults f1 and f2 can be isolated completely. If the curves f1 and f2 have a containment relationship as shown in (b) of Fig. 1, faults f1 and f2 can not be isolated anyhow. If the curves f1 and f2 have overlapping area as shown in (c) of Fig. 1, faults f1 and f2 can be isolated partly.

Fig. 1
figure 1

Normal curves of f1 and f2

Full size image

2.2 Fault-Pair Isolation Table

As Yang and Tian [22] has demonstrated that the fault-pair code technique is more accurate than the integer-coded technique in minimizing the size of test point set. We improved their method and proposed a new fault-pair isolation table technique to select the optimum test points.

As discussed above, normal curves of f1 and f2 have three different relative positions which show different fault isolation possibility. If the normal curves f1 and f2 have overlapping area, the fault isolation problem may be more difficult. We defined a new parameter to judge the fault isolation probability. Suppose the ambiguity gap of f1 is [Vf1min, Vf1max], and the ambiguity gap of f2 is [Vf2min, Vf2max] (Vf1min < Vf2min, Vf1max < Vf2max). As shown in Fig. 2, different cross areas of f1 and f2 have different meanings. If the response voltages fall into the interval of [Vf2min, Vf1max], f1 and f2 can not be isolated completely. Area A is the common parts of normal curve f1 and f2, the larger of this area the more difficult to isolate f1 and f2. Area B and C show different probability of f1 and f2 occur in this interval respectively. It can be concluded that the bigger of the area under each curve, the more probability of the fault occurs in this voltage region. If the response voltages fall into the interval of [Vf1min, Vf2min] or [Vf1max, Vf2max] (the corresponding area is D and E respectively), the faults f1 and f2 can be isolated absolutely. Therefore, we propose to calculate the shadow areas D and E of Fig. 2 to represent the fault isolation probability of f1 and f2. Since the area under the whole normal curve is 1 and the maximum sum value of shadow areas D and E is 2, we calculate the normalized fault isolation probability of f1 and f2 as follows:

Fig. 2
figure 2

Different cross areas of f1 and f2

Full size image
$$ \begin{array}{l}{P}_{FI}\left({f}_1,{f}_2\right)=\frac{\left( AreaD+ AreaE\right)}{2}\\ {}=\left({\displaystyle {\int}_{V_{f1 \min}}^{V_{f2 \min }}\frac{1}{\sqrt{2\pi}\sigma \left({f}_1\right)}{e}^{-\frac{{\left(x-\mu \left({f}_1\right)\right)}^2}{2{\sigma}^2\left({f}_1\right)}}dx+}{\displaystyle {\int}_{V_{f1 \max}}^{V_{f2 \max }}\frac{1}{\sqrt{2\pi}\sigma \left({f}_2\right)}{e}^{-\frac{{\left(x-\mu \left({f}_2\right)\right)}^2}{2{\sigma}^2\left({f}_2\right)}}dx}\right)/2\end{array} $$
(2)

If the curves f1 and f2 have no overlapping area as shown in (a) of Fig. 1, the fault isolation probability P FI (f 1, f 2) is 1, and this represents fault f1 and f2 can be isolated completely. If the curves f1 and f2 have a containment relationship as shown in (b) of Fig. 1, the fault isolation probability P FI (f 1, f 2) is 0, and this represents fault f1 and f2 can not be isolated anyhow. If the curves f1 and f2 have overlapping area as shown in (c) of Fig. 1, the fault isolation probability P FI (f 1, f 2) is between 0 and 1, and this represents faults f1 and f2 can be isolated partly. Therefore, it can be concluded that the bigger of the fault isolation probability value P FI (f 1, f 2), the more possibility to isolate fault f1 and f2.

By calculating the fault isolation probability values of any two faults, we can obtain the isolation probability of all fault pairs, and construct the fault-pair isolation table to select the optimum test points. In the proposed fault-pair isolation table, rows represent any possible fault pairs, and columns show the available test points. The values filled in the table are the defined fault isolation probability values, which can be calculated by formula (2). Different values in the fault-pair isolation table have different meanings. If the value is 1, it means that this pair of faults can be isolated completely by this test node. If the value is 0, it means that this pair of faults can not be isolated anyhow. If the value is between 0 and 1, it means this pair of faults can be partly isolated. From the table, we can clearly see the fault isolation capability of each candidate test point and find the special test points easily.

Lin and Elcherif [10] proposed the integer-coded fault dictionary technique in 1985. The ambiguity group is defined as any two faulty conditions that fall into the same ambiguity set if the gap between the voltage values produced by them is less than the ambiguity gap. For each fault, an integer code is generated from the numbers of ambiguity sets of each test point, and the same integer number represents all the faults that belong to the same ambiguity group in a given candidate test point. Since each candidate test point represents an independent measurement, the ambiguity groups of different test points can be numbered using the same integer without confusion [23].

Assume that Table 1 shows mean and standard deviation faulty voltage values (including fault-free case) of an analog circuit. Set w as 2, and use the formula (1) to calculate the ambiguity gaps of each test point. Take test point n1 as an example. The calculated ambiguity gaps of the test point n1 from f1 to f6 are [2.98, 3.02], [3.40, 3.80], [3.50, 3.90], [3.40, 4.20], [4.00, 4.40] and [0.94, 1.66]. Rearrange them from small to large. The first ambiguity gap [0.94, 1.66] does not overlap with any other ambiguity gaps, so it is numbered ambiguity group 0. The second ambiguity gap [2.98, 3.02] does not overlap with any other ambiguity gaps, so it is numbered ambiguity group 1. The other ambiguity gaps overlap together, and the corresponding faults fall into the same ambiguity group numbered ambiguity group 2. Finally we obtain the integer-coded fault dictionary shown in Table 2. From this table, we can find that only faults f1 and f6 can be isolated, and faults f2, f3, f4, f5 can not be isolated anyhow. This just reflects the shortage of the integer-coded table technique. However, our new proposed fault-pair isolation table technique can solve the problem. We will continue discussing this problem in Section 2.3.

Table 1 Fault dictionary
Full size table
Table 2 Integer-coded fault dictionary of Table 1 (w = 2)
Full size table

Use formula (2) to calculate the fault-pair isolation probability values of all the test points, and construct the fault-pair isolation table. Table 3 shows the fault-pair isolation table of Table 1. In this table, the column NIi represents the number of test points that can isolate the ith fault pair, and by searching for NIi = 1, we are able to find the special test point that can uniquely isolate the ith fault pair easily.

Table 3 Fault-pair isolation table of Table 1 (w = 2)
Full size table

2.3 Test Point Selection Algorithm Based on the Fault-Pair Isolation Table

In the proposed method, the fault-pair isolation table is derived from mean and standard deviation voltage values of the defined fault modes, the test points are selected based on the fault-pair isolation capability of the candidate test points. The strategy of the introduced method is that the special test points that can uniquely isolate some particular fault pairs should be added into Sopt first, and then judge whether these special test points in Sopt can isolate all the fault pairs or not. If they can, we have found the final solution; otherwise, more optimum test points should be selected. I1(nj) represents the number of 1’s associated with test point nj, which means the total number of fault pairs that can be isolated by test point nj. Is(nj) is the sum of fault-pair isolation probability values of test point nj, which represents the fault-pair isolation capability of test point nj. Therefore, the larger of these values represent the stronger fault-pair isolation capability of the test point. These particular meanings of I1(nj) and Is(nj) are used to select more optimum test points. The selected test points (columns) and all the fault pairs (rows) that can be isolated by test points of Sopt are removed from the fault-pair isolation table in the next step. Then, searching for the point with maximum value of I1(nj) and Is(nj) are used together to select the more optimum test points, until all the fault pairs are isolated or the remainder fault pairs can not be isolated unless more candidate test points are increased.

The steps of the proposed test point selection algorithm are illustrated as follows.

  1. Step 1)

    Initialize the desired test-point set Sopt as a null set, and let Sc consist of all the candidate test points. The fault dictionary is initialized based on the mean and standard deviation voltage values of all the defined fault mode samples (including fault-free case). The columns of dictionary represent NT test points, and the rows of dictionary are any possible fault pairs constructed by Nf fault modes. The appropriate interval parameter w is determined experimentally to confirm the ambiguity gaps by formula (1) for Nf fault modes.

  2. Step 2)

    Construct the fault-pair isolation table based on the fault-pair isolation capability calculated by formula (2).

  3. Step 3)

    Search for the fault pairs that correspond to NIi = 1. The test point that can uniquely isolate the ith fault pair is added into Sopt. The fault pairs (rows) that can be isolated by these test points in Sopt are all deleted from the fault-pair isolation table, and these test points (columns) are also removed from it. Go to Step 5.

  4. Step 4)

    I1(nj) of every test point in the fault-pair isolation table is calculated and the test point with the maximum I1(nj) is added into Sopt. In case of a tie, calculate Is(nj). The test point with larger Is(nj) is add into Sopt. The fault pairs (rows) isolated by this test point are deleted from the fault-pair isolation table, the test point (column) is also deleted from it. Go to Step 5.

  5. Step 5)

    Check the stop conditions. If the test points of Sopt can isolate all the fault pairs or the remainder fault pairs can not be isolated unless more candidate test points are increased, exit. Otherwise, go to Step 4.

It is important to note that NIi used in Step 3 was obtained after the fault-pair isolation table was constructed. Usually, some fault pairs can only be diagnosed by some certain test points in practice. In this case, Step 3 is able to help us find the final solution more accurately and efficiently. Under some special conditions, this step can even find the final solution directly. Although we need to run Step 4 to find more optimum test points sometimes, the size of the fault-pair isolation table has been dramatically decreased by Step 3, and this will surely help to save the computation time greatly. Our new algorithm provides a new criterion for analog circuit test point selection.

Such as the fault-pair isolation table shown in Table 3, by searching the NIi column for NIi = 1, we can easily find that fault pairs (f1, f2), (f1, f4), (f1, f6), (f2, f6) and (f3, f5) can only be distinguished by test point n1, and fault pairs (f2, f3), (f2, f4) and (f3, f4) can only be diagnosed by test point n2. Therefore, test point n1 and n2 should be added into Sopt according to Step 3. After checking for the stop conditions of Step 5, we can find that these two test points (n1 and n2) can isolate all the fault pairs and the algorithm finds the final solution directly. In this example, only one step (Step 3) can find all the optimum test points.

2.4 Algorithm Time Complexity Analysis

The time complexity of the proposed algorithm is less than O(N 2 f  ⋅ N T  ⋅ m), which will be proved in the following.

Since the algorithm needs to calculate every ambiguity gap for every fault mode in each test point, the time complexity of Step 1 is O(N f  ⋅ N T ) to get all the ambiguity gaps for N f fault modes in N T test points.

As discussed above, the fault-pair isolation table consists of N f  ⋅ (N f  − 1)/2 rows and N T  + 1 columns (including the column NIi), the time complexity of Step 2 during the construction of the fault-pair isolation table is O((N T  + 1) ⋅ N f  ⋅ (N f  − 1)/2) = O(N 2 f N T ).

In Step 3, since N f  ⋅ (N f  − 1)/2 rows in the table need to be searched, deleting the fault pairs (rows) isolated by the selected test points has the time complexity of O(N f  ⋅ (N f  − 1)/2) = O(N 2 f ).

In Step 4, since N f  ⋅ (N f  − 1)/2 rows and N T columns in the fault-pair isolation table need to be searched, the time complexity of calculating I1(nj) and Is(nj) are O(N T  ⋅ N f  ⋅ (N f  − 1)/2 + N T  ⋅ N f  ⋅ (N f  − 1)/2) = O(N T  ⋅ N 2 f ), and deleting the corresponding rows has the time complexity of O(N f  ⋅ (N f  − 1)/2) = O(N 2 f ). Therefore, the total time complexity of Step 4 is O(N T  ⋅ N 2 f ) + O(N 2 f ) = O(N 2 f  ⋅ N T )

Suppose that Step 4 is executed m iterations, the total time complexity of the proposed algorithm is:

$$ O\left({N}_f\cdot {N}_T+{N}_f^2{N}_T+{N}_f^2+{N}_f^2\cdot {N}_T\cdot m\right)=O\left({N}_f^2\cdot {N}_T\cdot m\right). $$

Because the isolated fault pairs (rows) are deleted in each iteration and the size of the fault-pair isolation table decreases gradually, the total time complexity is less than O(N 2 f  ⋅ N T  ⋅ m).

The time complexity of the proposed algorithm is the same as Yang’s [22] and Luo’s [11] method, but more complex than the methods proposed in references of [17, 23] and [13]. Because the time complexity of the construction of the fault-pair isolation table and the calculation of I1(nj) and Is(nj) are O(N 2 f  ⋅ N T ). For the on-line and off-line testing and fault diagnosing, the test point selection is the necessary preparation work. Once the optimum test points are selected and determined, it can be used for both SBT and SAT approaches. As the construction of the fault-pair isolation table is the key of our new algorithm and the calculation of I1(nj) and Is(nj) could help to select the optimum test points, the testability of the CUT and the accuracy of our method will be improved dramatically.

2.5 Improvements of the New Algorithm

As discussed above, the major improvements of our new algorithm can be summarized as follows:

  1. (a)

    A new formula for the calculation of the normalized fault-pair isolation probability is constructed and used properly.

  2. (b)

    A new fault-pair isolation table, the element of which has special meanings, is proposed.

  3. (c)

    A new criterion based on fault-pair isolation table for analog circuit test point selection is introduced.

  4. (d)

    The ambiguity gap construction method based on normal distribution is combined with the fault-pair code technique perfectly in the new algorithm to overcome the limitations of the integer-coded technique and obtain better results.

3 Experiment on the Circuits

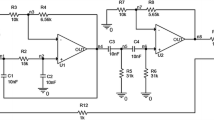
3.1 Bandpass Filter Circuit Example

The filter circuit with the nominal parameter values is shown in Fig. 3. This is the same analog circuit example as in references [11, 13, 17, 22]. The normal mode and the other defined fault modes are listed in Table 4. The excitation signal is a 1-kHz, 4-V sinusoidal wave. Totally, there are 23 potential faults f1 to f23 (including fault-free case) and 11 test points n1 to n11. The responses of voltage values at all test points for different faulty conditions are obtained by PSPICE simulation. During the simulations, to consider the effects of the tolerances, the resistor model “Rbreak” and the capacitor model “Cbreak” are used. The tolerance of resistor and capacitance are set as 5 and 10 % by editing their Spice model respectively. The Monte Carlo analysis is used to simulate the effects of the components’ tolerance. The tolerance distribution of the components is set as Gaussian distribution, and each the resistor and capacitance is varied within their tolerance. To obtain the simulation data, we use a 1Ω resistor to represent the short circuit fault, and a 100 MΩ resistor to represent the open circuit fault. 40 times of Monte Carlo analyses and 2 times of Worse-Case analyses are executed, and each fault mode gains 42 sample data.

Fig. 3
figure 3

Bandpass filter circuit

Full size image
Table 4 Fault modes of the bandpass filter circuit
Full size table

Since the interval parameter w is closely related to the ambiguity gap as discussed in Section 2, different values of w may lead to different results. Parameter w is set as 1.96 (with the area proportion of 95.45 %) in the first simulation and other different values are set in the next experiments.

3.1.1 Experiment on the Interval Parameter of 1.96

The initialized work is done in the first step of our algorithm. Since there are 23 potential faults and 11 test points, the candidate test-point set Sc is initialized as {n1, n2, n3, n4, n5, n6, n7, n8, n9, n10, n11}, NT = 11 and Nf = 23. The optimum test point set Sopt is initialized to a null set, and the parameter w is set as 1.96. After simulation and calculation, the constructed fault dictionary for the CUT is shown in Table 5. The formula (1) is used to calculate the ambiguity gaps for each fault mode of every test point. It can be found that the ambiguity gaps of the faults are bigger or smaller than 0.7 V in fact.

Table 5 Fault dictionary of the bandpass filter circuit
Full size table

In step 2, the fault-pair isolation table is constructed by the procedures introduced in Section 2. Table 6 shows a part of the obtained fault-pair isolation table. The formula (2) is used to calculate the normalized fault isolation probability of every fault pair. As discussed in Section 2, different values in the fault-pair isolation table have different meanings. The value is 1 means this pair of faults can be isolated completely, the value is 0 means this pair of faults cannot be isolated anyhow, and the value is between 0 and 1 means this pair of faults can be isolated partly.

Table 6 A part of fault-pair isolation table of the bandpass filter circuit
Full size table

In step 3, by checking the NIi column, the special test points n1, n5, n8 and n11 are selected first and add into Sopt. Because the fault pairs (f3, f5), (f3, f20), (f5, f20) and (f11, f19) can only be isolated by test point n1, (f8, f10) can only be isolated by test point n5, (f4, f12), (f9, f12), (f11, f12) and (f12, f23) can only be isolated by test point n8, (f1, f11), (f1, f15), (f1, f21), (f2, f15), (f4, f14), (f4, f15), (f4, f19), (f9, f14), (f9, f15), (f11, f14), (f11, f15), (f12, f15), (f14, f15), (f14, f21), (f15, f21) and (f15, f23) can only be isolated by test point n11. After removing the fault pairs (rows) that can be isolated by the test points of Sopt and deleting the corresponding selected test points (columns) of the fault-pair isolation table, the size of the table reduced greatly. The reduced fault-pair isolation table is shown in Table 7.

Table 7 Reduced fault-pair isolation table of the bandpass filter circuit
Full size table

After checking the stop conditions, more optimum test points should be selected and the algorithm goes to Step 4. I1(nj) of every candidate test point in the fault-pair isolation table is calculated respectively. The test points n9 and n10 have the same maximum I1(nj) = 17. In order to choose the test point that has better fault isolation capability, Is(nj) of test points n9 and n10 are calculated. Since n10 has larger Is(nj) = 17.53 and may have better performance in practice, test point n10 should be added into Sopt. After removing the isolated fault pairs (rows) and the selected optimum test point (column) of the fault-pair isolation table, the algorithm goes to Step 5 to check the stop conditions. As the remainder fault pairs cannot be completely isolated by the candidate test points anymore and the stop condition fulfills, the final solution is Sopt = {n1, n5, n8, n10, n11}. The obtained final fault-pair isolation table is shown in Table 8. From this table, we can clearly see that there are 22 fault pairs related to 9 different faults cannot be isolated completely. Therefore, it can be concluded that the proposed algorithm selected 5 optimum test points as the final solution, and can completely isolate 14 different kinds of faults (obtained by subtracting 9 from the total 23 faults).

Table 8 The final fault-pair isolation table of the bandpass filter circuit
Full size table

3.1.2 Experiment with Different Interval Parameters

Since different interval parameter values will lead to different ambiguity gaps and even different overlapped areas of the normal curves, the free interval parameter w should be determined experimentally. The test results with different w are shown in Table 9. The Sopt column of the table shows different final solutions with different interval parameter values, and the third column shows the amount of fault pairs that cannot be isolated. The last column shows the fault isolation degree which means the total number of faults that can be completely isolated by the chosen optimum test point set.

Table 9 Test results with different w for the bandpass filter circuit
Full size table

From Table 9, we can find that the larger parameter values have smaller fault isolation degrees. This is because the ambiguity gaps increase with the adding of the interval parameter w, and the fault-pair isolation probabilities, meanwhile, decrease. We can also find from Table 9 that the Sopt = {n1, n5, n8, n10, n11} repeats many times with different interval parameters. So the repeated test point set Sopt = {n1, n5, n8, n10, n11} can be considered as a candidate of the optimal test point set, which can be used to diagnose the CUT in practice.

3.1.3 Comparison with Other Methods

In this experiment, the proposed method is compared with other four reported methods. Since some reported methods are based on the integer-coded technique (Starzyk’s method [17], Pinjala’s method [13] and Luo’s method [11]), the integer-coded fault dictionary needs to be constructed first. The ambiguity gaps are calculated by formula (1), and the interval parameter is set as 2.2. The final results are listed in Table 10.

Table 10 Test results with different methods for the bandpass filter circuit (w = 2.2)
Full size table

As shown in Table 10, all the methods obtain the same fault isolation degree besides Yang’s [22] and our new method have the smallest size of the final optimum test point set. Our new method finds a different optimum test point set from the Yang’s [22] method, but both of the final solutions have the same high accuracy. This is to say that a CUT may have more than one different optimum test point sets.

From the above analysis, it can be concluded that the new proposed method is feasible and effective in finding the optimum test point set.

3.2 Leapfrog Filter Circuit Example

Figure 4 shows a leapfrog filter circuit. The tolerance of resistor and capacitance are set as 5 and 10 % respectively. The normal mode and the other defined fault modes are listed in Table 11. The excitation signal is a 1-kHz, 6-V sinusoidal wave. Totally, there are 20 potential faults f1 to f20 (including fault-free case) and 12 test points n1 to n12. The responses of voltage values at all test points for different faulty conditions are obtained by PSPICE simulation. 40 times of Monte Carlo analyses and 2 times of Worse-Case analyses are executed, and each fault mode gains 42 sample data.

Fig. 4
figure 4

Leapfrog filter circuit

Full size image
Table 11 Fault modes of the leapfrog filter circuit
Full size table

The test results with different interval parameter values are shown in Table 12. From the table, we can find that the fault isolation degree reduces and more test points are added into Sopt with the increase of the interval parameter values. This conclusion is the same as the bandpass filter example.

Table 12 Test results with different w for the leapfrog filter circuit
Full size table

The results with different methods are shown in Table 13 (the interval parameter w is set as 1). As shown in Table 13, Yang’s [22] method and our new method obtain the largest fault isolation degree, but the size of the Sopt obtained by our method is smaller than that of Yang’s [22]. Therefore, our new method finds the best final solution of all.

Table 13 Test results with different methods for the leapfrog filter circuit (w = 1)
Full size table

All the above experiment results demonstrate that the new proposed method has better accuracy and quality in finding the optimum test point set. It is an effective and feasible method in minimizing the size of the test point set of the analog circuit with the influence of component tolerance.

4 Statistical Experiments

Although the above experiments have shown the great advantage and ability of the proposed algorithm in finding the optimum test point set, there still no theoretical proof can be offered to demonstrate a specific non-exhaustive algorithm’s optimality [13, 17, 23]. The new proposed algorithm must statistically be tested on larger number of fault dictionaries to demonstrate its efficiency and qualities of generating optimum test point sets.

Such statistical experiments are carried out on the randomly computer-generated fault dictionaries and the final solutions are found by using Starzyk’s method [17], Pinjala’s method [13], Yang’s method [22], Luo’s method [11], the exhaustive method and the proposed new method respectively. All the algorithms are programmed by MATLAB and tested on an Intel 3.2 GHz processor computer. A total of 200 times’ statistical experiments are carried out. At every time of the experiment, 100 mean values, 100 standard deviation values and 20 test points’ data are needed. And all the mean and standard deviation values are randomly generated by MATLAB codes and vary in intervals [0.00, 10.00] and [0.00, 0.40] respectively. Since some of the methods are based on the integer-coded technique (Starzyk’s method [17], Pinjala’s method [13], Luo’s method [11] and the exhaustive method), the integer-coded fault dictionaries need to be constructed, too. The ambiguity gaps are calculated by formula (1), and the interval parameter w is set as 1. Table 14 shows the final results. From the table, we can find that the proposed method obtains the best solution of all. If the proposed method is adopted, two or three test points can isolate all the 100 faults in all the 200 times’ experiments. Yang’s [22] method also obtain good results, since three test points can isolate all the faults in all the experiments. But other methods (including the exhaustive method) need at least five test points to isolate all the faults, and this indicates that these solutions contain at least two redundant test points. Besides, in two simulated cases, except Yang’s [22] and our new proposed method, the other methods can not isolate all the faults fully, which is the shortage of the integer-coded technique.

Table 14 Statistical results of the solution accuracy
Full size table

Figure 5 illustrates the performance of the proposed algorithm and the integer-coded technique based exhaustive algorithm. This figure shows the relationship between the number of faults and the size of the final solutions. In Fig. 5a, the total number of candidate test points is 10. The two algorithms obtain the same accuracy solution at the beginning, but the size of the final solution found by the exhaustive algorithm increases dramatically when the fault number is larger than 40. The size of the final solution found by our proposed algorithm always keeps less than 4. Besides, when the fault number is larger than 120, the exhaustive algorithm makes all the faults undistinguishable, which is not right in fact. Therefore, our proposed algorithm has higher accuracy with the increase of the fault dictionary. The same conclusion can be drawn from Fig. 5b.

Fig. 5
figure 5

Statistical results of the proposed algorithm and the exhaustive algorithm

Full size image

Therefore, whether the data in the fault-pair isolation table are randomly computer generated or derived by a realistic circuit, our proposed algorithm can be used to choose the optimum set of test points if the fault-pair isolation table can be constructed properly.

5 Conclusion

Nowadays, the scale and complexity of the circuits are increasing with the fast development of the modern electronic industry, which has brought great difficulties and challenges to the fault diagnosis. Therefore, how to find a minimum set of test points efficiently to isolate all the faults to a desired degree becomes the key point. Since the circuit output responses follow the normal distribution, an accurate way for determining the fault ambiguity gap is used in this paper. Meanwhile, a new test point selection algorithm is proposed based on this ambiguity gap calculation method. In the algorithm, a new defined fault-pair isolation table is derived from the mean and standard deviation values of node voltage under different fault modes, and the optimum test points are selected based on the fault-pair isolation capability of the candidate test points. The time complexity of the proposed algorithm is proved to be less than O(N 2 f  ⋅ N T  ⋅ m). Carried out on the same trademark analog circuits, the proposed algorithm shows greater advantage in finding the final solutions than the other reported methods. Since no theoretical proof can be given to the optimality of the proposed algorithm, statistical experiments are utilized for its evaluation. The results demonstrate that our proposed method has better accuracy and quality in finding the optimum test point set. It is an effective and feasible method in minimizing the size of the test point set of the analog circuit with the influence of component tolerance. Therefore, it is particularly applicable to actual circuits and engineering practice.