Test Points Selection for Analog Fault Dictionary Techniques

Abstract

The test points selection problem for analog fault dictionary is researched extensively in many literatures. Various test points selection strategies and criteria for Integer-Coded fault wise table are described and compared in this paper. Firstly, the construction method of Integer-Coded fault wise table for analog fault dictionary is described. Secondly, theory and algorithms associated with these strategies and criteria are reviewed. Thirdly, the time complexity and solution accuracy of existing algorithms are analyzed and compared. Then, a more accurate test points selection strategy is proposed based on the existing strategies. Finally, statistical experiments are carried out and the accuracy and efficiency of different strategies and criteria are compared in a set of comparative tables and figures. Theoretical analysis and statistical experimental results given in this paper can provide an instruction for coding an efficient and accurate test points selection algorithm easily.

1 Introduction

On the one hand, test points selection is very important task for design for testability (DFT). On the other hand, fault dictionary is an important method of simulation before test (SBT) and this technique is a popular choice for fault diagnosis [8]. So the test points selection problem for fault dictionary are researched extensively in many literatures [1, 3, 5, 6, 8–11, 13, 14–16, 18]. The global minimum set of test points can only be guaranteed by an exhaustive search which is computationally expensive [11, 14]. As pointed out by Augusto et al. [3], the exhaustive search algorithm is limited to small or medium size analog systems. For large or medium systems, such as the dictionaries with more than 40 faults and more than 40 test points, the exhaustive search is impractical. The tradeoff between the desired degree of fault diagnosis and computation cost is to select a near-minimum set (or a local minimum set).

Lin and Elcherif [8] proposed an Integer-Coded fault wise table (or dictionary) technique. This technique is proven to be an effective tool for the optimum test points selection. The later test points selection algorithms [3, 5, 9–11, 14, 18] are all based on the Integer-Coded fault wise table technique. This technique was used to solve test points selection problem for analog fault dictionary technique first. But this technique can be used not only in circuit level fault diagnosis but also in system level fault diagnosis. In fact, the dependency matrix proposed in Deb et al. [4] is a system level binary fault dictionary. Binary fault dictionary is just a special Integer-Coded fault wise table (dictionary) [12, 17]. Don’t take the possibility of fault happening and test cost into consideration; sequential fault diagnosis problem is just a test points selection problem. So the test points selection algorithms proposed in literatures [3, 5, 9–11, 14, 18] could be used not only in circuit level but also in board level and system level. Each of these algorithms consists of a test points selection strategy and a test points selection criterion. Although the latest literatures [9, 14, 18] have provide statistical experiments to illustrate their algorithms’ superiority, these new test points selection criteria do not always overmatch the previous test points selection criteria as discussed later.

The construction method of Integer-Coded fault wise table for analog fault dictionary is illustrated in this section. In Section 2, existing test points selection algorithms are summarized at first. The accuracy and efficiency of every test points selection strategy and test points selection criterion is summarized and compared in Section 3. A new easy-execute algorithm, which can efficiently and accurately find the minimum test points set, is proposed in this section also. Statistical experiments are carried out in Section 4. Finally, conclusions are given in Section 5.

In fault dictionary, rows represent different faults (including the nominal case) and columns show the available test points. Assume that the voltages shown in Table 1 are obtained when a given net work is analyzed for the nominal condition (f ₀) as well as for eight faulty conditions (f ₁ to f ₈). Ambiguity group is defined that any two faulty conditions fall into the same ambiguity set if the gap between the voltage values produced by them is less than 0.7 V [6]. But it is necessary to point out that the voltage value span of an ambiguity group may be larger than 0.7 V. In column 2 of Table 1 for example, the voltage value gap produced by f ₆ and f ₄ is 0.4 V so they belong to one ambiguity set. Similarly, f ₄ and f ₅ belong to one ambiguity set also. Because f ₆ f ₄ are not distinguishable and f ₄ f ₅ are not distinguishable, so f ₆ f ₄ f ₅ are not distinguishable and belong to one ambiguity set although the voltage value gap produced by f ₆ and f ₅ is 0.9 V, which is larger than 0.7 V. The reader is referred to references [6, 10] for details.

Table 1 Fault dictionary

Table 2 indicates the ambiguity sets of Table 1. Lin and Elcherif [8] proposed an Integer-Coded fault wise table (or dictionary) for fault isolation phase. For each fault, a code is generated from the numbers of ambiguity sets of each test point. Considering test point n ₁ in Table 2, fault f ₄ is coded as “0”, faults {f ₁, f ₅, f ₆} are coded as “1”, faults {f ₀, f ₂} are coded as “2”, {f ₇, f ₈} are coded as “3” and f ₃ are coded as “4”. Then, Table 3 is derived.

Table 2 Ambiguity set of Table 1

Table 3 Integer-coded fault wise table

In this Integer-Coded fault wise table, the same integer number represents all the faults that belong to the same ambiguity group in a given column. Since each test point represents an independent measurement, ambiguity groups of each test point are independent and can be numbered using the same integers without confusion. The Integer-Coded table can also be regarded as an array of “N _F ” elements. If all the elements of this array are different, it means that each fault has unique integer number. Hence all faults can be diagnosed. If an entry of this array repeats, it indicates that these faults cannot be separated, with the set of test points used for making this array.

2 Test Points Selection Method

Test points selection methods for faulty dictionary technique can be classified into two categories: inclusive and exclusive [16]. In the inclusive approaches, the optimum set of test points (S _opt ) is initialized to be null, then an “ideal” test point based on a given criterion is added to it. The methods proposed in [6, 8–11, 14, 18] fall into inclusive category. While in exclusive methods, the desired optimum set is initialized to include all available test points at first. Then every test point will be checked one by one and will be deleted if it is redundant. The method proposed by Prasad and Babu [11] fall into exclusive method.

2.1 Inclusive Category

2.1.1 Algorithm 1[10]

• Step 1: Initialize S _opt as null set and let S _c consist of all candidate test points.

• Step 2: Draw out a test point n _j with $\mathop {Max}\limits_j \left( {N_{Aj} } \right)$ from S _c and add to S _opt .

• Step 3: Check whether the selected test points in S _opt are enough to diagnose the given set of faults. If yes, stop.

• Step 4: If the size of any one ambiguity set determined by S _opt is decreased after the inclusion of test point n _j , go to Step 2. Else, discard n _j from S _opt and go to Step 2.

2.1.2 Algorithm 2[3]

• Step 1: Initialize S _opt as null set and let S _c consist of all candidate test points.

• Step 2: Draw out a test point n _j with $\mathop {Min}\limits_j \left( {\mathop {Max}\limits_i \left( {F_{ij} } \right)} \right)$ from S _c and add to S _opt .

• Step 3: Check whether the selected test points in S _opt are enough to diagnose the given set of faults. If yes, stop.

• Step 4: If the size of any one ambiguity set determined by S _opt is decreased after the inclusion of test point n _j , go to Step 2. Else, discard n _j from S _opt and go to Step 2.

2.1.3 Algorithm 3[3]

• Step 1: Initialize S _opt as null set and let S _c consist of all candidate test points.

• Step 2: Draw out a test point n _j with $\mathop {Min}\limits_j \left( {s_j } \right)$ from S _c and add to S _opt , where

  $$s_j = \sum\limits_{i = 1}^{N_{Aj} } {^{{{\left( {{{F_{ij} - N_F } \mathord{\left/ {\vphantom {{F_{ij} - N_F } {N_{Aj} }}} \right. \kern-\nulldelimiterspace} {N_{Aj} }}} \right)^2 } \mathord{\left/ {\vphantom {{\left( {{{F_{ij} - N_F } \mathord{\left/ {\vphantom {{F_{ij} - N_F } {N_{Aj} }}} \right. \kern-\nulldelimiterspace} {N_{Aj} }}} \right)^2 } {N_{Aj} }}} \right. \kern-\nulldelimiterspace} {N_{Aj} }}} } $$

  (1)

• Step 3: Check whether the selected test points in S _opt are enough to diagnose the given set of faults. If yes, stop.

• Step 4: If the size of any one ambiguity set determined by S _opt is decreased after the inclusion of test point n _j , go to Step 2. Else, discard n _j from S _opt and go to Step 2.

2.1.4 Algorithm 4[9]

• Step 1: Initialize S _opt as null set and let S _c consist of all candidate test points.

• Step 2: Draw out a test point n _j with $\mathop {Max}\limits_j \left( {q_j } \right)$ from S _c and add to S _opt .

• Step 3: Check whether the selected test points in S _opt are enough to diagnose the given set of faults. If yes, stop.

• Step 4: In fault wise table (dictionary), eliminate rows that can be isolated by test points in S _opt together.

• Step 5: Calculate q _j for every test point n _j in S _c . Herein, q _j is the number of faults that can be isolated by n _j and test points in S _opt together. Go to Step 2.

The second sentence in this Step 5 may be confusing. The following example is used to explain this operation.

• Example 1: Considering the test points selection problem of Table 11.

Suppose that n ₁ have already added to S _opt viz. S _opt ={n ₁} and S _c ={n ₂,n ₃,n ₄,n ₅}. Obviously, all faults can’t be isolated by n ₁, so additional test points are needed. In Step 5, calculate q _j for every test point n _j in S _c . There is no fault can be isolated by n ₂ while n ₃ can isolate f ₃, n ₄ can isolate f ₂ and n ₅ can isolate f ₁. So one may get q ₂=0, q ₃=q ₄=q ₅=1 and draw that n ₃,n ₄ or n ₅ is better than n ₂. But when combined with test points in S _opt (viz. n ₁), all four faults can be isolated by n ₂, n ₃ can isolate {f ₂ f ₃}, n ₄ can isolate {f ₂ f ₃}, also, n ₅ can isolate {f ₀ f ₁}. So $q\prime _2 = 4$, $q\prime _3 = q\prime _4 = q\prime _5 = 2$. Obviously n ₂ should be added to S _opt according to Step 2. In Step 5, the q _j value is $q\prime$ value.

2.1.5 Algorithm 5[2]

• Step 1: Initialize S _opt as null set and let S _c consist of all candidate test points.

• Step 2: Draw out a test point n _j with $\mathop {Max}\limits_j \left( {I_j } \right)$ from S _c and add to S _opt , where

  $$\begin{array}{*{20}c} {I_{j} = - {\left( {\frac{{F_{{1j}} }}{{N_{F} }}\ln \frac{{F_{{1j}} }}{{N_{F} }} + \frac{{F_{{2j}} }}{{N_{F} }}\ln \frac{{F_{{2j}} }}{{N_{F} }} + \cdots \frac{{F_{{N_{{Aj}} j}} }}{{N_{F} }}\ln \frac{{F_{{N_{{Aj}} j}} }}{{N_{F} }}} \right)}} \\ { = \frac{{\ln N_{F} }}{{N_{F} }}{\sum\limits_{i = 1}^{N_{{Aj}} } {F_{{ij}} } } - \frac{1}{{N_{F} }}{\sum\limits_{i = 1}^{N_{{Aj}} } {F_{{ij}} \ln } }F_{{ij}} } \\ { = \ln N_{F} - \frac{1}{{N_{F} }}{\sum\limits_{i = 1}^{N_{{Aj}} } {F_{{ij}} \ln } }F_{{ij}} } \\ \end{array} $$

  (2)

• Step 3: Check whether the selected test points in S _opt are enough to diagnose the given set of faults. If yes, stop.

• Step 4: Partition the rows of the dictionary according to the ambiguity sets of S _opt and removing the rows that can be isolated by test points in S _opt together.

• Step 5: Calculate I _j for every test point in S _c . Go to Step 2.

2.1.6 Algorithm 6[13]

In Yang et al. [18], a heuristic Depth-first graph search algorithm is developed to solve the test points selection problem. Root node S contain all faults that to be diagnosed. First, use all candidate test points to expand S and the new generated graph nodes belong to Level 1. Second, on Level 1, select a graph node with maximum fault discrimination power as the one to be expanded for the second iteration. Finally, expand the selected graph node with all the test points except those used on the path from this node to the root node S. The new generated graph nodes belong to Level 2. Execute these steps iteratively until all faults are isolated. An example is used to illustrate this method.

Figure 1 is the expanded graph for Table 3. In this figure, x _i represents graph node and n _j is the test point used on the graph path. Every intermediate graph node x _i consists of two faults group. One group consists of isolated faults and the other consists of residual faults. Residual faults are subdivided into several ambiguity sets as shown in Fig. 1.

Fig. 1

Expanded graph

Initially let the graph G consist of the root node S. All potential faults (f ₀~f ₈) are contained in node S and belong to one ambiguity set (viz. N _AS =1). The root node S is expanded with all test points and the new four graph nodes (x ₁~x ₄) are shown on Level 1 in Fig. 1. Based on Level 1, Table 4 list the k _i (number of graph node that can isolate fault f _i ) value and information content of every fault, where information content is defined as:

$$I\left( {f_i } \right) = - \ln \left( {\frac{{k_i }}{{N_T }}} \right)$$

(3)

Table 4 k _i value and information content of every fault (N _T =4)

Faults f ₃ and f ₄ are isolated by graph node x ₁, so information content contained in x ₁ is I(x ₁)=I(f ₃)+I(f ₄). Information content for every graph node on Level 1 is shown in Table 5. Node x ₂ has the maximum information content, so it should be expanded in next step. Because test point n ₂ has been used on the path from root node to x ₂, the residual three test points {n ₁,n ₃,n ₄} are used to expand node x ₂ on the second level of Fig. 1.

Table 5 Fault discrimination power of every test point

Test points used on the path from goal node x ₈ to root node S make up of the final solution.

Obviously, each algorithm has its own test points selection criterion. One can call these criteria as fault discrimination power.

• Criterion1 $\mathop {Max}\limits_j \left( {N_{Aj} } \right)$

• Criterion2 $\mathop {Min}\limits_j \left( {\mathop {Max}\limits_i \left( {F_{ij} } \right)} \right)$

• Criterion3 $\mathop {Min}\limits_j \left( {s_j } \right)$

• Criterion4 $\mathop {Max}\limits_j \left( {q_j } \right)$

• Criterion5 $\mathop {Max}\limits_j \left( {I_j } \right)$

• Criterion6 $\mathop {Max}\limits_j \left( {I\left( {x_j } \right)} \right)$

2.2 Exclusive Category [3]

There are six candidate test points selection criteria for exclusive category also.

• Criterion7 $\mathop {Min}\limits_j \left( {N_{Aj} } \right)$

• Criterion8 $\mathop {Max}\limits_j \left( {\mathop {Max}\limits_i \left( {F_{ij} } \right)} \right)$

• Criterion9 $\mathop {Max}\limits_j \left( {s_j } \right)$

• Criterion10 $\mathop {Min}\limits_j \left( {q_j } \right)$

• Criterion11 $\mathop {Min}\limits_j \left( {I_j } \right)$

• Criterion12 $\mathop {Min}\limits_j \left( {I\left( {x_j } \right)} \right)$

• Step 1: Let S _opt consist of all candidate test points.

• Step 2: Draw out a test point n _j from S _opt by using any one of the exclusive criteria.

• Step 3: Check whether the residual test points in S _opt are enough to diagnose the given set of faults. If yes, go to Step 2. Else, add n _j to S _opt .

• Step 4: Repeat Step 2 to Step 3, till all test points are examined.

3 Algorithm Analysis and Statistical Experiments

3.1 Accuracy Analysis

Before the accuracy analysis, an example is considered at first.

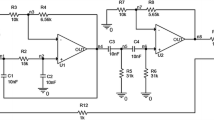
• Example 2: A band pass filter circuit example

Figure 2 is a band pass filter circuit, which is cited by literatures [3, 5, 9–11, 14, 18] as a benchmark circuit. The excitation signal is a 1 kHz, 4 V sinusoidal wave. Totally, there are eighteen potential catastrophic faults f ₁~f ₁₈ and eleven test points n ₁~n ₁₁. Voltage values at all nodes for different faulty conditions are obtained by simulation and the Integer-Coded fault wise table is constructed by procedures introduced in Section 1. The results are shown in Table 6. All seven strategies mentioned in Section 2 (six inclusive strategies and an exclusive strategy) are used to select optimum test points respectively. All the simulations are done by using Visual C+ + 6.0 codes. The results are listed in Table 7.

Fig. 2

A band pass filter circuit

Table 6 Integer-coded fault wise table for analog filter

Table 7 Final solution found by algorithms

The global minimum test points set is found by Algorithm 5, Algorithm 6 and Exclusive category. By using Algorithm 4, the final solution contains a redundant test point n ₇. Algorithm 1, Algorithm 2 and Algorithm 3 are even worse, since about three redundant test points are contained in the final solution. Obviously, the latter three inclusive strategies (and exclusive category) can more accurately find the optimum solution than the former three strategies. This conclusion was also proved by statistical experiments in literatures [9, 14, 18].

Because each algorithm (except for Exclusive category) has its own test points selection criterion, one may naturally conclude that the later three criteria (4~6) is better than the former criteria (1~3) based on the statistical experiment results. But this is not the fact as discussed in the following text.

3.1.1 Inclusive Category

As pointed out in Section 2, in the inclusive approaches, the optimum set of test points (S _opt ) is initialized to be null, then an “ideal” test points based on a given criterion is added to it. So test points selection criterion is an essential ingredient of inclusive algorithm. All the inclusive algorithms are greedy heuristic algorithms. Although each criterion evaluates the fault discrimination power of a test point from different point of view, but they are all just greedy heuristic functions and there is no theoretical proof can be offered to demonstrate a specific criterion’s optimality.

Besides test points selection criterion, test points selection strategy is another important ingredient of inclusive algorithm. A good test points selection strategy can improve the accuracy of a searching algorithm. For Algorithms 1, 2 and 3 mentioned in Section 2, the most important strategy lies in Step 4 and is called as Strategy 1 in this paper. According to Strategy 1, although a test point is evaluated as the best one in S _c , it will not be added to S _opt if it can not subdivide ambiguity sets determined by S _opt . In Example 2, after n ₈, n ₁₁, n ₇ and n ₅ are added to S _opt , n ₆ has the maximum fault discrimination power among the test points in S _c . By using Criterion 1, n ₆ is concluded as the best one and added to S _opt . Table 8 is the ambiguity sets information decided by the test points n ₈, n ₁₁, n ₇ and n ₅ together. Table 9 is the ambiguity sets information decided by test points n ₈, n ₁₁, n ₇, n ₅ and n ₆ together. Obviously, Table 8 and Table 9 have the same ambiguity sets information, say the new selected test point n ₆ has no contribution to S _opt . In other words, n ₆ is redundant test point for S _opt . By using Strategy 1, n ₆ will be eliminated from S _opt , so Strategy 1 can reduce the number of redundant test points of final solution set.

Table 8 Ambiguity sets information decided by {n ₈,n ₁₁,n ₇,n ₅}

Table 9 Ambiguity sets information decided by {n ₈,n ₁₁,n ₇,n ₅,n ₆}

Fault discrimination power of S _opt is determined by the all test points contained in it together. So simply adding a test point with best C _i to S _opt a maximum information increment of S _opt is not guaranteed and then global minimum test points set is less likely to be obtained. To overcome this shortcoming, Algorithm 4 provides another strategy in Step5 called as Strategy 2 in this paper. By using Strategy 2, fault discrimination power of a test point n _j is determined not by itself but by n _j and all test points in S _opt together. So if a test point n _j is to be added to S _opt , a maximum fault discrimination power increase of S _opt is guaranteed. In fact, Strategy 2 is also included in Algorithm 5 and Algorithm 6. In Algorithm 5, step 4 is the embodiment of Strategy 2. In Algorithm 6, graph node expanding process is based on the ambiguity sets information determined by S _opt , where S _opt consists of test points used on the path from current graph node to root node. So the selected node guarantees the maximum information increase to S _opt . Besides Strategy 2, Algorithms 4, 5 and 6 remove the faults that can be isolated by S _opt in each iteration. This can reduce these algorithms’ time and space complexities and is called as Strategy 3. Strategy 2 can further reduce redundant test points and in turn improve the solution accuracy. If Algorithms 1, 2 and 3 adopt Strategy 2 and 3, they can also more accurately find the optimum test point set. In Example 2, the new results are listed in Table 10. Compared to Table 7, improved algorithms (with Strategy 2 and Strategy 3) can more accurately find the optimum test point set.

Table 10 final solution found by improved algorithms

Although Strategy 2 can reduce the number of redundant test points, but the final solution may still have redundant test points. For example, there are still one or two redundant test points in final solutions in Table 10. As mentioned above, in the inclusive approaches, the optimum set of test points (S _opt ) is initialized to be null, then test point is added to it one by one. Although the new selected test point is not redundant for those selected test points, it cannot be guaranteed that one or more former selected test points is not redundant for the new set S _opt . In Table 10 for example, the final solution found by improved Algorithm 1 is {n ₁,n ₅,n ₈,n ₉,n ₁₁}. The selected order is n ₈→n ₉→n ₅→n ₁→n ₁₁. At first S _opt is initialized to be null, then test point n ₈ is added to S _opt . Obviously n ₈ is not redundant. But after n ₉,n ₅,n ₁,n ₁₁ are added to S _opt , n ₈ is a redundant test point for S _opt because that all faults can be isolated by n ₉,n ₅,n ₁,n ₁₁ without n ₈. So if only an algorithm belong to inclusive category, it cannot guarantee that there is no redundant test point contained in the final solution.

3.1.2 Exclusive Category

As mentioned in Section 2, exclusive algorithms examine all test points. Anyone redundant will be eliminated from S _opt . So the final solution found by exclusive category must have no redundant test points. It is needed to point out that a set without redundant test points does not mean that this set is a minimum set. An example is used to illustrate this viewpoint. Table 11 is a simple fault wise table. Both set S _{opt 1}={n ₁,n ₂} and set S _{opt 2}={n ₃,n ₄,n ₅} can isolate all faults and each set contains no redundant test points. Obviously, S _{opt 2} is not the minimum set.

Table 11 A simple fault wise table

For a practical complex system, there are many candidate test points (N _T ) in the design stage, but only a few physical test points (m) can be set, normally N _T > 2 m. As discussed above, exclusive method takes more time when N _T > 2m.

3.1.3 Combined Category

Based on the former discussion, considering test points set selection problem for a large-scale system, inclusive method is more efficient than exclusive method while exclusive method is more accurate than inclusive method.

To efficiently and accurately find the optimum test points set, an inclusive algorithm is executed at first, then exclusive algorithm is used to eliminate redundant test points in S _opt . This method is called as combined category. Table 12 lists the final solutions found by inclusive algorithms (Strategy 2 and Strategy 3 is adopted by every algorithm) and combined algorithms.

Table 12 Solutions found by original inclusive and combined algorithms

From Table 12, it can be seen that no matter which inclusive algorithm is executed, if only exclusive method is appended, the final solution contains no redundant test points. The combined method found the minimum set in this example.

3.2 Time Complexity

The complexities of Algorithm 1, Algorithm 2 and Algorithm 3 are dominated by Strategy 1. They all have the complexity of $O\left( {N_F p\log N_F } \right)$ [11], where p is the number of test points examined and $\begin{array}{*{20}l} {{m \leqslant p \leqslant N_{T} } \hfill} & {{{\left( {m = {\left| {S_{{opt}} } \right|}} \right)}} \hfill} \\ \end{array}$.

The complexity of Algorithms 4, 5 and 6 are dominated by Strategy 2. The process of calculating fault discriminate power q _j for every test point in S _c is the same with the process of checking whether a number repeats or not. There exist several efficient sequential algorithms such as quick sort, heap sort etc. [2][7] with time complexity of $O\left( {N_F \log N_F } \right)$ for calculating faulty discriminate power for one test point. Algorithms 4, 5 and 6 examine every test point in S _c for each iteration, so these algorithms have the time complexity of $O\left( {N_F p\prime \log N_F } \right)$, where $p\prime = N_T + \left( {N_T - 1} \right) + \cdots \left( {N_T - m + 1} \right)$. Because the case of N _T >2m is considered in this paper, there will be $p\prime > > m$. So the total time complexity of Algorithms 4, 5 and 6 is $O\left( {N_F mN_T \log N_F } \right)$.

Exclusive category has the complexity of $O\left( {N_F \left( {p + m} \right)\log N_F } \right)$, where m is the number of test points contained in S _opt . As pointed out in Prasad et al. [11],

$$N_T > 2m;\,{\text{exclusive}}\,{\text{method}}\,{\text{takes}}\,{\text{more}}\,{\text{time}}.$$

(1)

$$N_T > 2m;\,{\text{exclusive}}\,{\text{method}}\,{\text{takes}}\,{\text{less}}\,{\text{time}}.$$

(1)

As discussed above, the time complexity of inclusive algorithm is $O\left( {N_F p\log N_F } \right)$ or $O\left( {N_F p\prime \log N_F } \right)$. Suppose that the final solution found by an inclusive algorithm contains m test points, using exclusive method to examine all test points in S _opt will take $O\left( {N_F m\log N_F } \right)$ complexity. So the time complexity of combined method is

$$O\left( {N_F p\log N_F } \right)\; + \;O\left( {N_F m\log N_F } \right)$$

$${\text{or}}\,O\left( {N_F p\prime\log N_F } \right)\; + \;O\left( {N_F m\log N_F } \right)$$

Because $p\prime > > m$ and p >> m, the total time complexity of combined algorithm is still $O\left( {N_F p\log N_F } \right)$ or $O\left( {N_F p\prime \log N_F } \right)$.

The following three conclusions can be drawn according to the theoretical analysis in this Section.

• Conclusion 1: Every test points selection criterion is just greedy heuristic function and there is no theoretical proof can be offered to demonstrate a specific criterion’s optimality. Any specific criterion has no superior in the final solution to others.

• Conclusion 2: Strategy 2 is superior in the accuracy to Strategy 1 while Strategy 1 is more efficient than Strategy 2.

• Conclusion 3: When combined with exclusive strategy, either Strategy 1 or Strategy 2 can improve the accuracy of the final solution and do not increase the time complexity.

Besides the theoretical proof, the statistical experiments are also provided to prove the above conclusions in Section 4.

4 Statistical Experiments

Statistical experiments are carried out on the randomly computer-generated Integer-Coded dictionaries by using the inclusive category (adopting six criteria, Strategy 1 and Strategy 2 respectively) and combined category respectively. All the simulations are done by using Visual C++ 6.0 codes. All the execution times in this paper are obtained using an Intel 1.6 GHz processor, 512 M RAM and Microsoft Windows XP operating system.

• Experiment 1: Totally, there are 100 Integer-Coded fault wise tables and each table has 1,000 simulated faults, 100 test points, and six ambiguity sets per test point.

Table 13 lists the results of Strategy 1 by using six different criteria respectively. It can be seen that by using Strategy 1 and Criterion 1 (the second column of Table 13), 17 simulated fault wise tables (17% of the simulated cases) need seven test points to isolated all faults, 61 simulated fault wise tables need eight test points to isolated all faults, 22 simulated fault wise tables need nine test points to isolated all faults. Comparing different columns of Table 13, one can see that the size of final solutions found by six different criteria are all varying between seven and nine. In about 14–19% of the simulated fault wise tables, the size of final solutions is seven. In most (about 60–71%) of the simulated cases, the final solutions consist of eight test points. In the rest (about 15–22%) of the simulated cases, the size of the final solutions is nine. So it can be drawn that if the same strategy is adopted, the accuracy of final solutions found by different criteria have no dramatic differences (viz. in the accuracy of finding final solution, no one specific criterion is superior to others). Besides the accuracy, the computation time of different criterion has no notable difference also. This gives that in the time efficiency, no one specific criterion is superior to the others. This conclusion can also be drawn according to Tables 14, 15 and 16.

Table 13 Statistical results of inclusive category (by using strategy 1)

Table 14 Statistical results of combined category (by using strategy 1 and exclusive category)

Table 15 Statistical results of inclusive category (by using strategy 2)

Table 16 Statistical results of combined category (by using strategy 2 and exclusive category)

By comparing column 2 of Table 14 to column 2 of Table 13, it can be seen that the combined category improves the accuracy of final solutions substantially. By using combined category and Criterion 1, the size of final solutions is no more than 8. While if inclusive category and the same criterion are adopted, one will draw that there are 22 simulated cases need nine test points to isolate all faults as shown in Table 13. Additionally, to isolate all faults, 83% of the simulated dictionaries only need seven test points by using combined category while 83% (61%+22%) of the simulated dictionaries need eight or nine test points by using inclusive category. In Fig. 3, Criterion 3 is the common criterion adopted by Strategy 1 and Combined category. In 66% of the simulated cases, it is concluded that eight test points are necessary by using strategy 1. However in most (90%) of the simulated cases, it is concluded that only seven test points are enough to isolate all faults. Additionally, in 17% of the simulated cases the size of final solution found by Strategy 1 is 9 while the size of final solution is no more than 8 if the Combined category is used.

Fig. 3

Statistical results of strategy 1 and combined category

So it can be drawn that combined category has superiority in the final solutions’ accuracy to inclusive category. Comparing the other corresponding columns of Tables 13 and 14 (viz. the other five criteria are adopted respectively), the same conclusion can be drawn.

Computation time per dictionary is averagely about 195 ms by using inclusive category and 218 ms by using combined category. So the combined category need little more time than inclusive category. This conclusion is consistent with the former time complexity analysis given in Section 3.2. So it can be drawn that the combined category is superior to the inclusive categories. This conclusion can also be drawn by comparing Table 15 to Table 16.

From Table 15 it can be seen that the size of final solutions found by Strategy 2 is no more than seven while more than 80% of simulated cases need eight or nine test points by using Strategy 1 in Table 13. So Strategy 2 can improve the solutions’ accuracy dramatically and this conclusion is consistent with the former accuracy analysis given in Section 3.1.2. Figure 4 is used to illustrate this conclusion.

Fig. 4

Statistical results of strategy 1 and strategy 2

The size (number of selected test points) of the final solutions found by Strategy 2 is no more than 7 while the the size of the final solutions found by Strategy 1 is no less than 7. Obviously, Strategy 2 can improve the accuracy of final solution substantially. The same conclusion can be drawn when the other criteria are adopted respectively (by comparing other corresponding columns of Tables 13 and 15).

At the same time the computation time of Strategy 2 is about six times as much as that of Strategy 1. The same conclusion can also be drawn by comparing Table 14 to Table 15. This is consistent with former theoretical analysis. So Strategy 2 is superior in solution accuracy to Strategy 1 while Strategy 1 is superior in time efficiency to Strategy 2.

It can be argued that the ambiguity sets number of a fault wise table is seldom a constant. For example, the ambiguity sets contained in each test points in Table 6 vary in number from 3 to 9. So to validate former conclusions, another set of simulations are carried out in this paper.

• Experiment 2: Totally, there are 100 Integer-Coded fault wise tables and each table has 1,000 simulated faults, 40 test points. Ambiguity sets number per test point can vary form 1 to 10 randomly.

Table 17 lists the results of inclusive category by using six different criteria respectively. Comparing the different columns of this table, one cannot say which specific criterion is better than the others. This proves the conclusion that no one specific criterion is superior to the others again.

Table 17 Statistical results of inclusive category (by using strategy 1)

By comparing Table 17 with Table 18 or by comparing Table 19 with Table 20, it can be drawn that the combined category can improve the solution accuracy without taking too much additional computation time. Similarly, conclusion that Strategy 2 is superior to Strategy 1 in solution accuracy can also be drawn by comparing Table 17 with Table 19 or by comparing Table 18 with Table 20.

Table 18 Statistical results of combined category (by using strategy 1 and exclusive category)

Table 19 Statistical results of inclusive category (by using strategy 2)

Table 20 Statistical results of combined category (by using strategy 2 and exclusive category)

5 Conclusion

Heuristic test points selection methods for faulty dictionary technique can be classified into two categories: inclusive and exclusive. Either in inclusive category or in exclusive category, every greedy search algorithm consists of a test points selection strategy and a test points selection criterion. The time complexity and solution accuracy of these algorithms, strategies and criteria are analyzed and compared extensively in this paper. Theoretical analysis and statistical experimental results give the following three conclusions.

• Conclusion 1: In the accuracy and efficiency of finding final solution, no one specific criterion is superior to the others.

• Conclusion 2: Strategy 2 is superior in the accuracy to Strategy 1 while Strategy 1 is more time efficient than Strategy 2.

• Conclusion 3: When combined with exclusive strategy, either Strategy 1 or Strategy 2 can improve the accuracy of the final solution and does not increase the time complexity.

Above conclusions provide an instruction for coding a test points selection algorithm. Conclusion 1 shows that any criterion can be adopted without affecting the accuracy and the efficiency of an algorithm. So a criterion that can be calculated easily, such as Criterion 1, is suggested to be chosen. Based on Conclusion 2 and Conclusion 3, if an efficient algorithm is required, Strategy 1 plus exclusive strategy is a good choice. If the solution’s accuracy is required, Strategy 2 plus exclusive strategy should be adopted. No matter Strategy 1 or Strategy 2 are adopted, the combined strategy proposed in this paper can guaranty that the final solution contain no redundant test points.

Additionally, conclusions drawn in this paper show that a new strategy rather than a new criterion should be focused on in future work.