A Novel Test Point Selection Method for Analog Fault Dictionary Techniques

Abstract

Most of the recently reported test point selection algorithms for analog fault dictionary techniques are based on integer-coded table (ICT) technique. Hence, the accuracy of these algorithms is closely related to the accuracy of the ICT technique. Unfortunately, this technique is not accurate, especially when the size of fault dictionary is large. This paper proposes an accurate fault-pair Boolean table technique for the test point selection problem. First, the approach to transform the fault dictionary into a fault-pair Boolean table is introduced. Then, a test point selection algorithm based on the fault-pair Boolean table is proposed. Thirdly, several example circuits are used to illustrate the proposed algorithm. Simulated results indicate that the proposed method is more accurate than the other methods. Therefore, it is a good solution for minimizing the size of the test point set.

1 Introduction

Methods for the fault diagnosis of analog circuits are usually classified into two main categories [3]: simulation before test (SBT) and simulation after test (SAT). The probabilistic method and fault dictionary techniques fall into SBT, and optimization, fault verification and parameter identification techniques fall into SAT. Among the various fault diagnosis methods, one of the most widely used SBT methods is the fault dictionary method [6]. This method is applicable to both hard and soft fault detection and consists of three important phases [12]. First, in the construction of a fault dictionary, all potential faults are listed and the stimuli type (i.e., dc, ac, or time domain), shape, frequency, and amplitude are selected. A circuit under test (CUT) is then simulated for the fault-free case and all fault cases. The fault signatures (i.e., output response or a set of responses or other parameters that are derived from output responses) are generated when a test program is executed on a unit having a fault. The fault features of the responses are stored and organized in the dictionary for fault diagnosis. The second phase is test point selection. In this phase, an optimum test point set is required to achieve the desired degree of fault diagnosis. The third phase is fault isolation. At this stage, the same stimuli as those used in constructing the dictionary are applied to the fault CUT. The measured values at selected test points or calculated signatures are compared with those stored in the dictionary to match the fault(s) to one of the predefined faults or to a set of faults according to preset criteria [12]. This paper focuses on the second phase.

The problem of test point selection for the analog fault dictionary technique has been studied extensively [1, 2, 4–6, 8–13, 15–17]. Varghese et al. [15] proposed a heuristic method for test point selection based on the concept of confidence levels determined by using distance concepts. The concept of ambiguity groups and developed logical rules to select test points was proposed by Hochwald and Bastian [5]. Stenbakken and Souders proposed a method of QR factorization of a circuit sensitivity matrix [13]. Abderrahman et al. [13] used sequential quadratic programming and constraint logic programming to generate the test set. Lin and Elcherif [6] proposed two heuristic methods based on the two criteria proposed by Hochward and Bastian. Spaandonk and Kevenaar [11] proposed looking for a set of test points by combining the decomposition method of a system sensitivity matrix and an iterative algorithm. Prasad and Babu [12] proposed four algorithms for inclusive approaches and three strategies for exclusive approaches. Based on the fault detection table and computing the information content of every node, Pinjala and Kim [8] proposed an approach to get the near-minimum test sets. An entropy-based approach was proposed by Starzyk, et al. [12]. Golonek and Rutkowsk [4] proposed a genetic-algorithm-based test point selection method. Most test point selection algorithms and strategies [4, 6, 8–10, 12, 16, 17] mentioned above are based on the ICT technique. Hence, the accuracy of these algorithms is closely related to the accuracy of the ICT technique.

Since a single-fault situation is mostly encountered in fault diagnosis, only if the method works for this situation can it be generalized to solving multiple soft fault cases. Hence, this paper mainly focuses on tolerance handling in the presence of single faults. Section 2 illustrates the ICT technique and its shortcoming, and a new fault-pair Boolean table technique is proposed to overcome this shortcoming. A test point selection algorithm based on the fault-pair Boolean table is given in this section as well. Section 3 presents several simulated results and demonstrates the superiority in the computational efficiency and solution quality of the proposed method by comparing it with the other reported methods. Section 4 concludes this work.

The nomenclature of this paper is as follows:

n _j :

The jth test point.

I(n _j ):

Count of the number of 1′ s associated with test point n _j .

N _T :

Number of candidate test points.

f _i :

The ith fault.

N _F :

Number of all potential faults (including the nominal case).

S _opt :

Desired test point set.

S _C :

Candidate test point set.

NT _i :

Number of test points that can isolate the ith fault pair.

2 Fault-Pair Boolean Table

Most of the reported test point selection algorithms and strategies [4, 6, 8–10, 12, 16, 17] are based on the ICT technique. This technique was first proposed by Lin and Elcherif [6]. According to this technique [6, 9, 12], an ambiguity group is defined as any two faulty conditions that fall into the same ambiguity group if the gap between the voltage values produced by them is less than 0.7 volts. If the two fault components belong to one ambiguous group, they are undistinguishable. Faults that belong to the same ambiguity group in a given column are coded as the same integer. In this table, the same integer number represents all the faults that belong to the same ambiguity group in a given column. Since each test point represents an independent measurement, ambiguity groups of different test points are independent and can be numbered using the same integers without confusion. The detailed description of this technique can be found in the literature [6, 9, 12].

2.1 The Shortage of ICT Technique

Assume that Table 1 shows faulty (including fault free) voltage values of a network. Faults f ₀ and f ₂ are isolated by test point n ₁ because the voltage gap produced by them is larger than 0.7 volts. Hence, the fault pair (f ₀, f ₂) is isolated by n ₁. Similarly, the fault pairs (f ₀, f ₃) and (f ₁, f ₃) are isolated by n ₁. The residual fault pairs (f ₀, f ₁), (f ₁, f ₂) and (f ₂, f ₃) are isolated by test point n ₂. Thus, test point set {n ₁, n ₂} can isolate all faults.

Table 1 Fault dictionary

If the ICT technique is adopted, we will conclude that not all of the faults can be isolated. For example, on test point n ₁ of Table 1, faults f ₀ and f ₁ are coded as 0. The voltage gap produced by faults f ₁ and f ₂ is 0.6 volts (smaller than the 0.7-volt criterion). Hence, they fall into one ambiguous group. Since f ₁ is coded as 0, f ₂ should also be coded as 0 according to the ICT technique [6, 12]. Similarly, f ₃ is coded as 0. Table 2 shows the results. In this table, all the faults are coded as 000. Therefore, all the faults are undistinguishable. Based on this table, regardless of which test point selection algorithm is used, we cannot get any solution.

Table 2 Integer-coded table

Apparently, the traditional ICT technique induces a wrong conclusion in this example. The fault-pair Boolean table technique proposed in the following section can overcome this shortcoming.

2.2 Fault-Pair Boolean Table Technique

In the proposed fault-pair Boolean table, rows represent any possible fault pairs, and columns show the available test points. A fault dictionary that consists of N _F faults has $C_{{N_F}}^2 = \frac{{{N_F} \times \left( {{N_F} - 1} \right)}}{2}$ fault pairs. Each test point n _j is represented by a binary column vector d of dimension $\frac{{{N_f} \times \left( {{N_f} - 1} \right)}}{2}$. Test point n _j isolates the ith $\left( {1 \leqslant i \leqslant \frac{{{N_f} \times \left( {{N_f} - 1} \right)}}{2}} \right)$ fault pair if the ith component of the test vector d _ij is 1.

According to the 0.7-volt criterion, f ₀ and f ₁ cannot be isolated by n ₁ in Table 1; hence, the corresponding component d ₁₁ of Table 3 is 0. Similarly, two other fault pairs (f ₁, f ₂) and (f ₂, f ₃) cannot be isolated by n ₁, and d ₁₄ and d ₁₆ are 0. These three fault pairs can be isolated by test point n ₂; therefore, d ₂₁ = d ₂₄ = d ₂₆ = 1. The other components of Table 5 are derived in the same way. Since all six fault pairs can be isolated by n ₁ and n ₂ together, test point set {n ₁, n ₂} is the optimum solution.

Table 3 Fault-pair Boolean table

It is important to note that in the present era of low-voltage analog circuits, the 0.7-volt criterion seems to be excessive. Supposedly, 0.2 volts gap should be enough to distinguish two faults; therefore, this gap is adopted in some literature [14, 16]. Hence, the 0.2-volt criterion is adopted in the following text. The problem of whether this criterion is the best criterion or not falls into the first phase of fault dictionary techniques, and its discussion is beyond the scope of this paper.

2.3 Test Point Set Selection Algorithm

The global minimum set of test points can only be guaranteed by an exhaustive search method [12], which is computationally expensive and impractical. This paper handle the near optimum test point set selection problem. The popular choice is the greedy search algorithm [4, 8–10, 12, 17]. The main idea of the greedy search algorithm for the test point selection problem can be illustrated as follows. The optimum test point set (S _opt ) is initialized to null. Then, the best test point among the candidate test point set (S _C ) is drawn from S _C , and added into S _opt . If the test points in S _opt are not sufficient to diagnose the fault pairs, the best test point among S _C is drawn from S _C and added into S _opt . The above steps are repeatedly executed until all fault pairs are isolated. Whether a test point is the best one or not is evaluated by a test point evaluation criterion [16]. The test point evaluation criterion used in this paper is a measure known as information content I(n _j ). Test point n ₁ in Table 3 can distinguish three fault pairs (f ₀, f ₂), (f ₀, f ₃) and (f ₁, f ₃). Hence, I(n ₁) = 3. Similarly, I(n ₂) = 3 and I(n ₃) = 2. The I(n _j ) value is easy to calculate, and $\mathop {{\max }}\limits_j (I({n_j}))$ is chosen as the test point evaluation criterion in this paper.

Only one test point n ₂ can isolate the 4th fault pair (f ₁, f ₂) in Table 3; hence, NT ₄ = 1. Therefore, this test point is necessary for fault isolation, and it should be added into the desired optimum test point set (S _opt ). According to the above discussion, the proposed test point selection algorithm based on the fault-pair Boolean table technique can be illustrated as follows.

• Step 1) The optimum test point set S _opt is initialized to a null set.

• Step 2) For each fault pair that corresponds to NT _i  = 1, the test point that can uniquely isolate the ith fault pair is added into S _opt . The rows (fault pairs) that can be isolated by this test point are deleted from the fault-pair Boolean table, and the test point is removed from the fault-pair Boolean table. Go to Step 4.

• Step 3) I(n _j ) of every test point in the fault-pair Boolean table is calculated, and the test point with $\mathop {{\max }}\limits_j (I({n_j}))$ is added into S _opt . The rows (fault pairs) isolated by this test point are deleted. The point is also deleted.

• Step 4) If all the fault pairs are isolated, exit. Otherwise, go to Step 3.

It is important to note that NT _i used in Step 2 and the I(n _j ) value for the first iteration were obtained after the fault-pair table was constructed.

Usually, in an actual analog circuit, some faults can be diagnosed only by a certain test point. In this case, Step 2 helps the algorithm more accurately and efficiently finds the final solution. If there is only one optimum solution, the proposed algorithm can find the global optimum solution by using just one step, viz. Step 2. Even there are more than one optimum, Step 2 dramatically decreases the size of the fault-pair Boolean table. For example, in Table 2 from [12], f ₁ and f ₃ can be distinguished only by test point n ₁, f ₈ and f ₁₀ are diagnosed by only one test point n ₅, f ₁₅ and f ₁₆ are isolated by exclusive test point n ₉, and f ₀ and f ₁₄ are discerned by n ₁₁. Therefore, n ₁, n ₅, n ₉, and n ₁₁ should be added into S _opt according to Step 2. These four test points isolate all faults. In this example, only one step (Step 2) can find the optimum solution.

Theorem 1

The time complexity of the proposed algorithm is less than $O\left( {N_F^2{N_T}m} \right)$.

Proof

As discussed in Section 2.2, the fault-pair table consists of $\frac{{{N_F} \times \left( {{N_F} - 1} \right)}}{2}$ rows. Hence, in Step 2, deleting the rows (fault pairs) isolated by the selected test points has the time complexity of $O\left( {\frac{{{N_F} \times \left( {{N_F} - 1} \right)}}{2}} \right) = O\left( {N_F^2} \right)$. In Step 3, the time complexity of calculating I(n _j ) is $O\left( {N_F^2 \times {N_T}} \right)$, and deleting rows has the time complexity of $O\left( {N_F^2} \right)$. Suppose that Step 3 is executed for m iterations, viz. |S _opt | = m, the total complexity of the proposed algorithm is $O\left( {N_F^2 + N_F^2 \times {N_T} \times m} \right) = O\left( {N_F^2{N_T}m} \right)$. Because the isolated faults are deleted in each iteration, the size of the fault-pair table decreases gradually. Therefore, the total complexity is less than $O\left( {N_F^2 + N_F^2 \times {N_T} \times m} \right) = O\left( {N_F^2{N_T}m} \right)$.

3 Simulation Examples

3.1 Simulations on Circuits

Example 1

A band pass filter circuit example

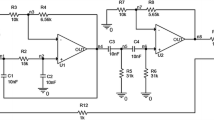
The filter circuit shown in Fig. 1 is stimulated by a 1 kHz, 4 V sinusoidal wave. A total of 23 faulty conditions f ₀–f ₂₂ and eleven test points n ₁–n ₁₁ are examined. Voltage values at all the test points for different faulty conditions are simulated by using PSPICE. The results are shown in Table 4. The fault-pair Boolean table, Table 5, is constructed by using the procedures introduced in Section 2.2

Fig. 1

A band pass filter circuit

Table 4 AC voltage fault dictionary (Unit: V)

Table 5 Fault-pair Boolean table

In Step 1 of the proposed algorithm, the optimum test point set S _opt is initialized to a null set. In Step 2, NT ₁₃ = 1, and n ₁₁ is the only one test point that isolates the 13th fault pair (f ₀, f ₁₃). Hence, n ₁₁ is added into S _opt . The rows isolated by n ₁₁ are deleted from Table 5. For example, the 1st fault pair (f ₀, f ₁) and the 2nd fault pair (f ₀, f ₂), isolated by n ₁₁, are removed. Test point n ₁₁ is also removed from Table 5. Similarly, n ₁ and n ₅ should be added into S _opt , and then S _opt = {n ₁, n ₅, n ₁₁}. After all the fault pairs isolated by the test point set S _opt are removed from Table 5, three rows shown in Table 6 remain.

Table 6 Residual fault pairs

In Step 3, the I(n _j ) value is calculated, and the results are shown in the final row of this table. Test point n ₈, which has the maximum I(n _j ) value among the candidate test points, is added into S _opt , and then S _opt = {n ₁, n ₅, n ₈, n ₁₁}. So far, all fault pairs are isolated. The optimum solution is found when the proposed algorithm is executed for only one iteration. If the integer-coded technique is adopted, the size of the test point set found by other algorithms, including the exhaustive method, is larger than 4. The results are shown below.

Graph search algorithm [17]:

$$ {S_{opt}} = \left\{ {{n_1},{n_5},{n_6},{n_9},{n_{11}}} \right\} $$

Pinjala’s algorithm [8]:

$$ {S_{opt}} = \left\{ {{n_1},{n_5},{n_8},{n_9},{n_{11}}} \right\} $$

Starzyk’s algorithm [12]:

$$ {S_{opt}} = \left\{ {{n_1},{n_5},{n_8},{n_9},{n_{11}}} \right\} $$

The exhaustive algorithm [17]:

$$ {S_{opt}} = \left\{ {{n_1},{n_5},{n_6},{n_9},{n_{11}}} \right\} $$

Obviously, the proposed method more accurately finds the solution than the other algorithms.

Example 2

Leapfrog filter circuit example

Figure 2 shows a Leapfrog filter circuit. A total of 20 potential faults are examined. All 12 test points are assumed to be accessible for the purpose of demonstration. The excitation signal is a f = 1 kHz, V _p  = 6 V sinusoidal wave. The tolerance of resistors and capacitors is 5% and 10%, respectively. High and Low faulty voltage limits on every test point of each individual fault are calculated by using a worst-case analysis. The measurement accuracy is ±5%. Table 7 shows the results of worst-case analysis. The voltage signature of every fault varies between its high and low faulty voltage limit. For example, the signature area of fault condition R3Open on test point n ₂ is (4.17, 3.09). If two faults have overlapping signature areas, these two faults are undistinguishable. On test point n ₂, the nominal case and R3Open cannot be diagnosed because their signature areas have the common intersection (4.17, 3.48). The undistinguished faults are listed in Table 8. Based on Tables 7, 8, and 9 is obtained by using the proposed fault-pair technique.

Fig. 2

A Leapfrog filter circuit

Table 7 Fault dictionary (Unit:V)

Table 8 Faults number

Table 9 A part of fault-pair Boolean table

It is easy to see from Table 9 that test points n ₂, n ₄, n ₆, n ₈, and n ₁₂ are necessary to isolate (f ₀, f ₄), (f ₃, f ₅), (f ₅, f ₆), (f ₀, f ₈) and (f ₀, f ₇), respectively. Hence, S _opt = {n ₂, n ₄, n ₆, n ₈, n ₁₂}. So far the test points in S _opt isolate all the fault pairs. It means that when the proposed algorithm runs to Step 2 in the first iteration, the final solution is found. The computation time is only about 0.9 ms.

In this example, all the other algorithms, including the graph search algorithm [17], Pinjala’s algorithm [8], and the entropy-based algorithm [12] also find the optimum solution. However, these algorithms run for 5 iterations, and the computation time is about 2.1 ms. This result justifies the former deduction that Step 2 helps the proposed algorithm more accurate and efficient than the other ICT-based algorithms.

Example 3

A linear net

The fault dictionary technique is traditionally used to diagnose catastrophic faults; however, it can also be used to diagnose the soft fault of linear circuits. Hence, the proposed fault-pair technique and test point selection algorithm are also applicable to the soft fault diagnosis problem.

Assume n ₁ and n ₂ are two different test points (except for the reference point) in a linear circuit N, the fault set is $F = \left\{ {{f_0},{f_1}, \cdots {f_n}} \right\}$,where f ₀ is the nominal case, and f _i denotes a faulty condition of the i ^th component. In the nominal case, the voltage values measured on n ₁ and n ₂ are V ₀₁ and V ₀₂, respectively. For any other faulty condition f _i , the node voltage function must cross (V ₀₁,V ₀₂). The node voltage function for f _i is expressed as follows [7]:

$$ {V_1} - {V_{10}} = {A_i}\left( {{V_2} - {V_{20}}} \right), $$

(1)

where A _i is the slope of formula (1) on the V ₁–V ₂ plane. ${\theta_i} = \arctan {A_i}\left( { - {{90}^0} \leqslant {\theta_i} \leqslant {{90}^0}} \right)$ is selected as the fault model.

Figure 3 shows a linear voltage-dividing circuit. The potential fault components are listed in Table 10. The A _i value for every component on each plane is obtained by simulation. In this table, P _j denotes the j ^th plane. For example, P ₁ is the V _n1–V _n2 plane, P ₂ denotes the V _n1–V _n3 plane, P ₁₀ is the V _n4–V _n5 plane, and so on. The components in Table 11 are the θ values of all potential fault components.

Fig. 3

A linear voltage-dividing circuit

Table 10 Slope value

Table 11 θ values

Assume that any two faulty components are distinguishable if the angle degree difference they produce is larger than 10°. The problem of whether 10° is the best criterion or not falls into the first phase of fault dictionary techniques. This problem is beyond the scope of this paper. The fault-pair Boolean table, Table 12, is constructed by using the procedures introduced in Section 2.2

Table 12 Fault-pair Boolean table

The proposed algorithm is used to select the minimum plane set from Table 13. Because no fault pair has NT _i  = 1, Step 2 is overleaped. In Step 3, P ₄, which has the maximum I(P ₄) value 36, is added into S _opt . Because all 36 fault pairs are isolated by${S_{opt}} = \left\{ {{P_4}} \right\},\,{S_{opt}} = \left\{ {{n_1},\,{n_5}} \right\}$ is the final solution.

Table 13 Statistical simulation results

The component parameter randomly varies within its tolerance range (x_i ± x_i 10%). Assume that R1 = 4.4 k, R2 = 3.1 k, R3 = 2.8 k, R4 = 2.9 k, R5 = 3.3 k, R6 = 13.1 k, R7 = 6.2 k, R8 = 5.4 k, R9 = 5.8 k, and R10 = 3.2 k. When the circuit works steadily, the voltages on the two selected test points t ₁and t ₅ are ${V_{{t_1}0}} = {7}.{\hbox{756V}}$, ${V_{{t_5}0}} = {481}.{\hbox{4mV}}$, respectively. When R4 fails, R4 = 2 K, for example, the faulty voltage values are ${V_{{t_1}0}} = {7}.{\hbox{728V}}$, ${V_{{t_5}0}} = {536}.{\hbox{3mV}}$. According to expression (1), the fault signature is $A = \frac{{0.5363 - 0.4814}}{{7.728 - 7.756}} \approx - 1.96 = > \theta = - {11.1^0}$. Table 11 shows that on the selected plane ${P_4},\,\theta = - {11.1^0}$ falls into the signature area of R4, viz. -7.1 ± 5°. Hence, faulty component R4 is diagnosed accurately.

In fact, regardless of what type of measurement is carried out; and what kind of failure needs to be diagnosed, if only the fault dictionary can be constructed, then the fault-pair Boolean table is applicable, and the proposed algorithm can be used to select the minimum columns to discriminate the rows.

3.2 Statistical Simulation Examples

In the former three examples, the proposed algorithm more accurately finds the minimum test point set than the other methods. In this subsection, its accuracy is also examined on extensive randomly computer-generated fault dictionaries. Besides, for comparison, five latest test point selection algorithms are also examined on the same dictionaries. All the simulations are done by using MATLAB codes in an Intel 1.6 GHz processor, 512 M RAM and the Microsoft Windows XP operating system.

Statistical Simulation Example 1

A total of 100 fault dictionaries are examined. Every dictionary consists of 100 simulated faults and 20 test points. Every component of these dictionaries is randomly generated by MATLAB codes and varies between 0.00 and 5.00 volts. First, these dictionaries are transformed into integer-coded and fault-pair tables. Then, the proposed algorithm is carried out on the fault-pair tables, and the other algorithms are carried out on the integer-coded tables. Table 13 shows the simulation results. It can be seen that if the proposed method A ₆ is adopted, three test points that isolate all the faults in all 100 simulated fault dictionaries (100% of the simulated cases) are sufficient, however, if the other algorithms (A ₁ ~ A ₅) including the exhaustive algorithm are used, the sizes of final solutions are larger than 7, which indicates that these solutions contain at least four redundant test points. Besides, in eight simulated cases, the integer-coded technique leads to an erroneous conclusion that faults cannot be isolated fully.

Table 14 shows the time complexity of every algorithm, cited in [16] except for A ₆. The time complexity of algorithm A ₄ is hard to obtain and can be examined only by statistical simulations. It can be seen that the time complexity of proposed algorithm A ₆ is larger than that of A ₁, A ₂, and A ₃; however, it is much smaller than that of A ₅. In this example, the complexity of A ₆ is $O\left( {\frac{{{N_F}^2m{N_T}}}{{{N_F}m{N_T}{{\log }_2}\left( {{N_F}} \right)}}} \right) = O\left( {\frac{{100}}{{{{\log }_2}\left( {100} \right)}}} \right) \approx 6.7$ times more than that of A ₁, A ₂ and A ₃; however, it is much smaller than that of A ₅. For the eight no-solution cases, the average computation time of which is listed in Table 15. In these cases, the time complexity of A ₅ is o(2²⁰ ·100log100); therefore, its executing time is larger than 1 h.

Table 14 Time complexity

Table 15 Average computation time

Although the execution time of the proposed algorithm is greater than that of other near optimum algorithms, since we do not execute this algorithm in real-time but rather do it offline, the proposed algorithm is still a computationally viable algorithm. For example, the execution time for a 100 × 20 size fault dictionary is only about 0.2 s.

Statistical Simulation Example 2

Figure 4 illustrates the performance of the proposed algorithm and the ICT-based exhaustive method. This figure shows the relationship between the number of faults and the size of the final solution. In Fig. 4(a), the total number of candidate test points is 20. If the fault number is smaller than 40, no difference exists between the proposed algorithm and the ICT-based exhaustive algorithm. When the fault number is larger than 40, the size of the final solution found by the exhaustive algorithm increases dramatically; however, if the proposed method is adopted, the size of the final solution increases slowly. Besides, when the fault number is larger than 120, the ICT technique makes all the faults undistinguishable. Hence, with an increase in the dictionary size, the ICT technique cannot accurately find the final solution whereas the proposed algorithm exhibits an excellent accuracy. The same conclusion is drawn from Fig. 4(b).

Fig. 4

Statistical results of the proposed method and the exhaustive algorithm based on Integer-Coded technique

4 Conclusion

Modern densely-loaded circuit boards have posed problems for fault diagnosis with in-circuit testers because only limited physical access to the boards is allowed. Therefore, a method that can select a minimum test point set is badly needed to reduce the number of test points. The recently reported test point selection algorithms that based on the ICT technique are claimed to be applicable to a large fault dictionary. Unfortunately, as pointed out in Section 2, the ICT technique leads to an erroneous conclusion when the fault dictionary is large. Therefore, the integer-coded technique is not applicable to large size fault dictionary. Based on these considerations, the main focus and contributions of this paper are listed as follows:

• A new fault-pair Boolean table technique that can fully take advantage of the fault discrimination power of the test points is proposed.

• A test point selection algorithm that fits for the fault-pair Boolean table is introduced.

• This paper proves that the faulty dictionary technique can be used to diagnose not only catastrophic faults but also parameter faults.

The proposed algorithm is succinct, easy to program and execute. Its accuracy has is proved by theoretical analysis and statistical simulations. Thus, it is particularly applicable to actual circuits and engineering applications.